Numerical Analysis of the Process of Drawing Thin-Walled CuSn8 Alloy Tubes on a Cylindrical Plug
Abstract
1. Introduction
2. Materials and Methods
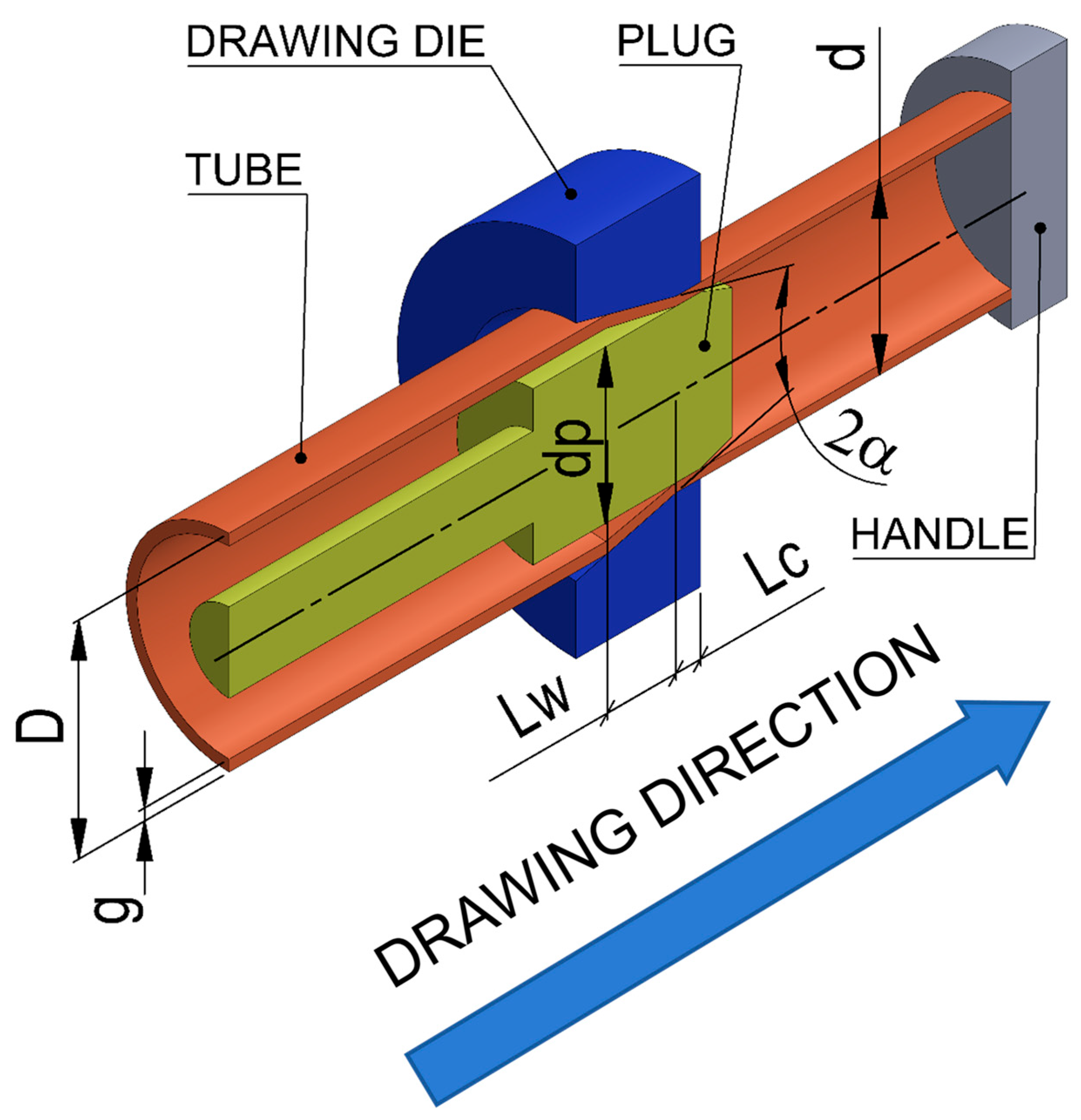
2.1. Computer Simulation
2.2. Experimental Studies
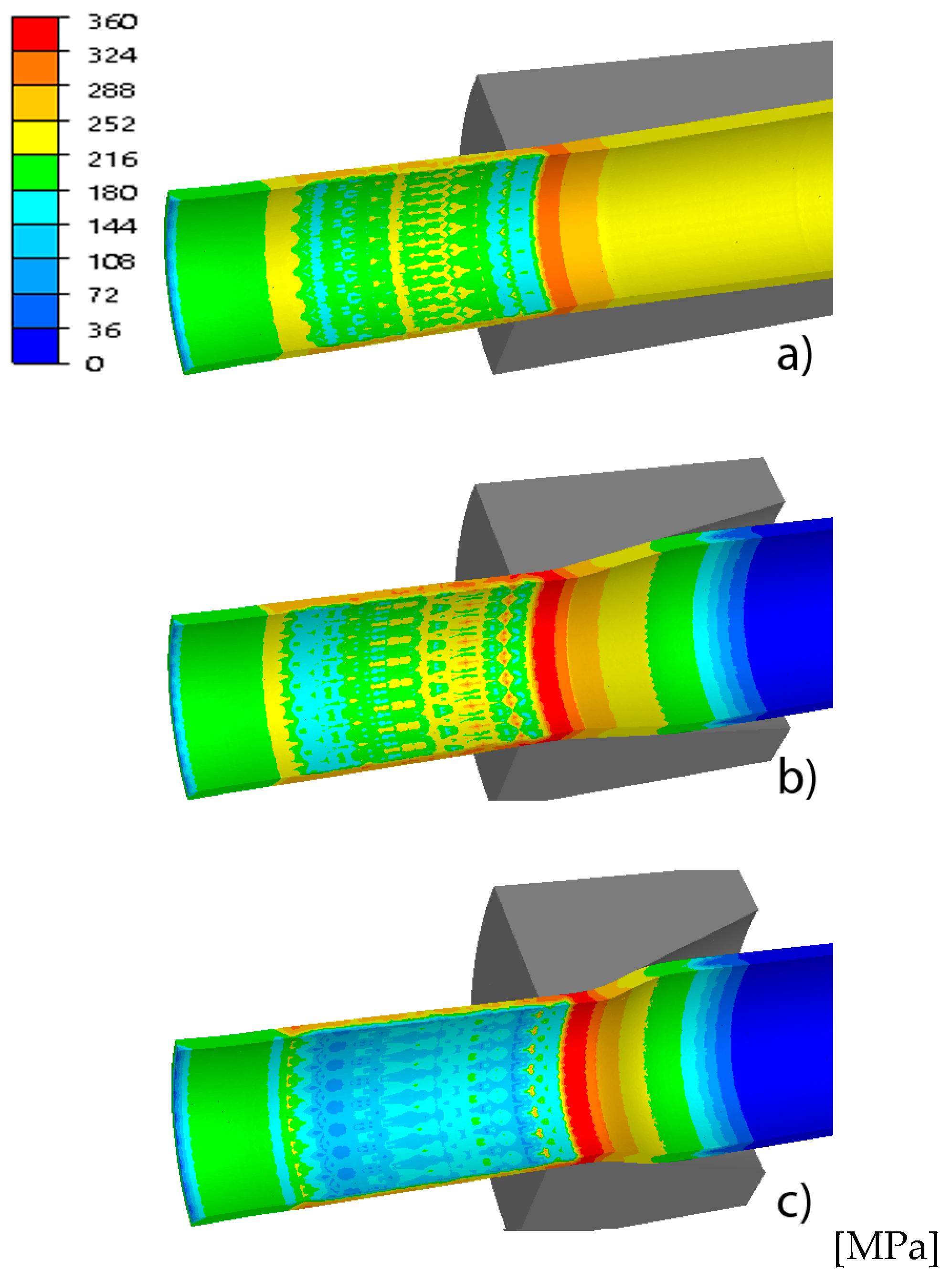
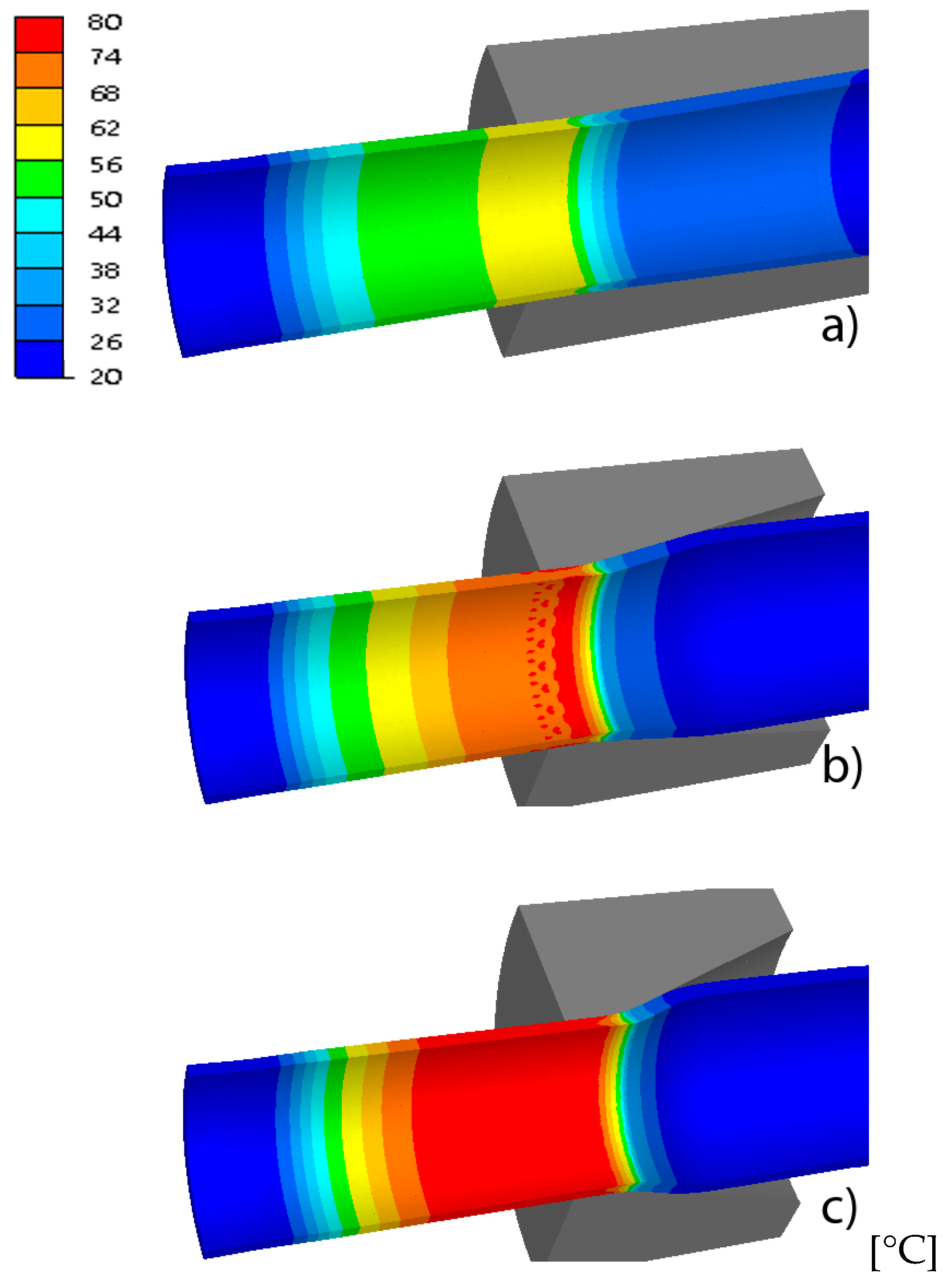
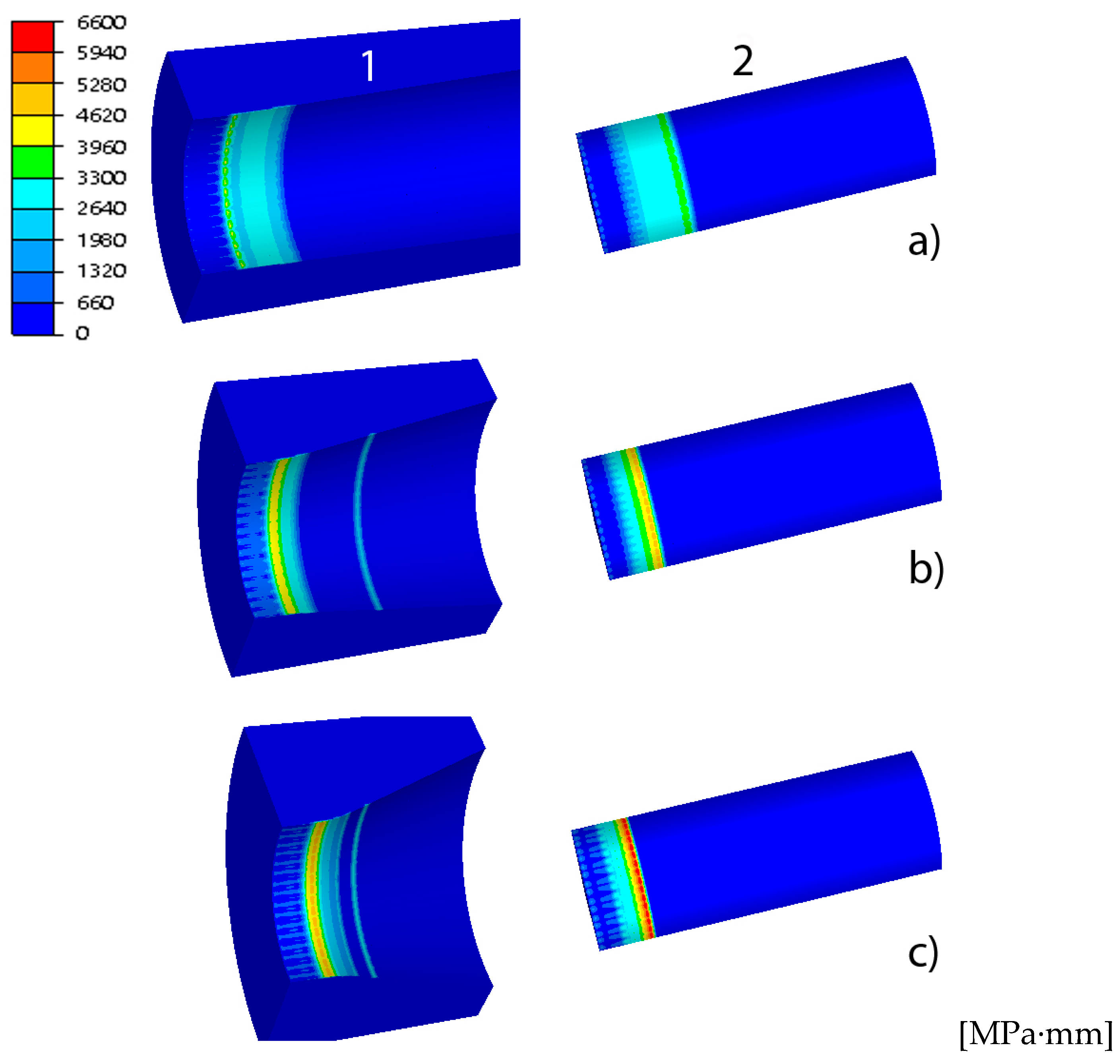
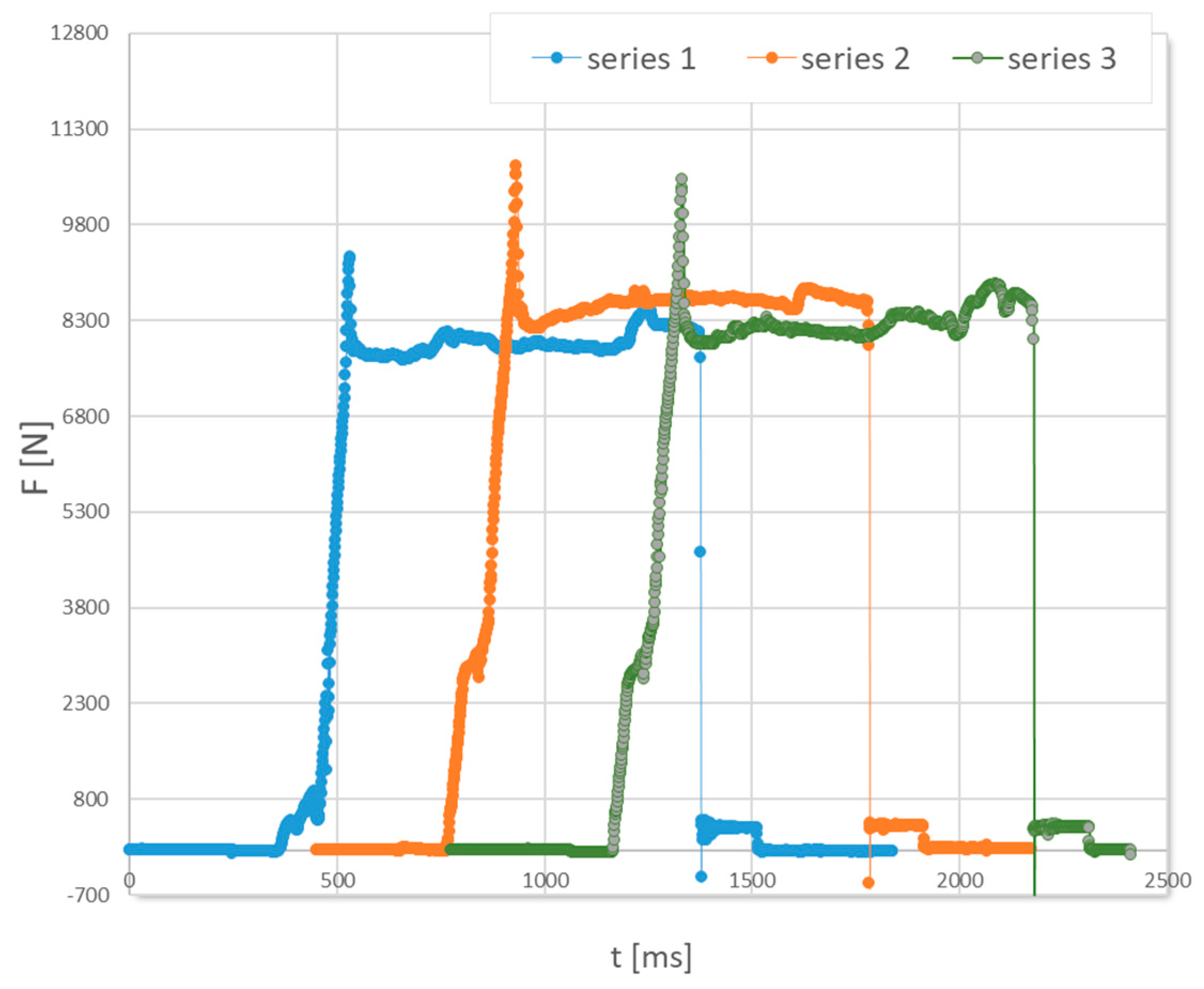
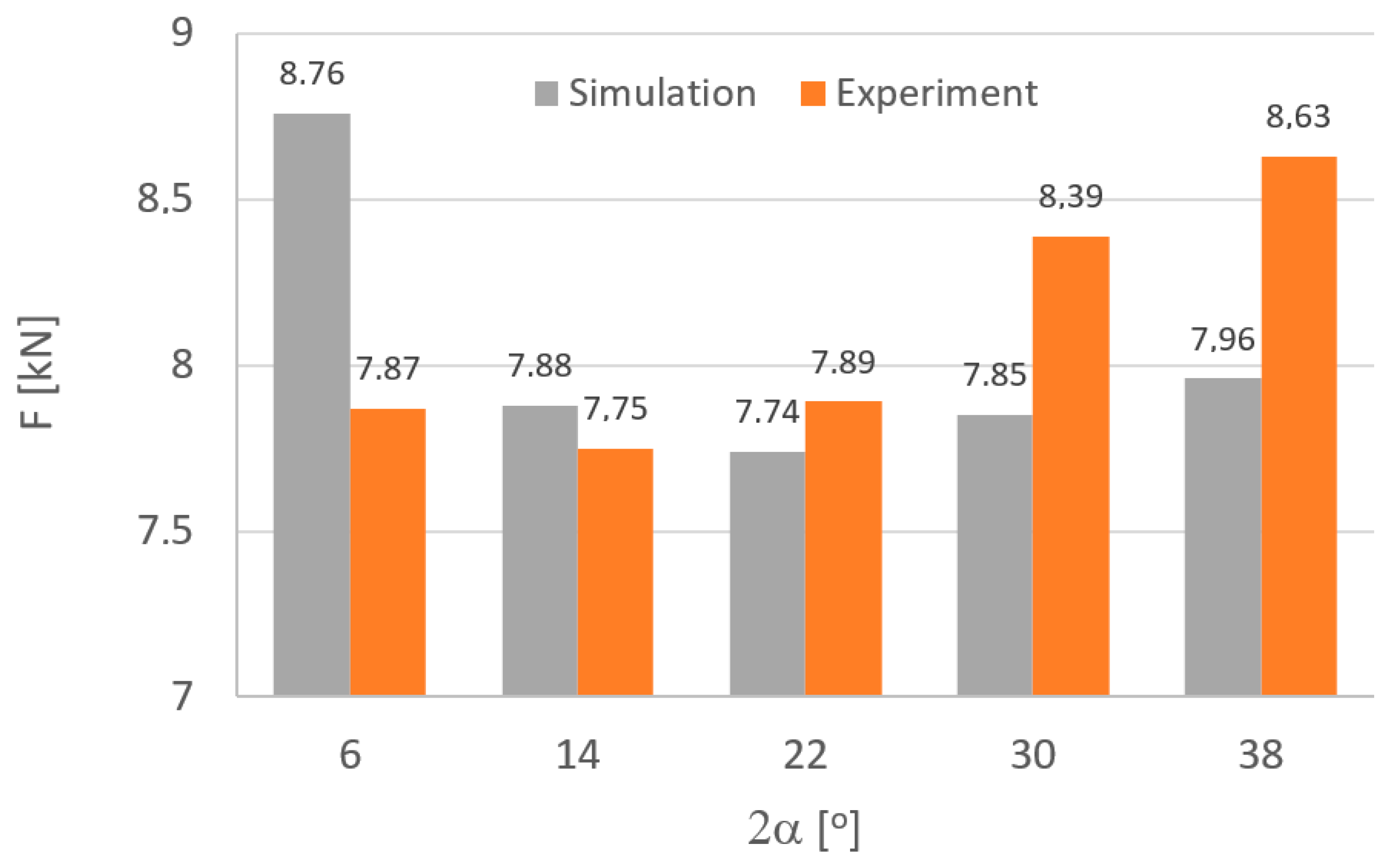
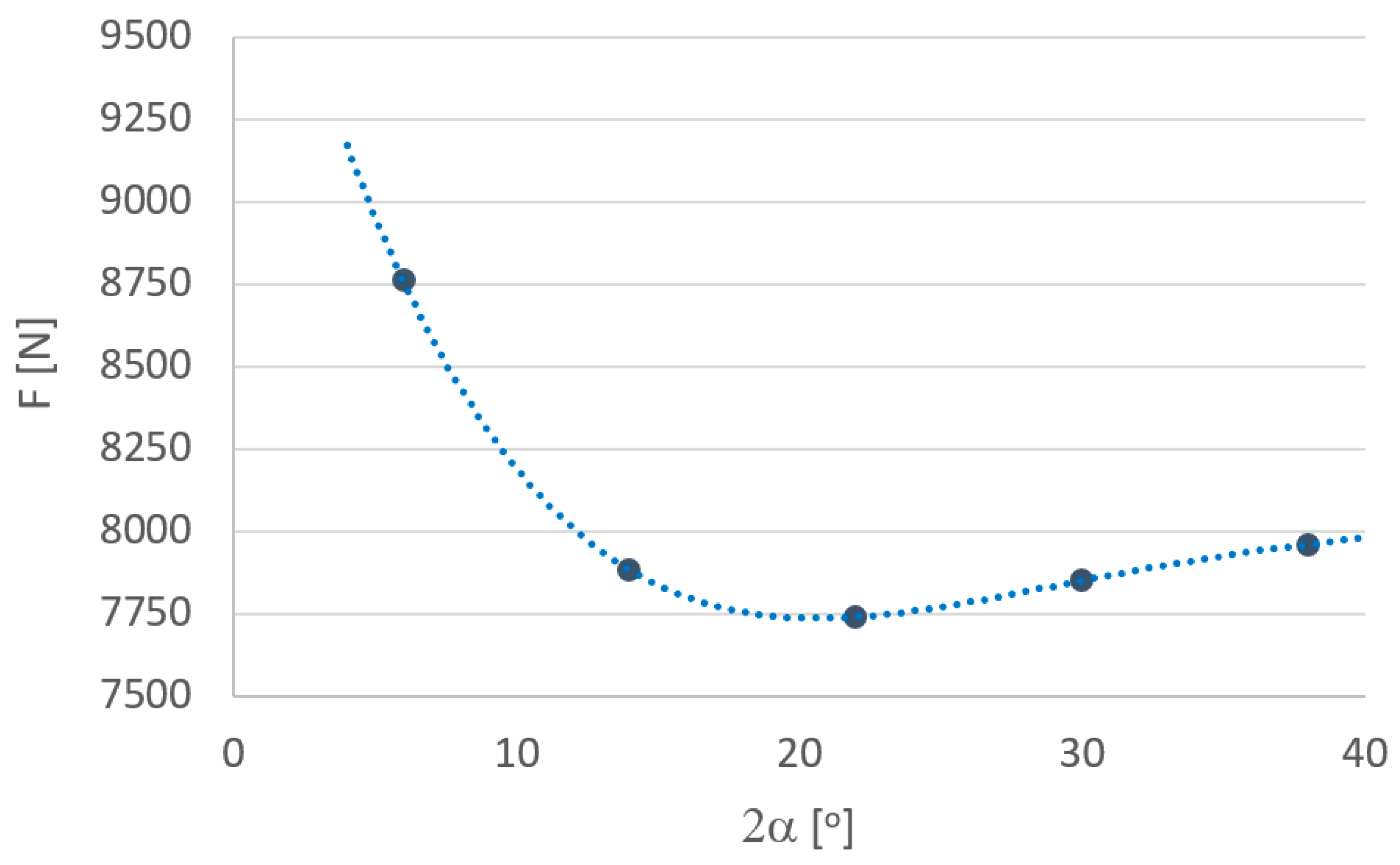
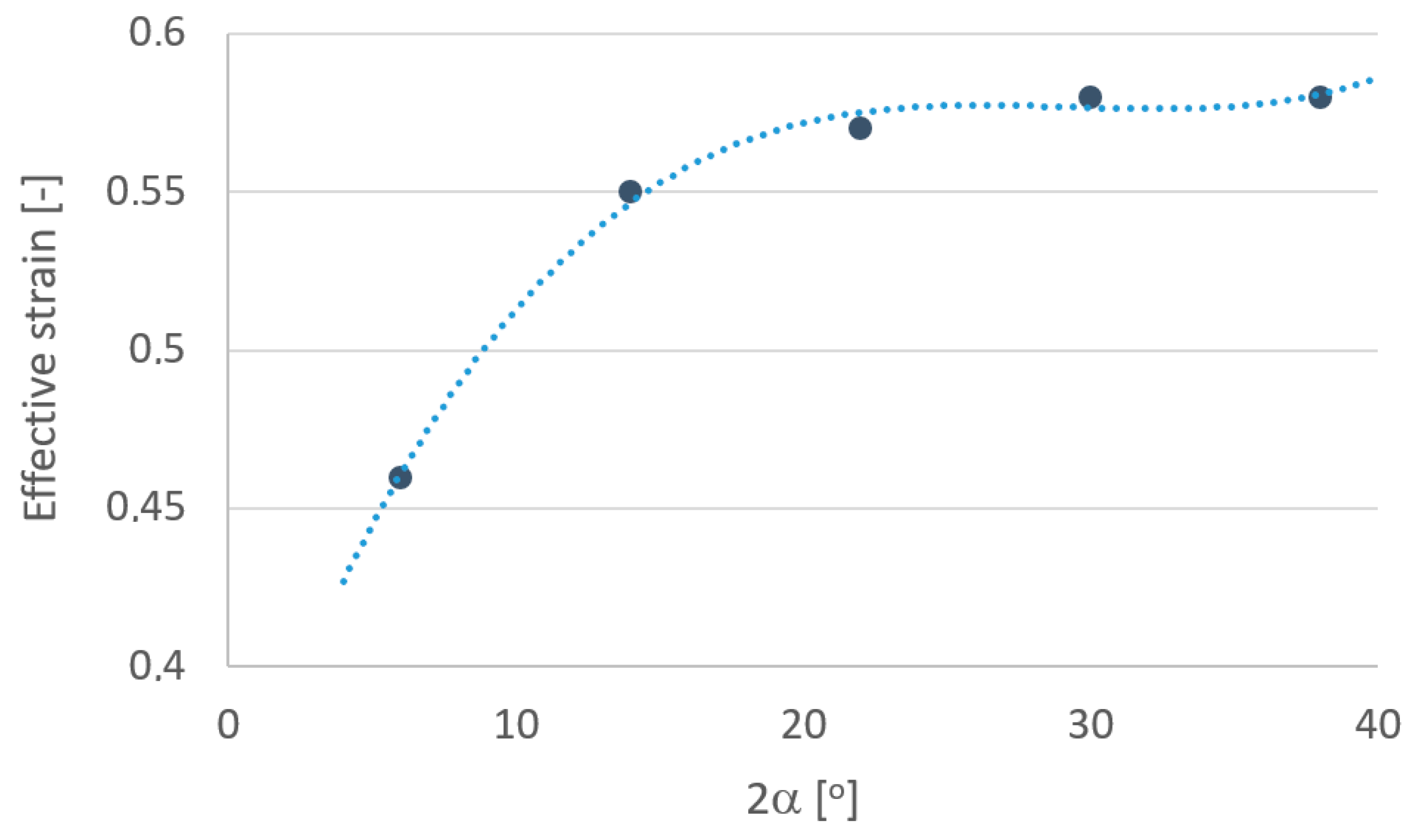
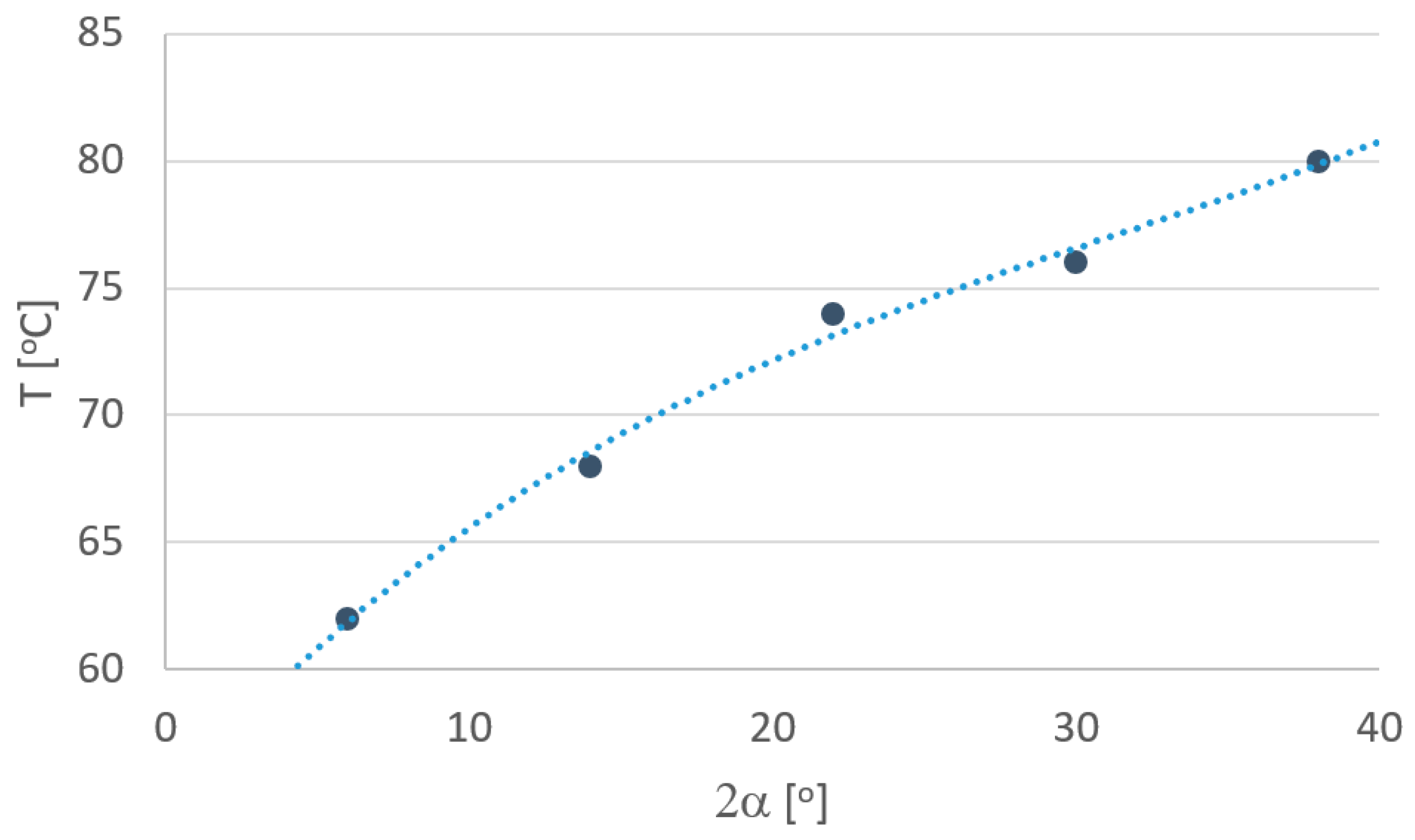
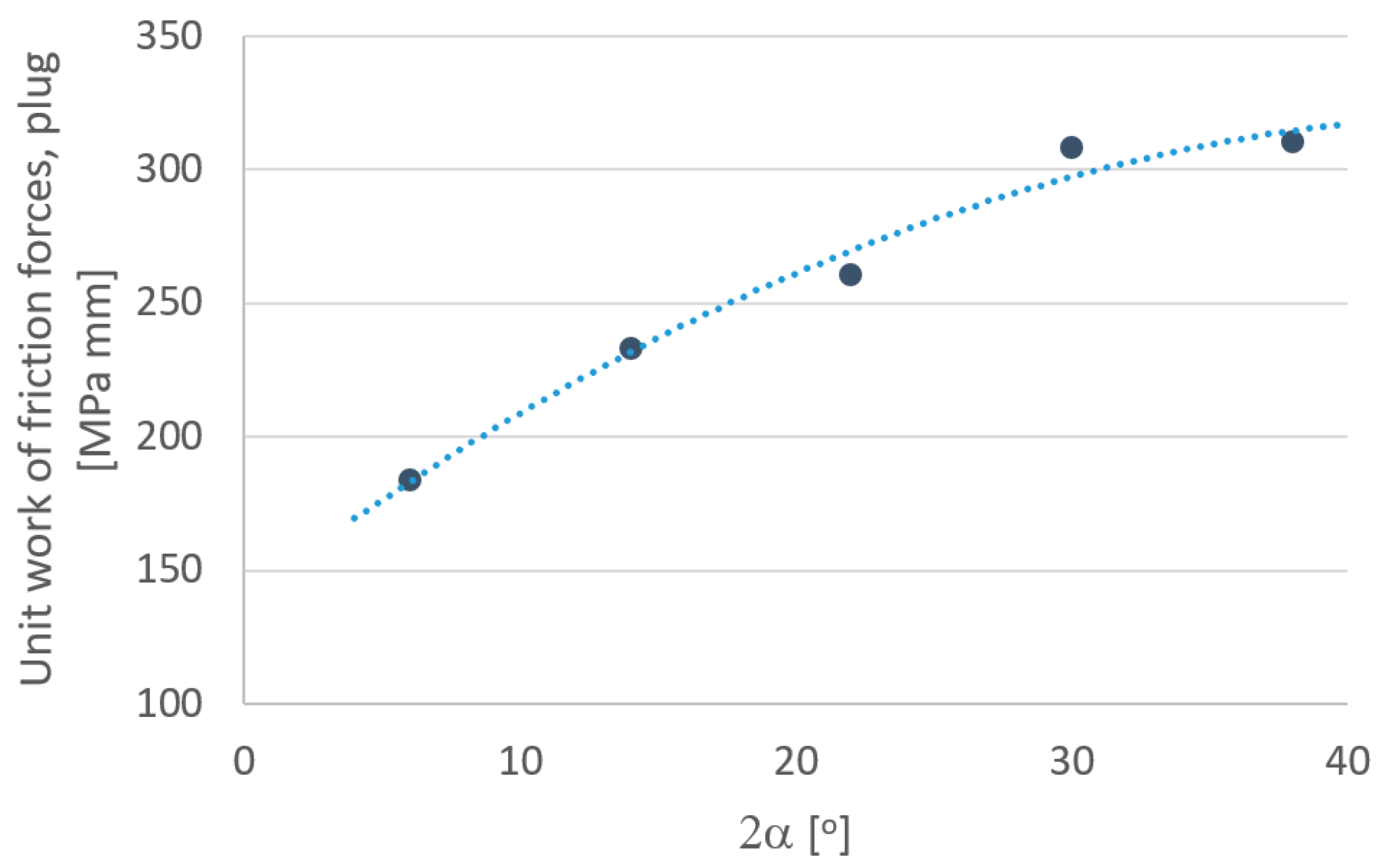
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rubio, E.M.; Camacho, A.M.; Pérez, R.; Marín, M.M. Guidelines for Selecting Plugs Used in Thin-Walled Tube Drawing Processes of Metallic Alloys. Metals 2017, 7, 572. [Google Scholar] [CrossRef]
- Palengat, M.; Chagnon, G.; Favier, D.; Louche, H.; Linardon, C.; Plaideau, C. Cold drawing of 316L stainless steel thin-walled tubes: Experiments and finite element analysis. Int. J. Mech. Sci. 2013, 70, 69–78. [Google Scholar] [CrossRef]
- Favier, D.; Liu, Y.; Orgeas, L.; Sandel, A.; Debove, L.; Comte-Gaz, P. Influence of thermomechanical processing on the superelastic properties of a Ni-rich nitinol shape memory alloy. Mater. Sci. Eng. A Struct. 2006, 429, 130–136. [Google Scholar] [CrossRef]
- Guillot, M.; Fafard, M.; Girard, S.; Rahem, A.; D’Amours, G. Experimental Exploration of the Aluminum Tube Drawing Process for Producing Variable Wall Thickness Components used in Light Structural Applications. SAE Tech. Pap. 2010, 1, 0222. [Google Scholar] [CrossRef]
- Łuksza, J. Elementy Ciągarstwa; AGH: Kraków, Poland, 2001. [Google Scholar]
- Knap, F.; Karuzel, R.; Cieślak, Ł. Ciągnienie Drutów, Prętów i Rur; Metalurgia Nr 36; Wydawnictwo Wydziału Inżynierii Procesowej, Materiałowej i Fizyki Stosowanej, Politechniki Częstochowskiej: Częstochowa, Poland, 2004. [Google Scholar]
- Knap, F.; Golis, B.; Pilarczyk, J.W. Wybrane Zagadnienia z Teorii i Praktyki Ciągnienia; Cz. 3. Ciągnienie Stalowych Prętów i Rur; Politechnika Częstochowska: Częstochowa, Poland, 1993. [Google Scholar]
- Pernis, R.; Kasala, J. The influence of the die and floating plug geometry on the drawing process of tubing. Int. J. Adv. Manuf. Technol. 2013, 65, 1081–1089. [Google Scholar] [CrossRef]
- Farahani, N.; Parvizi, A.; Barooni, A.; Naeini, S. Optimum curved die profile for tube drawing process with fixed conical plug. J. Adv. Manuf. Technol. 2018, 97, 1–11. [Google Scholar] [CrossRef]
- Sadok, L.; Pietrzyk, M. Zagadnienie zmiany grubości ścianki w procesie swobodnego ciągnienia rur. Arch. Hut. 1979, 24, 255–264. [Google Scholar]
- Sadok, L.; Pietrzyk, M. Analiza pracy korka swobodnego w obszarze odkształcenia. Hutnik 1981, 48, 62–65. [Google Scholar]
- Hatalak, R.; Kazana, W. Kryteria doboru trzpieni swobodnych do ciągnienia rur drobnowymiarowych. Rudy I Met. Nieżelazne 1992, 2, 44–47. [Google Scholar]
- Kapustová, M.; Sobota, R.; Necpal, M. The influence of technological parameters on drawing force at cold drawing of steel tubes using fem simulation. Solid State Phenom. 2019, 294, 124–128. [Google Scholar] [CrossRef]
- Kazanecki, J. Wytwarzanie Rur Bez Szwu; Wydawnictwo AGH: Kraków, Poland, 2003. [Google Scholar]
- Sińczak, J. (Ed.) Procesy Przeróbki Plastycznej. Ćwiczenia Laboratoryjne; Wydawnictwo Naukowe AKAPIT: Kraków, Poland, 2001. [Google Scholar]
- Łuksza, J.; Sadok, L. Wybrane Zagadnienia z Ciągarstwa. In Skrypty Uczelniane; AGH: Kraków, Poland, 1986. [Google Scholar]
- Gülseren, B.; Bychkov, O.; Frolov, I.; Schaper, M.; Grydin, O. Sinking of Ultra-Thick-Walled Double-Layered Aluminium Tubes. Arch. Metall. Mater. 2018, 63, 365–370. [Google Scholar] [CrossRef]
- Suliga, M.; Wartacz, R.; Hawryluk, M. The Multi-Stage Drawing Process of Zinc-Coated Medium-Carbon Steel Wires in Conventional and Hydrodynamic Dies. Materials 2020, 13, 4871. [Google Scholar] [CrossRef] [PubMed]
- Suliga, M.; Wartacz, R.; Hawryluk, M.; Kostrzewa, J. The Effect of Drawing in Conventional and Hydrodynamic Dies on Structure and Corrosion Resistance of Hot-Dip Galvanized Zinc Coatings on Medium-Carbon Steel Wire. Materials 2022, 15, 6728. [Google Scholar] [CrossRef]
- Foadian, F.; Carradó, A.; Palkowski, H. Precision tube production: Influencing the eccentricity and residual stresses by tilting andshifting. J. Mater. Process. Technol. 2015, 222, 155–162. [Google Scholar] [CrossRef]
- Al-Hamdany, N.; Brokmeier, H.-G.; Salih, M.; Zhong, Z.; Schwebke, B.; Schell, N.; Gan, W. Crystallographic texture gradient along the wall thickness of an SF-copper tube. Mater. Charact. 2018, 139, 125–133. [Google Scholar] [CrossRef]
- Brokmeier, H.-G.; Carradò, A.; Al-Hamdany, N.; Pirling, T.; Wimpory, R.; Schell, N.; Palkowski, H. Texture gradient in a copper tube at maximum and minimum wall thickness. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Dresden, Germany, 24–29 August 2014; IOP Publishing: Bristol, UK, 2015; Volume 82, p. 012102. [Google Scholar]
- Bajor, T.; Muskalski, Z.; Suliga, M. Research on the drawing process with a large total deformation wires of AZ31 alloy. J. Phys. Conf. Ser. 2010, 240, 012107. [Google Scholar] [CrossRef]
- Park, H.; Lee, D.N. Deformation and annealing textures of drawn Al–Mg–Si alloy tubes. J. Mater. Process. Technol. 2001, 113, 551–555. [Google Scholar] [CrossRef]
- Khani, S.; Palkowski, H.; Carradò, A.; Foadian, F. Experimental Investigation on Local and Global Texture Evolution in Drawing Seamless Copper Tubes. Appl. Mech. 2023, 4, 93–108. [Google Scholar] [CrossRef]
- Foadian, F.; Carradó, A.; Pirling, T.; Palkowski, H. Residual stresses evolution in Cu tubes, cold drawn with tilted dies—Neutron diffraction measurements and finite element simulation. Mater. Des. 2016, 107, 163–170. [Google Scholar] [CrossRef]
- Akchurin, R.Z.; Bogatov, A.A.; Salikhyanov, D.R.; Ovchinnikov, A.S. Development and Introduction of Technology and Equipment for Multiple Drawing of Copper Alloy Thin-Walled Tube on a Long Movable Mandrel Without Intermediate Heat Treatment. Metallurgist 2019, 62, 1039–1047. [Google Scholar] [CrossRef]
- Neves, F.O.; Button, S.T.; Caminaga, C.; Gentile, F.C. Numerical and experimental analysis of tube drawing with fixed plug. J. Braz. Soc. Mech. Sci. Eng. 2005, 27, 426–431. [Google Scholar] [CrossRef]
- Hoff, N.J. Approximate analysis of structures in the presence of moderately large steps deformation. Q. Appl. Math. 1954, 2, 49–58. [Google Scholar] [CrossRef]
- Kocańda, A. Określenie trwałości narzędzia w obróbce plastycznej metali. In Informatyka w Technologii Metali; Pieli, A., Grosmana, F., Kusiaka, J., Pietrzyka, M., Eds.; Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 2003; pp. 148–188. [Google Scholar]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Milenin, A. Matematicheskaja model’ processa iznosa valkov pri gorjachej prokatke profilej. In Udoskonalenija Procesiv ta Obladannja Obrobotki Tiskom v Metalurgij i Mashinobuduvanii; Tematichnij zbornik naukovikh prac, ed.; Donbaska derzhavna mashinobidivna akademija (DDMA): Kramatorsk, Ukraine, 2006; pp. 409–414. [Google Scholar]





| Material | YS/ MPa | UTS/ MPa | TEL/ % |
|---|---|---|---|
| Tensile test | 155 | 387 | 80 |
| Material | K | m1 | m2 |
|---|---|---|---|
| CuSn8 | 280 | 0.1 | 0.46 |
| Variant | Drawing Angle 2α [o] | Length of the Calibration Part Lc [mm] | Length of the Calibration Part Lc [%] | Drawing Die Diameter D [mm] | Cylindrical Plug Diameter dp [mm] |
|---|---|---|---|---|---|
| I | 6 | 4 | 26 | 15.20 | 13.65 |
| II | 14 | 4 | 26 | 15.20 | 13.65 |
| III | 22 | 4 | 26 | 15.20 | 13.65 |
| IV | 30 | 4 | 26 | 15.20 | 13.65 |
| V | 38 | 4 | 26 | 15.20 | 13.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suliga, M.; Mróz, S.; Szota, P.; Wasilewski, M.; Jaroszewski, K. Numerical Analysis of the Process of Drawing Thin-Walled CuSn8 Alloy Tubes on a Cylindrical Plug. Materials 2025, 18, 2754. https://doi.org/10.3390/ma18122754
Suliga M, Mróz S, Szota P, Wasilewski M, Jaroszewski K. Numerical Analysis of the Process of Drawing Thin-Walled CuSn8 Alloy Tubes on a Cylindrical Plug. Materials. 2025; 18(12):2754. https://doi.org/10.3390/ma18122754
Chicago/Turabian StyleSuliga, Maciej, Sebastian Mróz, Piotr Szota, Mateusz Wasilewski, and Konrad Jaroszewski. 2025. "Numerical Analysis of the Process of Drawing Thin-Walled CuSn8 Alloy Tubes on a Cylindrical Plug" Materials 18, no. 12: 2754. https://doi.org/10.3390/ma18122754
APA StyleSuliga, M., Mróz, S., Szota, P., Wasilewski, M., & Jaroszewski, K. (2025). Numerical Analysis of the Process of Drawing Thin-Walled CuSn8 Alloy Tubes on a Cylindrical Plug. Materials, 18(12), 2754. https://doi.org/10.3390/ma18122754






