Lignocellulosic Byproducts as Bio-Adsorbents for Lead Removal
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
- Dry nut shells of walnut and chestnut obtained as waste material at one dry fruit processing mill, and
- Wood and burnt wood obtained from local pine (Pinus pinaster) forests. Burnt pine wood is abundant due to wildfires that have occurred in the region in the last years.
2.2. Adsorbent Material Characterization
2.2.1. Powder X-Ray Diffraction (PXRD) Analysis
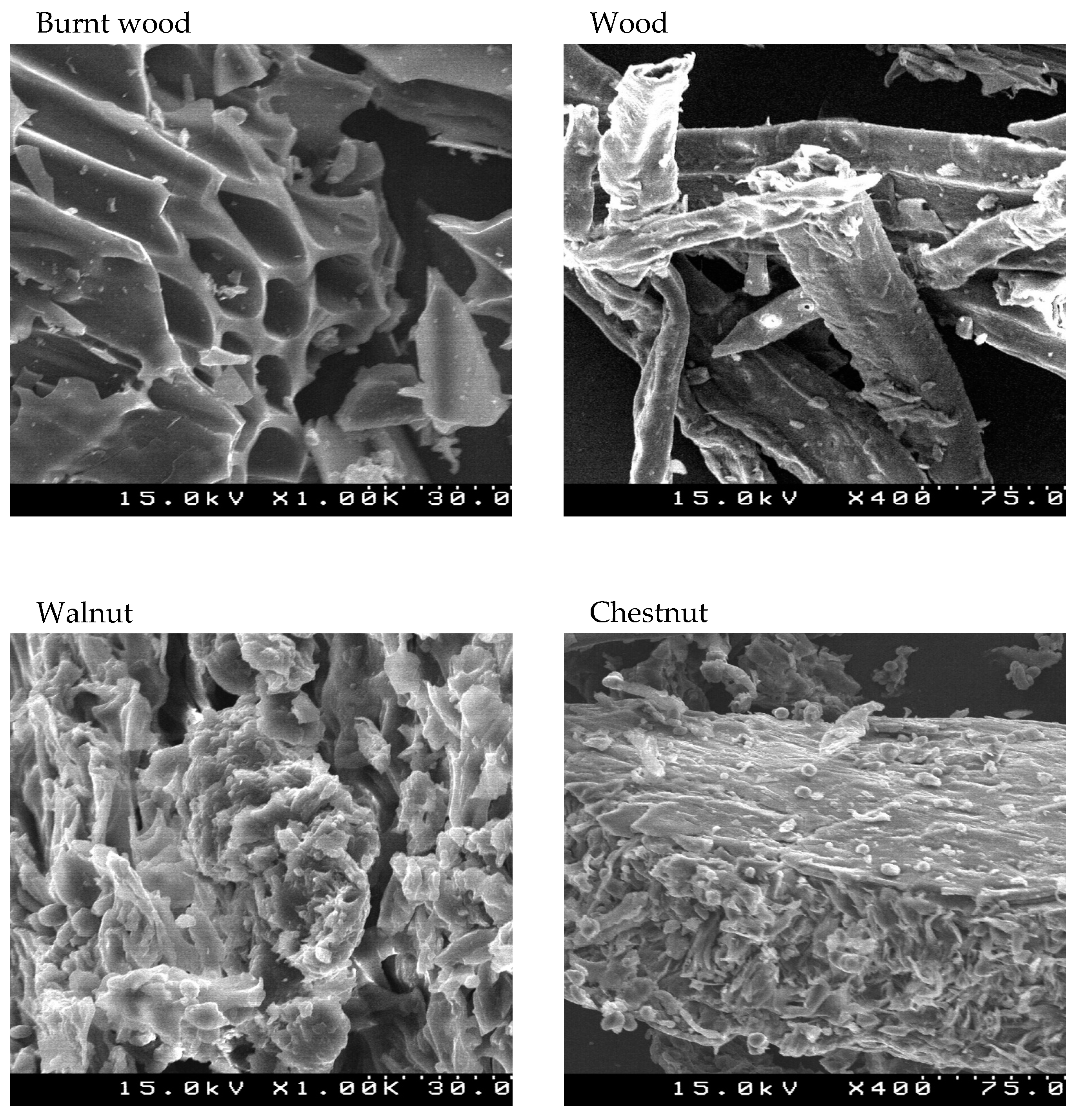
2.2.2. Scanning Electron Microscopy and Energy Dispersive Spectroscopy (SEM–EDS)
2.2.3. BET Surface Area Analysis
2.2.4. Thermogravimetric Analysis
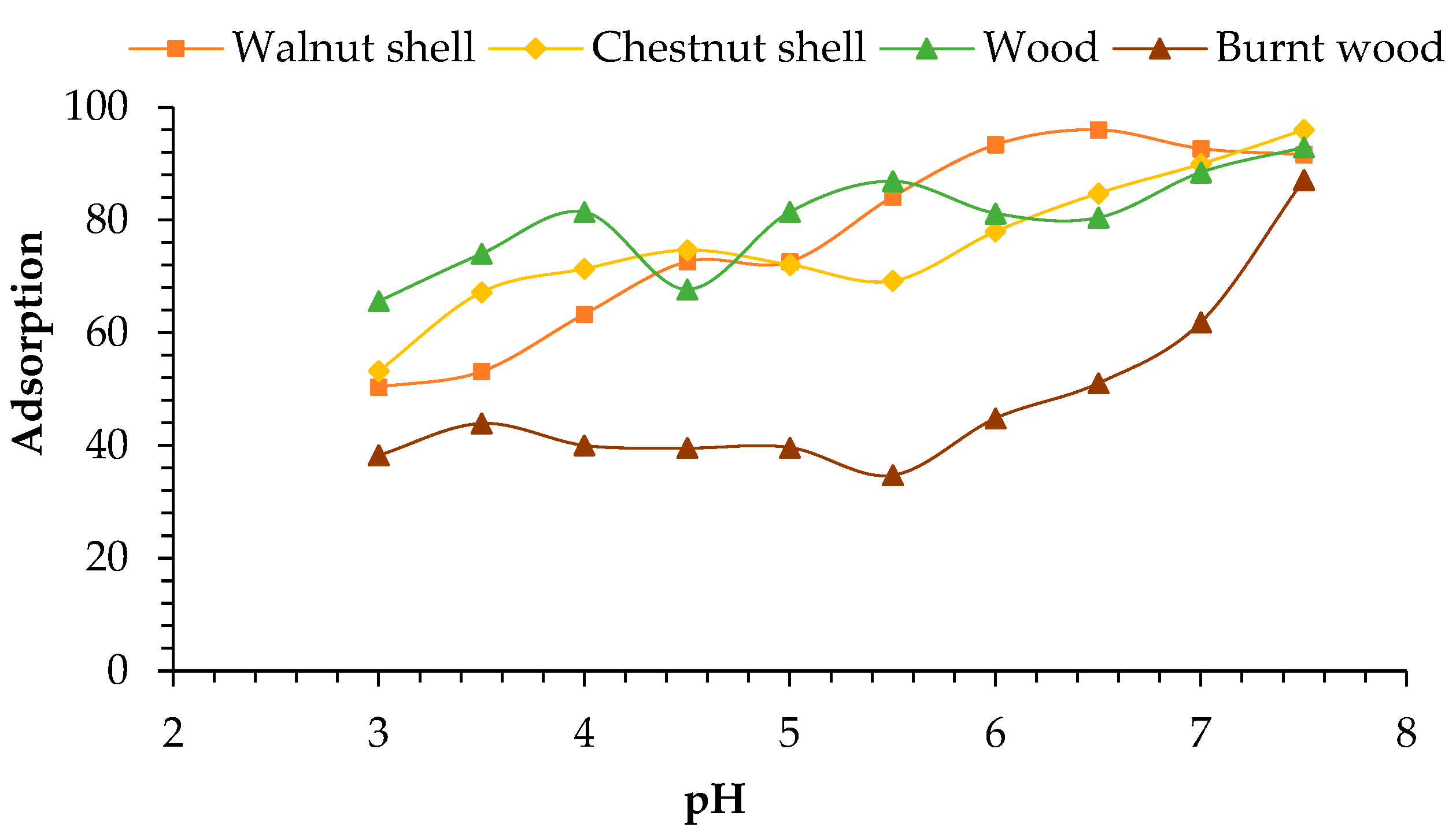
2.3. pH Optimization
2.4. Adsorption Isotherms
2.5. Adsorption Kinetics
3. Results
3.1. Characterization of Materials
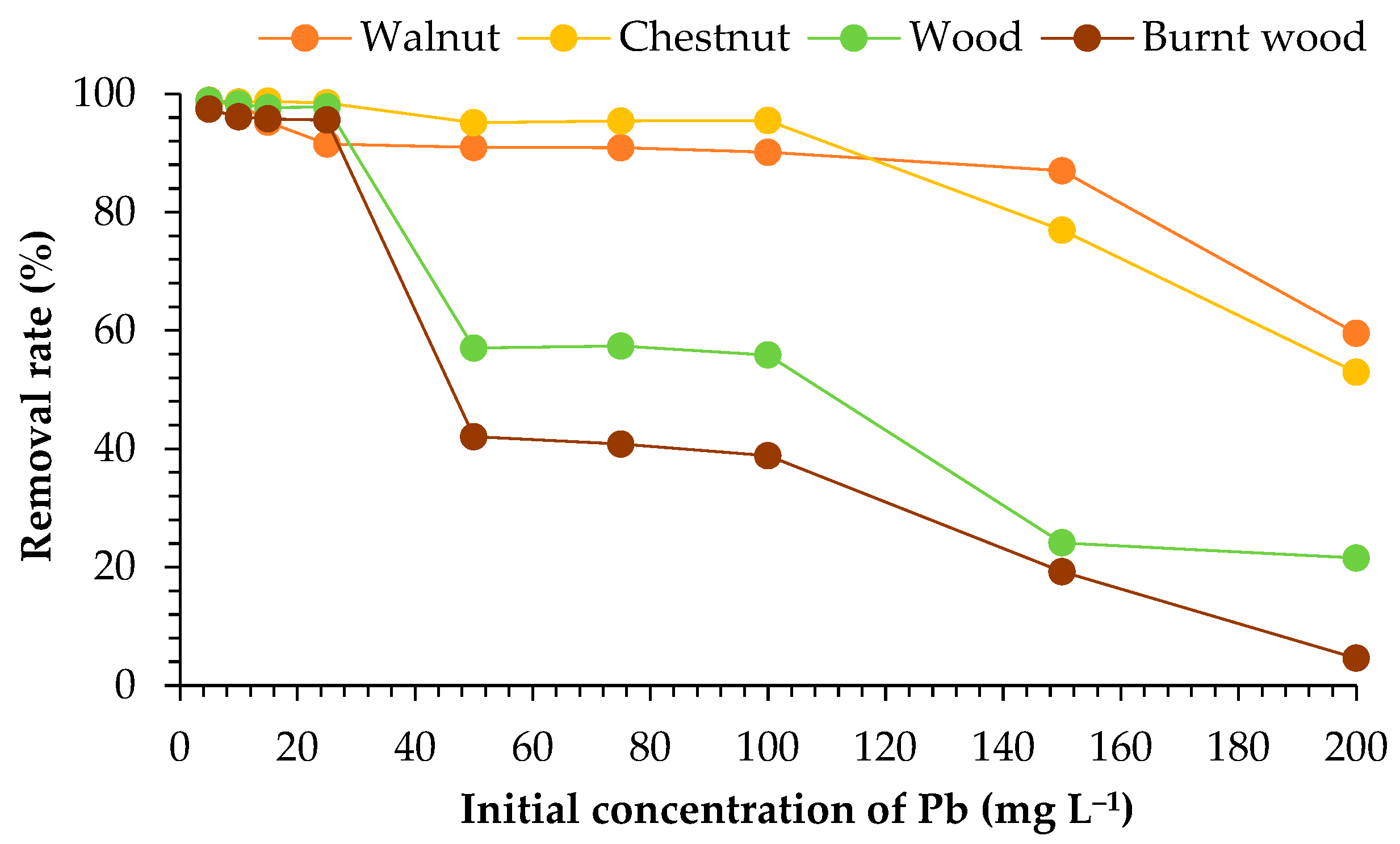
3.2. Initial Concentration of Pb Ions
3.3. Adsorption Isotherms
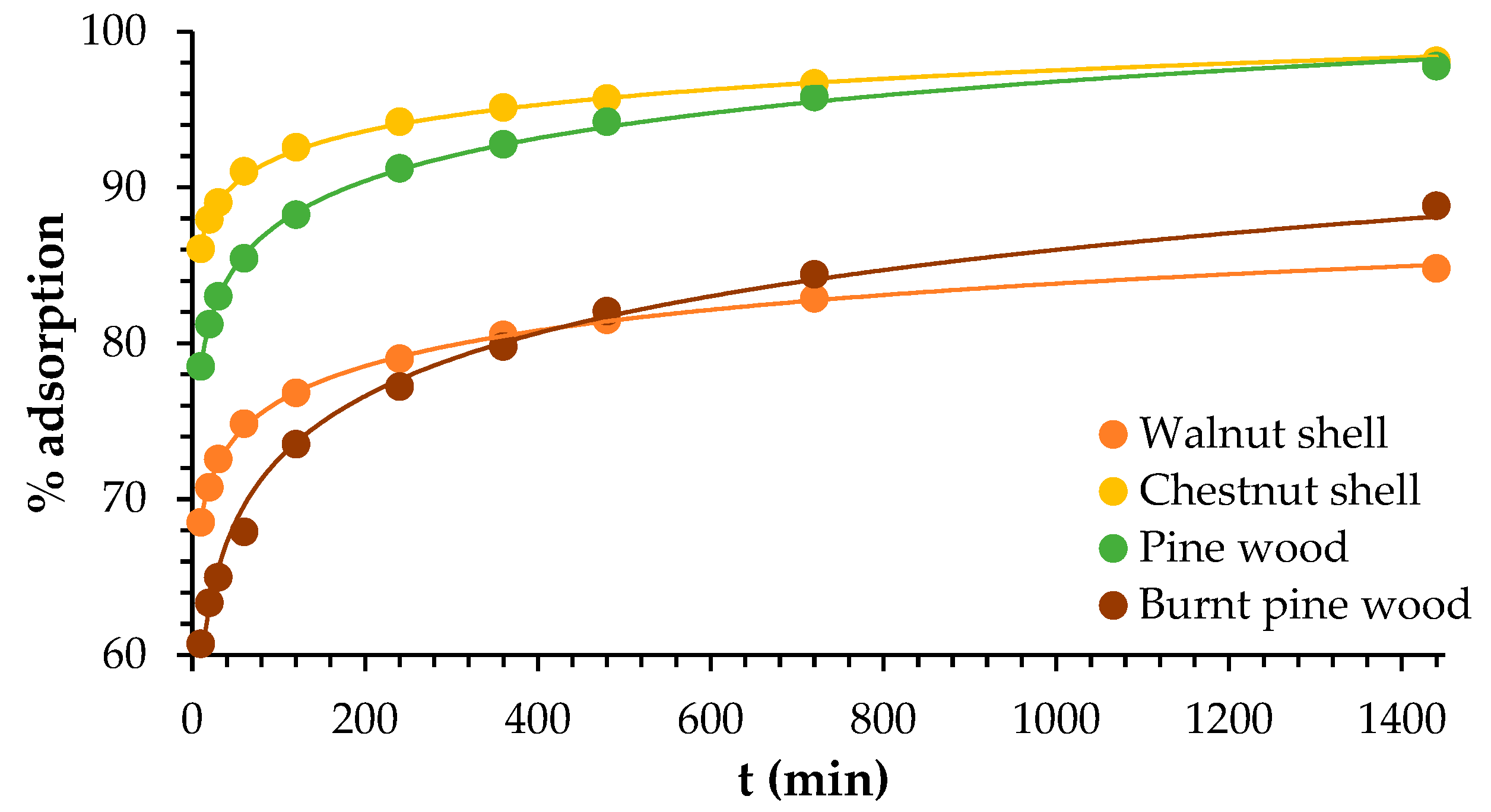
3.4. Adsorption Kinetics
4. Discussion
4.1. Characterization of Materials
4.2. Initial Concentration of Pb Ions
4.3. Adsorption Isotherms
4.4. Adsorption Kinetics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Wang, X.; Zhao, G.; Chen, C.; Chai, Z.; Alsaedi, A.; Hayat, T.; Wang, X. Metal–Organic Framework-Based Materials: Superior Adsorbents for the Capture of Toxic and Radioactive Metal Ions. Chem. Soc. Rev. 2018, 47, 2322–2356. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Gu, Y.; Xie, D.; Qin, W.; Zhang, H.; Wang, G.; Zhang, Y.; Zhao, H. A Hierarchical Hybrid Monolith: MoS42−-Intercalated NiFe Layered Double Hydroxide Nanosheet Arrays Assembled on Carbon Foam for Highly Efficient Heavy Metal Removal. J. Mater. Chem. A 2019, 7, 12869–12881. [Google Scholar] [CrossRef]
- EEA. Industrial Pollutant Releases to Water in Europe; European Environment Agency: Copenhagen, Denmark, 2022. [Google Scholar]
- Basu, M.; Guha, A.K.; Ray, L. Adsorption of Lead on Cucumber Peel. J. Clean. Prod. 2017, 151, 603–615. [Google Scholar] [CrossRef]
- Jones, H.H. American Conference of Governmental Industrial Hygienists’ Proposed Threshold Limit Value for Noise. Am. Ind. Hyg. Assoc. J. 1968, 29, 537–540. [Google Scholar] [CrossRef]
- Levin, R.; Brown, M.J.; Kashtock, M.E.; Jacobs, D.E.; Whelan, E.A.; Rodman, J.; Schock, M.R.; Padilla, A.; Sinks, T. Lead Exposures in U.S. Children, 2008: Implications for Prevention. Environ. Health Perspect. 2008, 116, 1285–1293. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Lead and Copper Rule. Available online: https://www.epa.gov/dwreginfo/lead-and-copper-rule (accessed on 17 November 2022).
- APA. Metais Pesados. Available online: https://apambiente.pt/ar-e-ruido/metais-pesados (accessed on 12 February 2025).
- IARC Working Group on the Evaluation of Carcinogenic Risks to Humans. Inorganic and Organic Lead Compounds; International Agency for Research on Cancer: Lyon, France, 2006. [Google Scholar]
- Escudero-Oñate, C.; Poch, J.; Villaescusa, I. Adsorption of Cu(II), Ni(II), Pb(II) and Cd(II) from Ternary Mixtures: Modelling Competitive Breakthrough Curves and Assessment of Sensitivity. Environ. Process. 2017, 4, 833–849. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Basic Information About Lead in Drinking Water. Available online: https://www.epa.gov/ground-water-and-drinking-water/basic-information-about-lead-drinking-water (accessed on 12 February 2025).
- Buragohain, M.; Bhuyan, B.; Sarma, H.P. Seasonal Variations of Lead, Arsenic, Cadmium and Aluminium Contamination of Groundwater in Dhemaji District, Assam, India. Env. Monit. Assess. 2010, 170, 345–351. [Google Scholar] [CrossRef]
- Alamgir, A.; Khan, M.A.; Schilling, J.; Shaukat, S.S.; Shahab, S. Assessment of Groundwater Quality in the Coastal Area of Sindh Province, Pakistan. Env. Monit. Assess. 2016, 188, 78. [Google Scholar] [CrossRef]
- Puglla, E.P.; Guaya, D.; Tituana, C.; Osorio, F.; García-Ruiz, M.J. Biochar from Agricultural By-Products for the Removal of Lead and Cadmium from Drinking Water. Water 2020, 12, 2933. [Google Scholar] [CrossRef]
- Kinuthia, G.K.; Ngure, V.; Beti, D.; Lugalia, R.; Wangila, A.; Kamau, L. Levels of Heavy Metals in Wastewater and Soil Samples from Open Drainage Channels in Nairobi, Kenya: Community Health Implication. Sci. Rep. 2020, 10, 8434. [Google Scholar] [CrossRef]
- Araújo, C.S.T.; Almeida, I.L.S.; Rezende, H.C.; Marcionilio, S.M.L.O.; Léon, J.J.L.; de Matos, T.N. Elucidation of Mechanism Involved in Adsorption of Pb(II) onto Lobeira Fruit (Solanum lycocarpum) Using Langmuir, Freundlich and Temkin Isotherms. Microchem. J. 2018, 137, 348–354. [Google Scholar] [CrossRef]
- Novais, R.M.; Buruberri, L.H.; Seabra, M.P.; Labrincha, J.A. Novel Porous Fly-Ash Containing Geopolymer Monoliths for Lead Adsorption from Wastewaters. J. Hazard. Mater. 2016, 318, 631–640. [Google Scholar] [CrossRef]
- Ferreira, J.M.; da Silva, F.L.H.; Alsina, O.L.S.; Oliveira, L.d.S.C.; Cavalcanti, E.B.; Gomes, W.C. Estudo do equilíbrio e cinética da biossorção do pb2+ por saccharomyces cerevisiae. Quím. Nova 2007, 30, 1188–1193. [Google Scholar] [CrossRef]
- Ahmad, K.; Shah, H.-R.; Khan, M.S.; Iqbal, A.; Potrich, E.; Amaral, L.S.; Rasheed, S.; Nawaz, H.; Ayub, A.; Naseem, K.; et al. Lead in Drinking Water: Adsorption Method and Role of Zeolitic Imidazolate Frameworks for Its Remediation: A Review. J. Clean. Prod. 2022, 368, 133010. [Google Scholar] [CrossRef]
- Amin, M.; Chetpattananondh, P. Biochar from Extracted Marine Chlorella Sp. Residue for High Efficiency Adsorption with Ultrasonication to Remove Cr(VI), Zn(II) and Ni(II). Bioresour. Technol. 2019, 289, 121578. [Google Scholar] [CrossRef]
- Bangari, R.S.; Singh, A.K.; Namsani, S.; Singh, J.K.; Sinha, N. Magnetite-Coated Boron Nitride Nanosheets for the Removal of Arsenic(V) from Water. ACS Appl. Mater. Interfaces 2019, 11, 19017–19028. [Google Scholar] [CrossRef]
- Haase, M.F.; Jeon, H.; Hough, N.; Kim, J.H.; Stebe, K.J.; Lee, D. Multifunctional Nanocomposite Hollow Fiber Membranes by Solvent Transfer Induced Phase Separation. Nat. Commun. 2017, 8, 1234. [Google Scholar] [CrossRef]
- Wang, Y.; Dang, Q.; Liu, C.; Yu, D.; Pu, X.; Wang, Q.; Gao, H.; Zhang, B.; Cha, D. Selective Adsorption toward Hg(II) and Inhibitory Effect on Bacterial Growth Occurring on Thiosemicarbazide-Functionalized Chitosan Microsphere Surface. ACS Appl. Mater. Interfaces 2018, 10, 40302–40316. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, S.; Qiao, J.; Kołodyńska, D.; Ju, Y.; Zhang, M.; Cai, M.; Deng, D.; Dionysiou, D.D. Malic Acid-Enhanced Chitosan Hydrogel Beads (mCHBs) for the Removal of Cr(VI) and Cu(II) from Aqueous Solution. Chem. Eng. J. 2018, 353, 225–236. [Google Scholar] [CrossRef]
- Guo, L.; Liang, L.; Wang, Y.; Liu, M. Biosorption of Pb2+ from Aqueous Solution by Rice Straw Modified with Citric Acid. Environ. Prog. Sustain. Energy 2016, 35, 359–367. [Google Scholar] [CrossRef]
- Sharaf El-Deen, G.E.; Sharaf El-Deen, S.E.A. Kinetic and Isotherm Studies for Adsorption of Pb(II) from Aqueous Solution onto Coconut Shell Activated Carbon. Desalination Water Treat. 2016, 57, 28910–28931. [Google Scholar] [CrossRef]
- Lee, M.-E.; Park, J.H.; Chung, J.W. Comparison of the Lead and Copper Adsorption Capacities of Plant Source Materials and Their Biochars. J. Environ. Manag. 2019, 236, 118–124. [Google Scholar] [CrossRef] [PubMed]
- Alhogbi, B.G. Potential of Coffee Husk Biomass Waste for the Adsorption of Pb(II) Ion from Aqueous Solutions. Sustain. Chem. Pharm. 2017, 6, 21–25. [Google Scholar] [CrossRef]
- Sahoo, R.K.; Jena, S. Removal of Pb(II) from Aqueous Solution Using Fruits Peel as a Low Cost Adsorbent. Int. J. Sci. Eng. Technol. 2017, 5, 5–13. [Google Scholar]
- Ince, M.; İnce, O.K. An Overview of Adsorption Technique for Heavy Metal Removal from Water/Wastewater: A Critical Review. Int. J. Pure Appl. Sci. 2017, 3, 10–19. [Google Scholar] [CrossRef]
- Cruz-Lopes, L.P.; Macena, M.; Esteves, B.; Guiné, R.P.F. Ideal pH for the Adsorption of Metal Ions Cr6+, Ni2+, Pb2+ in Aqueous Solution with Different Adsorbent Materials. Open Agric. 2021, 6, 115–123. [Google Scholar] [CrossRef]
- Macena, M.W. Análise do Potencial de Adsorção de iões Metálicos em Solução Aquosa por Resíduos Lenhocelulósicos. Master’s Thesis, Polytechnic Institute of Viseu, Viseu, Portugal, 2021. [Google Scholar]
- Ju, X.; Bowden, M.; Brown, E.E.; Zhang, X. An Improved X-Ray Diffraction Method for Cellulose Crystallinity Measurement. Carbohydr. Polym. 2015, 123, 476–481. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Liu, Y.-X.; Lu, H.-H.; Yang, R.-Q.; Yang, S.-M. Competitive Adsorption of Pb(II), Cu(II), and Zn(II) Ions onto Hydroxyapatite-Biochar Nanocomposite in Aqueous Solutions. J. Solid. State Chem. 2018, 261, 53–61. [Google Scholar] [CrossRef]
- Pelekani, C.; Snoeyink, V.L. Competitive Adsorption between Atrazine and Methylene Blue on Activated Carbon: The Importance of Pore Size Distribution. Carbon 2000, 38, 1423–1436. [Google Scholar] [CrossRef]
- Erdoğan, S.; Önal, Y.; Akmil-Başar, C.; Bilmez-Erdemoğlu, S.; Sarıcı-Özdemir, Ç.; Köseoğlu, E.; İçduygu, G. Optimization of Nickel Adsorption from Aqueous Solution by Using Activated Carbon Prepared from Waste Apricot by Chemical Activation. Appl. Surf. Sci. 2005, 252, 1324–1331. [Google Scholar] [CrossRef]
- Deng, Y.; Huang, S.; Dong, C.; Meng, Z.; Wang, X. Competitive Adsorption Behaviour and Mechanisms of Cadmium, Nickel and Ammonium from Aqueous Solution by Fresh and Ageing Rice Straw Biochars. Bioresour. Technol. 2020, 303, 122853. [Google Scholar] [CrossRef] [PubMed]
- Poonam; Bharti, S.K.; Kumar, N. Kinetic Study of Lead (Pb2+) Removal from Battery Manufacturing Wastewater Using Bagasse Biochar as Biosorbent. Appl. Water Sci. 2018, 8, 119. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, S.; Yao, P.; Chen, Y.; Xu, X.; Li, T.; Gong, G. Removal of Pb(II) from Aqueous Solutions by Phytolacca americana L. Biomass as a Low Cost Biosorbent. Arab. J. Chem. 2018, 11, 99–110. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y.; Tao, Y.; Yu, Y.; Jiang, H.; Lian, H. Comparative Study of Adsorption of Pb(II) on Native Garlic Peel and Mercerized Garlic Peel. Env. Sci. Pollut. Res. 2014, 21, 2054–2063. [Google Scholar] [CrossRef]
- Mishra, P.C.; Patel, R.K. Removal of Lead and Zinc Ions from Water by Low Cost Adsorbents. J. Hazard. Mater. 2009, 168, 319–325. [Google Scholar] [CrossRef]
- Amar, M.B.; Walha, K.; Salvadó, V. Evaluation of Olive Stones for Cd(II), Cu(II), Pb(II) and Cr(VI) Biosorption from Aqueous Solution: Equilibrium and Kinetics. Int. J. Environ. Res. 2020, 14, 193–204. [Google Scholar] [CrossRef]
- Gundogdu, A.; Ozdes, D.; Duran, C.; Bulut, V.N.; Soylak, M.; Senturk, H.B. Biosorption of Pb(II) Ions from Aqueous Solution by Pine Bark (Pinus Brutia Ten.). Chem. Eng. J. 2009, 153, 62–69. [Google Scholar] [CrossRef]
- Ekinci, S.; İlter, Z.; Ercan, S.; Çınar, E.; Çakmak, R. Magnetite Nanoparticles Grafted with Murexide-Terminated Polyamidoamine Dendrimers for Removal of Lead (II) from Aqueous Solution: Synthesis, Characterization, Adsorption and Antimicrobial Activity Studies. Heliyon 2021, 7, e06600. [Google Scholar] [CrossRef]
- Long, M.; Jiang, H.; Li, X. Biosorption of Cu2+, Pb2+, Cd2+ and Their Mixture from Aqueous Solutions by Michelia Figo Sawdust. Sci. Rep. 2021, 11, 11527. [Google Scholar] [CrossRef]
- Aziz, N.A.A.; Jayasuriya, N.; Fan, L. Adsorption Study on Moringa Oleifera Seeds and Musa Cavendish as Natural Water Purification Agents for Removal of Lead, Nickel and Cadmium from Drinking Water. IOP Conf. Ser. Mater. Sci. Eng. 2016, 136, 012044. [Google Scholar] [CrossRef]
- Medellin-Castillo, N.A.; Padilla-Ortega, E.; Regules-Martínez, M.C.; Leyva-Ramos, R.; Ocampo-Pérez, R.; Carranza-Alvarez, C. Single and Competitive Adsorption of Cd(II) and Pb(II) Ions from Aqueous Solutions onto Industrial Chili Seeds (Capsicum annuum) Waste. Sustain. Environ. Res. 2017, 27, 61–69. [Google Scholar] [CrossRef]
- Mouni, L.; Merabet, D.; Bouzaza, A.; Belkhiri, L. Adsorption of Pb(II) from Aqueous Solutions Using Activated Carbon Developed from Apricot Stone. Desalination 2011, 276, 148–153. [Google Scholar] [CrossRef]
- Sekar, M.; Sakthi, V.; Rengaraj, S. Kinetics and Equilibrium Adsorption Study of Lead(II) onto Activated Carbon Prepared from Coconut Shell. J. Colloid Interface Sci. 2004, 279, 307–313. [Google Scholar] [CrossRef] [PubMed]
- Rabiee Abyaneh, M.; Nabi Bidhendi, G.; Daryabeigi Zand, A. Pb(ΙΙ), Cd(ΙΙ), and Mn(ΙΙ) Adsorption onto Pruning-Derived Biochar: Physicochemical Characterization, Modeling and Application in Real Landfill Leachate. Sci. Rep. 2024, 14, 3426. [Google Scholar] [CrossRef]
- Thirumavalavan, M.; Lai, Y.-L.; Lin, L.-C.; Lee, J.-F. Cellulose-Based Native and Surface Modified Fruit Peels for the Adsorption of Heavy Metal Ions from Aqueous Solution: Langmuir Adsorption Isotherms. J. Chem. Eng. Data 2010, 55, 1186–1192. [Google Scholar] [CrossRef]
- Langmuir, I. The Adsorption of Gases on Plane Surfaces of Glass, Mica and Platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Freundlich, H.M.F. Over the Adsorption in Solution. J. Phys. Chem. 1906, 57, 1100–1107. [Google Scholar]
- Pelekani, C.; Snoeyink, V.L. Competitive Adsorption in Natural Water: Role of Activated Carbon Pore Size. Water Res. 1999, 33, 1209–1219. [Google Scholar] [CrossRef]
- Mamchenko, A.V.; Yakimova, T.I.; Koganovskii, A.M. The Mechanism of the Filling of the Micropores in Activated Charcoals during the Adsorption of Organic Substances Dissolved in Water. Russ. J. Phys. Chem. 1982, 56, 741. [Google Scholar]
- Sousa, F.W.; Oliveira, A.G.; Ribeiro, J.P.; Rosa, M.F.; Keukeleire, D.; Nascimento, R.F. Green Coconut Shells Applied as Adsorbent for Removal of Toxic Metal Ions Using Fixed-Bed Column Technology. J. Environ. Manag. 2010, 91, 1634–1640. [Google Scholar] [CrossRef]
- Teoh, Y.P.; Khan, M.A.; Choong, T.S. Kinetic and Isotherm Studies for Lead Adsorption from Aqueous Phase on Carbon Coated Monolith. Chem. Eng. J. 2013, 217, 248–255. [Google Scholar] [CrossRef]
- Largitte, L.; Pasquier, R. A Review of the Kinetics Adsorption Models and Their Application to the Adsorption of Lead by an Activated Carbon. Chem. Eng. Res. Des. 2016, 109, 495–504. [Google Scholar] [CrossRef]

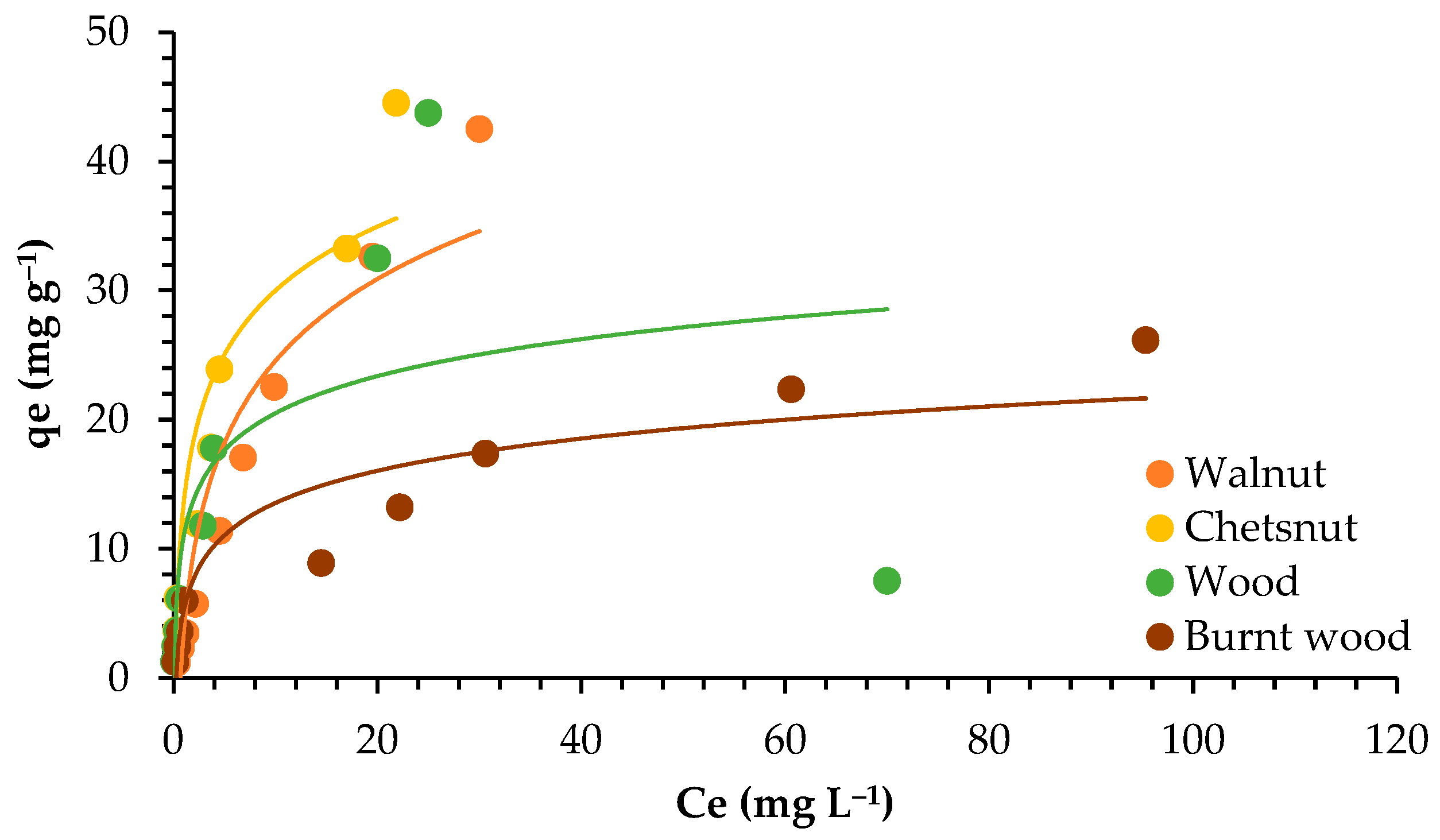
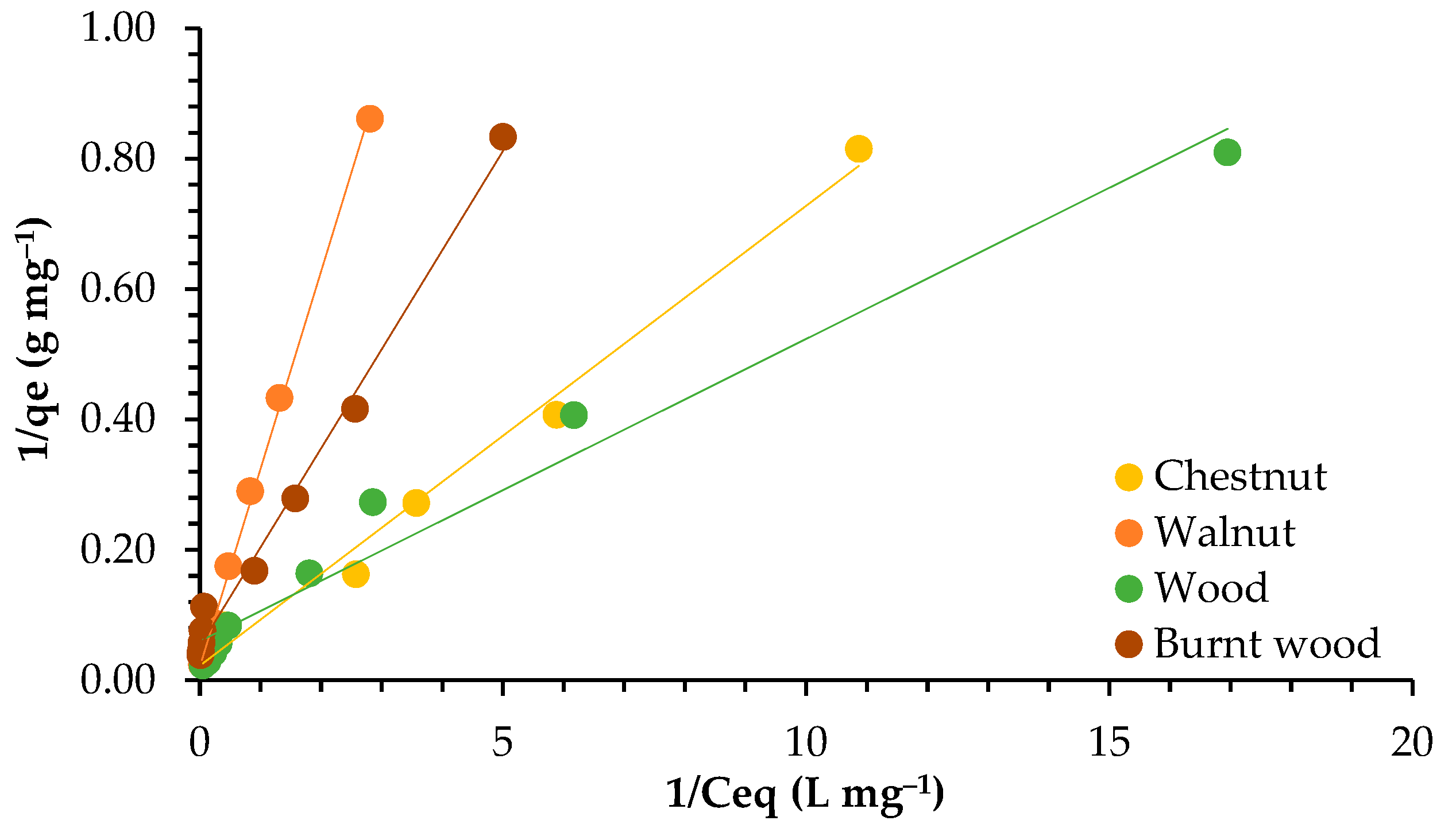
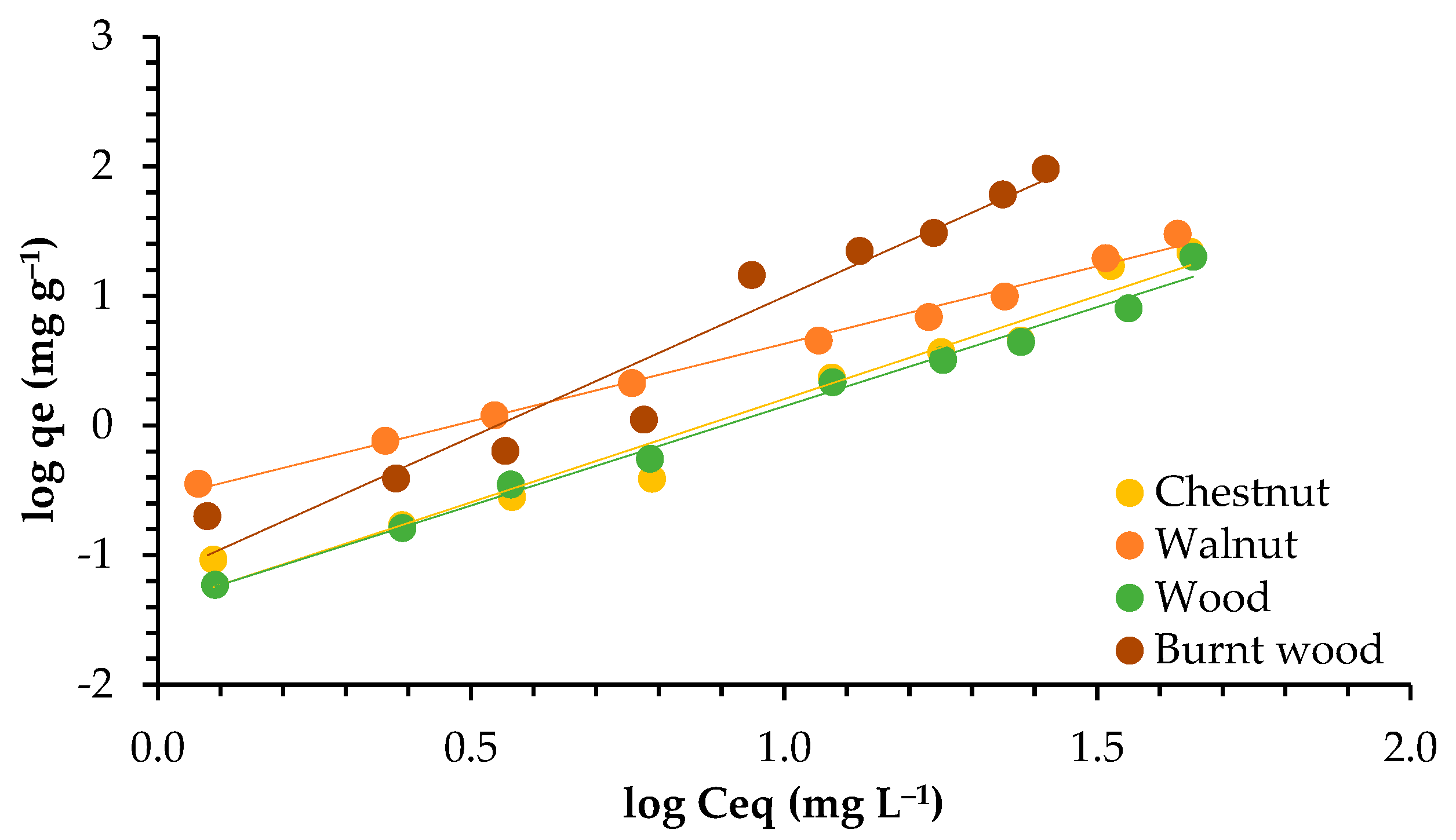

| Models | Parameters | Walnut | Chestnut | Wood | Burnt Wood |
|---|---|---|---|---|---|
| Langmuir | qmax (mg g−1) | 47.393 | 44.444 | 16.639 | 19.084 |
| KL (L mg−1) | 0.070 | 0.319 | 1.295 | 0.345 | |
| R2 | 0.999 | 0.992 | 0.970 | 0.991 | |
| Freundlich | KF (mg1−nLn g−1) | 2.990 | 7.483 | 8.002 | 3.621 |
| n | 1.205 | 1.648 | 1.545 | 2.289 | |
| R2 | 0.993 | 0.967 | 0.991 | 0.946 |
| Pseudo-First-Order | Pseudo-Second-Order | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| k1 (L min−1) | qe calc (mg g−1) | qe exp (mg g−1) | R2 | k2 (g mg−1.min) | h (mg g−1.min) | qe calc (mg g−1) | qe exp (mg g−1) | R2 | |
| Walnut | 2.50 × 10−3 | 0.546 | 4.84 | 0.956 | 2.46 × 10−2 | 0.575 | 4.84 | 4.84 | 1.000 |
| Chestnut | 2.20 × 10−3 | 0.675 | 5.12 | 0.966 | 2.13 × 10−2 | 0.527 | 4.98 | 5.12 | 1.000 |
| Wood | 1.90 × 10−3 | 1.156 | 4.25 | 0.977 | 1.07 × 10−2 | 0.169 | 3.98 | 4.25 | 0.998 |
| Burnt wood | 1.80 × 10−3 | 0.907 | 3.85 | 0.971 | 1.47 × 10−2 | 0.191 | 3.61 | 3.85 | 0.999 |
| Elovich | Intraparticle Diffusion | |||||
|---|---|---|---|---|---|---|
| a | b | R2 | C | Kdif | R2 | |
| Walnut | 9.94 × 1010 | 6.84 | 0.956 | 4.23 | 0.019 | 0.924 |
| Chestnut | 1.05 × 1012 | 7.67 | 0.990 | 4.37 | 0.021 | 0.942 |
| Wood | 1.00 × 104 | 4.44 | 0.905 | 2.99 | 0.035 | 0.978 |
| Burnt wood | 1.09 × 105 | 5.59 | 0.908 | 2.84 | 0.027 | 0.970 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macena, M.; Pereira, H.; Grosche, L.; Esteves, B.; Santos-Vieira, I.; Cruz-Lopes, L. Lignocellulosic Byproducts as Bio-Adsorbents for Lead Removal. Materials 2025, 18, 2320. https://doi.org/10.3390/ma18102320
Macena M, Pereira H, Grosche L, Esteves B, Santos-Vieira I, Cruz-Lopes L. Lignocellulosic Byproducts as Bio-Adsorbents for Lead Removal. Materials. 2025; 18(10):2320. https://doi.org/10.3390/ma18102320
Chicago/Turabian StyleMacena, Morgana, Helena Pereira, Lucas Grosche, Bruno Esteves, Isabel Santos-Vieira, and Luísa Cruz-Lopes. 2025. "Lignocellulosic Byproducts as Bio-Adsorbents for Lead Removal" Materials 18, no. 10: 2320. https://doi.org/10.3390/ma18102320
APA StyleMacena, M., Pereira, H., Grosche, L., Esteves, B., Santos-Vieira, I., & Cruz-Lopes, L. (2025). Lignocellulosic Byproducts as Bio-Adsorbents for Lead Removal. Materials, 18(10), 2320. https://doi.org/10.3390/ma18102320











