Thermo-Oxidative Aging Effects on Hyperelastic Behavior of EPDM Rubber: A Constitutive Modeling Approach
Abstract
1. Introduction
2. Material and Methods
2.1. Material and Specimen
2.2. Test Methods
3. Results
4. Discussion
4.1. Hyperelastic Constitutive Modeling
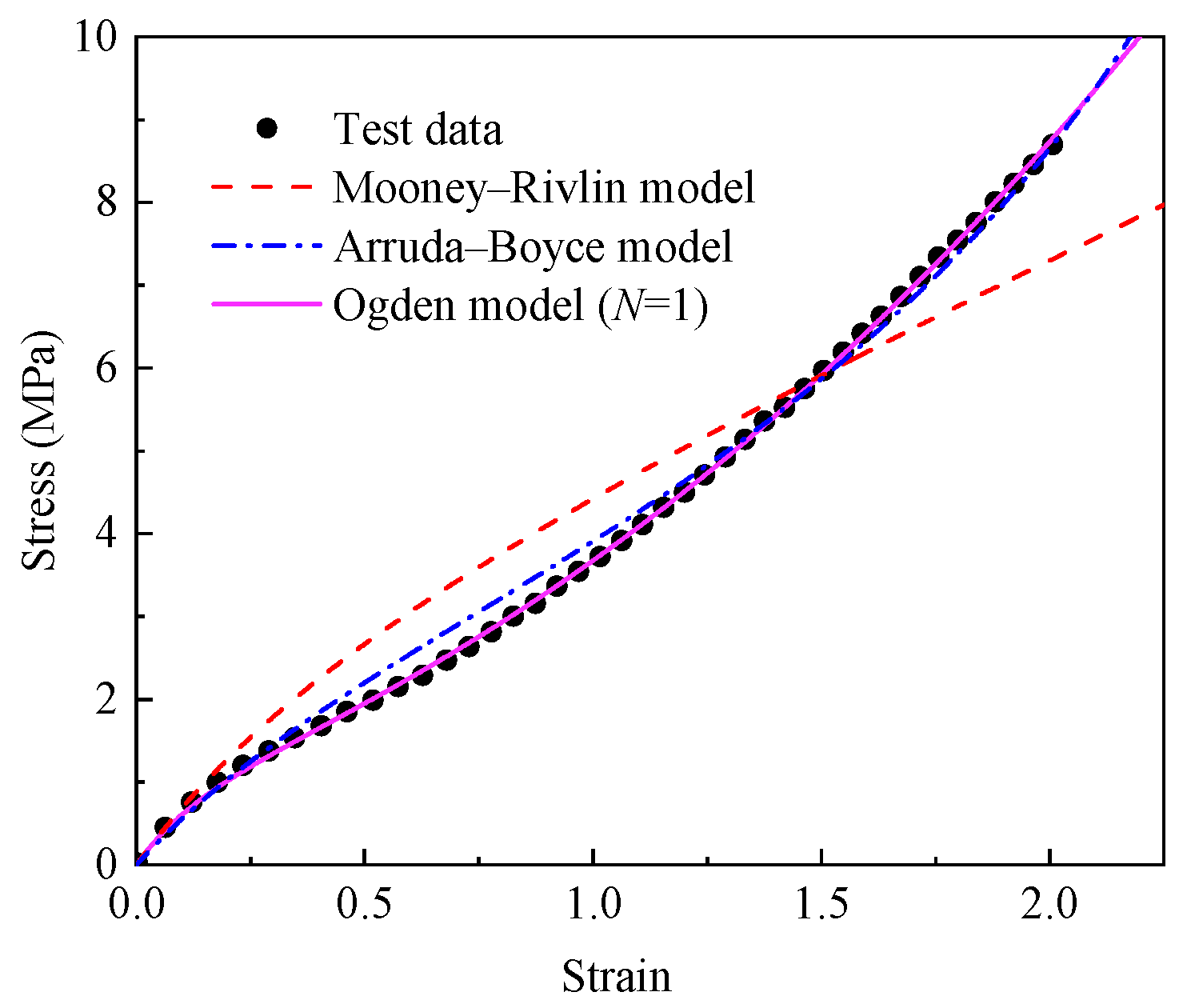
4.1.1. Mooney–Rivlin Model
4.1.2. Arruda–Boyce Model
4.1.3. Ogden Model
4.1.4. Model Comparison
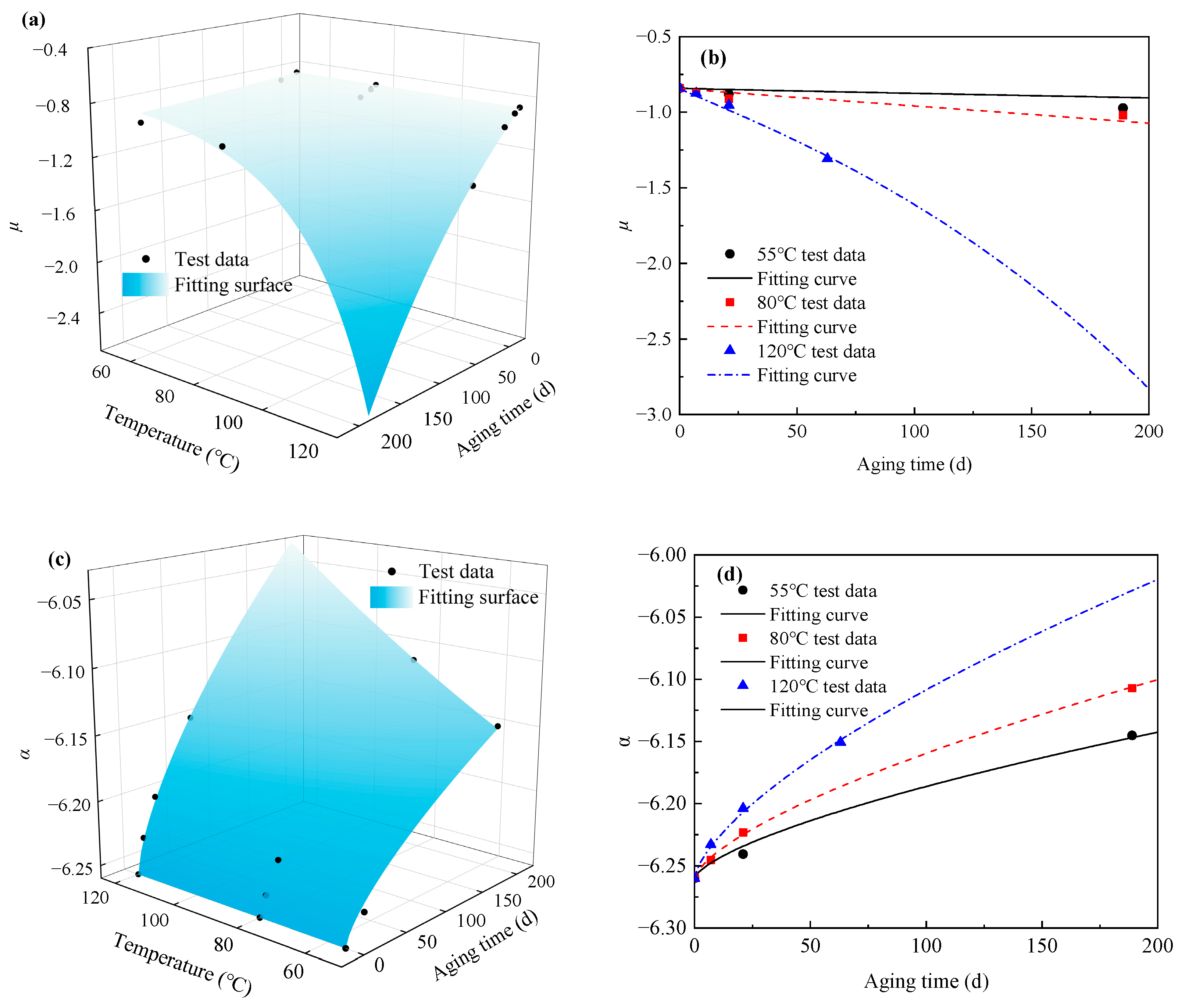
4.2. Effect of the Temperature and Aging Time on the Model Parameters
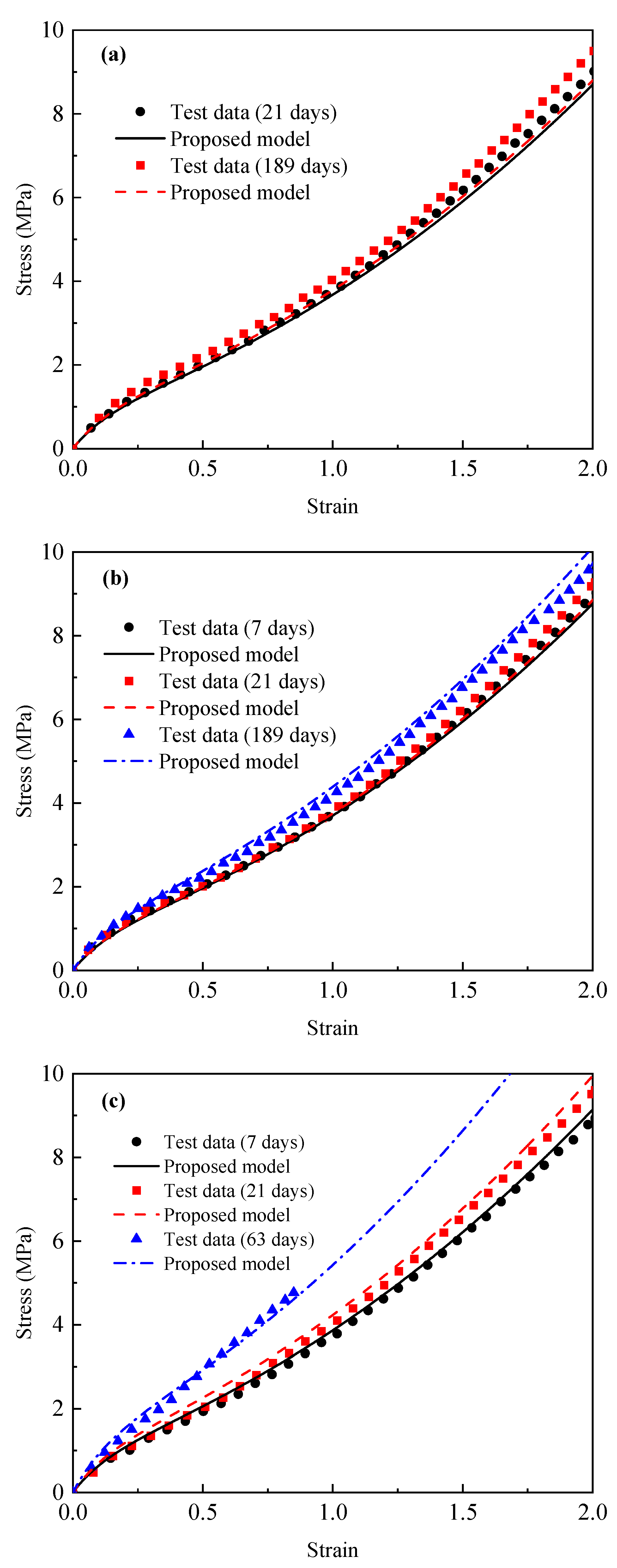
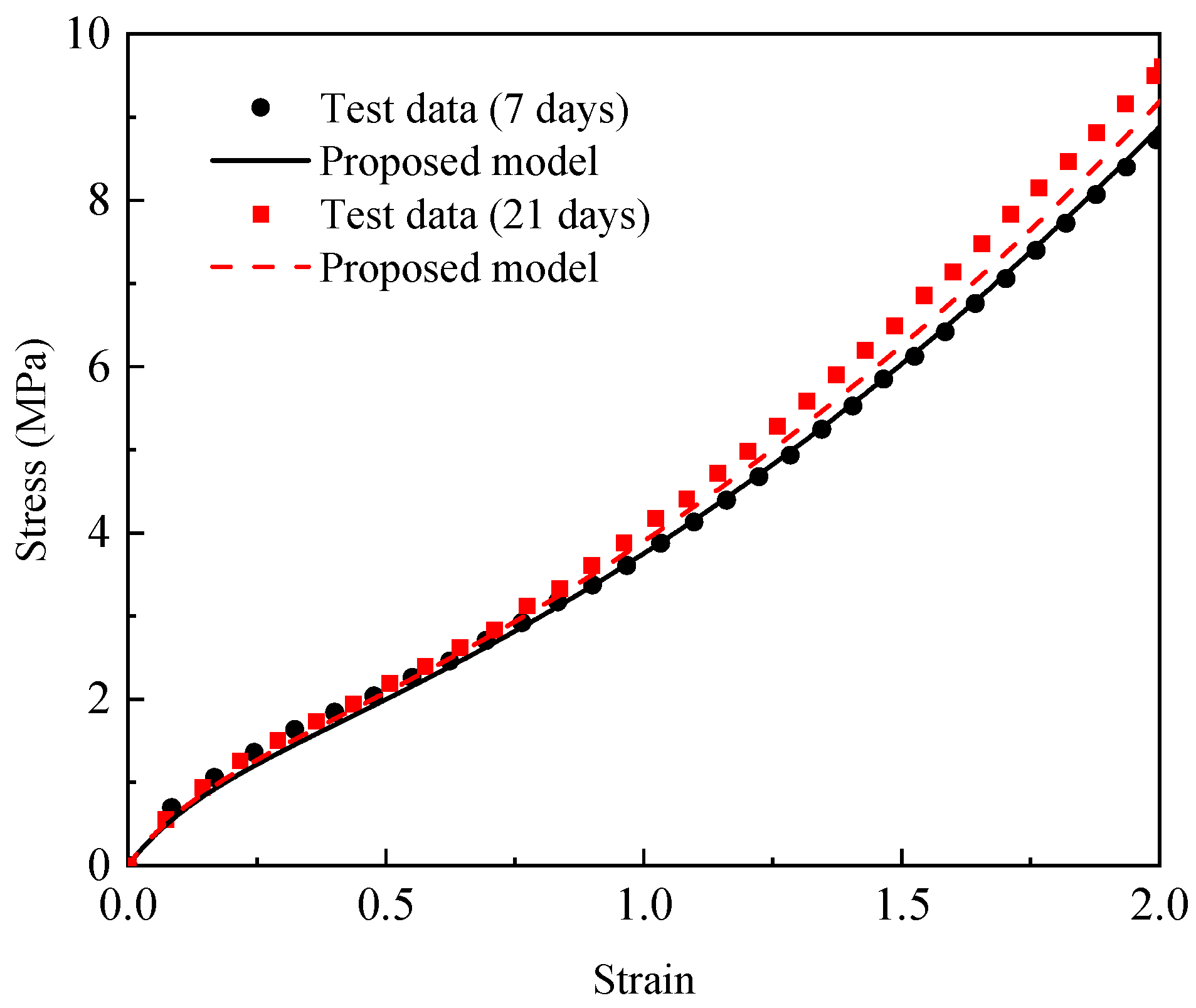
4.3. Model Verification
5. Conclusions
- The tensile stress–strain curve of EPDM rubber exhibits a typical S-shape large deformation characteristic. EPDM rubber gradually hardens when the aging time and aging temperature increases.
- The fitting performance of the Mooney–Rivlin, Arruda–Boyce, and Ogden models was evaluated using the R2, MAPE, and RMSE. The results show that the Ogden model more accurately describes the hyperelastic behavior of unaged EPDM rubber.
- An improved Ogden model was proposed. This model extends the aging time correlation of the parameters through the Dakin dynamic relationship and the aging temperature correlation of parameters through the Arrhenius relationship.
- In the strain range of 200%, the proposed model was able to capture the hyperelastic behavior of EPDM rubber when considering the influence of thermo-oxidative aging well.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, Z.; Chen, J.; Zhang, K. Lifetime Prediction of EPDM Sealing Materials with Thermal Aging Under Constant Compression. J. Phys. Conf. Ser. 2024, 2842, 012008. [Google Scholar] [CrossRef]
- Huang, X.; Gu, J.; Li, M.; Yu, X.; Liu, Y.; Xu, G. A Leakage Prediction Model for Sealing Performance Assessment of EPDM O-Rings under Irradiation Conditions. Polymers 2023, 15, 3073. [Google Scholar] [CrossRef] [PubMed]
- Hough, P.; van der Aar, N.; Qiu, Z. Compounding and Mixing Methodology for Good Performance of EPDM in Tire Sidewalls. Tire Sci. Technol. 2020, 48, 2–21. [Google Scholar] [CrossRef]
- Cho, J.K.; Sun, H.; Seo, H.W.; Chung, J.; Seol, M.; Kim, S.; Kim, R.; Park, I.; Suhr, J.; Park, J.C.; et al. Heat Dissipative Mechanical Damping Properties of EPDM Rubber Composites Including Hybrid Fillers of Aluminium Nitride and Boron Nitride. Soft Matter. 2020, 16, 6812–6818. [Google Scholar] [CrossRef]
- Bouguedad, D.; Mekhaldi, A.; Jbara, O.; Rondot, S.; Hadjadj, A.; Douglade, J.; Dony, P. Physico-Chemical Study of Thermally Aged EPDM Used in Power Cables Insulation. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3207–3215. [Google Scholar] [CrossRef]
- Assink, R.A.; Gillen, K.T.; Sanderson, B. Monitoring the Degradation of a Thermally Aged EPDM Terpolymer by 1 H NMR Relaxation Measurements of Solvent Swelled Samples. Polymer 2002, 43, 1349–1355. [Google Scholar] [CrossRef]
- Hu, Q.; Chen, Q.; Song, P.; Gong, X.; Chen, J.; Zhao, Y. Performance of Thermal-Oxidative Aging on the Structure and Properties of Ethylene Propylene Diene Monomer (EPDM) Vulcanizates. Polymers 2023, 15, 2329. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of Elastic Properties of Carbon-Black-Filled Rubber Vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Ogden, R.W. Large Deformation Isotropic Elasticity: On the Correlation of Theory and Experiment for Compressible Rubberlike Solids. Proc. R. Soc. A 1972, 328, 567–583. [Google Scholar] [CrossRef]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A Three-Dimensional Constitutive Model for the Large Stretch Behavior of Rubber Elastic Materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Elasticity of a Network of Long-Chain Molecules. I. Trans. Faraday Soc. 1943, 39, 36. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.; Zhang, Y.; Chen, J.; Zhang, L.; Li, F. A Comparative Study of 85 Hyperelastic Constitutive Models for Both Unfilled Rubber and Highly Filled Rubber Nanocomposite Material. Nano Mater. Sci. 2022, 4, 64–82. [Google Scholar] [CrossRef]
- Dal, H.; Açıkgöz, K.; Badienia, Y. On the Performance of Isotropic Hyperelastic Constitutive Models for Rubber-Like Materials: A State of the Art Review. Appl. Mech. Rev. 2021, 73, 020802. [Google Scholar] [CrossRef]
- Beda, T. An Approach for Hyperelastic Model-Building and Parameters Estimation a Review of Constitutive Models. Eur. Polym. J. 2014, 50, 97–108. [Google Scholar] [CrossRef]
- Shaw, J.A.; Jones, A.S.; Wineman, A.S. Chemorheological Response of Elastomers at Elevated Temperatures: Experiments and Simulations. J. Mech. Phys. Solids 2005, 53, 2758–2793. [Google Scholar] [CrossRef]
- Wineman, A.; Shaw, J. Coupled Thermal- and Deformation-Induced Degradation in Planar Rubber Membranes Under Radial Loading. Math. Mech. Solids 2019, 24, 3103–3124. [Google Scholar] [CrossRef]
- Mohammadi, H.; Dargazany, R. A Micro-Mechanical Approach to Model Thermal Induced Aging in Elastomers. Int. J. Plast. 2019, 118, 1–16. [Google Scholar] [CrossRef]
- Mohammadi, H.; Morovati, V.; Poshtan, E.; Dargazany, R. Understanding Decay Functions and their Contribution in Modeling of Thermal-Induced Aging of Cross-Linked Polymers. Polym. Degrad. Stab. 2020, 175, 109108. [Google Scholar] [CrossRef]
- Chaabane, M.; Ding, N.; Zaïri, F. An Approach to Assess the Thermal Aging Effects On the Coupling Between Inelasticity and Network Alteration in Filled Rubbers. Int. J. Non-Linear Mech. 2021, 136, 103783. [Google Scholar] [CrossRef]
- Andrews, R.D.; Tobolsky, A.V.; Hanson, E.E. The Theory of Permanent Set at Elevated Temperatures in Natural and Synthetic Rubber Vulcanizates. J. Appl. Phys. 1946, 17, 352–361. [Google Scholar] [CrossRef]
- Tobolsky, A.V.; Prettyman, I.B.; Dillon, J.H. Stress Relaxation of Natural and Synthetic Rubber Stocks. J. Appl. Phys. 1944, 15, 380–395. [Google Scholar] [CrossRef]
- Naumann, C. Chemisch-Mechanisch Gekoppelte Modellierung und Simulation Oxidativer Alterungsvorgänge in Gummibauteilen. Ph.D. Dissertation, Technische Universität Chemnitz, Chemnitz, Germany, 2016. [Google Scholar]
- Heczko, J.; Kottner, R.; Kossa, A. Rubber Ageing at Elevated Temperature—Model Calibration. Eur. J. Mech.-A/Solids 2021, 89, 104320. [Google Scholar] [CrossRef]
- Jalalpour, A.; Arghavani, J.; Naghdabadi, R. Thermo-Oxidative Aging of Natural Rubber: Experimental Study and a Thermodynamically Consistent Mechanical-Chemical-Diffusion Model. Contin. Mech. Thermodyn. 2024, 36, 1579–1595. [Google Scholar] [CrossRef]
- Johlitz, M.; Diercks, N.; Lion, A. Thermo-Oxidative Ageing of Elastomers: A Modelling Approach Based On a Finite Strain Theory. Int. J. Plast. 2014, 63, 138–151. [Google Scholar] [CrossRef]
- Lion, A.; Johlitz, M. On the Representation of Chemical Ageing of Rubber in Continuum Mechanics. Int. J. Solids Struct. 2012, 49, 1227–1240. [Google Scholar] [CrossRef]
- Musil, B.; Johlitz, M.; Lion, A. On the Ageing Behaviour of NBR: Chemomechanical Experiments, Modelling and Simulation of Tension Set. Contin. Mech. Thermodyn. 2020, 32, 369–385. [Google Scholar] [CrossRef]
- Musil, B.; Böhning, M.; Johlitz, M.; Lion, A. On the Inhomogenous Chemo-Mechanical Ageing Behaviour of Nitrile Rubber: Experimental Investigations, Modelling and Parameter Identification. Contin. Mech. Thermodyn. 2020, 32, 127–146. [Google Scholar] [CrossRef]
- Dippel, B.; Johlitz, M.; Lion, A. Ageing of Polymer Bonds: A Coupled Chemomechanical Modelling Approach. Contin. Mech. Thermodyn. 2014, 26, 247–257. [Google Scholar] [CrossRef]
- Bouaziz, R.; Ahose, K.D.; Lejeunes, S.; Eyheramendy, D.; Sosson, F. Characterization and Modeling of Filled Rubber Submitted to Thermal Aging. Int. J. Solids Struct. 2019, 169, 122–140. [Google Scholar] [CrossRef]
- Lejeunes, S.; Eyheramendy, D.; Boukamel, A.; Delattre, A.; Méo, S.; Ahose, K.D. A Constitutive Multiphysics Modeling for Nearly Incompressible Dissipative Materials: Application to Thermo–Chemo-Mechanical Aging of Rubbers. Mech. Mech. Time-Depend. Mater. 2018, 22, 51–66. [Google Scholar] [CrossRef]
- N’guyen, T.A.; Lejeunes, S.; Eyheramendy, D.; Boukamel, A. A Thermodynamical Framework for the Thermo-Chemo-Mechanical Couplings in Soft Materials at Finite Strain. Mech. Mater. 2016, 95, 158–171. [Google Scholar] [CrossRef]
- Li, Q.; Xu, Z.; Dong, Y.; He, Z.; He, J.; Yan, X. Hyperelastic Hybrid Molecular Chain Model of Thermal-Oxidative Aging Viscoelastic Damping Materials Based on Physical–Chemical Process. J. Eng. Mech. 2023, 149, 04022099. [Google Scholar] [CrossRef]
- Li, Q.; Xu, Z.; Tong, Q.; Dong, Y.; Xu, Y.; Lu, Y. Mechanical Properties of Viscoelastic Materials Subjected to Thermal-Oxidative Aging: An Experimental and Theoretical Study. J. Appl. Polym. Sci. 2023, 140, e54667. [Google Scholar] [CrossRef]
- Shakiba, M.; Najmeddine, A. Physics-Based Constitutive Equation for Thermochemically Aged Elastomers Based On Crosslink Density Evolution. J. Mech. Mater. Struct. 2022, 17, 229–246. [Google Scholar] [CrossRef]
- Zhi, J.; Wang, Q.; Zhang, M.; Zhou, Z.; Liu, A.; Jia, Y. Coupled Analysis On Hyper-Viscoelastic Mechanical Behavior and Macromolecular Network Alteration of Rubber During Thermo-Oxidative Aging Process. Polymer 2019, 171, 15–24. [Google Scholar] [CrossRef]
- Korba, A.G.; Kumar, A.; Barkey, M. A Hyper-Elastic Thermal Aging Constitutive Model for Rubber-Like Materials. J. Elastomers Plast. 2020, 52, 677–700. [Google Scholar] [CrossRef]
- Hu, X.; Yang, X.; Jiang, X.; Song, K. Constitutive Model for Thermal-Oxygen-Aged EPDM Rubber Based on the Arrhenius Law. Polymers 2024, 16, 2608. [Google Scholar] [CrossRef]
- Lou, W.; Xie, C.; Guan, X. Thermal-Aging Constitutive Model for a Silicone Rubber Foam Under Compression. Polym. Degrad. Stab. 2022, 198, 109873. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Liu, R.; Chen, M.; Zhang, C.; Li, X.; Li, W.; Wang, H. Compressive Stress-Hydrothermal Aging Behavior and Constitutive Model of Shield Tunnel EPDM Rubber Material. Constr. Build. Mater. 2022, 320, 126298. [Google Scholar] [CrossRef]
- Ha-Anh, T.; Vu-Khanh, T. Prediction of Mechanical Properties of Polychloroprene During Thermo-Oxidative Aging. Polym. Test. 2005, 24, 775–780. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, F.; Guo, J.; Xue, J.; Yi, Z. Sealing Properties of EPDM Intercalation Composite Rings in High Temperature. Lubr. Eng. 2014, 39, 129–132. (In Chinese) [Google Scholar]
- ISO 37:2024; Rubber, Vulcanized or Thermoplastic-Determination of Tensile Stress-Strain Properties. International Organization for Standardization: Geneva, Switzerland, 2024.
- Li, Z.; Chen, Z.; Sun, W.; Liu, Y.; Wang, X.; Lin, J.; Wang, J.; He, S. Properties of EPDM Nanocomposites Reinforced with Modified Montmorillonite. Polymers 2024, 16, 2381. [Google Scholar] [CrossRef]
- Alipour, A.; Naderi, G.; Ghoreishy, M.H. Effect of Nanoclay Content and Matrix Composition On Properties and Stress–Strain Behavior of NR/EPDM Nanocomposites. J. Appl. Polym. Sci. 2013, 127, 1275–1284. [Google Scholar] [CrossRef]
- Wang, S.; Xu, J.; Li, H.; Liu, J.; Zhou, C. The Effect of Thermal Aging On the Mechanical Properties of Ethylene Propylene Diene Monomer Charge Coating. Mech. Time-Depend. Mater. 2022, 28, 321–336. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Jiang, D. A Rate-Dependent Aging Constitutive Model of EPDM Rubber. Colloid Polym. Sci. 2024, 302, 1037–1052. [Google Scholar] [CrossRef]
- Cui, Z.; Liu, W.; Tan, L.; Sun, G.; Hu, X. Evidence for non-Arrhenius Behavior of EPDM Rubber by Combining Arrhenius and Time–Temperature Superposition (TTS) Extrapolations. RSC Adv. 2024, 14, 5216–5221. [Google Scholar] [CrossRef] [PubMed]
- Valanis, K.C.; Landel, R.F. The Strain-Energy Function of a Hyperelastic Material in Terms of the Extension Ratios. J. Appl. Phys. 1967, 38, 2997–3002. [Google Scholar] [CrossRef]
- Destrade, M.; Dorfmann, L.; Saccomandi, G. The Ogden Model of Rubber Mechanics: 50 Years of Impact On Nonlinear Elasticity. Phil. Trans. R. Soc. A 2022, 380, 20210332. [Google Scholar] [CrossRef]
- Gallareta, J.G.; González-Menorca, C.; Muñoz, P.; Vasic, M.V. Advancements in Soft Sensor Technologies for Quality Control in Process Manufacturing: A Review. IEEE Sens. J. 2025, in press. [CrossRef]
- Dakin, T.W. Electrical Insulation Deterioration Treated as a Chemical Rate Phenomenon. Trans. Am. Inst. Electr. Eng. 1948, 67, 113–122. [Google Scholar] [CrossRef]


| Ingredients | Value [phr] |
|---|---|
| EPDM | 100 |
| Carbon black | 30 |
| Organo-modified montmorillonite | 25 |
| Compatibilizers | 10 |
| Zinc oxide | 5 |
| Antioxidant | 3 |
| Vulcanizator | 3 |
| Aging Temperature (°C) | Aging Time (Days) | |||
|---|---|---|---|---|
| 55 °C | 0 | 21 | 189 | / |
| 80 °C | 0 | 7 | 21 | 189 |
| 120 °C | 0 | 7 | 21 | 63 |
| Model | R2 | RMSE (MPa) | MAPE (%) |
|---|---|---|---|
| Mooney–Rivlin | 0.9229 | 0.6668 | 17.2422 |
| Arruda–Boyce | 0.9971 | 0.1293 | 4.7118 |
| Ogden (N = 1) | 0.9998 | 0.0331 | 1.5281 |
| Aging Temperature (°C) | Aging Time (d) | μ | α |
|---|---|---|---|
| 55 | 21 | −0.88 | −6.24 |
| 189 | −0.972 | −6.145 | |
| 80 | 7 | −0.87 | −6.243 |
| 21 | −0.9122 | −6.223 | |
| 189 | −1.021 | −6.107 | |
| 120 | 7 | −0.875 | −6.233 |
| 21 | −0.9545 | −6.209 | |
| 63 | −1.308 | −6.151 |
| Parameter | R2 | RMSE | MAPE (%) |
|---|---|---|---|
| μ | 0.9976 | 0.0025 | 0.0286 |
| α | 0.9397 | 0.032 | 2.5557 |
| Aging Temperature (°C) | Aging Time (d) | R2 | RMSE (MPa) | MAPE (%) |
|---|---|---|---|---|
| 55 °C | 21 | 0.9941 | 0.1908 | 3.7157 |
| 189 | 0.9769 | 0.3869 | 7.9223 | |
| 80 °C | 7 | 0.9977 | 0.1176 | 3.3618 |
| 21 | 0.9941 | 0.1969 | 4.2133 | |
| 189 | 0.9937 | 0.2110 | 3.7725 | |
| 120 °C | 7 | 0.9974 | 0.1278 | 3.9492 |
| 21 | 0.9936 | 0.2143 | 6.4662 | |
| 63 | 0.9895 | 0.1347 | 7.2237 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Z.; Huang, X.; Zhang, K.; Yan, S.; Chen, J.; He, R.; Li, J.; Zhong, W. Thermo-Oxidative Aging Effects on Hyperelastic Behavior of EPDM Rubber: A Constitutive Modeling Approach. Materials 2025, 18, 2236. https://doi.org/10.3390/ma18102236
Xie Z, Huang X, Zhang K, Yan S, Chen J, He R, Li J, Zhong W. Thermo-Oxidative Aging Effects on Hyperelastic Behavior of EPDM Rubber: A Constitutive Modeling Approach. Materials. 2025; 18(10):2236. https://doi.org/10.3390/ma18102236
Chicago/Turabian StyleXie, Zhaonan, Xicheng Huang, Kai Zhang, Shunping Yan, Junhong Chen, Ren He, Jiaxing Li, and Weizhou Zhong. 2025. "Thermo-Oxidative Aging Effects on Hyperelastic Behavior of EPDM Rubber: A Constitutive Modeling Approach" Materials 18, no. 10: 2236. https://doi.org/10.3390/ma18102236
APA StyleXie, Z., Huang, X., Zhang, K., Yan, S., Chen, J., He, R., Li, J., & Zhong, W. (2025). Thermo-Oxidative Aging Effects on Hyperelastic Behavior of EPDM Rubber: A Constitutive Modeling Approach. Materials, 18(10), 2236. https://doi.org/10.3390/ma18102236







