Numerical Investigation on the Performance of Compressible Fluid Systems in Mitigating Close-Field Blast Effects on a Fiber Circle
Abstract
1. Introduction
2. Numerical Methodologies
2.1. Introduction of Numerical Models
2.2. Material Models
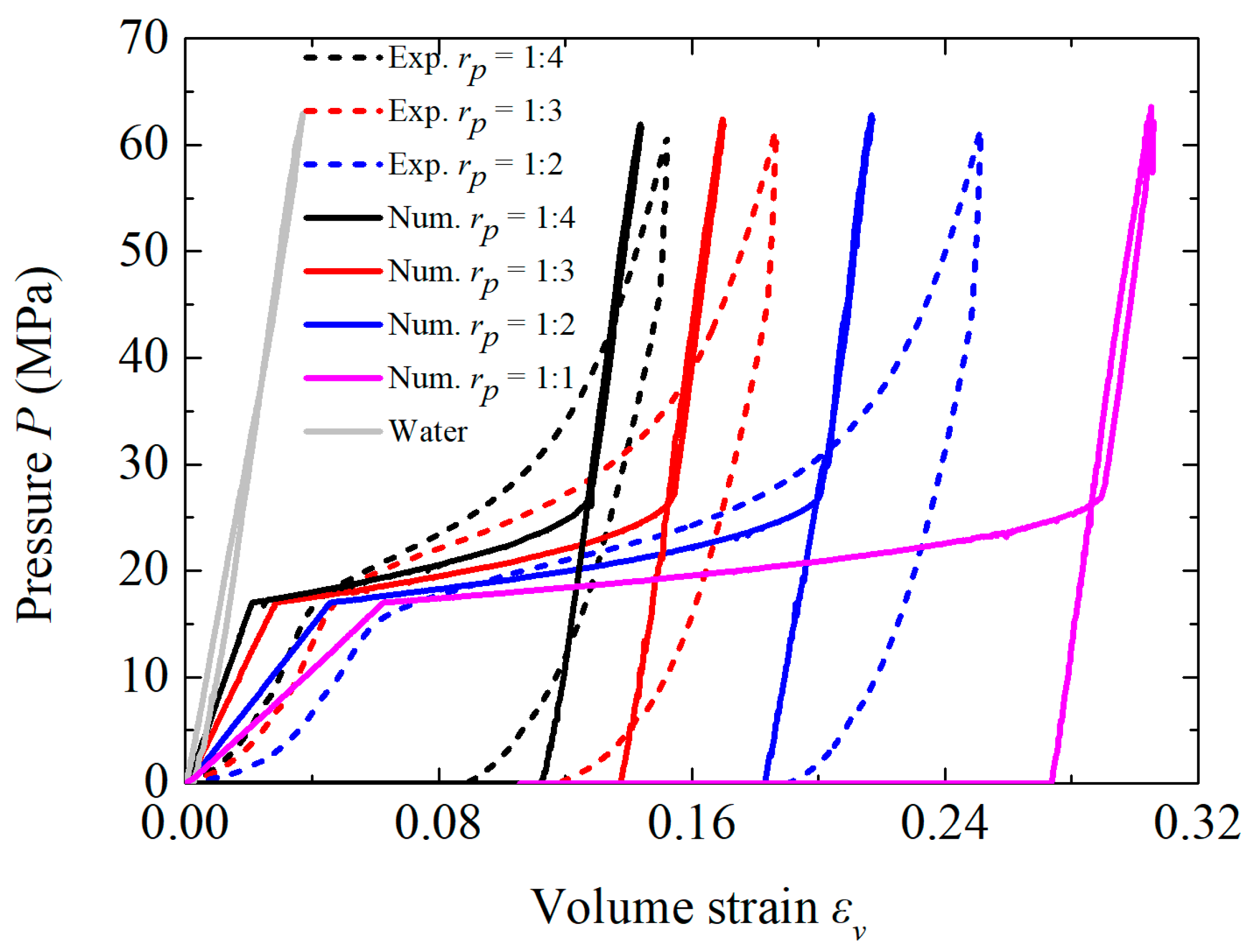
2.2.1. Nanoporous Material Liquid System
2.2.2. Fiber-Reinforced Cross-Ply Composite
2.2.3. Air and TNT Explosive
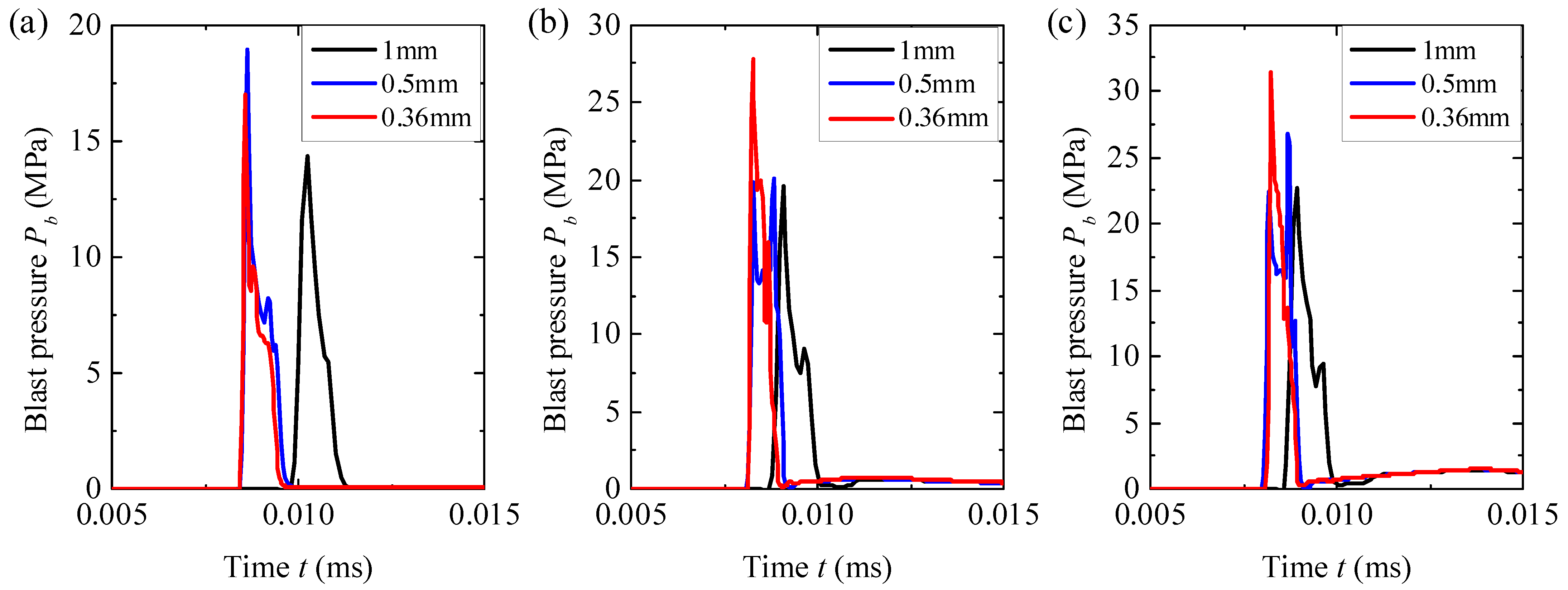
2.3. Blast Loading and Its Mesh Dependence
3. Numerical Results and Analyses
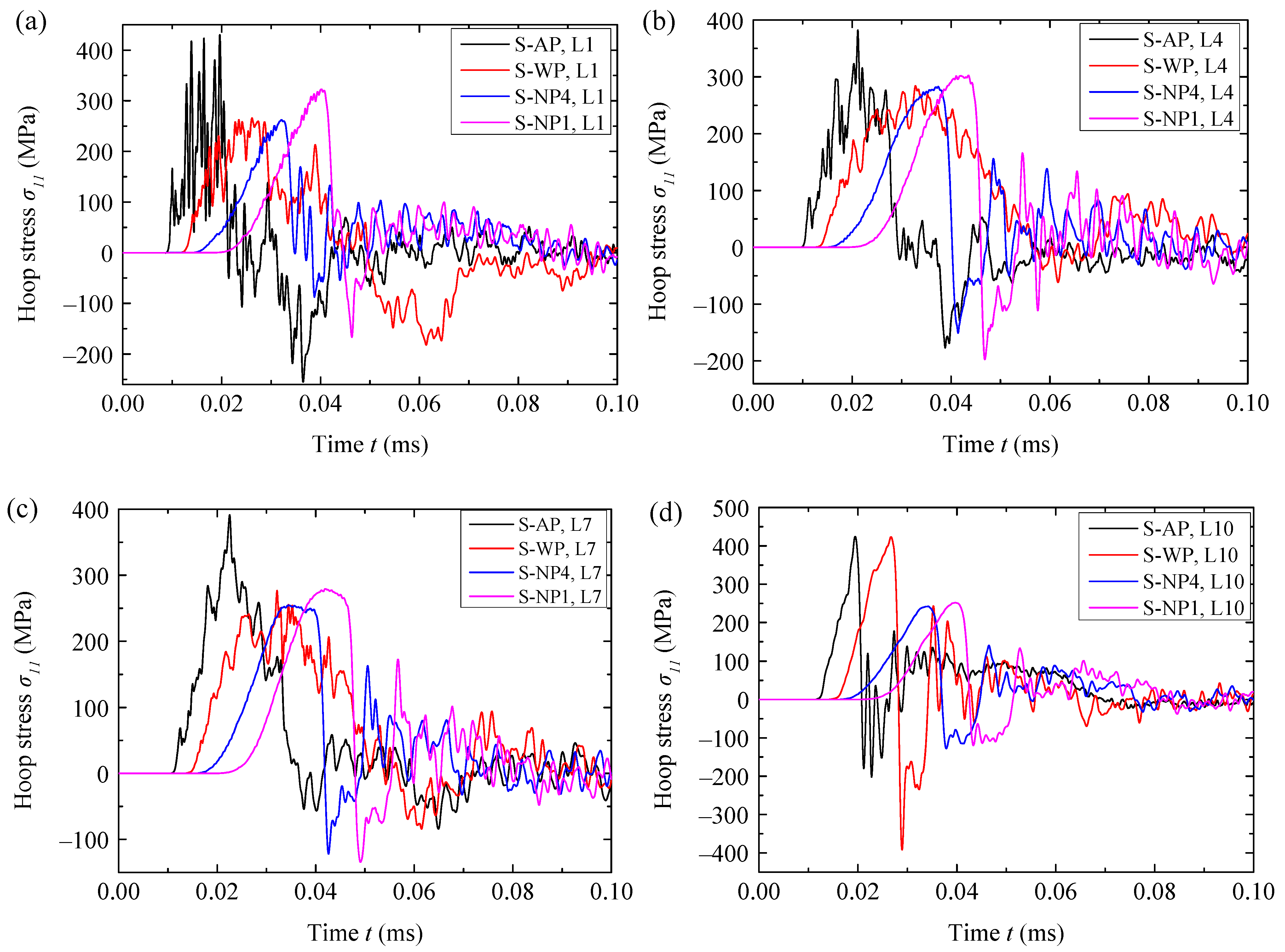
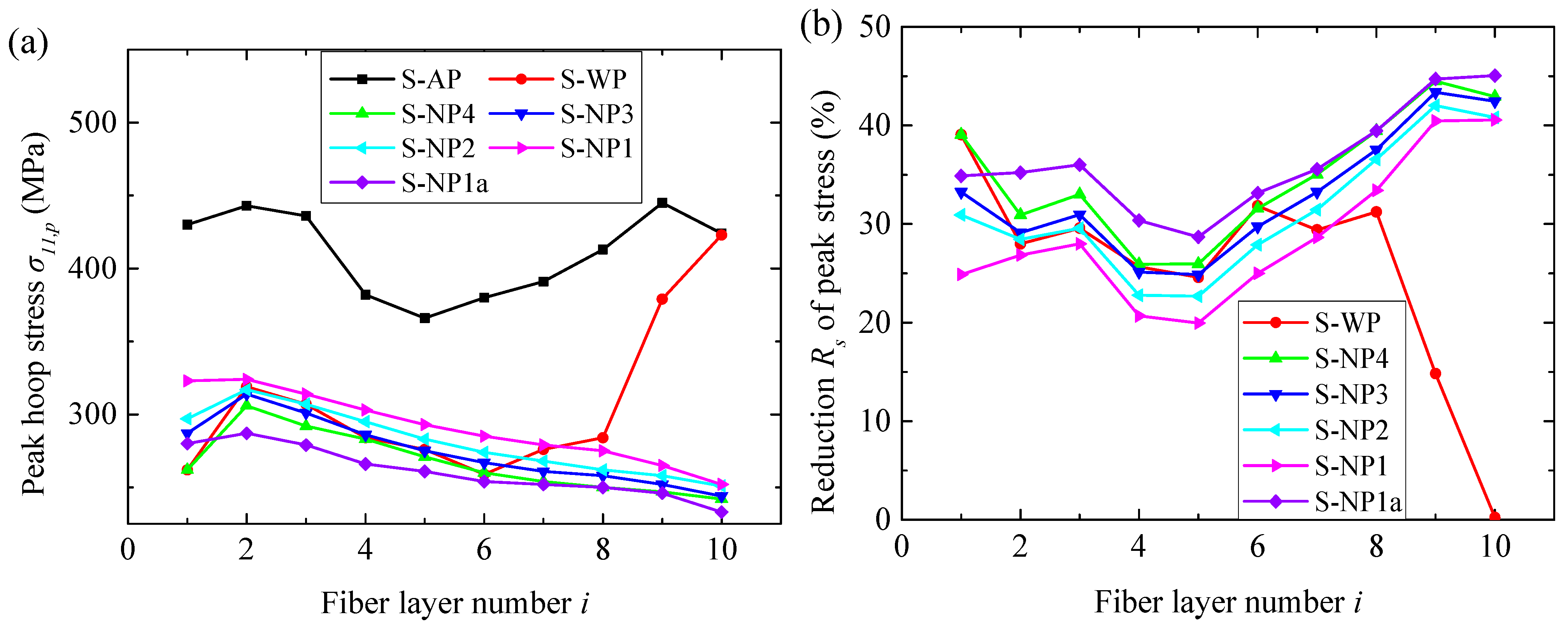
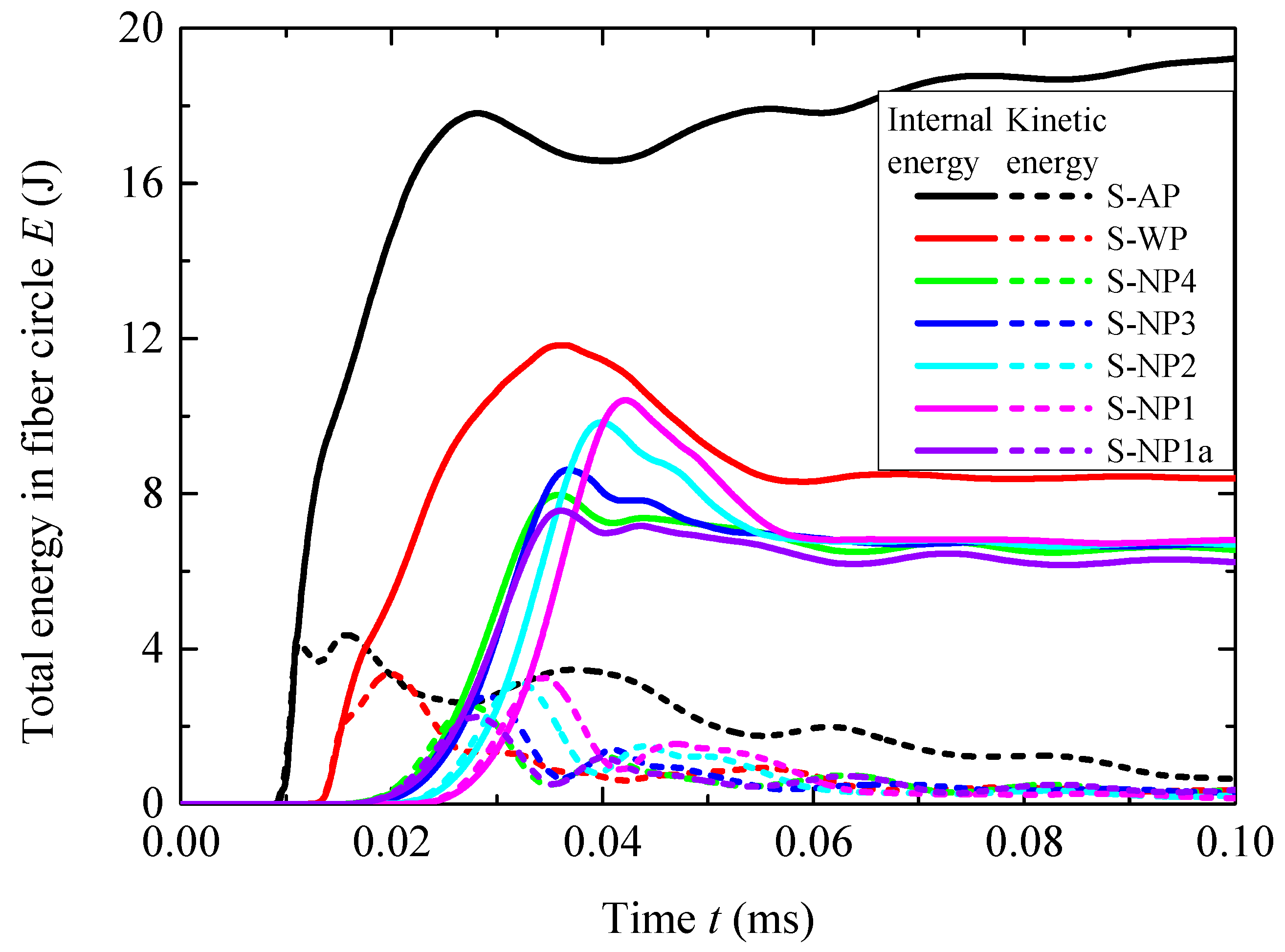
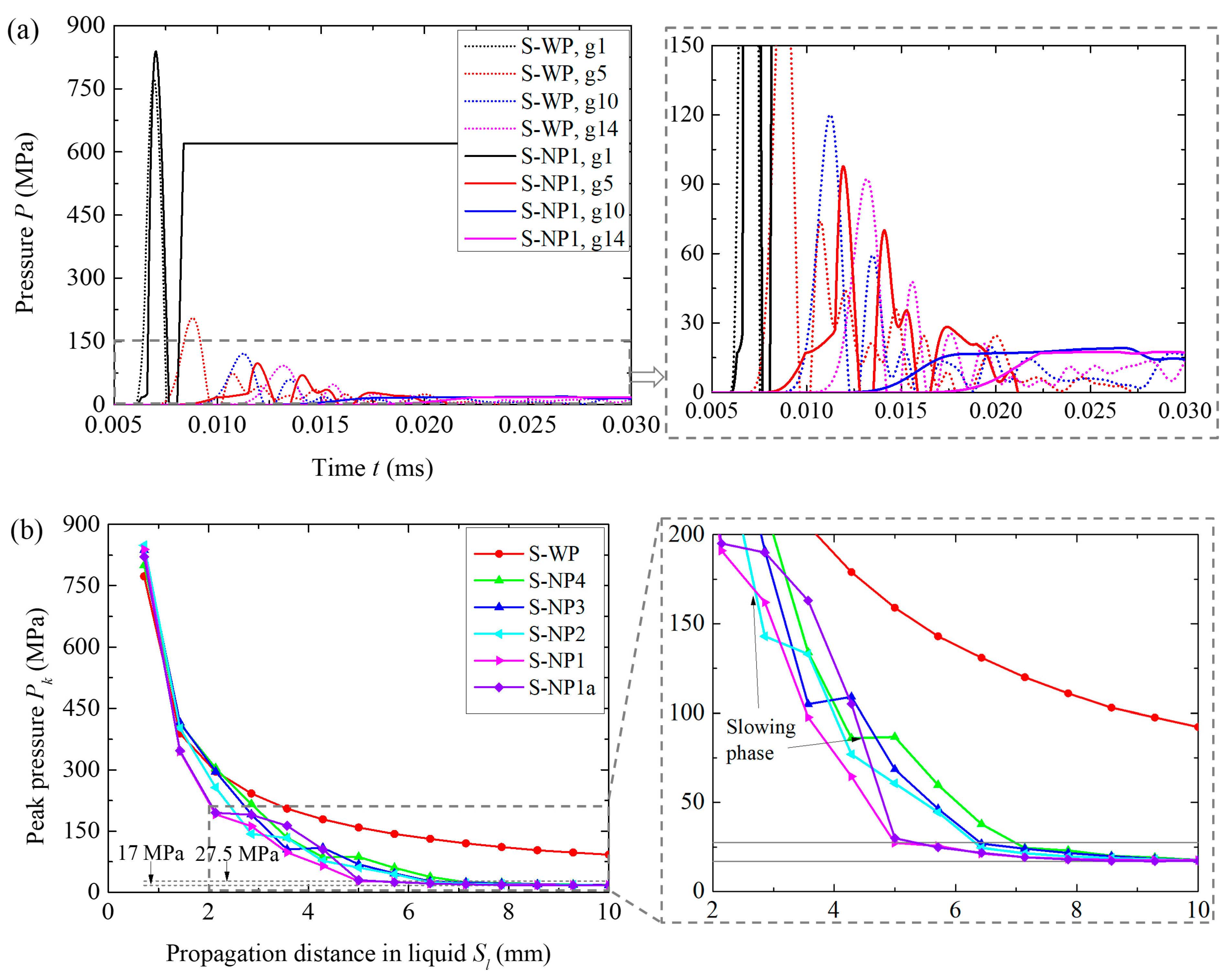
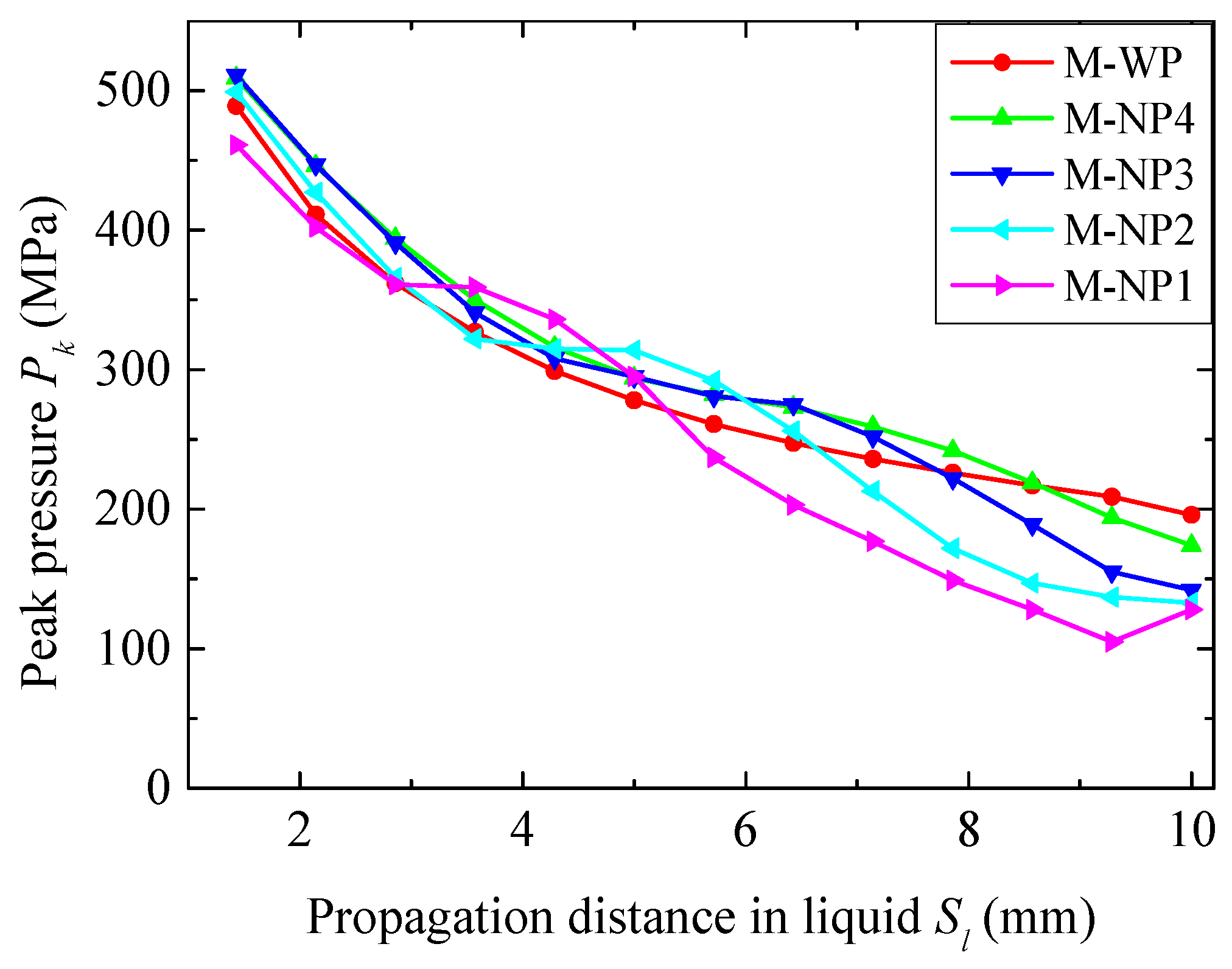
3.1. Using the TNT Charge of 3.80 g
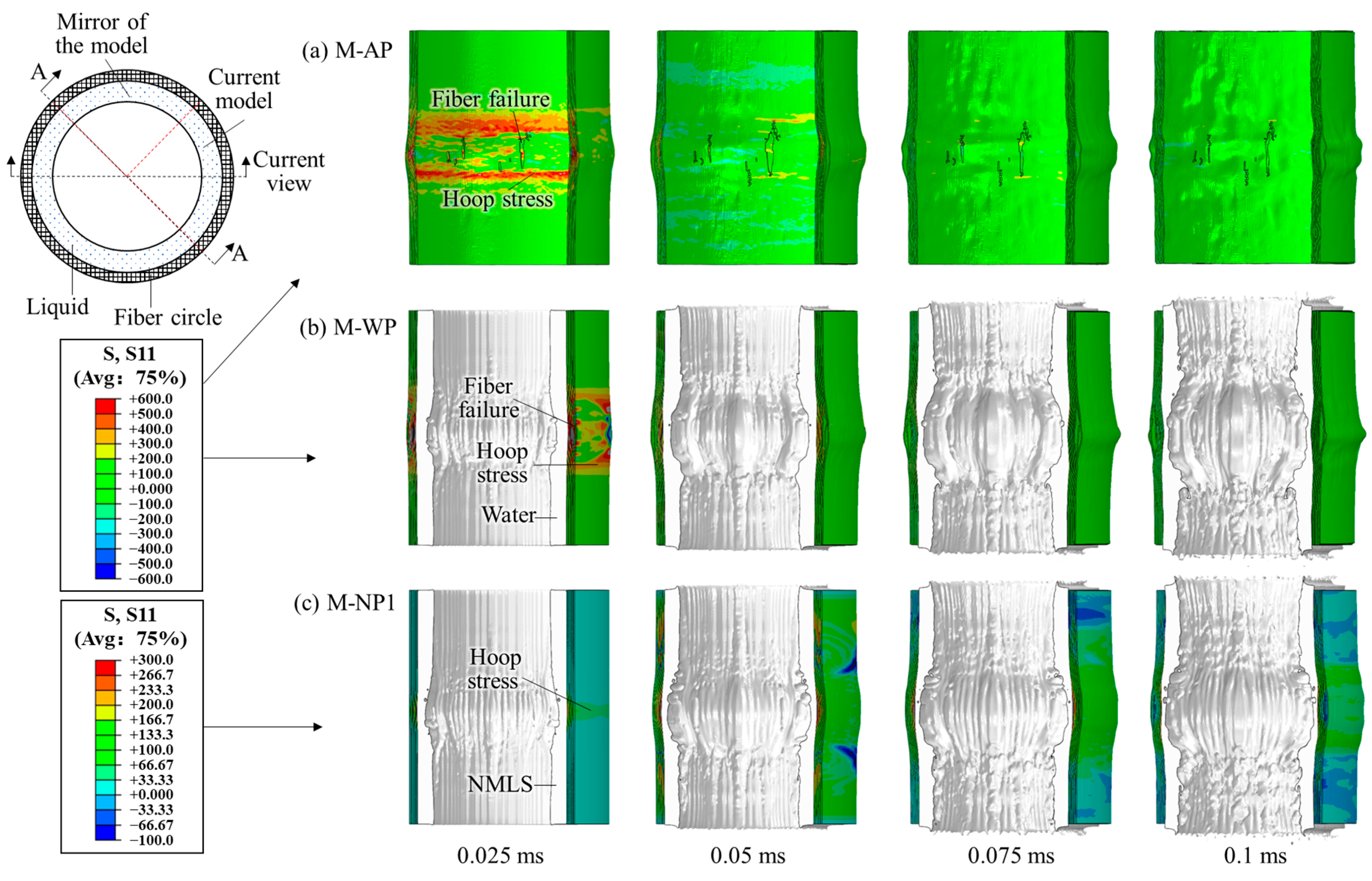
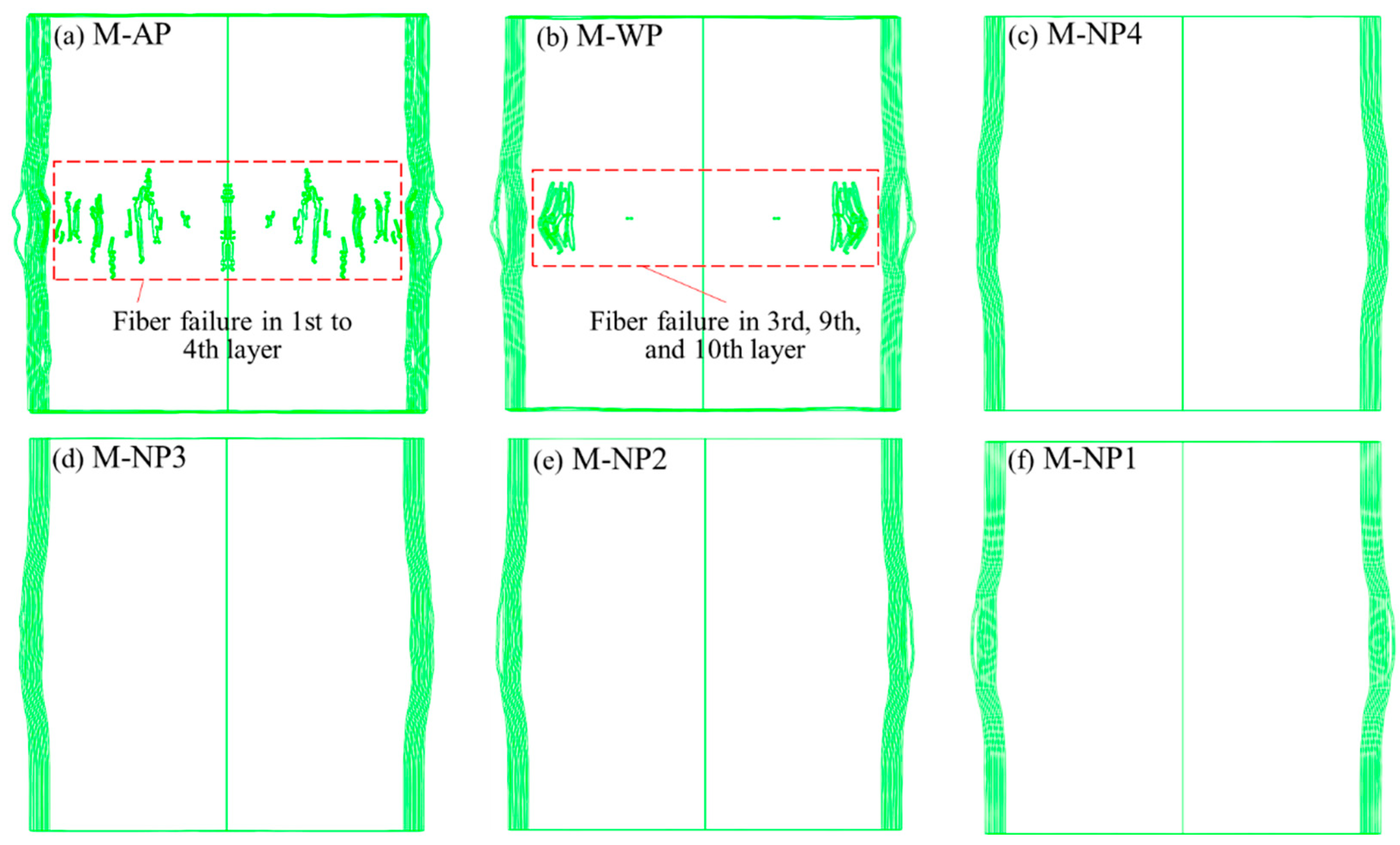
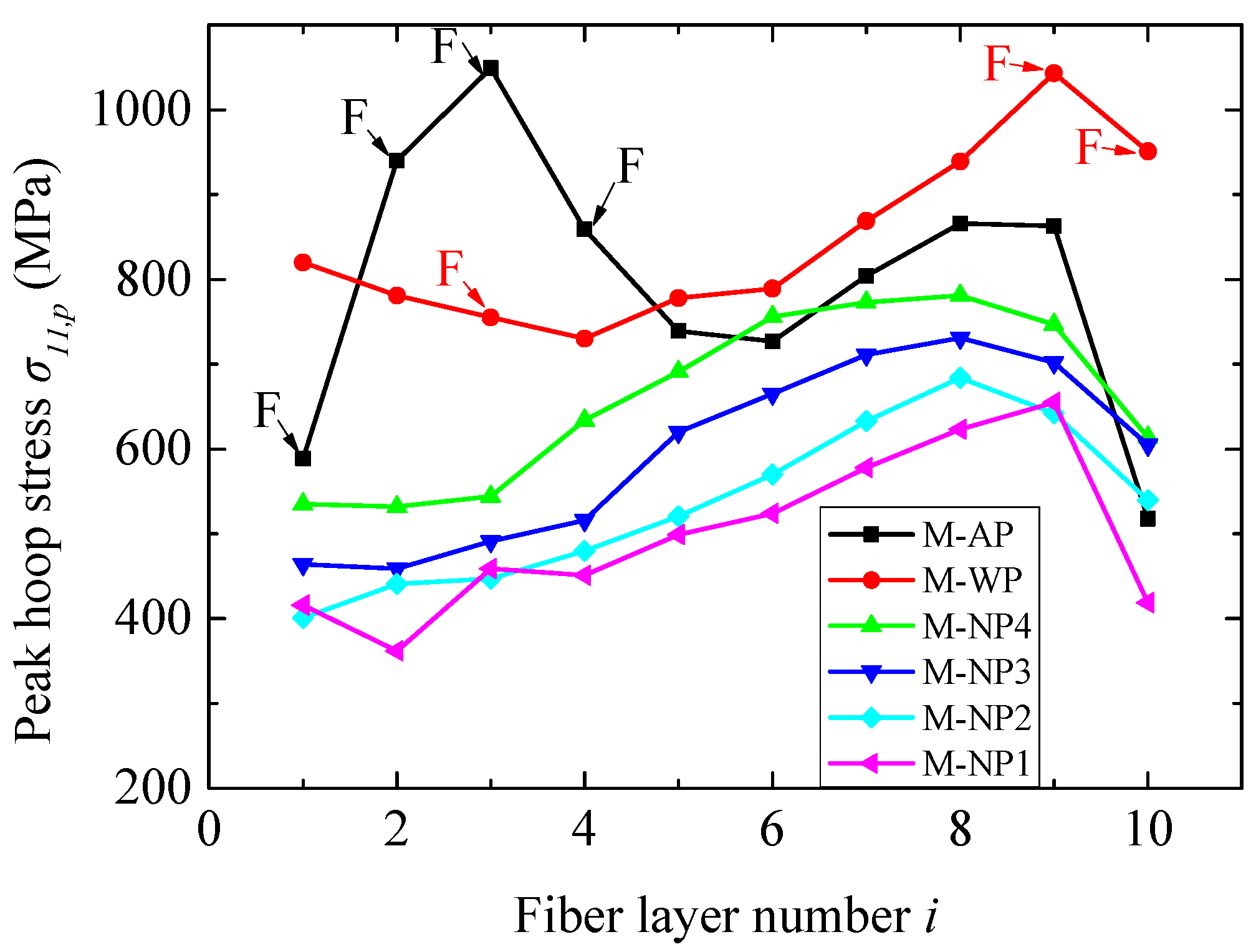
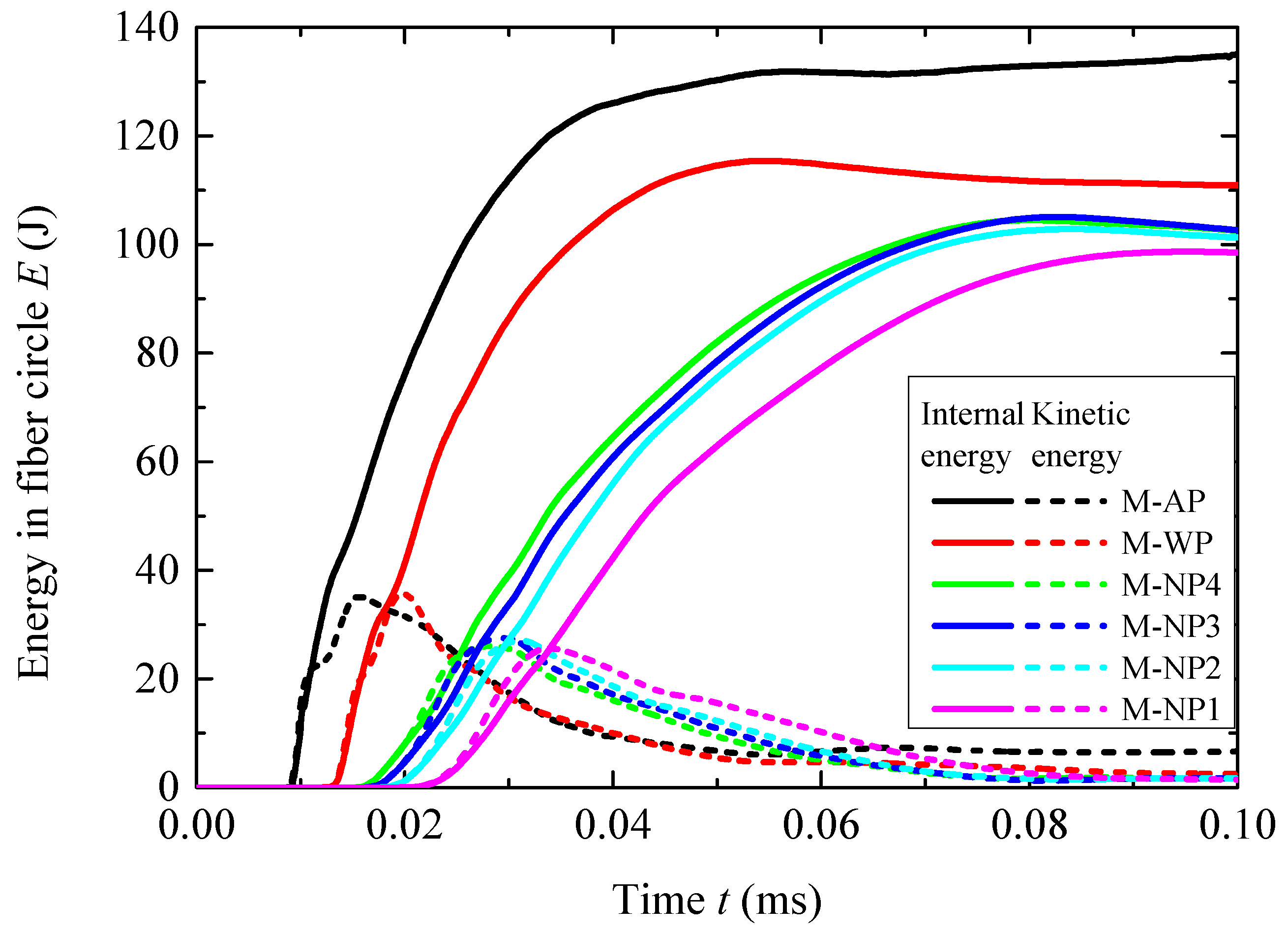
3.2. Using the TNT Charge of 7.68 g
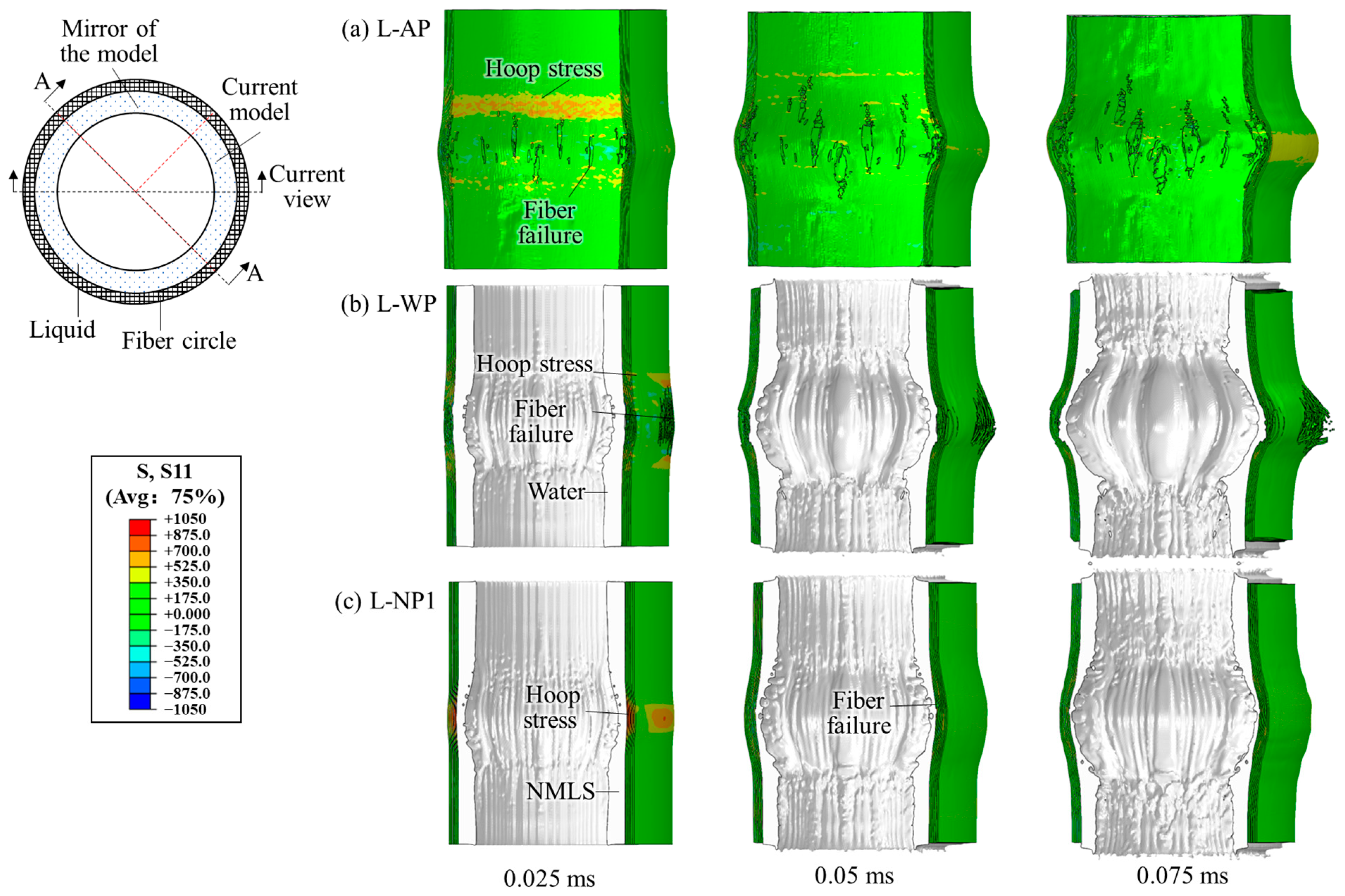
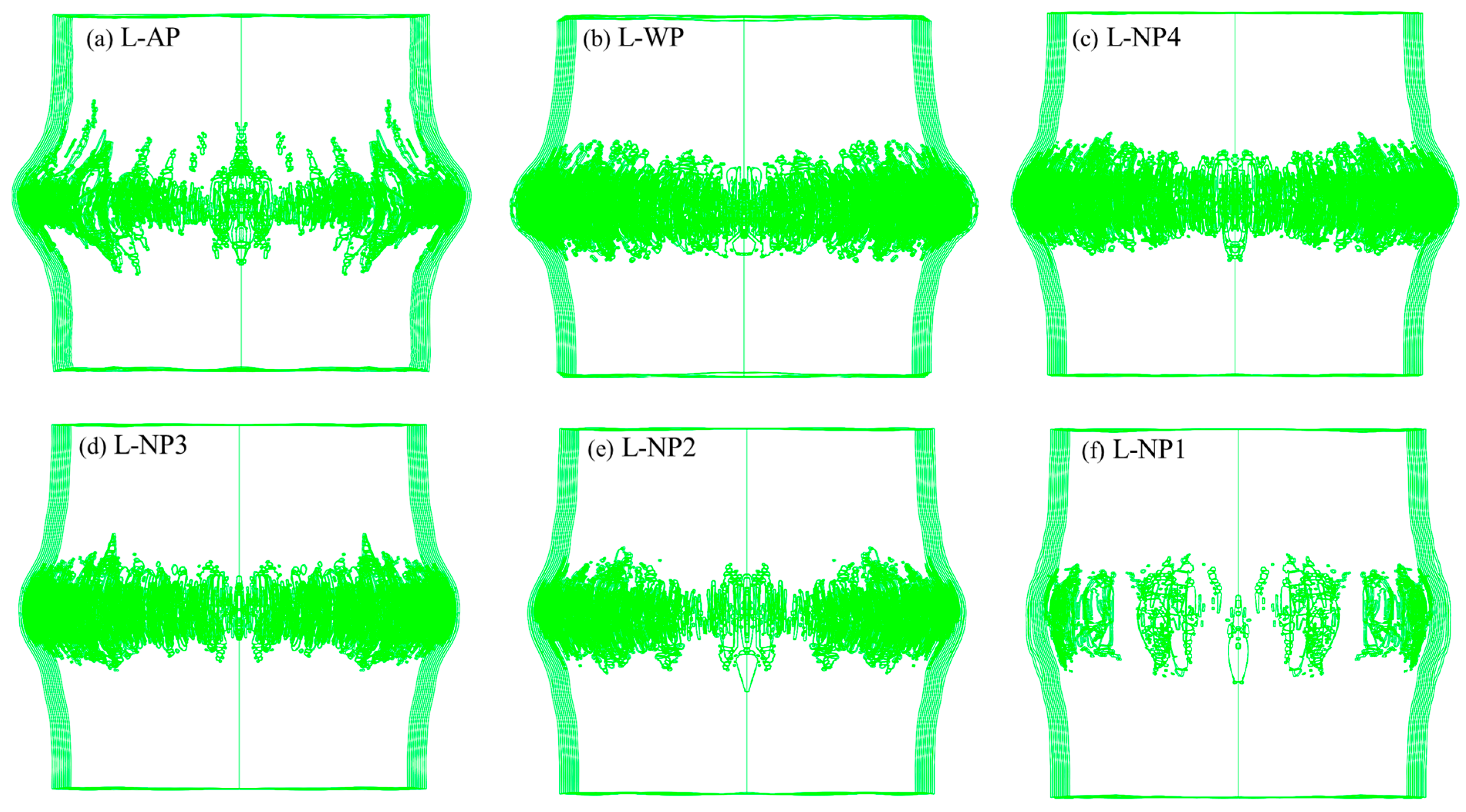
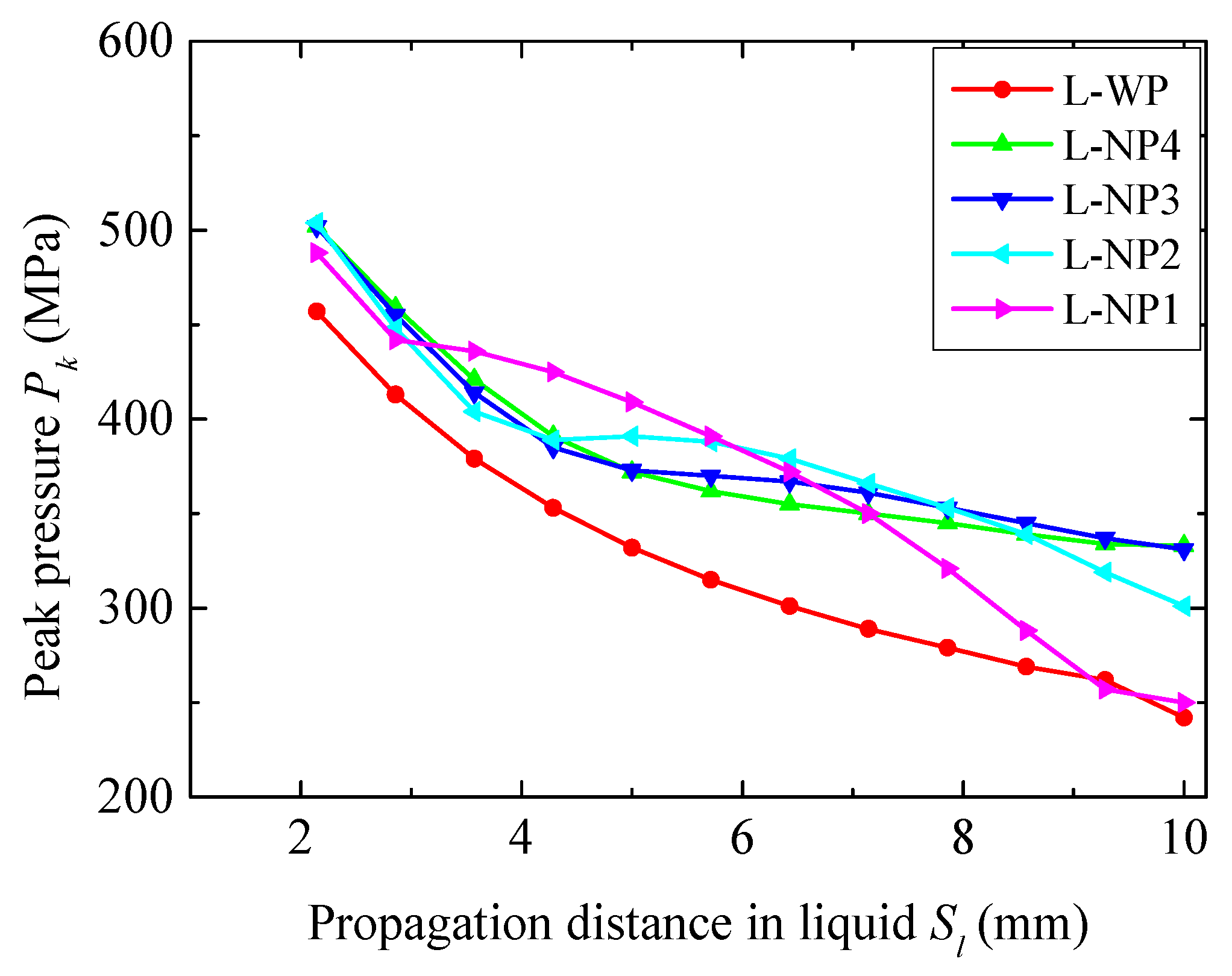
3.3. Using the TNT Charge of 11.52 g
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Form/meaning |
| AP | Fiber-ply alone structure |
| CEL | Coupled Eulerian–Lagrangian |
| EASs | Energy absorption systems |
| EOS | Equation of state |
| IEDs | Improvised explosive devices |
| JWL | Jones–Wilkins–Lee |
| NMLS | Nanoporous material liquid system |
| NMLSs | Nanoporous material liquid systems |
| N1 | NMLS with a particle–water mass ratio of 1:1 |
| N2 | NMLS with a particle–water mass ratio of 1:2 |
| N3 | NMLS with a particle–water mass ratio of 1:3 |
| N4 | NMLS with a particle–water mass ratio of 1:4 |
| NP | NMLS fiber-ply structure |
| NP1 | NP with NMLS N1 |
| NP2 | NP with NMLS N2 |
| NP3 | NP with NMLS N3 |
| NP4 | NP with NMLS N4 |
| UHMWPE | Ultra-high-molecular-weight polyethylene |
| WP | Water fiber-ply structure |
References
- Khlistunov, I.A.; Belogorlov, A.A. Influence of the characteristics of a nanoporous material on nonwetting-liquid flow under an impulse action. J. Eng. Phys. Thermophys. 2024, 97, 1514–1520. [Google Scholar] [CrossRef]
- Cao, G. Nanofluidic energy damper: Modeling, simulation and analysis. J. Micromechanics Mol. Phys. 2022, 7, 237–259. [Google Scholar] [CrossRef]
- Huang, W.; Bi, Y.; Liu, Y.; Yang, P.; Liu, J. Tunable mechanical performance of nanoporous energy absorption composite material. Smart Mater. Struct. 2025, 34, 025016. [Google Scholar] [CrossRef]
- Han, A.; Qiao, Y. Pressure-induced infiltration of aqueous solutions of multiple promoters in a nanoporous silica. J. Am. Chem. Soc. 2006, 128, 10348–10349. [Google Scholar] [CrossRef]
- Cao, G. Working Mechanism of nanoporous energy absorption system under high speed loading. J. Phys. Chem. C 2012, 116, 8278–8286. [Google Scholar] [CrossRef]
- Han, A.; Kong, X.; Qiao, Y. Pressure induced liquid infiltration in nanopores. J. Appl. Phys. 2006, 100, 014308. [Google Scholar] [CrossRef]
- Han, A.; Punyamurtula, V.K.; Kim, T.; Qiao, Y. The upper limit of energy density of nanoporous materials functionalized liquid. J. Mater. Eng. Perform. 2008, 17, 326–329. [Google Scholar] [CrossRef]
- Kong, X.; Surani, F.B.; Qiao, Y. Energy absorption of nanoporous silica particles in aqueous solutions of sodium chloride. Phys. Scr. 2006, 74, 531–534. [Google Scholar] [CrossRef]
- Cao, G.X. Nanofluidic energy absorption system: A review. Adv. Mech. 2017, 47, 201707. [Google Scholar]
- Chen, X.; Surani, F.B.; Kong, X.; Punyamurtula, V.K.; Qiao, Y. Energy absorption performance of steel tubes enhanced by a nanoporous material functionalized liquid. Appl. Physic Lett. 2006, 89, 241918. [Google Scholar] [CrossRef]
- Chordiya, Y.M.; Goel, M.D.; Matsagar, V.A. Assessment of energy absorption for different foams subjected to low-velocity impact. Sādhanā Acad. Proc. Eng. Sci. 2023, 48, 157. [Google Scholar] [CrossRef]
- Kong, X.; Qiao, Y. Thermal effects on pressure-induced infiltration of a nanoporous system. Philos. Mag. Lett. 2005, 85, 331–337. [Google Scholar] [CrossRef]
- Surani, F.B.; Kong, X.; Panchal, D.B.; Qiao, Y. Energy absorption of a nanoporous system subjected to dynamic loadings. Appl. Phys. Lett. 2005, 87, 163111. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, Z.; Xu, J.; Xu, X.; Liu, C.; Li, Y. A candidate of mechanical energy mitigation system: Dynamic and quasi-static behaviors and mechanisms of zeolite β/water system. Mater. Des. 2015, 66, 545–551. [Google Scholar] [CrossRef]
- Lu, W. Recent Experimental Advances in solid–liquid composites for impact and blast mitigation. J. Compos. Sci. 2024, 8, 462. [Google Scholar] [CrossRef]
- Li, M.; Li, J.; Barbat, S.; Baccouche, R.; Lu, W. Enhanced filler-tube wall interaction in liquid nanofoam-filled thin-walled tubes. Compos. Struct. 2018, 200, 120–126. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, Y.; Wen, Y.; He, T. The quasi-static and dynamic impact study of energy absorptions of crush tubes with silica aerogel liquid system as fillers. Microporous Mesoporous Mater. 2022, 341, 112097. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, J.; Zhao, C.; Li, Y. Exploring a new candidate of energy absorber: Thin-walled tube structures filled with nanoporous material functionalized liquid. In Proceedings of the 2014 IRCOBI Conference, Berlin, Germany, 10–12 September 2014; pp. 578–586. [Google Scholar]
- Liu, Y.; Schaedler, T.A.; Jacobsen, A.J.; Chen, X. Quasi-static energy absorption of hollow microlattice structures. Compos. Part B 2014, 67, 39–49. [Google Scholar] [CrossRef]
- Liu, Y.; Schaedler, T.A.; Jacobsen, A.J.; Lu, W.; Qiao, Y.; Chen, X. Quasi-static crush behavior of hollow microtruss filled with NMF liquid. Compos. Struct. 2014, 115, 29–40. [Google Scholar] [CrossRef]
- Xu, B.; Chen, X.; Lu, W.; Zhao, C.; Qiao, Y. Non-dissipative energy capture of confined liquid in nanopores. Appl. Phys. Lett. 2014, 104, 203107. [Google Scholar] [CrossRef]
- Xu, B.; Qiao, Y.; Chen, X. Mitigating impact/blast energy via a novel nanofluidic energy capture mechanism. J. Mech. Phys. Solids 2014, 62, 194–208. [Google Scholar] [CrossRef]
- Vladimir, D.B.; Anton, A.B.; Vladimir, N.T. Response of a nanofluid system based on a porous medium to an impact loading. Colloids Surf. A Physicochem. Eng. Asp. 2018, 537, 540–548. [Google Scholar] [CrossRef]
- 24. Hibbitt, Karlsson & Sorensen, Inc. ABAQUS Version 6.14 Documentation; Dassault Systemes Simulia Corp.: Providence, RI, USA, 2019. [Google Scholar]
- Borman, V.D.; Grekhov, A.M.; Troyan, V.I. Investigation of the percolation transition in a nonwetting liquid-nanoporous medium system. J. Exp. Theor. Phys. 2000, 91, 170–181. [Google Scholar] [CrossRef]
- Liu, L.; Chen, X.; Lu, W.; Han, A.; Qiao, Y. Infiltration of electrolytes in molecular-sized nanopores. Phys. Rev. Lett. 2009, 102, 184501. [Google Scholar] [CrossRef]
- Qiao, Y.; Liu, L.; Chen, X. Pressurized liquid in nanopores: A modified laplace-young equation. Nano Lett. 2009, 9, 984–988. [Google Scholar] [CrossRef]
- Kong, X.; Surani, F.B.; Qiao, Y. Effects of addition of ethanol on the infiltration pressure of a mesoporous silica. J. Mater. Res. 2005, 20, 1042–1045. [Google Scholar] [CrossRef]
- Herrmann, W. Constitutive equation for the dynamic compaction of ductile porous materials. J. Appl. Phys. 1968, 40, 2490–2499. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, L.F.; Zhang, Q.; Zhang, L.; Song, H.; Gao, X.; Sun, B.; Liu, H.; Song, H. A thermodynamically complete multiphase equation of state for dense and porous metals at wide ranges of temperature and pressure. Chin. Phys. B 2025, 34, 036401. [Google Scholar] [CrossRef]
- Russell, B.P.; Karthikeyan, K.; Deshpande, V.S.; Fleck, N. The high strain rate response of Ultra High Molecular-weight Polyethylene: From fibre to laminate. Int. J. Impact Eng. 2013, 60, 1–9. [Google Scholar] [CrossRef]
- Nguyen, L.H.; Lässig, T.R.; Ryan, S.; Riedel, W.; Mouritz, A.P.; Orifici, A.C. A methodology for hydrocode analysis of ultra-high molecular weight polyethylene composite under ballistic impact. Compos. Part A Appl. Sci. Manuf. 2016, 84, 224–235. [Google Scholar] [CrossRef]
- Chen, J.K.; Allahdadi, F.A.; Sun, C.T. A quadratic yield function for fiber-reinforced composites. J. Compos. Mater. 1997, 31, 788–811. [Google Scholar] [CrossRef]
- Zhu, W.; Yao, W.; Huang, G.; Zhou, Y.; Li, W.; Wang, X. Numerical investigation on effects of blast loading on anti-fragment performance of hollow cylindrical UHMWPE cross-ply laminate. Compos. Struct. 2025, 351, 118565. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, T.; Zhu, W.; Bian, X.-B.; Huang, G.-Y. Evaluation of blast mitigation effects of hollow cylindrical barriers based on water and foam. Compos. Struct. 2022, 282, 115016. [Google Scholar] [CrossRef]
- Hu, J.; Chen, Z.; Zhang, X.; Wei, Y.; Liang, X.; Liang, J.; Ma, G.; Wang, Q.; Long, Y. Underwater explosion in centrifuge part I: Validation and calibration of scaling laws. Sci. China Technol. Sci. 2017, 60, 1638–1657. [Google Scholar] [CrossRef]
- Zhang, L. Performance of the Explosive Materials and Testing on Explosion Effect; University of Science and Technology of China Press: Hefei, China, 2006. [Google Scholar]
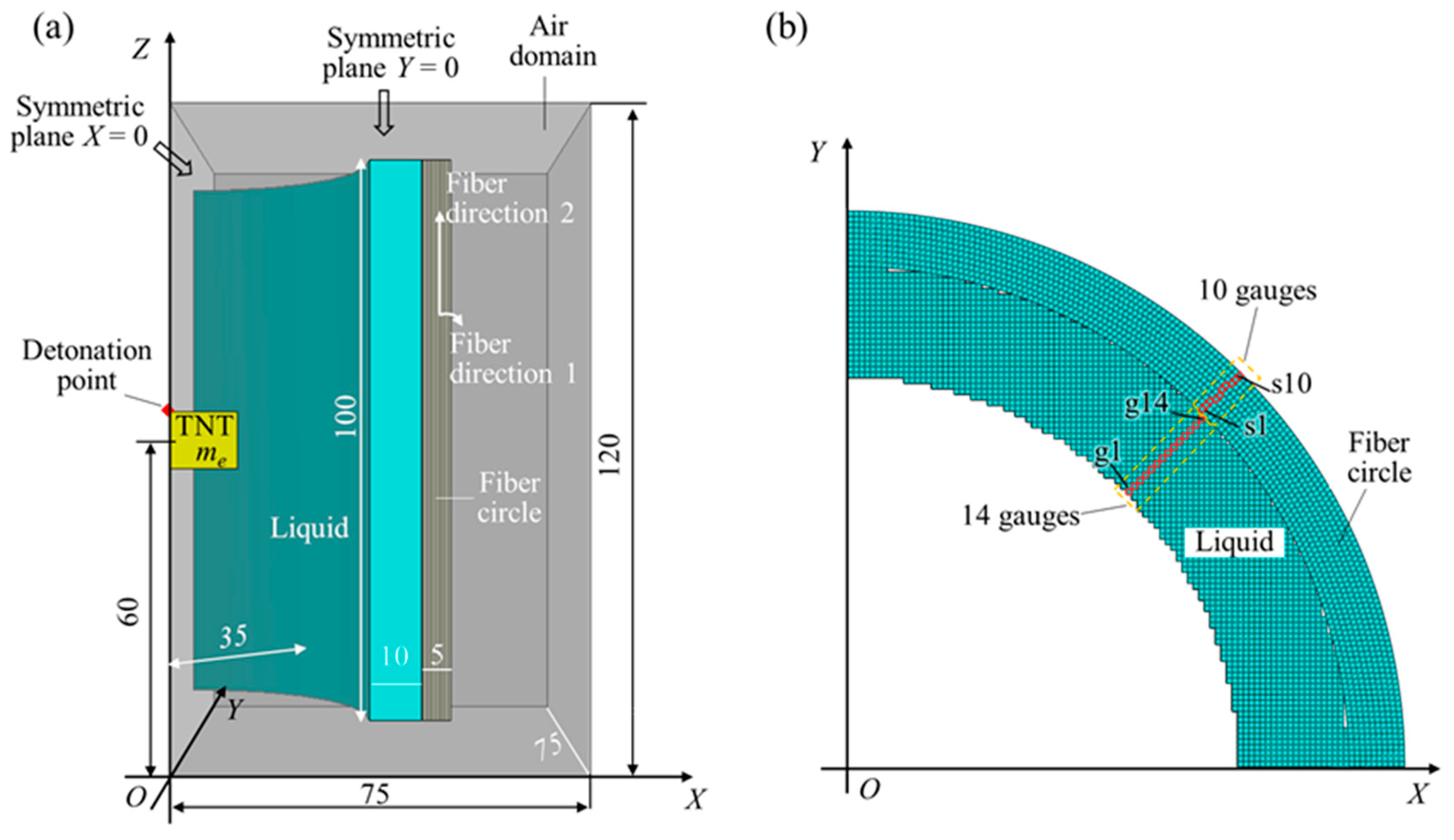


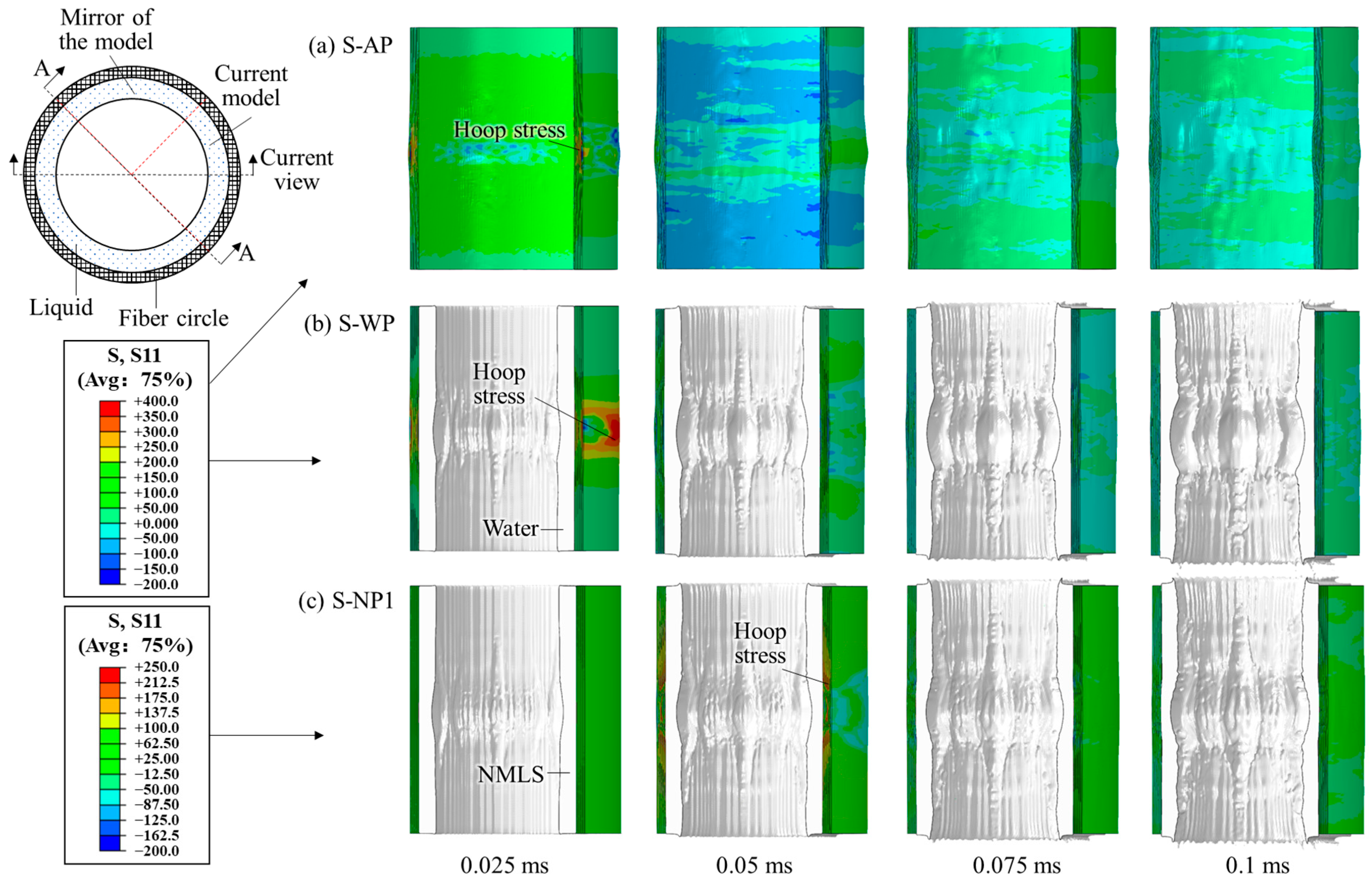
| No. | Name | Charge Size (mm) | Charge Mass (g) | Liquid | Liquid Mass (g) | Fiber Mass (g) |
|---|---|---|---|---|---|---|
| 1 | S-AP | Φ25 × 5 | 3.80 | None | 0 | 146.4 g |
| 2 | S-WP | Water | 249.4 | |||
| 3 | S-NP1 | N1 | ||||
| 4 | S-NP2 | N2 | ||||
| 5 | S-NP3 | N3 | ||||
| 6 | S-NP4 | N4 | ||||
| 7 | S-AP | Φ25 × 10 | 7.68 | None | 0 | |
| 8 | M-WP | Water | 249.4 | |||
| 9 | M-NP1 | N1 | ||||
| 10 | M-NP2 | N2 | ||||
| 11 | M-NP3 | N3 | ||||
| 12 | M-NP4 | N4 | ||||
| 13 | L-AP | Φ25 × 15 | 11.52 | None | 0 | |
| 14 | L-WP | Water | 249.4 | |||
| 15 | L-NP1 | N1 | ||||
| 16 | L-NP2 | N2 | ||||
| 17 | L-NP3 | N3 | ||||
| 18 | L-NP4 | N4 |
| Particle–Water Ratio rp | EOS Us–Up | EOS Compaction | ||||
|---|---|---|---|---|---|---|
| Reference Density ρ0 (g/cm3) | Reference Sound Speed c0 (m/s) | Reference Sound Speed in the Porous Material cp0 (m/s) | Porosity n0 | Infiltration Pressure Pin (MPa) | Compaction Pressure at Which All Nanopores Are Filled with Water Pc (MPa) | |
| 1:1 | 1.377 | 1500 | 400 | 0.274 | 17 | 27.5 |
| 1:2 | 1.224 | 1500 | 500 | 0.183 | 17 | 27.5 |
| 1:3 | 1.159 | 1500 | 800 | 0.137 | 17 | 27.5 |
| 1:4 | 1.124 | 1500 | 1000 | 0.110 | 17 | 27.5 |
| 0 (Water) | 1 | 1500 | - | - | - | - |
| Parameter | Density ρ | Gas Constant R | Air Pressure P0 | Specific Heat Cv |
|---|---|---|---|---|
| Value | 1.225 kg/m3 | 287.058 J/(kg·K) | 0.101325 MPa | 718 J/(kg·K) |
| Parameter | Density ρ | Detonation Velocity D | Fitting Coefficient | Detonation Energy Density e | ||||
|---|---|---|---|---|---|---|---|---|
| A | B | ω | R1 | R2 | ||||
| Value | 1630 kg/m3 | 6930 m/s | 373.77 GPa | 3.75 GPa | 0.35 | 4.15 | 0.9 | 3,681,000 kJ/kg |
| Name | Peak Internal Energy Eip (J) | Peak Kinetic Energy Ekp (J) | Reduction Ri in Eip (%) | Reduction Rk in Ekp (%) |
|---|---|---|---|---|
| S-AP | 17.8 | 4.36 | - | |
| S-WP | 11.8 | 3.35 | 33.7 | 23.2 |
| S-NP4 | 7.97 | 2.54 | 55.2 | 41.7 |
| S-NP3 | 8.61 | 2.77 | 51.6 | 36.5 |
| S-NP2 | 9.84 | 3.12 | 44.7 | 28.4 |
| S-NP1 | 10.4 | 3.25 | 41.6 | 25.5 |
| S-NP1a | 7.56 | 2.24 | 57.5 | 48.6 |
| Name | Peak Internal Energy Eip (J) | Peak Kinetic Energy Ekp (J) | Reduction Ri in Eip (%) | Reduction Rk in Ekp (%) |
|---|---|---|---|---|
| M-AP | 131.9 | 35.1 | - | - |
| M-WP | 115.4 | 35.7 | 12.5 | −1.7 |
| M-NP4 | 104.5 | 26.1 | 20.8 | 25.6 |
| M-NP3 | 105.1 | 27.5 | 20.3 | 21.7 |
| M-NP2 | 102.8 | 27.1 | 22.1 | 22.8 |
| M-NP1 | 98.7 | 25.7 | 25.2 | 26.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Yao, W.; Liu, J.; Zheng, Y.; Li, W.; Wang, X. Numerical Investigation on the Performance of Compressible Fluid Systems in Mitigating Close-Field Blast Effects on a Fiber Circle. Materials 2025, 18, 2204. https://doi.org/10.3390/ma18102204
Zhu W, Yao W, Liu J, Zheng Y, Li W, Wang X. Numerical Investigation on the Performance of Compressible Fluid Systems in Mitigating Close-Field Blast Effects on a Fiber Circle. Materials. 2025; 18(10):2204. https://doi.org/10.3390/ma18102204
Chicago/Turabian StyleZhu, Wei, Wenjin Yao, Jian Liu, Yu Zheng, Wenbin Li, and Xiaoming Wang. 2025. "Numerical Investigation on the Performance of Compressible Fluid Systems in Mitigating Close-Field Blast Effects on a Fiber Circle" Materials 18, no. 10: 2204. https://doi.org/10.3390/ma18102204
APA StyleZhu, W., Yao, W., Liu, J., Zheng, Y., Li, W., & Wang, X. (2025). Numerical Investigation on the Performance of Compressible Fluid Systems in Mitigating Close-Field Blast Effects on a Fiber Circle. Materials, 18(10), 2204. https://doi.org/10.3390/ma18102204






