1. Introduction
The permittivity of fibers plays a crucial role in various electromagnetic applications involving woven and non-woven fabrics. This includes electromagnetic functional textiles [
1], fiber-reinforced composites used in circuits [
2], and fabric antennas [
3]. The permittivity of these fibrous materials corresponds to their interaction with electromagnetic fields, thereby significantly affecting key properties like signal transmission, electromagnetic shielding effectiveness, and the performance of antennas.
A fibrous medium featuring fibers significantly smaller than the wavelength of propagating electromagnetic radiation can be treated (under the quasi-static assumption) as an effective medium. In consequence, the medium exhibits a characteristic effective permittivity . This effective permittivity is influenced by diverse factors, such as the solid volume fraction of fibers and the permittivity of the fibers and host medium, as well as the orientation and geometry of the fiber microstructure.
Describing
by using mixing relations [
4,
5] involves employing either probability distribution relations based on the micromechanical bounds or mixing relations based on the Effective Media Approximation (EMA relations) [
4]. Probability distribution relations involve correlating
with weighting parameters based on empirical data and micromechanical bounds. These micromechanical bounds, such as Hashin–Shtrikman or Wiener bounds [
5], are used to establish limits on the possible values for
in isotropic and anisotropic media, respectively. However, it is important to note that the accuracy of probability distribution relations depends significantly on the data acquisition process. This necessitates an experimental methodology that is capable of measuring the anisotropic
of samples. Consequently, the fitting procedure should only account for the inclusion in which their orientations correspond to those in the measured samples. For other samples, a thorough characterization is required whenever their orientation varies.
EMA relations offer a practical alternative approach for estimating
. Unlike probability distribution relations that rely on empirical data, EMA relations utilize semi-analytical functions to estimate
. EMA relations assume that mixtures are composed of spherical or ellipsoidal inclusions embedded in a continuous medium, which are equally exposed to a volume-averaged electric field [
6]. It is important to note that to maintain a valid mean electric field, significant attenuation of the field amplitude must be avoided. This condition is satisfied when the size of the inclusions is significantly smaller than the skin depth of the electromagnetic radiation.
The EMA framework estimates the macroscopic dielectric properties of materials by averaging the contributions of their individual inclusions. This framework relies on the principle that when a dielectric inclusion is placed in a uniform electric field
, it induces a secondary electric field within the inclusion. This induced field causes charges within the inclusion to align, generating a dipole moment
, which, in turn, alters the surrounding electric field. For moderate applied fields, the relationship between incident
and generated
is linear, given by
, where
is the polarizability of the inclusion. The Clausius-Mossotti formula [
4] relates the macroscopic
of a material to the combined contributions of the
of its microscopic inclusions. For one or more inclusion species, it is expressed as
where
is the permittivity of the continuous medium (host phase), and
is the number density of dipoles of the
i-th component (or species). In addition, the polarizability of a spherical inclusion is expressed as
[
4], where
is the volume of the sphere, and
is the permittivity of the inclusion, respectively. The Clausius–Mossotti formula, using the polarizability of a spherical inclusion, is commonly referred to as the Maxwell–Garnett (MG) mixing relation [
4]. The MG approach assumes a system with a low volume fraction of particles that are sufficiently spaced apart. This relation reads as
where
is volume fraction of the
i-th component given by
.
Other frequently used EMA relations include the Bruggeman–Landauer (BL) mixing relation [
4,
5,
6]. The BL relation is derived from the MG relation by assuming that
and treating the host medium as an inclusion phase, such that
[
7]. The Bruggeman approach considers the interactions between induced dipoles of particles in a concentrated particle system. Unlike the MG relation, the BL relation symmetrically treats the volume fraction dispersion of the inclusions
and host medium
. For a multiphase mixture, the BL relation is given as
Both MG and BL relations produce good estimates of permittivity in isotropic media. However, fibrous media characterized by a dominant fiber orientation exhibit anisotropic behavior, leading to the requirement of a second-rank tensor description for precise representation of their effective permittivity. Anisotropic EMA relations provide a means to estimate the permittivity tensor by incorporating ellipsoidal inclusions and considering their spatial orientation with respect to their ellipsoidal depolarization factors. Nevertheless, when dealing with microstructures that are geometrically not analogous to ellipsoids (i.e., curved fibers), the effectiveness of EMA relations in providing reliable estimates diminishes. In such cases, alternative approaches are typically preferred to accurately estimate the effective permittivity.
For geometries other than spheres or ellipsoids, an alternative approach involves using numerical calculations to determine the polarizability of the inclusions. After deriving a polarizability expression, it can be integrated into the Clausius–Mossotti formula to calculate
. While analytical expressions for the scattered fields can be derived for spherical and ellipsoidal inclusions, more complex inclusion shapes require numerical calculations to obtain polarizability expressions. These calculations are essential to identify higher-order functions that accurately represent the induced dipole moment. In such cases, the induced dipole moment is numerically approximated and expressed in relation to the volume and the permittivity of both the inclusions and the host media [
8,
9,
10]. This approach is effective for estimating
in cases where inclusions share the same geometry. However, its applicability is limited in most fibrous media, as the varying curvature of fibers results in significant geometric differences from one inclusion to another.
Recent advancements in effective media theory, such as the Bragg–Pippard (BP) theory and Strong Property Fluctuation Theory (SPFT), address the limitations of conventional models like MG and BL [
11]. BP improves on MG with depolarization dyadics that match actual particle shapes. SPFT treats inclusions as constitutive property fluctuations, using volume integral equations and statistical measures to derive effective parameters. Despite these advancements, challenges persist in characterizing inclusions with complicated structures [
11], highlighting the need for further innovation to address the diversity and intricacy of modern composite materials.
Lastly, another approach to estimate
, particularly for non-spheroidal inclusions, involves characterizing the inclusion’s geometric shape. One approach to describing these shapes is through the spectral density function method [
12]. Another viable option is employing mixing relations that directly establish a correlation between
and the specific topology of the inclusions [
13,
14]. An example of this approach is a topological relation that has shown good
estimations for both isotropic (i.e., open-cell foams [
13]) and anisotropic (straight filaments [
14]) media. The corresponding topological mixing relation is
where
is a scalar complex-valued correlation parameter containing the topological details of the microstructure of the inclusions. Specifically,
integrates the volume fraction, orientation, geometry, and permittivity contrast between the inclusions and the continuous medium. In the case of isotropic media,
can be represented as a single value, sufficiently covering all these parameters. In contrast, for anisotropic media, it is necessary to detail the orientation of the inclusions in addition to the other parameters, i.e.,
. Thus, specifying
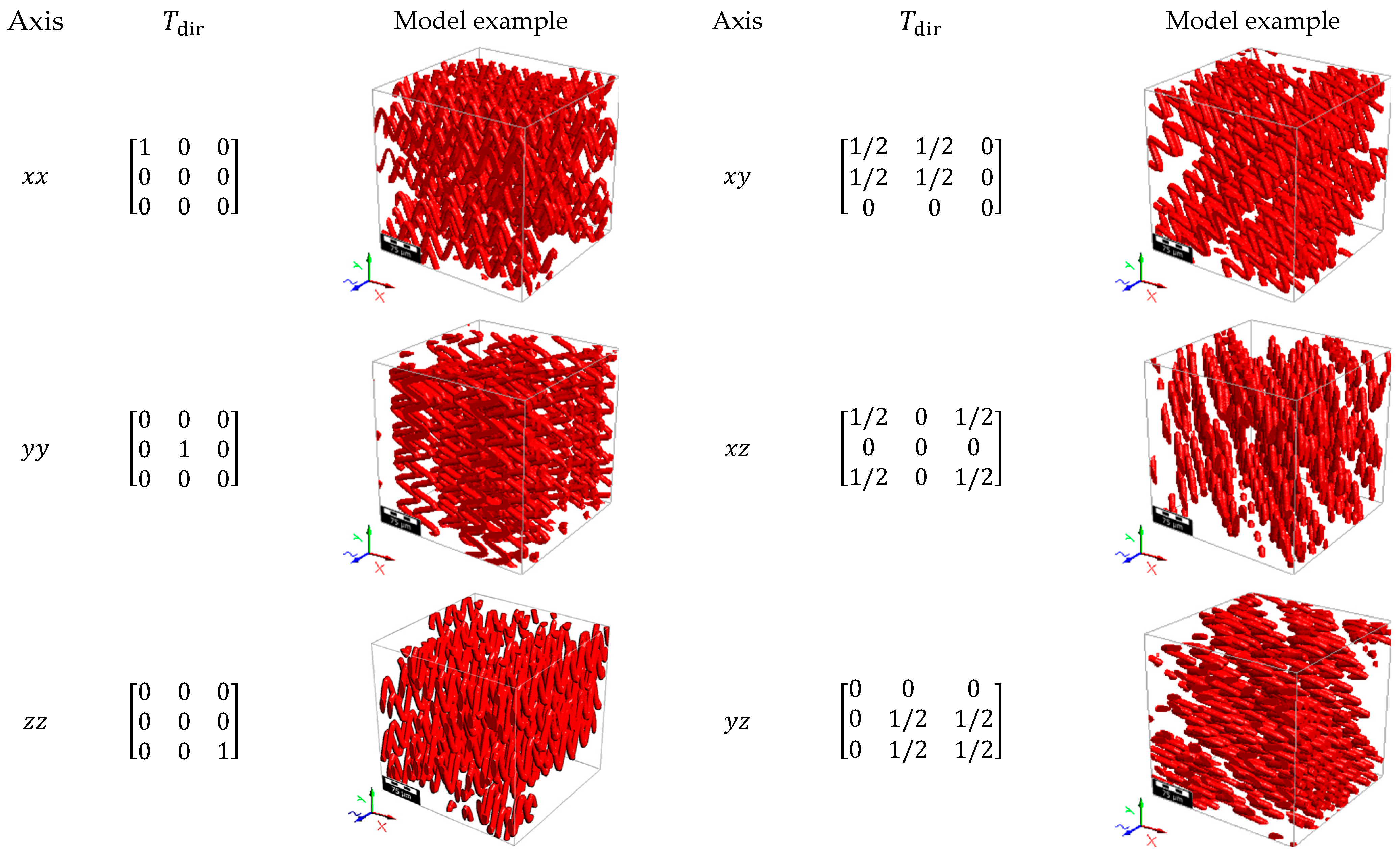
to the principal Λ-directions (Λ = xx,
or
) is achieved as
where
and
denote the following components: the orientation tensor
after a rotation to the principal Λ-directions and the geometrical correlation parameter
respectively. Note that
refers to the absolute value of
. Accordingly, the inclusion’s geometry is represented as
while their orientation is characterized by
As implied previously,
denotes the orientation tensor after it has undergone a rotation, with the subscript
indicating the direction of the rotation. The original (non-rotated) orientation tensor
, describing the average inclusion directions, is given by
The rotated orientation tensor
is computed using matrix multiplication with the basic rotation matrices
,
and
. Specifically
, where
is the combined rotation matrix
expressed as
The re-orientation towards the Λ-directions is accomplished by specifying the following Euler angles: (), (), and (). For reference, corresponds to the initial orientation tensor .
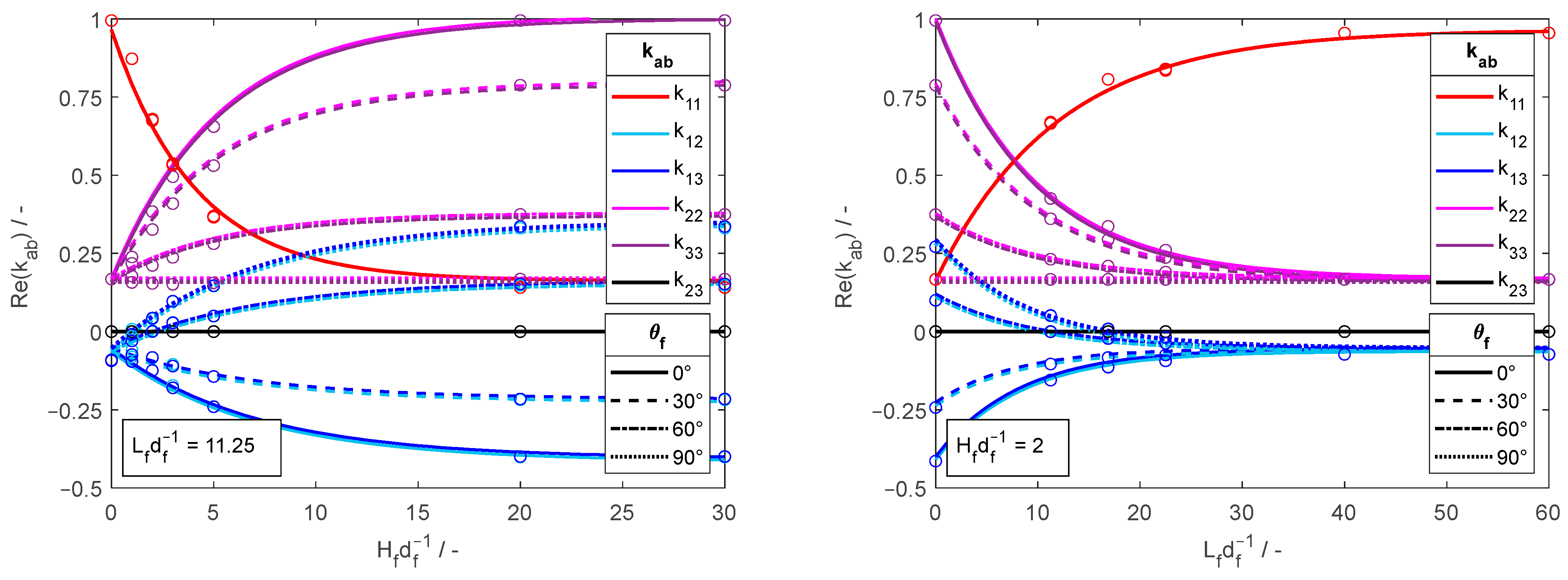
Consequently, for anisotropic media, where the permittivity Λ-components (diagonal components of the tensor) are required, the topological relation is formulated as
This relation facilitates the redirection of the inclusions through tensor rotation of , enabling the permittivity evaluation in any specified Λ-direction. Note that both and are symmetric, meaning and .
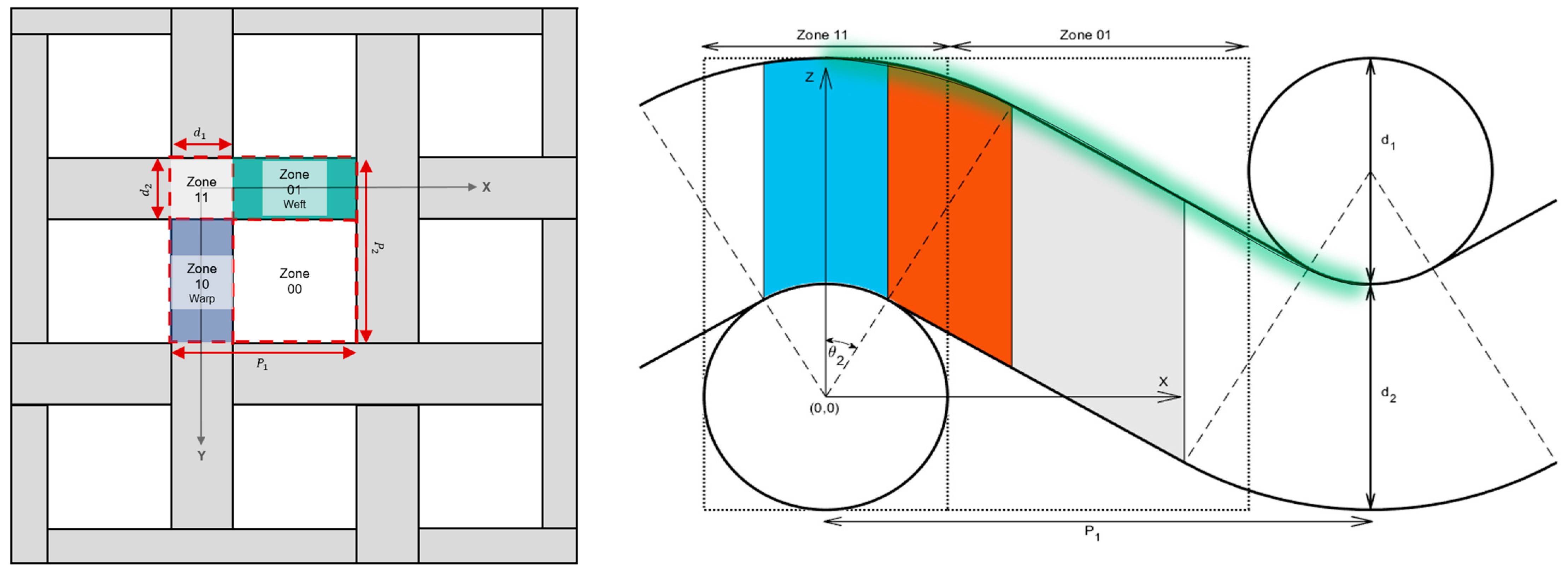
Finally, in addition to mixing relations, the dielectric properties of materials with inclusions (e.g., fabrics [
15,
16]) can also be determined by using an electrical capacitance approach. This approach involves correlating the effective dielectric constant
(real part of
) with the capacitance
observed in a parallel plate capacitor, that is
where
and
are the parallel area and gap between parallel plates, respectively. The calculation of
involves describing the total length of fiber material between the parallel plates by considering the weave pattern of the interlaced fibers [
15]. However, this approach is best suited for estimating the permittivity of materials with inclusions arranged in a well-defined structure, i.e., woven fibers with a repeating weave. Conversely, it is not suitable for randomly oriented fibers found in non-woven fabrics.
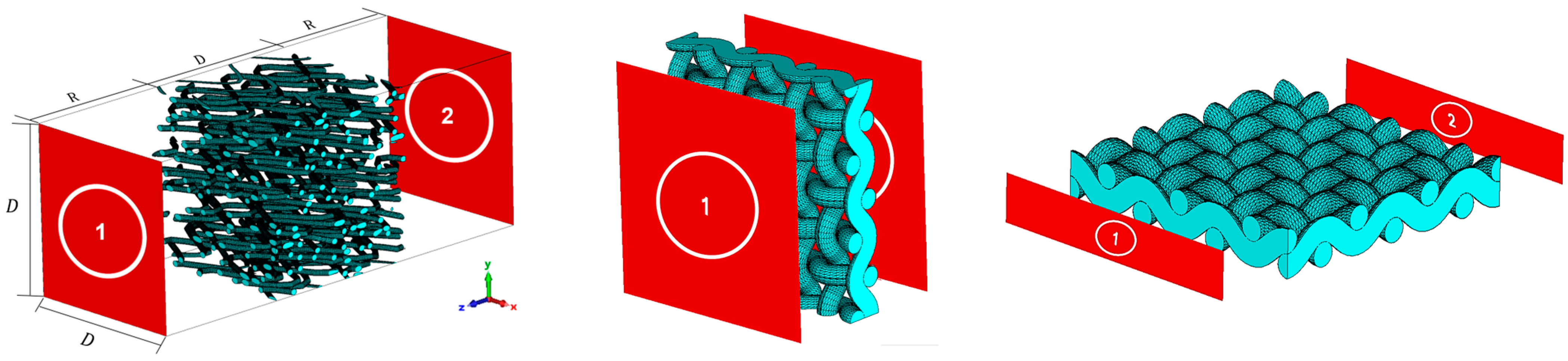
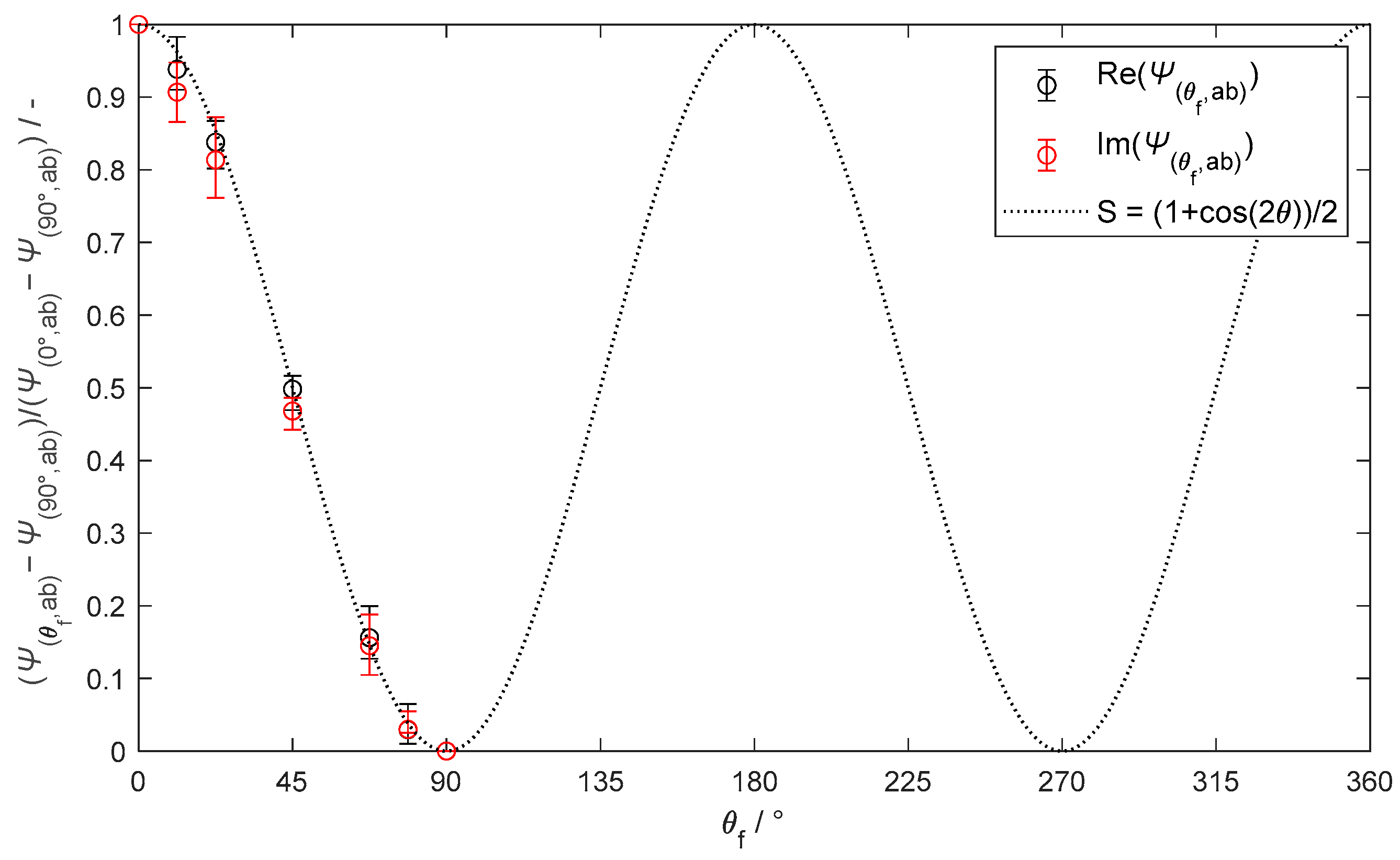
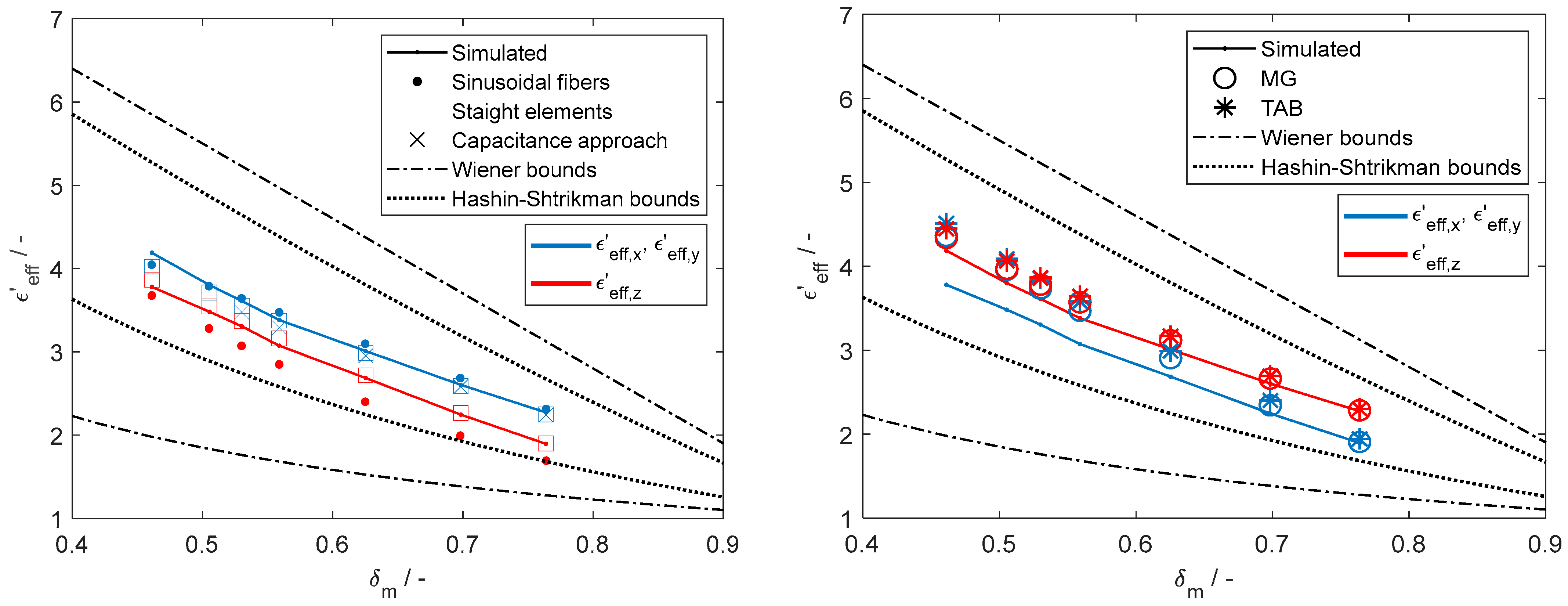
This work investigates the structural geometry and orientation of anisotropic fibrous media, introducing two novel approaches for estimating εeff:
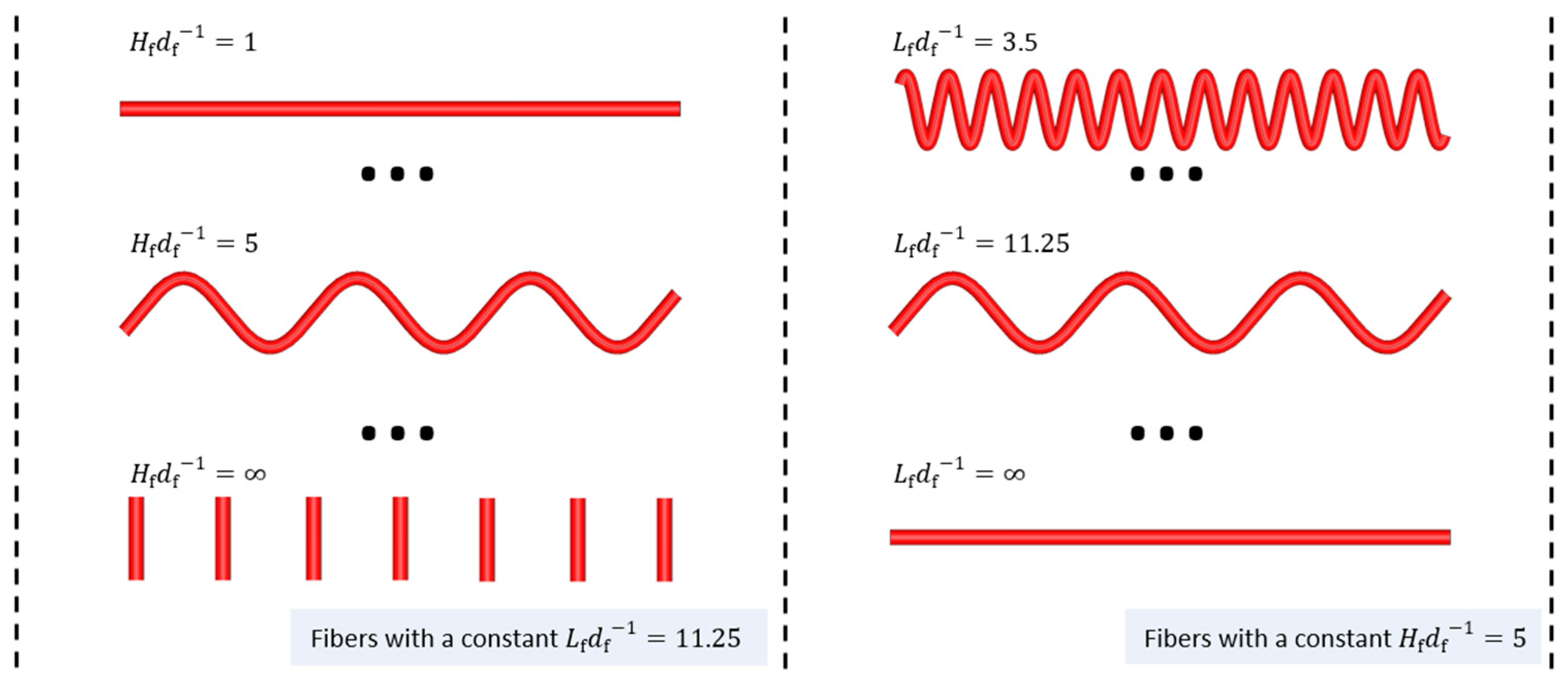
The first approach considers sinusoidal wave-curved fibers. Unlike conventional EMA models assuming ellipsoidal inclusions, the proposed wave-curved model captures complex fiber undulations, providing higher accuracy.
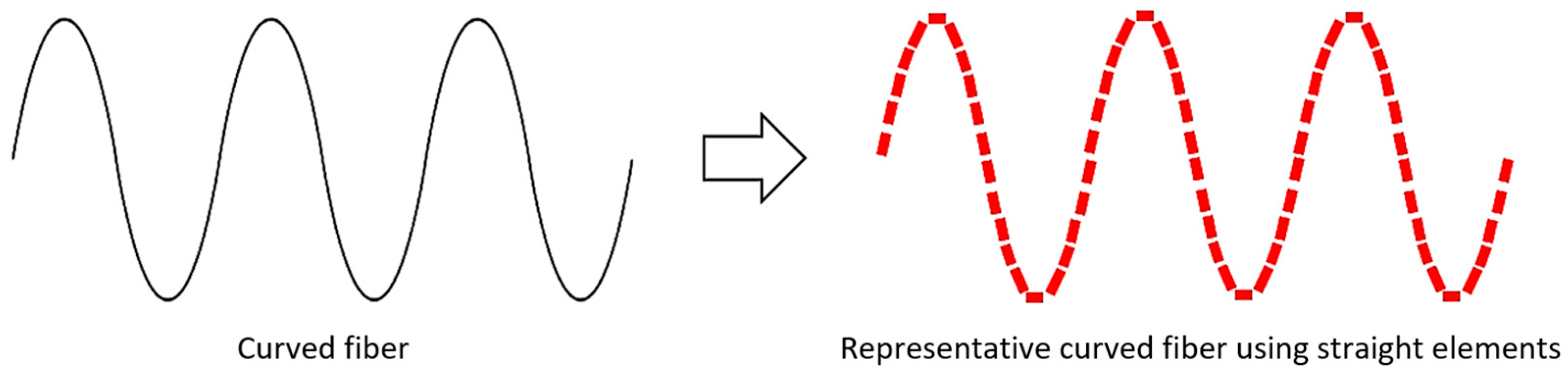
The second approach treats fibers as a collection of interconnected straight elements, overcoming the first approach’s limitation to strictly consider sinusoidal waves and enabling the approximation of any curvature without an explicit geometric characterization.
In addition, the present investigation focuses on assessing the accuracy of these approaches in estimating εeff for various fibrous media, as follows:
Dispersed fibers: εeff estimates from the proposed approaches with the conventional EMA models and electromagnetic wave propagation simulations to assess accuracy for spread-out fibers.
Plain-woven fabrics: the comparison for woven fabrics is similar to that for dispersed fibers, including the proposed approaches, EMA conventional mixing relations, and numerical calculations, with the addition of a theoretical capacitance model for woven constructions.
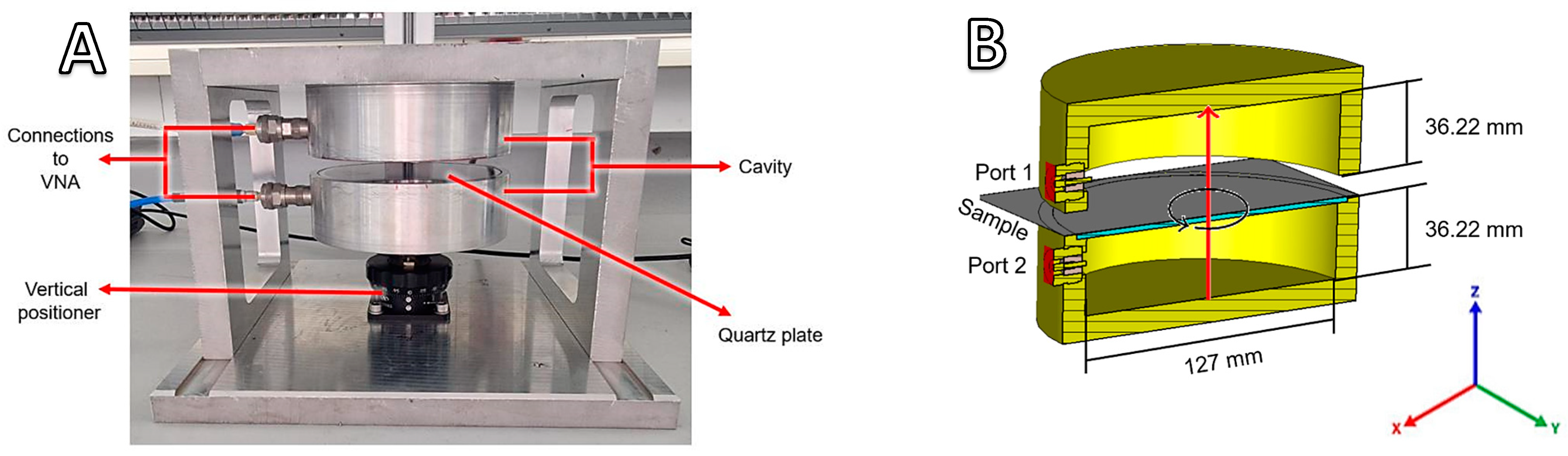
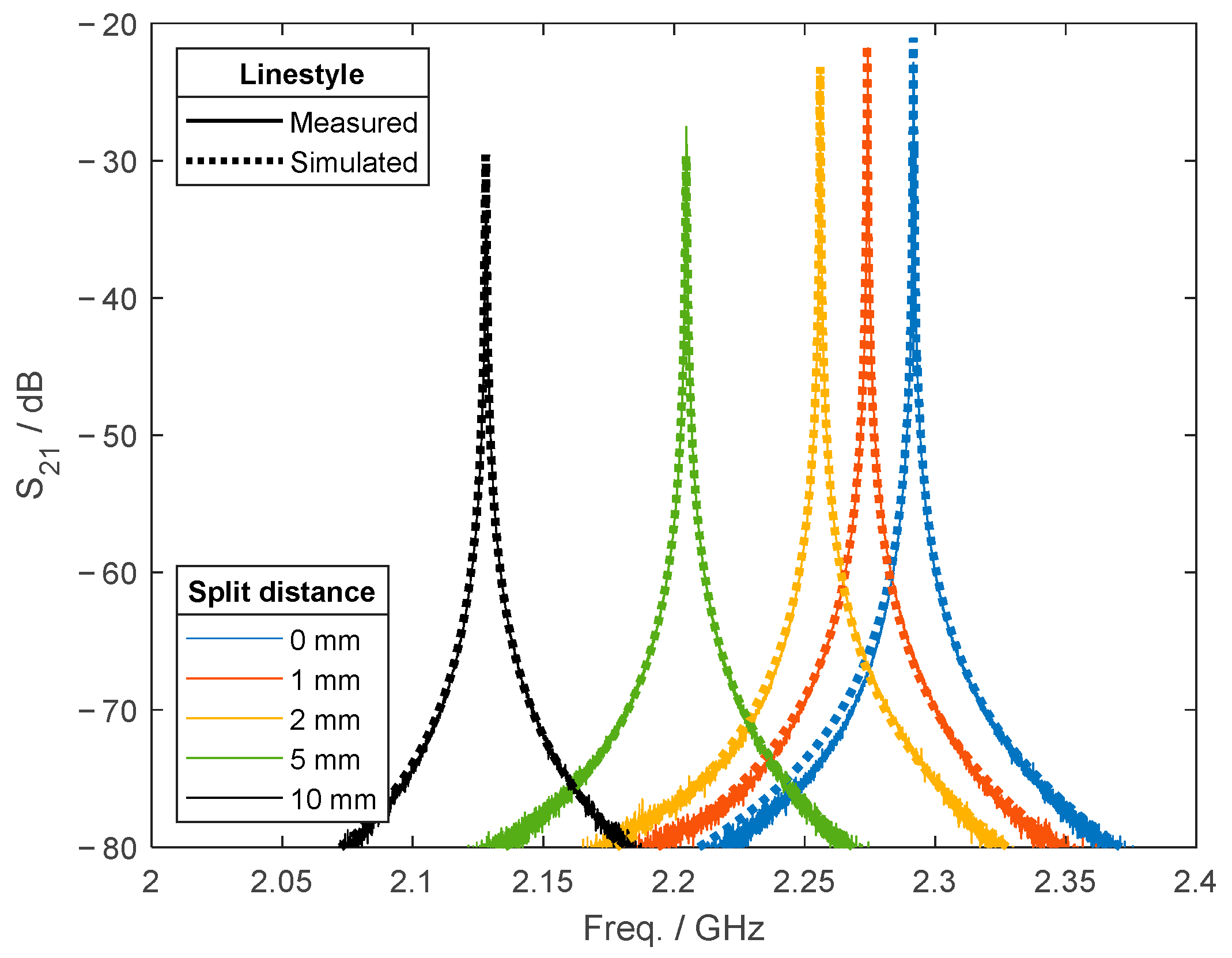
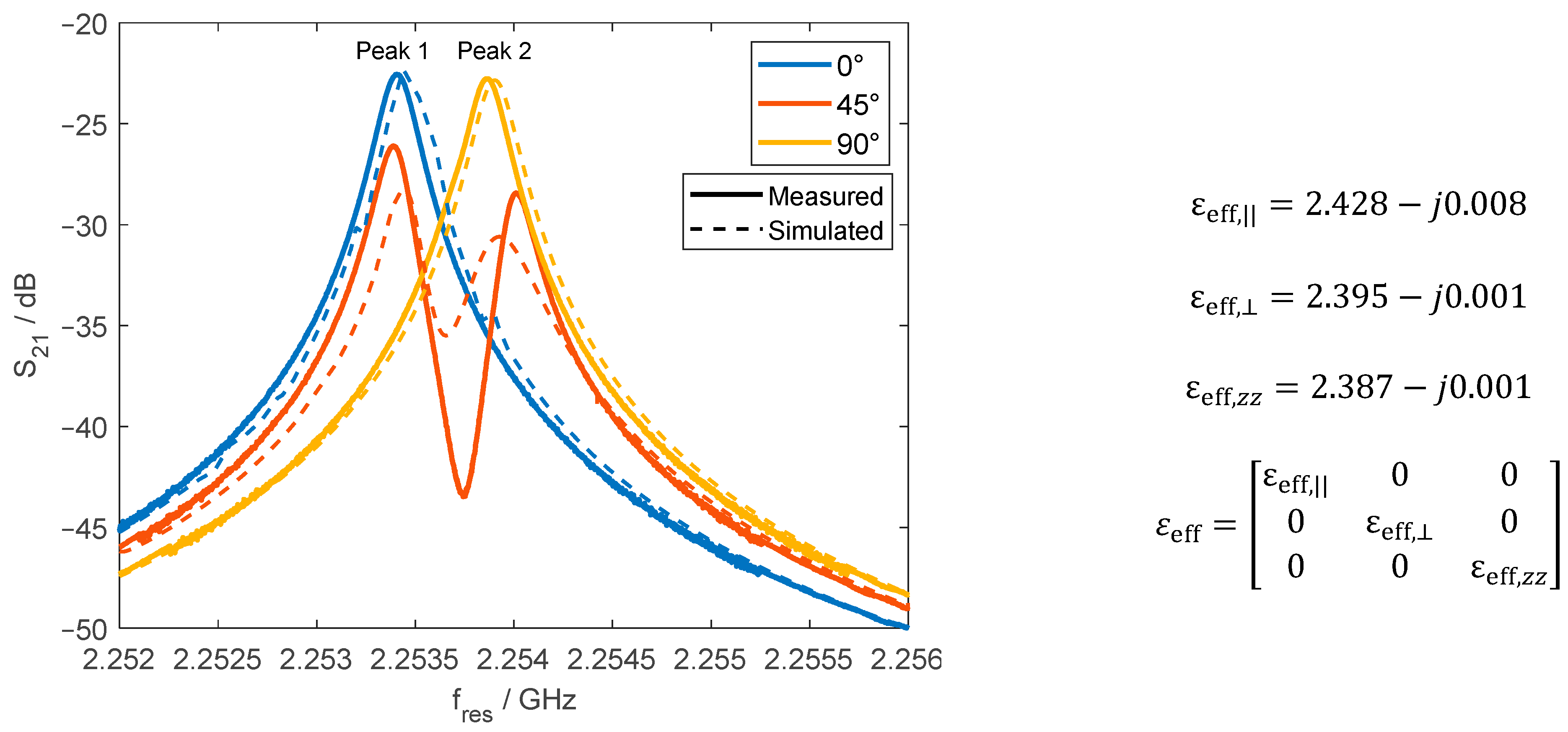
Experimental woven fabrics: The resonance frequency of a woven alumina fabric in a microwave resonator is compared experimentally with that from numerical simulations, where the permittivity of the fabric is estimated using the proposed approaches applied for woven fabrics.
The manuscript’s structure is outlined as follows:
Section 2 presents the methodologies used for estimating
εeff, including numerical calculations, conventional EMA models, the proposed novel approaches, and a revised capacitance model from the literature. This section also describes the experimental procedure and characteristics of a fibrous sample used for experimental confirmation.
Section 3 compares the methods’ estimates, emphasizing which approach provides the best estimates for simulated dispersed fibers, simulated woven fabrics, and an experimental alumina fabric.
Section 4 summarizes the key findings and limitations of the analyzed approaches.