Mechanical Properties of Lattice Structures with a Central Cube: Experiments and Simulations
Abstract
1. Introduction
2. Experiments
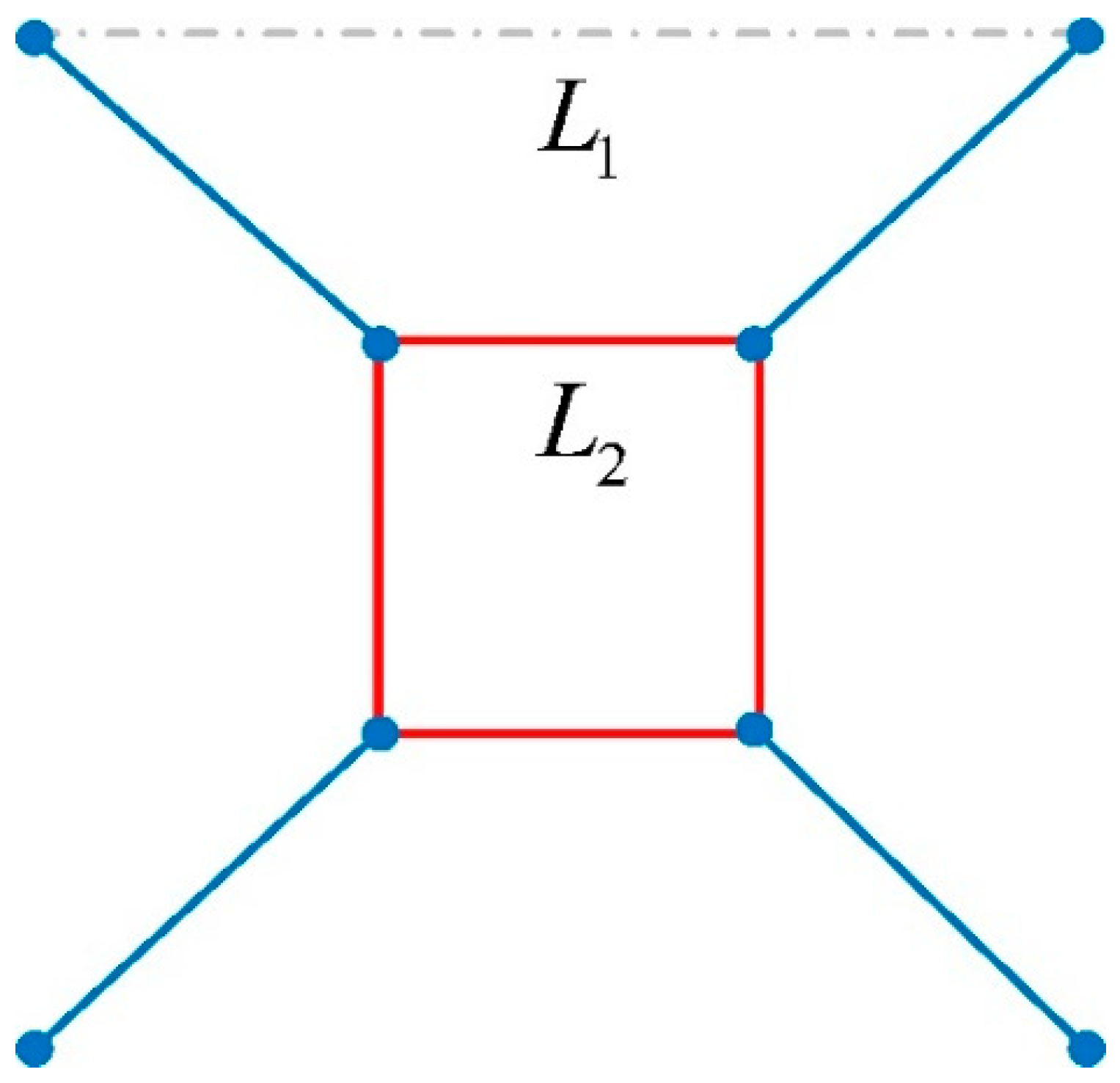
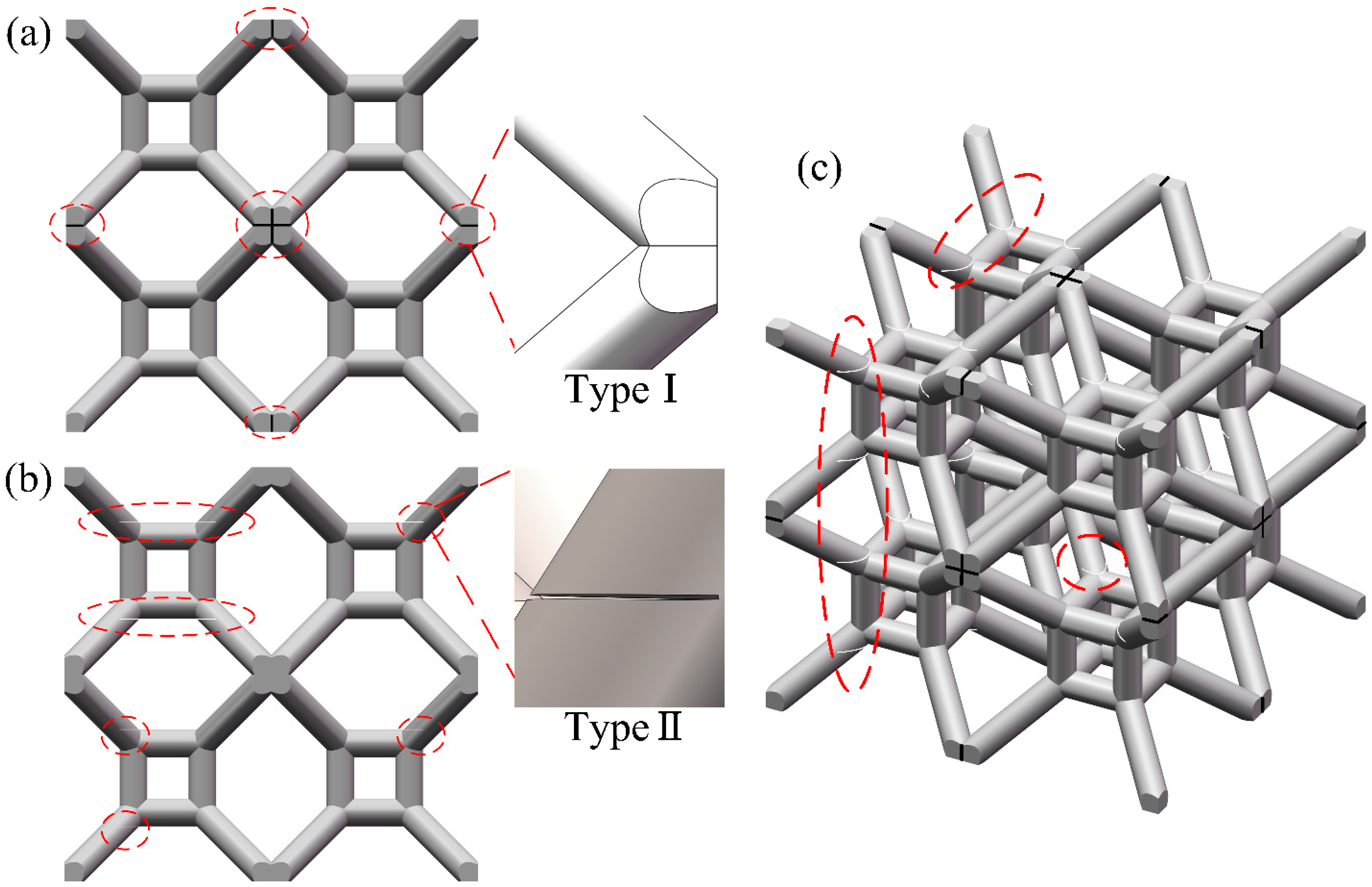
2.1. Design of Lattice Structures
2.2. Additive Manufacturing of Lattice Structures
2.3. Mechanical Tests
2.4. Preliminary Analysis
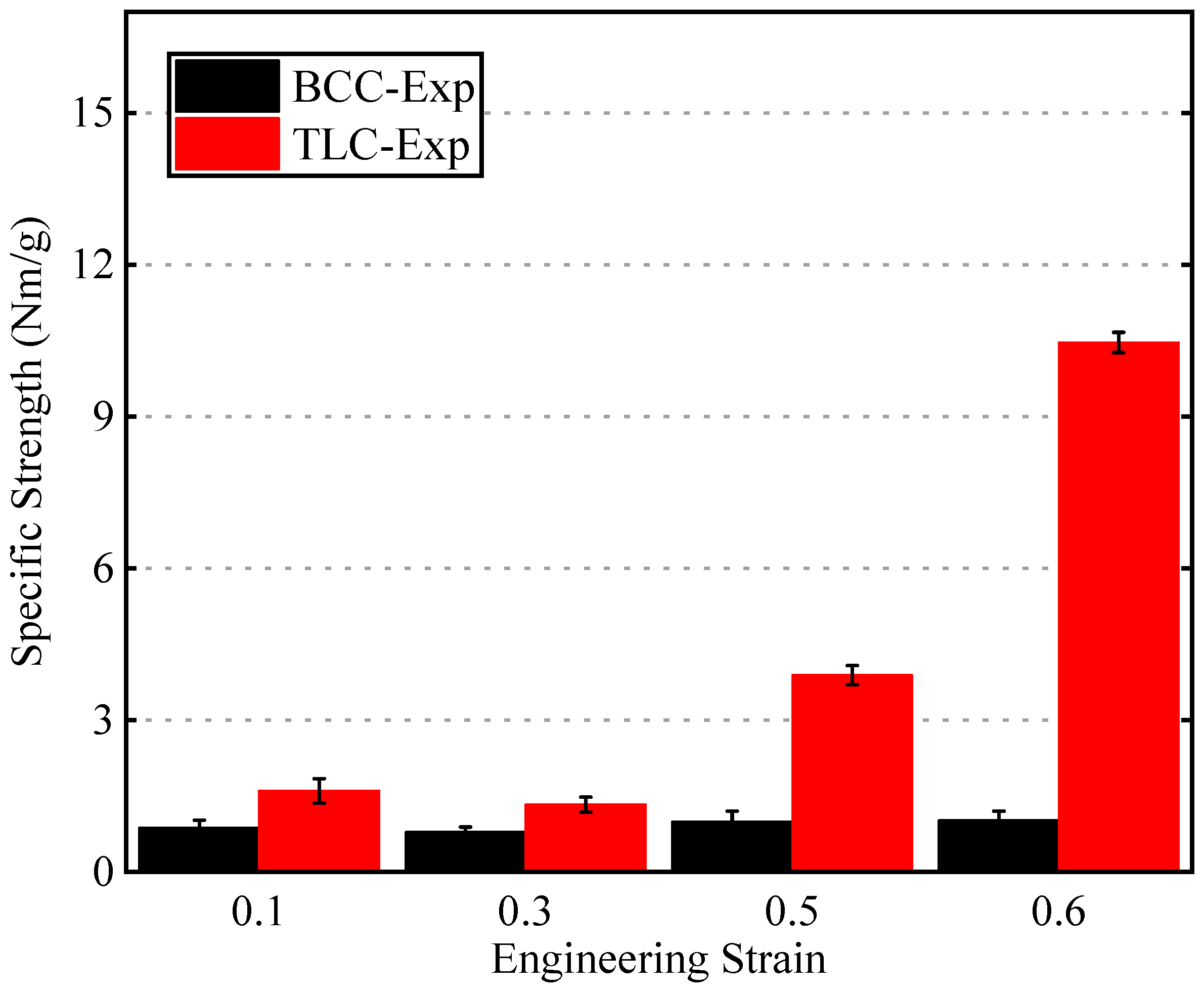
2.4.1. Energy Absorption and Specific Strength
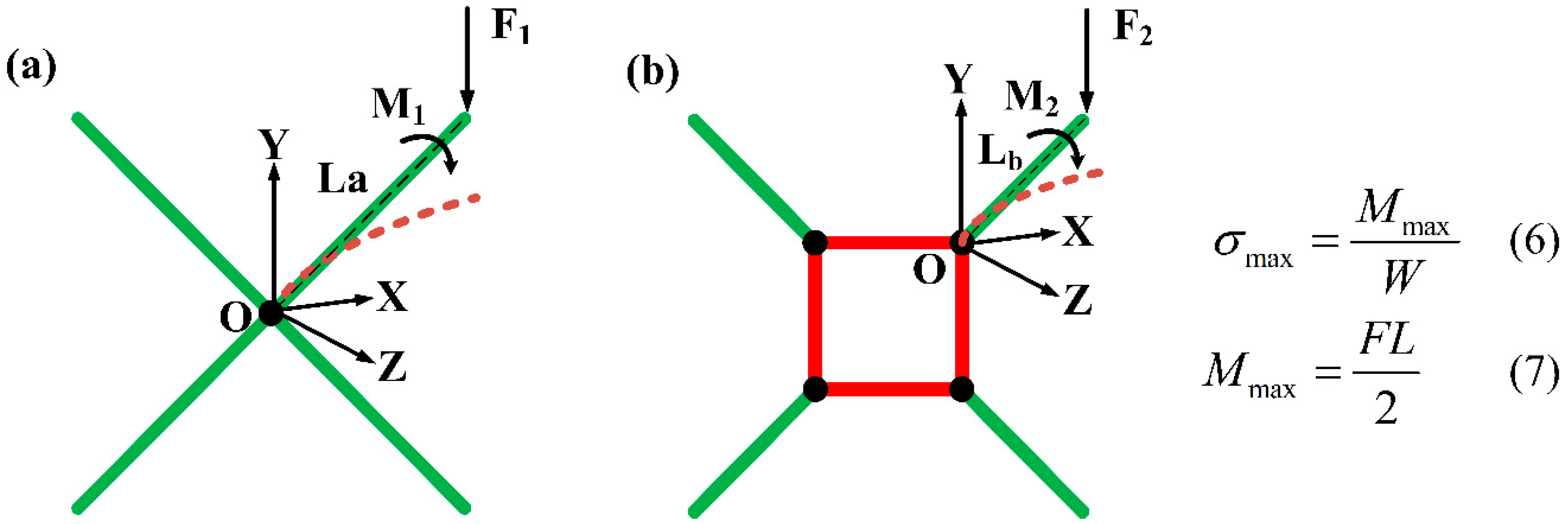
2.4.2. Bending Strength of Struts
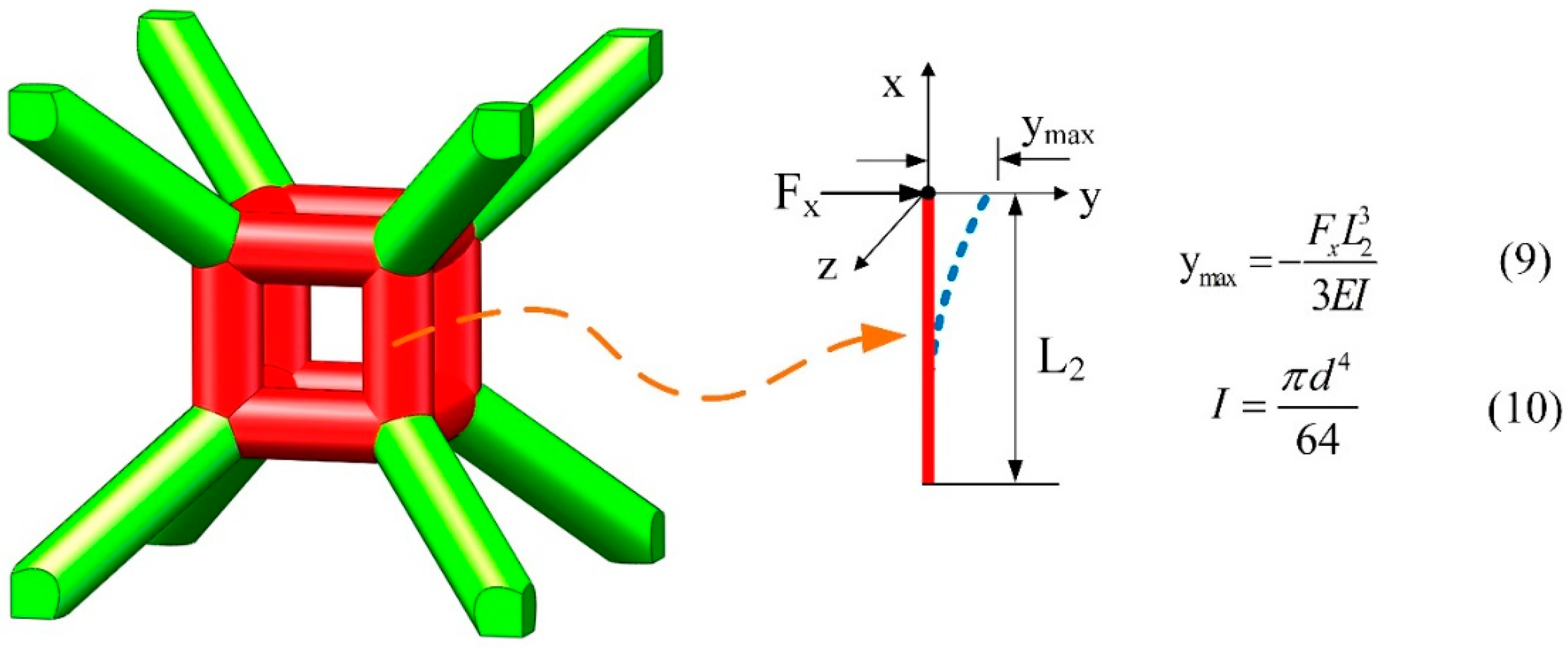
2.4.3. Deflection of Vertical Central Struts
3. Finite Element Modeling
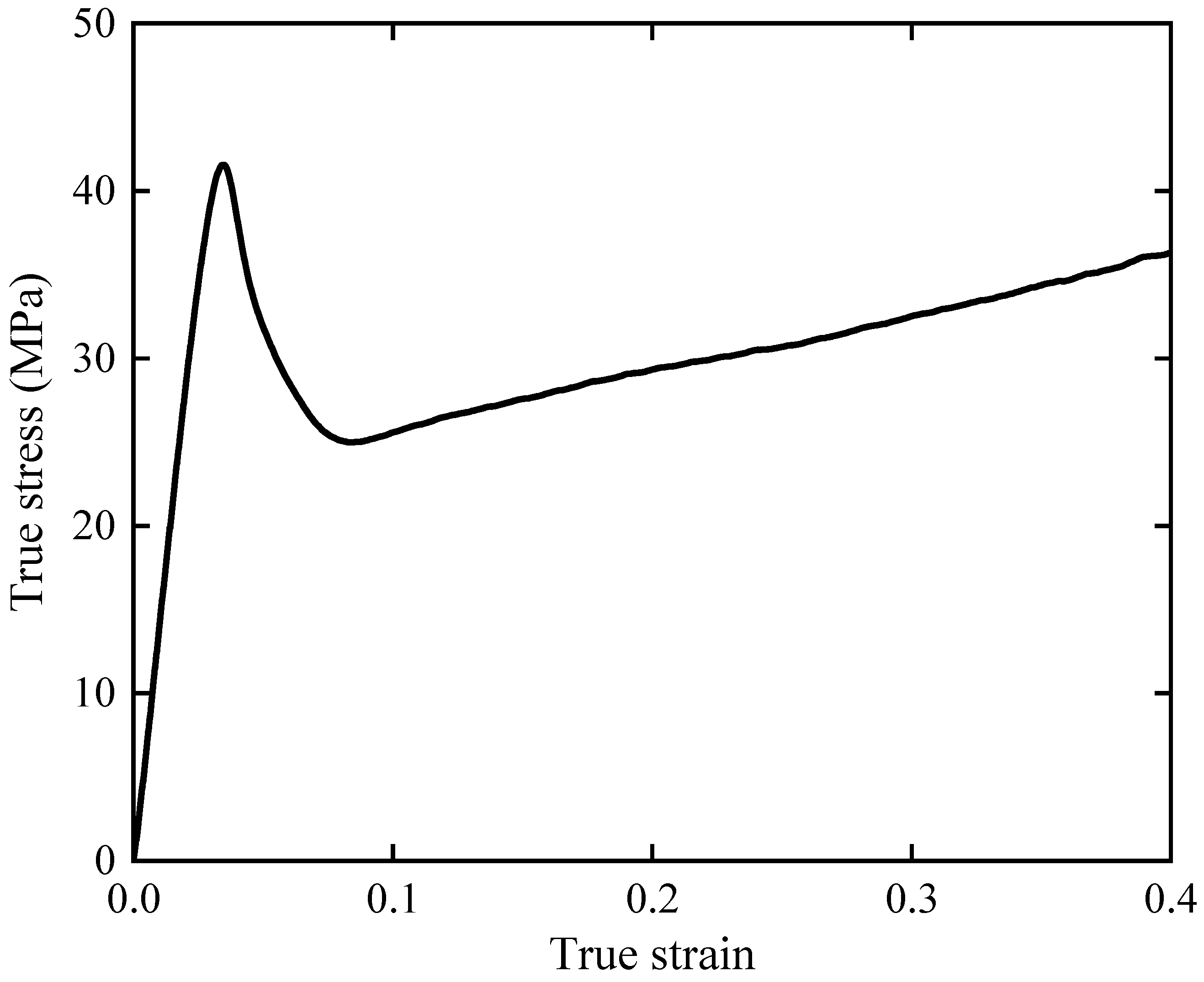
3.1. Material Properties
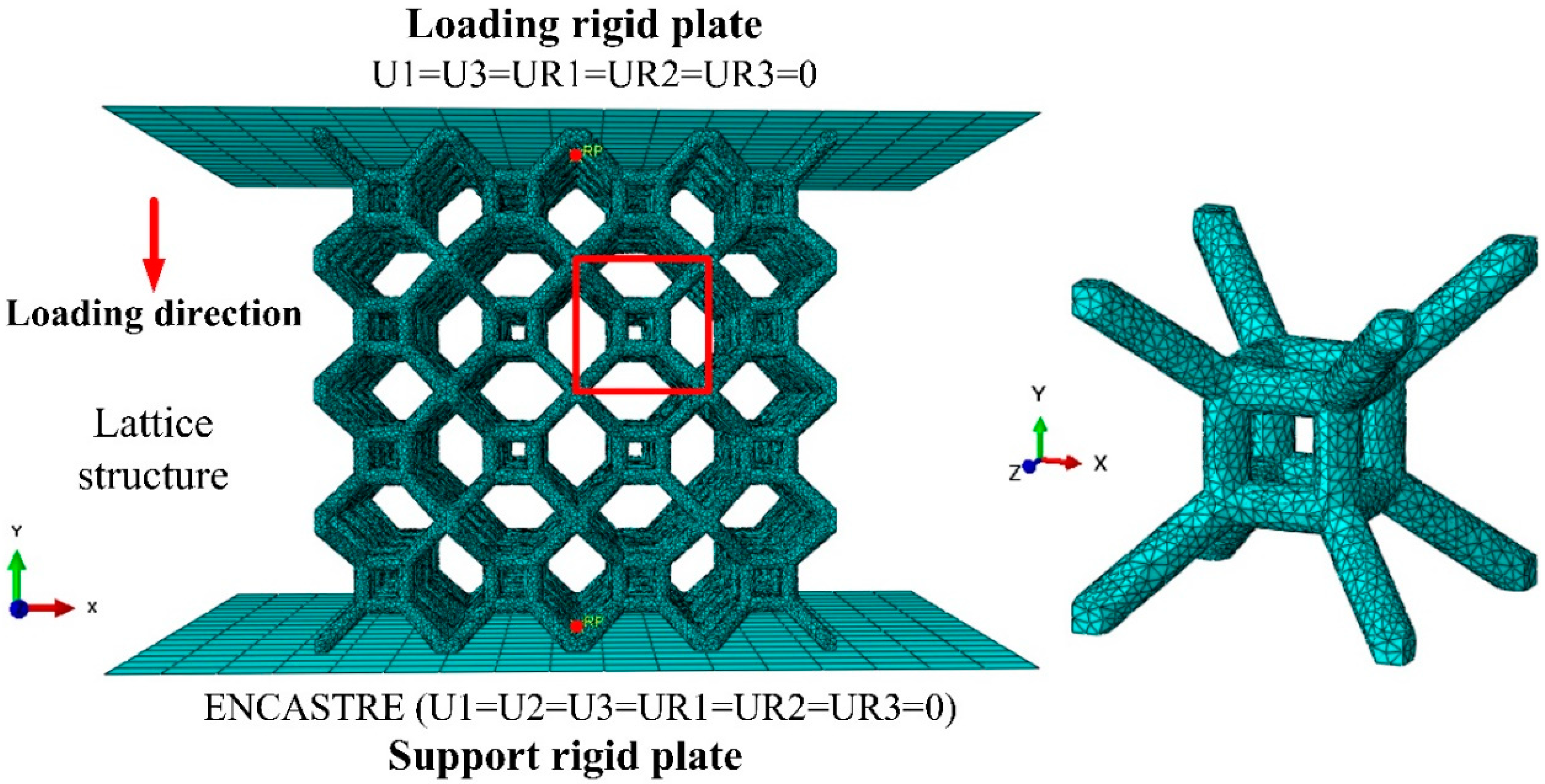
3.2. Finite Element Model
4. Results and Discussion
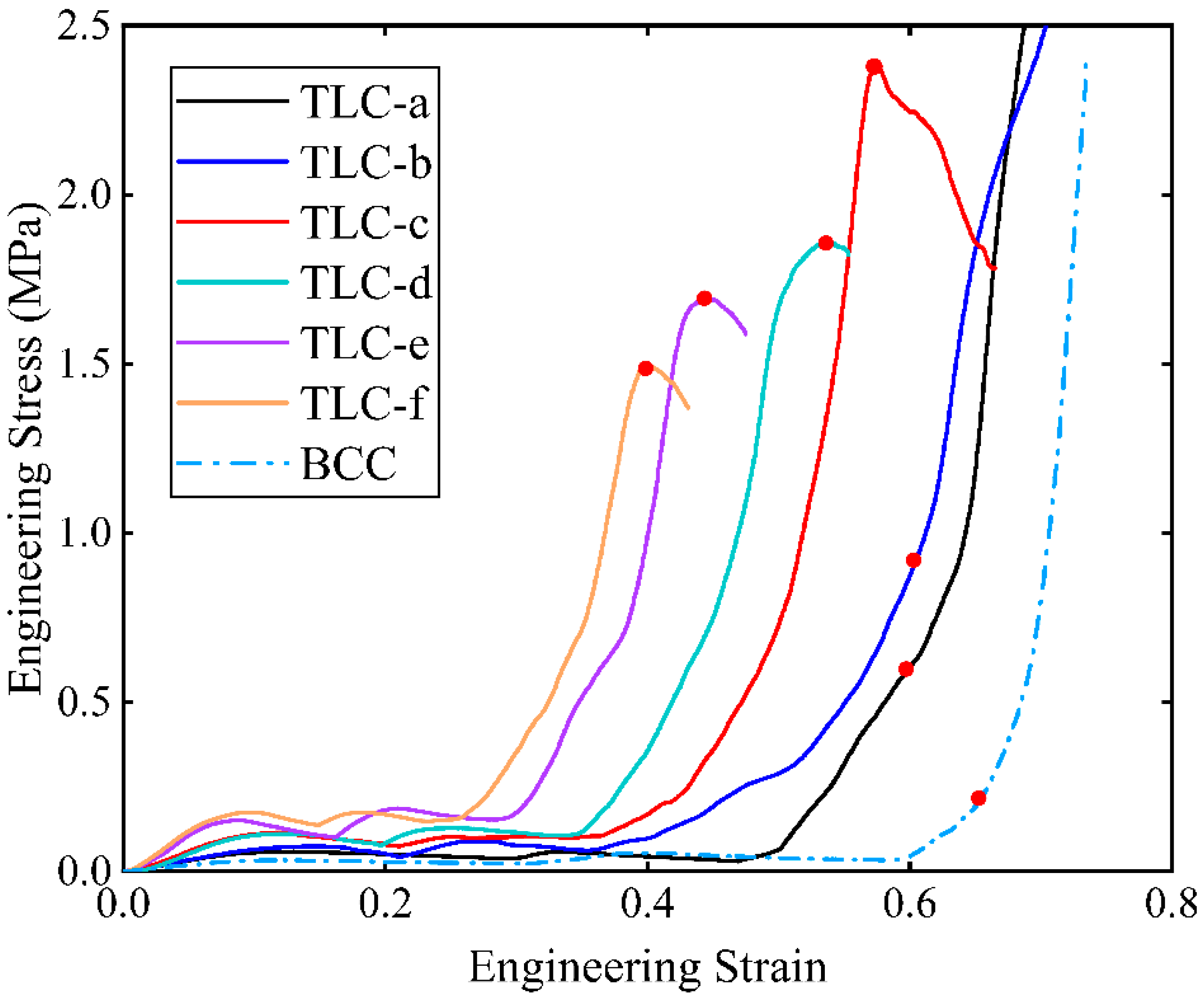
4.1. The Optimal Size of the Central Cubic Truss in the TLC Structure
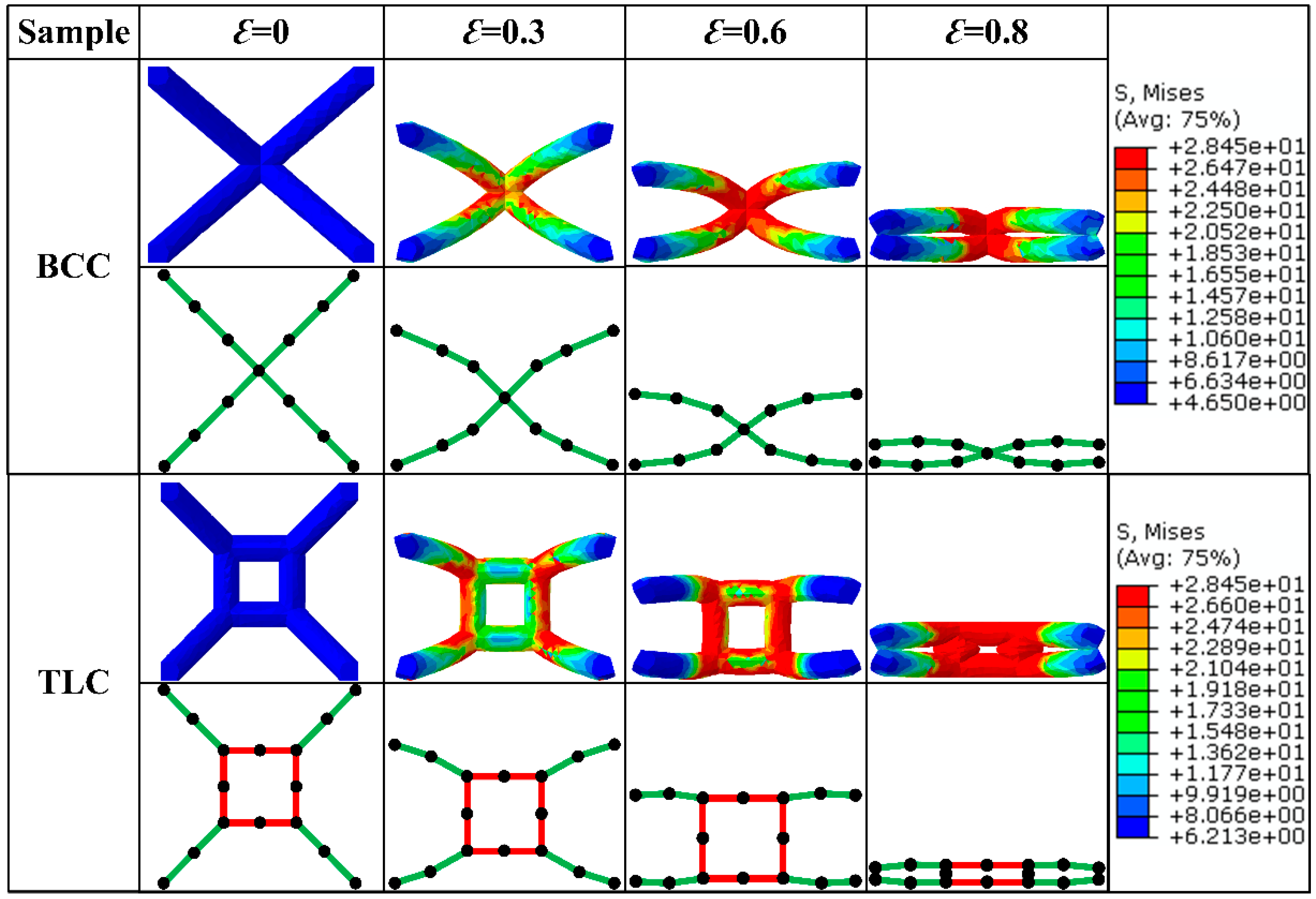
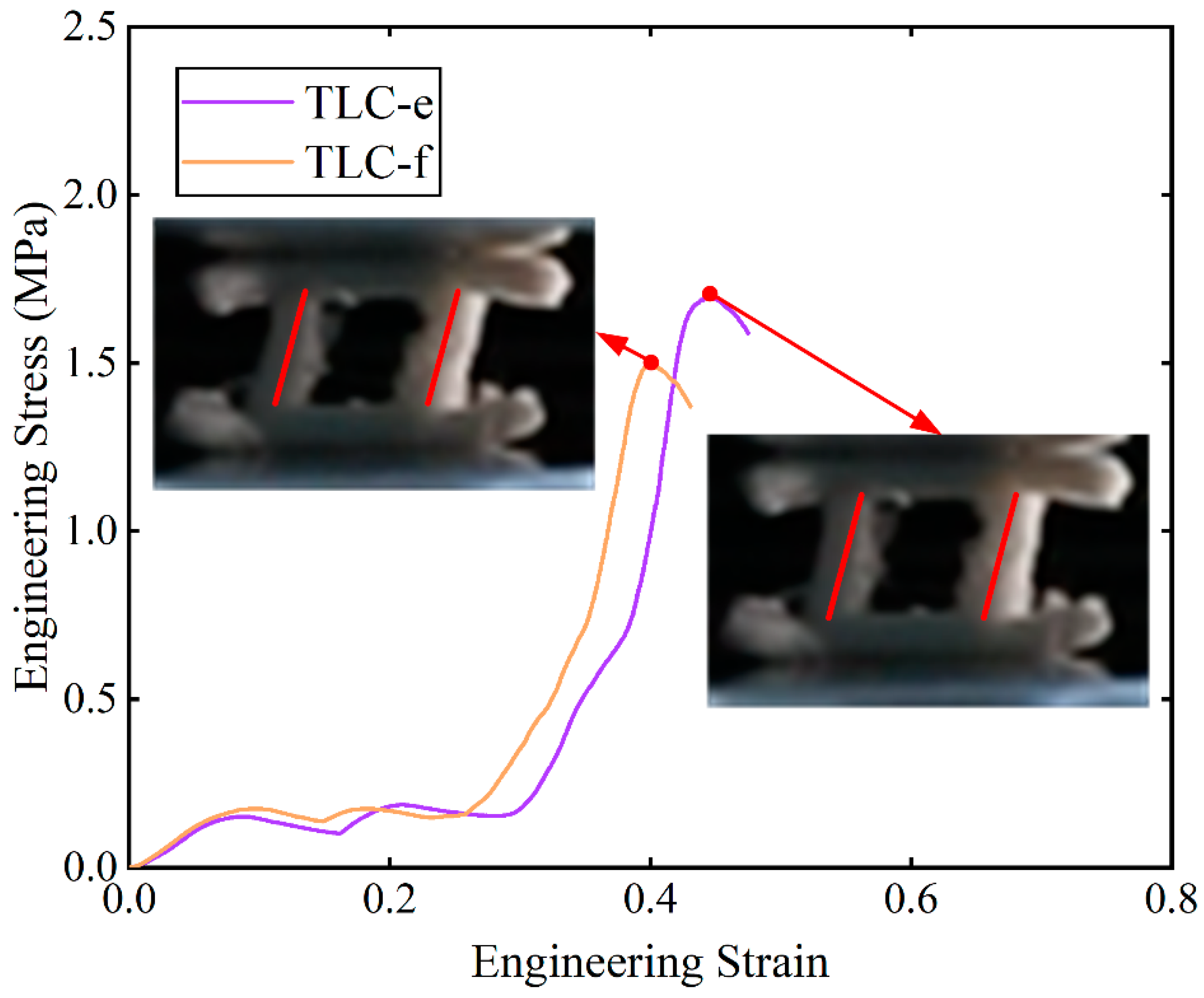
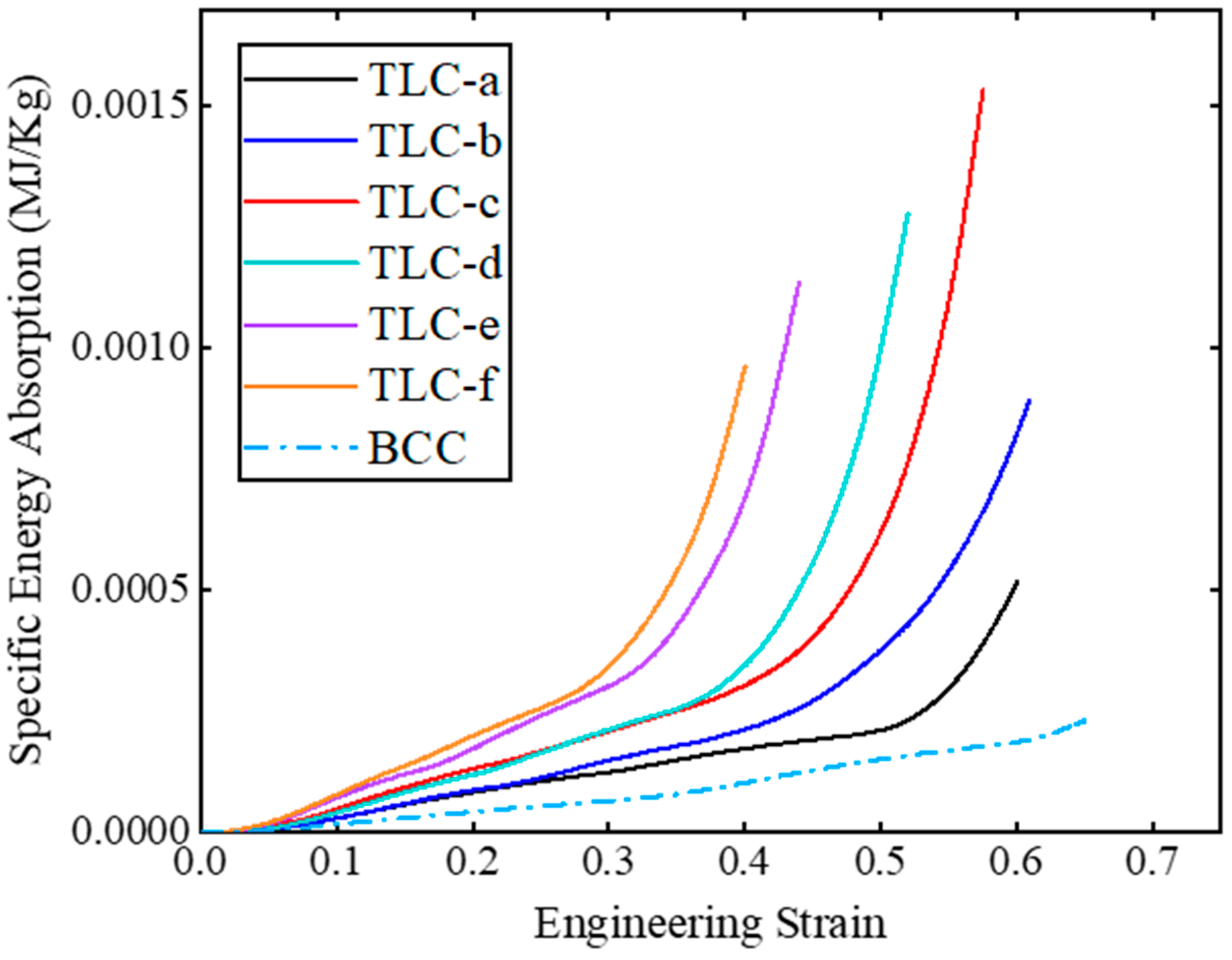
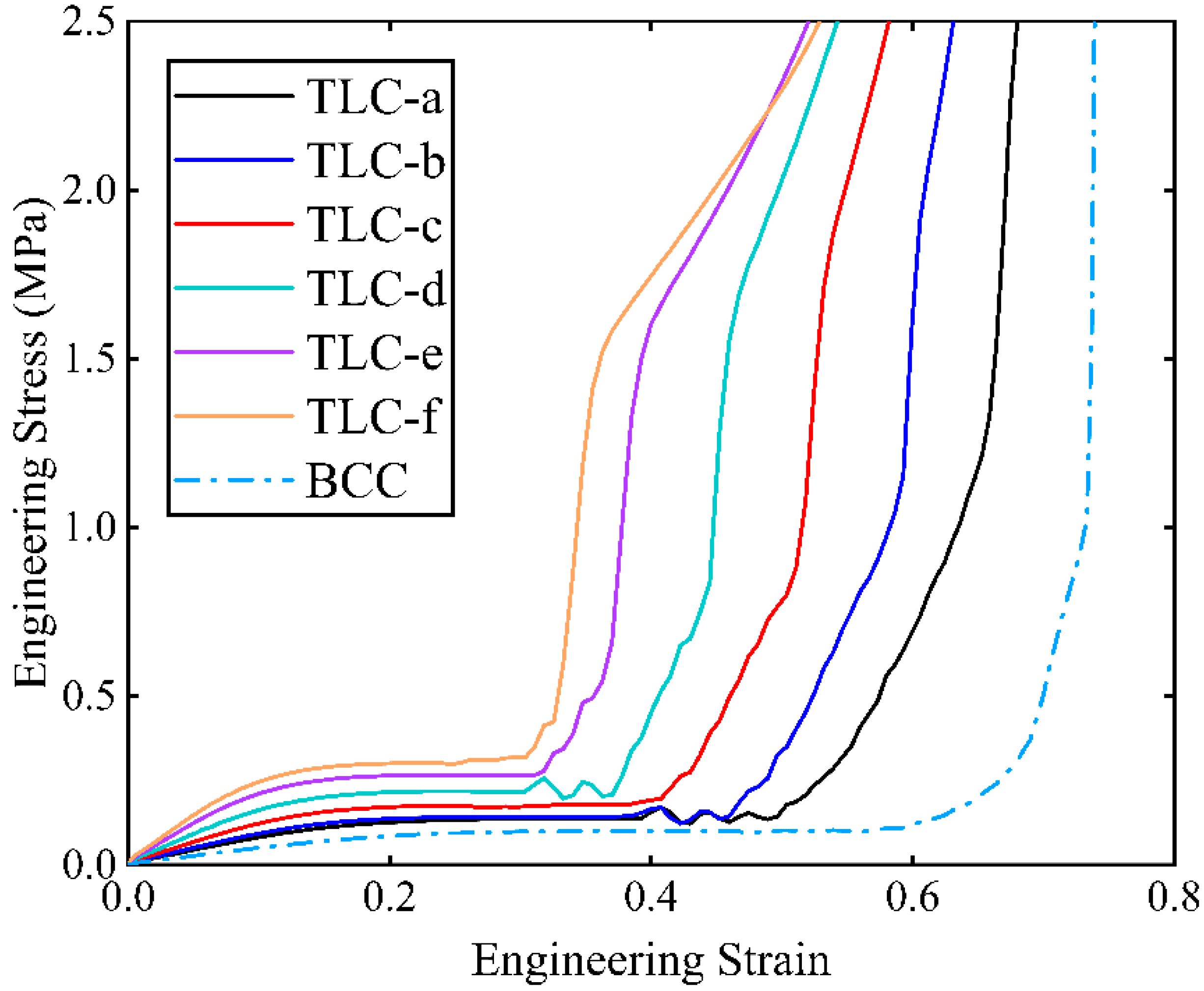
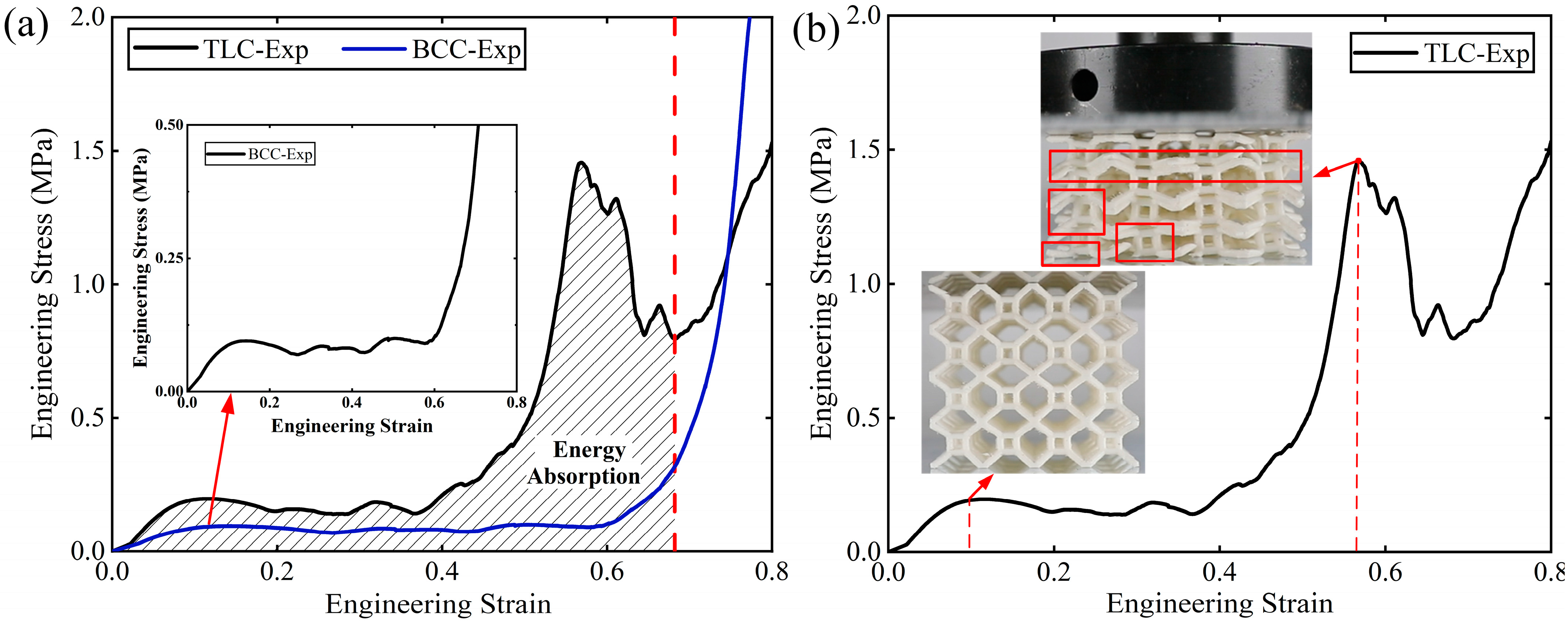
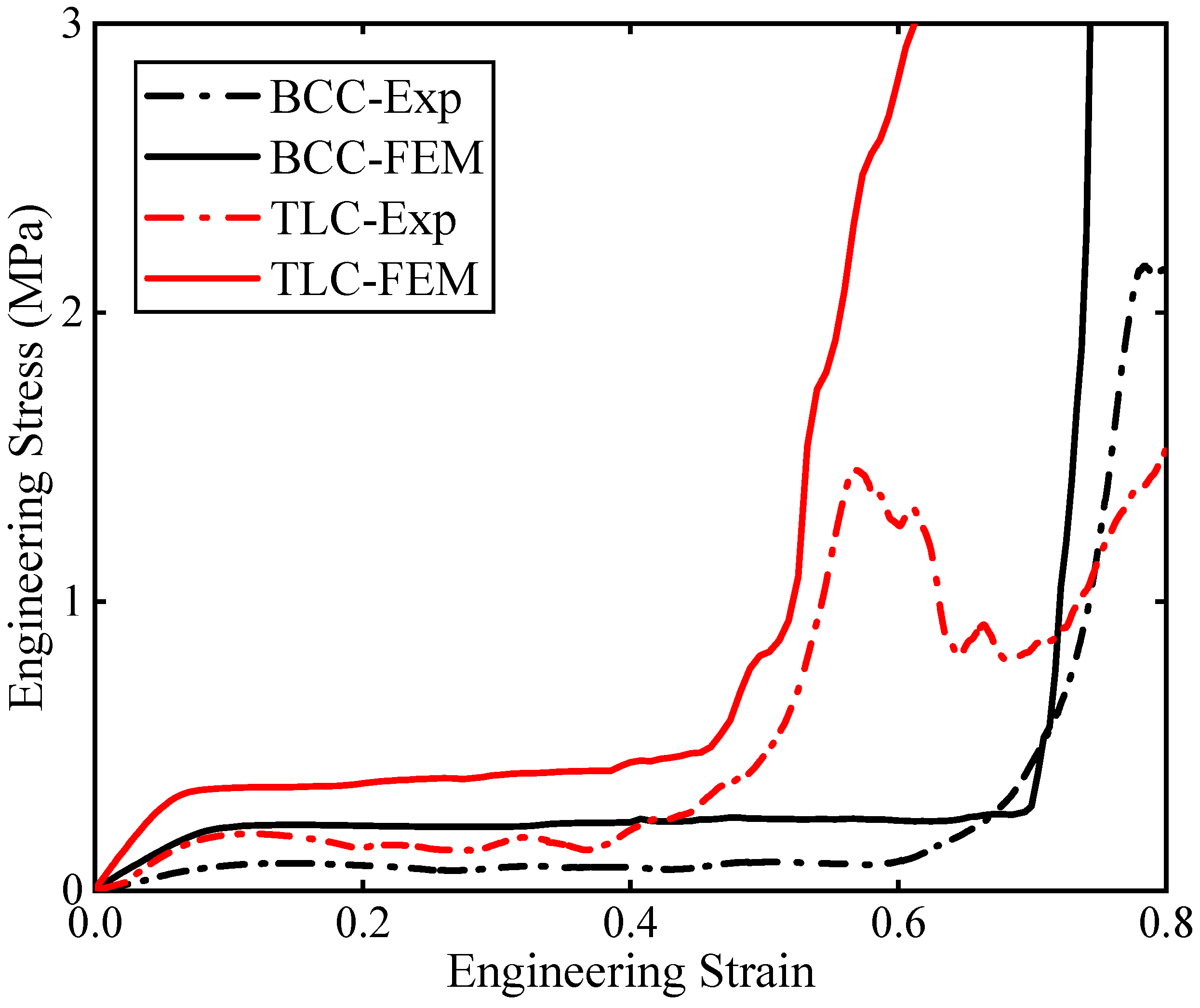
4.2. Experimental Results for 4 × 4 × 4 Structures
4.3. Finite Element Modeling for Lattice Structures with Defects
4.3.1. Establishment of the Finite Element Model for Lattice Structures with Microcracks
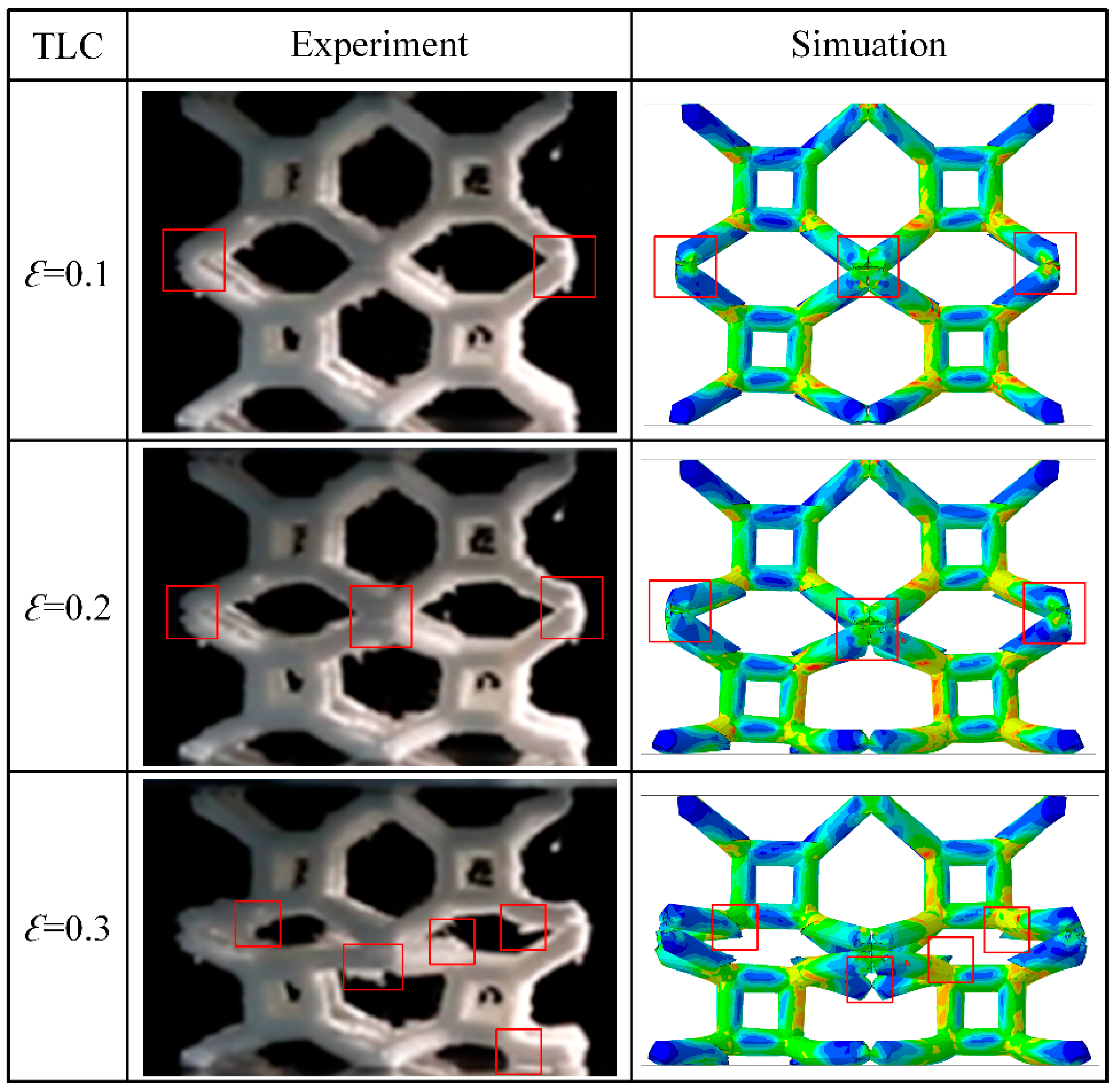
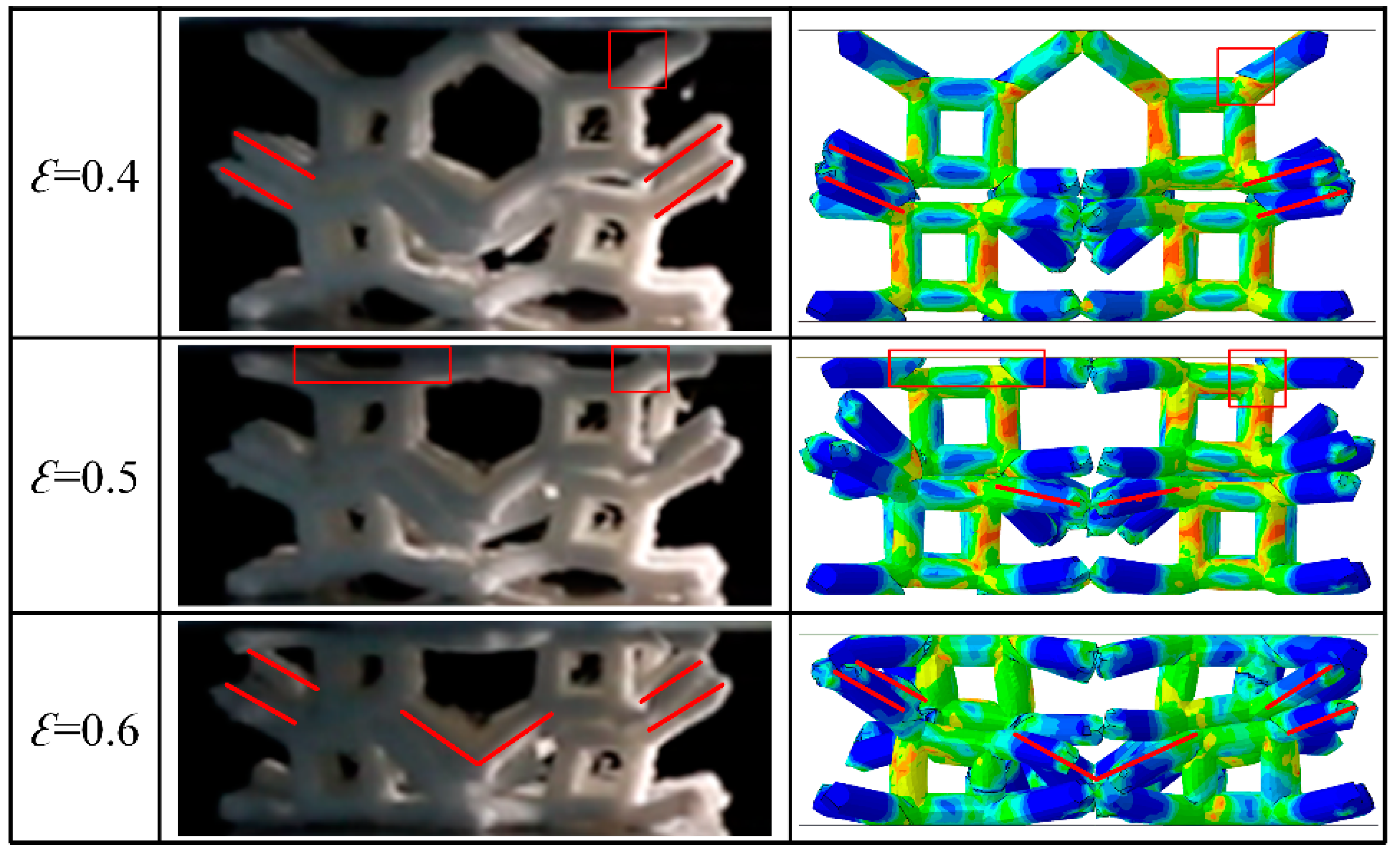
4.3.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashby, M.; Evans, A.; Fleck, N.; Gibson, L.; Hutchinson, J.; Wadley, H.; Delale, F. Reviewer Metal Foams: A Design Guide. Appl. Mech. Rev. 2001, 54, B105–B106. [Google Scholar] [CrossRef]
- Wadley, H.N. Multifunctional Periodic Cellular Metals. Philos. Transact. A Math. Phys. Eng. Sci. 2006, 364, 31–68. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F.; Harley, B.A. Cellular Materials in Nature and Medicine; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-521-19544-7. [Google Scholar]
- Craster, R.; Guenneau, S. Acoustic Metamaterials: Negative Refraction, Imaging, Lensing and Cloaking; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Khelif, A.; Adibi, A. (Eds.) Phononic Crystals: Fundamentals and Applications; Springer: New York, NY, USA, 2016; ISBN 978-1-4614-9392-1. [Google Scholar]
- Babaee, S.; Viard, N.; Wang, P.; Fang, N.X.; Bertoldi, K. Harnessing Deformation to Switch on and off the Propagation of Sound. Adv. Mater. Deerfield Beach Fla 2016, 28, 1631–1635. [Google Scholar] [CrossRef] [PubMed]
- Reyes, R.L.; Ghim, M.-S.; Kang, N.-U.; Park, J.-W.; Gwak, S.-J.; Cho, Y.-S. Development and Assessment of Modified-Honeycomb-Structure Scaffold for Bone Tissue Engineering. Addit. Manuf. 2022, 54, 102740. [Google Scholar] [CrossRef]
- Hajare, D.M.; Gajbhiye, T.S. Additive Manufacturing (3D Printing): Recent Progress on Advancement of Materials and Challenges. Mater. Today Proc. 2022, 58, 736–743. [Google Scholar] [CrossRef]
- Song, S.; Xiong, C.; Zheng, J.; Yin, J.; Zou, Y.; Zhu, X. Compression, Bending, Energy Absorption Properties, and Failure Modes of Composite Kagome Honeycomb Sandwich Structure Reinforced by PMI Foams. Compos. Struct. 2021, 277, 114611. [Google Scholar] [CrossRef]
- Landi, D.; Zefinetti, F.C.; Spreafico, C.; Regazzoni, D. Comparative Life Cycle Assessment of Two Different Manufacturing Technologies: Laser Additive Manufacturing and Traditional Technique. Procedia CIRP 2022, 105, 700–705. [Google Scholar] [CrossRef]
- Zhong, R.; Ren, X.; Yu Zhang, X.; Luo, C.; Zhang, Y.; Min Xie, Y. Mechanical Properties of Concrete Composites with Auxetic Single and Layered Honeycomb Structures. Constr. Build. Mater. 2022, 322, 126453. [Google Scholar] [CrossRef]
- Wei, Y.-L.; Yang, Q.-S.; Liu, X.; Tao, R. Multi-Bionic Mechanical Metamaterials: A Composite of FCC Lattice and Bone Structures. Int. J. Mech. Sci. 2022, 213, 106857. [Google Scholar] [CrossRef]
- Yang, J.; Chen, X.; Sun, Y.; Zhang, J.; Feng, C.; Wang, Y.; Wang, K.; Bai, L. Compressive Properties of Bidirectionally Graded Lattice Structures. Mater. Des. 2022, 218, 110683. [Google Scholar] [CrossRef]
- Feng, G.; Li, S.; Xiao, L.; Song, W. Energy Absorption Performance of Honeycombs with Curved Cell Walls under Quasi-Static Compression. Int. J. Mech. Sci. 2021, 210, 106746. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, Y.; Fan, S.; Yang, N.; Wu, N. Design and Optimization of Graded Lattice Structures with Load Path-Oriented Reinforcement. Mater. Des. 2023, 227, 111776. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Xu, Y.; Zhang, W.; Zhu, J. Compressive Behavior and Energy Absorption of Polymeric Lattice Structures Made by Additive Manufacturing. Front. Mech. Eng. 2020, 15, 319–327. [Google Scholar] [CrossRef]
- Zhang, J.; Hong, R.; Wang, H. 3D-Printed Functionally-Graded Lattice Structure with Tunable Removal Characteristics for Precision Polishing. Addit. Manuf. 2022, 59, 103152. [Google Scholar] [CrossRef]
- Caiazzo, F.; Alfieri, V.; Campanelli, S.L.; Errico, V. Additive Manufacturing and Mechanical Testing of Functionally-Graded Steel Strut-Based Lattice Structures. J. Manuf. Process. 2022, 83, 717–728. [Google Scholar] [CrossRef]
- Plocher, J.; Panesar, A. Effect of Density and Unit Cell Size Grading on the Stiffness and Energy Absorption of Short Fibre-Reinforced Functionally Graded Lattice Structures. Addit. Manuf. 2020, 33, 101171. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Zhang, D.Z.; Zhai, W. TPMS-Based Interpenetrating Lattice Structures: Design, Mechanical Properties and Multiscale Optimization. Int. J. Mech. Sci. 2023, 244, 108092. [Google Scholar] [CrossRef]
- Dong, L. Mechanical Responses of Ti-6Al-4V Truss Lattices Having a Combined Simple-Cubic and Body-Centered-Cubic (SC-BCC) Topology. Aerosp. Sci. Technol. 2021, 116, 106852. [Google Scholar] [CrossRef]
- Yang, X.; Gong, Y.; Zhao, L.; Zhang, J.; Hu, N. Compressive Mechanical Properties of Layer Hybrid Lattice Structures Fabricated by Laser Powder Bed Fusion Technique. J. Mater. Res. Technol. 2023, 22, 1800–1811. [Google Scholar] [CrossRef]
- Chen, X.; Ji, Q.; Wei, J.; Tan, H.; Yu, J.; Zhang, P.; Laude, V.; Kadic, M. Light-Weight Shell-Lattice Metamaterials for Mechanical Shock Absorption. Int. J. Mech. Sci. 2020, 169, 105288. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Zhang, D.Z.; Zhai, W. Design, Mechanical Properties and Optimization of Lattice Structures with Hollow Prismatic Struts. Int. J. Mech. Sci. 2023, 238, 107842. [Google Scholar] [CrossRef]
- Zhong, H.Z.; Song, T.; Li, C.W.; Das, R.; Gu, J.F.; Qian, M. Understanding the Superior Mechanical Properties of Hollow-Strut Metal Lattice Materials. Scr. Mater. 2023, 228, 115341. [Google Scholar] [CrossRef]
- Xiao, L.; Feng, G.; Li, S.; Mu, K.; Qin, Q.; Song, W. Mechanical Characterization of Additively-Manufactured Metallic Lattice Structures with Hollow Struts under Static and Dynamic Loadings. Int. J. Impact Eng. 2022, 169, 104333. [Google Scholar] [CrossRef]
- Červinek, O.; Pettermann, H.; Todt, M.; Koutný, D.; Vaverka, O. Non-Linear Dynamic Finite Element Analysis of Micro-Strut Lattice Structures Made by Laser Powder Bed Fusion. J. Mater. Res. Technol. 2022, 18, 3684–3699. [Google Scholar] [CrossRef]
- Liu, X.; Wada, T.; Suzuki, A.; Takata, N.; Kobashi, M.; Kato, M. Understanding and Suppressing Shear Band Formation in Strut-Based Lattice Structures Manufactured by Laser Powder Bed Fusion. Mater. Des. 2021, 199, 109416. [Google Scholar] [CrossRef]
- Bai, L.; Xu, Y.; Chen, X.; Xin, L.; Zhang, J.; Li, K.; Sun, Y. Improved Mechanical Properties and Energy Absorption of Ti6Al4V Laser Powder Bed Fusion Lattice Structures Using Curving Lattice Struts. Mater. Des. 2021, 211, 110140. [Google Scholar] [CrossRef]
- Zhu, S.; Ma, L.; Wang, B.; Hu, J.; Zhou, Z. Lattice Materials Composed by Curved Struts Exhibit Adjustable Macroscopic Stress-Strain Curves. Mater. Today Commun. 2018, 14, 273–281. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and Specific Energy Absorption of Additively-Manufactured Metallic BCC Metamaterials Composed of Tapered Beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Gu, X.; Zhou, Y.; Yin, Y.; Tan, Q.; Li, M.; Zhang, M.-X. Mechanical Performance of a Node Reinforced Body-Centred Cubic Lattice Structure Manufactured via Selective Laser Melting. Scr. Mater. 2020, 189, 95–100. [Google Scholar] [CrossRef]
- Topologically Optimized Lattice Structures with Superior Fatigue Performance. Int. J. Fatigue 2022, 165, 107188. [CrossRef]
- Ma, X.; Zhang, D.Z.; Luo, T.; Zheng, X.; Zhou, H. Novel Optimal Design-Making Model of Additive Manufactured Lattice Structures Based on Mechanical Physical Model. Mater. Today Commun. 2024, 38, 107823. [Google Scholar] [CrossRef]
- Sun, Z.; Gong, Y.; Bian, Z.; Zhang, J.; Zhao, L.; Hu, N. Mechanical Properties of Bionic Lattice and Its Hybrid Structures Based on the Microstructural Design of Pomelo Peel. Thin-Walled Struct. 2024, 198, 111715. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Ashby, M.F.; Fleck, N.A. Foam Topology: Bending versus Stretching Dominated Architectures. Acta Mater. 2001, 49, 1035–1040. [Google Scholar] [CrossRef]
- Karamooz Ravari, M.R.; Kadkhodaei, M.; Badrossamay, M.; Rezaei, R. Numerical Investigation on Mechanical Properties of Cellular Lattice Structures Fabricated by Fused Deposition Modeling. Int. J. Mech. Sci. 2014, 88, 154–161. [Google Scholar] [CrossRef]
- Kaur, M.; Yun, T.G.; Han, S.M.; Thomas, E.L.; Kim, W.S. 3D Printed Stretching-Dominated Micro-Trusses. Mater. Des. 2017, 134, 272–280. [Google Scholar] [CrossRef]
- Carlton, H.D.; Volkoff-Shoemaker, N.A.; Messner, M.C.; Barton, N.R.; Kumar, M. Incorporating Defects into Model Predictions of Metal Lattice-Structured Materials. Mater. Sci. Eng. A 2022, 832, 142427. [Google Scholar] [CrossRef]
- Gautam, R.; Idapalapati, S.; Feih, S. Printing and Characterisation of Kagome Lattice Structures by Fused Deposition Modelling. Mater. Des. 2018, 137, 266–275. [Google Scholar] [CrossRef]
- Li, D.; Qin, R.; Chen, B.; Zhou, J. Analysis of Mechanical Properties of Lattice Structures with Stochastic Geometric Defects in Additive Manufacturing. Mater. Sci. Eng. A 2021, 822, 141666. [Google Scholar] [CrossRef]
- Computational Modelling of Strut Defects in SLM Manufactured Lattice Structures. Mater. Des. 2019, 171, 107671. [CrossRef]
- Sun, Z.P.; Guo, Y.B.; Shim, V.P.W. Influence of Printing Direction on the Dynamic Response of Additively-Manufactured Polymeric Materials and Lattices. Int. J. Impact Eng. 2022, 167, 104263. [Google Scholar] [CrossRef]
- Alghamdi, A.; Maconachie, T.; Downing, D.; Brandt, M.; Qian, M.; Leary, M. Effect of Additive Manufactured Lattice Defects on Mechanical Properties: An Automated Method for the Enhancement of Lattice Geometry. Int. J. Adv. Manuf. Technol. 2020, 108, 957–971. [Google Scholar] [CrossRef]
- Bacciaglia, A.; Ceruti, A.; Liverani, A. Structural Analysis of Voxel-Based Lattices Using 1D Approach. 3D Print. Addit. Manuf. 2022, 9, 365–379. [Google Scholar] [CrossRef]
- Amirpour, M.; Battley, M. Study of Manufacturing Defects on Compressive Deformation of 3D-Printed Polymeric Lattices. Int. J. Adv. Manuf. Technol. 2022, 122, 2561–2576. [Google Scholar] [CrossRef]
- Cao, X.; Jiang, Y.; Zhao, T.; Wang, P.; Wang, Y.; Chen, Z.; Li, Y.; Xiao, D.; Fang, D. Compression Experiment and Numerical Evaluation on Mechanical Responses of the Lattice Structures with Stochastic Geometric Defects Originated from Additive-Manufacturing. Compos. Part B Eng. 2020, 194, 108030. [Google Scholar] [CrossRef]
- Yang, H.; Wang, W.; Li, C.; Qi, J.; Wang, P.; Lei, H.; Fang, D. Deep Learning-Based X-Ray Computed Tomography Image Reconstruction and Prediction of Compression Behavior of 3D Printed Lattice Structures. Addit. Manuf. 2022, 54, 102774. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Meng, J.; Zhou, H.; Liu, Y.; Zhang, X.; Wang, P.; Fang, D. Evaluation of Compressive Properties of SLM-Fabricated Multi-Layer Lattice Structures by Experimental Test and μ-CT-Based Finite Element Analysis. Mater. Des. 2019, 169, 107685. [Google Scholar] [CrossRef]
- Zanini, F.; Sorgato, M.; Savio, E.; Carmignato, S. Dimensional Verification of Metal Additively Manufactured Lattice Structures by X-Ray Computed Tomography: Use of a Newly Developed Calibrated Artefact to Achieve Metrological Traceability. Addit. Manuf. 2021, 47, 102229. [Google Scholar] [CrossRef]
- Geng, L.; Wu, W.; Sun, L.; Fang, D. Damage Characterizations and Simulation of Selective Laser Melting Fabricated 3D Re-Entrant Lattices Based on in-Situ CT Testing and Geometric Reconstruction. Int. J. Mech. Sci. 2019, 157–158, 231–242. [Google Scholar] [CrossRef]
- Tkac, J.; Toth, T.; Molnar, V.; Dovica, M.; Fedorko, G. Observation of Porous Structure’s Deformation Wear after Axial Loading with the Use of Industrial Computed Tomography (CT). Measurement 2022, 200, 111631. [Google Scholar] [CrossRef]
- Dallago, M.; Winiarski, B.; Zanini, F.; Carmignato, S.; Benedetti, M. On the Effect of Geometrical Imperfections and Defects on the Fatigue Strength of Cellular Lattice Structures Additively Manufactured via Selective Laser Melting. Int. J. Fatigue 2019, 124, 348–360. [Google Scholar] [CrossRef]
- Sun, Z.P.; Guo, Y.B.; Shim, V.P.W. Characterisation and Modeling of Additively-Manufactured Polymeric Hybrid Lattice Structures for Energy Absorption. Int. J. Mech. Sci. 2021, 191, 106101. [Google Scholar] [CrossRef]
- Anisotropic Compression Behaviors of Bio-Inspired Modified Body-Centered Cubic Lattices Validated by Additive Manufacturing—ScienceDirect. Available online: https://www.sciencedirect.com/science/article/pii/S1359836822001093 (accessed on 8 October 2022).
- Wang, P.; Yang, F.; Li, P.; Zheng, B.; Fan, H. Design and Additive Manufacturing of a Modified Face-Centered Cubic Lattice with Enhanced Energy Absorption Capability. Extreme Mech. Lett. 2021, 47, 101358. [Google Scholar] [CrossRef]
- Yang, X.; Ma, W.; Zhang, Z.; Liu, S.; Tang, H. Ultra-High Specific Strength Ti6Al4V Alloy Lattice Material Manufactured via Selective Laser Melting. Mater. Sci. Eng. A 2022, 840, 142956. [Google Scholar] [CrossRef]
- ASTM D638; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2022.
- Wang, Z. Recent Advances in Novel Metallic Honeycomb Structure. Compos. Part B 2019, 166, 731–741. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.A.W. Compressive Behaviour of Stainless Steel Micro-Lattice Structures. Int. J. Mech. Sci. 2013, 68, 125–139. [Google Scholar] [CrossRef]
- Chen, Y.; Ye, L.; Zhang, Y.X.; Fu, K. Compression Behaviours of 3D-Printed CF/PA Metamaterials: Experiment and Modelling. Int. J. Mech. Sci. 2021, 206, 106634. [Google Scholar] [CrossRef]
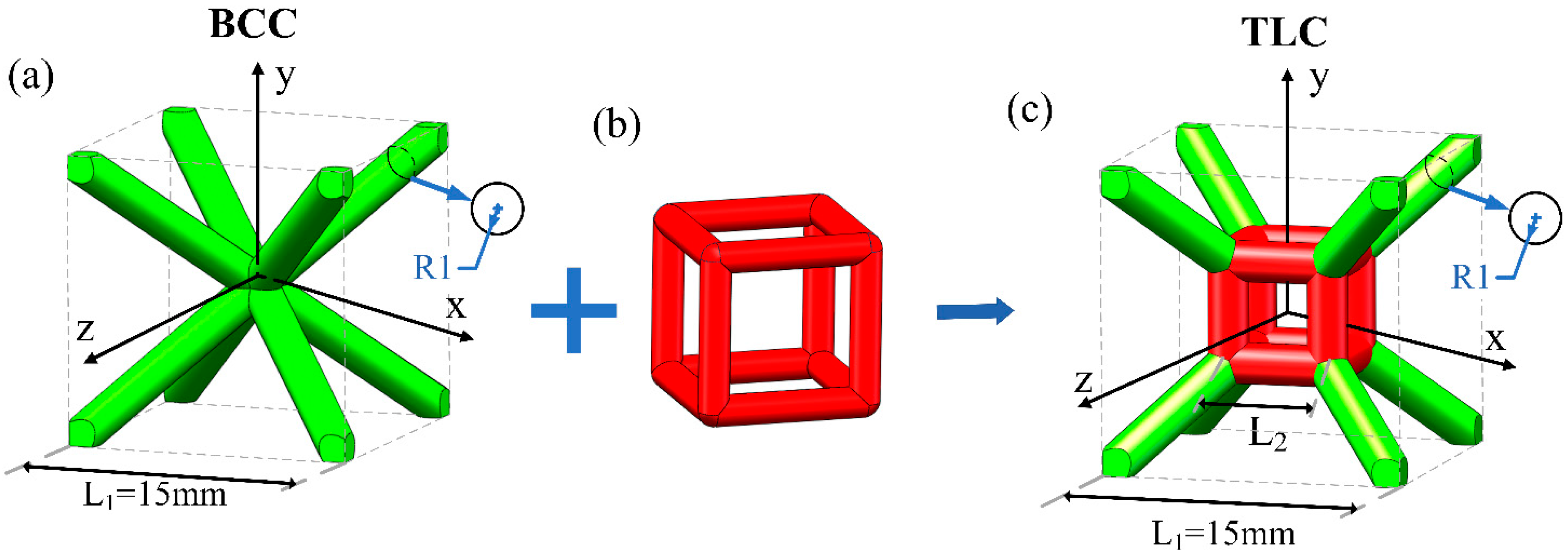









| Structure | Volume | Theoretical Mass | Actual Mass | Relative Density | Apparent Density |
|---|---|---|---|---|---|
| BCC | 18.37 cm3 | 21.70 g | 21.55 g | 0.0850 | 0.0998 |
| TLC | 22.11 cm3 | 26.09 g | 26.11 g | 0.1024 | 0.1209 |
| Elastic Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | Yield Strength (MPa) |
|---|---|---|---|
| 1.85 | 0.35 | 1200 | 42 |
| Plastic strain | 0 | 0.0045 | 0.012 | 0.021 | 0.034 | 0.132 | 0.2 | 0.3 |
| Plastic stress (MPa) | 40 | 36 | 32 | 29 | 26 | 28 | 30 | 34 |
| 3/15 a | 4/15 b | 5/15 c | 6/15 d | 7/15 e | 7.5/15 f | |
|---|---|---|---|---|---|---|
| 15 mm | 15 mm | 15 mm | 15 mm | 15 mm | 15 mm | |
| 3 mm | 4 mm | 5 mm | 6 mm | 7 mm | 7.5 mm |
| Initial Flow Stress at a Strain of 0.1 | Maximum Stress | |
|---|---|---|
| Experiment | 0.14 | 1.64 |
| Ideal structure | 0.31(121% ↑) | 3.00 (83% ↑) |
| Model A | 0.20 (43% ↑) | 2.15 (31% ↑) |
| Model B | 0.26 (86% ↑) | 1.87 (14% ↑) |
| Model C | 0.19 (36% ↑) | 1.55 (6% ↓) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Ma, Y.; Liu, P.; Chen, Y. Mechanical Properties of Lattice Structures with a Central Cube: Experiments and Simulations. Materials 2024, 17, 1329. https://doi.org/10.3390/ma17061329
Guo S, Ma Y, Liu P, Chen Y. Mechanical Properties of Lattice Structures with a Central Cube: Experiments and Simulations. Materials. 2024; 17(6):1329. https://doi.org/10.3390/ma17061329
Chicago/Turabian StyleGuo, Shuai, Yuwei Ma, Peng Liu, and Yang Chen. 2024. "Mechanical Properties of Lattice Structures with a Central Cube: Experiments and Simulations" Materials 17, no. 6: 1329. https://doi.org/10.3390/ma17061329
APA StyleGuo, S., Ma, Y., Liu, P., & Chen, Y. (2024). Mechanical Properties of Lattice Structures with a Central Cube: Experiments and Simulations. Materials, 17(6), 1329. https://doi.org/10.3390/ma17061329





