Mechanistic Analysis of Reflective Cracking Potential in Electrified Pavement with Inductive Charging System
Abstract
:1. Introduction
2. Objective and Scope
3. Development of Finite Element Model
3.1. Structure of Electrified Pavement
3.2. Development of Finite Element Models
3.3. Climate Inputs and Temperature Prediction
3.4. Pavement Material Properties
3.5. Crack Initiation and Propagation
3.6. Modeling of Layer Interfaces
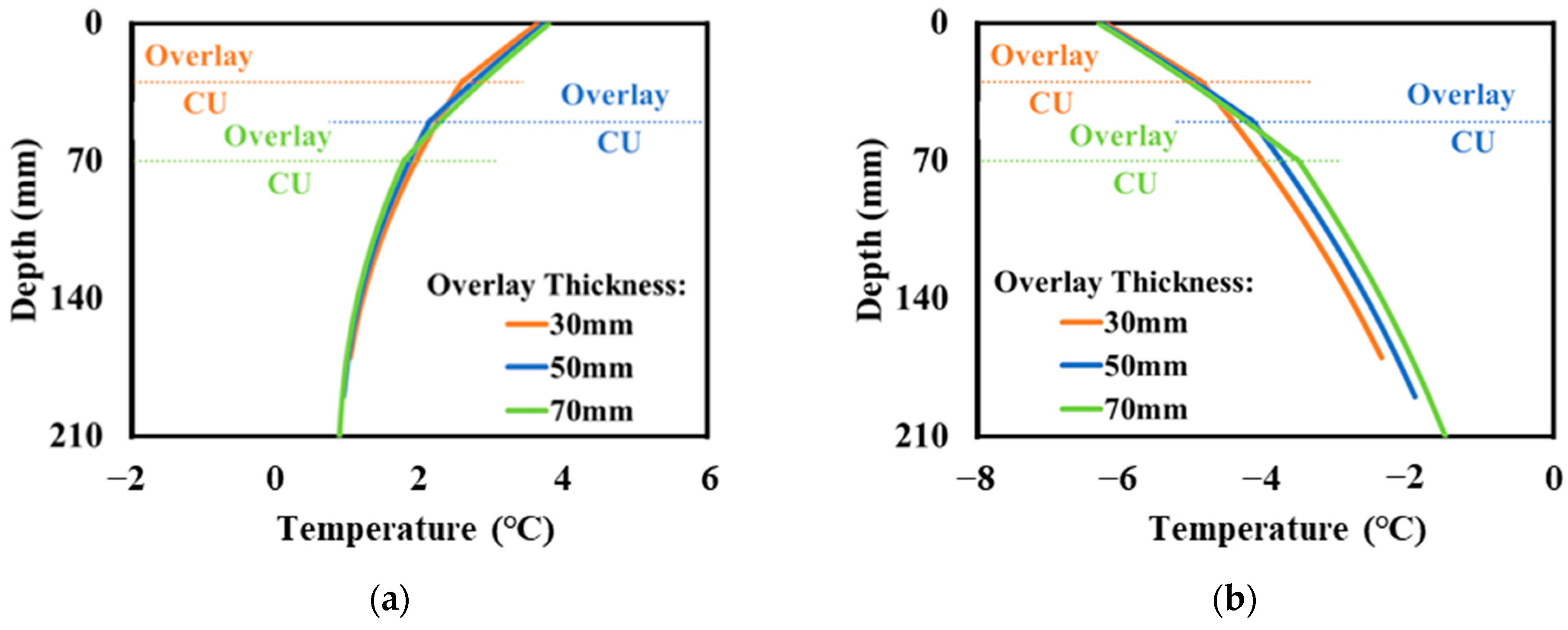
4. Temperature Profiles in Electrified Pavement
5. Parametric Study of Electrified Pavement Design
5.1. Effect of Embedment Depth of Charging Unit
5.2. Effect of Charging Unit Width
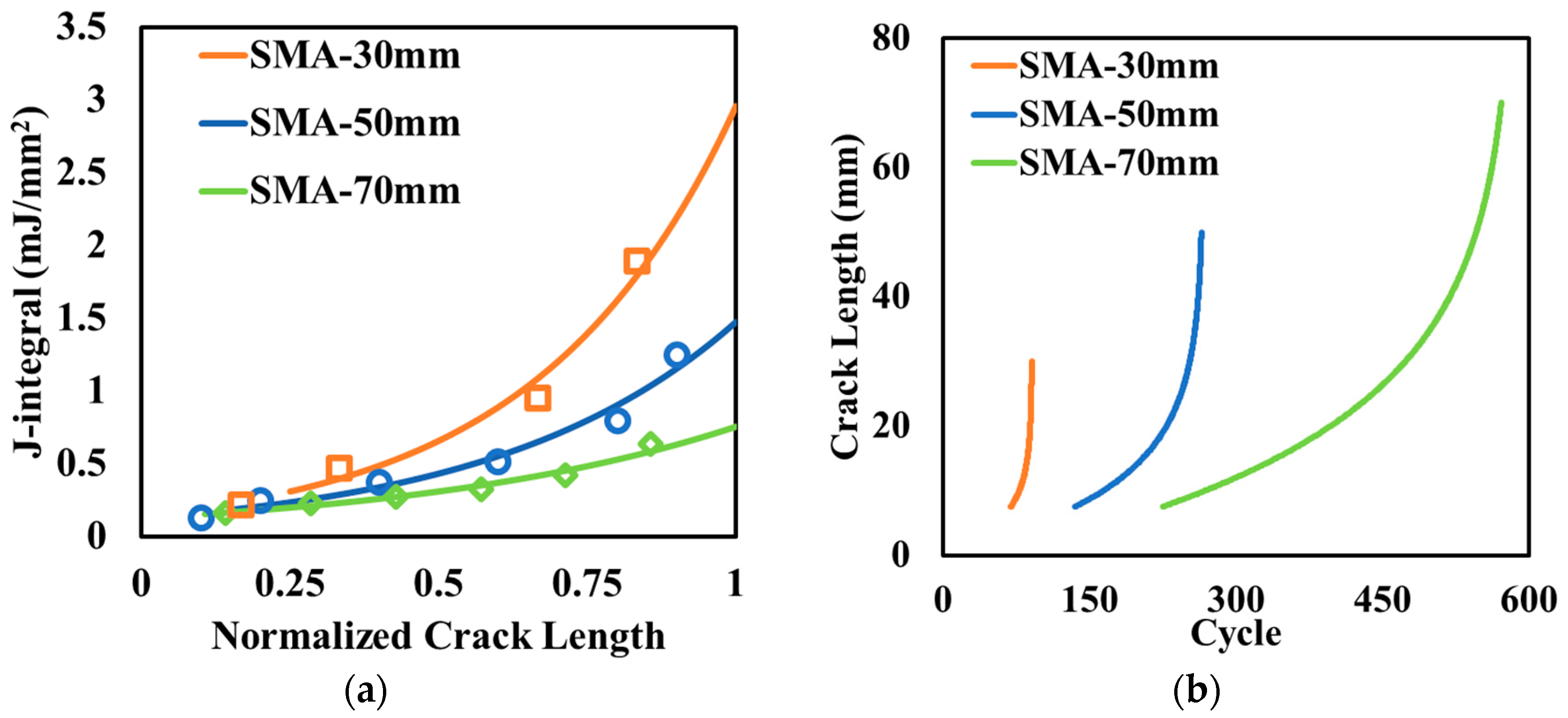
5.3. Effect of Charging Unit Thickness
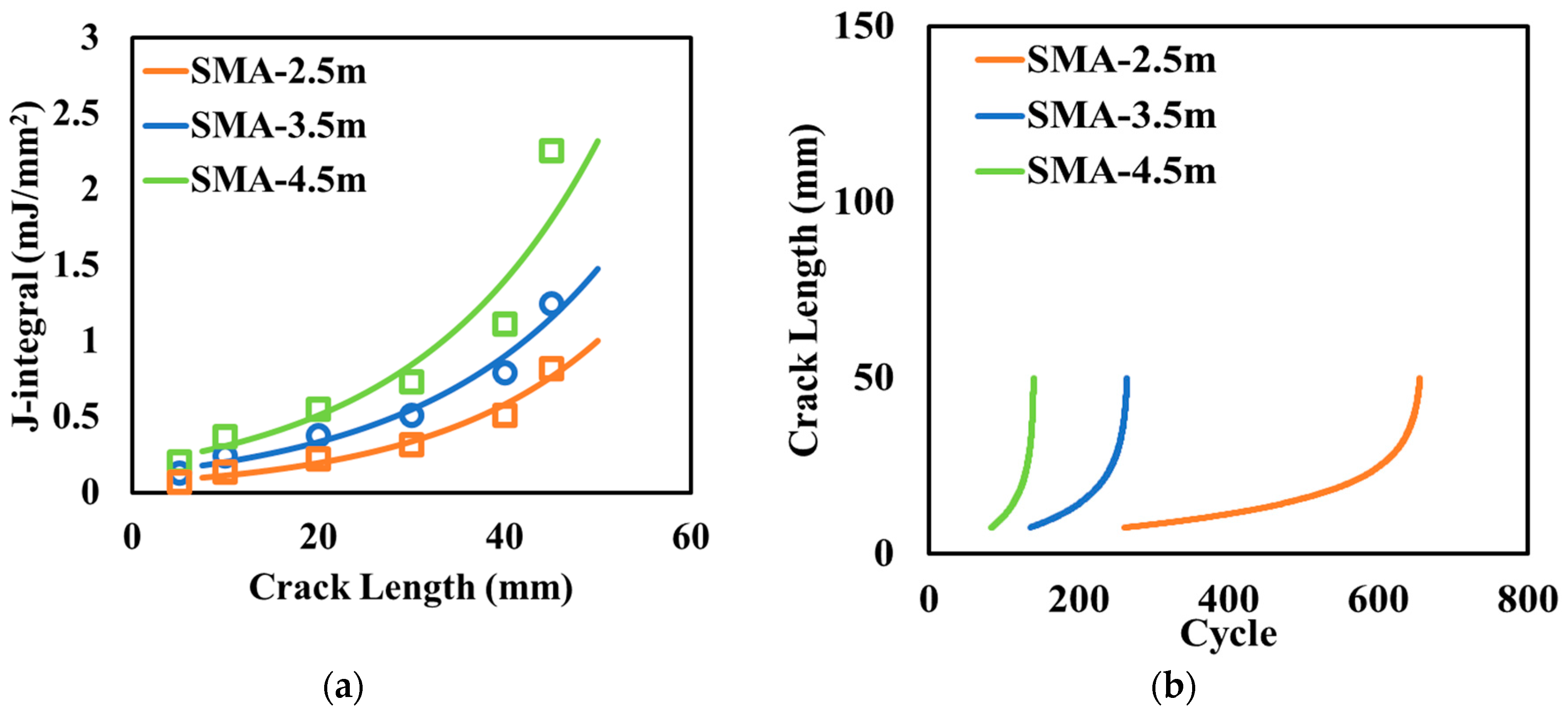
5.4. Effect of Charging Unit Length
6. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, F.; Taylor, N.; Kringos, N. Electrification of roads: Opportunities and challenges. Appl. Energy 2015, 150, 109–119. [Google Scholar] [CrossRef]
- Darabi, Z.; Ferdowsi, M. Impact of plug-in hybrid electric vehicles on electricity demand profile. In Smart Power Grids; Springer: Berlin/Heidelberg, Germany, 2011; pp. 319–349. [Google Scholar] [CrossRef]
- Andwari, A.M.; Pesiridis, A.; Rajoo, S.; Martinez-Botas, R.; Esfahanian, V. A review of Battery Electric Vehicle technology and readiness levels. Renew. Sustain. Energy Rev. 2017, 78, 414–430. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, W.; Yin, Y. Deployment of stationary and dynamic charging infrastructure for electric vehicles along traffic corridors. Transp. Res. Part C Emerg. Technol. 2017, 77, 185–206. [Google Scholar] [CrossRef]
- Barth, H.; Jung, M.; Braun, M.; Schmülling, B.; Reker, U. Concept evaluation of an inductive charging system for electric ve-hicles. In Proceedings of the 3rd European Conference Smart Grids and E-Mobility, Munich, Germany, 17–18 October 2011. [Google Scholar]
- Panchal, C.; Stegen, S.; Lu, J. Review of static and dynamic wireless electric vehicle charging system. Eng. Sci. Technol. 2018, 21, 922–937. [Google Scholar] [CrossRef]
- Systems Control Technology. Roadway Powered Electric Vehicle Project: Track Construction and Testing Program Phase 3D; UC Berkeley: California Partners for Advanced Transportation Technology: Berkeley, CA, USA, 1994. [Google Scholar]
- Shin, J.; Shin, S.; Kim, Y.; Ahn, S.; Lee, S.; Jung, G.; Jeon, S.-J.; Cho, D.-H. Design and implementation of shaped magnet-ic-resonance-based wireless power transfer system for roadway-powered moving electric vehicles. IEEE Trans. Ind. Electron. 2013, 61, 1179. [Google Scholar] [CrossRef]
- Beeldens, A.; Hauspiec, P.; Perikd, H. Inductive Charging through Concrete Roads: A Belgian Case Study and Application. In Proceedings of the 1st European Road Infrastructure Congress, Leeds, UK, 18–20 October 2016. [Google Scholar]
- Ceravolo, R.; Miraglia, G.; Surace, C.; Zanotti Fragonara, L. A computational methodology for assessing the time-dependent structural performance of electric road infrastructures. Comput.-Aided Civ. Infrastruct. Eng. 2016, 31, 701–716. [Google Scholar] [CrossRef]
- Nguyen, M.L.; Hornych, P.; Kerzrého, J.P.; Perez, S. Full scale test on prefabricated slabs for electrical supply by induction of urban transport systems. Transp. Res. Arena Paris 2014, 5, 239–252. [Google Scholar] [CrossRef]
- Dinh, N.N.; Yang, E.H.; Lechner, B. Precast electrified roadway pavement systems using engineered cementitious composites. In Proceedings of the 12th International Symposium on Concrete Roads Prague, Prague, Czech Republic, 23–26 September 2014. [Google Scholar]
- Soares, L.; Wang, H. A study on renewed perspectives of electrified road for wireless power transfer of electric vehicles. Renew. Sustain. Energy Rev. 2022, 158, 112110. [Google Scholar] [CrossRef]
- Chabot, A.; Deep, P. 2D Multilayer solution for an electrified road with a built-in charging box. Road Mater. Pavement Des. 2019, 20 (Suppl. S2), S590–S603. [Google Scholar] [CrossRef]
- Chen, J.Q.; Wang, H.; Xie, P.Y. Pavement temperature prediction: Theoretical models and critical affecting factors. Appl. Therm. Eng. 2019, 158, 113755. [Google Scholar] [CrossRef]
- Jimenez-Relinque, E.; Grande, M.; Rubiano, F.; Castellote, M. Durability and Safety Performance of Pavements with Added Photocatalysts. Appl. Sci. 2021, 11, 11277. [Google Scholar] [CrossRef]
- Lei, J.; Feng, F.; Xu, S.; Wen, W.; He, X. Study on mechanical properties of modified polyurethane concrete at different tem-peratures. Appl. Sci. 2022, 12, 3184. [Google Scholar] [CrossRef]
- Pyshyev, S.; Miroshnichenko, D.; Chipko, T.; Donchenko, M.; Bogoyavlenska, O.; Lysenko, L.; Miroshnychenko, M.; Prysia-zhnyi, Y. Use of Lignite Processing Products as Additives to Road Petroleum Bitumen. ChemEngineering 2024, 8, 27. [Google Scholar] [CrossRef]
- Kalwar, K.A.; Aamir, M.; Mekhilef, S. Inductively coupled power transfer (ICPT) for electric vehicle charging—A review. Renew. Sustain. Energy Rev. 2015, 47, 462–475. [Google Scholar] [CrossRef]
- Xie, P.; Wang, H. Finite element analysis of thermal-induced reflective cracking in composite pavement with mitigation strate-gies. Eng. Fract. Mech. 2022, 266, 108396. [Google Scholar] [CrossRef]
- ABAQUS/Standard User’s Manual, Version 6.14; Hibbitt, Karlsson & Sorenson, Inc.: Pawtucket, RI, USA, 2014.
- Xie, P.; Wang, H. Analysis of temperature variation and thermally induced reflective cracking potential in composite pavements. Transp. Res. Rec. 2020, 2674, 177–188. [Google Scholar] [CrossRef]
- West, R.; Timm, D.; Powell, B.; Heitzman, M.; Tran, N.; Rodezno, C.; Watson, D.; Leiva, F.; Vargas, A.; Willis, R.; et al. Phase V (2012–2014) NCAT Test Track Findings; National Center for Asphalt Technology (NCAT): Auburn, AL, USA, 2018. [Google Scholar]
- Yin, F.; West, R. Performance and Life-Cycle Cost Benefits of Stone Matrix Asphalt; NCAT Report 18-03; National Center for Asphalt Technology (NCAT): Auburn, Alabama, 2018. [Google Scholar]
- Jacobs, M.M.J. Crack Growth in Asphaltic Mixes. Ph.D. Dissertation, Delft University of Technology, Delft, The Netherlands, 1995. [Google Scholar]
- Kim, Y.R.; Daniel, J.S.; Wen, H. Fatigue Performance Evaluation of WesTrack Asphalt Mixtures Using Viscoelastic Continuum Damage Approach; Final Report; North Carolina Department of Transportation: Raleigh, NC, USA, 2002. [Google Scholar]
- Chen, F.; Balieu, R.; Córdoba, E.; Kringos, N. Towards an understanding of the structural performance of future electrified roads: A finite element simulation study. Int. J. Pavement Eng. 2019, 20, 204–215. [Google Scholar] [CrossRef]
- Lytton, R.L.; Uzan, J.; Fernando, E.G.; Roque, R.; Hiltunen, D.; Stoffels, S.M. Development and Validation of Performance Prediction Models and Specifications for Asphalt Binders and Paving Mixes; Strategic Highway Research Program: Washington, DC, USA, 1993.
- Lv, S.; Xia, C.; Liu, C.; Zheng, J.; Zhang, F. Fatigue equation for asphalt mixture under low temperature and low loading fre-quency conditions. Constr. Build. Mater. 2019, 211, 1085–1093. [Google Scholar] [CrossRef]
- Kuai, H.; Lee, H.J.; Zi, G.; Mun, S. Application of generalized J-integral to crack propagation modeling of asphalt concrete under repeated loading. Transp. Res. Rec. 2009, 2127, 72–81. [Google Scholar] [CrossRef]
- Baek, J.; Ozer, H.; Wang, H.; Al-Qadi, I.L. Effects of interface conditions on reflective cracking development in hot-mix asphalt overlays. Road Mater. Pavement Des. 2010, 11, 307–334. [Google Scholar] [CrossRef]
- Amirpour, M.; Kim, S.; Battley, M.P.; Kelly, P.; Bickerton, S.; Covic, G. Coupled electromagnetic-thermal analysis of roadway inductive power transfer pads within a model pavement. Appl. Therm. Eng. 2021, 189, 116710. [Google Scholar] [CrossRef]
- American Concrete Pavement Association. Design and Construction of Joints for Concrete Streets; Concrete Information; American Concrete Pavement Association: Rosemont, IL, USA, 1992. [Google Scholar]
- Machura, P.; Li, Q. A critical review on wireless charging for electric vehicles. Renew. Sustain. Energy Rev. 2019, 104, 209–234. [Google Scholar] [CrossRef]
- Yin, H. Reflective Cracking Phase III Comprehensive Report; FAA: Washington, DC, USA, 2017.
- Guo, L.; Wang, H. A novel design of partially magnetized pavement for wireless power transfer to electric vehicles with im-proved efficiency and cost saving. Energy Convers. Manag. 2022, 252, 115080. [Google Scholar] [CrossRef]

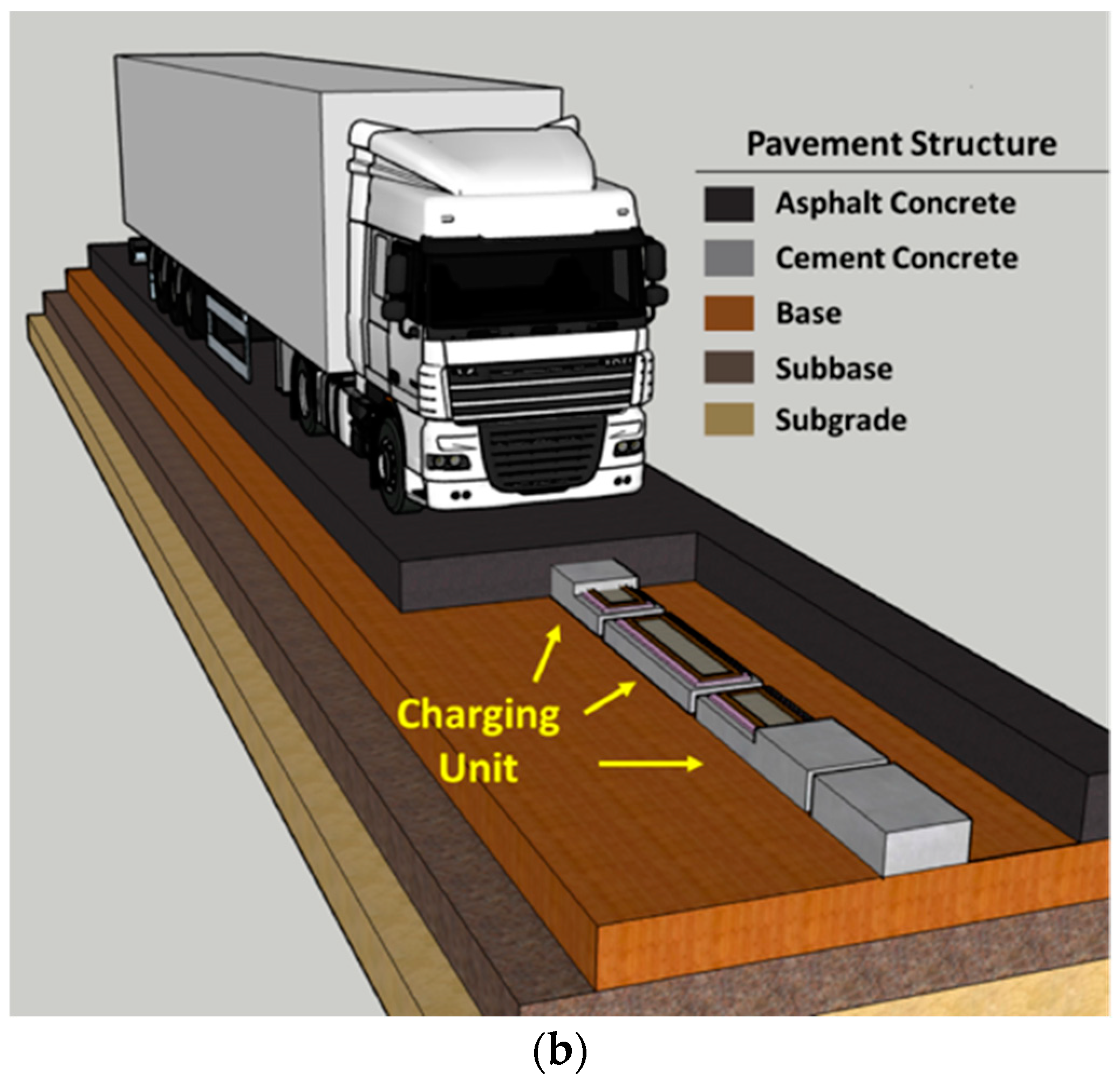
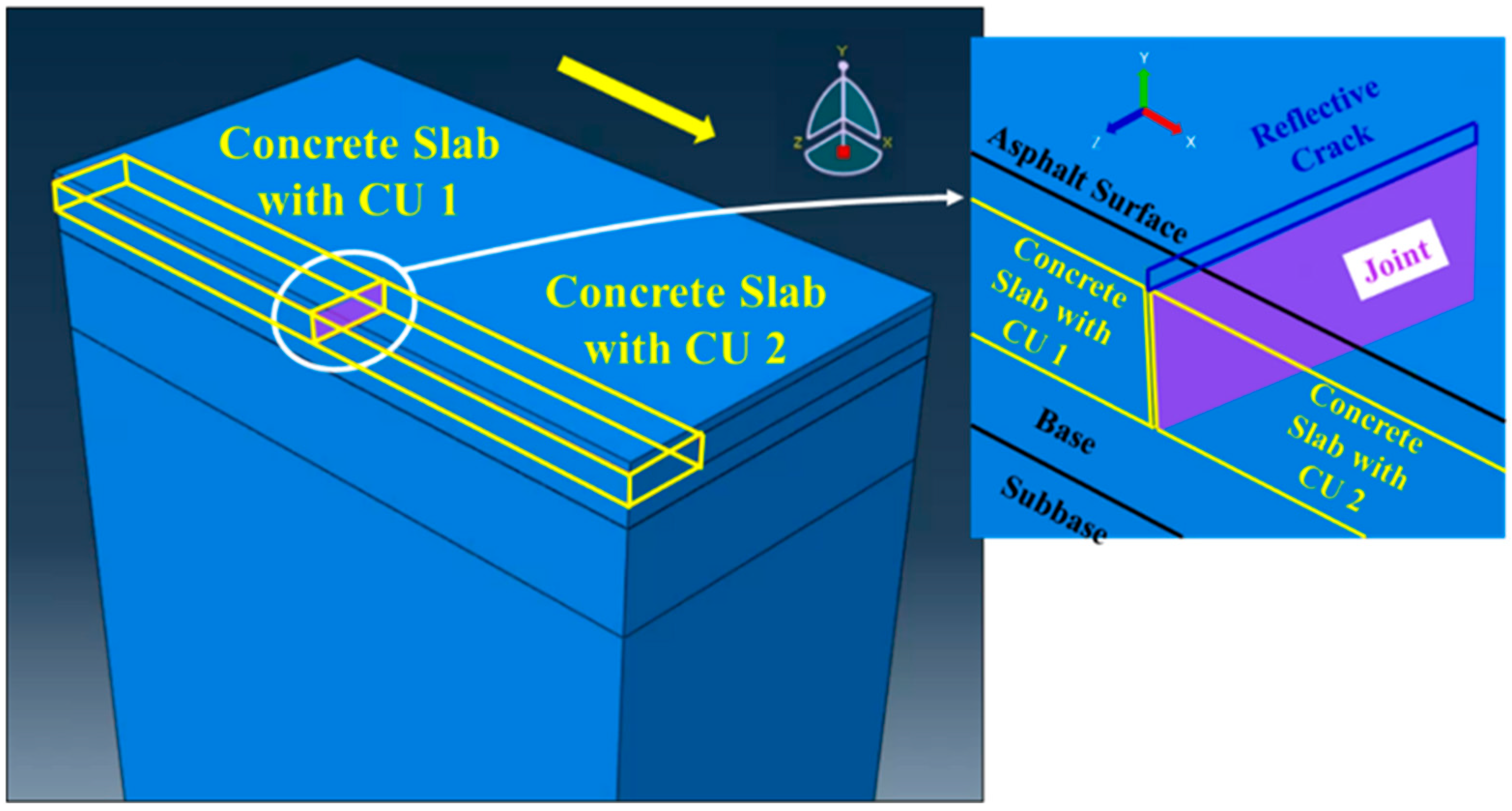
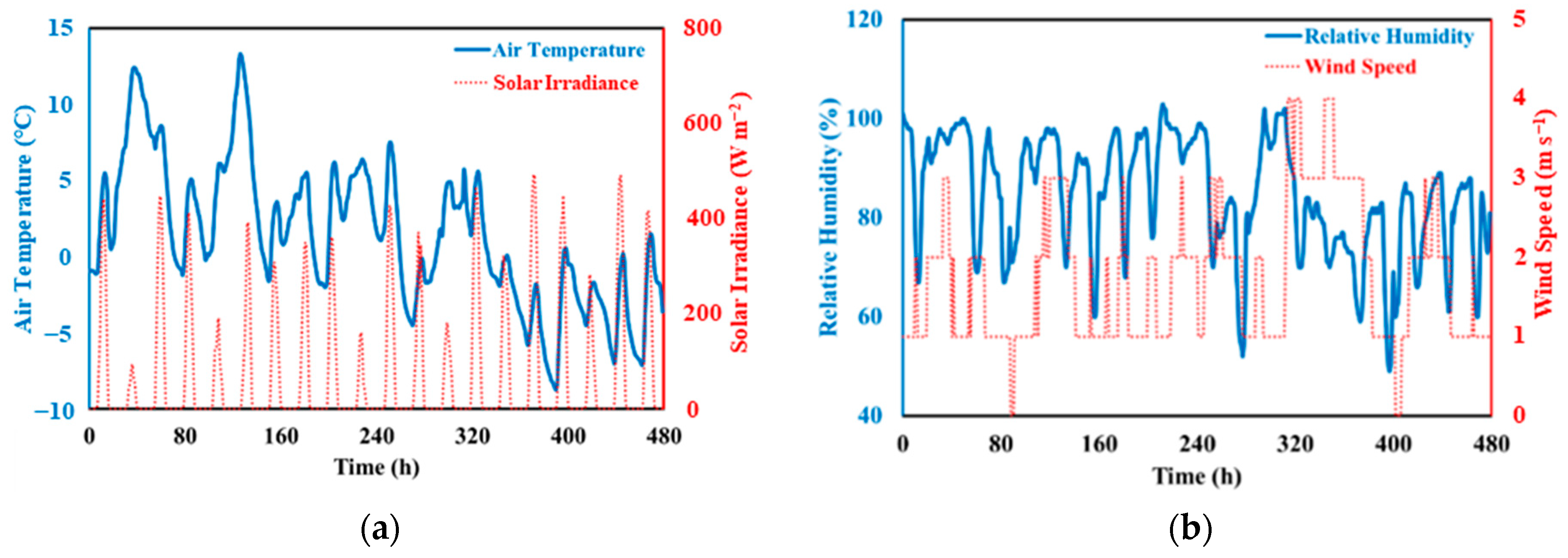
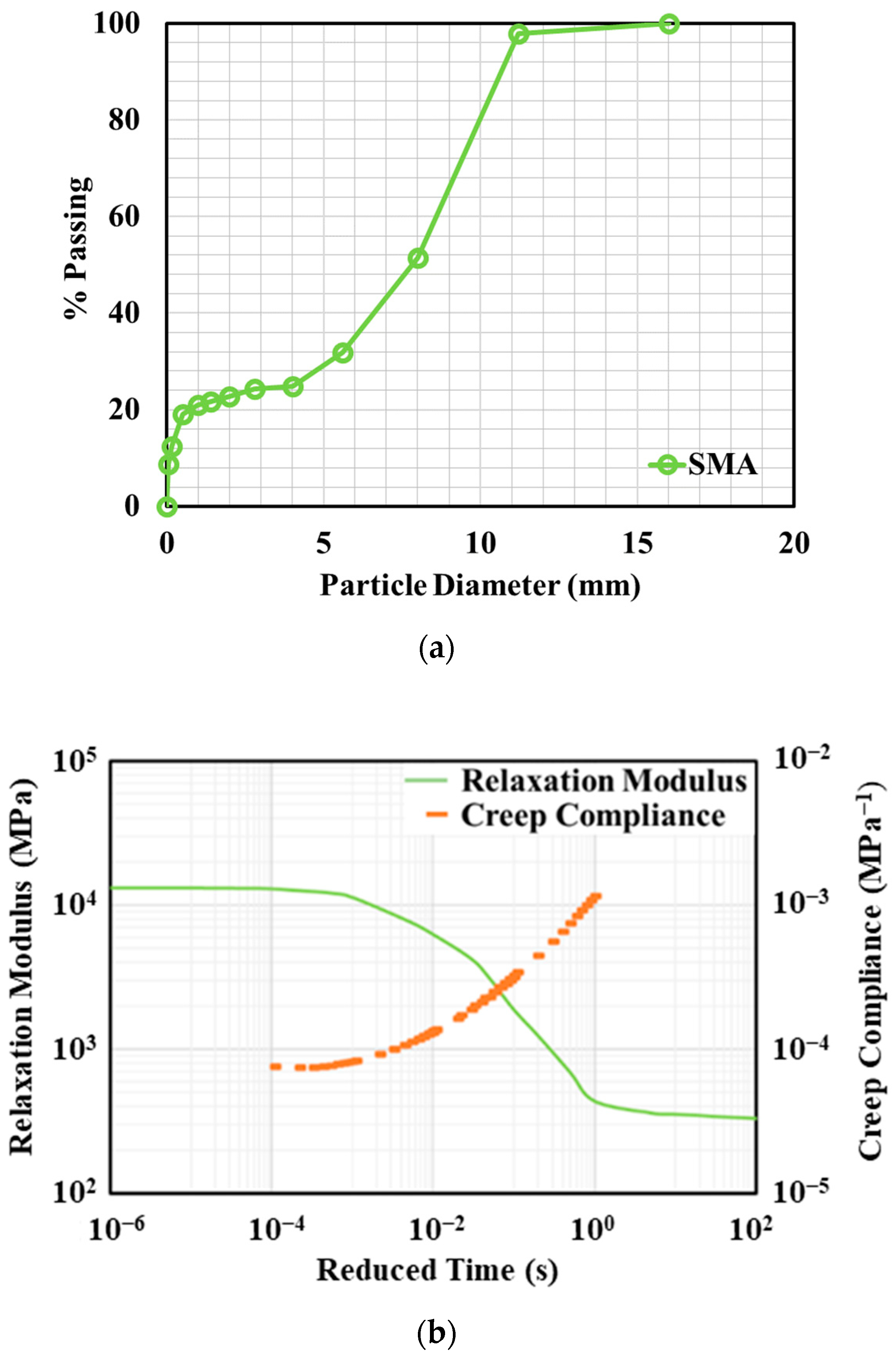


| Existing Asphalt/Surface Layer | Concrete with CU | Granular Base | Granular Subbase | Subgrade | ||
|---|---|---|---|---|---|---|
| Density (kg·m−3) | 2300 | 2401 | 2200 | 2100 | 1800 | |
| Modulus (MPa) | Viscoelastic | 27500 | 350 | 200 | 69 | |
| Poisson’s Ratio | 0.35 | 0.15 | 0.35 | 0.35 | 0.4 | |
| Conductivity (W m−1K−1) | 1.3 | 2.5 | 1.56 | 1.43 | 1.56 | |
| Specific heat (kJ kg−1K−1) | 0.92 | 0.88 | 0.91 | 0.94 | 1.04 | |
| Expansion coefficient (°C−1) | 2 × 10−5 | 0.98 × 10−5 | n/a | n/a | n/a | |
| Fracture parameters—A | 1.91 × 10−6 | n/a | n/a | n/a | n/a | |
| Fracture parameters—n | 2.035 | n/a | n/a | n/a | n/a | |
| Charging Lane Width (mm) | 3700 | |
|---|---|---|
| Asphalt surface over concrete slabs | Thickness (mm) | 30, 50, 70 |
| Concrete slabs with charging units | Thickness (mm) | 100, 140, 180 |
| Width (mm) | 400, 600, 800 | |
| Joint spacing (mm) | 2500, 3500, 4500 | |
| Layers below concrete slabs | Base layer thickness (mm) | 100 |
| Subbase layer thickness (mm) | 500 | |
| Subgrade layer thickness (mm) | 3000 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, P.; Wang, H. Mechanistic Analysis of Reflective Cracking Potential in Electrified Pavement with Inductive Charging System. Materials 2024, 17, 4282. https://doi.org/10.3390/ma17174282
Xie P, Wang H. Mechanistic Analysis of Reflective Cracking Potential in Electrified Pavement with Inductive Charging System. Materials. 2024; 17(17):4282. https://doi.org/10.3390/ma17174282
Chicago/Turabian StyleXie, Pengyu, and Hao Wang. 2024. "Mechanistic Analysis of Reflective Cracking Potential in Electrified Pavement with Inductive Charging System" Materials 17, no. 17: 4282. https://doi.org/10.3390/ma17174282
APA StyleXie, P., & Wang, H. (2024). Mechanistic Analysis of Reflective Cracking Potential in Electrified Pavement with Inductive Charging System. Materials, 17(17), 4282. https://doi.org/10.3390/ma17174282








