Prediction of Mechanical Properties of Lattice Structures: An Application of Artificial Neural Networks Algorithms
Abstract
1. Introduction
- (1)
- For the prediction of structural mechanical properties, researchers usually use the equivalent voxel method [18] to construct the dataset, which is usually characterized by a large amount of input data and unclear relationships between the data. Therefore, this paper will be based on the topology between different lattice structures, which can greatly reduce the size of the input dataset and ensure validity at the same time.
- (2)
- Meanwhile, this paper is based on experimental results and adopts the finite element calculation method, which greatly expands the sample size of the dataset and helps the accuracy of the validation. Considering the maturity of current neural network research, this paper adopts the artificial neural network method to ensure the reliability of the results.
- (3)
- This prediction method classifies the structure of Gibson–Ashby model for the first time. And based on the classified models, machine learning is carried out separately, and better prediction results are finally obtained. It can provide directional support for subsequent lattice structure optimization design.
2. Method
2.1. Artificial Neural Network Algorithm
2.2. ANN Dataset
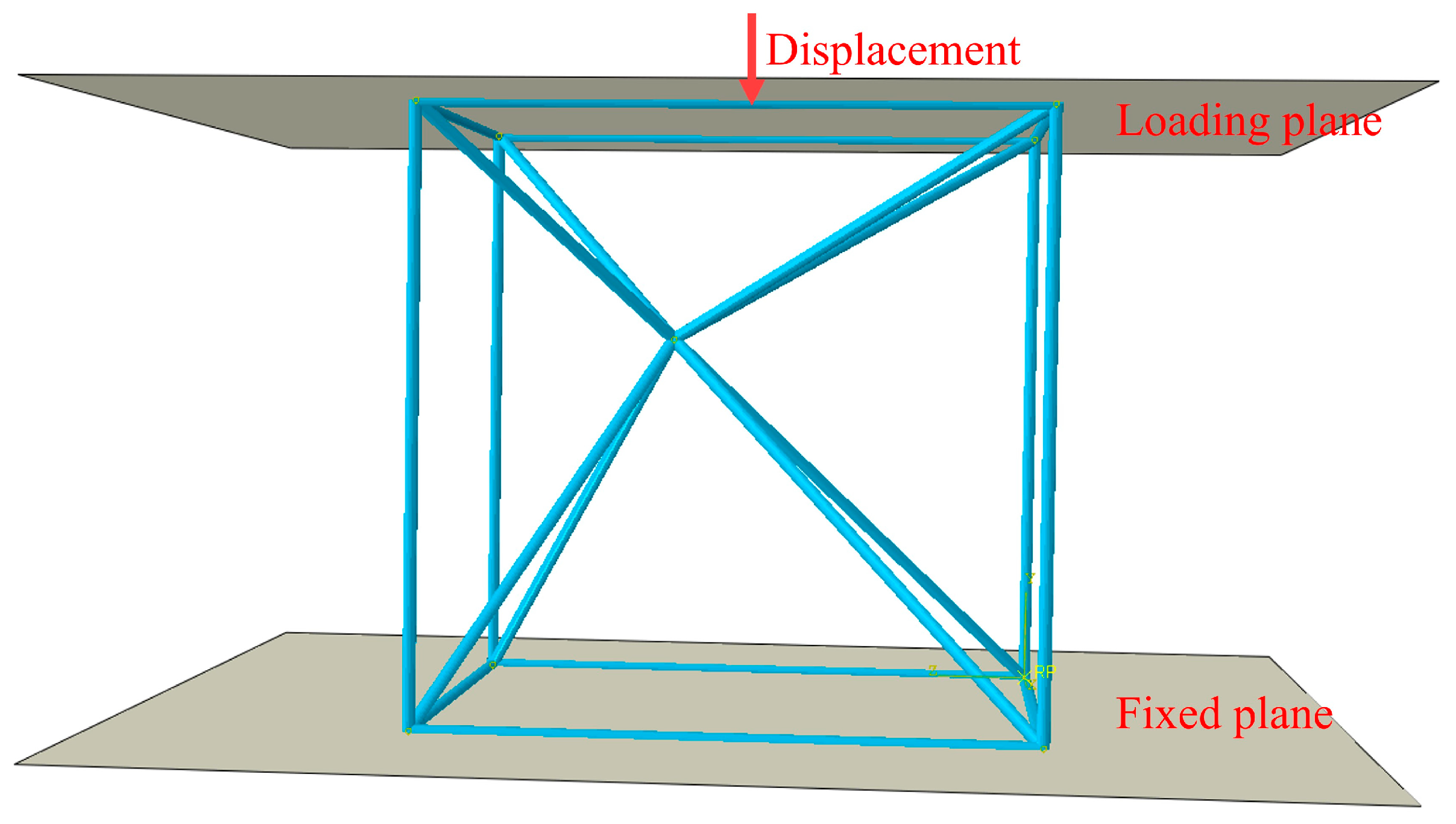
2.3. Finite Element Method Calculation
3. Result and Discussion
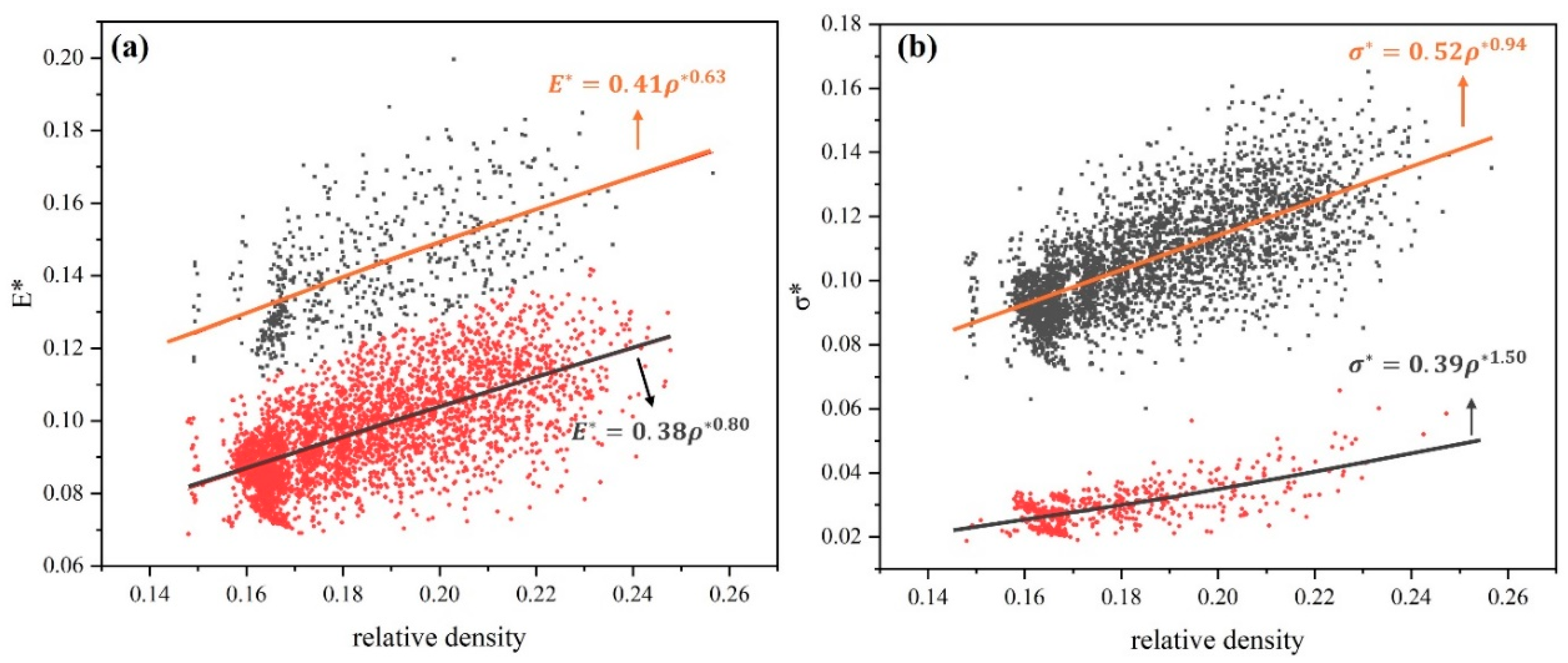
3.1. Mechanical Properties
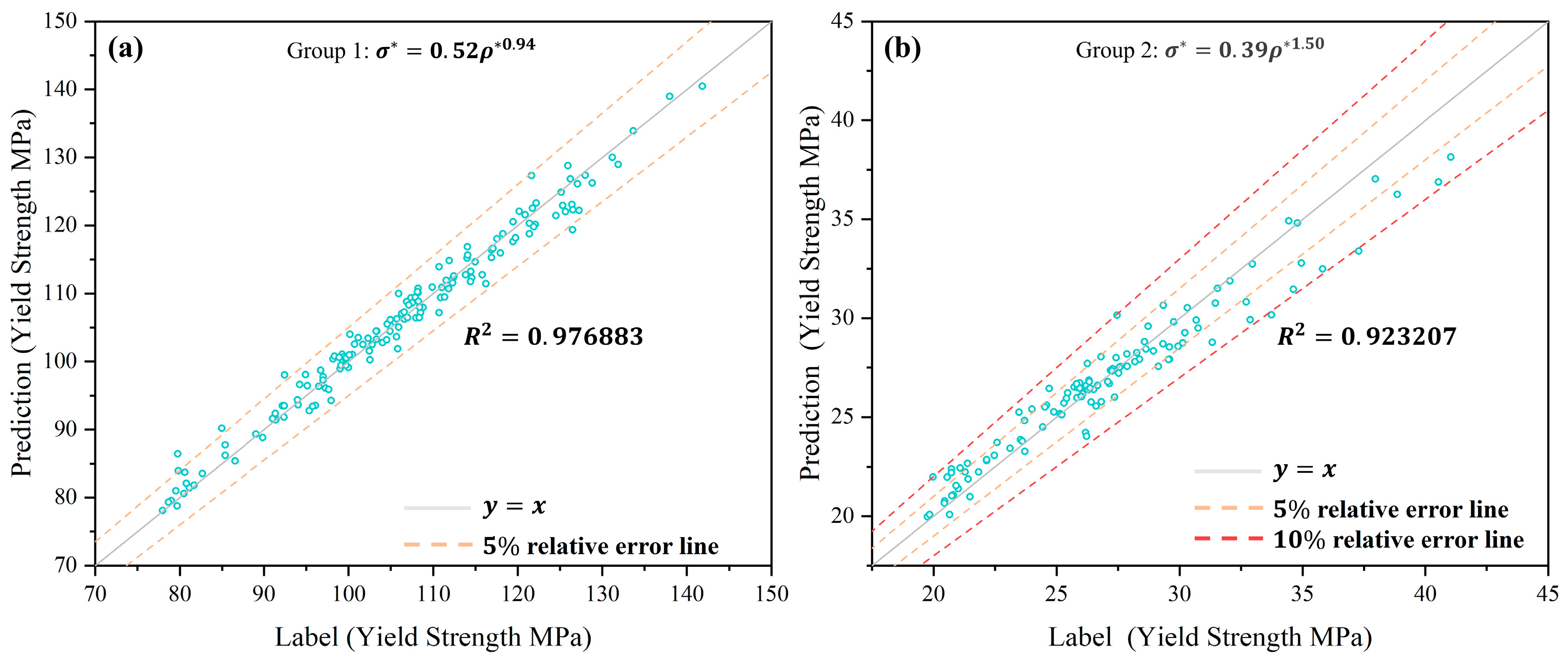
3.2. The Prediction of ANN
3.3. ANN Application Deployment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, L.; Yang, F.; Jin, Y.; Li, P.; Zhang, S.; Xue, K.; Lu, G.; Fan, H. Multifunctional hybrid plate lattice structure with high energy absorption and excellent sound absorption. Mater. Des. 2024, 241, 112946. [Google Scholar] [CrossRef]
- Zhang, L.; Lei, H.; Wang, F.; Wang, P.; Duan, S.; Zhao, Z. Twist design of lattice structure fabricated by powder bed fusion to adjust the energy absorption behavior. Compos. Struct. 2024, 342, 118244. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Li, Z.; Zhang, T.; Zhou, H.; Ren, Z. Design, mechanical properties, and optimization of BCC lattice structures with taper struts. Compos. Struct. 2022, 295, 115830. [Google Scholar] [CrossRef]
- Totaro, G.; Gürdal, Z. Optimal design of composite lattice shell structures for aerospace applications. Aerosp. Sci. Technol. 2009, 13, 157–164. [Google Scholar] [CrossRef]
- Zhu, L.; Li, N.; Childs, P.R.N. Light-weighting in aerospace component and system design. Propuls. Power Res. 2018, 7, 103–119. [Google Scholar] [CrossRef]
- Smeets, B.J.R.; Fagan, E.M.; Matthews, K.; Telford, R.; Murray, B.R.; Pavlov, L.; Weafer, B.; Meier, P.; Goggins, J. Structural testing of a shear web attachment point on a composite lattice cylinder for aerospace applications. Compos. B Eng. 2021, 212, 108691. [Google Scholar] [CrossRef]
- Geetha, M.; Singh, A.K.; Asokamani, R.; Gogia, A.K. Ti based biomaterials, the ultimate choice for orthopaedic implants—A review. Prog. Mater Sci. 2009, 54, 397–425. [Google Scholar] [CrossRef]
- Murr, L.E. Open-cellular metal implant design and fabrication for biomechanical compatibility with bone using electron beam melting. J. Mech. Behav. Biomed. Mater. 2017, 76, 164–177. [Google Scholar] [CrossRef]
- Costa, M.R.; Sohouli, A.; Suleman, A. Multi-scale and multi-material topology optimization of gradient lattice structures using surrogate models. Compos. Struct. 2022, 289, 115402. [Google Scholar] [CrossRef]
- Chen, L.; Che, J.; Liang, S.; Wang, Y. Multiscale topology optimization of gradient lattice structure based on volume parametric modeling. Compos. Struct. 2024, 328, 117746. [Google Scholar] [CrossRef]
- Christiansen, R.E.; Wang, F.; Sigmund, O. Topological Insulators by Topology Optimization. Phys. Rev. Lett. 2019, 122, 234502. [Google Scholar] [CrossRef] [PubMed]
- Noda, M.; Matsushima, K.; Yamada, T. Orientation optimization via topological derivatives in combination with multi-material topology optimization based on extended level set method. Comput. Methods Appl. Mech. Eng. 2024, 418, 116585. [Google Scholar] [CrossRef]
- Norato, J.A. Topology optimization with supershapes. Struct. Multidiscip. Optim. 2018, 58, 415–434. [Google Scholar] [CrossRef]
- Iaccarino, P.; Maresca, E.; Morganti, S.; Auricchio, F.; Di Maio, E. Topologically Optimized Graded Foams. Adv. Eng. Mater. 2024, 26, 2301798. [Google Scholar] [CrossRef]
- Zhang, T.; Cheng, X.; Guo, C.; Dai, N. Toughness-improving design of lattice sandwich structures. Mater. Des. 2023, 226, 111600. [Google Scholar] [CrossRef]
- Xu, S.; Shen, J.; Zhou, S.; Huang, X.; Xie, Y.M. Design of lattice structures with controlled anisotropy. Mater. Des. 2016, 93, 443–447. [Google Scholar] [CrossRef]
- Wu, J.; Wang, W.; Gao, X. Design and Optimization of Conforming Lattice Structures. IEEE Trans. Vis. Comput. Graph. 2021, 27, 43–56. [Google Scholar] [CrossRef]
- Liu, C.; Li, S. High-resolution topology optimization method of multi-morphology lattice structures based on three-dimensional convolutional neural networks (3D-CNN). Struct. Multidiscip. Optim. 2023, 66, 235. [Google Scholar] [CrossRef]
- Horváth, D.; Gmitra, M.; Vávra, I. Neural network approach to magnetic dot arrays modeling. J. Magn. Magn. Mater. 2001, 231, 273–286. [Google Scholar] [CrossRef]
- Pan, Y.; Billings, S.A.; Zhao, Y. The identification of coupled map lattice models for autonomous cellular neural network patterns. Int. J. Bifurc. Chaos 2008, 18, 985–996. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, C.; Deng, C. An improved GNN using dynamic graph embedding mechanism: A novel end-to-end framework for rolling bearing fault diagnosis under variable working conditions. Mech. Syst. Sig. Process. 2023, 200, 110534. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, Y.; Niu, H.; Cheng, X.; Zhao, P.; Bao, J. GNNs for mechanical properties prediction of strut-based lattice structures. Int. J. Mech. Sci. 2024, 269, 109082. [Google Scholar] [CrossRef]
- Hestroffer, J.M.; Charpagne, M.-A.; Latypov, M.I.; Beyerlein, I.J. Graph neural networks for efficient learning of mechanical properties of polycrystals. Comput. Mater. Sci. 2023, 217, 111894. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, J.; Alippi, C.; Ding, S.X.; Shardt, Y.; Peng, T.; Yang, C. Graph neural network-based fault diagnosis: A review. arXiv 2021, arXiv:2111.08185. [Google Scholar]
- Zhang, Y.; Wang, Z.; Zhu, J.; Yang, Y.; Rao, M.; Song, W.; Zhuo, Y.; Zhang, X.; Cui, M.; Shen, L.; et al. Brain-inspired computing with memristors: Challenges in devices, circuits, and systems. Appl. Phys. Rev. 2020, 7, 011308. [Google Scholar] [CrossRef]
- Cheng, J.; Tegge, A.N.; Baldi, P. Machine Learning Methods for Protein Structure Prediction. IEEE Rev. Biomed. Eng. 2008, 1, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Jordan, M.I.; Mitchell, T.M. Mitchell, Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Peng, X.-L.; Xu, B.-X. Data-driven inverse design of composite triangular lattice structures. Int. J. Mech. Sci. 2024, 265, 108900. [Google Scholar] [CrossRef]
- Yu, G.; Xiao, L.; Song, W. Deep learning-based heterogeneous strategy for customizing responses of lattice structures. Int. J. Mech. Sci. 2022, 229, 107531. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, B.; Zhu, H.; Fan, H. Structure genome based machine learning method for woven lattice structures. Int. J. Mech. Sci. 2023, 245, 108134. [Google Scholar] [CrossRef]
- Wu, C.; Luo, J.; Zhong, J.; Xu, Y.; Wan, B.; Huang, W.; Fang, J.; Steven, G.P.; Sun, G.; Li, Q. Topology optimisation for design and additive manufacturing of functionally graded lattice structures using derivative-aware machine learning algorithms. Addit. Manuf. 2023, 78, 103833. [Google Scholar] [CrossRef]
- Suzuki, A.; Nakatani, H.; Kobashi, M. Machine learning surrogate modeling toward the design of lattice-structured heat sinks fabricated by additive manufacturing. Mater. Des. 2023, 230, 111969. [Google Scholar] [CrossRef]
- Wu, Y.; Mao, Z.; Feng, Y. Energy absorption prediction for lattice structure based on D2 shape distribution and machine learning. Compos. Struct. 2023, 319, 117136. [Google Scholar] [CrossRef]
- Teimouri, A.; Challapalli, A.; Konlan, J.; Li, G. Machine learning assisted design and optimization of plate-lattice structures with superior specific recovery force. Giant 2024, 18, 100282. [Google Scholar] [CrossRef]
- Jalali, S.K.; Beigrezaee, M.J.; Misseroni, D.; Pugno, N.M. A modified Gibson-Ashby model for functionally graded lattice structures. Mech. Mater. 2024, 188, 104822. [Google Scholar] [CrossRef]
- Zhong, H.; Song, T.; Li, C.; Das, R.; Gu, J.; Qian, M. The Gibson-Ashby model for additively manufactured metal lattice materials: Its theoretical basis, limitations and new insights from remedies. Curr. Opin. Solid State Mater. Sci. 2023, 27, 101081. [Google Scholar] [CrossRef]
- Uhlířová, T.; Pabst, W. Conductivity and Young’s modulus of porous metamaterials based on Gibson-Ashby cells. Scr. Mater. 2019, 159, 1–4. [Google Scholar] [CrossRef]
- Zhong, H.; Das, R.; Gu, J.; Qian, M. Low-density, high-strength metal mechanical metamaterials beyond the Gibson-Ashby model, Mater. Today 2023, 68, 96–107. [Google Scholar] [CrossRef]
- Maskery, I.; Aremu, A.O.; Parry, L.; Wildman, R.D.; Tuck, C.J.; Ashcroft, I.A. Effective design and simulation of surface-based lattice structures featuring volume fraction and cell type grading. Mater. Des. 2018, 155, 220–232. [Google Scholar] [CrossRef]
- Ren, X.; Xiao, L.; Hao, Z. Multi-property cellular material design approach based on the mechanical behaviour analysis of the reinforced lattice structure. Mater. Des. 2019, 174, 107785. [Google Scholar] [CrossRef]
- Dwivedi, K.; Joshi, S.; Nair, R.; Sapre, M.S.; Jatti, V. Optimizing 3D printed diamond lattice structure and investigating the influence of process parameters on their mechanical integrity using nature-inspired machine learning algorithms. Mater. Today Commun. 2024, 38, 108233. [Google Scholar] [CrossRef]
- Xiao, L.; Shi, G.; Song, W. Machine learning predictions on the compressive stress–strain response of lattice-based metamaterials. Int. J. Solids Struct. 2024, 300, 112893. [Google Scholar] [CrossRef]
- Hu, E.; Seetoh, I.P.; Lai, C.Q. Machine learning assisted investigation of defect influence on the mechanical properties of additively manufactured architected materials. Int. J. Mech. Sci. 2022, 221, 107190. [Google Scholar] [CrossRef]
- Ma, S.; Tang, Q.; Liu, Y.; Feng, Q. Prediction of Mechanical Properties of Three-Dimensional Printed Lattice Structures Through Machine Learning. J. Comput. Inf. Sci. Eng. 2022, 22, 031008. [Google Scholar] [CrossRef]
- Gongora, A.E.; Friedman, C.; Newton, D.K.; Yee, T.D.; Doorenbos, Z.; Giera, B.; Duoss, E.B.; Han, T.Y.-J.; Sullivan, K.; Rodriguez, J.N. Accelerating the design of lattice structures using machine learning. Sci. Rep. 2024, 14, 13703. [Google Scholar] [CrossRef]
- Asami, K.; Roth, S.; Krukenberg, M.; Röver, T.; Herzog, D.; Emmelmann, C. Predictive modeling of lattice structure design for 316L stainless steel using machine learning in the L-PBF process. J. Laser Appl. 2023, 35, 042046. [Google Scholar] [CrossRef]
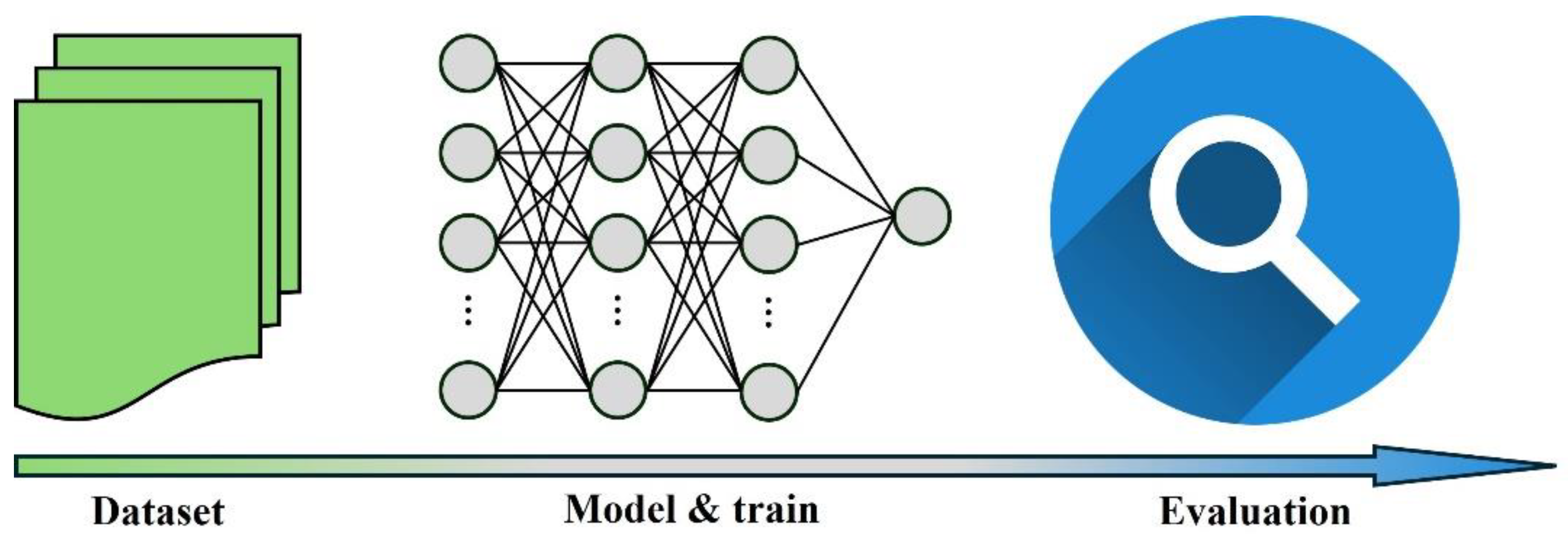


| No | ML Model | Dataset Type | Input Parameters | Comparison |
|---|---|---|---|---|
| 1 | ANN | Topology feature | 23 | This work |
| 2 [28] | ANN | Geometric feature | 3 | Poor generalizability to other lattice structures |
| 3 [33] | ANN | Shape features | 1000 | Too large data inputs for deployment of applications and lightweight operation |
| 4 [32] | NN | Digital visualization | 400 | Too large data inputs for deployment of applications and lightweight operation |
| 5 [30] | SG-based machine learning | Geometric feature | 3 | Poor generalizability to other different structures |
| 6 [22] | GNN | Topology feature | 55 | large data inputs |
| 7 [34] | DNN | Representative volume Element | 20 | Only for plate–lattice structures |
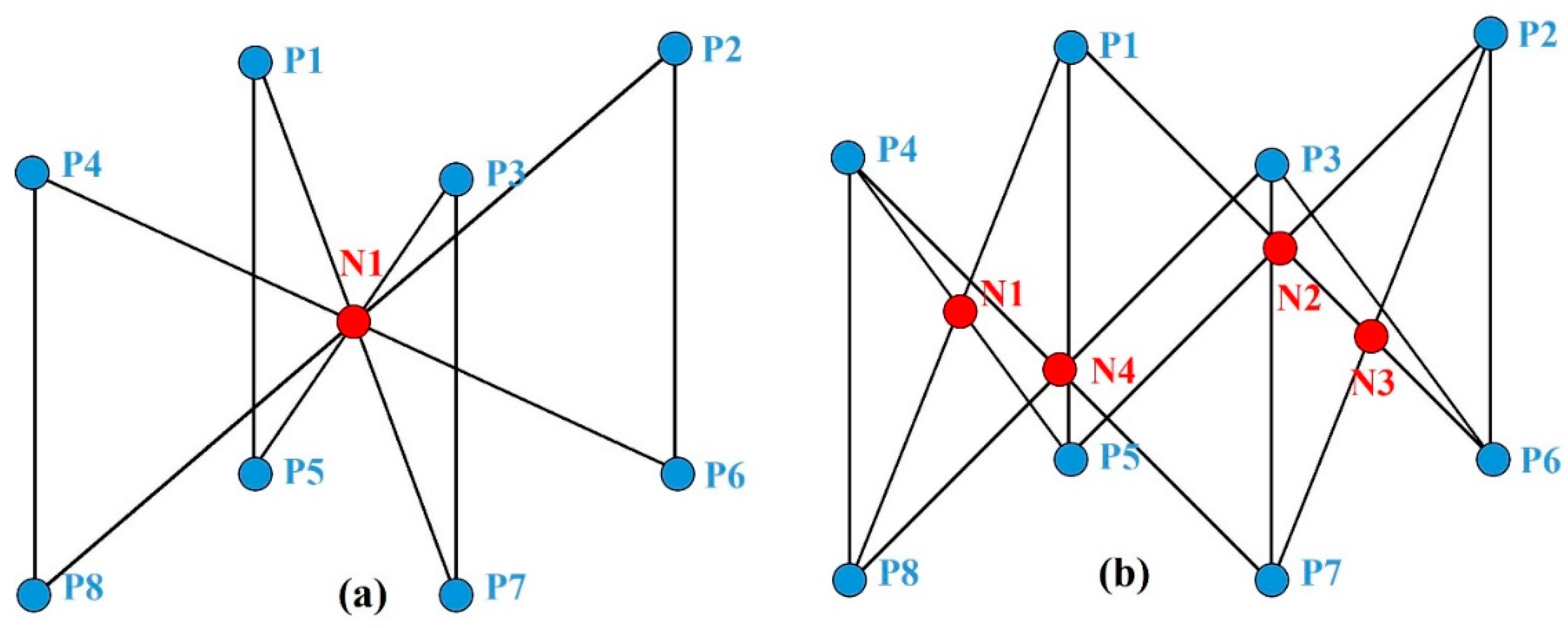
| Internal Node | Number of Data | Yield Strength (MPa) | Young’s Modulus (MPa) |
|---|---|---|---|
| N1 | 1000 | From FEM | From FEM |
| N1, N2 | 1000 | From FEM | From FEM |
| N1, N2, N3 | 1000 | From FEM | From FEM |
| N1, N2, N3, N4 | 1000 | From FEM | From FEM |
| Elastic | Johnson–Cook Plastic | |||
|---|---|---|---|---|
| Young’s Modulus | Poisson’s Ratio | A | B | N |
| 107 GPa | 0.3 | 1567 Mpa | 952 Mpa | 0.4 |
| Group Type | 1# Layer | 2# Layer | Activation Function | Iterations |
|---|---|---|---|---|
| 233 | 253 | ReLU | 1000 | |
| 69 | 0 | Sigmoid | 1000 |
| Group Type | 1# Layer | 2# Layer | Activation Function | Iterations |
|---|---|---|---|---|
| 72 | 295 | ReLU | 1000 | |
| 300 | 251 | tanh | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, J.; Li, M.; Shen, J. Prediction of Mechanical Properties of Lattice Structures: An Application of Artificial Neural Networks Algorithms. Materials 2024, 17, 4222. https://doi.org/10.3390/ma17174222
Bai J, Li M, Shen J. Prediction of Mechanical Properties of Lattice Structures: An Application of Artificial Neural Networks Algorithms. Materials. 2024; 17(17):4222. https://doi.org/10.3390/ma17174222
Chicago/Turabian StyleBai, Jiaxuan, Menglong Li, and Jianghua Shen. 2024. "Prediction of Mechanical Properties of Lattice Structures: An Application of Artificial Neural Networks Algorithms" Materials 17, no. 17: 4222. https://doi.org/10.3390/ma17174222
APA StyleBai, J., Li, M., & Shen, J. (2024). Prediction of Mechanical Properties of Lattice Structures: An Application of Artificial Neural Networks Algorithms. Materials, 17(17), 4222. https://doi.org/10.3390/ma17174222








