Negative Magnetoresistance in Hopping Regime of Lightly Doped Thermoelectric SnSe
Abstract
1. Introduction
2. Materials and Methods
3. Results
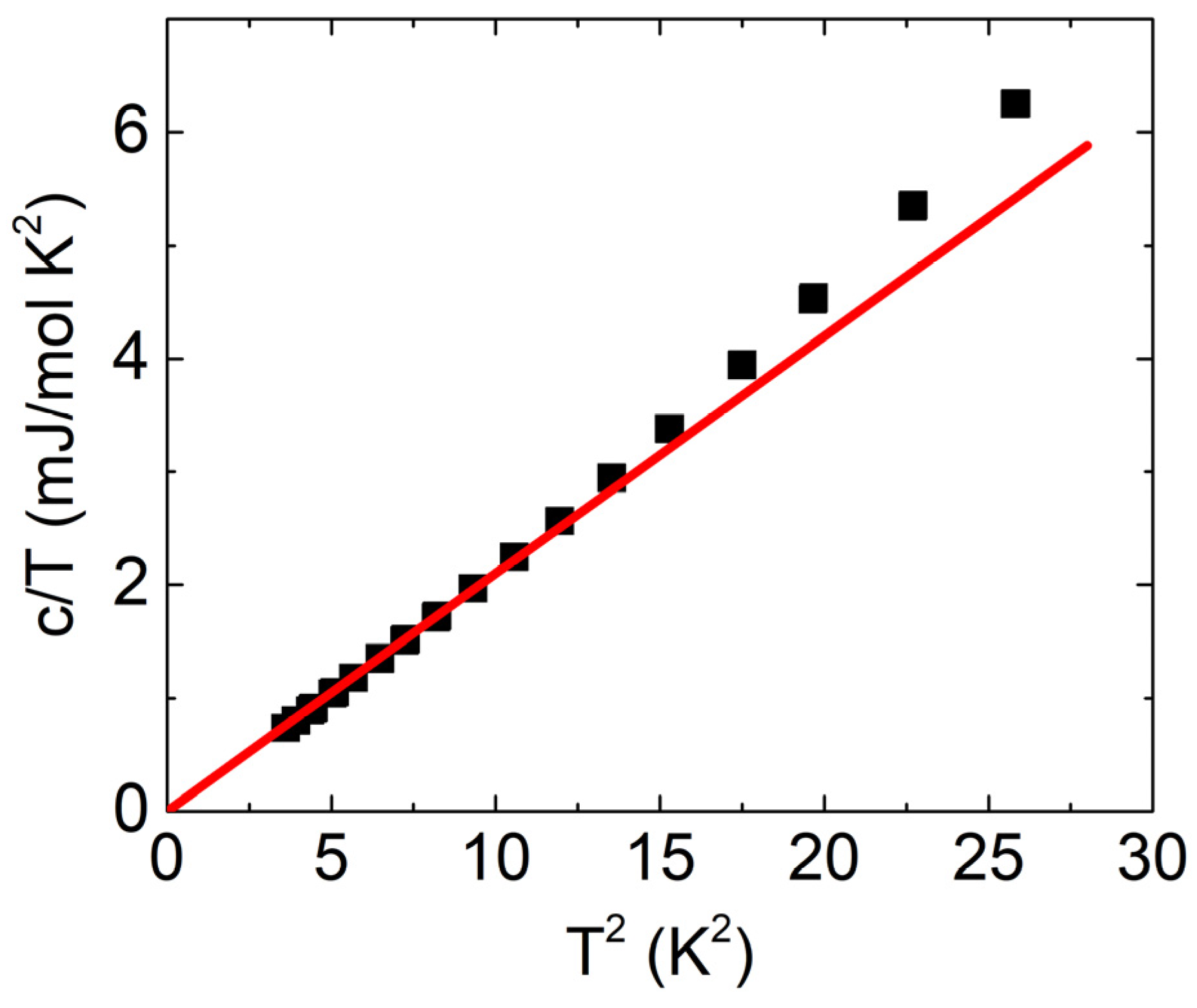
3.1. Specific Heat
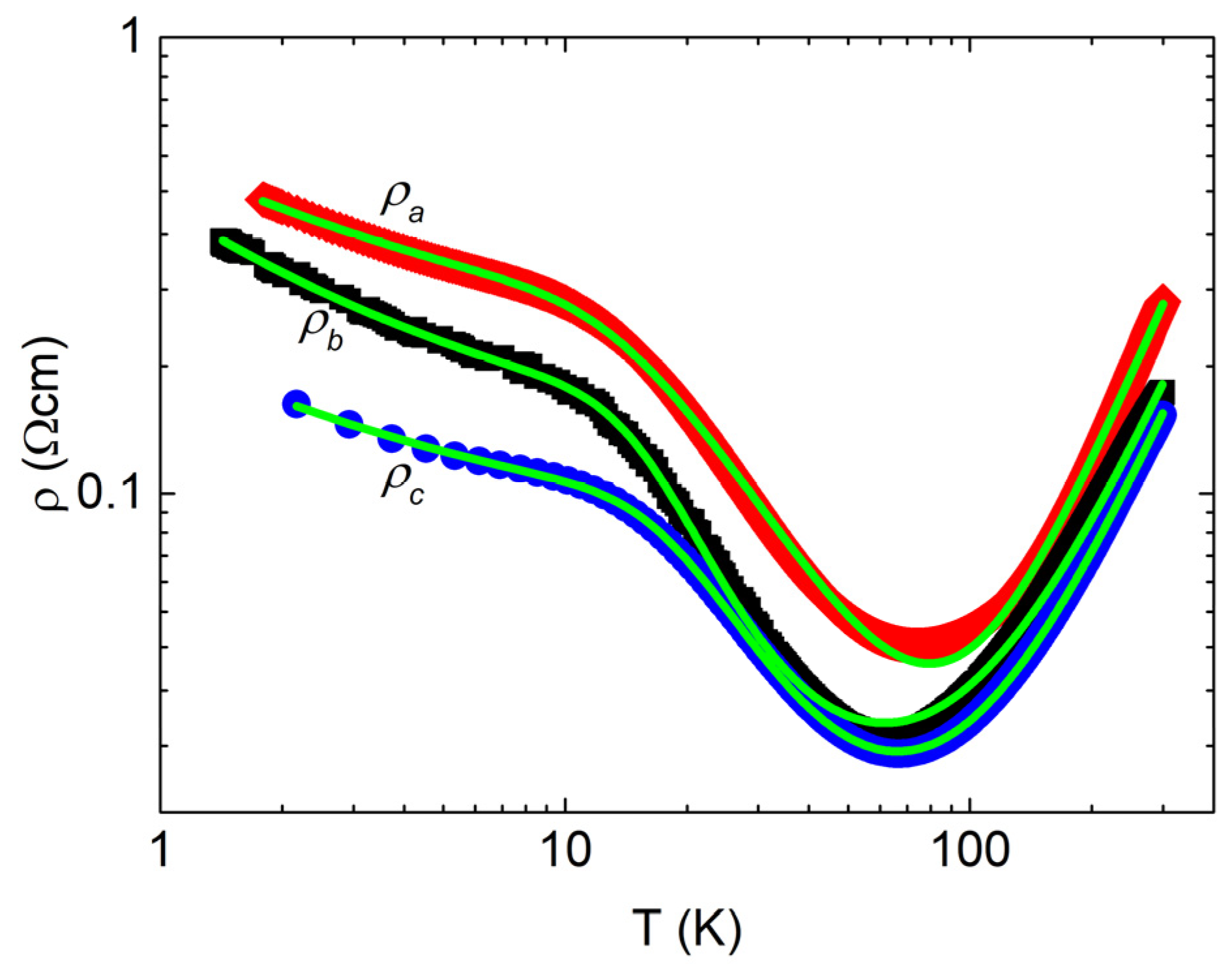
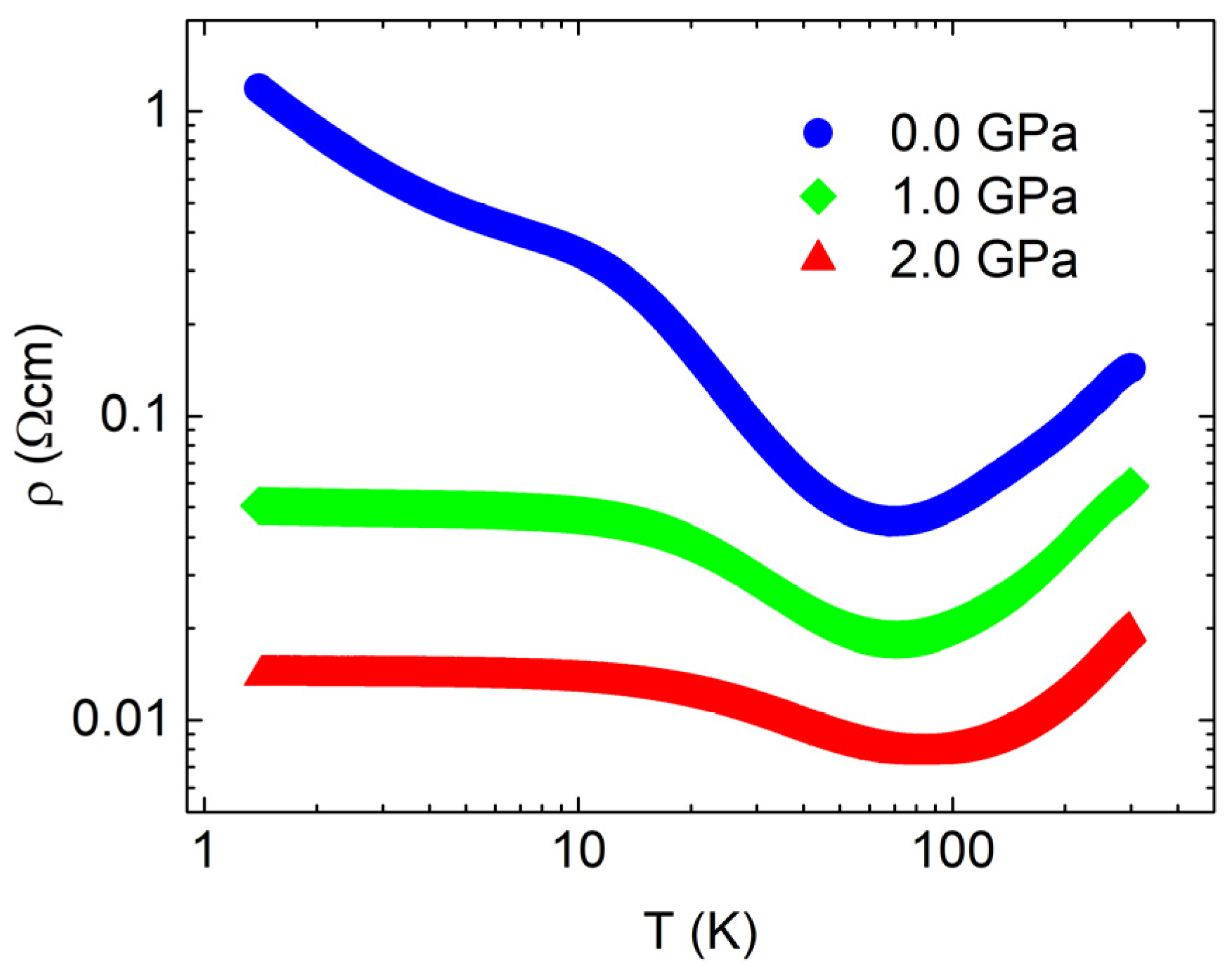
3.2. Electronic Transport
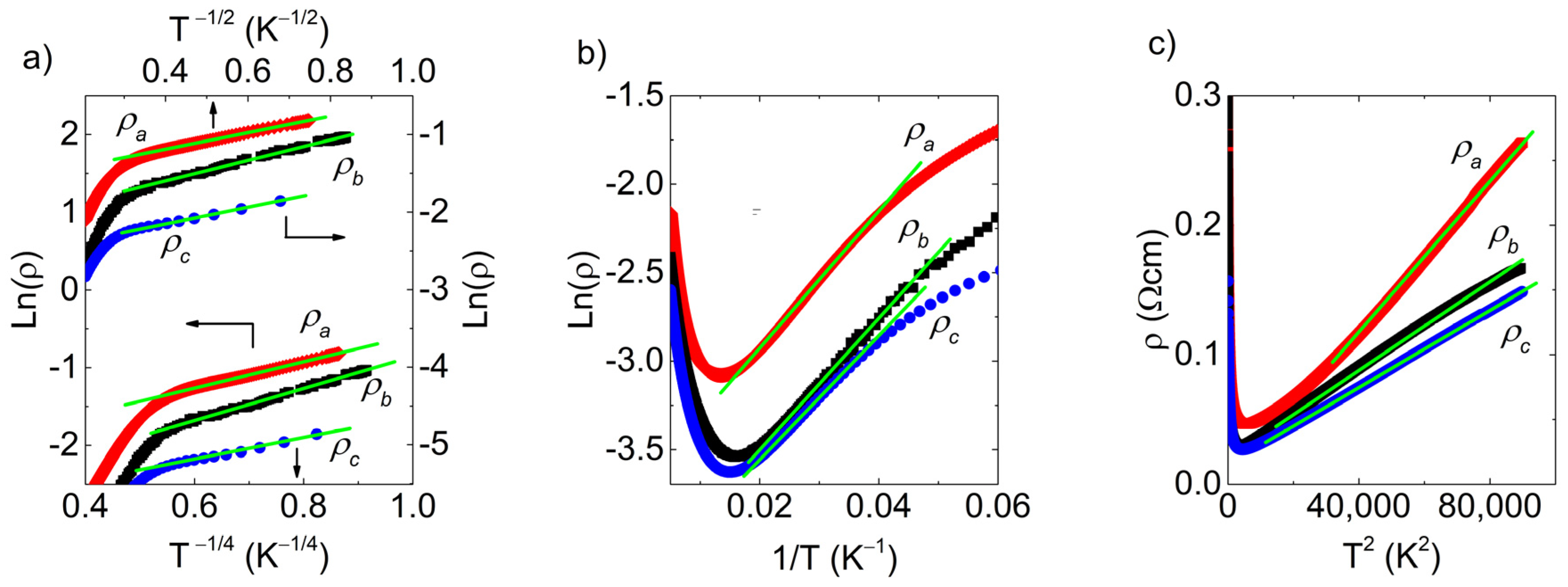
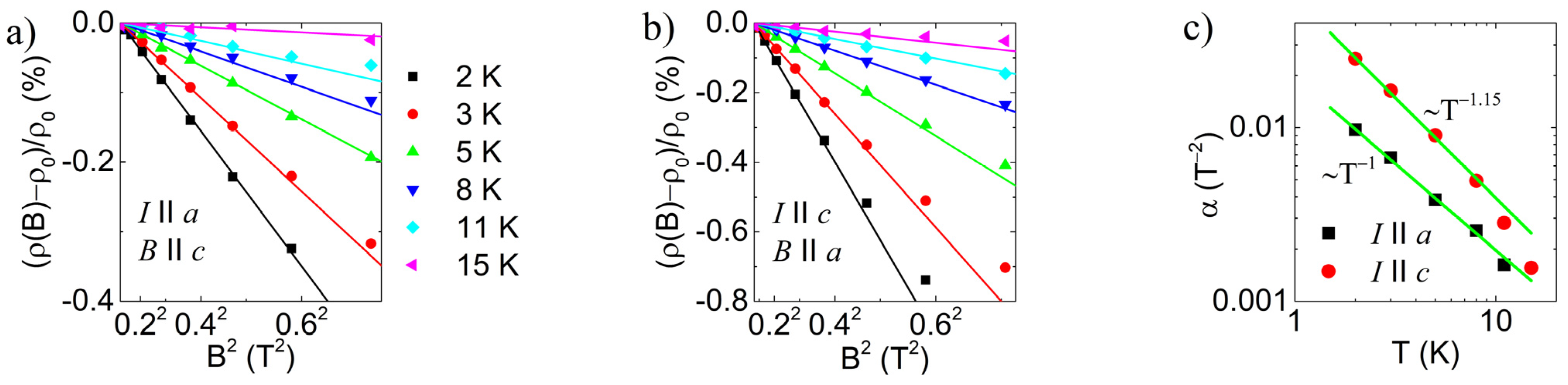
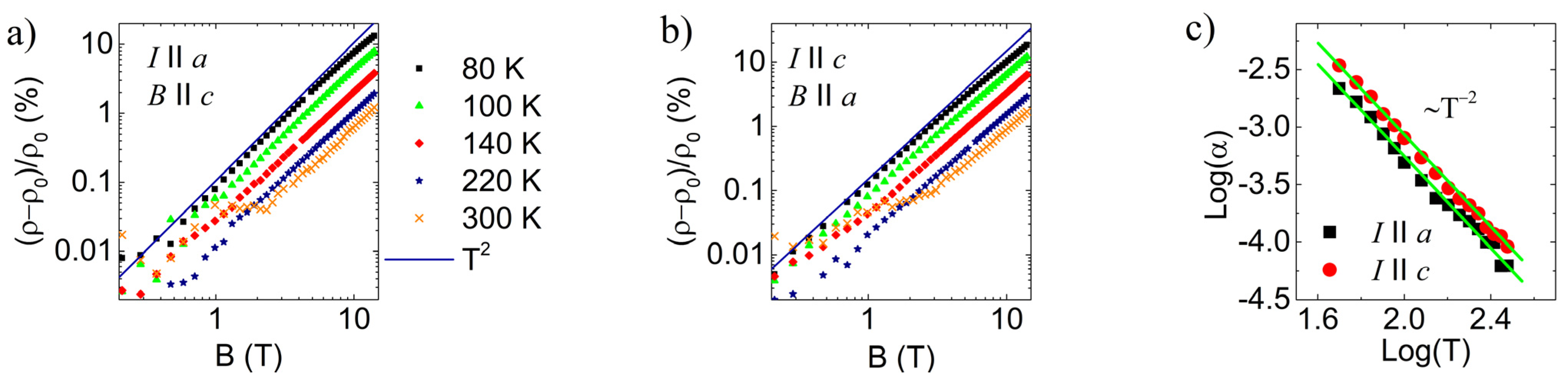
4. Discussion
Magneto-Transport
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, L.-D.; Lo, S.-H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow Thermal Conductivity and High Thermoelectric Figure of Merit in SnSe Crystals. Nature 2014, 508, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Loa, I.; Husband, R.J.; Downie, R.A.; Popuri, S.R.; Bos, J.-W.G. Structural Changes in Thermoelectric SnSe at High Pressures. J. Phys. Condens. Matter 2015, 27, 072202. [Google Scholar] [CrossRef] [PubMed]
- Popuri, S.R.; Pollet, M.; Decourt, R.; Morrison, F.D.; Bennett, N.S.; Bos, J.W.G. Large Thermoelectric Power Factors and Impact of Texturing on the Thermal Conductivity in Polycrystalline SnSe. J. Mater. Chem. C Mater. 2016, 4, 1685–1691. [Google Scholar] [CrossRef]
- Wei, P.-C.; Bhattacharya, S.; He, J.; Neeleshwar, S.; Podila, R.; Chen, Y.Y.; Rao, A.M. The Intrinsic Thermal Conductivity of SnSe. Nature 2016, 539, E1–E2. [Google Scholar] [CrossRef]
- Wu, D.; Wu, L.; He, D.; Zhao, L.-D.; Li, W.; Wu, M.; Jin, M.; Xu, J.; Jiang, J.; Huang, L.; et al. Direct Observation of Vast Off-Stoichiometric Defects in Single Crystalline SnSe. Nano Energy 2017, 35, 321–330. [Google Scholar] [CrossRef]
- Ibrahim, D.; Vaney, J.-B.; Sassi, S.; Candolfi, C.; Ohorodniichuk, V.; Levinsky, P.; Semprimoschnig, C.; Dauscher, A.; Lenoir, B. Reinvestigation of the Thermal Properties of Single-Crystalline SnSe. Appl. Phys. Lett. 2017, 110, 032103. [Google Scholar] [CrossRef]
- Kutorasinski, K.; Wiendlocha, B.; Kaprzyk, S.; Tobola, J. Electronic Structure and Thermoelectric Properties of n- and p-Type SnSe from First-Principles Calculations. Phys. Rev. B 2015, 91, 205201. [Google Scholar] [CrossRef]
- Chen, X.; Lu, P.; Wang, X.; Zhou, Y.; An, C.; Zhou, Y.; Xian, C.; Gao, H.; Guo, Z.; Park, C.; et al. Topological Dirac Line Nodes and Superconductivity Coexist in SnSe at High Pressure. Phys. Rev. B 2017, 96, 165123. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, X.; Sun, H.; Sun, B.; Liu, B.; Liu, H.; Kong, L.; Ma, H. Effect of High Pressure on Thermoelectric Performance and Electronic Structure of SnSe via HPHT. J. Alloys Compd. 2016, 667, 123–129. [Google Scholar] [CrossRef]
- Yan, J.; Ke, F.; Liu, C.; Wang, L.; Wang, Q.; Zhang, J.; Li, G.; Han, Y.; Ma, Y.; Gao, C. Pressure-Driven Semiconducting-Semimetallic Transition in SnSe. Phys. Chem. Chem. Phys. 2016, 18, 5012–5018. [Google Scholar] [CrossRef]
- Yu, H.; Dai, S.; Chen, Y. Enhanced Power Factor via the Control of Structural Phase Transition in SnSe. Sci. Rep. 2016, 6, 26193. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, J.; Wang, H. Anisotropic Thermal Expansion of SnSe from First-Principles Calculations Based on Grüneisen’s Theory. Phys. Chem. Chem. Phys. 2017, 19, 15187–15193. [Google Scholar] [CrossRef]
- Wei, P.-C.; Bhattacharya, S.; Liu, Y.-F.; Liu, F.; He, J.; Tung, Y.-H.; Yang, C.-C.; Hsing, C.-R.; Nguyen, D.-L.; Wei, C.-M.; et al. Thermoelectric Figure-of-Merit of Fully Dense Single-Crystalline SnSe. ACS Omega 2019, 4, 5442–5450. [Google Scholar] [CrossRef]
- Chattopadhyay, T.; Pannetier, J.; von Schnering, H.G. Neutron Diffraction Study of the Structural Phase Transition in SnS and SnSe. J. Phys. Chem. Solids 1986, 47, 879–885. [Google Scholar] [CrossRef]
- Jin, M.; Chen, Z.; Tan, X.; Shao, H.; Liu, G.; Hu, H.; Xu, J.; Yu, B.; Shen, H.; Xu, J.; et al. Charge Transport in Thermoelectric SnSe Single Crystals. ACS Energy Lett. 2018, 3, 689–694. [Google Scholar] [CrossRef]
- Liu, F.; Parajuli, P.; Rao, R.; Wei, P.C.; Karunarathne, A.; Bhattacharya, S.; Podila, R.; He, J.; Maruyama, B.; Priyadarshan, G.; et al. Phonon Anharmonicity in Single-Crystalline SnSe. Phys. Rev. B 2018, 98, 224309. [Google Scholar] [CrossRef]
- Shi, G.; Kioupakis, E. Quasiparticle Band Structures and Thermoelectric Transport Properties of p-Type SnSe. J. Appl. Phys. 2015, 117, 065103. [Google Scholar] [CrossRef]
- Jian Zhang, J.Z.; Zhu, H.; Wu, X.; Cui, H.; Li, D.; Jiang, J.; Gao, C.; Wang, Q.; Cui, Q. Plasma-Assisted Synthesis and Pressure-Induced Structural Transition of Single-Crystalline SnSe Nanosheets. Nanoscale 2015, 7, 10807–10816. [Google Scholar] [CrossRef]
- Wang, S.; Hui, S.; Peng, K.; Bailey, T.P.; Liu, W.; Yan, Y.; Zhou, X.; Tang, X.; Uher, C. Low Temperature Thermoelectric Properties of p-Type Doped Single-Crystalline SnSe. Appl. Phys. Lett. 2018, 112, 142102. [Google Scholar] [CrossRef]
- Tayari, V.; Senkovskiy, B.V.; Rybkovskiy, D.; Ehlen, N.; Fedorov, A.; Chen, C.Y.; Avila, J.; Asensio, M.; Perucchi, A.; Di Pietro, P.; et al. Quasi-Two-Dimensional Thermoelectricity in SnSe. Phys. Rev. B 2018, 97, 045424. [Google Scholar] [CrossRef]
- Nishimura, T.; Sakai, H.; Mori, H.; Akiba, K.; Usui, H.; Ochi, M.; Kuroki, K.; Miyake, A.; Tokunaga, M.; Uwatoko, Y.; et al. Large Enhancement of Thermoelectric Efficiency Due to a Pressure-Induced Lifshitz Transition in SnSe. Phys. Rev. Lett. 2019, 122, 226601. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, A.; Ogiso, O.; Matsumoto, R.; Tanaka, M.; Hara, H.; Tanaka, H.; Takeya, H.; Lee, C.-H.; Takano, Y. Influence of Oxidation in Starting Material Sn on Electric Transport Properties of SnSe Single Crystals. J. Phys. Soc. Jpn. 2018, 87, 065001. [Google Scholar] [CrossRef]
- Duvjir, G.; Min, T.; Thi Ly, T.; Kim, T.; Duong, A.-T.; Cho, S.; Rhim, S.H.; Lee, J.; Kim, J. Origin of p-Type Characteristics in a SnSe Single Crystal. Appl. Phys. Lett. 2017, 110, 262106. [Google Scholar] [CrossRef]
- Lin, X.; Fauqué, B.; Behnia, K. Scalable T2 Resistivity in a Small Single-Component Fermi Surface. Science (1979) 2015, 349, 945–948. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Wang, T.; Xu, Z.; Wu, J.; Hu, W.; Ren, Z.; Liu, S.; Behnia, K.; Lin, X. T-Square Resistivity without Umklapp Scattering in Dilute Metallic Bi2O2Se. Nat. Commun. 2020, 11, 3846. [Google Scholar] [CrossRef]
- Zhang, H.-F.; Lv, Y.-Y.; Xu, L.; Luo, Y.-C.; Lu, H.-M.; Wang, C.W.; Liu, Z.K.; Zhou, J.; Chen, Y.B.; Yao, S.-H. Modulating Electrical Transport Properties of SnSe Crystal to Improve the Thermoelectric Power Factor by Adjusting Growth Method. Appl. Phys. Lett. 2020, 116, 092103. [Google Scholar] [CrossRef]
- Okamoto, H. Se-Sn (Selenium-Tin). J. Phase Equilibria 1998, 19, 293. [Google Scholar] [CrossRef]
- Huang, X.R. LauePt, a Graphical-User-Interface Program for Simulating and Analyzing White-Beam X-Ray Diffraction Laue Patterns. J. Appl. Cryst. Crystallogr. 2010, 43, 926–928. [Google Scholar] [CrossRef]
- Sist, M.; Zhang, J.; Brummerstedt Iversen, B. Crystal Structure and Phase Transition of Thermoelectric SnSe. Acta Cryst. Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 310–316. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Jazbec, S.; Koželj, P.; Vrtnik, S.; Jagličić, Z.; Popčević, P.; Ivkov, J.; Stanić, D.; Smontara, A.; Feuerbacher, M.; Dolinšek, J. Electrical, Magnetic, and Thermal Properties of the δ-FeZn10 Complex Intermetallic Phase. Phys. Rev. B 2012, 86, 064205. [Google Scholar] [CrossRef]
- Stanić, D.; Popčević, P.; Smiljanić, I.; Bihar, Ž.; Bilušić, A.; Batistić, I.; Ivkov, J.; Hegen, M.; Feuerbacher, M. Thermal Conductivity of Taylor Phase Al3(Mn,Pd) Complex Metallic Alloys. Croat. Chem. Acta 2010, 83, 81–86. [Google Scholar]
- Baggioli, M.; Zaccone, A. Universal Origin of Boson Peak Vibrational Anomalies in Ordered Crystals and in Amorphous Materials. Phys. Rev. Lett. 2019, 122, 145501. [Google Scholar] [CrossRef]
- Popuri, S.R.; Pollet, M.; Decourt, R.; Viciu, M.L.; Bos, J.W.G. Evidence for Hard and Soft Substructures in Thermoelectric SnSe. Appl. Phys. Lett. 2017, 110, 253903. [Google Scholar] [CrossRef]
- Logothetidis, S.; Polatoglou, H.M. Ellipsometric Studies of the Dielectric Function of SnSe and a Simple Model of the Electronic Structure and the Bonds of the Orthorhombic IV-VI Compounds. Phys. Rev. B 1987, 36, 7491–7499. [Google Scholar] [CrossRef]
- Pletikosić, I.; Von Rohr, F.; Pervan, P.; Das, P.K.; Vobornik, I.; Cava, R.J.; Valla, T. Band Structure of the IV-VI Black Phosphorus Analog and Thermoelectric SnSe. Phys. Rev. Lett. 2018, 120, 156403. [Google Scholar] [CrossRef]
- Shklovskii, B.I.; Efros, A.L. Electronic Properties of Doped Semiconductors; Springer: Berlin/Heidelberg, Germany, 1984; Volume 45, ISBN 978-3-662-02405-8. [Google Scholar]
- Mott, N. Metal-Insulator Transitions, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1990; ISBN 9780429094880. [Google Scholar]
- Schoepe, W. Variable-Range Hopping Conduction in Doped Germanium at Very Low Temperatures and High Magnetic Fields. Z. Für Phys. B Condens. Matter 1988, 71, 455–463. [Google Scholar] [CrossRef]
- Lisunov, K.G.; Arushanov, E.; Thomas, G.A.; Bucher, E.; Schön, J.H. Variable-Range Hopping Conductivity and Magnetoresistance in n-CuGaSe2. J. Appl. Phys. 2000, 88, 4128–4134. [Google Scholar] [CrossRef]
- Essaleh, L.; Wasim, S.M.; Marín, G.; Rincón, C.; Amhil, S.; Galibert, J. Mott Type Variable Range Hopping Conduction and Magnetoresistance in p-Type CuIn3Te5 Semiconductor Compound. J. Appl. Phys. 2017, 122, 015702. [Google Scholar] [CrossRef]
- Benzaquen, M.; Walsh, D.; Mazuruk, K. Low-Field Magnetoresistance of n-Type GaAs in the Variable-Range Hopping Regime. Phys. Rev. B 1988, 38, 10933–10936. [Google Scholar] [CrossRef]
- Zhang, Y.; Sarachik, M.P. Negative Magnetoresistance in the Variable-Range-Hopping Regime in n-Type CdSe. Phys. Rev. B 1991, 43, 7212–7215. [Google Scholar] [CrossRef] [PubMed]
- Biskupski, G. Positive and Negative Magnetoresistance in the Variable-Range-Hopping Regime of Doped Semiconductors. Philos. Mag. B 1992, 65, 723–728. [Google Scholar] [CrossRef]
- Wasim, S.M.; Essaleh, L.; Galibert, J.; Leotin, J. Magnetoresistance in the Variable Range Hopping Conduction Regime in n-Type CuInSe2. Jpn. J. Appl. Phys. 1993, 32, 453. [Google Scholar] [CrossRef]
- Arushanov, E.; Siebentritt, S.; Schedel-Niedrig, T.; Lux-Steiner, M.C. Hopping Conductivity in p-CuGaSe2 Films. J. Appl. Phys. 2006, 100, 063715. [Google Scholar] [CrossRef]
- Fukuyama, H.; Yoshida, K. Negative Magnetoresistance in the Anderson Localized States. J. Phys. Soc. Jpn. 1979, 46, 102–105. [Google Scholar] [CrossRef]
- Raikh, M.E.; Wessels, G.F. Single-Scattering-Path Approach to the Negative Magnetoresistance in the Variable-Range-Hopping Regime for Two-Dimensional Electron Systems. Phys. Rev. B 1993, 47, 15609–15621. [Google Scholar] [CrossRef]
- Sakai, A.; Kanno, T.; Yotsuhashi, S.; Adachi, H.; Tokura, Y. Thermoelectric Properties of Electron-Doped KTaO3. Jpn. J. Appl. Phys. 2009, 48, 097002. [Google Scholar] [CrossRef]
- Chan, M.K.; Veit, M.J.; Dorow, C.J.; Ge, Y.; Li, Y.; Tabis, W.; Tang, Y.; Zhao, X.; Barišić, N.; Greven, M. In-Plane Magnetoresistance Obeys Kohler’s Rule in the Pseudogap Phase of Cuprate Superconductors. Phys. Rev. Lett. 2014, 113, 177005. [Google Scholar] [CrossRef]
- Kumar, A.; Yudson, V.I.; Maslov, D.L. Quasiparticle and Nonquasiparticle Transport in Doped Quantum Paraelectrics. Phys. Rev. Lett. 2021, 126, 076601. [Google Scholar] [CrossRef]

| Crystal Direction | ||||||
|---|---|---|---|---|---|---|
| a | 0.108 | 1.6 | 0.024 | 40.7 | −0.007 | 3.02 |
| a * | 0.163 | 1.3 | 0.078 | 45.3 | −0.064 | 2.90 |
| b | 0.054 | 2.1 | 0.015 | 36.4 | 0.022 | 1.68 |
| b * | 0.047 | 2.2 | 0.0037 | 75.9 | 0.013 | 1.74 |
| c | 0.048 | 1.4 | 0.015 | 34.4 | 0.015 | 1.49 |
| c * | 0.043 | 1.5 | 0.0057 | 75.2 | 0.063 | 1.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zorić, M.; Dhami, N.S.; Bader, K.; Gille, P.; Smontara, A.; Popčević, P. Negative Magnetoresistance in Hopping Regime of Lightly Doped Thermoelectric SnSe. Materials 2023, 16, 2863. https://doi.org/10.3390/ma16072863
Zorić M, Dhami NS, Bader K, Gille P, Smontara A, Popčević P. Negative Magnetoresistance in Hopping Regime of Lightly Doped Thermoelectric SnSe. Materials. 2023; 16(7):2863. https://doi.org/10.3390/ma16072863
Chicago/Turabian StyleZorić, Marija, Naveen Singh Dhami, Kristian Bader, Peter Gille, Ana Smontara, and Petar Popčević. 2023. "Negative Magnetoresistance in Hopping Regime of Lightly Doped Thermoelectric SnSe" Materials 16, no. 7: 2863. https://doi.org/10.3390/ma16072863
APA StyleZorić, M., Dhami, N. S., Bader, K., Gille, P., Smontara, A., & Popčević, P. (2023). Negative Magnetoresistance in Hopping Regime of Lightly Doped Thermoelectric SnSe. Materials, 16(7), 2863. https://doi.org/10.3390/ma16072863







