Atomic-Scale Insights into the Deformation Mechanism of the Microstructures in Precipitation-Strengthening Alloys
Abstract
1. Introduction
2. Model and Simulation Details
2.1. Phase-Field Crystal Model
2.2. Simulation Details
3. Results and Discussion
3.1. Deformation Mechanisms of Microstructure at Different Lattice Misfits
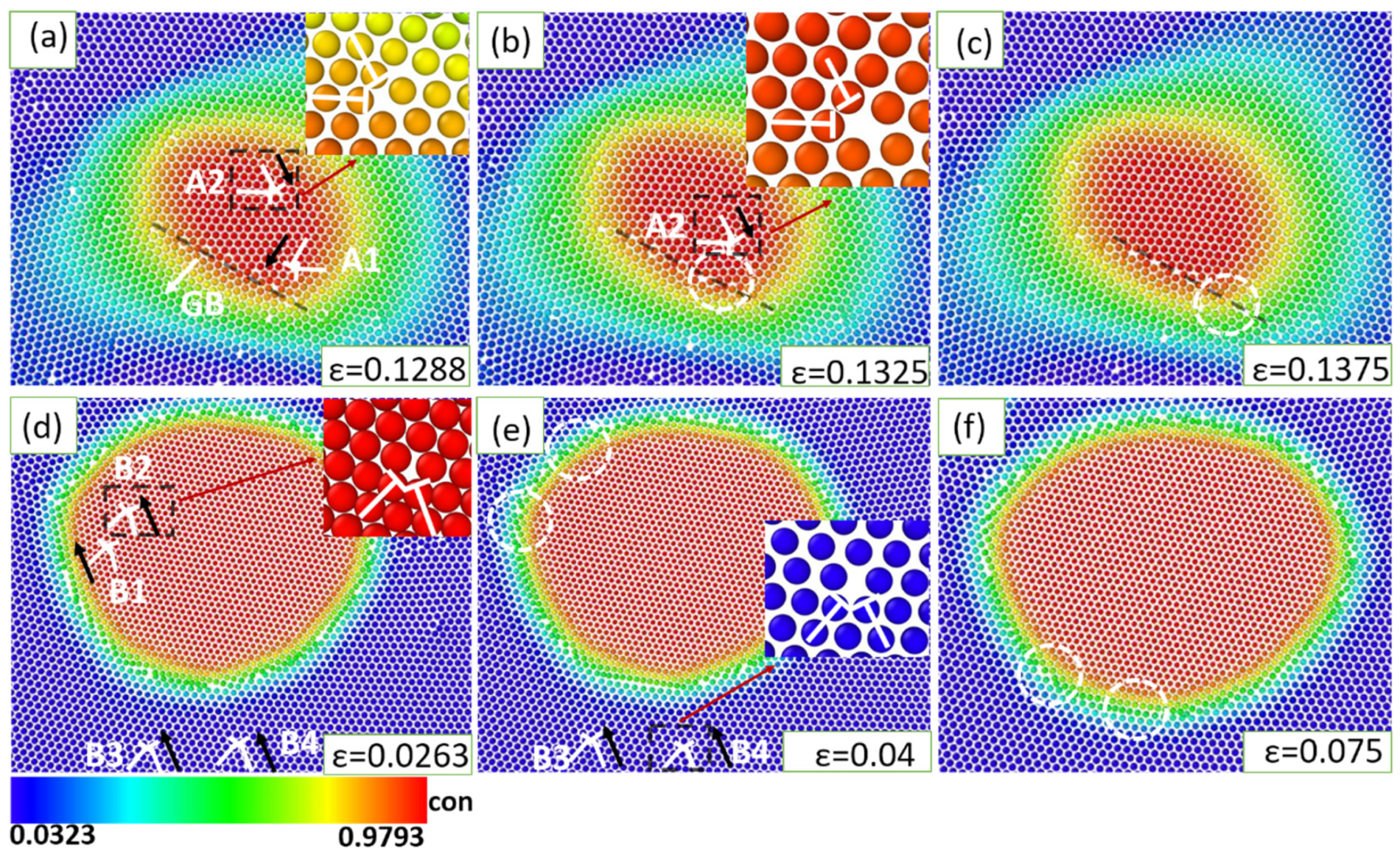
3.1.1. Precipitate-GB Interactions
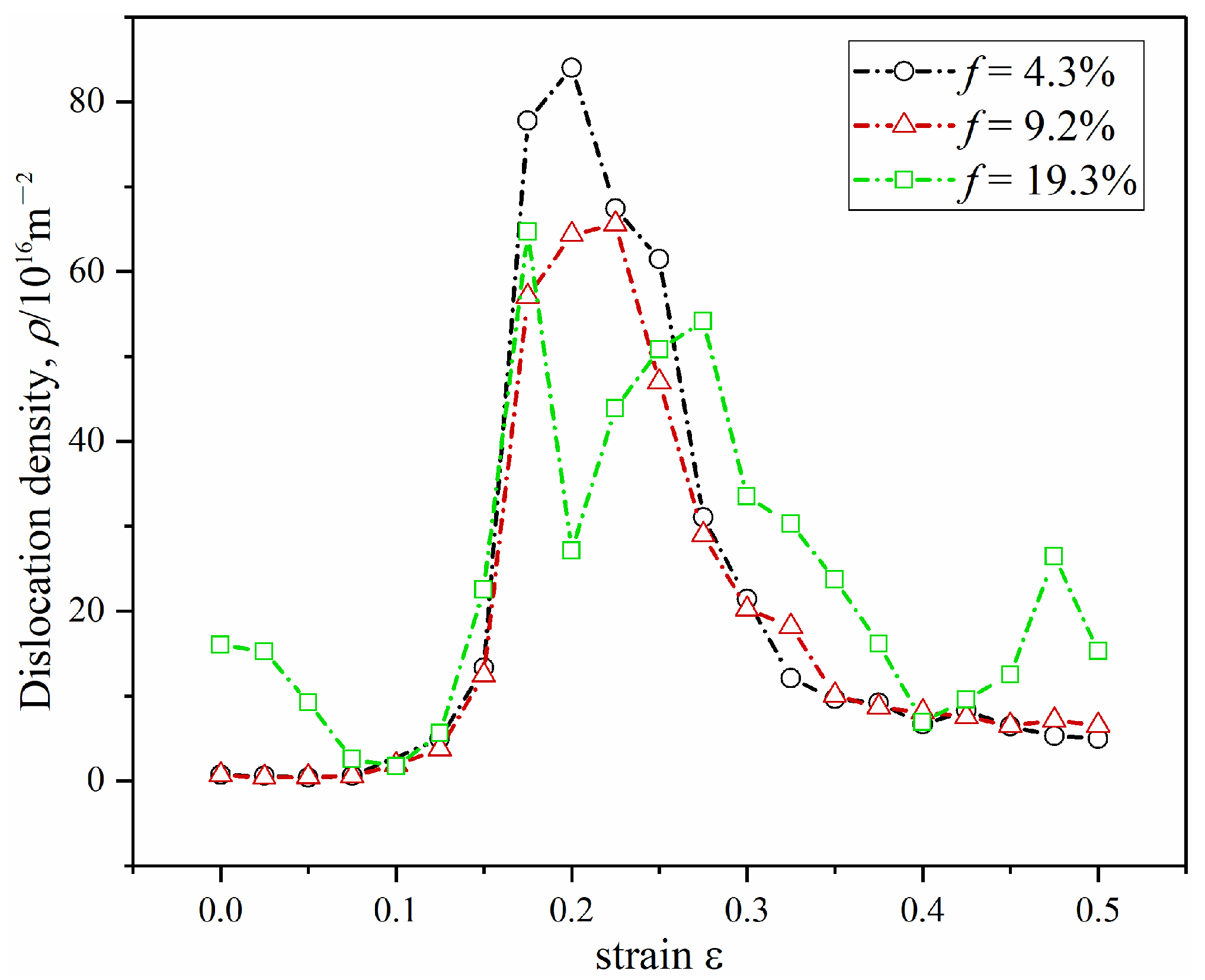
3.1.2. The Dislocation-GB/Precipitate Interactions
3.2. Deformation Mechanisms at Higher Strain Rate
3.3. Deformation Mechanisms of Precipitate-Matrix Phase Interface
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, X.; Cao, X.; Luan, J.; Jiao, Z.; Liu, C.; Zhang, Z. Synergy of strengthening and toughening of a Cu-rich precipitate-strengthened steel. Mater. Sci. Eng. A 2022, 832, 142487. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Pang, S.; Li, X.; Dong, C.; Liaw, P.K. Coherent Precipitation and Strengthening in Compositionally Complex Alloys: A Review. Entropy 2018, 20, 878. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Z.; Timokhina, I.; Pereloma, E. Clustering, nano-scale precipitation and strengthening of steels. Prog. Mater. Sci. 2020, 118, 100764. [Google Scholar] [CrossRef]
- Stornelli, G.; Gaggia, D.; Rallini, M.; Di Schino, A. Heat treatment effect on maraging steel manufactured by laser powder bed fusion technology: Microstructure and mechanical properties. Acta Met. Slovaca 2021, 27, 122–126. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Y.; Chen, D.; Sun, L.; Chen, L.; Tong, X.; Liu, C.; Zhang, Z. Nanoscale precipitation and its influence on strengthening mechanisms in an ultra-high strength low-carbon steel. Int. J. Plast. 2018, 113, 99–110. [Google Scholar] [CrossRef]
- Chambrin, N.; Dalverny, O.; Cloue, J.-M.; Brucelle, O.; Alexis, J. In Situ Ageing with the Platform Preheating of AlSi10Mg Alloy Manufactured by Laser Powder-Bed Fusion Process. Metals 2022, 12, 2148. [Google Scholar] [CrossRef]
- Marlaud, T.; Deschamps, A.; Bley, F.; Lefebvre, W.; Baroux, B. Influence of alloy composition and heat treatment on precipitate composition in Al-Zn-Mg-Cu alloys. Acta Mater. 2010, 58, 248–260. [Google Scholar] [CrossRef]
- Lee, S.-H.; Jung, J.-G.; Baik, S.-I.; Seidman, D.; Kim, M.-S.; Lee, Y.-K.; Euh, K. Precipitation strengthening in naturally aged Al-Zn-Mg-Cu alloy. Mater. Sci. Eng. a-Struct. Mater. Prop. Microstruct. Process. 2021, 803, 140719. [Google Scholar] [CrossRef]
- Rios, P.; Fonseca, G. Grain boundary pinning by Al6Mn precipitates in an Al–1wt%Mn alloy. Scr. Mater. 2004, 50, 71–75. [Google Scholar] [CrossRef]
- Wang, N.; Ji, Y.; Wang, Y.; Wen, Y.; Chen, L.-Q. Two modes of grain boundary pinning by coherent precipitates. Acta Mater. 2017, 135, 226–232. [Google Scholar] [CrossRef]
- Ahmadi, M.; Povoden-Karadeniz, E.; Öksüz, K.; Falahati, A.; Kozeschnik, E. A model for precipitation strengthening in multi-particle systems. Comput. Mater. Sci. 2014, 91, 173–186. [Google Scholar] [CrossRef]
- Randle, V.; Ralph, B. Interactions of grain boundaries with coherent precipitates during grain growth. Acta Met. 1986, 34, 891–898. [Google Scholar] [CrossRef]
- Bai, S.; Di, H.; Liu, Z. Dislocation interaction with Omega phase in crept Al-Cu-Mg-Ag alloys. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2016, 651, 399–405. [Google Scholar] [CrossRef]
- Hirouchi, T.; Takaki, T.; Tomita, Y. Effects of temperature and grain size on phase-field-crystal deformation simulation. Int. J. Mech. Sci. 2010, 52, 309–319. [Google Scholar] [CrossRef]
- Williams, K.R.; Fisher, S.B. The interaction of dislocation loop and γ’ precipitate in nickel based alloys. Radiat. Eff. 1975, 25, 97–103. [Google Scholar] [CrossRef]
- Bahl, S.; Xiong, L.; Allard, L.; Michi, R.; Poplawsky, J.; Chuang, A.; Singh, D.; Watkins, T.; Shin, D.; Haynes, J.; et al. Aging behavior and strengthening mechanisms of coarsening resistant metastable theta’ precipitates in an Al-Cu alloy. Mater. Des. 2021, 198, 109378. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Zaefferer, S.; Raabe, D. Coupling of Electron Channeling with EBSD: Toward the Quantitative Characterization of Deformation Structures in the SEM. Jom 2013, 65, 1229–1236. [Google Scholar] [CrossRef]
- Kobayashi, M.; Miura, H. 3D/4D characterization of strain distribution evolving within the microstructure during plastic deformation. Curr. Opin. Solid State Mater. Sci. 2020, 24, 100835. [Google Scholar] [CrossRef]
- Yang, J.; Liu, C.; Ma, P.; Chen, L.; Zhan, L.; Yan, N. Superposed hardening from precipitates and dislocations enhances strength-ductility balance in Al-Cu alloy. Int. J. Plast. 2022, 158, 103413. [Google Scholar] [CrossRef]
- Chrominski, W.; Lewandowska, M. Influence of dislocation structures on precipitation phenomena in rolled Al-Mg-Si alloy. Mater. Sci. Eng. a-Struct. Mater. Prop. Microstruct. Process. 2020, 793, 139903. [Google Scholar] [CrossRef]
- Liao, Y.; Ye, C.; Gao, H.; Kim, B.-J.; Suslov, S.; Stach, E.A.; Cheng, G.J. Dislocation pinning effects induced by nano-precipitates during warm laser shock peening: Dislocation dynamic simulation and experiments. J. Appl. Phys. 2011, 110, 023518. [Google Scholar] [CrossRef]
- Shaha, S.; Czerwinski, F.; Kasprzak, W.; Friedman, J.; Chen, D.; Shalchi-Amirkhiz, B. Interaction between nano-precipitates and dislocations during high temperature deformation of Al-Si alloys. J. Alloy. Compd. 2017, 712, 219–224. [Google Scholar] [CrossRef]
- Baruah, M.; Borah, A. Processing and precipitation strengthening of 6xxx series aluminium alloys: A review. Int. J. Mater. Sci. 2020, 1, 40–48. [Google Scholar] [CrossRef]
- Tan, F.; Fang, Q.; Li, J.; Wu, H. Interaction of precipitate with shear–coupled grain boundary migration. Acta Mech. 2019, 231, 237–250. [Google Scholar] [CrossRef]
- Marenych, O.; Kostryzhev, A. Strengthening Mechanisms in Nickel-Copper Alloys: A Review. Metals 2020, 10, 1358. [Google Scholar] [CrossRef]
- Cepeda-Jiménez, C.; Castillo-Rodríguez, M.; Pérez-Prado, M. Origin of the low precipitation hardening in magnesium alloys. Acta Mater. 2018, 165, 164–176. [Google Scholar] [CrossRef]
- Mukherji, D.; Gilles, R.; Barbier, B.; Del Genovese, D.; Hasse, B.; Strunz, P.; Wroblewski, T.; Fuess, H.; Rösler, J. Lattice misfit measurement in Inconel 706 containing coherent γ′ and γ″ precipitates. Scr. Mater. 2003, 48, 333–339. [Google Scholar] [CrossRef]
- Thompson, A.; Brooks, J. The mechanism of precipitation strengthening in an iron-base superalloy. Acta Met. 1982, 30, 2197–2203. [Google Scholar] [CrossRef]
- Peng, J.; Li, Z.; Fu, L.; Ji, X.; Pang, Z.; Shan, A. Carbide precipitation strengthening in fine-grained carbon-doped FeCoCrNiMn high entropy alloy. J. Alloy. Compd. 2019, 803, 491–498. [Google Scholar] [CrossRef]
- Lai, Y.; Fan, W.; Yin, M.; Wu, C.; Chen, J. Structures and formation mechanisms of dislocation-induced precipitates in relation to the age-hardening responses of Al-Mg-Si alloys. J. Mater. Sci. Technol. 2019, 41, 127–138. [Google Scholar] [CrossRef]
- Biswas, A.; Siegel, D.J.; Wolverton, C.; Seidman, D.N. Precipitates in Al–Cu alloys revisited: Atom-probe tomographic experiments and first-principles calculations of compositional evolution and interfacial segregation. Acta Mater. 2011, 59, 6187–6204. [Google Scholar] [CrossRef]
- Maciejewski, K.; Jouiad, M.; Ghonem, H. Dislocation/precipitate interactions in IN100 at 650 °C. Mater. Sci. Eng. A 2013, 582, 47–54. [Google Scholar] [CrossRef]
- Liu, H.; Gao, Y.; Qi, L.; Wang, Y.; Nie, J.-F. Phase-Field Simulation of Orowan Strengthening by Coherent Precipitate Plates in an Aluminum Alloy. Met. Mater. Trans. A 2015, 46, 3287–3301. [Google Scholar] [CrossRef]
- Li, J.; Chen, H.; Fang, Q.; Jiang, C.; Liu, Y.; Liaw, P.K. Unraveling the dislocation–precipitate interactions in high-entropy alloys. Int. J. Plast. 2020, 133, 102819. [Google Scholar] [CrossRef]
- Liao, M.; Li, B.; Horstemeyer, M.F. Interaction Between Basal Slip and a Mg17Al12 Precipitate in Magnesium. Met. Mater. Trans. A 2014, 45, 3661–3669. [Google Scholar] [CrossRef]
- Huo, J.-R.; Yang, H.-Y.; Wang, J.; He, C.-Z. Computational simulation of al-based alloy surface structure dislocation: The first-principles calculation and atomic pair-potential lattice dynamics calculation. Mod. Phys. Lett. B 2021, 35, 2150143. [Google Scholar] [CrossRef]
- Wu, K.-A.; Voorhees, P.W. Phase field crystal simulations of nanocrystalline grain growth in two dimensions. Acta Mater. 2012, 60, 407–419. [Google Scholar] [CrossRef]
- Yamanaka, A.; McReynolds, K.; Voorhees, P.W. Phase field crystal simulation of grain boundary motion, grain rotation and dislocation reactions in a BCC bicrystal. Acta Mater. 2017, 133, 160–171. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, K.; Zhang, H.; Tian, X.; Jiang, Q.; Murugadoss, V.; Hou, H. Dislocation motion in plastic deformation of nano polycrystalline metal materials: A phase field crystal method study. Adv. Compos. Hybrid Mater. 2022, 5, 2546–2556. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, L.; Deng, Q.; Zhou, W.; Luo, Z.; Lin, K. Phase field crystal simulation of dislocation configuration evolution in dynamic recovery in two dimensions. Acta Mater. 2016, 117, 238–251. [Google Scholar] [CrossRef]
- Fallah, V.; Korinek, A.; Ofori-Opoku, N.; Raeisinia, B.; Gallerneault, M.; Provatas, N.; Esmaeili, S. Atomic-scale pathway of early-stage precipitation in Al-Mg-Si alloys. Acta Mater. 2015, 82, 457–467. [Google Scholar] [CrossRef]
- Fallah, V.; Ofori-Opoku, N.; Stolle, J.; Provatas, N.; Esmaeili, S. Simulation of early-stage clustering in ternary metal alloys using the phase-field crystal method. Acta Mater. 2013, 61, 3653–3666. [Google Scholar] [CrossRef]
- Elder, K.R.; Provatas, N.; Berry, J.; Stefanovic, P.; Grant, M. Phase-field crystal modeling and classical density functional theory of freezing. Phys. Rev. B 2007, 75, 064107. [Google Scholar] [CrossRef]
- Greenwood, M.; Ofori-Opoku, N.; Rottler, J.; Provatas, N. Modeling structural transformations in binary alloys with phase field crystals. Phys. Rev. B 2011, 84, 064104. [Google Scholar] [CrossRef]
- Greenwood, M.; Rottler, J.; Provatas, N. Phase-field-crystal methodology for modeling of structural transformations. Phys. Rev. E 2011, 83, 031601. [Google Scholar] [CrossRef]
- Huang, Z.-F.; Elder, K.; Provatas, N. Phase-field-crystal dynamics for binary systems: Derivation from dynamical density functional theory, amplitude equation formalism, and applications to alloy heterostructures. Phys. Rev. E 2010, 82, 021605. [Google Scholar] [CrossRef]
- Ofori-Opoku, N.; Fallah, V.; Greenwood, M.; Esmaeili, S.; Provatas, N. Multicomponent phase-field crystal model for structural transformations in metal alloys. Phys. Rev. B 2013, 87, 134105. [Google Scholar] [CrossRef]
- Granasy, L.; Tegze, G.; Toth, G.; Pusztai, T. Phase-field crystal modelling of crystal nucleation, heteroepitaxy and patterning. Philos. Mag. 2011, 91, 123–149. [Google Scholar] [CrossRef]
- Fallah, V.; Korinek, A.; Ofori-Opoku, N.; Provatas, N.; Esmaeili, S. Atomistic investigation of clustering phenomenon in the Al–Cu system: Three-dimensional phase-field crystal simulation and HRTEM/HRSTEM characterization. Acta Mater. 2013, 61, 6372–6386. [Google Scholar] [CrossRef]
- Stefanovic, P.; Haataja, M.; Provatas, N. Phase field crystal study of deformation and plasticity in nanocrystalline materials. Phys. Rev. E 2009, 80, 046107. [Google Scholar] [CrossRef]
- Shuai, X.; Wang, Z.J.; Mao, H.; Tang, S.; Kong, Y.; Du, Y. Atomic-scale study of compositional and structural evolution of early-stage grain boundary precipitation in Al–Cu alloys through phase-field crystal simulation. J. Mater. Sci. 2021, 56, 12700–12715. [Google Scholar] [CrossRef]
- Shuai, X.; Mao, H.; Tang, S.; Kong, Y.; Du, Y. Growth modes of grain boundary precipitate in aluminum alloys under different lattice misfits. J. Mater. Sci. 2022, 57, 2744–2757. [Google Scholar] [CrossRef]
- Dehghan-Manshadi, A.; Dippenaar, R. The Behavior of Precipitates during Hot-Deformation of Low-Manganese, Titanium-Added Pipeline Steels. Metall. Mater. Trans. a-Phys. Metall. Mater. Sci. 2010, 41A, 3291–3296. [Google Scholar] [CrossRef]
- Gong, X.; Luo, S.; Li, S.; Wu, C. Dislocation-Induced Precipitation and Its Strengthening of Al-Cu-Li-Mg Alloys with High Mg. Acta Metall. Sin. -Engl. Lett. 2021, 34, 597–605. [Google Scholar] [CrossRef]
- Chen, L.; Shen, J. Applications of semi-implicit Fourier-spectral method to phase field equations. Comput. Phys. Commun. 1998, 108, 147–158. [Google Scholar] [CrossRef]
- Hirouchi, T.; Takaki, T.; Tomita, Y. Development of numerical scheme for phase field crystal deformation simulation. Comput. Mater. Sci. 2009, 44, 1192–1197. [Google Scholar] [CrossRef]
- Sakaguchi, N.; Shibayama, T.; Kinoshita, H.; Takahashi, H. Atomistic dynamical observation of grain boundary structural changes under electron irradiation. J. Nucl. Mater. 2002, 307–311, 1003–1006. [Google Scholar] [CrossRef]
- Bernstein, N. The influence of geometry on grain boundary motion and rotation. Acta Mater. 2008, 56, 1106–1113. [Google Scholar] [CrossRef]
- Tayon, W.A.; Nygren, K.E.; Crooks, R.E.; Pagan, D.C. In-situ study of planar slip in a commercial aluminum-lithium alloy using high energy X-ray diffraction microscopy. Acta Mater. 2019, 173, 231–241. [Google Scholar] [CrossRef]
- Zhu, A.; Chen, J.; Starke, E. Precipitation strengthening of stress-aged Al-xCu alloys. Acta Mater. 2000, 48, 2239–2246. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Lu, J. Atomic-scale study of dislocation-grain boundary interactions in Cu bicrystal by Berkovich nanoindentation. Mater. Sci. Eng. A 2022, 840, 143012. [Google Scholar] [CrossRef]
- Bratov, V.; Borodin, E. Comparison of dislocation density based approaches for prediction of defect structure evolution in aluminium and copper processed by ECAP. Mater. Sci. Eng. A 2015, 631, 10–17. [Google Scholar] [CrossRef]
- Ni, S.; Wang, Y.; Liao, X.; Alhajeri, S.; Li, H.; Zhao, Y.; Lavernia, E.; Ringer, S.; Langdon, T.; Zhu, Y. Grain growth and dislocation density evolution in a nanocrystalline Ni–Fe alloy induced by high-pressure torsion. Scr. Mater. 2011, 64, 327–330. [Google Scholar] [CrossRef]
- Tandon, R.; Mehta, K.; Manna, R.; Mandal, R. Effect of tensile straining on the precipitation and dislocation behavior of AA7075T7352 aluminum alloy. J. Alloy. Compd. 2022, 904, 163942. [Google Scholar] [CrossRef]
- Lee, W.-S.; Chen, T.-H. Rate-dependent deformation and dislocation substructure of Al–Sc alloy. Scr. Mater. 2006, 54, 1463–1468. [Google Scholar] [CrossRef]
- Thirathipviwat, P.; Nozawa, S.; Furusawa, M.; Onuki, Y.; Hasegawa, M.; Matsumoto, K.; Sato, S. In-situ neutron diffraction study on a dislocation density in a correlation with strain hardening in Al–Mg alloys. Mater. Sci. Eng. A 2022, 855, 143956. [Google Scholar] [CrossRef]
- Zuiko, I.; Kaibyshev, R. Deformation structures and strengthening mechanisms in an Al-Cu alloy subjected to extensive cold rolling. Mater. Sci. Eng. A 2017, 702, 53–64. [Google Scholar] [CrossRef]
- Jia, B.W.; Tan, K.H.; Loke, W.K.; Wicaksono, S.; Yoon, S.F. Effects of surface reconstruction on the epitaxial growth of III-Sb on GaAs using interfacial misfit array. Appl. Surf. Sci. 2017, 399, 220–228. [Google Scholar] [CrossRef]


| Parameters | Symbols | Values/Expressions |
|---|---|---|
| Reference density | 0.01 | |
| Reference composition | c0 | 0.5 |
| Polynomial fitting parameters | 1.4, 1 | |
| Entropy of mixing coefficient | 0.005 | |
| Parameters for correlation function | 0.8, | |
| Gradient energy coefficient | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.; Tang, S.; Kong, Y.; Shuai, X.; Mao, H.; Du, Y. Atomic-Scale Insights into the Deformation Mechanism of the Microstructures in Precipitation-Strengthening Alloys. Materials 2023, 16, 1841. https://doi.org/10.3390/ma16051841
Wei C, Tang S, Kong Y, Shuai X, Mao H, Du Y. Atomic-Scale Insights into the Deformation Mechanism of the Microstructures in Precipitation-Strengthening Alloys. Materials. 2023; 16(5):1841. https://doi.org/10.3390/ma16051841
Chicago/Turabian StyleWei, Chenshuang, Sai Tang, Yi Kong, Xiong Shuai, Hong Mao, and Yong Du. 2023. "Atomic-Scale Insights into the Deformation Mechanism of the Microstructures in Precipitation-Strengthening Alloys" Materials 16, no. 5: 1841. https://doi.org/10.3390/ma16051841
APA StyleWei, C., Tang, S., Kong, Y., Shuai, X., Mao, H., & Du, Y. (2023). Atomic-Scale Insights into the Deformation Mechanism of the Microstructures in Precipitation-Strengthening Alloys. Materials, 16(5), 1841. https://doi.org/10.3390/ma16051841






