Measurement and In-Depth Analysis of Higher Harmonic Generation in Aluminum Alloys with Consideration of Source Nonlinearity
Abstract
1. Introduction
2. Plane Wave Solutions and Nonlinearity Parameters
3. Elements of Absolute Nonlinearity Parameter Measurement
3.1. Receiver Calibration Measurement
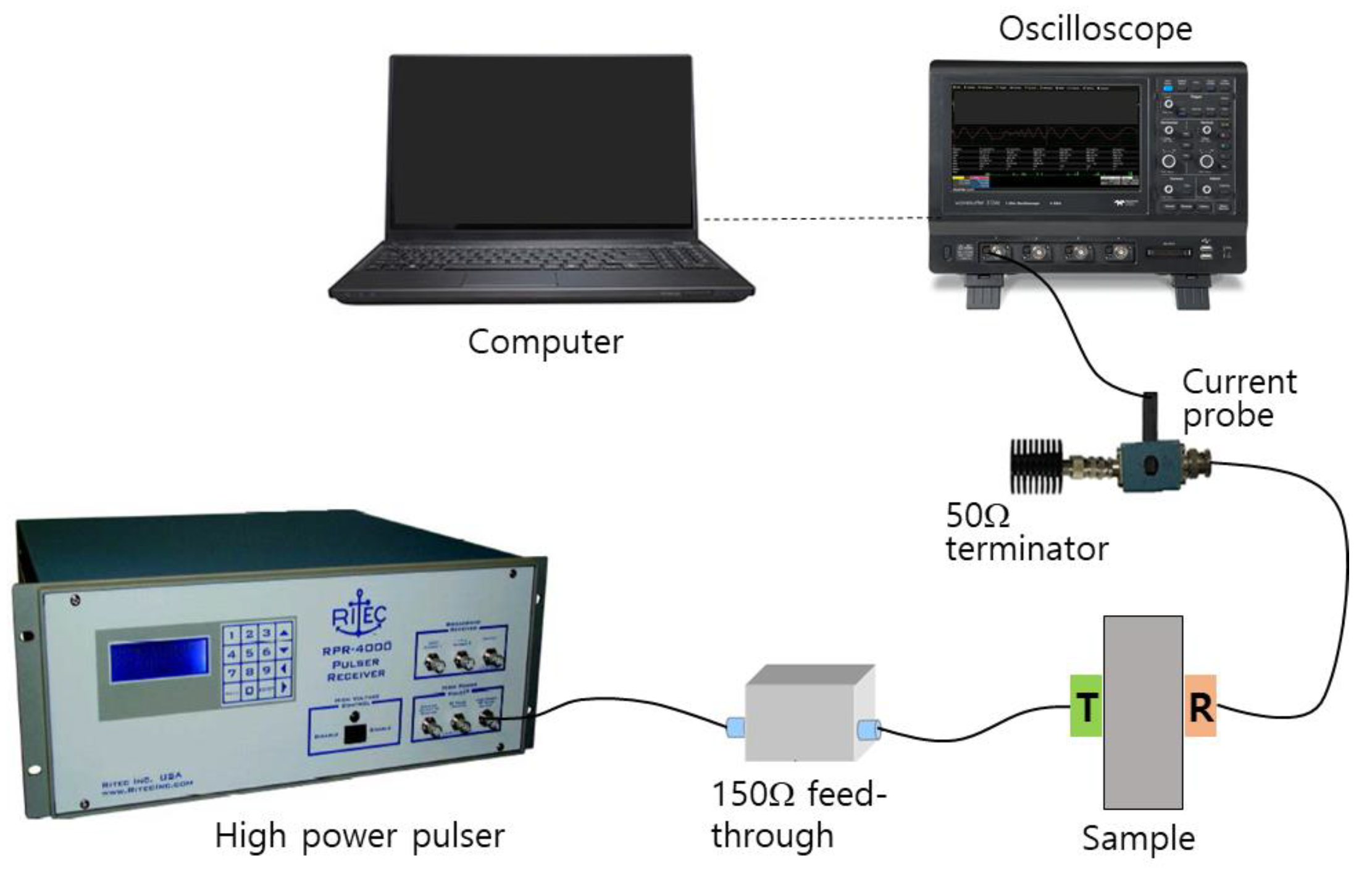
3.2. Harmonic Generation Measurement
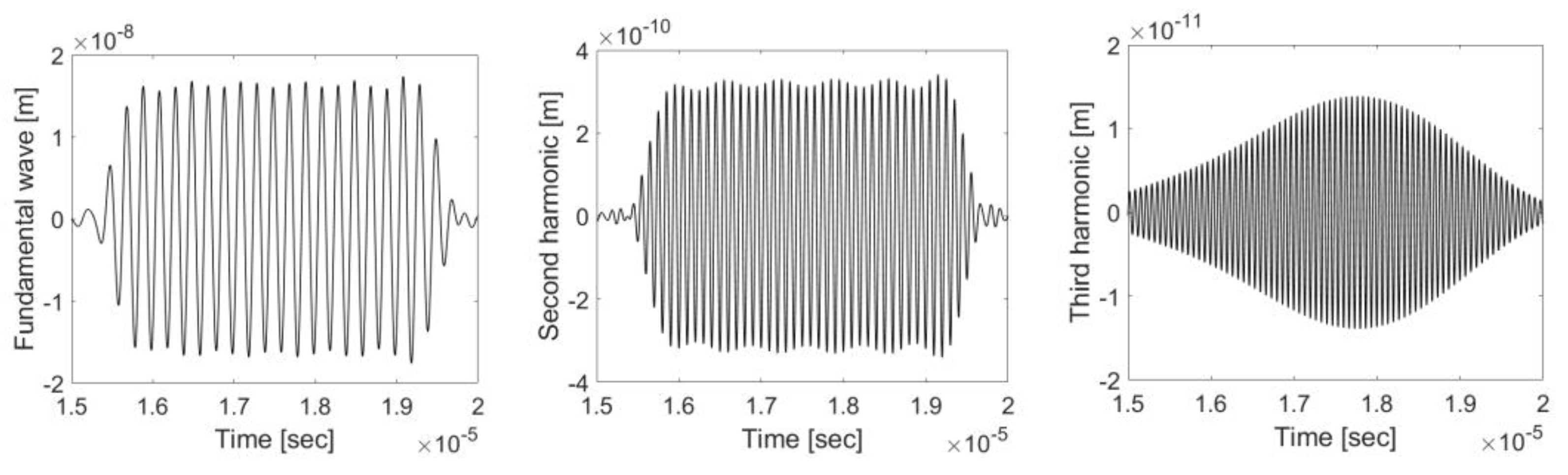
3.3. Measurement of Harmonic Displacement Amplitude
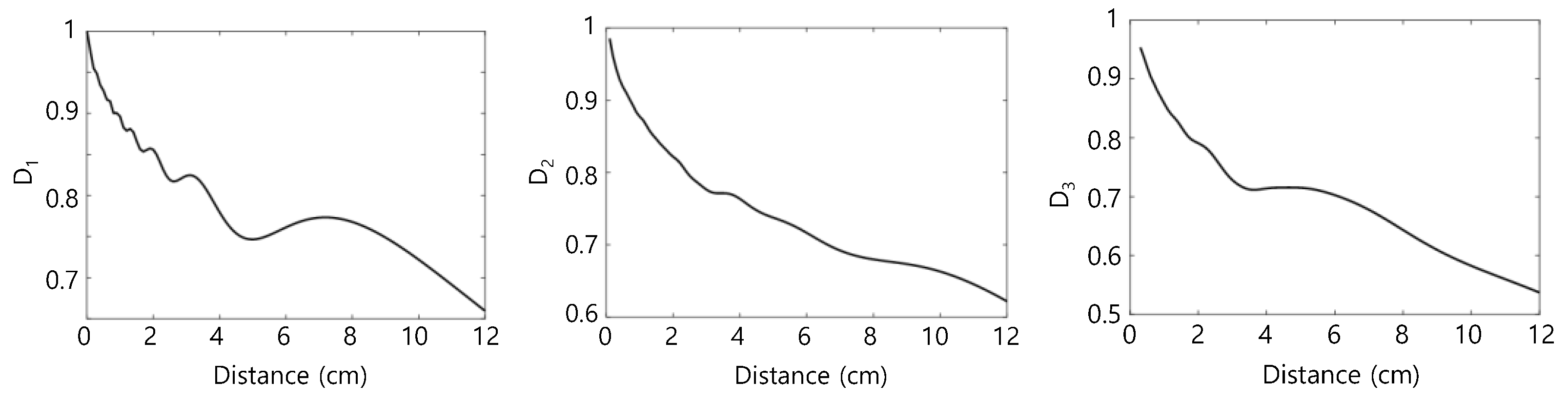
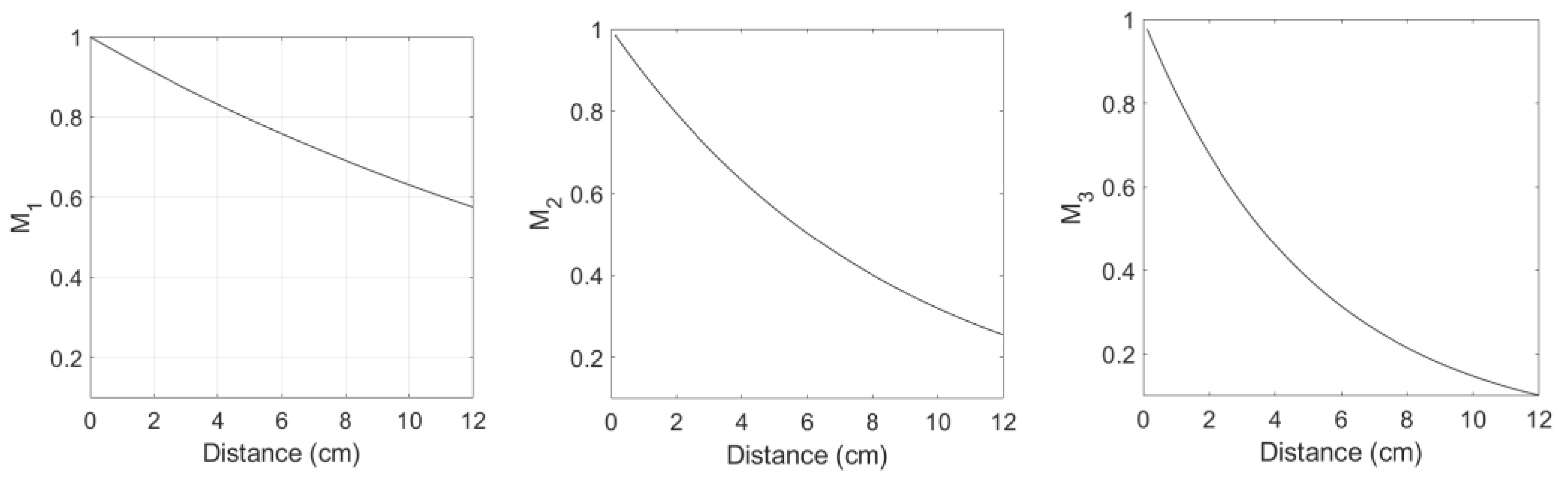
3.4. Diffraction and Attenuation Corrections
3.5. Check of Source Nonlinearity and Correction
3.6. Comments on Contact Method of Nonlinear Ultrasound Testing
4. Results and Discussion
4.1. Diffraction Correction and Attenuation Correction
4.2. Receiver Transfer Function
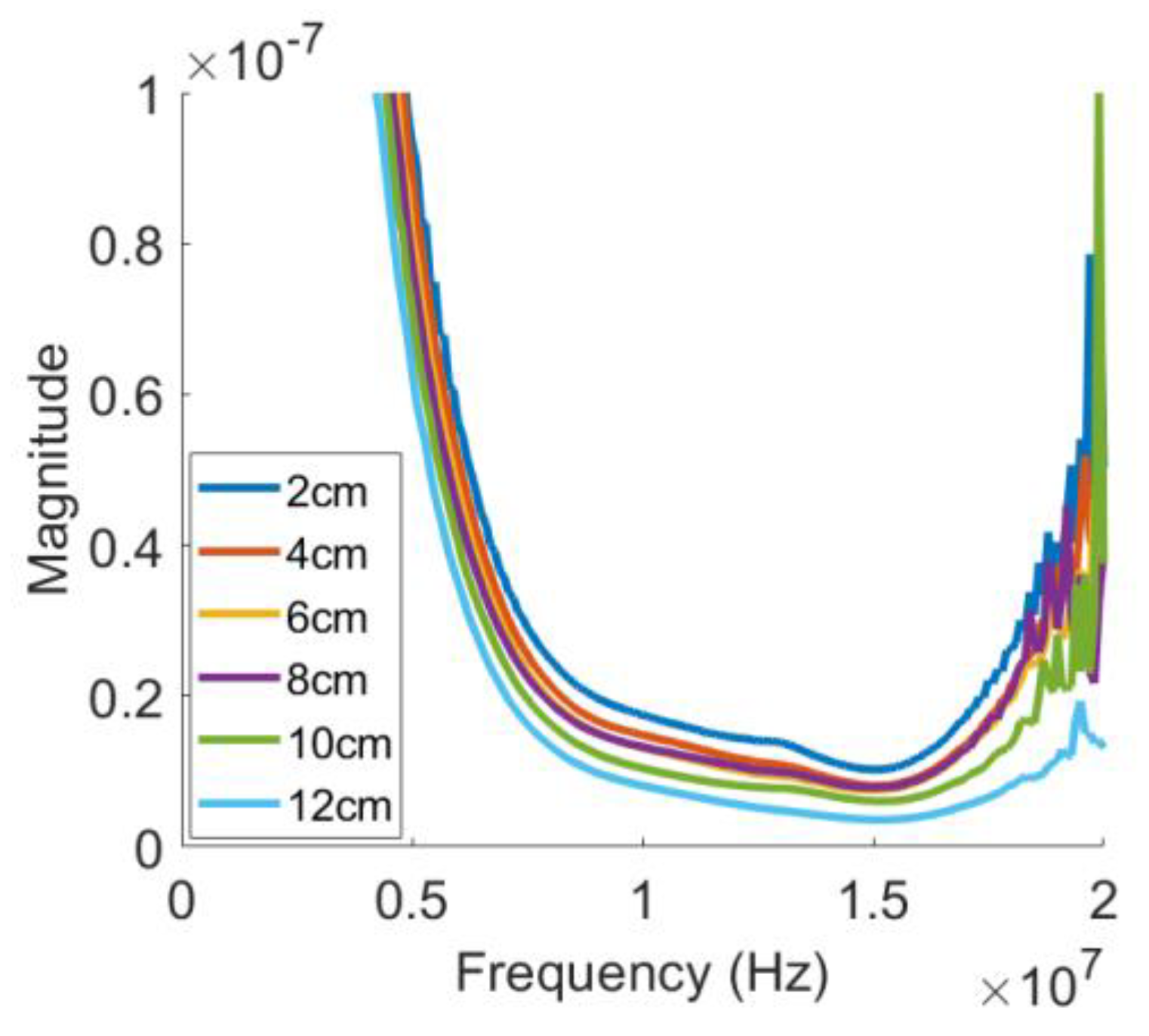
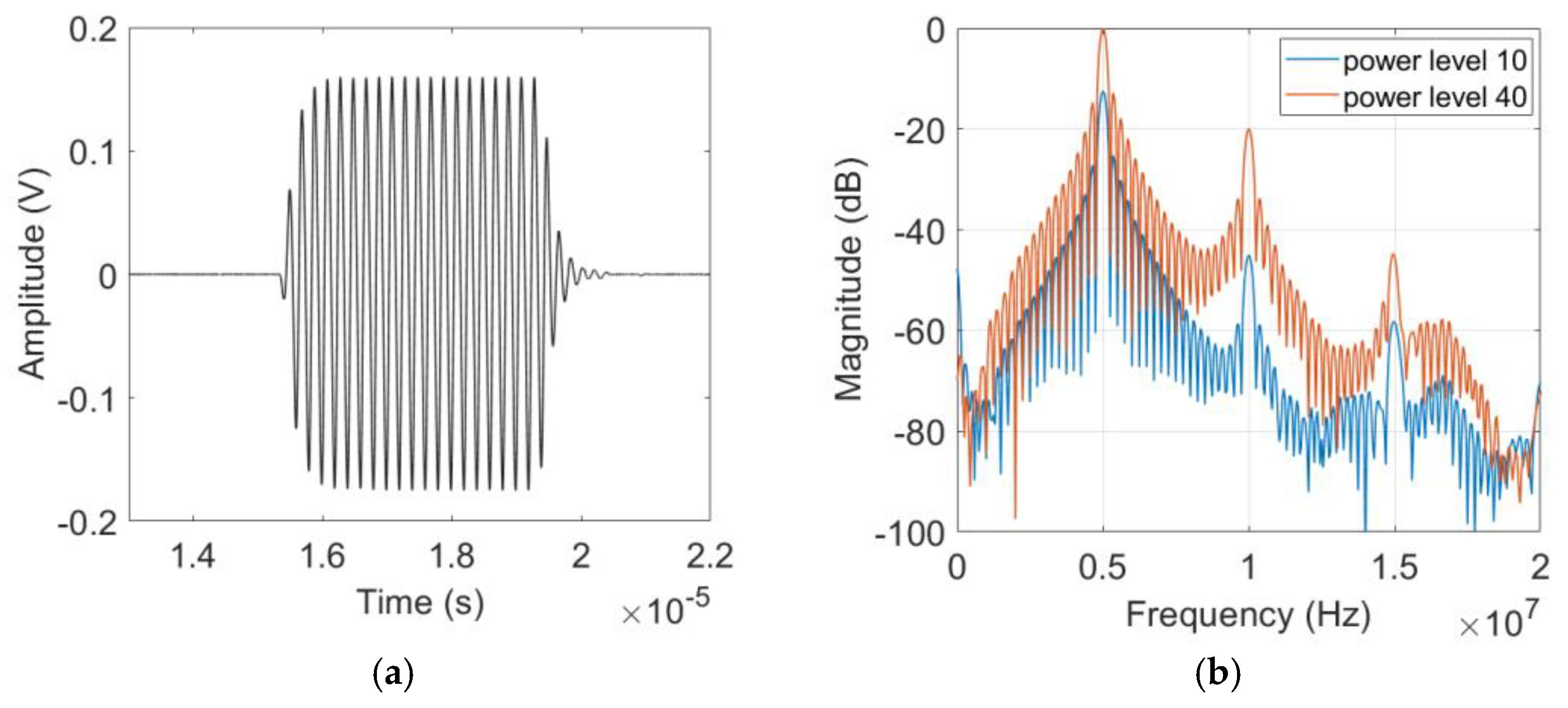
4.3. Received Waveform and Frequency Spectrum
4.4. Calculation of Absolute Displacement
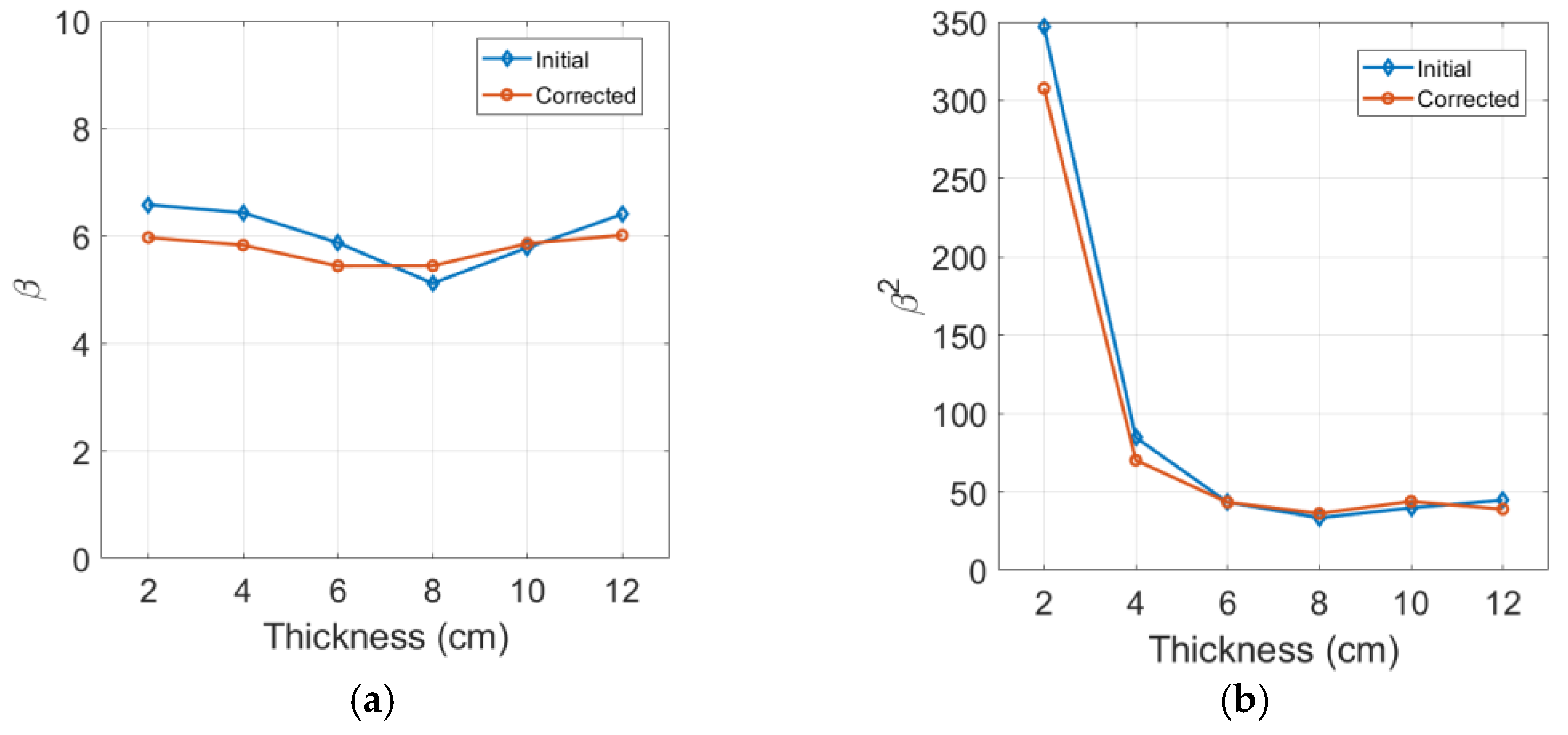
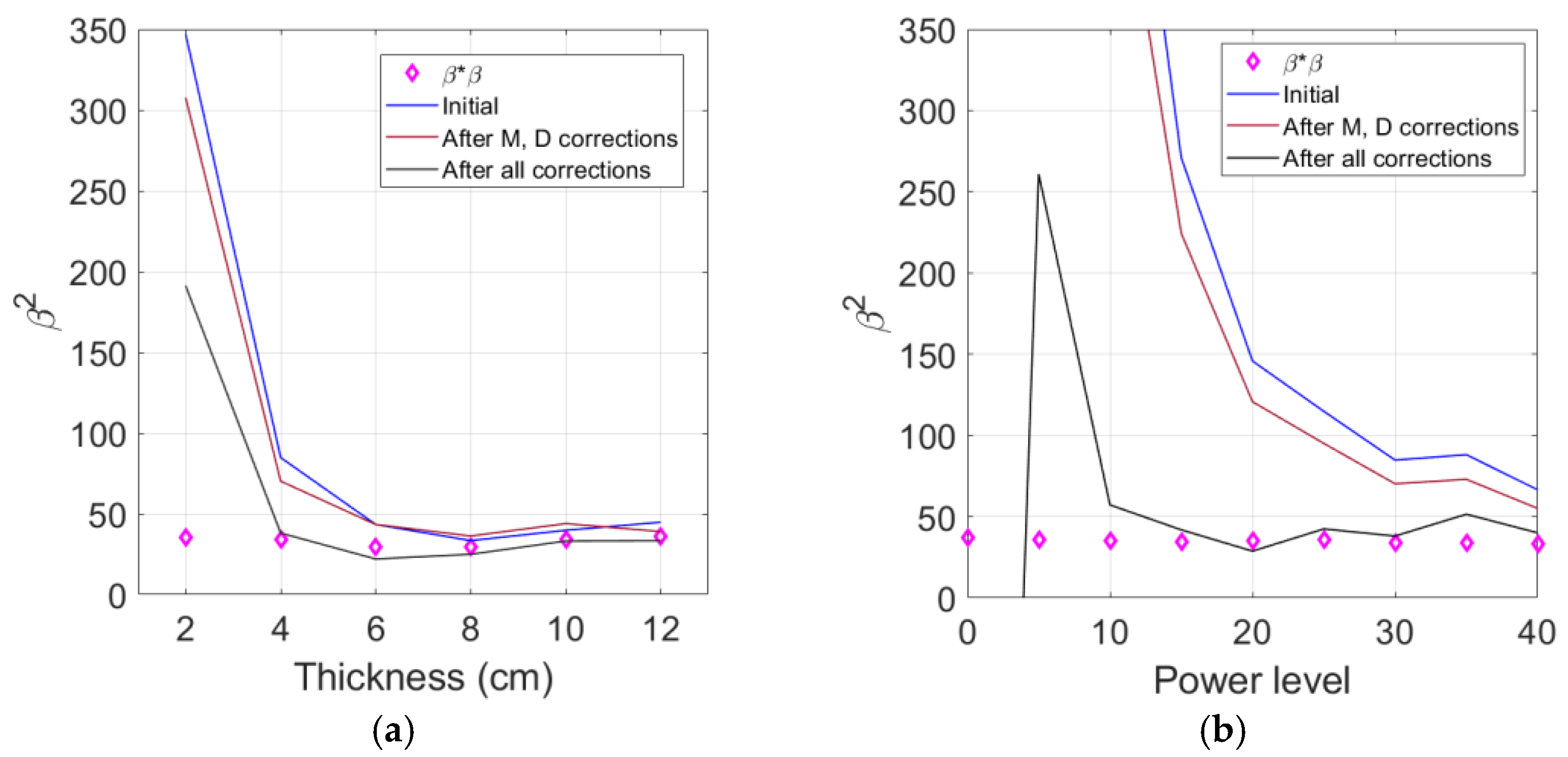
4.5. Effects of Diffraction and Attenuation Corrections on
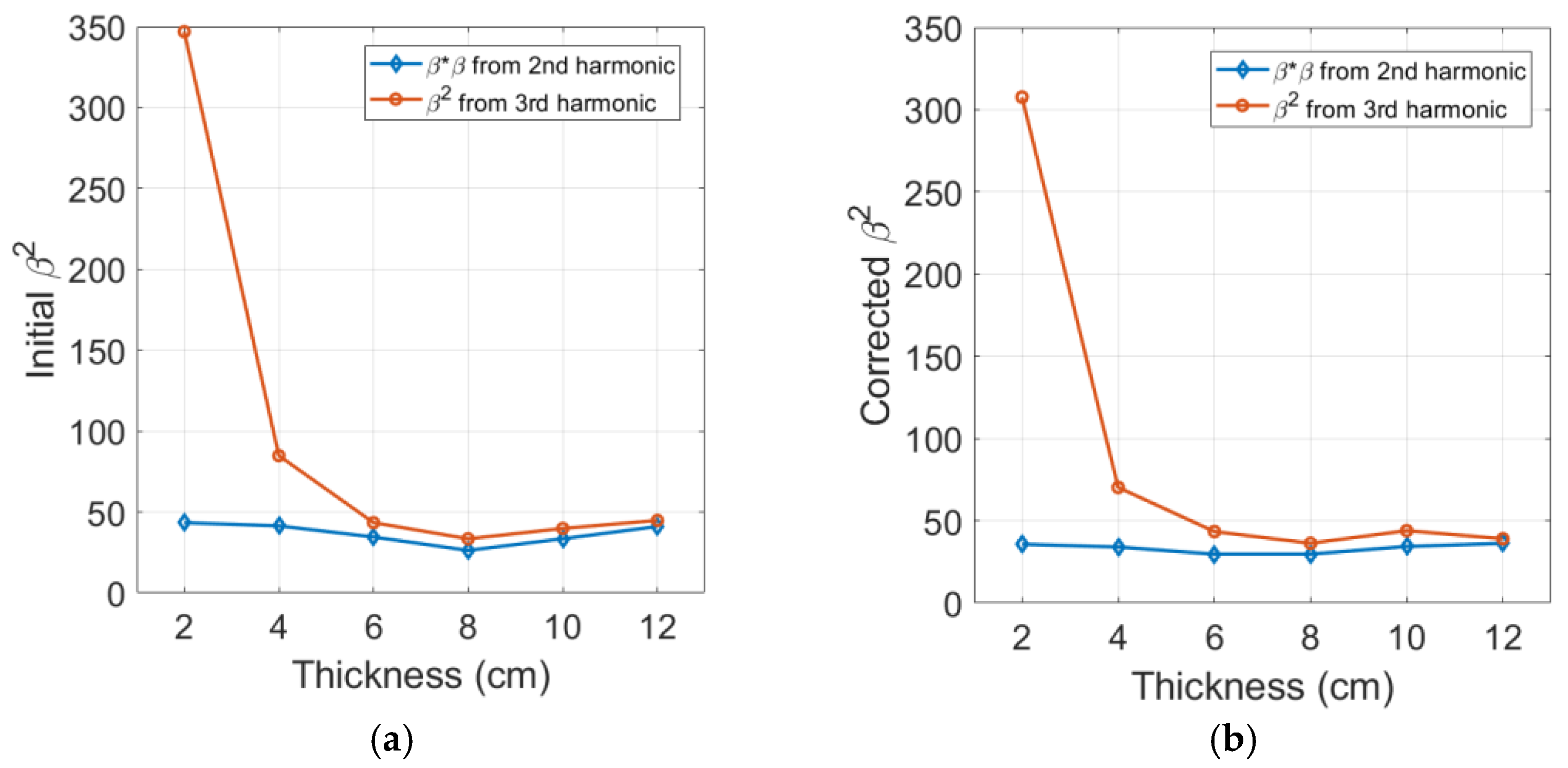
4.6. Comparison of Cubic Nonlinearity Paramter and Square of Quadratic Nonlinearity Parameter
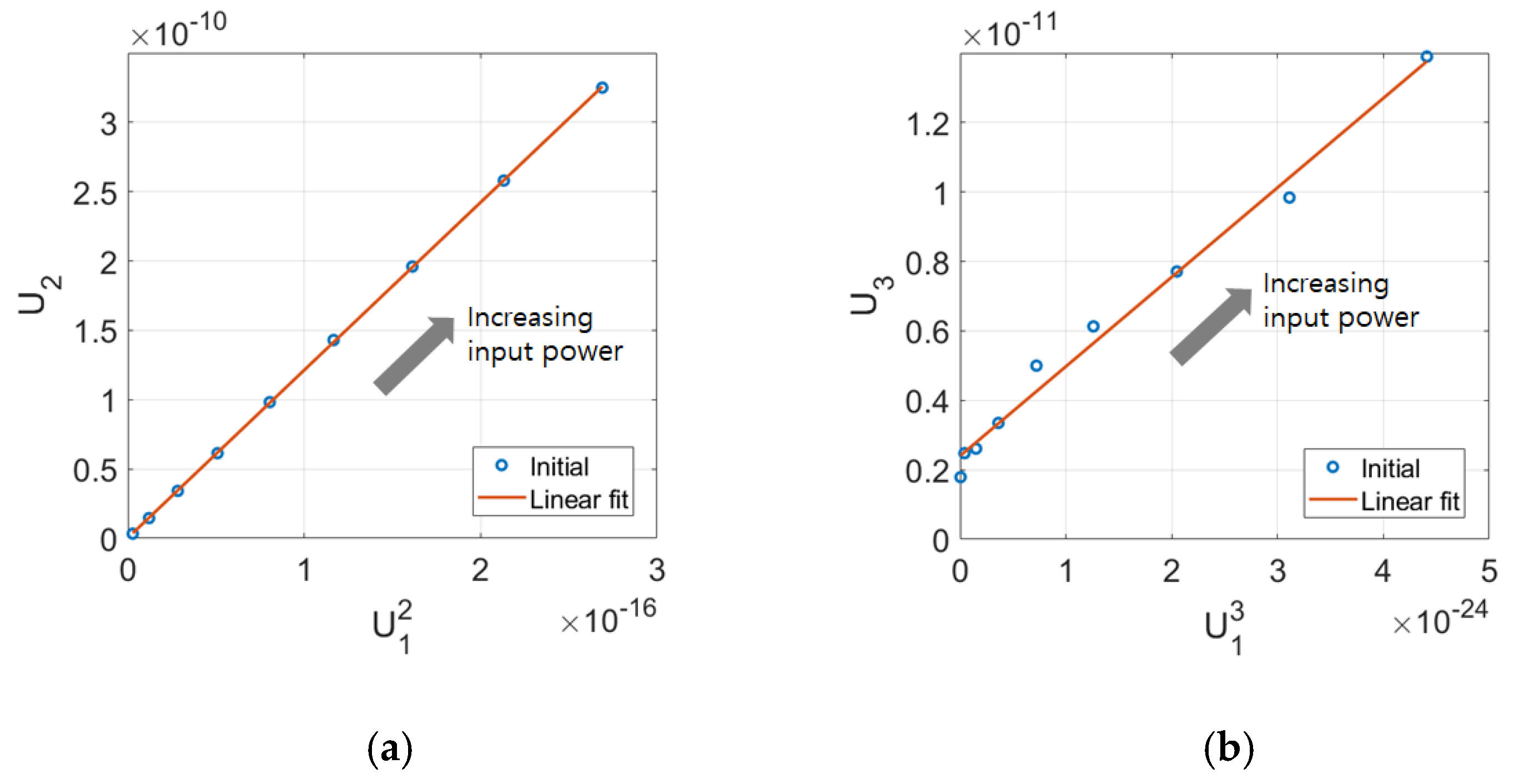
4.7. Source Nonlinearity Check and Correction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thompson, R.B.; Buck, D.; Thompson, D.O. Higher harmonics of finite amplitude ultrasonic waves in Solids. J. Acoust. Soc. Am. 1976, 59, 1087–1094. [Google Scholar] [CrossRef]
- Gebrekidan, S.B.; Kang, T.; Kim, H.-J.; Song, S.-J. Nonlinear ultrasonic characterization of early degradation of fatigued Al6061-T6 with harmonic generation technique. Ultrasonics 2018, 85, 23–30. [Google Scholar] [CrossRef]
- Zhu, B.; Lee, J. A Study on Fatigue State Evaluation of Rail by the Use of Ultrasonic Nonlinearity. Materials 2019, 12, 2698. [Google Scholar] [CrossRef]
- Zhang, L.; Oskoe, S.K.; Li, H.; Ozevin, D. Combined Damage Index to Detect Plastic Deformation in Metals Using Acoustic Emission and Nonlinear Ultrasonics. Materials 2018, 11, 2151. [Google Scholar] [CrossRef]
- Kawashima, K. Harmonic Imaging of Plastic Deformation in Thin Metal Plates Using Nonlinear Ultrasonic Method. Jpn. J. Appl. Phys. 2011, 50, 07HC14. [Google Scholar] [CrossRef]
- Ren, G.; Kim, G.; Jhang, K. Relationship between second and third-order acoustic nonlinear parameters in relative measurement. Ultrasonics 2015, 56, 539–544. [Google Scholar] [CrossRef]
- Kamali, N.; Mahdav, A.; Chi, S.-W. Numerical study on how heterogeneity affects ultrasound high harmonics generation. Nondestruct. Test. Eval. 2020, 35, 158–176. [Google Scholar] [CrossRef]
- Shah, A.A.; Ribakov, Y. Non-linear ultrasonic evaluation of damaged concrete based on higher order harmonic generation. Mater. Des. 2009, 30, 4095–4102. [Google Scholar] [CrossRef]
- Chillara, V.K.; Lissenden, C.J. On some aspects of material behavior relating microstructure and ultrasonic higher harmonic generation. Int. J. Eng. Sci. 2015, 94, 59–70. [Google Scholar] [CrossRef]
- Hikata, A.; Sewell, F., Jr.; Elbaum, C. Generation of ultrasonic second and third harmonics due to dislocation ii. Phys. Rev. 1966, 151, 035003. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Effect of precipitate coherency strains on acoustic harmonic generation. J. Appl. Phys. Lett. 1997, 81, 2957–2962. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Determination of precipitate nucleation and growth rates from ultrasonic harmonic generation. Appl. Phys. Lett. 2000, 77, 1952–1954. [Google Scholar] [CrossRef]
- Lissenden, C.J.; Liu, Y.; Choi, G.W.; Yao, X. Effect of Localized Microstructure Evolution on Higher Harmonic Generation of Guided Waves. J. Nondestruct. Eval. 2014, 33, 178–186. [Google Scholar] [CrossRef]
- Zhao, G.; Jiang, M.; Luo, Y.; Sui, Q. Third harmonic approximate phase velocity matching nonlinear early fatigue damage detection. Measurement 2022, 189, 110518. [Google Scholar] [CrossRef]
- Li, W.; Xu, C.; Cho, Y. Third harmonic generation of shear horizontal guided waves propagation in plate-like structures. J. Korean Soc. Nondestruct. Test. 2016, 36, 149–154. [Google Scholar] [CrossRef]
- Wen, F.; Shan, S.; Cheng, L. Third harmonic shear horizontal waves for material degradation monitoring. Struct. Health Monit. 2021, 20, 475–483. [Google Scholar] [CrossRef]
- Achenbach, J.D.; Wang, Y. Far-field resonant third harmonic surface wave on a half-space of incompressible material of cubic nonlinearity. J. Mech. Phys. Solids 2018, 120, 5–15. [Google Scholar] [CrossRef]
- Wang, Y.; Achenbach, J.D. Interesting effects in harmonic generation by plane elastic waves. Acta Mech. Sin. 2017, 33, 754–762. [Google Scholar] [CrossRef]
- Jeong, H.; Barnard, D.; Cho, S.; Zhang, S.; Li, X. Receiver calibration and the nonlinearity parameter measurement of thick solid samples with diffraction and attenuation corrections. Ultrasonics 2017, 81, 147–157. [Google Scholar] [CrossRef]
- Cho, S.; Jeong, H.; Zhang, S.; Li, X. Dual Element Transducer Approach for Second Harmonic Generation and Material Nonlinearity Measurement of Solids in the Pulse-Echo Method. J. Nondestruct. Eval. 2020, 39, 62. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Jeong, H.; Cho, S. Investigation of material nonlinearity measurements using the third-harmonic generation. IEEE Trans. Instrum. Meas. 2019, 68, 3635–3646. [Google Scholar] [CrossRef]
- Kube, C.M.; Arguelles, A.P. Ultrasonic harmonic generation from materials with up to cubic nonlinearity. J. Acoust. Soc. Am. 2017, 142, EL224–EL230. [Google Scholar] [CrossRef]
- Dace, G.E.; Thompson, R.B.; Buck, O. Measurement of the acoustic harmonic generation for materials characterization using contact transducers. Rev. Prog. Quant. Nondestruct. Eval. 1992, 11, 2069–2076. [Google Scholar]
- Vila, M.; Meulen, F.V.; Dos Santos, S.; Haumesser, L.; Bou Matar, O. Contact phase modulation method for acoustic nonlinear parameter measurement in solid. Ultrasonics 2004, 42, 1061–1065. [Google Scholar] [CrossRef] [PubMed]
- Robin, G.; Meulen, F.V.; Wilkie-Chancellier, N.; Martinez, L.; Haumesser, L.; Fortineau, J.; Griesmar, P.; Lethiecq, M.; Feuillard, G. Ultrasonic self-calibrated method applied to monitoring of sol–gel transition. Ultrasonics 2012, 52, 622–627. [Google Scholar] [CrossRef] [PubMed]
- Rogers, P.H.; Van Buren, A.L. An exact expression for the Lommel-diffraction correction integral. J. Acoust. Soc. Am. 1974, 55, 724–728. [Google Scholar] [CrossRef]
- Williams, A.O., Jr. The piston source at high frequencies. J. Acoust. Soc. Am. 1951, 23, 1–6. [Google Scholar] [CrossRef]
- Chakrapani, S.K.; Howard, A.; Barnard, D. Influence of surface roughness on the measurement of acoustic nonlinearity parameter of solids using contact piezoelectric transducers. Ultrasonics 2018, 84, 112–118. [Google Scholar] [CrossRef]
- Sun, L.; Kulkarni, S.S.; Achenbach, J.D.; Krishnaswamy, S. Technique to minimize couplant-effect in acoustic nonlinearity measurements. J. Acoust. Soc. Am. 2006, 120, 2500–2505. [Google Scholar] [CrossRef]
- Jeong, H.; Zhang, S.; Cho, S.; Li, X. Assessment of Acoustic Nonlinearity Parameters Using an Optimized Data-Fitting Method with Multi-Gaussian Beam Model-Based Diffraction Corrections. Res. Nondestruct. Valuat. 2016, 27, 230–250. [Google Scholar] [CrossRef]
- Song, D.-G.; Choi, S.; Kim, T.; Jhang, K.-Y. Compensation of a Second Harmonic Wave Included in an Incident Ultrasonic Wave for the Precise Measurement of the Acoustic Nonlinearity Parameter. Sensors 2021, 21, 3203. [Google Scholar] [CrossRef]
- Torello, D.; Thiele, S.; Matlack, K.H.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Diffraction, attenuation, and source corrections for nonlinear Rayleigh wave ultrasonic measurements. Ultrasonics 2015, 56, 417–426. [Google Scholar] [CrossRef]
- Tang, S.C.; Clement, G.T. A Harmonic Cancellation Technique for an Ultrasound Transducer Excited by a Switched-Mode Power Converter. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 359–367. [Google Scholar] [CrossRef]
- Mostavi, A.; Kabir, M.; Ozevin, D. The integration of superlattices and immersion nonlinear ultrasonics to enhance damage detection threshold. Appl. Phys. Lett. 2017, 111, 201905. [Google Scholar] [CrossRef]
- Tian, Y.; Shen, Y.; Rao, D.; Xu, W. Metamaterial improved nonlinear ultrasonics for fatigue damage detection. Smart Mater. Struct. 2019, 28, 075038. [Google Scholar] [CrossRef]
- Sandeep Kumar, S.R.; Krishnadas, V.K.; Balasubramaniam, K.; Rajagopal, P. Waveguide metamaterial rod as mechanical acoustic filter for enhancing nonlinear ultrasonic detection. APL Mater. 2021, 9, 061115. [Google Scholar]
- Smith, E.J.; Matlack, K.H. Metal additively manufactured phononic materials as ultrasonic filters in nonlinear ultrasound measurements. J. Acoust. Soc. Am. 2021, 149, 3739–3750. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, H.; Shin, H.; Zhang, S.; Li, X. Measurement and In-Depth Analysis of Higher Harmonic Generation in Aluminum Alloys with Consideration of Source Nonlinearity. Materials 2023, 16, 4453. https://doi.org/10.3390/ma16124453
Jeong H, Shin H, Zhang S, Li X. Measurement and In-Depth Analysis of Higher Harmonic Generation in Aluminum Alloys with Consideration of Source Nonlinearity. Materials. 2023; 16(12):4453. https://doi.org/10.3390/ma16124453
Chicago/Turabian StyleJeong, Hyunjo, Hyojeong Shin, Shuzeng Zhang, and Xiongbing Li. 2023. "Measurement and In-Depth Analysis of Higher Harmonic Generation in Aluminum Alloys with Consideration of Source Nonlinearity" Materials 16, no. 12: 4453. https://doi.org/10.3390/ma16124453
APA StyleJeong, H., Shin, H., Zhang, S., & Li, X. (2023). Measurement and In-Depth Analysis of Higher Harmonic Generation in Aluminum Alloys with Consideration of Source Nonlinearity. Materials, 16(12), 4453. https://doi.org/10.3390/ma16124453







