Nondestructive Evaluation of Residual Stress in Shot Peened Inconel Using Ultrasonic Minimum Reflection Measurement
Abstract
:1. Introduction
2. Theory
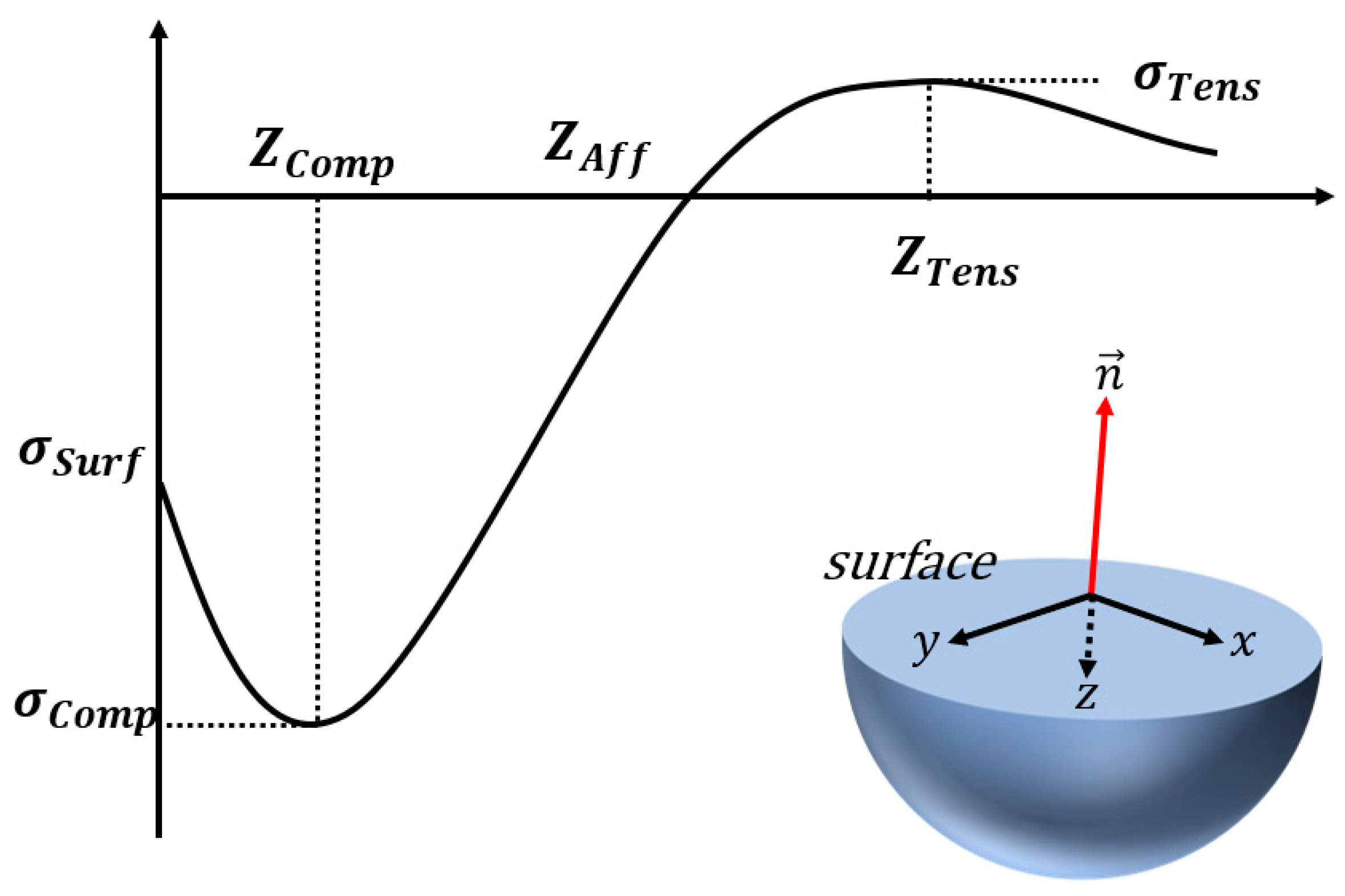
2.1. Characteristics of Residual Stress by Shot Peening
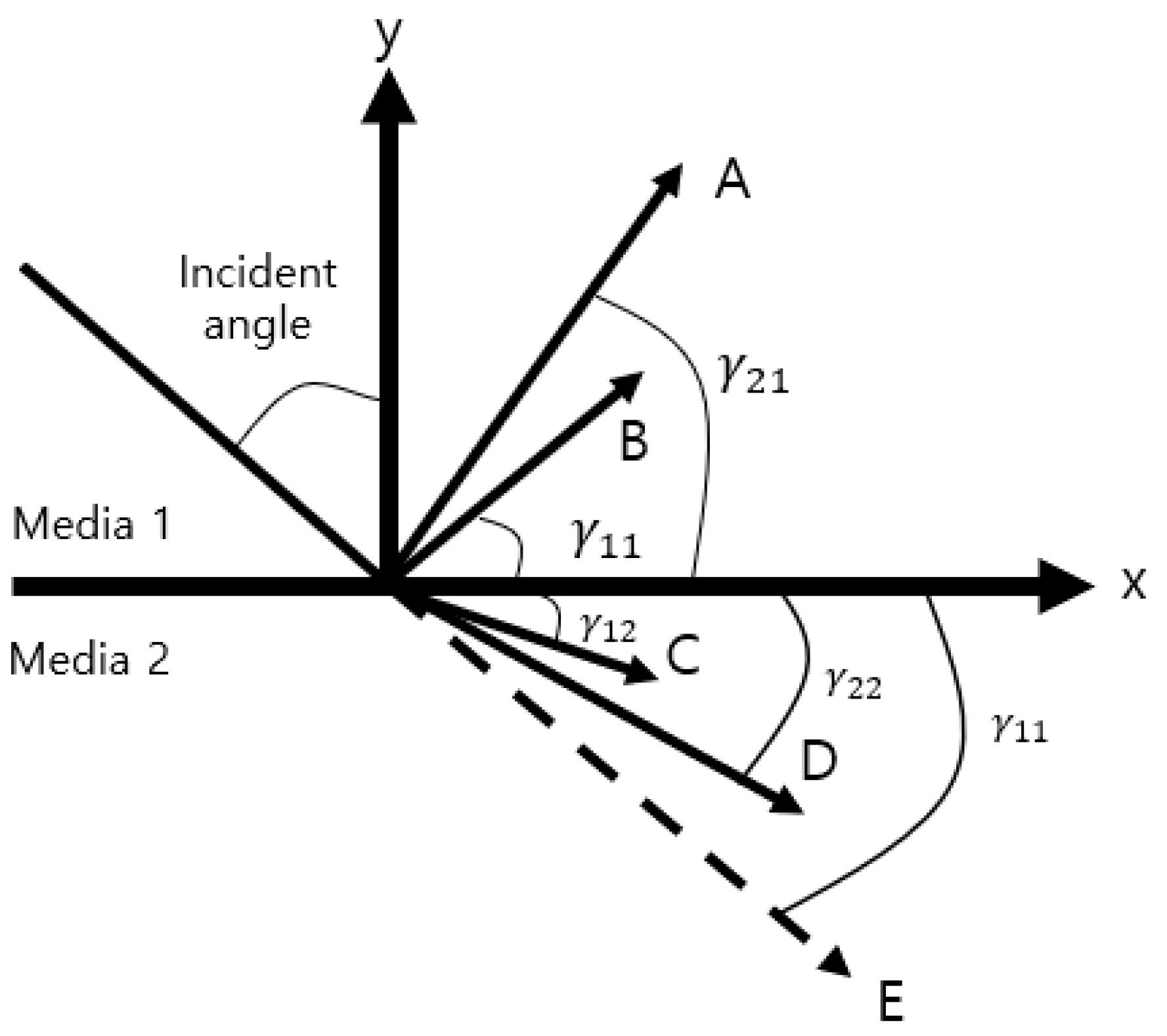
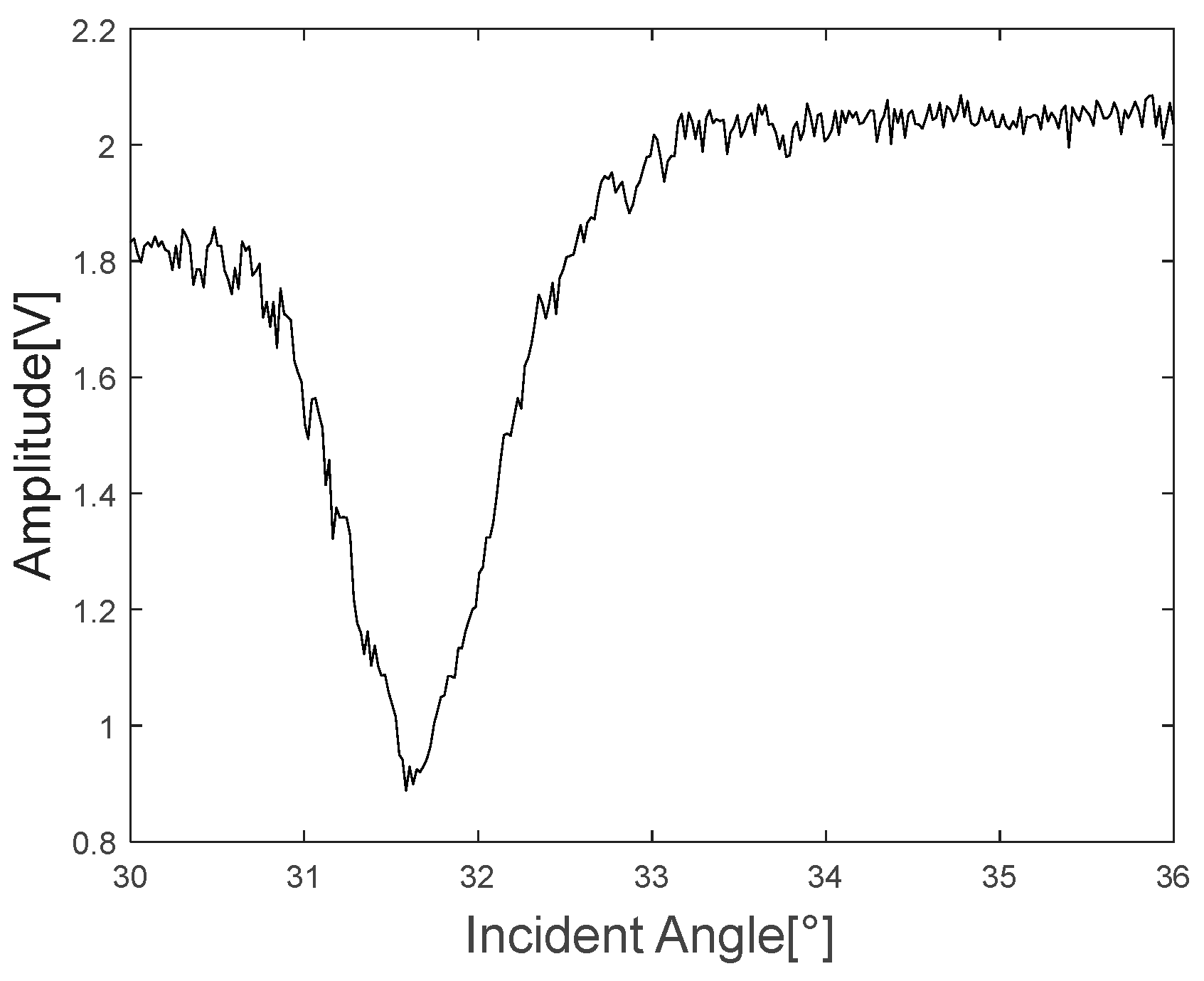
2.2. Minimum Reflection Method and Measurement
2.3. Relationship between Minimum Reflection and Rayleigh Wave Velocity
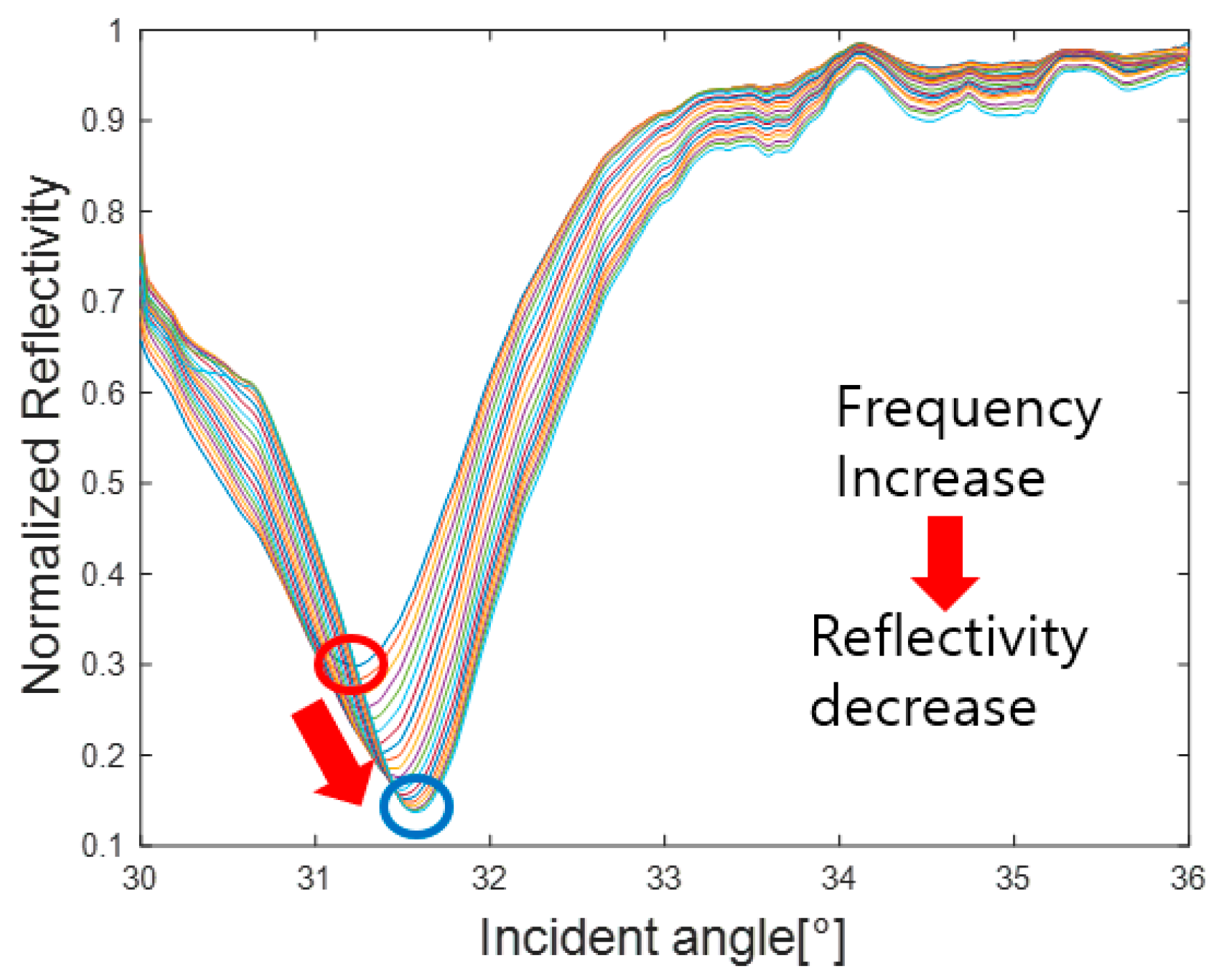
2.4. Relation between Rayleigh Wave Dispersion and Residual Stress Change According to Depth
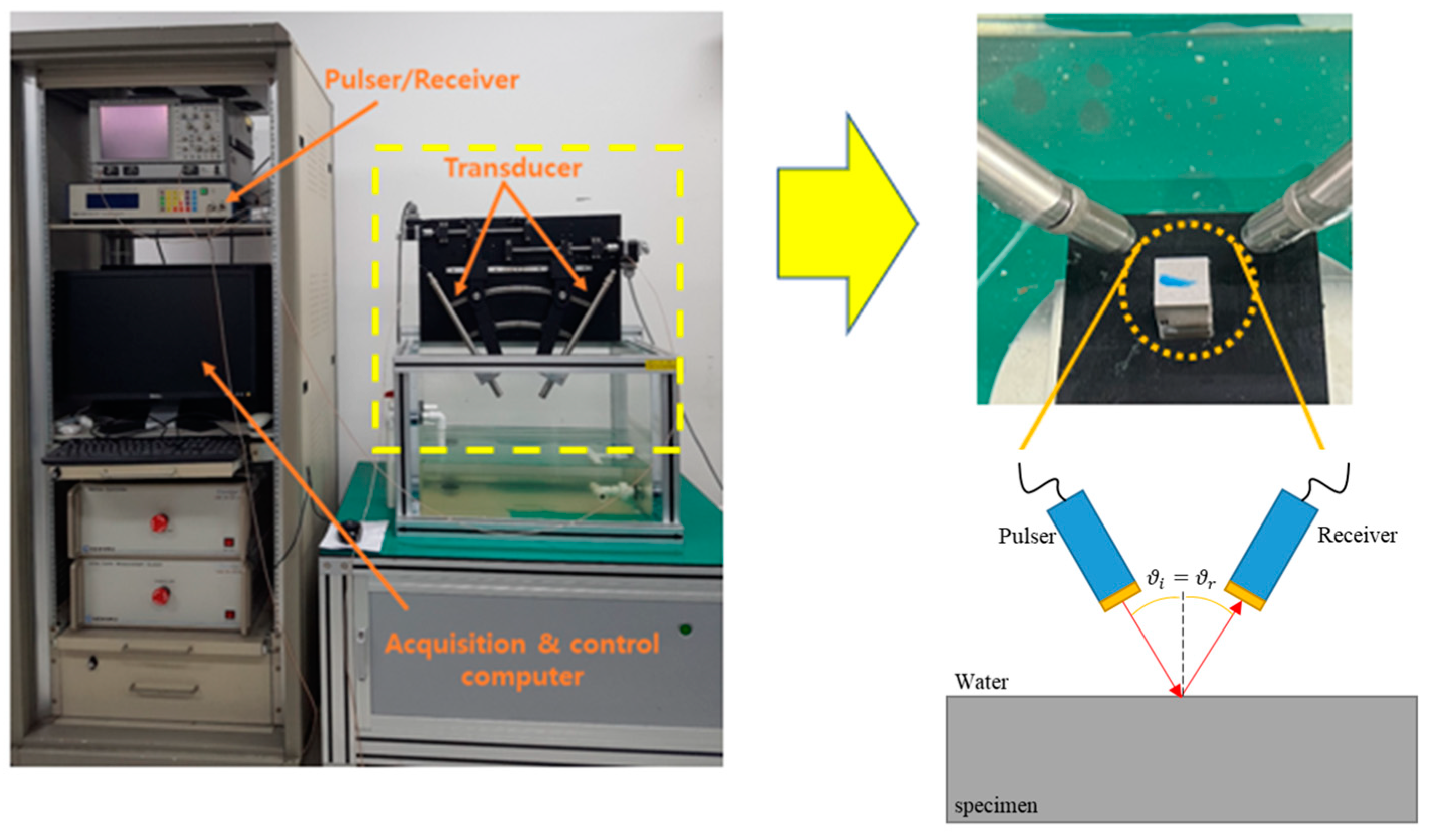
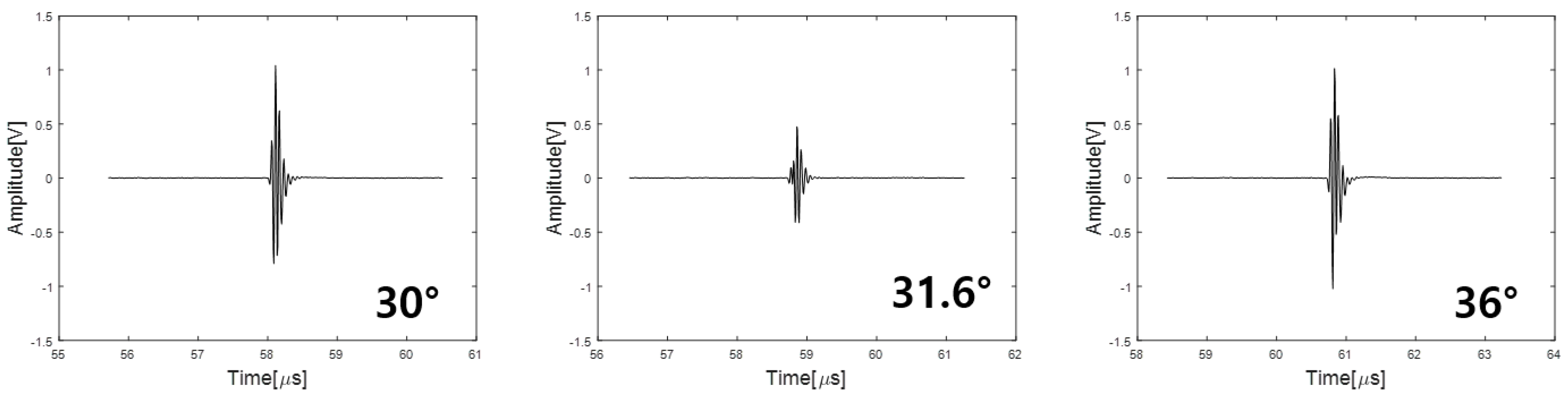
3. Ultrasonic Minimum Reflection Measurement
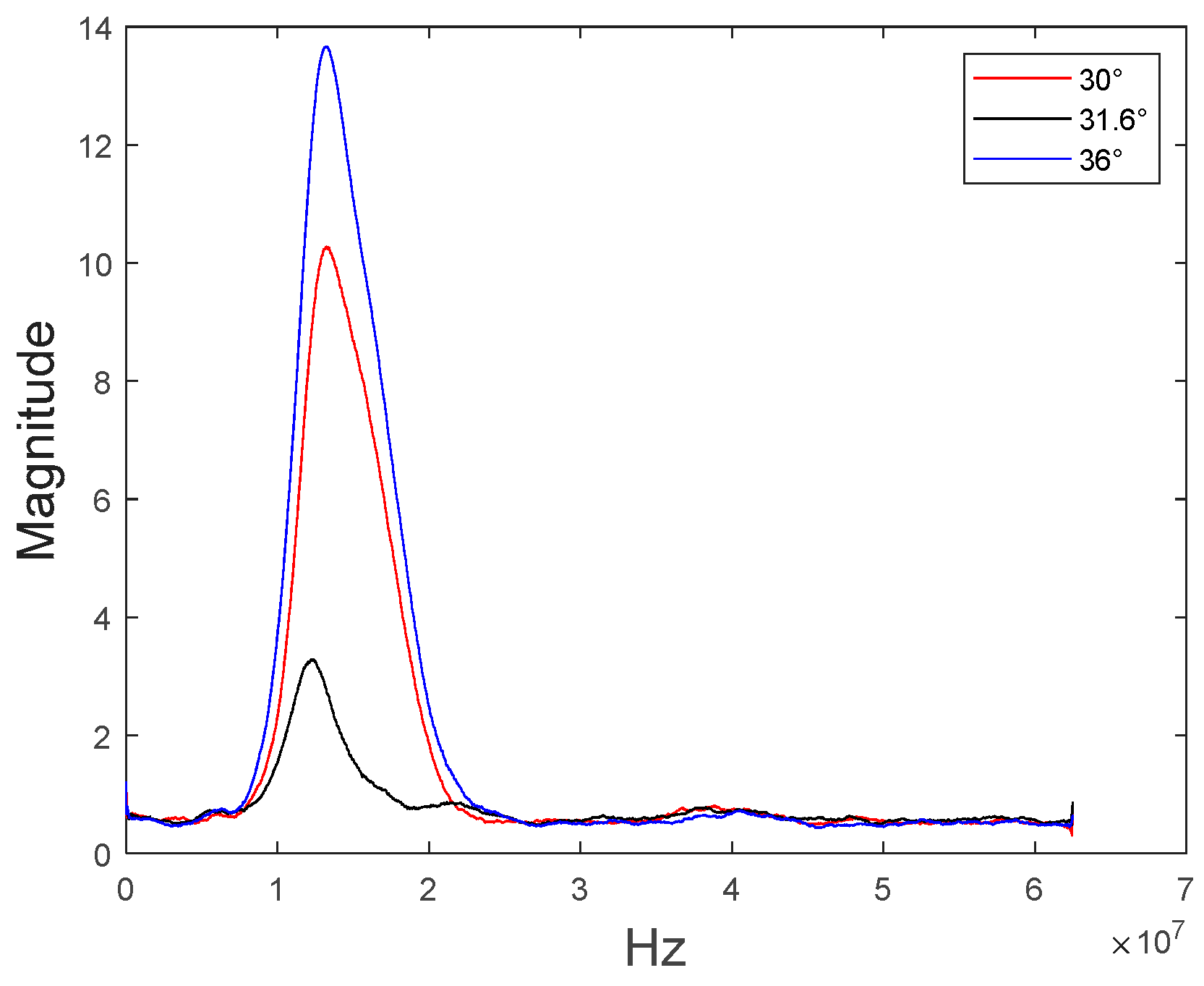
4. Rayleigh Wave Dispersion Determination
5. Inverse Analysis
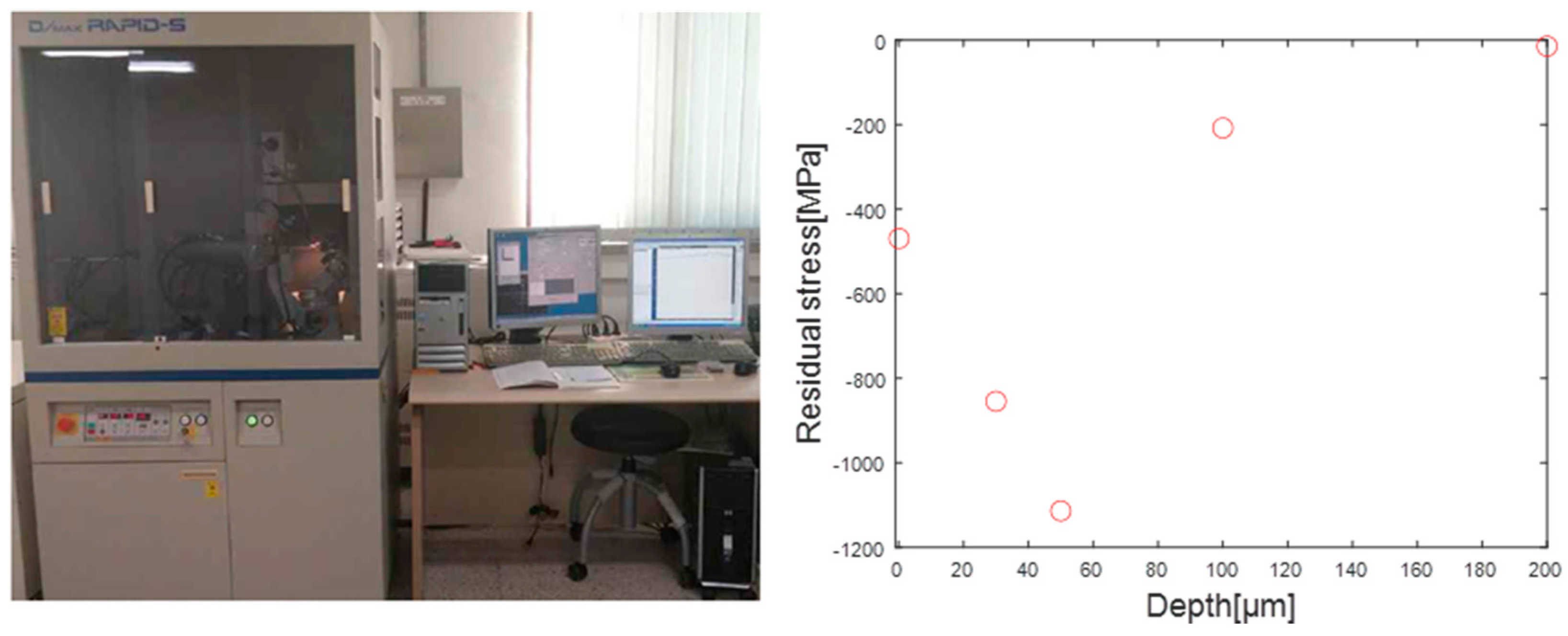
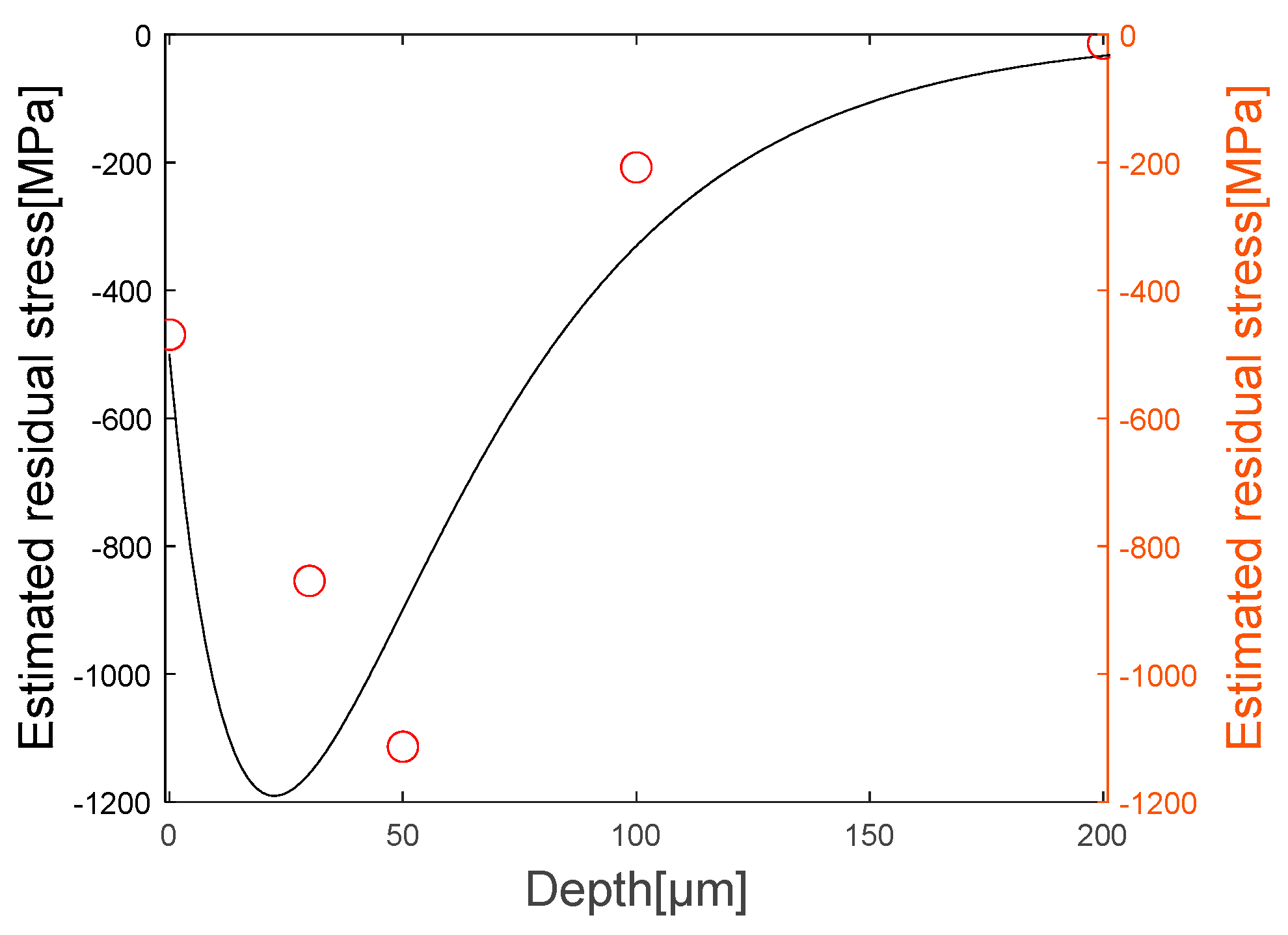
6. Comparison with XRD Measurement
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klotz, T.; Delbergue, D.; Bocher, P.; Levesque, M.; Brochu, M. Surface characteristics and fatigue behavior of shot peened Inconel 718. Int. J. Fatigue 2018, 110, 10–21. [Google Scholar] [CrossRef]
- Maleki, E.; Unal, O.; Guagliano, M.; Bagherifard, S. The effects of shot peening, laser shock peening and ultrasonic nanocrystal surface modification on the fatigue strength of Inconel 718. Mat. Sci. Eng. A—Struct. 2021, 810, 141029. [Google Scholar] [CrossRef]
- Sanda, A.; Garcia Navas, V.; Gonzalo, O. Surface state of Inconel 718 ultrasonic shot peened: Effect of processing time, material and quantity of shot balls and distance from radiating surface to sample. Mater. Des. 2011, 32, 2213–2220. [Google Scholar] [CrossRef]
- Lee, T.K. Nondestructive Evaluation of Residual Stress in Shot Peened Inconel Specimen Using Rayleigh Wave. Ph.D. Thesis, Sungkyunkwan University, Seoul, Republic of Korea, 2019. [Google Scholar]
- Frishman, A.M.; Lo, C.H.; Shen, Y.; Nakagawa, N. A scaling law for nondestructive evaluation of shot peening induced surface material property deviation. AIP Conf. Proc. 2009, 1096, 1341–1348. [Google Scholar]
- Im, S.W.; Lee, E.T.; Shim, H.J.; Kim, J.W.; Chang, I.H. Residual Stress Evaluation Caused by Press Forming and Welding of 600MPa Class Circular Steel Tube Using Hole-Drilling Strain Gage Method. J. Korean Soc. Steel Constr. 2006, 18, 625–631. [Google Scholar]
- Shen, Y.; Lee, C.; Lo, C.; Frishman, A.M.; Nakagawa, N. Conductivity profile determination by eddy current for shot-peened superalloy surfaces toward residual stress assessment. AIP Conf. Proc. 2007, 894, 1229–1236. [Google Scholar]
- Chandrasekar, R. Swept Frequency Eddy Current (SFEC) Measurements of Inconel 718 as a Function of Microstructure and Residual Stress. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2013. [Google Scholar]
- Kim, D.Y. A Study on Ultrasonic Nondestructive Diagnostic Methods for Thermal Degradation and Thin Coating Characterization of Mechanical Components; Sungkyunkwan University: Seoul, Republic of Korea, 2019. [Google Scholar]
- Kim, H.J.; Song, S.J.; Choi, J.H.; Kwon, S.D. Investigation of Non-specular Reflection of Rayleigh Waves for Evaluation of the Material Properties of Surface Area. New Phys. Sae Mulli 2012, 62, 179–184. [Google Scholar] [CrossRef]
- Becker, F.L.; Richardson, R.L. Research Techniques in Nondestructive Testing; Academic Press: New York, NY, USA, 1973; Volume 1, pp. 91–130. [Google Scholar]
- Husson, D. A perturbation theory for the acoustoelastic effect of surface waves. J. Appl. Phys. 1985, 57, 1562–1568. [Google Scholar] [CrossRef]
- Ditri, J.J.; Hongerholt, D. Stress distribution determination in isotropic materials via inversion of ultrasonic Rayleigh wave dispersion data. Int. J. Solids. Struct. 1996, 33, 2437–2451. [Google Scholar] [CrossRef]
- Siamak, A.; Rasool, M. Improvement in accuracy of the measurements of residual stresses due to circumferential welds in thin-walled pipe using Rayleigh wave method. Nucl. Eng. Des. 2009, 239, 2201–2208. [Google Scholar]
- Sergey, G.; Marek, R.; Bernd, K. Towards In-Situ Determination of Rayleigh Wave Acoustoelastic Constants for Surface Treated Materials Characterization, Collection: QNDE 2019-6880. Available online: https://www.iastatedigitalpress.com/qnde/article/id/8598/ (accessed on 26 May 2023).
- Bernd, K.; Martin, B. Rayleigh Wave Velocity Dispersion for Characterization of Surface Treated Aero Engine Alloys. ECNDT 2010-08. Available online: https://www.ndt.net/search/docs.php3?id=9058 (accessed on 26 May 2023).
- Lee, T.G.; Kim, H.J.; Song, S.J.; Kwon, S.D. Residual Stress Evaluation of a Shot Peening Specimen by Using a Rayleigh Wave. New Phys. Sae Mulli 2016, 66, 179–184. [Google Scholar] [CrossRef]
- Jassby, K.; Kishoni, D. Experimental technique for measurement of stress-acoustic coefficients of Rayleigh waves. Exp. Mech. 1983, 23, 74–80. [Google Scholar] [CrossRef]
- Jassby, K.; Saltoun, D. Use of ultrasonic Rayleigh waves for the measurement of applied biaxial surface stresses in aluminium 2024-T351 alloy. Mater. Eval. 1982, 40, 198–205. [Google Scholar]
- Duquennoy, M.; Ouaftouh, M.; Ourak, M. Determination of stresses in alu-minium alloy using optical detection of Rayleigh waves. Ultrasonics 1999, 37, 365–372. [Google Scholar] [CrossRef]
- Hirao, M.; Fukuoka, H.; Hori, K. Acoustoelastic effect of Rayleigh surface wave in isotropic material. J. Appl. Mech. 1981, 48, 119–124. [Google Scholar] [CrossRef]
- Trung, H. Prediction of Residual Stress Depth Profile Using Ultrasonic Minimum Reflection Measurement. Master’s Thesis, Sungkyunkwan University, Seoul, Republic of Korea, 2020. [Google Scholar]
- Gallitelli, D.; Boyer, V.; Gelineau, M.; Colaitis, Y. Simulation of shot peening: From process parameters to residual stress fields in a structure. Comptes Rendus Mec. 2016, 344, 355–374. [Google Scholar] [CrossRef]
- Schmerr, L.W. Fundamentals of Ultrasonic Nondestructive Evaluation; Plenum Press: New York, NY, USA; London, UK, 1998; pp. 91–97. ISBN 0-306-45752-0. [Google Scholar]
- Rjelka, M.; Barth, M.; Reinert, S.; Koehler, B.; Bamberg, J.; Baron, H.U.; Hessert, R. Third Order Elastic Constants and Rayleigh Wave Dispersion of Shot Peened Aero-Engine Materials. Mater. Sci. Forum 2013, 768, 201–208. [Google Scholar] [CrossRef]
- Min, C.H.; Park, H.I.; Bae, S.R. Experimental Vibration Analysis for Viscoelastic Ally Damped Circular Cylindrical Shell Using Nonlinear Least Square Method. J. Ocean Eng. Technol. 2008, 21, 41–46. [Google Scholar]






| Variable (Symbol) | Assumption Value | Variable (Symbol) | Assumption Value |
|---|---|---|---|
| 2800 [m/s] | −606 [GPa] | ||
| 5900 [m/s] | −479 [GPa] | ||
| 2900 [m/s] | 80 [GPa] | ||
| −527 [GPa] | 121 [GPa] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.-W.; Lee, T.-G.; Yeom, Y.-T.; Kwon, S.-D.; Kim, H.-H.; Lee, K.-Y.; Kim, H.-J.; Song, S.-J. Nondestructive Evaluation of Residual Stress in Shot Peened Inconel Using Ultrasonic Minimum Reflection Measurement. Materials 2023, 16, 5075. https://doi.org/10.3390/ma16145075
Choi Y-W, Lee T-G, Yeom Y-T, Kwon S-D, Kim H-H, Lee K-Y, Kim H-J, Song S-J. Nondestructive Evaluation of Residual Stress in Shot Peened Inconel Using Ultrasonic Minimum Reflection Measurement. Materials. 2023; 16(14):5075. https://doi.org/10.3390/ma16145075
Chicago/Turabian StyleChoi, Yeong-Won, Taek-Gyu Lee, Yun-Taek Yeom, Sung-Duk Kwon, Hun-Hee Kim, Kee-Young Lee, Hak-Joon Kim, and Sung-Jin Song. 2023. "Nondestructive Evaluation of Residual Stress in Shot Peened Inconel Using Ultrasonic Minimum Reflection Measurement" Materials 16, no. 14: 5075. https://doi.org/10.3390/ma16145075
APA StyleChoi, Y.-W., Lee, T.-G., Yeom, Y.-T., Kwon, S.-D., Kim, H.-H., Lee, K.-Y., Kim, H.-J., & Song, S.-J. (2023). Nondestructive Evaluation of Residual Stress in Shot Peened Inconel Using Ultrasonic Minimum Reflection Measurement. Materials, 16(14), 5075. https://doi.org/10.3390/ma16145075







