Optimization of Reinforcing Patch Effects on Cracked Plates Using Analytical Modeling and Taguchi Design
Abstract
1. Introduction
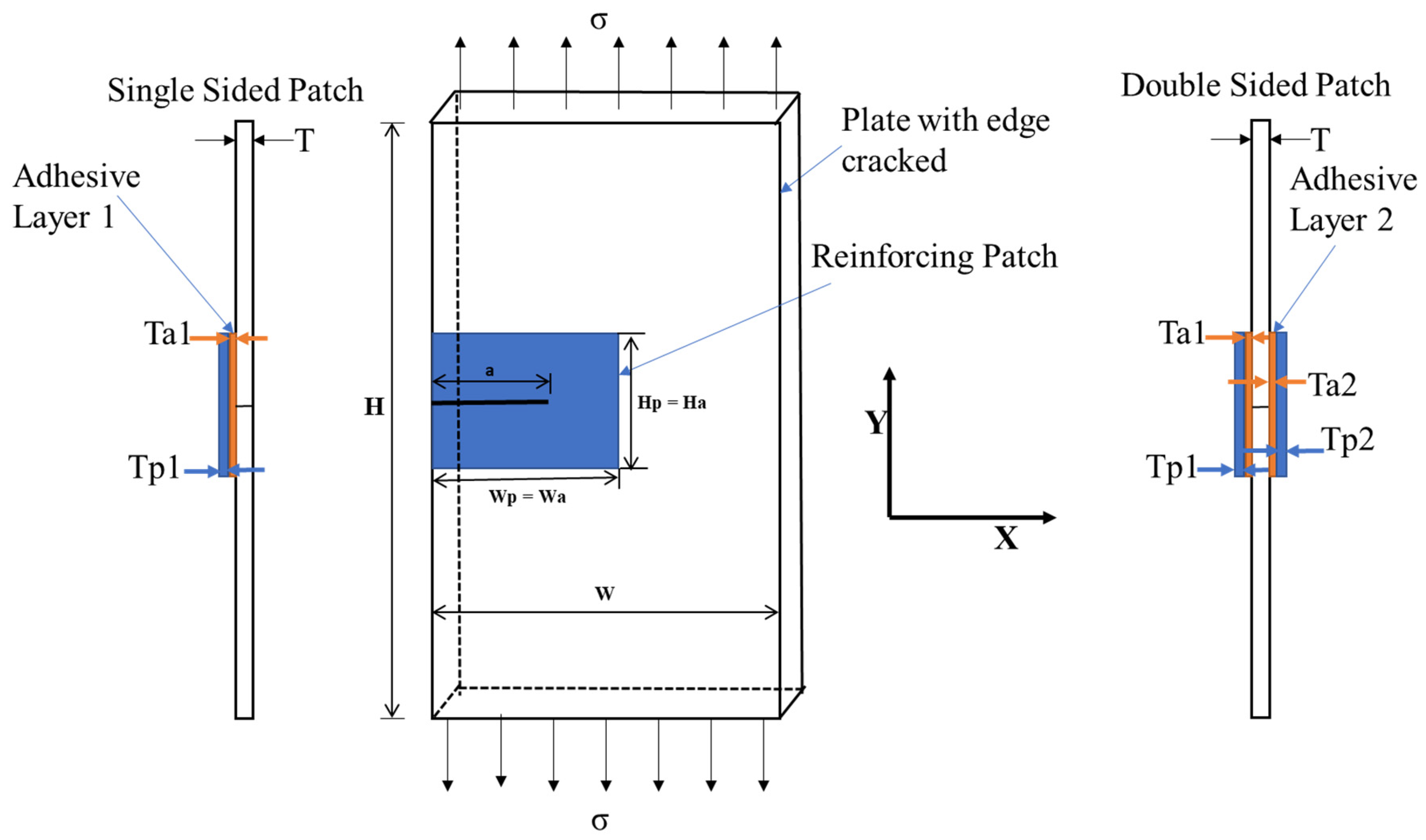
2. Problem Formulation
3. Mathematical Modeling
3.1. Stress Intensity Factor for Cracked Plate without Reinforcing Patch
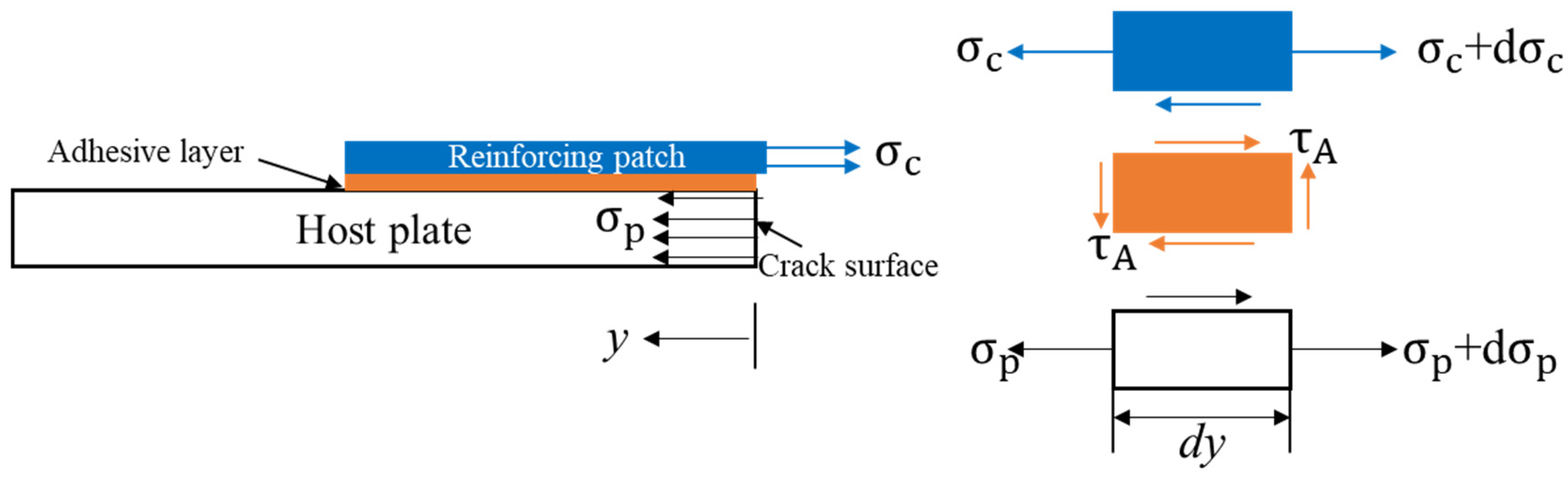
3.2. Stress Intensity Factor for Cracked Plates with Single and Double Reinforcing Patches
- The adhesive bond’s shared tension stress was very negligible and overlooked.
- The plate and patch both experienced the same tension strain since there were no force-lag effects between the two materials.
- Only shear deformation of the adhesive bond was observed, and the adhesive thickness and shear stress were distributed equally.
- Flexural deformation of the plate and the patch was ignored in preference for the elastic continuum represented by the plate and patch.
4. Taguchi Design
Taguchi’s Orthogonal Array
5. Results and Discussion
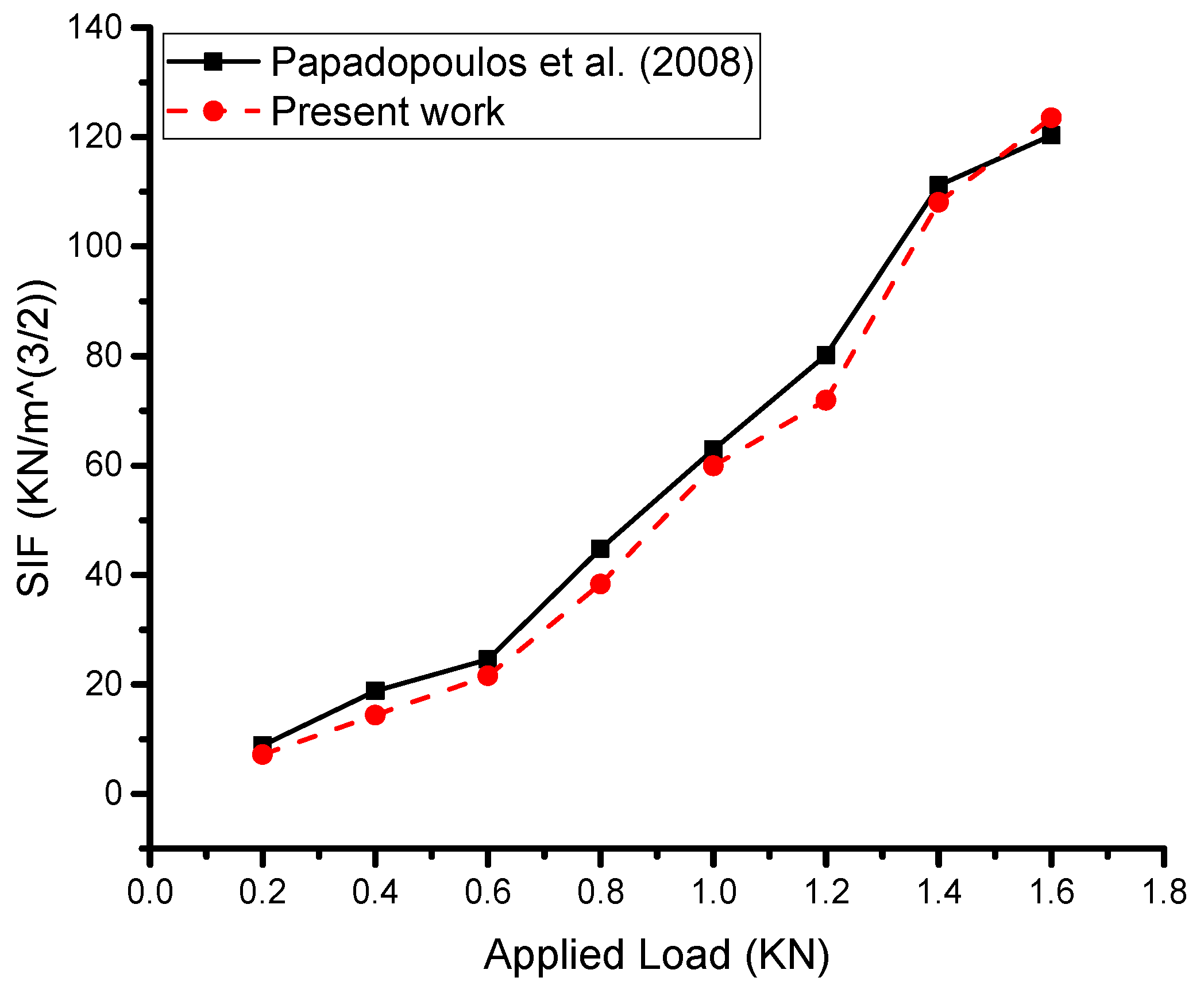
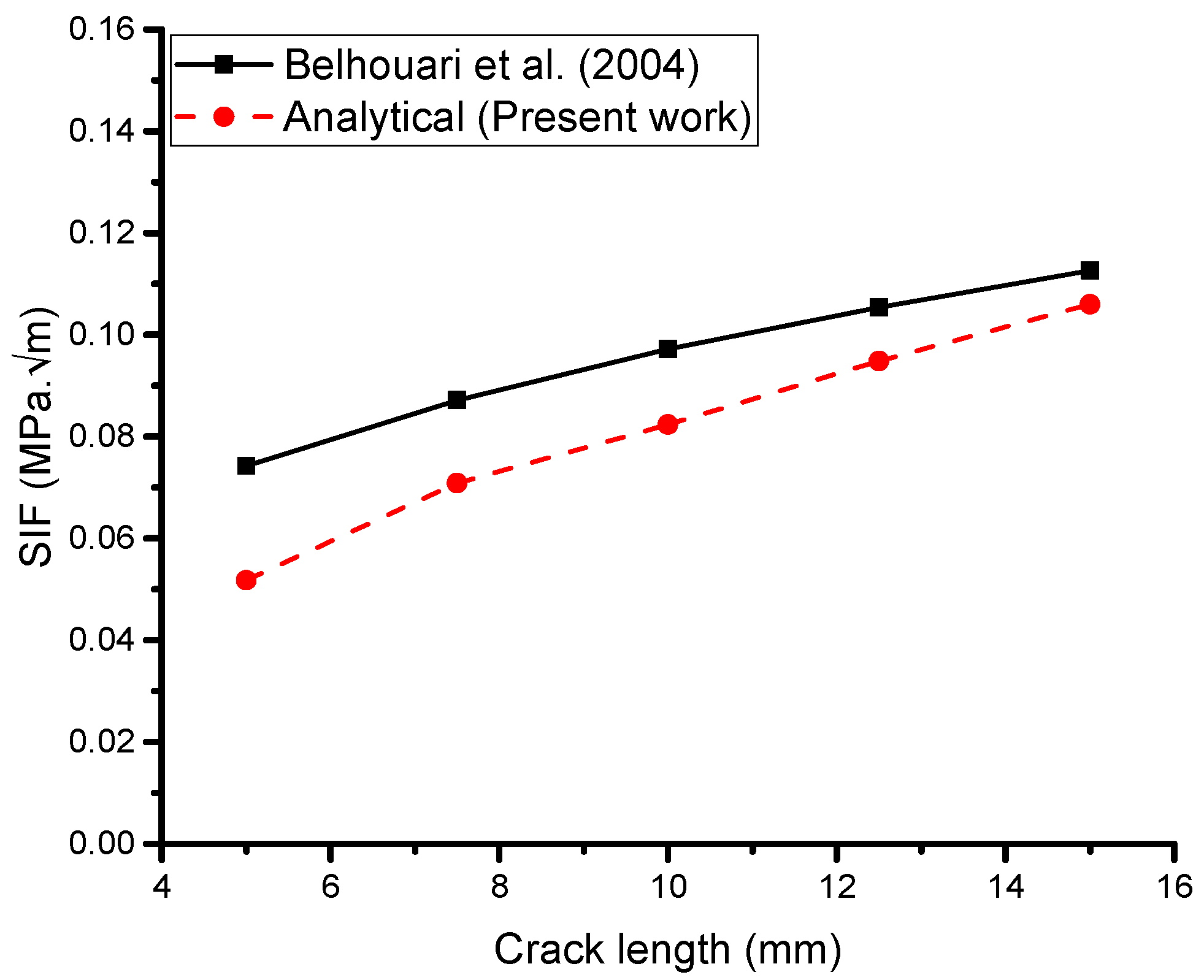
5.1. Benchmark Validation of the Present Analytical Model
5.2. Reduction in and Comparison of SIF Performance
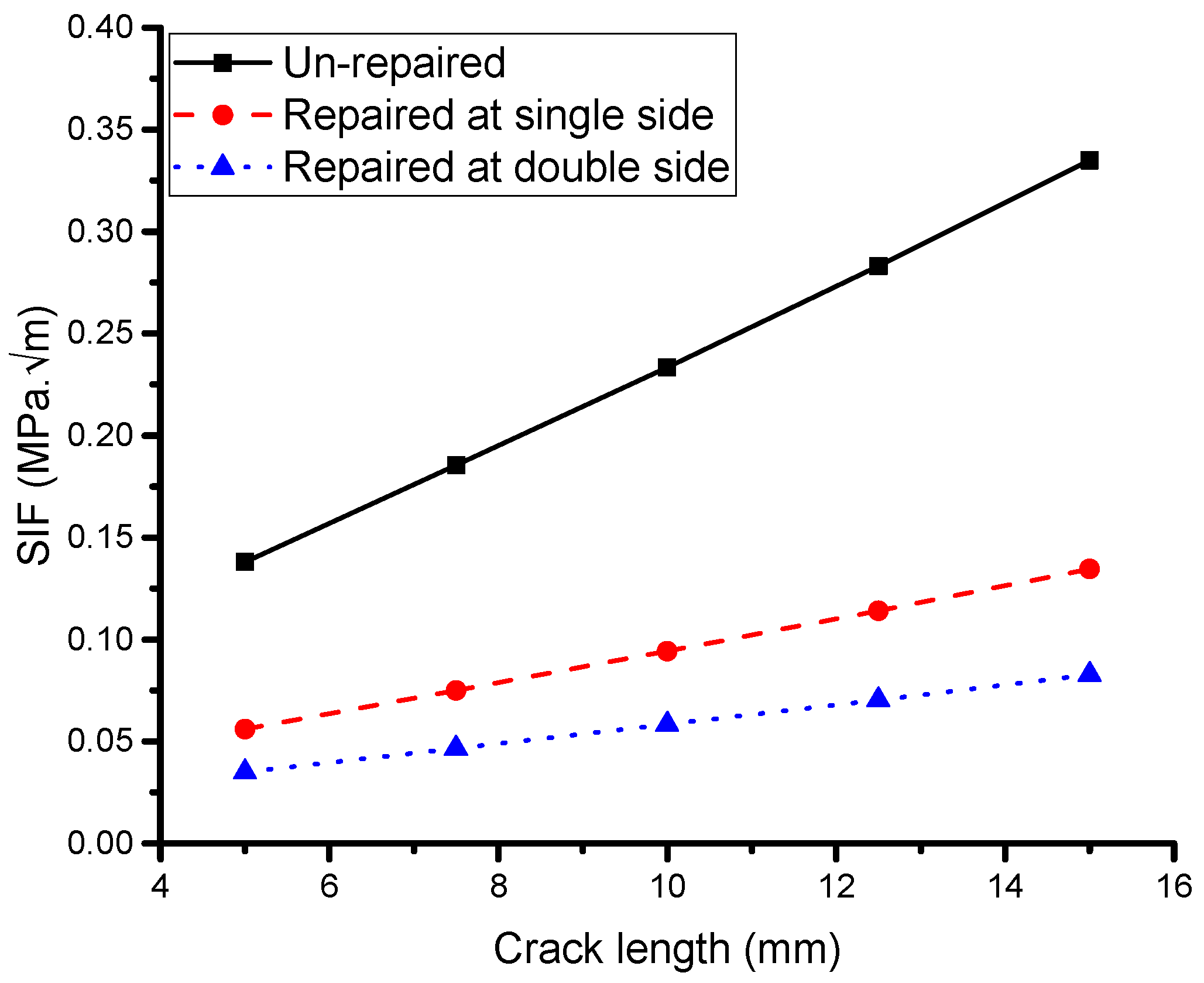
5.2.1. Effect of Crack Length
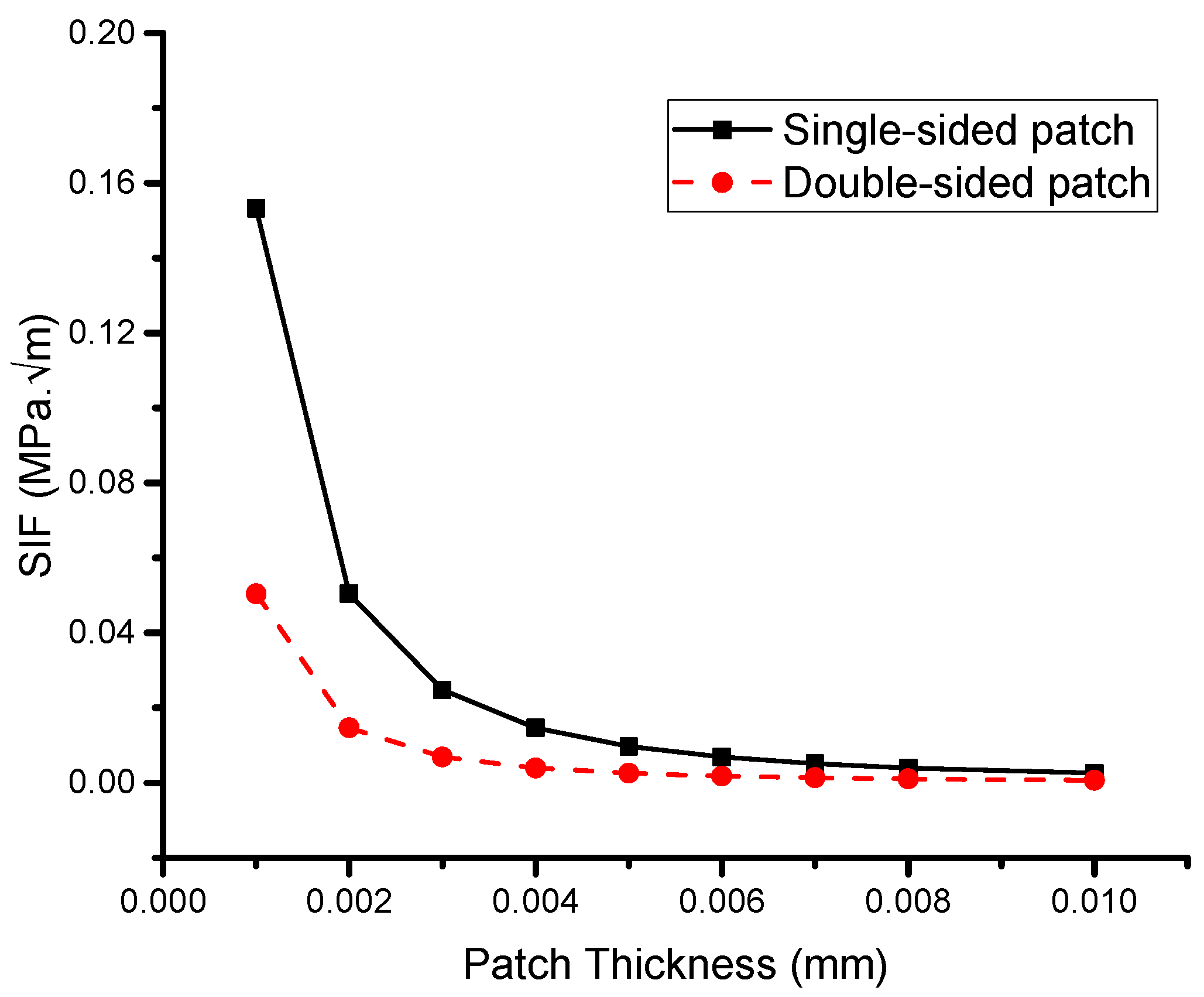
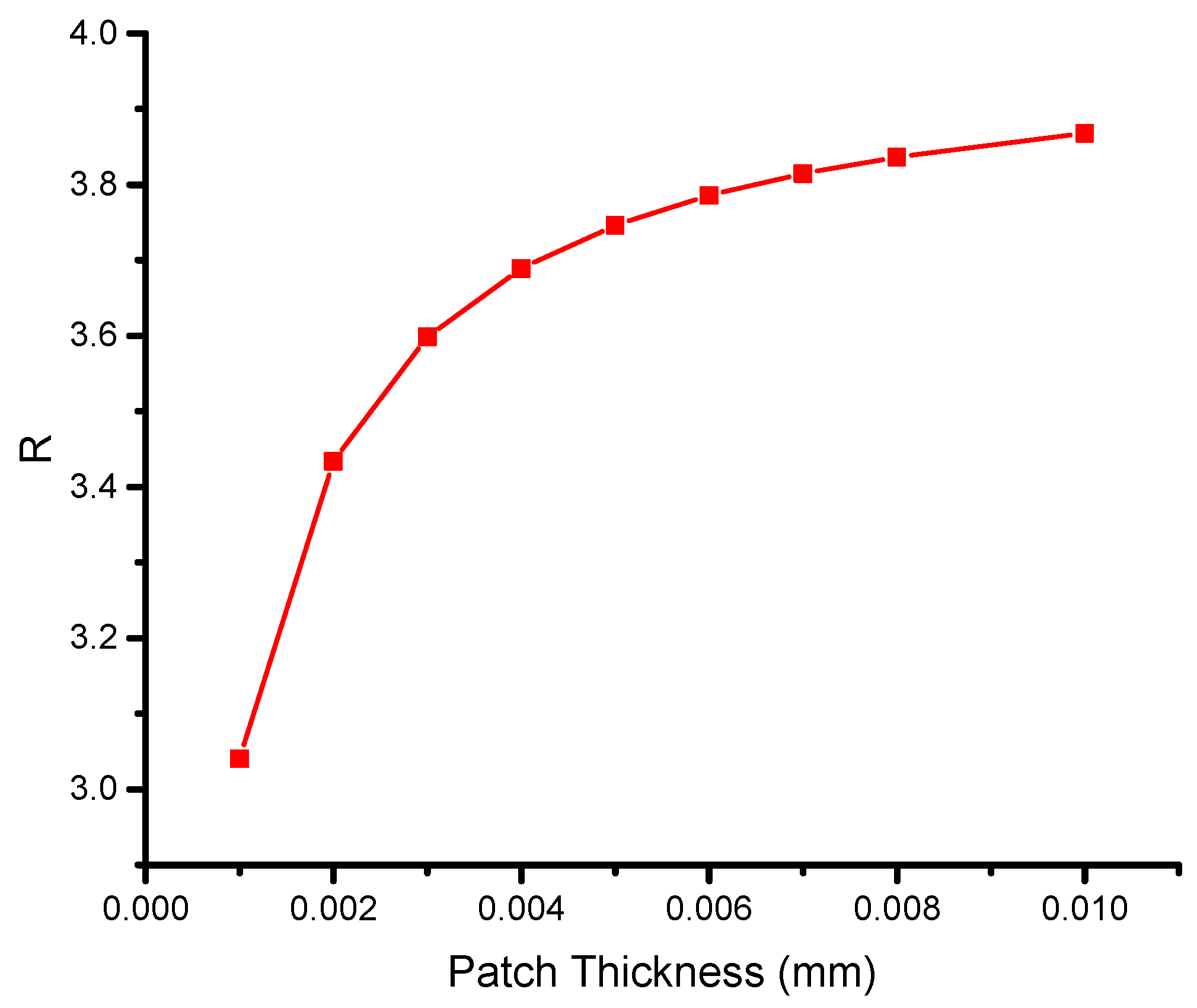
5.2.2. Effect of Patch Thickness
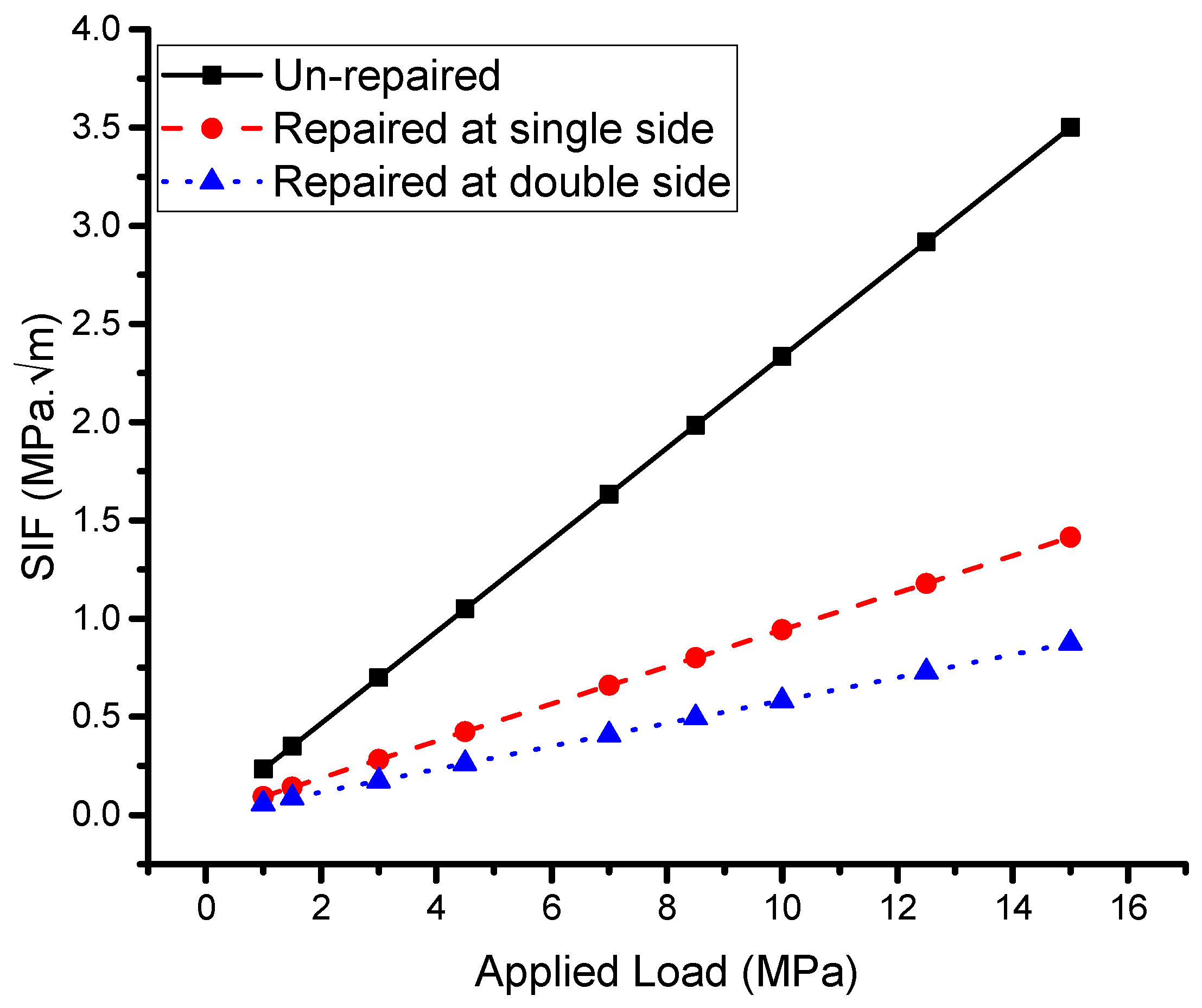
5.2.3. Effect of Applied Load
5.3. Optimization Results
5.3.1. Development of Linear Regression Equation
5.3.2. Analysis of Taguchi Design
Main Effect Plot
Contour Plots
5.3.3. Analysis of Variance
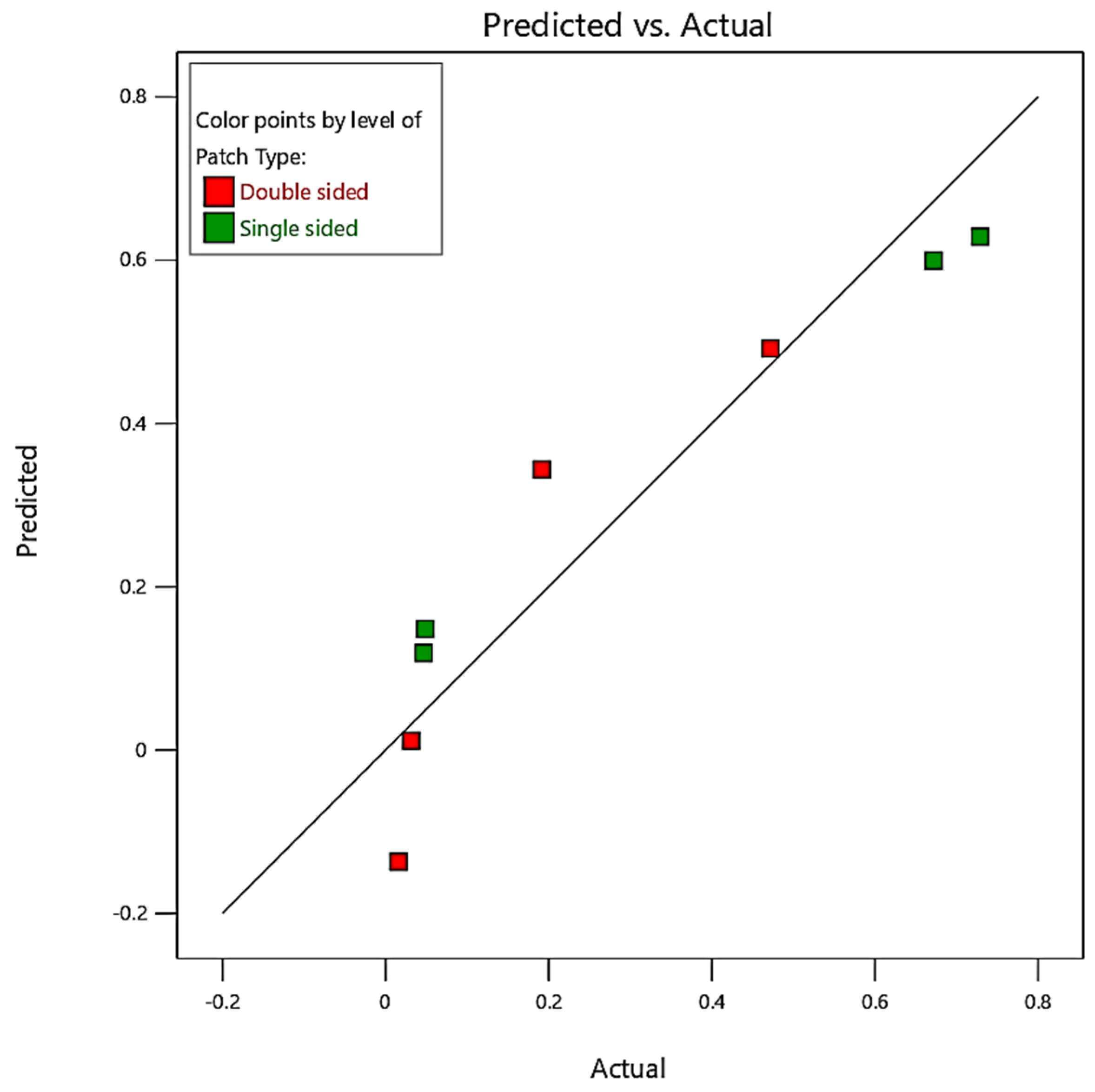
5.3.4. Prediction Results
Prediction Plot
Optimal Parameters Prediction
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| ANOVA | Analysis of variance |
| ERR | Energy relies rate |
| FE | Finite element |
| LEFM | Linear elastic factor mechanics |
| MS | Mean square |
| NSIF | Normalized stress intensity factor |
| SCF | Stress concentration factor |
| SE | Standard error |
| SERR | Strain energy release rate |
| SIF | Stress intensity factor |
| SS | Sum of square |
| VIF | Variance inflation factor |
References
- Starke, E.A.; Staleyt, J.T. Application of modern aluminum alloy to aircraft. Prog. Aerosp. Sci. 1996, 32, 131–172. [Google Scholar] [CrossRef]
- Ahmad, F.; Mehboob, H.; Abbassi, F.; Hong, J.; Zghal, J.; Mehboob, A. Numerical investigation to evaluate the energy effect on the impact resistance of an aircraft carbon fiber-reinforced polymer composite. Mech. Adv. Mater. Struct. 2021, 29, 4457–4467. [Google Scholar] [CrossRef]
- Nayak, N.V. Composite materials in aerospace design. Mater. Des. 2014, 4, 1–10. [Google Scholar] [CrossRef]
- Katnam, K.B.; Da Silva, L.F.M.; Young, T.M. Bonded repair of composite aircraft structures: A review of scientific challenges and opportunities. Prog. Aerosp. Sci. 2013, 61, 26–42. [Google Scholar] [CrossRef]
- Baker, A. Bonded composite repair of fatigue-cracked primary aircraft structure. Compos. Struct. 1999, 47, 431–443. [Google Scholar] [CrossRef]
- Wang, C.H.; Rose, L.R.F.; Callinan, R. Analysis of out-of-plane bending in one-sided bonded repair. Int. J. Solids Struct. 1998, 35, 1653–1675. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, K.W.; Seo, D.C.; Lee, S.B. Calculation of Stress Intensity Factor Using Weight Function Method for a Patched Crack. Eng. Fract. Mech. 2000, 183–187, 103–108. [Google Scholar] [CrossRef]
- Bouiadjra, B.B.; Belhouari, M.; Serier, B. Computation of the stress intensity factors for repaired cracks with bonded composite patch in mode I and mixed mode. Compos. Struct. 2002, 56, 401–406. [Google Scholar] [CrossRef]
- Belhouari, M.; Bouiadjra, B.B.; Megueni, A.; Kaddouri, K. Comparison of double and single bonded repairs to symmetric composite structures: A numerical analysis. Compos. Struct. 2004, 65, 47–53. [Google Scholar] [CrossRef]
- Hosseini-Toudeshky, H.; Mohammadi, B.; Sadeghi, G.; Daghyani, H.R. Numerical and experimental fatigue crack growth analysis in mode-I for repaired aluminum panels using composite material. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1141–1148. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Badalouka, B.; Souyiannis, J. Experimental study of the reduction at crack-tip stress intensity factor K_I by bonded patch. Int. J. Fract. 2008, 149, 199–205. [Google Scholar] [CrossRef]
- Aabid, A.; Ibrahim, Y.E.; Hrairi, M. Optimization of Structural Damage Repair with Single and Double-Sided Composite Patches through the Finite Element Analysis and Taguchi Method. Materials 2023, 16, 1581. [Google Scholar] [CrossRef] [PubMed]
- Yala, A.A.; Megueni, A. Optimisation of composite patches repairs with the design of experiments method. Mater. Des. 2009, 30, 200–205. [Google Scholar] [CrossRef]
- Yala, A.A.; Demouche, N.; Beddek, S.; Hamid, K. Full Analysis of All Composite Patch Repairing Design Parameters. Iran. J. Mater. Sci. Eng. 2018, 15, 70–77. [Google Scholar] [CrossRef]
- Guruprasad, K. Numerical estimation of stress intensity factor. Eng. Fract. Mech. 1987, 27, 559–569. [Google Scholar]
- Ahn, J.S.; Basu, P.K.; Woo, K.S. Analysis of cracked aluminum plates with one-sided patch repair using p -convergent layered model. Finite Elem. Anal. Des. 2010, 46, 438–448. [Google Scholar] [CrossRef]
- Bouiadjra, B.B.; Achour, T.; Berrahou, M.; Ouinas, D.; Feaugas, X. Numerical estimation of the mass gain between double symmetric and single bonded composite repairs in aircraft structures. Mater. Des. 2010, 31, 3073–3077. [Google Scholar] [CrossRef]
- Rabinovitch, O.; Frostig, Y. Fracture mechanics approach to geometrically nonlinear debonding problems in RC beams strengthened with composite materials. Adv. Struct. Eng. 2006, 9, 765–777. [Google Scholar] [CrossRef]
- Mhamdia, R.; Bouadjra, B.B.; Serier, B.; Ouddad, W.; Feaugas, X.; Touzain, S. Stress intensity factor for repaired crack with bonded composite patch under thermo-mechanical loading. J. Reinf. Plast. Compos. 2011, 30, 416–424. [Google Scholar] [CrossRef]
- Albedah, A.; Bouiadjra, B.B.; Mhamdia, R.; Benyahia, F.; Es-saheb, M. Comparison between double and single sided bonded composite repair with circular shape. Mater. Des. 2011, 32, 996–1000. [Google Scholar] [CrossRef]
- Ergun, E.; Tasgetiren, S.; Topcu, M. Stress intensity factor estimation of repaired aluminum plate with bonded composite patch by combined genetic algorithms and FEM under temperature effects. Indian J. Eng. Mater. Sci. 2012, 19, 17–23. [Google Scholar]
- Kwon, Y.W.; Lee, W.Y.; Mcgee, A.S.; Hart, D.C. Analytical Model for Prediction of Reduced Strain Energy Release Rate of Single-Side-Patched Plates. Appl. Compos. Mater. 2013, 20, 1321–1339. [Google Scholar] [CrossRef]
- Aabid, A.; Hrairi, M.; Ali, J.S.M.; Abuzaid, A. Numerical Analysis of Cracks Emanating From Hole in Plate Repaired by Composite Patch. Int. J. Mech. Prod. Eng. Res. Dev. 2018, 4, 238–243. [Google Scholar]
- Aabid, A.; Hrairi, M.; Ali, J.S.M.; Abuzaid, A. Effect of Bonded Composite Patch on the Stress Intensity Factors for a Center-cracked Plate. IIUM Eng. J. 2019, 20, 211–221. [Google Scholar] [CrossRef]
- Aabid, A.; Hrairi, M.; Ali, J.S.M. Optimization of composite patch repair for center-cracked rectangular plate using design of experiments method. Mater. Today Proc. 2019, 27, 1713–1719. [Google Scholar] [CrossRef]
- Liu, X.; Wu, J.; Xi, J.; Yu, Z. Bonded repair optimization of cracked aluminum alloy plate by microwave cured carbon-aramid fiber/epoxy sandwich composite patch. Materials 2019, 12, 1655. [Google Scholar] [CrossRef] [PubMed]
- Aabid, A.; Hrairi, M.; Ali, J.S.M.; Abuzaid, A. Stress Concentration Analysis of a Composite Patch on a Hole in an Isotropic Plate. Int. J. Mech. Prod. Eng. Res. Dev. 2018, 6, 249–255. [Google Scholar]
- Aabid, A.; Hrairi, M.; Dawood, M.S.I.S. Modeling Different Repair Configurations of an Aluminum Plate with a Hole. Int. J. Recent Technol. Eng. 2019, 7, 235–240. [Google Scholar]
- Aabid, A.; Hrairi, M.; Abuzaid, A.; Syed, J.; Ali, M. Estimation of stress intensity factor reduction for a center-cracked plate integrated with piezoelectric actuator and composite patch. Thin-Walled Struct. 2021, 158, 107030. [Google Scholar] [CrossRef]
- Baker, A.A. A Proposed Approach for Certification of Bonded Composite Repairs to Flight-Critical Airframe Structure. Appl. Compos. Mater. 2011, 18, 337–369. [Google Scholar] [CrossRef]
- Rao, P.S.; Hardiman, M.; O’Dowd, N.P.; Sebaey, T.A. Comparison of progressive damage between thermoset and thermoplastic CFRP composites under in-situ tensile loading. J. Compos. Mater. 2021, 55, 1473–1484. [Google Scholar] [CrossRef]
- Alshahrani, H.; Sebaey, T.A. Effect of Embedded Thin-Plies on the Charpy Impact Properties of CFRP Composites. Polymers 2022, 14, 1929. [Google Scholar] [CrossRef] [PubMed]
- Sebaey, T.A.; Kumar, D.; Mehboob, H. Internally stiffened foam- filled carbon fi ber reinforced composite tubes under impact loading for energy absorption applications. Compos. Struct. 2021, 255, 112910. [Google Scholar] [CrossRef]
- Rose, L.R.F. An application of the inclusion analogy for bonded reinforcements. Int. J. Solids Struct. 1981, 17, 827–838. [Google Scholar] [CrossRef]
- Ricci, F.; Franco, F.; Monrefusco, N. Bonded Composite Patch Repairs on Cracked Aluminum Plates: Theory, Modeling and Experiments. In Advances in Composite Materials—Ecodesign and Analysis; IntechOpen: London, UK, 2011; pp. 445–464. [Google Scholar] [CrossRef]
- Ouinas, D.; Hebbar, A.; Olay, J.V. Fracture Mechanics Modelling of Cracked Aluminium Panel Repaired with Bonded Composite Circular Patch. J. Appl. Sci. 2006, 6, 2088–2095. [Google Scholar] [CrossRef]
- Fekirini, H.; Bouiadjra, B.B.; Belhouari, M.; Boutabout, B.; Serier, B. Numerical analysis of the performances of bonded composite repair with two adhesive bands in aircraft structures. Compos. Struct. 2008, 82, 84–89. [Google Scholar] [CrossRef]
- Madani, K.; Touzain, S.; Feaugas, X.; Benguediab, M.; Ratwani, M. Stress distribution in a 2024-T3 aluminum plate with a circular notch, repaired by a graphite/epoxy composite patch. Int. J. Adhes. Adhes. 2009, 29, 225–233. [Google Scholar] [CrossRef]
- Kumar, A.M.; Hakeem, S.A. Optimum design of symmetric composite patch repair to centre cracked metallic sheet. Compos. Struct. 2000, 49, 285–292. [Google Scholar] [CrossRef]
- Tada, H.; Paris, P.C.; Irwin, G.R. The Stress Analysis of Cracks Handbook, 3rd ed.; ASME: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Rose, L.R.F.; Wang, C.H. Analytical Methods for Designing Composite Repairs. Adv. Bond. Compos. Repair Met. Aircr. Struct. 2002, 1–2, 137–175. [Google Scholar] [CrossRef]
- Wang, H.T.; Wu, G.; Pang, Y.Y. Theoretical and numerical study on stress intensity factors for FRP-strengthened steel plates with double-edged cracks. Sensors 2018, 18, 2356. [Google Scholar] [CrossRef] [PubMed]
- Rose, L.R.F. Theoretical analysis of crack patching. In Bonded Repair of Aircraft Structures; Springer: Berlin/Heidelberg, Germany, 1988; pp. 77–106. [Google Scholar]
- Aabid, A.; Hrairi, M.; Ali, J.S.M.; Sebaey, T.A. A Review on Reductions in the Stress-Intensity Factor of Cracked Plates Using Bonded Composite Patches. Materials 2022, 15, 3086. [Google Scholar] [CrossRef] [PubMed]
- Rice, J.R. Some remarks on elastic crack-tip stress fields. Int. J. Solids Struct. 1972, 8, 751–758. [Google Scholar] [CrossRef]
- Zheng, Y. Experimental and Theoretical Research on Fatigue Behavior of Steel Structures Strengthened with CFRP. Ph.D. Thesis, Tsinghua University, Beijing, China, 2007. [Google Scholar]
- Crew, R.F.A.E.; Cutler, E.D.W. Statistical Methods; Springer: London, UK, 1934. [Google Scholar]
- Fischer, R.A. Statistical Methods for Research Workers; Oliver & Boyd: London, UK, 1925; pp. 241–271. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Swenson, D.; James, M. FRANC2D/L: A Crack Propagation Simulator for Plane Layered Structures; Kansas State University: Manhattan, KS, USA, 1998. [Google Scholar]
- Klug, J.; Maley, S.; Sun, C.T. Characterization of fatigue behavior of bonded composite repairs. J. Aircr. 2012, 36, 1016–1022. [Google Scholar] [CrossRef]
- Umamaheswar, T.V.R.S.; Singh, R. Modelling of a patch repair to a thin cracked sheet. Eng. Fract. Mech. 1999, 62, 267–289. [Google Scholar] [CrossRef]
- Ting, T.; Jones, R.; Chiu, W.K.; Marshall, I.H.; Greer, J.M. Composite repairs to rib stiffened panels. Compos. Struct. 1999, 47, 737–743. [Google Scholar] [CrossRef]
- Chung, K.H.; Yang, W.H.; Cho, M.R. Fracture Mechanics Analysis of Cracked Plate Repaired by Composite Patch. Key Eng. Mater. 2000, 183–187, 43–48. [Google Scholar] [CrossRef]


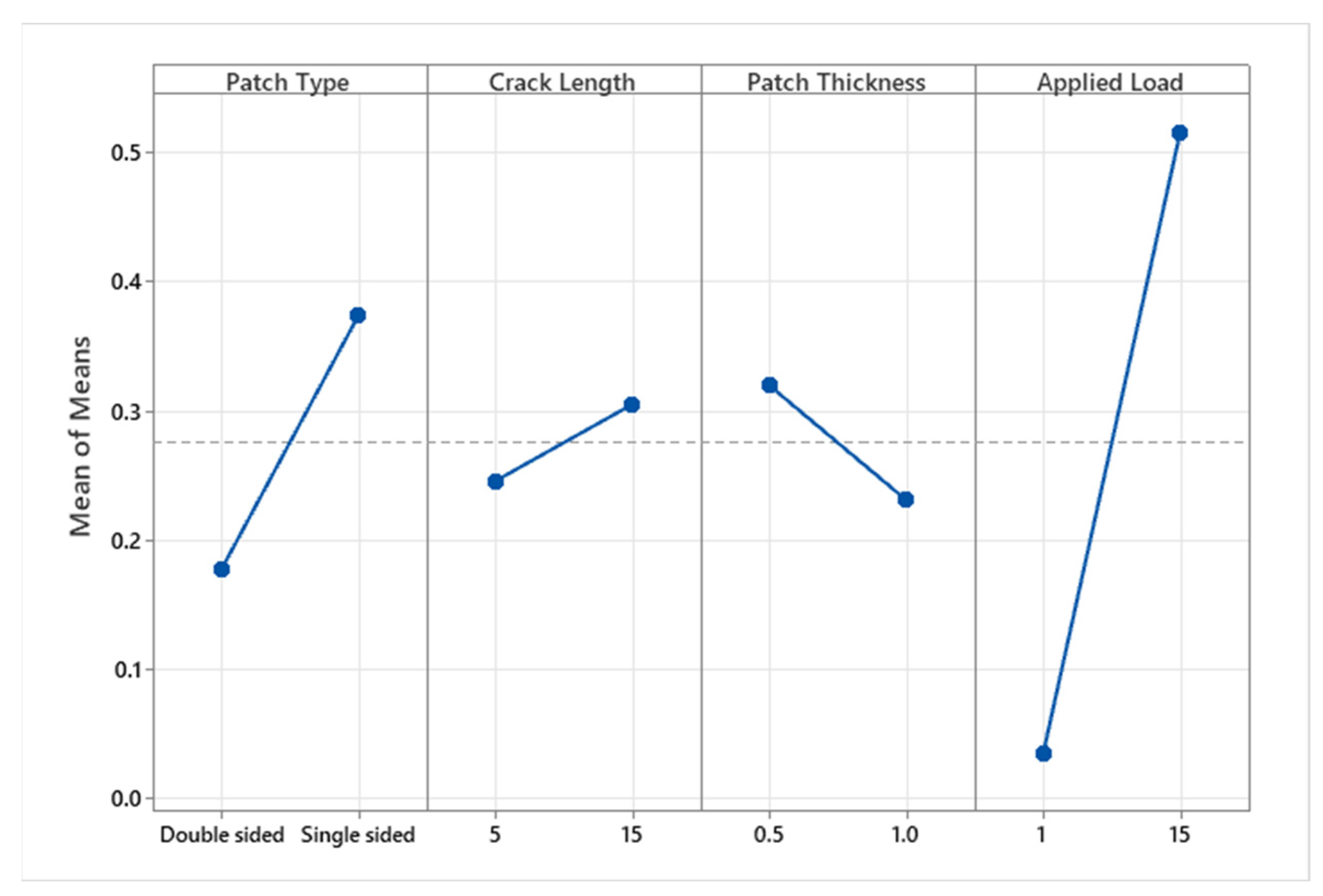
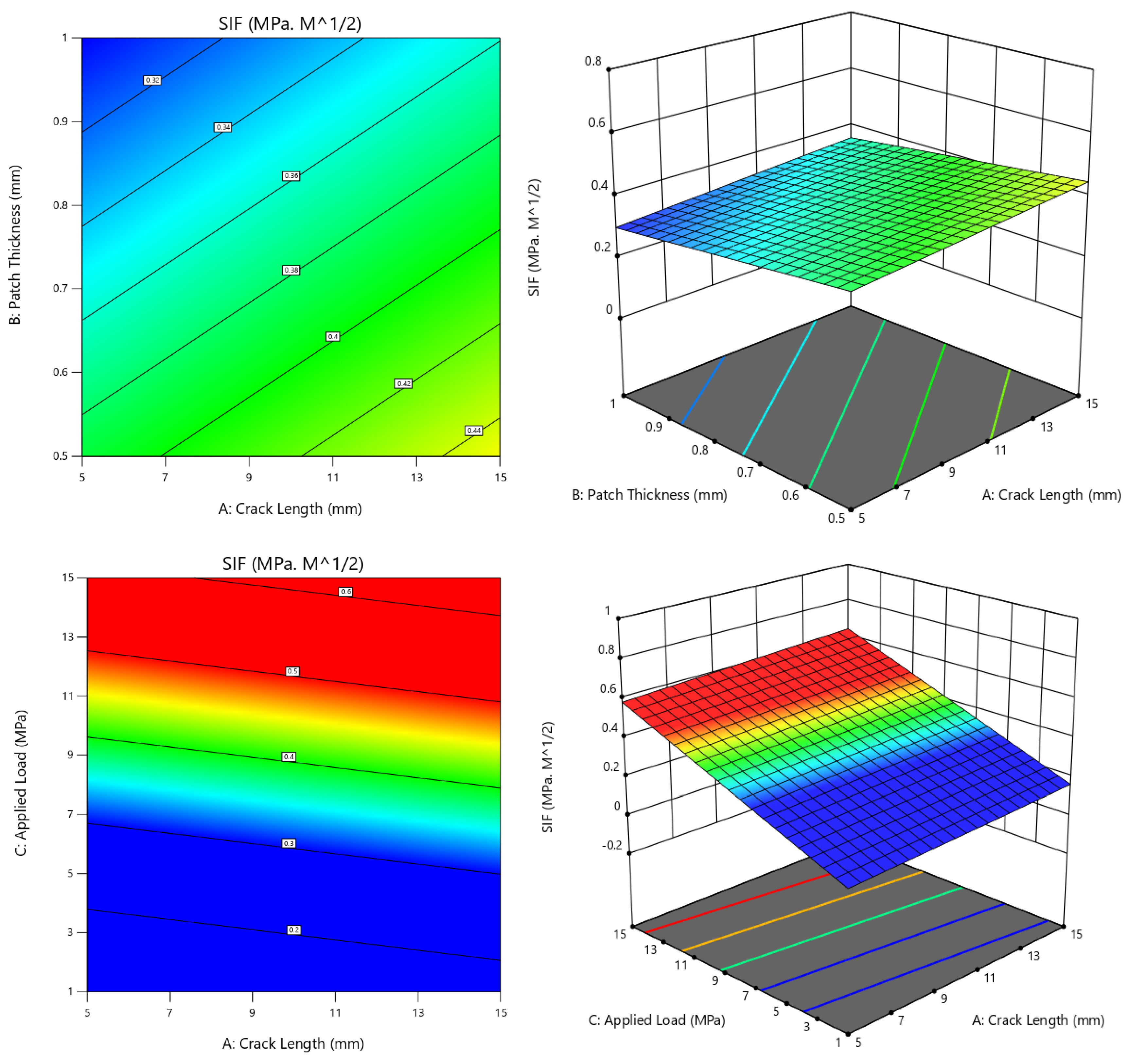
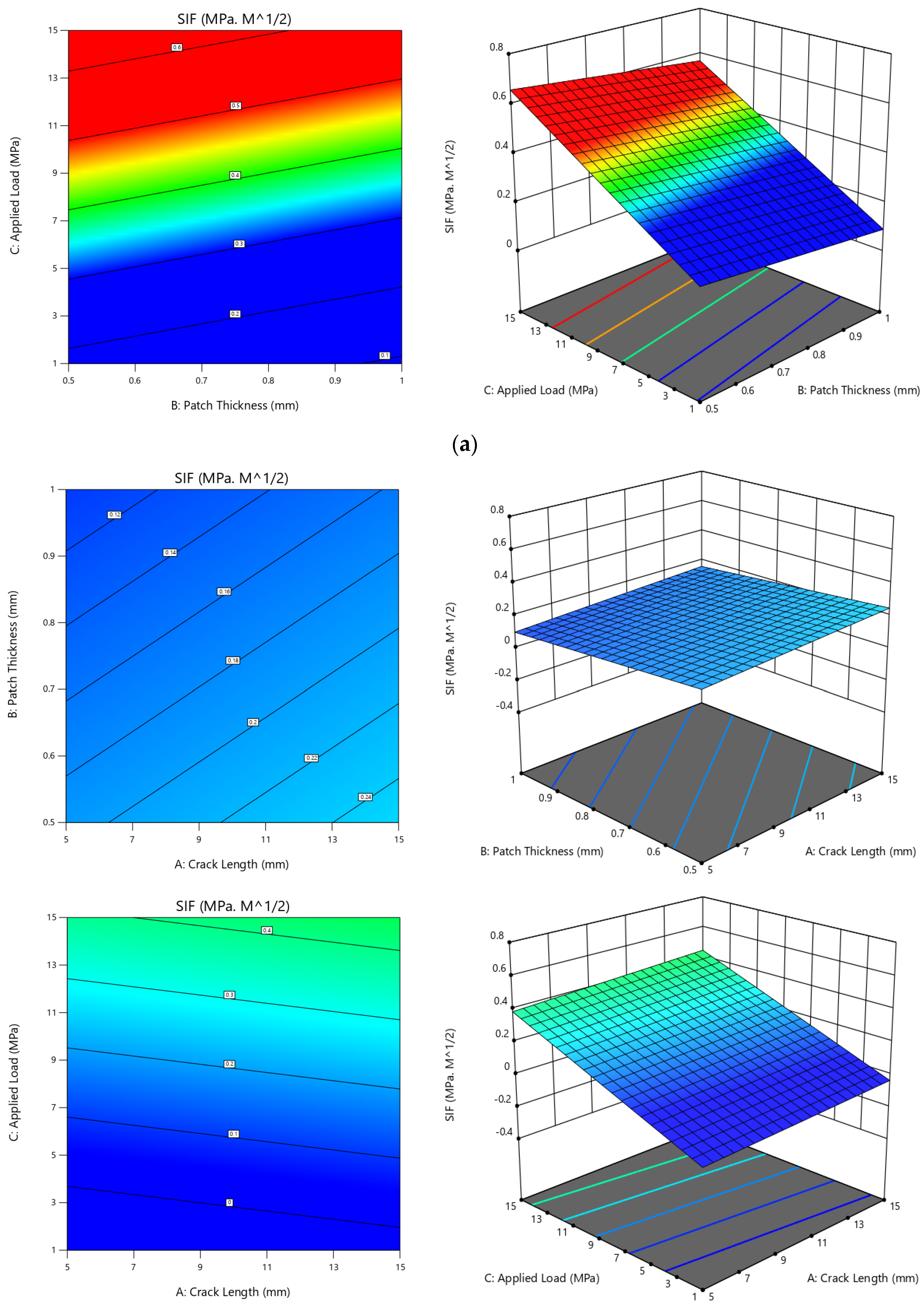
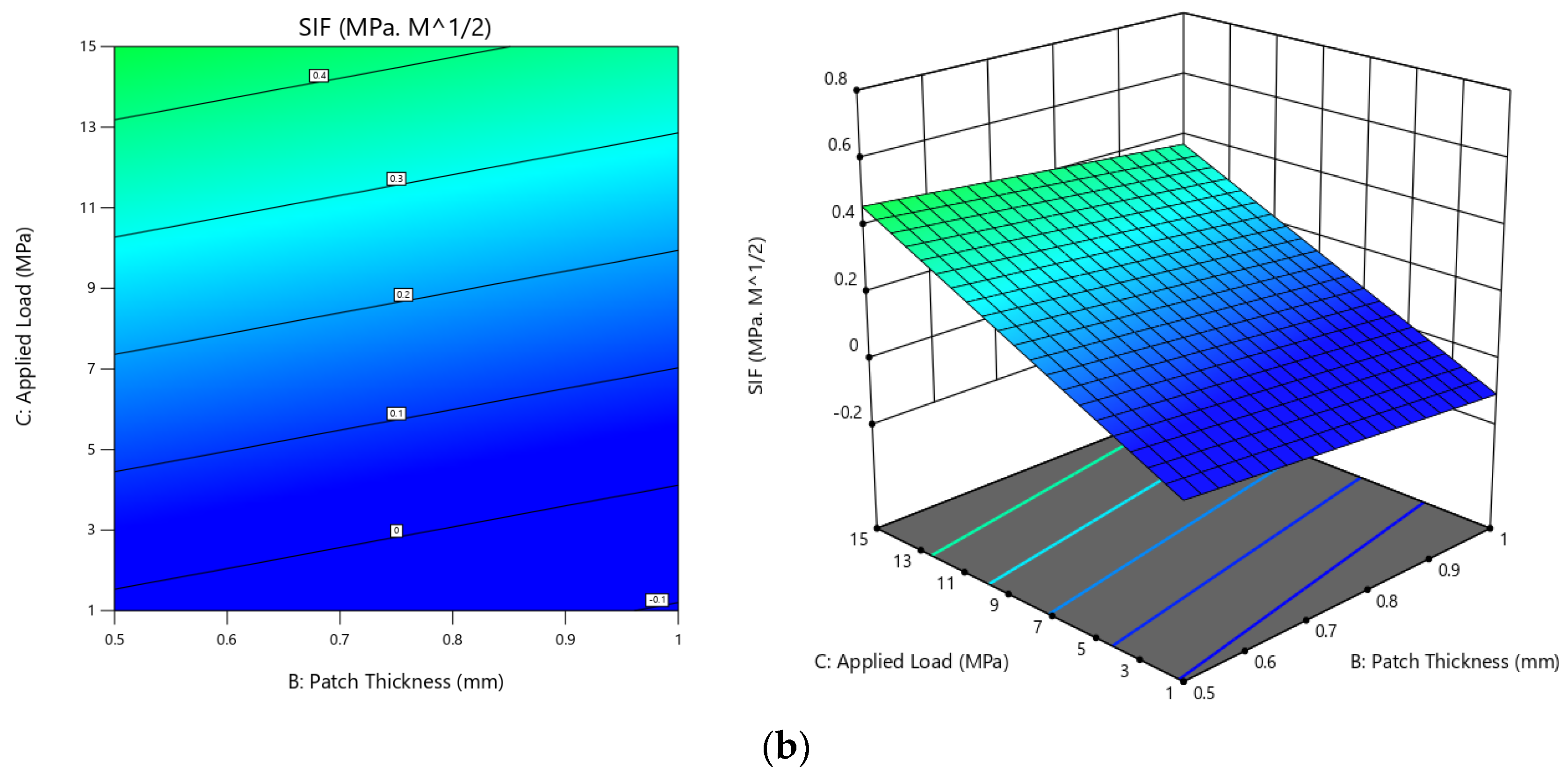

| Parameter | Patch Type | Crack Length (mm) | Patch Thickness (mm) | Applied Load (MPa) |
|---|---|---|---|---|
| Level 1 | Single-sided | 5 | 0.5 | 1 |
| Level 2 | Double-sided | 15 | 1 | 15 |
| Run | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| Coded Values | A | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 |
| B | 1 | 1 | 2 | 2 | 1 | 1 | 2 | 2 | |
| C | 1 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | |
| D | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | |
| Run | Patch Type | Crack Length (m) | Patch Thickness (m) | Applied Load (MPa) | SIF (MPa. m1/2) |
|---|---|---|---|---|---|
| 1 | Single-sided | 5 | 0.5 | 1 | 0.048594527 |
| 2 | Single-sided | 5 | 0.5 | 15 | 0.728977448 |
| 3 | Single-sided | 15 | 1 | 1 | 0.046735684 |
| 4 | Single-sided | 15 | 1 | 15 | 0.672010353 |
| 5 | Double-sided | 5 | 1 | 1 | 0.015778775 |
| 6 | Double-sided | 5 | 1 | 15 | 0.191442929 |
| 7 | Double-sided | 15 | 0.5 | 1 | 0.031467357 |
| 8 | Double-sided | 15 | 0.5 | 15 | 0.472010353 |
| Run | Selected Parameter | Fit | SE Fit | Resid. | Std. Resid. | ||||
|---|---|---|---|---|---|---|---|---|---|
| Patch Type | Crack Length (m) | Patch Thickness (m) | Applied Load (MPa) | ||||||
| 1 | Single-sided | 5 | 0.5 | 1 | 0.049 | 0.149 | 0.127 | −0.100 | −1.01 |
| 2 | Single-sided | 5 | 0.5 | 15 | 0.729 | 0.629 | 0.127 | 0.100 | 1.01 |
| 3 | Single-sided | 15 | 1 | 1 | 0.047 | 0.119 | 0.127 | −0.072 | −0.73 |
| 4 | Single-sided | 15 | 1 | 15 | 0.672 | 0.600 | 0.127 | 0.072 | 0.73 |
| 5 | Double-sided | 5 | 1 | 1 | 0.016 | −0.137 | 0.127 | 0.152 | 1.55 |
| 6 | Double-sided | 5 | 1 | 15 | 0.191 | 0.344 | 0.127 | −0.152 | −1.55 |
| 7 | Double-sided | 15 | 0.5 | 1 | 0.031 | 0.012 | 0.127 | 0.020 | 0.20 |
| 8 | Double-sided | 15 | 0.5 | 15 | 0.472 | 0.492 | 0.127 | −0.020 | −0.20 |
| Source | DF | Seq SS | Contribution | Adj. SS | Adj. MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Patch type | 1 | 0.077150 | 12.07% | 0.077150 | 0.077150 | 2.98 | 0.183 |
| Crack length | 1 | 0.007047 | 1.10% | 0.007047 | 0.007047 | 0.27 | 0.638 |
| Patch thickness | 1 | 0.015760 | 2.46% | 0.015760 | 0.015760 | 0.61 | 0.492 |
| Applied load | 1 | 0.461696 | 72.21% | 0.461696 | 0.461696 | 17.82 | 0.024 |
| Error | 3 | 0.077717 | 12.16% | 0.077717 | 0.025906 | ||
| Total | 7 | 0.639369 | 100.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aabid, A. Optimization of Reinforcing Patch Effects on Cracked Plates Using Analytical Modeling and Taguchi Design. Materials 2023, 16, 4348. https://doi.org/10.3390/ma16124348
Aabid A. Optimization of Reinforcing Patch Effects on Cracked Plates Using Analytical Modeling and Taguchi Design. Materials. 2023; 16(12):4348. https://doi.org/10.3390/ma16124348
Chicago/Turabian StyleAabid, Abdul. 2023. "Optimization of Reinforcing Patch Effects on Cracked Plates Using Analytical Modeling and Taguchi Design" Materials 16, no. 12: 4348. https://doi.org/10.3390/ma16124348
APA StyleAabid, A. (2023). Optimization of Reinforcing Patch Effects on Cracked Plates Using Analytical Modeling and Taguchi Design. Materials, 16(12), 4348. https://doi.org/10.3390/ma16124348







