Modeling Elastomer Compression: Exploring Ten Constitutive Equations
Abstract
1. Introduction
2. Selected Constitutive Models
2.1. Neo-Hookean Model
2.2. Mooney–Rivlin Model (Two-Parameter)
- The elastomer is incompressible and isotropic (in an unstrained state).
- The strain energy function must depend on even powers of λi (λi—principal stretch ratio).
2.3. Mooney–Rivlin Model (Three-Parameter)
2.4. Signiorini Model
2.5. Yeoh Model
2.6. James, Green and Simpson Model
2.7. Ogden Model
2.8. Arruda–Boyce Model
2.9. Gent Model
2.10. Marlow Model
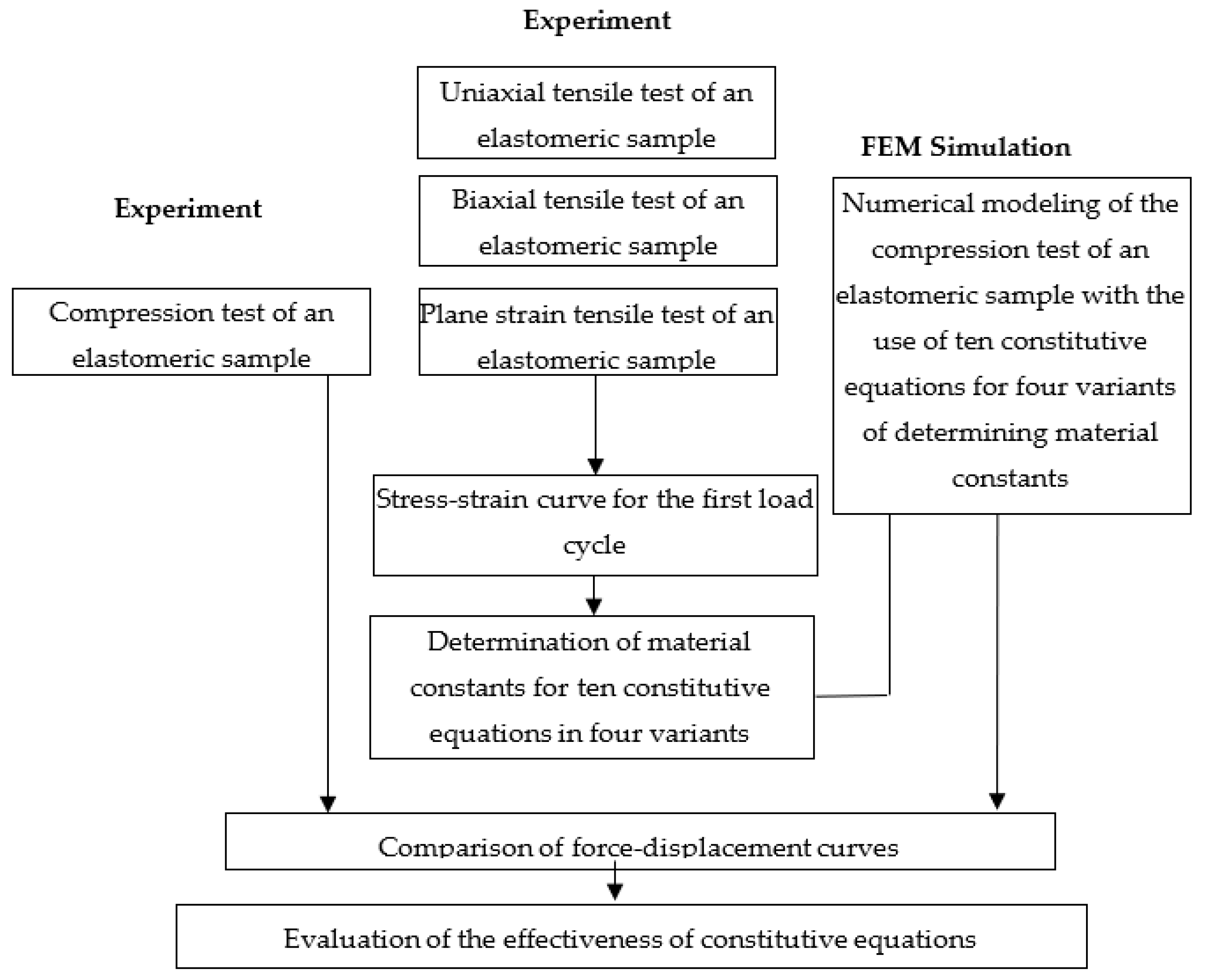
3. Methods
4. Experimental Work
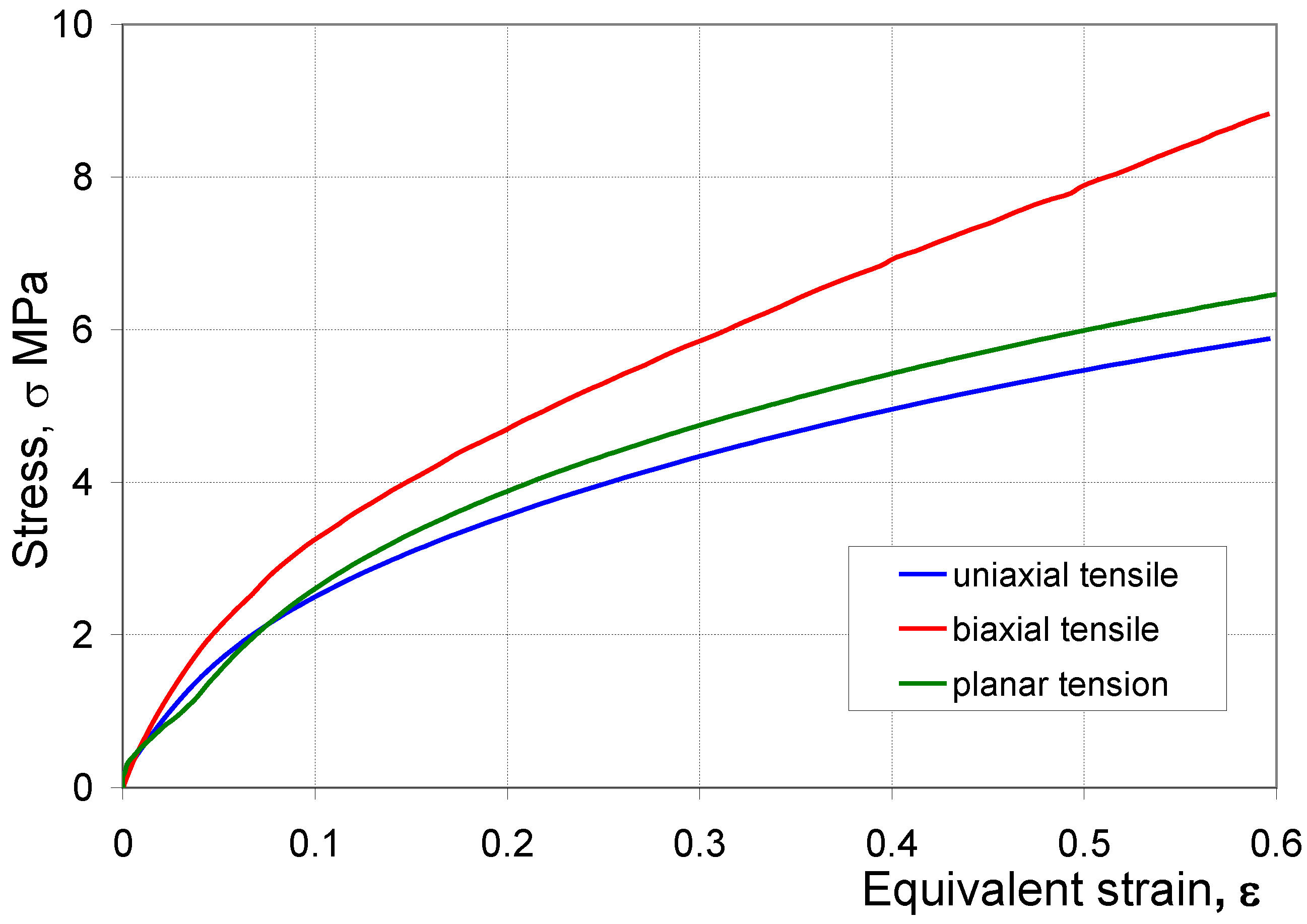
4.1. Uniaxial Tensile Test
4.2. Biaxial Tensile Test
4.3. Plane Strain Tensile Test
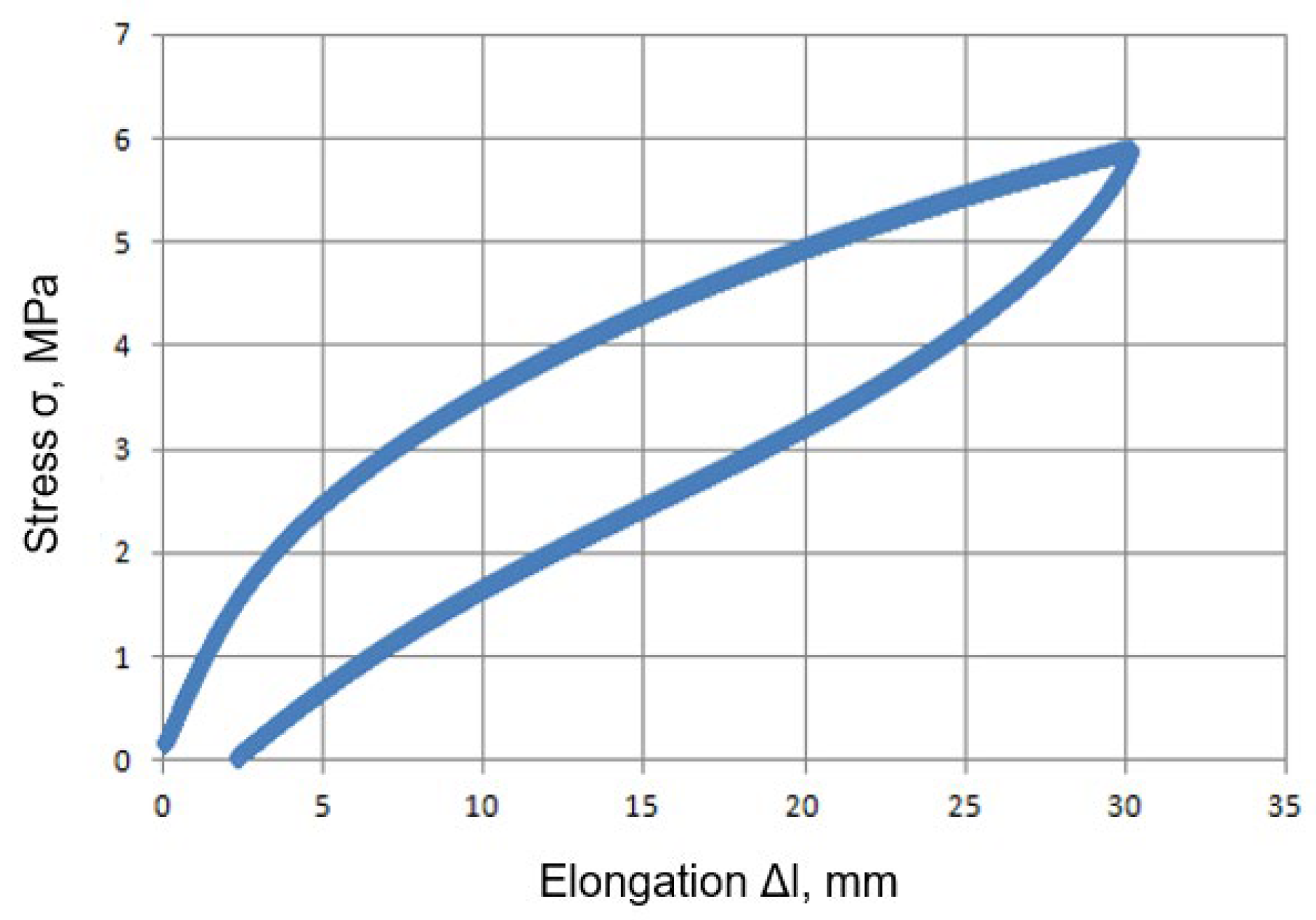
4.4. Stress–Strain Curve
5. Determination of the Constants in the Constitutive Equations
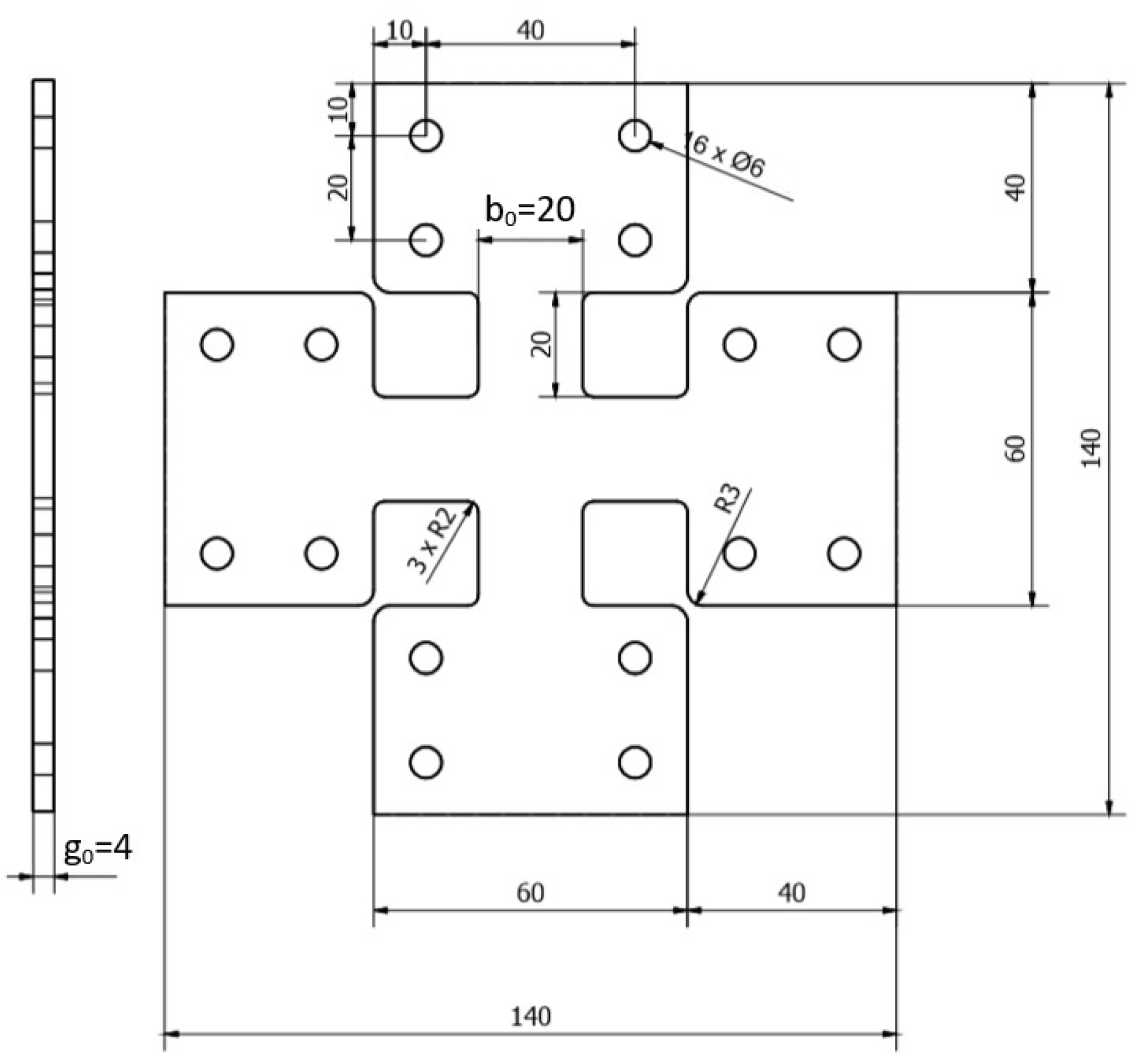
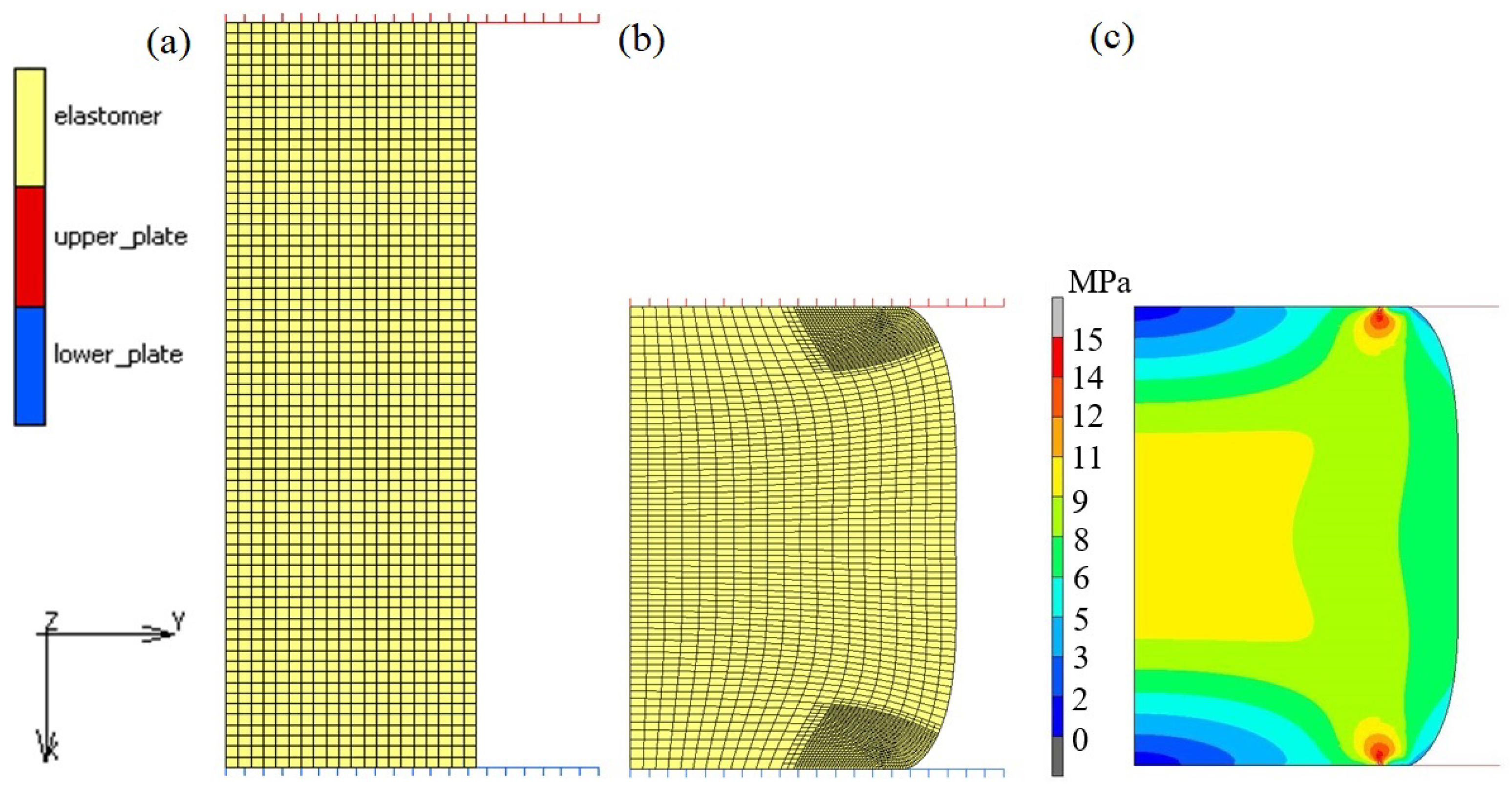
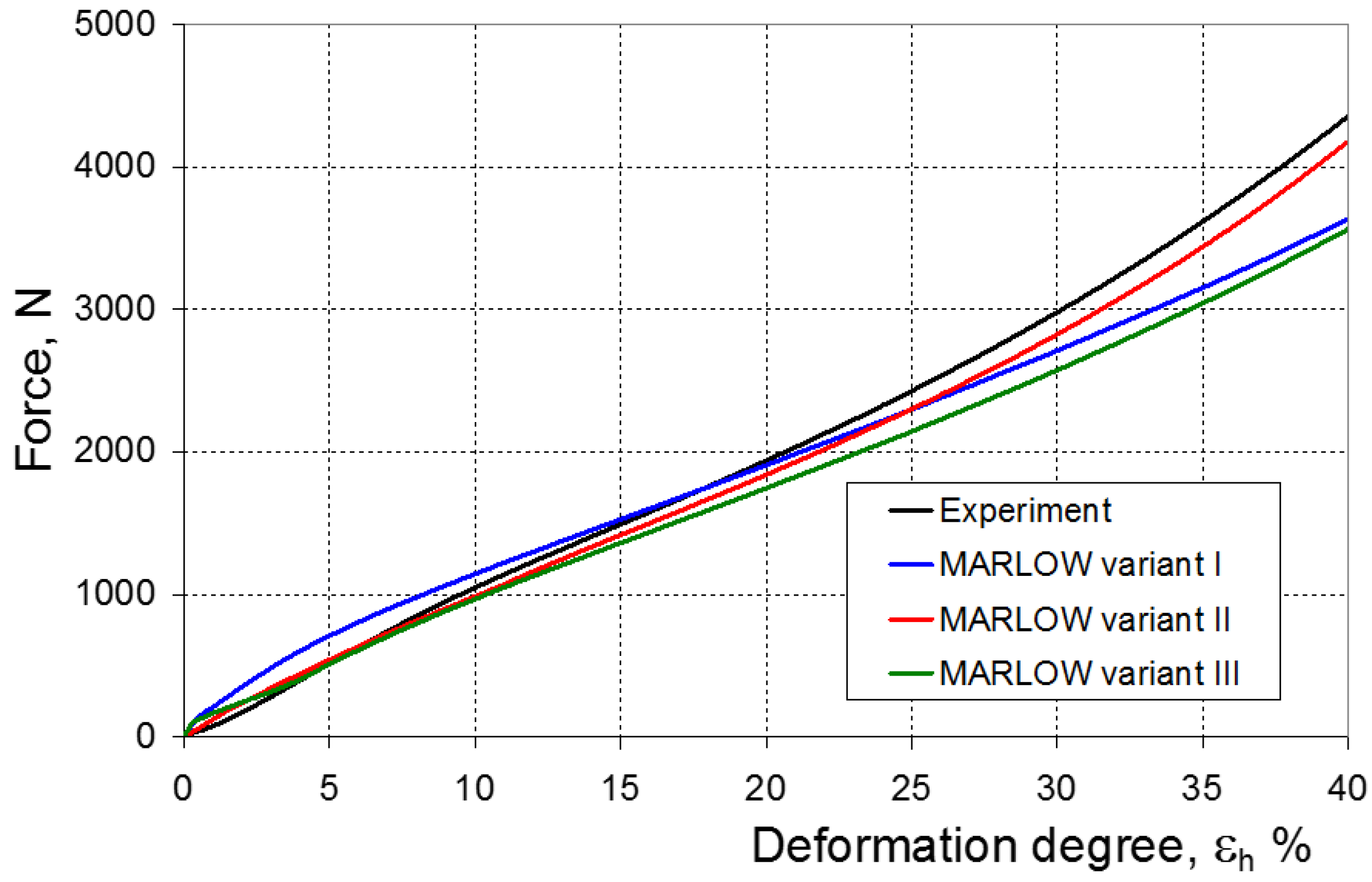
6. Experimental and Numerical Compression Test
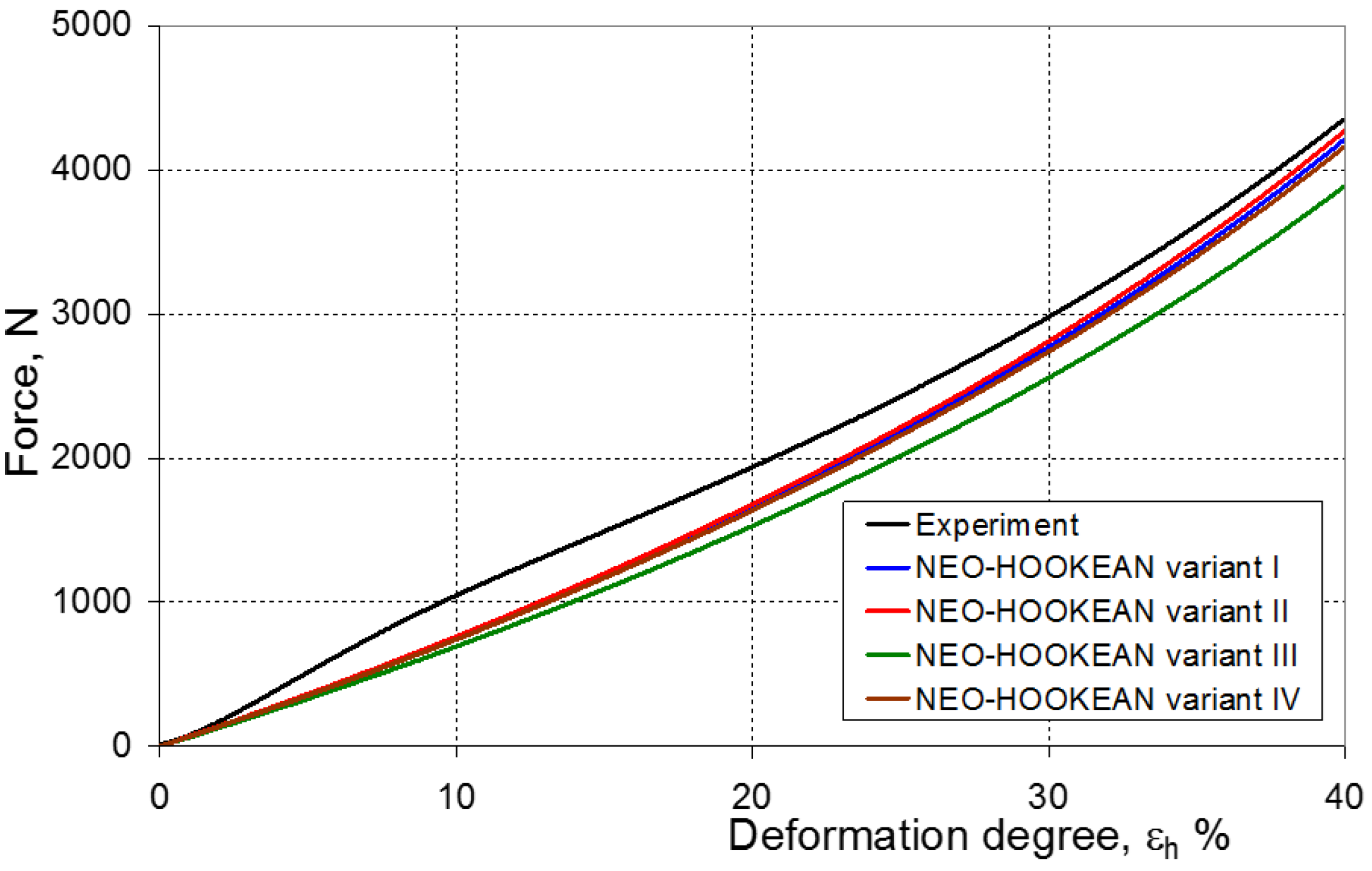
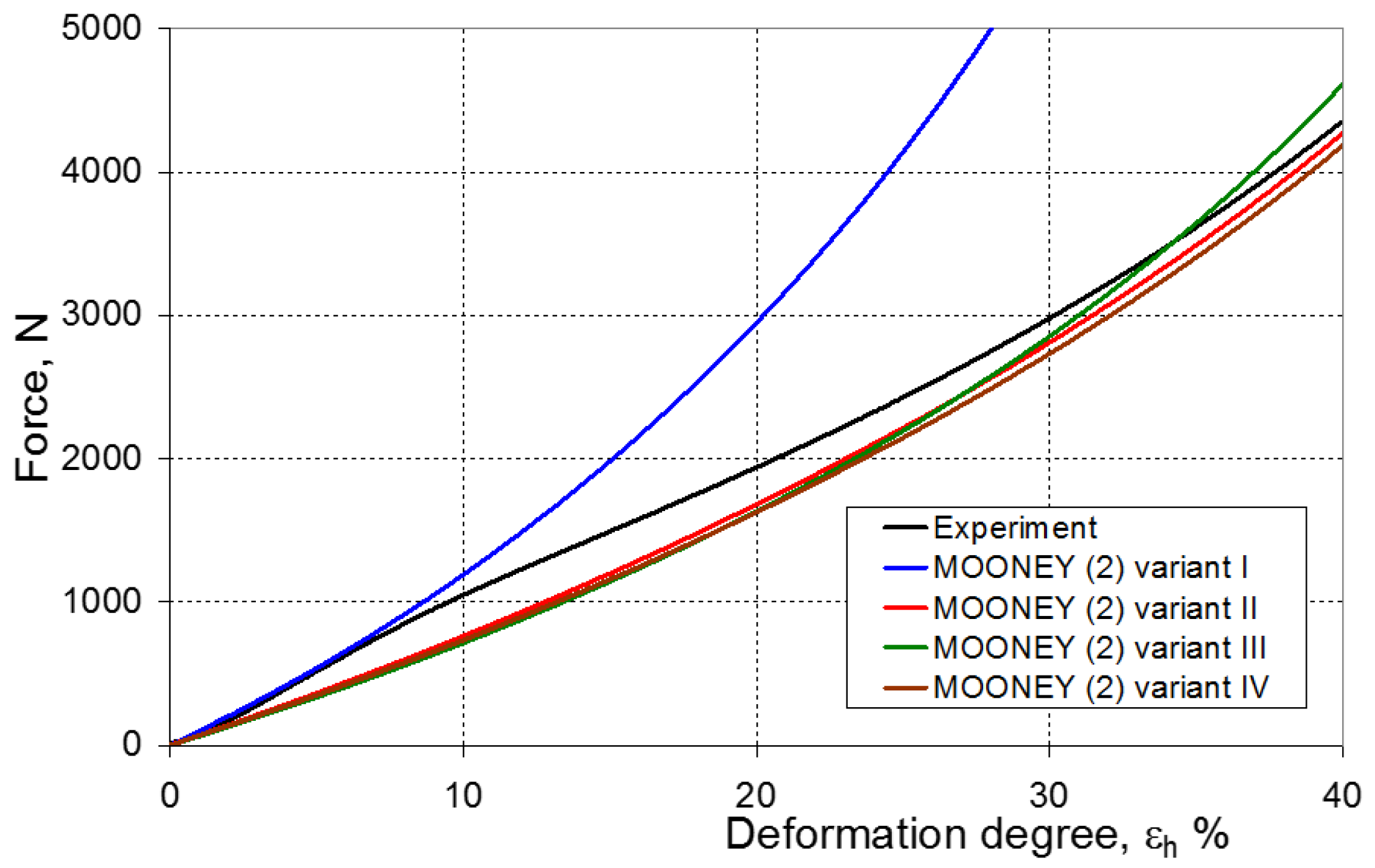
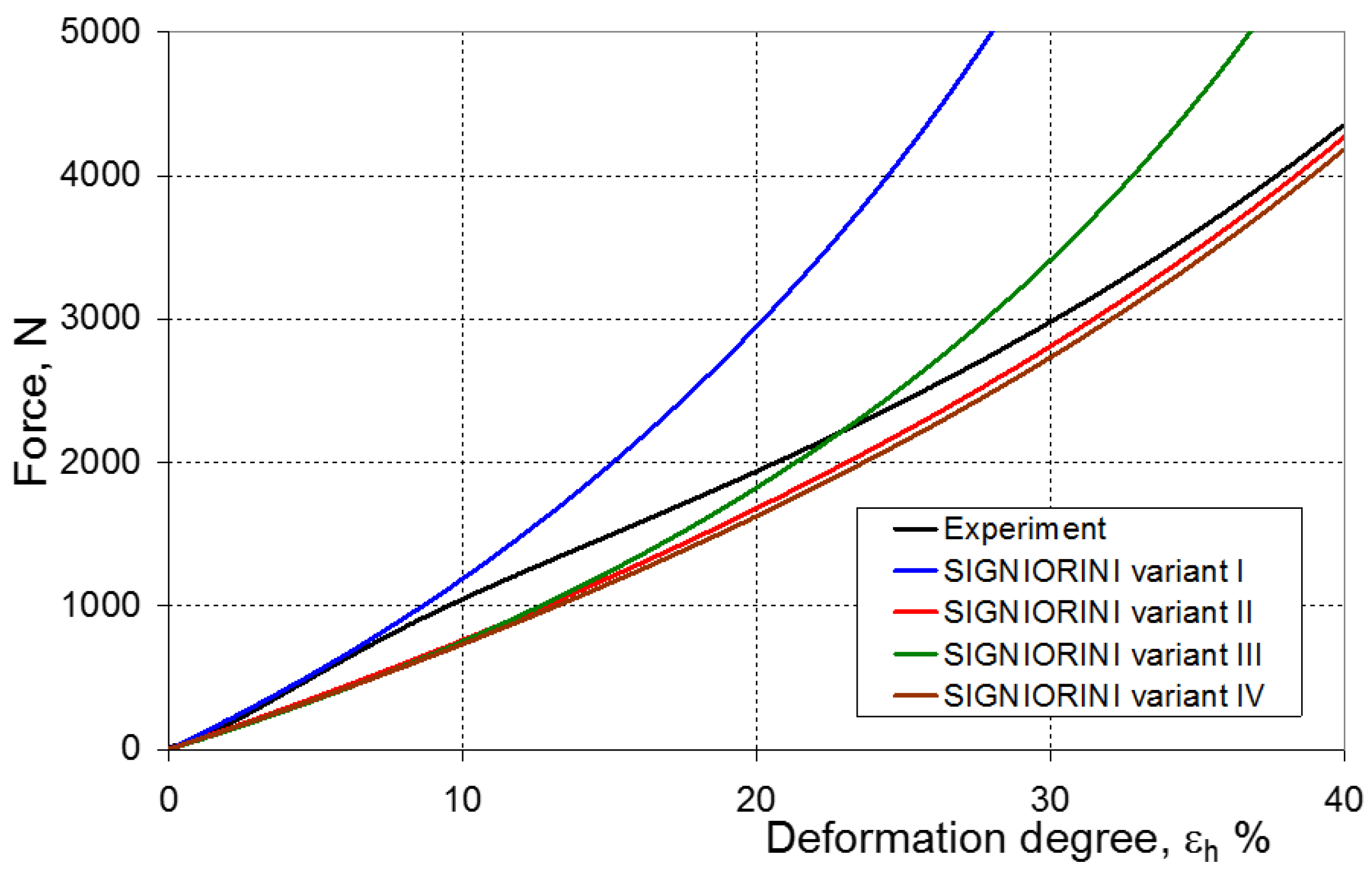
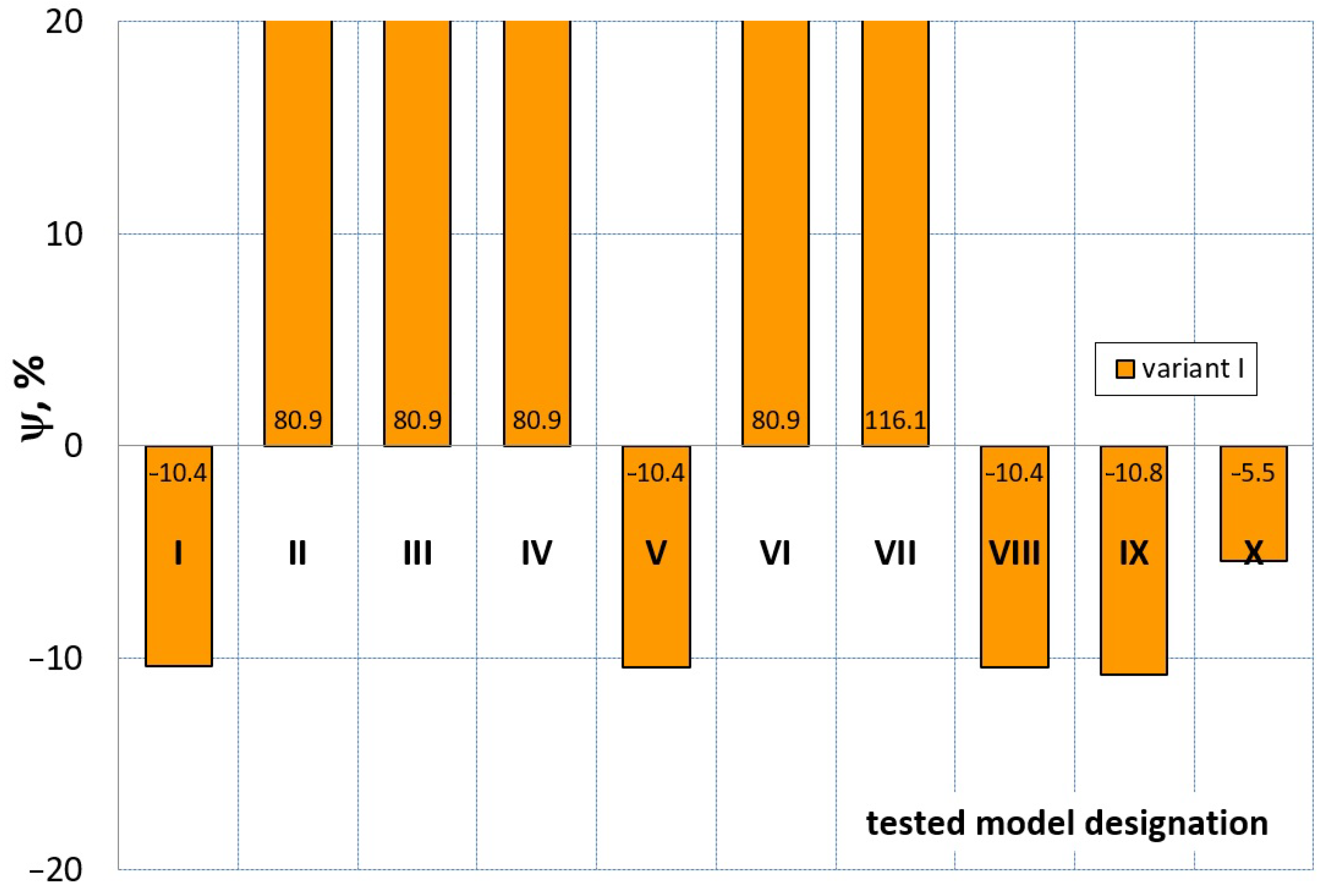
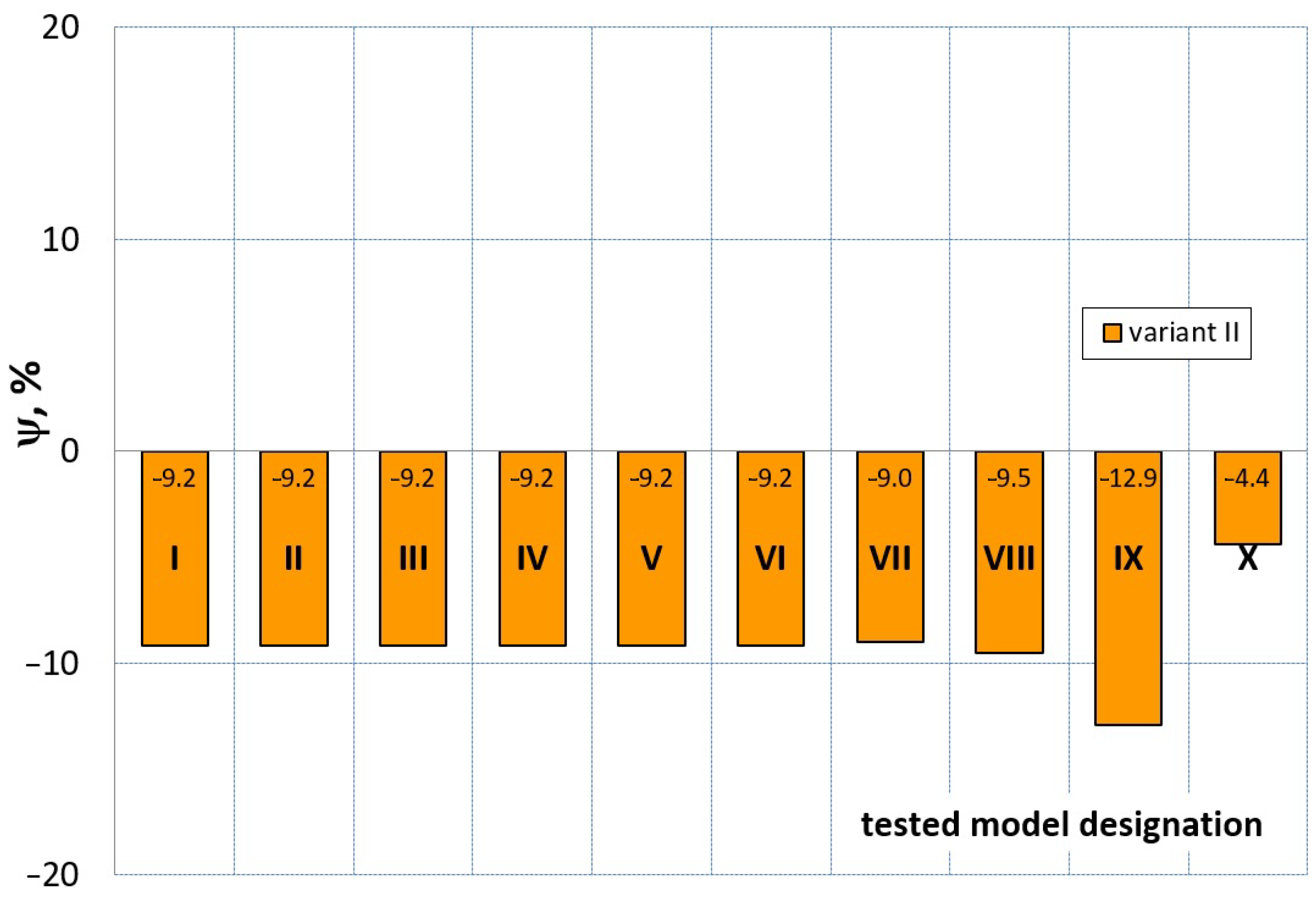
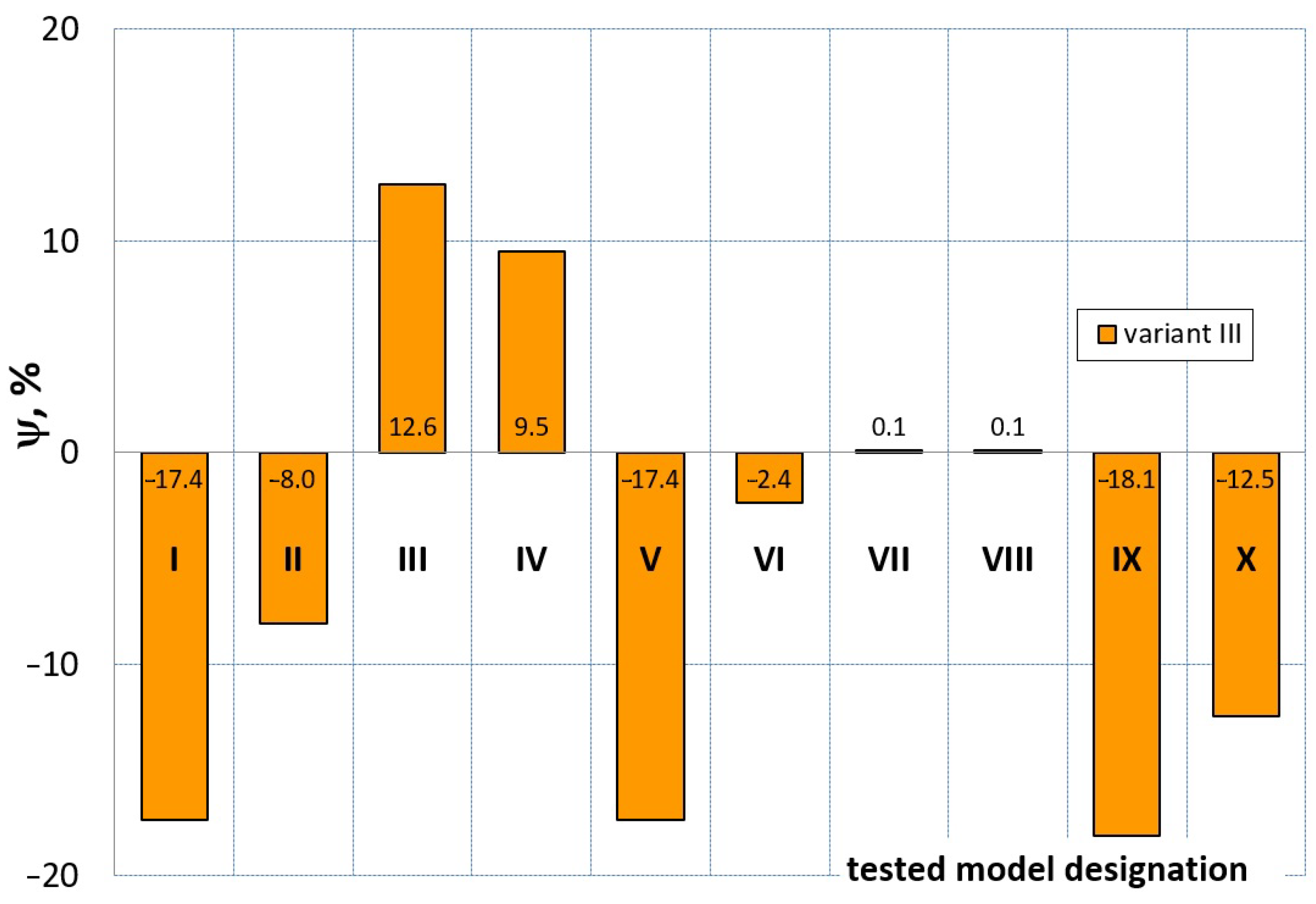
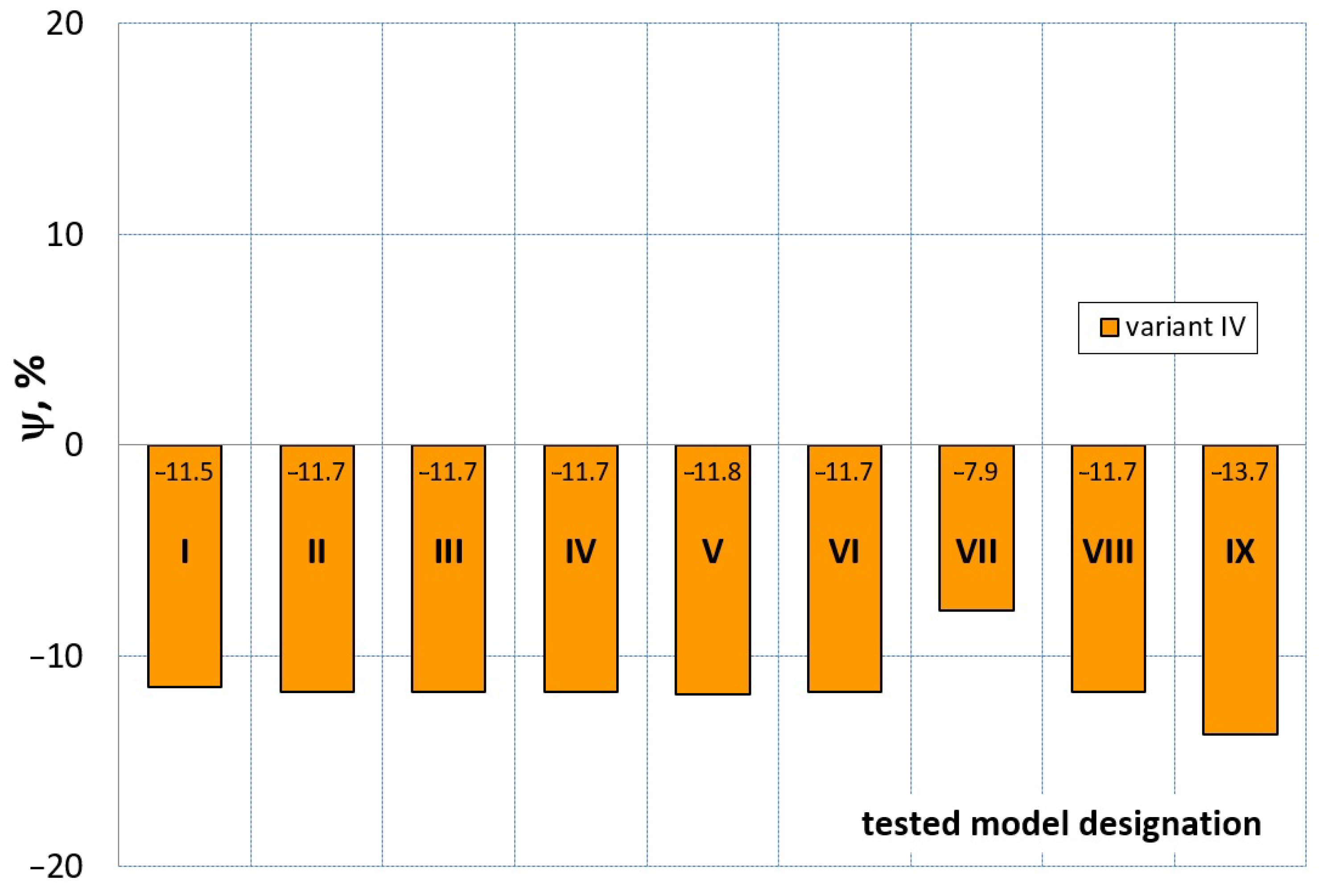
7. Evaluation of the Compression Test Modeling Effectiveness
- ψ = 0—force–displacement curves (calculated and experimental) coincide, which means the complete convergence of the results of FEM calculations with the experiment;
- ψ > 0—there is a discrepancy between the force–displacement curves, and the value of the calculated force is greater than the value of the experimental force;
- ψ < 0—there is a discrepancy in the course of the force–displacement curve, and the calculated force values are smaller than the force values in the experiment.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elias, H.G. An Introduction to Polymer Science; VCH Publishers: Weinheim, Germany, 1997; pp. 333–354. [Google Scholar]
- Shanks, R.A.; Kong, I. General Purpose Elastomers: Structure, Chemistry, Physics and Performance. In Advances in Elastomers I. Advanced Structured Materials; Visakh, P., Thomas, S., Chandra, A., Mathew, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 11. [Google Scholar] [CrossRef]
- Gajewski, M.; Szczerba, R.; Jemioło, S. Modelling of elastomeric bearings with application of Yeoh hyperelastic material model. Procedia Eng. 2015, 111, 220–227. [Google Scholar] [CrossRef]
- Ahmad, D.; Ajaj, R.M. Multiaxial mechanical characterization of latex skin for morphing wing application. Polym. Test. 2022, 106, 107408. [Google Scholar] [CrossRef]
- Ahmad, D.; Sahu, S.K.; Patra, K. Fracture toughness, hysteresis and stretchability of dielectric elastomers under equibiaxial and biaxial loading. Polym. Test. 2019, 79, 106038. [Google Scholar] [CrossRef]
- Huri, D.; Mankovits, T. Comparison of the material models in rubber finite element analysis. IOP Conf. Ser. Mater. Sci. Eng. 2018, 393, 012018. [Google Scholar] [CrossRef]
- Bin Du, X.; Zhao, Y.Q.; Lin, F.; Xiao, Z. Parameters Determination of Mooney-Rivlin Model for Rubber Material of Mechanical Elastic Wheel. Appl. Mech. Mater. 2017, 872, 198–203. [Google Scholar]
- Aidy, A.; Hosseini, M.; Sahari, B.B. A review and comparison on some rubber elasticity models. J. Sci. Ind. Res. 2010, 69, 495–500. [Google Scholar]
- Boyce, M.C.; Arruda, E.M. Constitutive Models of Rubber Elasticity: A Review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Khajehsaeid, H.; Arghavani, J.; Naghdabadi, R. A hyperelastic constitutive model for rubber-like materials. Eur. J. Mech. A/Solids 2013, 38, 144–151. [Google Scholar] [CrossRef]
- Mooney, M. A Theory of Large Elastic Deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials IV. further developments of the general theory. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1948, 241, 379–397. [Google Scholar] [CrossRef]
- MSC Marc®. Volume A: Theory and User Information; MSC. Software Corporation: Newport Beach, CA, USA, 2020. [Google Scholar]
- Dorfmann, A.; Muhr, A. Constitutive Models for Rubber III; CRC Press: London, UK, 2003. [Google Scholar]
- Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- James, A.G.; Green, A.; Simpson, G.M. Strain energy functions of rubber. I. Characterization of gum vulcanizates. J. Appl. Polym. Sci. 1975, 19, 2033–2058. [Google Scholar] [CrossRef]
- James, A.G.; Green, A. Strain energy functions of rubber. II. The characterization of filled vulcanizates. J. Appl. Polym. Sci. 1975, 19, 2319–2330. [Google Scholar] [CrossRef]
- Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1972, 326, 565–584. [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Ellis Horwood: Chichester, UK, 1984. [Google Scholar]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Gent, A.N. A New Constitutive Relation for Rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Ahmad, D.; Ajaj, R.M. A Multiaxial Fracture of Ecoflex Skin with Different Shore Hardness for Morphing Wing Application. Polymers 2023, 15, 1526. [Google Scholar] [CrossRef]
- Ahmad, D.; Kumar, D.; Ajaj, R.M. Multiaxial Deformations of Elastomeric Skins for Morphing Wing Applications: Theoretical Modeling and Experimental Investigations. Polymers 2022, 14, 4891. [Google Scholar] [CrossRef]
- Jemioło, S.; Gajewski, M.; Szczerba, R. Application of hyperselasticity and FEM in modeling of elastomer bridge bearings. In Modern Structural Mechanics with Applications to Civil Engineering; Warsaw University of Technology: Warsaw, Poland, 2015; pp. 99–122. [Google Scholar]
- Kut, S.; Ryzińska, G.; Niedziałek, B. The Influence of Material Model of the Polyurethane Elastomer on the FEM Calculations Quality for the Various Modes of Loading. Arch. Met. Mater. 2017, 62, 523–530. [Google Scholar] [CrossRef]
- MSC Software. Experimental Elastomer Analysis; MSC Software Corporation: Newport Beach, CA, USA, 2010. [Google Scholar]
- MSC Software. MSC Marc Volume B, Element Library; MSC Software Corporation: Newport Beach, CA, USA, 2020. [Google Scholar]
- MSC Software. Nonlinear Finite Element Analysis of Elastomers; MSC Software Corporation: Newport Beach, CA, USA, 2016. [Google Scholar]
- Jaszak, P. Modelowanie Gumy za Pomocą Metody Elementów Skończonych. Elastomery 2016, 20, 31–39. (In Polish) [Google Scholar]
- Seibert, H.; Scheffer, T.; Diebels, S. Biaxial testing of elastomers—Experimental setup, measurement and experimental optimisation of specimen’s shape. Tech. Mech. 2014, 34, 72–89. [Google Scholar]
- Testing and Analysis: Equibiaxial Stretching of Elastomeric Sheets. An Analytical Verification of Experimental Technique. Available online: www.axelproducts.com (accessed on 17 September 2022).
- Amborski, J.; Wołejsza, Z.; Osiński, J. Analiza numeryczna i badania elastomerowego tłumika drgań. Trans. Inst. Aviat. 2006, 1–2, 99–105. (In Polish) [Google Scholar]
- Palmieri, G.; Chiappini, G.; Sasso, M.; Papalini, S. Hyperelastic Materials Characterization by Planar Tension Tests and Full-field Strain Measurement. In Proceedings of the SEM Annual Conference, Albuquerque, Mexico, 1–4 June 2009. [Google Scholar]
- Testing and Analysis: Testing Elastomers for Hyperelastic Material Models in Finite Element Analysis. Available online: www.axelproducts.com (accessed on 17 September 2022).
- Kneć, M.; Golewski, P. Sample Holder for Biaxial Stretching on Uniaxial. Machines. Patent RP 225039, 28 February 2017. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]









| No | Model | Variant I–IV | Material Constants | Coeficient of Determination | ||||
|---|---|---|---|---|---|---|---|---|
| C10 | C01 | C11 | C20 | C30 | R2 | |||
| 1 | NEO-HOOKEAN | I | 2.872 | - | - | - | - | 0.987 |
| II | 2.912 | - | - | - | - | 0.996 | ||
| III | 2.65 | 0.993 | ||||||
| IV | 2.838 | - | - | - | - | 0.992 | ||
| 2 | MOONEY (2) | I | 7.521 × 10−13 | 4.097 | - | - | - | 0.993 |
| II | 2.912 | 2.147 × 10−8 | - | - | - | 0.996 | ||
| III | 1.938 | 0.712 | 0.993 | |||||
| IV | 2.717 | 0.080 | - | - | - | 0.992 | ||
| 3 | MOONEY (3) | I | 1.047 × 10−8 | 4.096 | 1.586 × 10−9 | - | - | 0.993 |
| II | 2.912 | 2.803 × 10−8 | 1.462 × 10−9 | - | - | 0.996 | ||
| III | 0.340 | 2.310 | 1.686 × 10−8 | 0.993 | ||||
| IV | 2.717 | 0.080 | 3.860 × 10−8 | - | - | 0.992 | ||
| 4 | SIGNIORINI | I | 1.314 × 10−6 | 4.097 | - | 7.065 × 10−8 | - | 0.993 |
| II | 2.912 | 6.276 × 10−8 | - | 3.643 × 10−8 | - | 0.996 | ||
| III | 0.585 | 2.065 | - | 5.271 × 10−9 | - | 0.993 | ||
| IV | 2.718 | 0.079 | - | 2.456 × 10−8 | - | 0.992 | ||
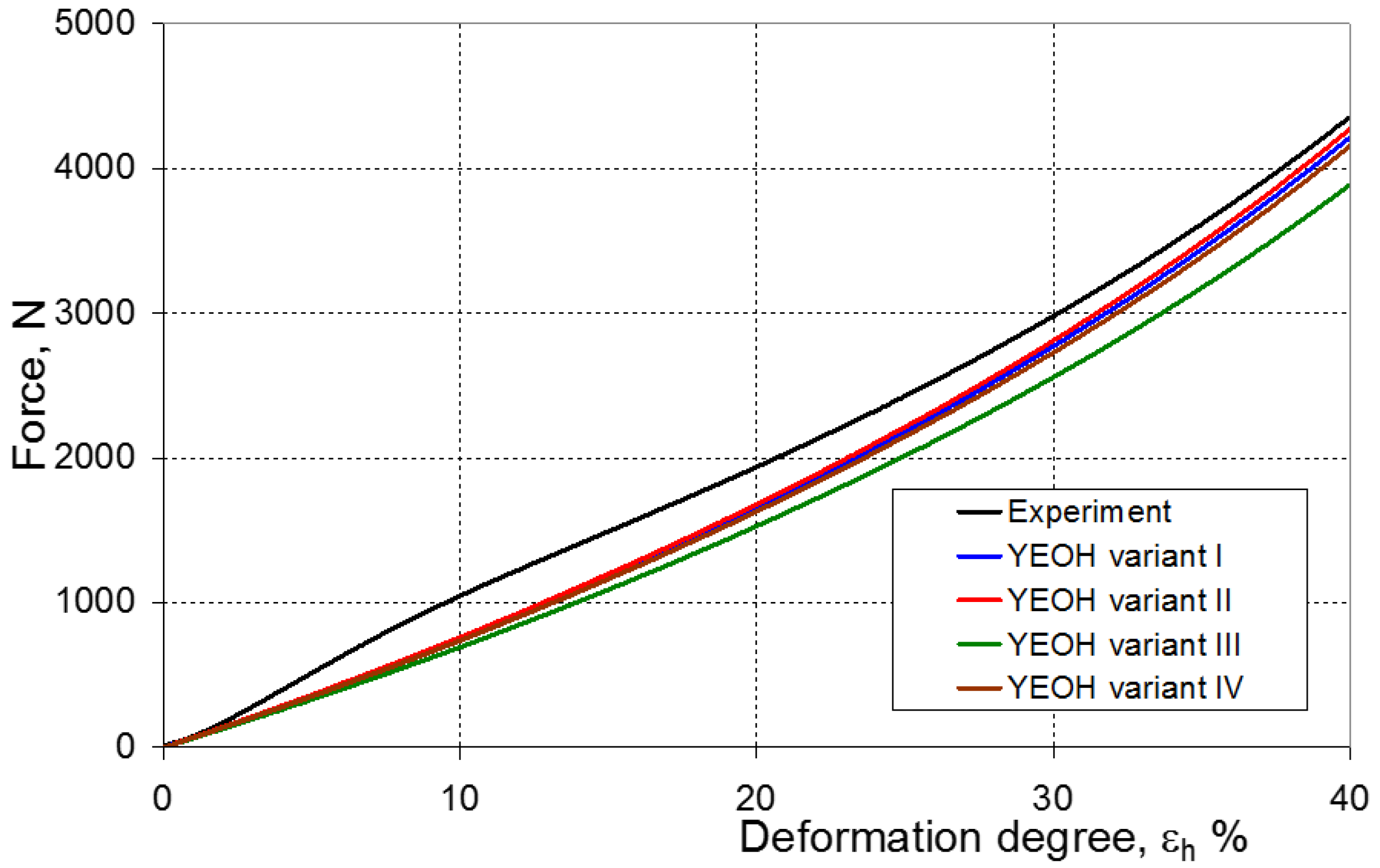
| 5 | YEOH | I | 2.872 | - | - | 1.419 × 10−9 | 2.767 × 10−9 | 0.987 |
| II | 2.912 | - | - | 5.538 × 10−10 | 2.893 × 10−10 | 0.996 | ||
| III | 2.65 | - | - | 2.002 × 10−8 | 1.048 × 10−7 | 0.993 | ||
| IV | 2.825 | - | - | 1.148 × 10−8 | 0.003 | 0.992 | ||
| 6 | JAMES–GREEN–SIMPSON | I | 1.304 × 10−7 | 4.096 | 2.339 × 10−7 | 1.565 × 10−7 | 2.006 × 10−8 | 0.993 |
| II | 2.912 | 4.574 × 10−8 | 5.843 × 10−8 | 1.378 × 10−8 | 2.359 × 10−7 | 0.996 | ||
| III | 1.500 | 1.150 | 1.292 × 10−8 | 1.378 × 10−8 | 1.317 × 10−8 | 0.993 | ||
| IV | 2.717 | 0.080 | 2.302 × 10−12 | 1.624 × 10−12 | 2.085 × 10−7 | 0.992 | ||
| No | Model | Variant I–IV | The Number of Components of the Function N | Material Constants | Coeficient of Determination | |
|---|---|---|---|---|---|---|
| µn | αn | R2 | ||||
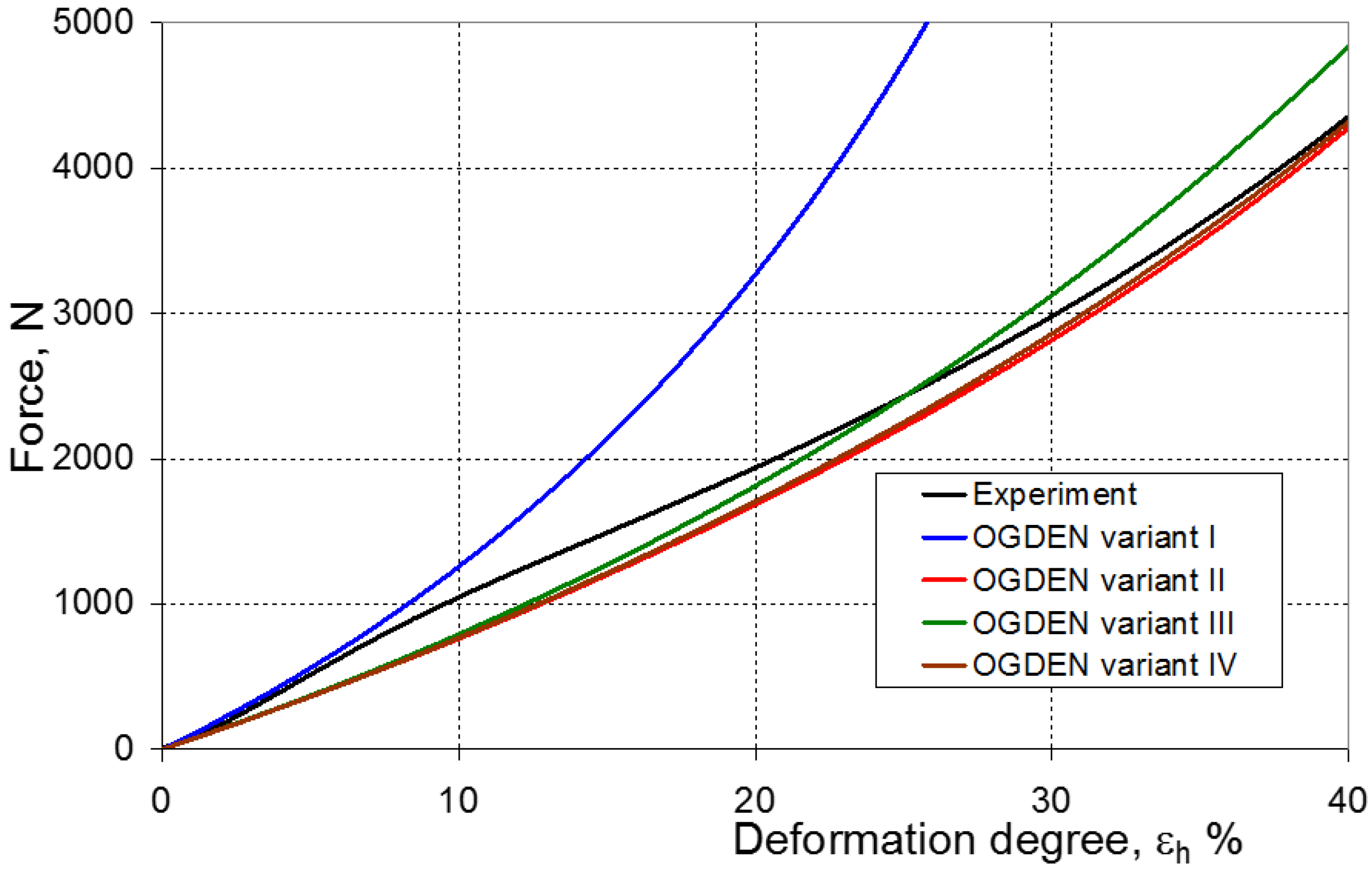
| 7 | OGDEN | I | 2 | −5.809 | −2.896 | 0.993 |
| 4.762 × 10−5 | 0.054 | |||||
| II | −1.104 × 10−5 | −0.142 | 0.996 | |||
| 6.033 | 1.931 | |||||
| III | 289.102 | 0.040 | 0.995 | |||
| 0.055 | 0.044 | |||||
| IV | −1.440 × 10−4 | −4.11 × 10−2 | 0.992 | |||
| 8.416 | 1.376 | |||||
| 8.416 | 1.376 | |||||
| 8.416 | 1.376 | |||||
| 8.416 | 1.376 | |||||
| No | Model | Variant I–IV | Material Constants | Coeficient of Determination | |
|---|---|---|---|---|---|
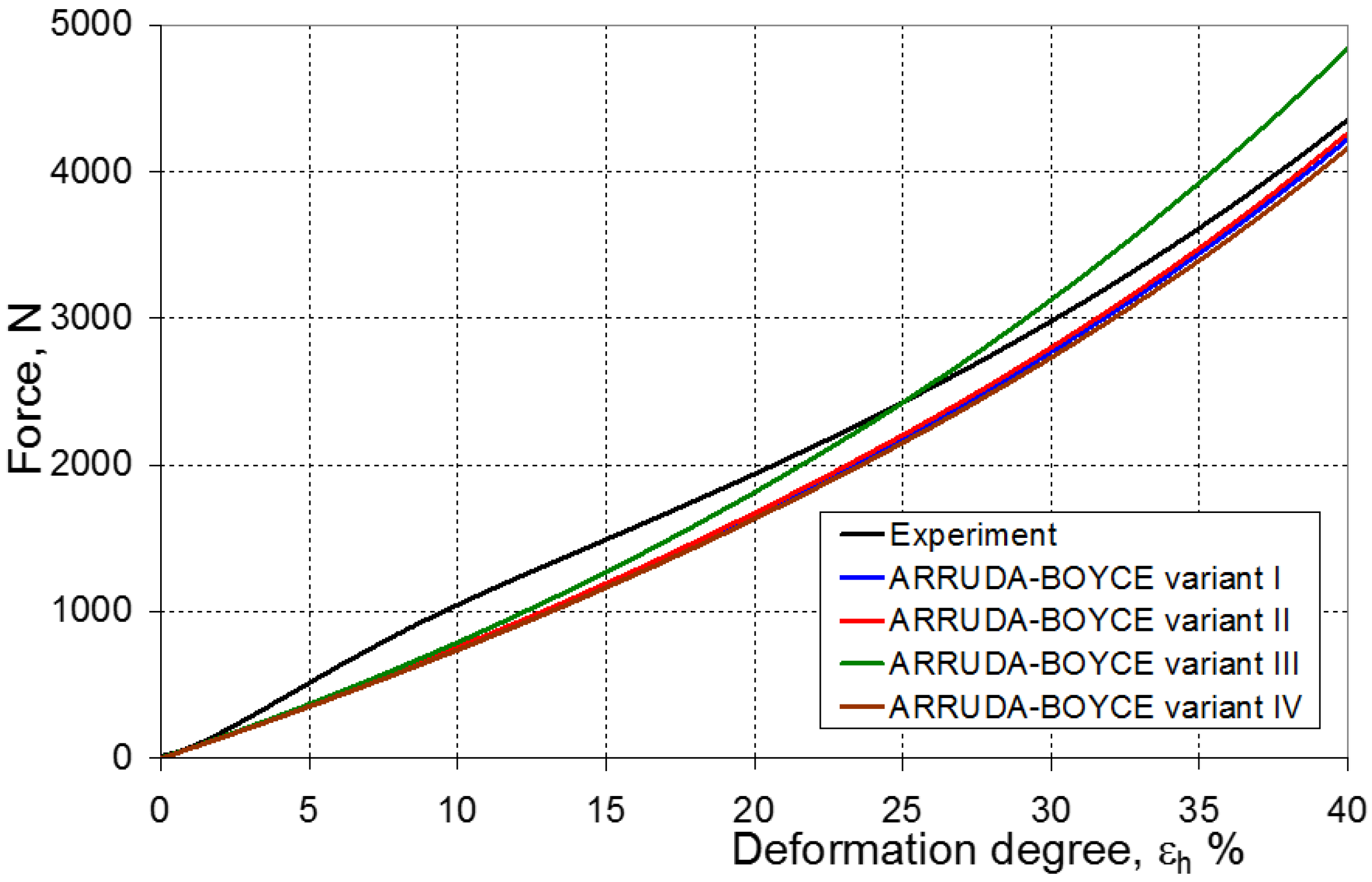
| 8 | ARRUDA–BOYCE | NKΘ | N | R2 | |
| I | 5.638 | 37.966 | 0.987 | ||
| II | 5.727 | 52.440 | 0.996 | ||
| III | 5.204 | 39.525 | 0.993 | ||
| IV | 5.589 | 52.4399 | 0.992 | ||
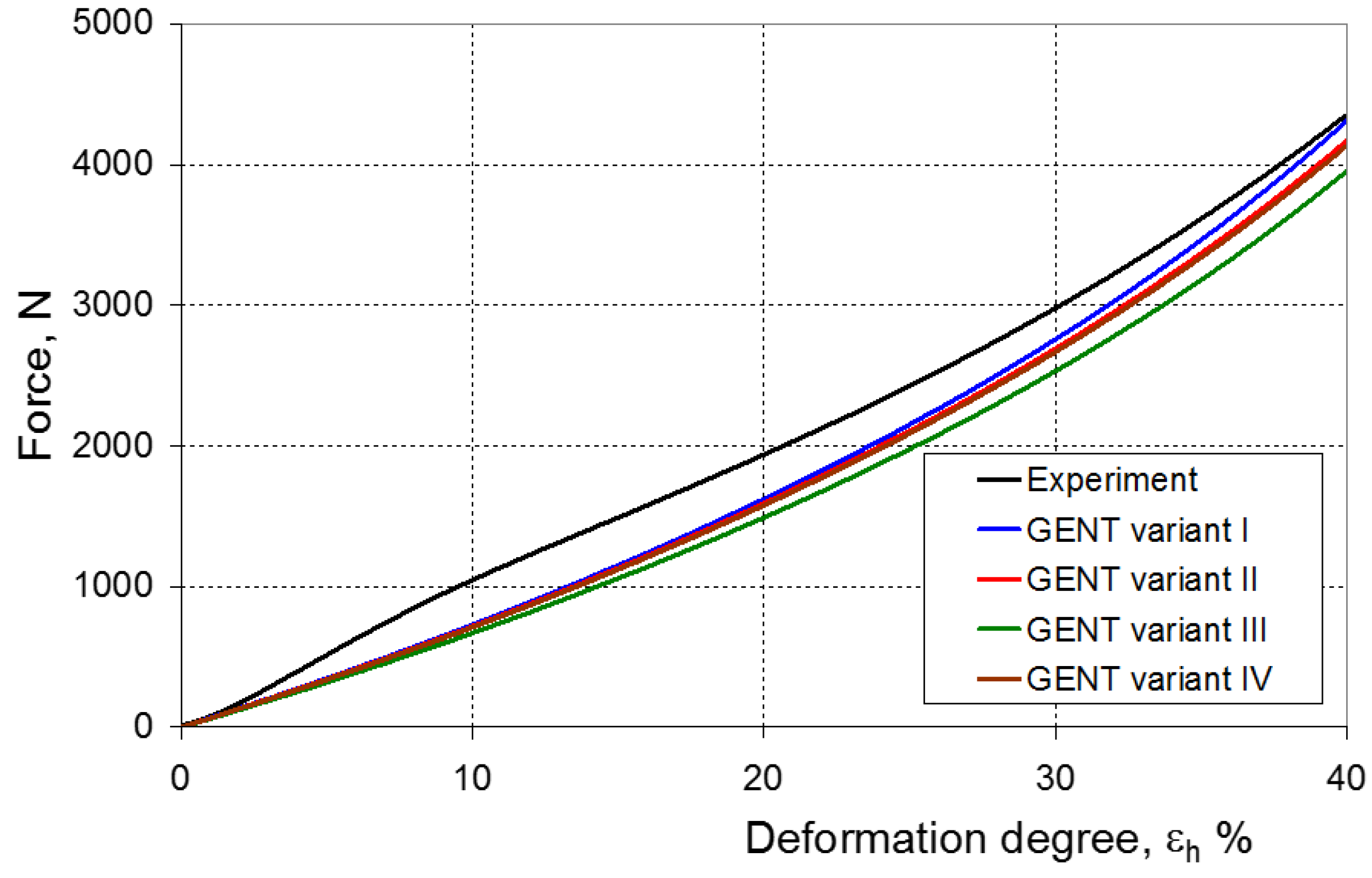
| 9 | GENT | E | I_M | ||
| I | 16.688 | 18.998 | 0.986 | ||
| II | 16.433 | 26.220 | 0.995 | ||
| III | 15.344 | 19.762 | 0.992 | ||
| IV | 16.284 | 26.220 | 0.991 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kut, S.; Ryzińska, G. Modeling Elastomer Compression: Exploring Ten Constitutive Equations. Materials 2023, 16, 4121. https://doi.org/10.3390/ma16114121
Kut S, Ryzińska G. Modeling Elastomer Compression: Exploring Ten Constitutive Equations. Materials. 2023; 16(11):4121. https://doi.org/10.3390/ma16114121
Chicago/Turabian StyleKut, Stanisław, and Grażyna Ryzińska. 2023. "Modeling Elastomer Compression: Exploring Ten Constitutive Equations" Materials 16, no. 11: 4121. https://doi.org/10.3390/ma16114121
APA StyleKut, S., & Ryzińska, G. (2023). Modeling Elastomer Compression: Exploring Ten Constitutive Equations. Materials, 16(11), 4121. https://doi.org/10.3390/ma16114121






