Investigating the Retrofitting Effect of Fiber-Reinforced Plastic and Steel Mesh Casting on Unreinforced Masonry Walls
Abstract
1. Introduction
2. Experimental Section
2.1. Preparing Prisms for Testing
2.1.1. Glass Fiber Sample
2.1.2. Ferrocement Strip Samples Casting
2.2. Testing of Brick and Prisms
2.2.1. Compressive Strength Test of Brick
2.2.2. Prism Flexure Test
2.2.3. Prism Diagonal Compression Test
2.2.4. Compressive Strength Test of Prism
3. Results and Discussion
3.1. Brick Compression Strength
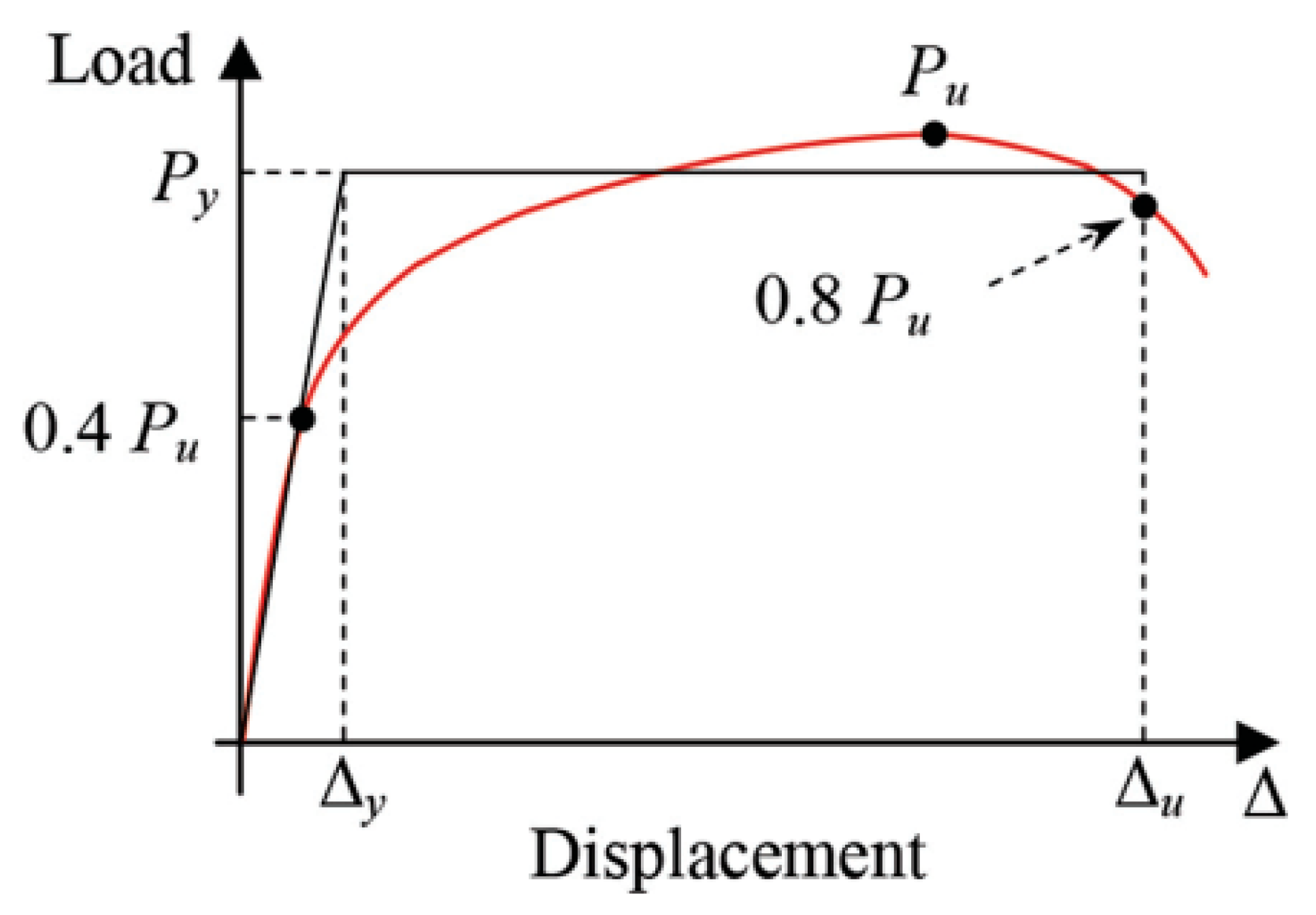
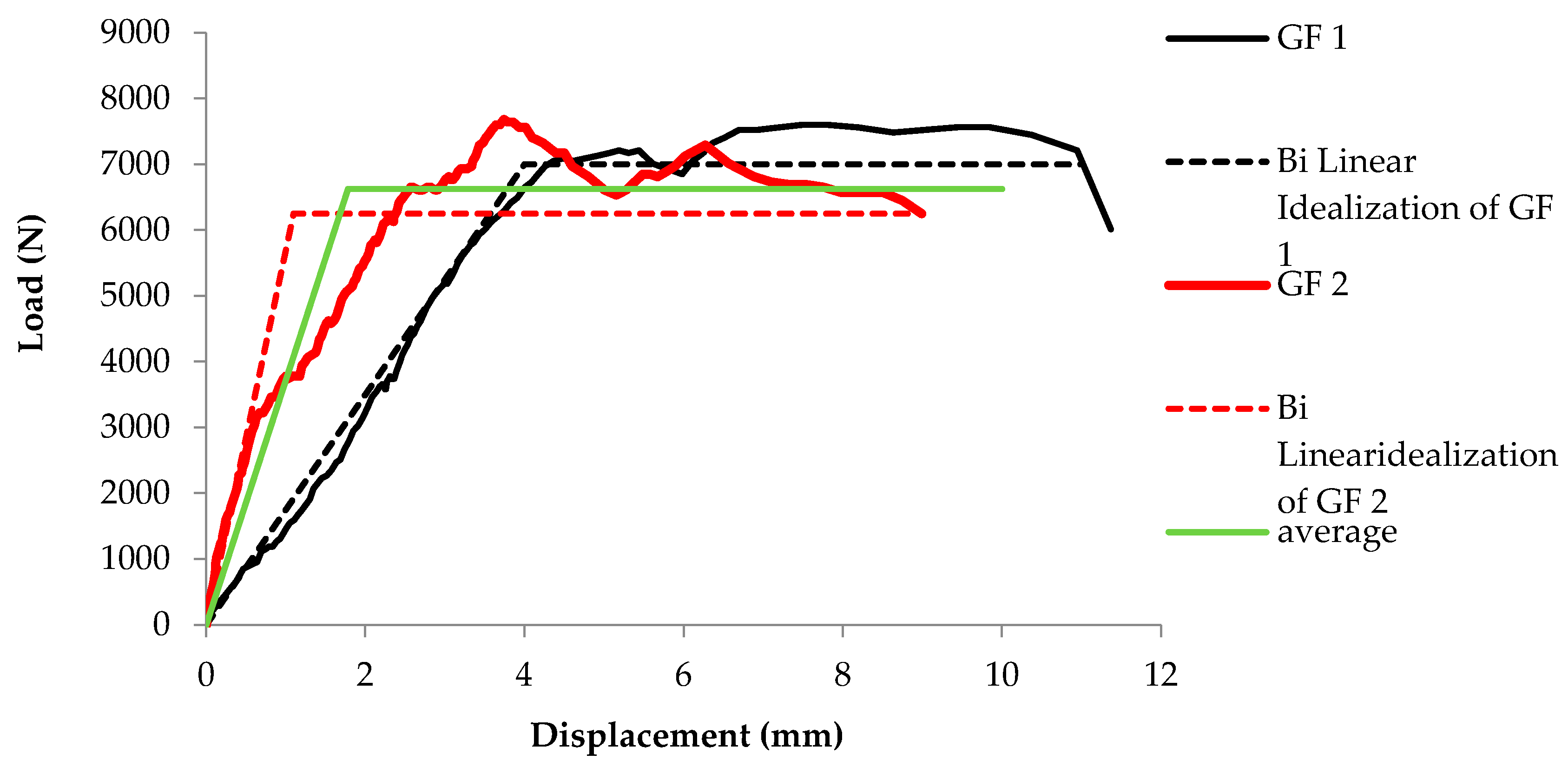
3.2. Prism Flexural Strength Adopting Bilinear Idealization Approach
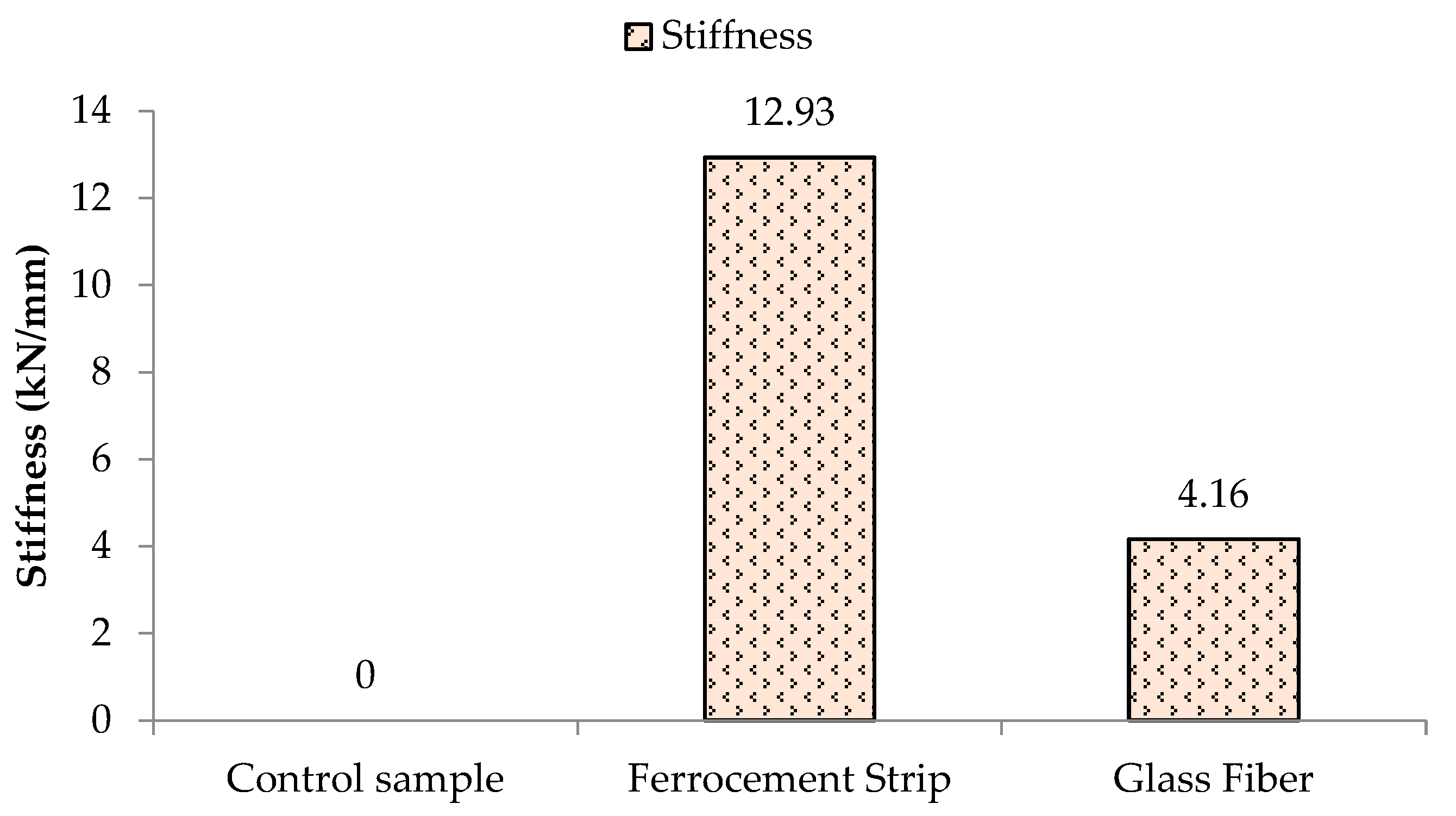
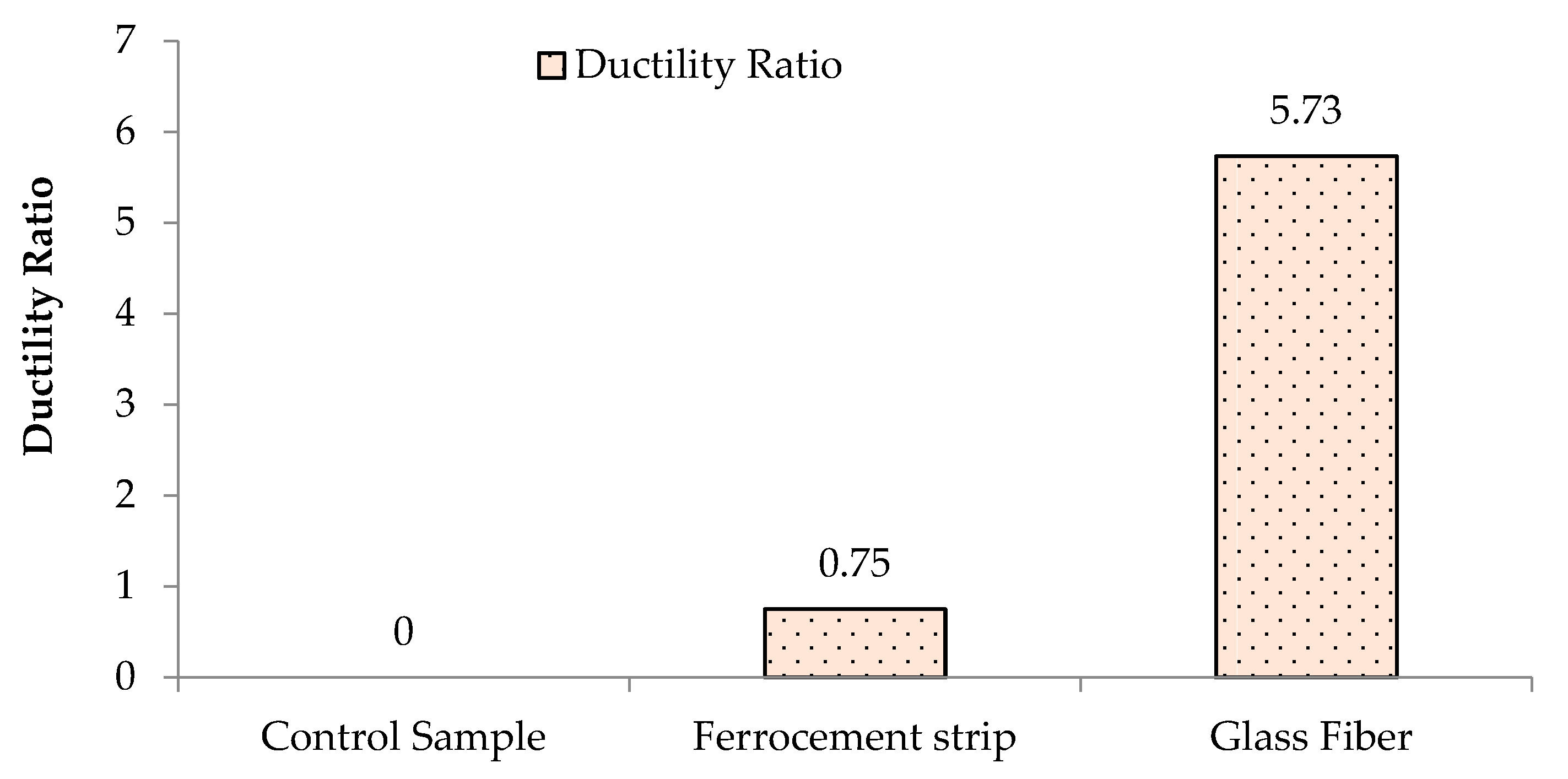
3.3. Stiffness and Ductility of Prisms
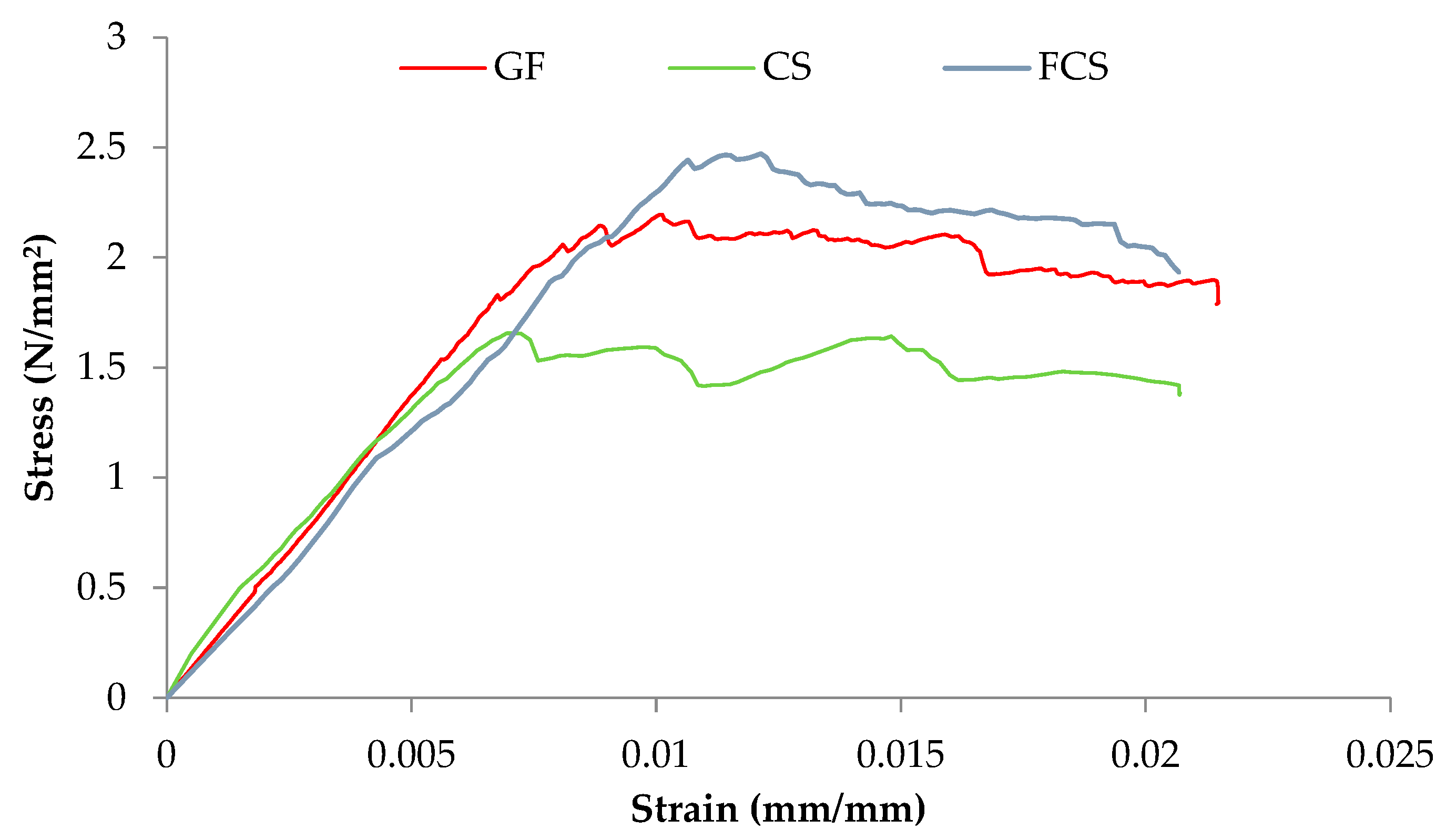
3.4. Elastic Modulus (E) of Prisms
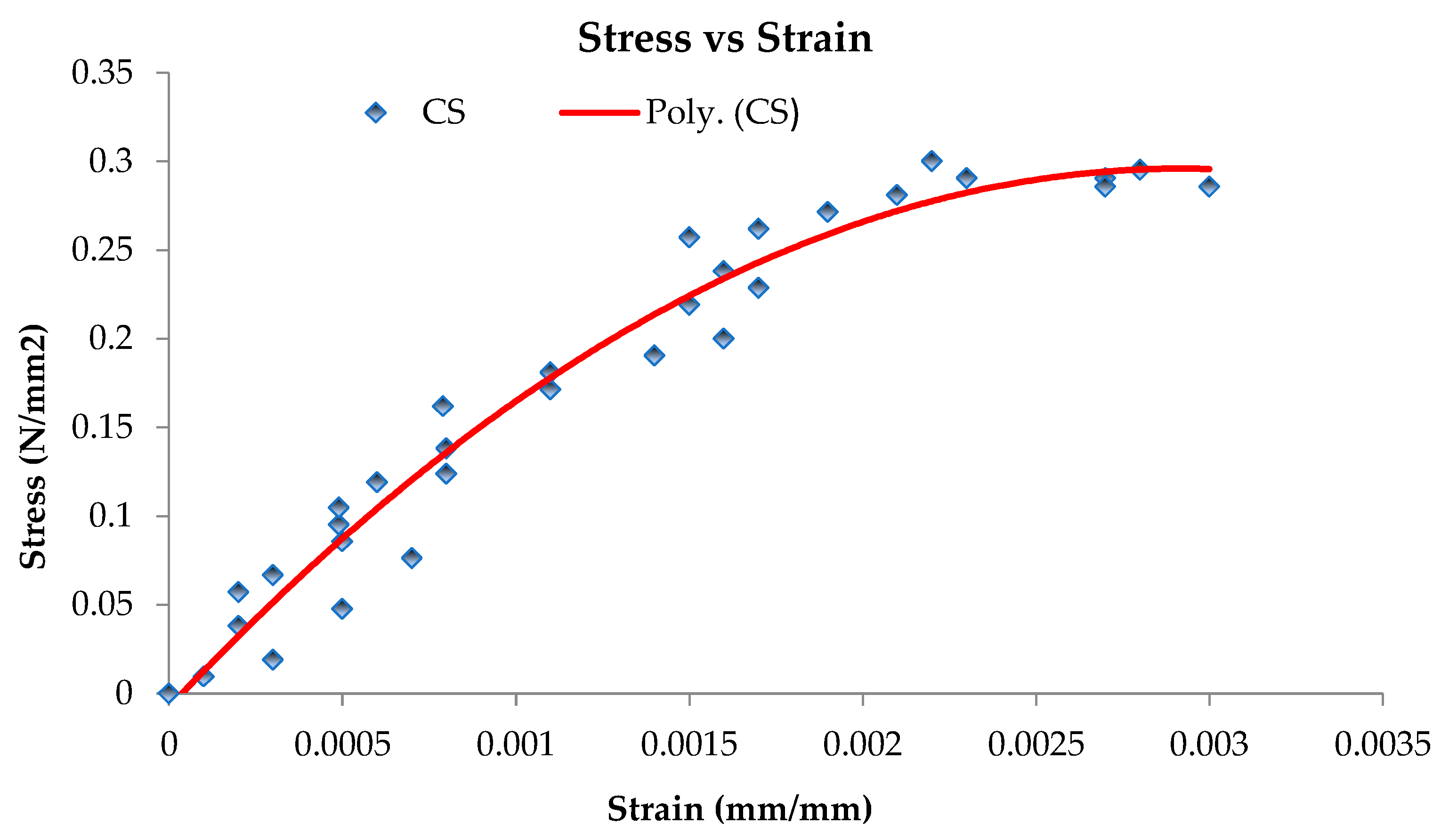
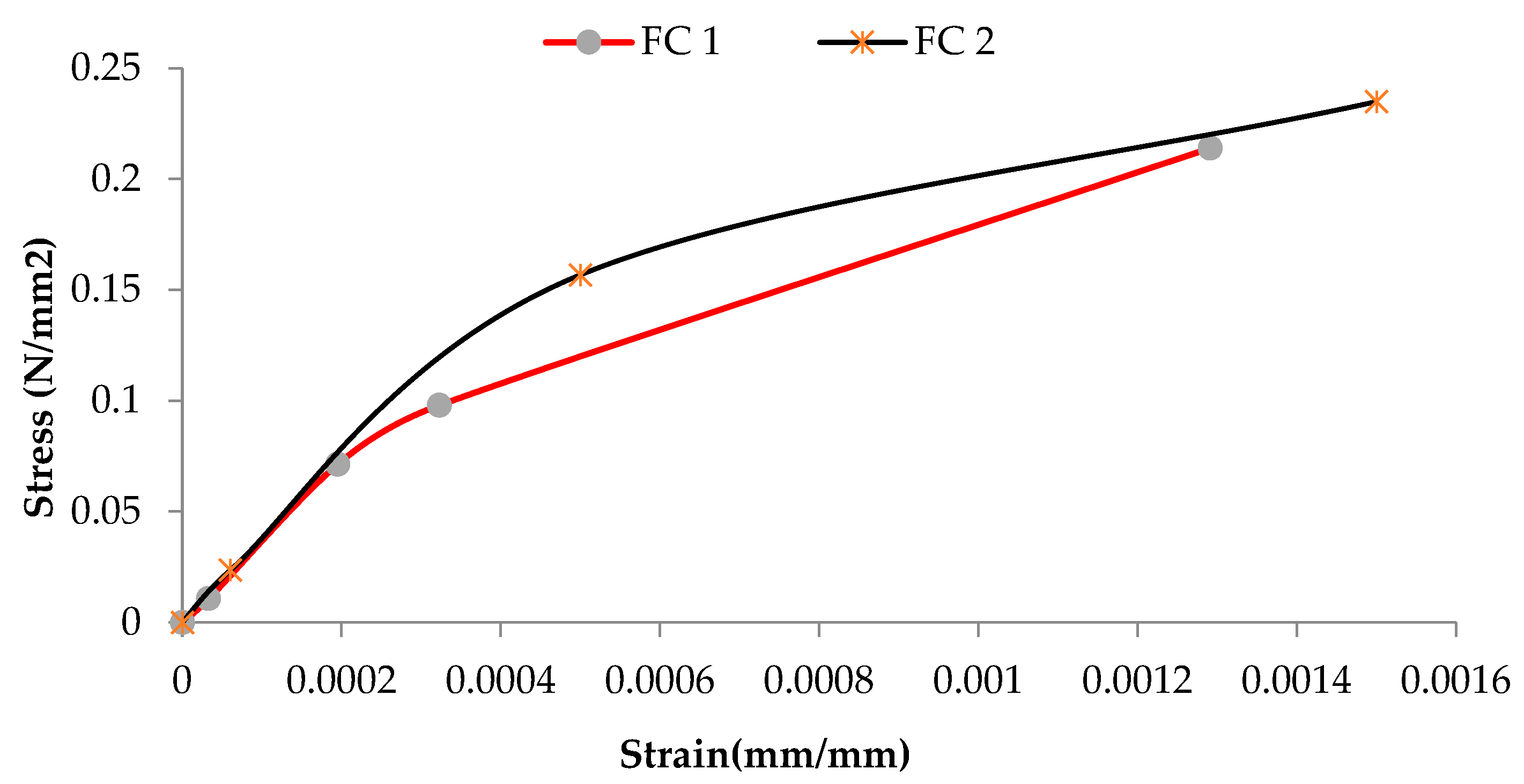
3.5. Shear Modulus (G) of Prisms
4. Conclusions
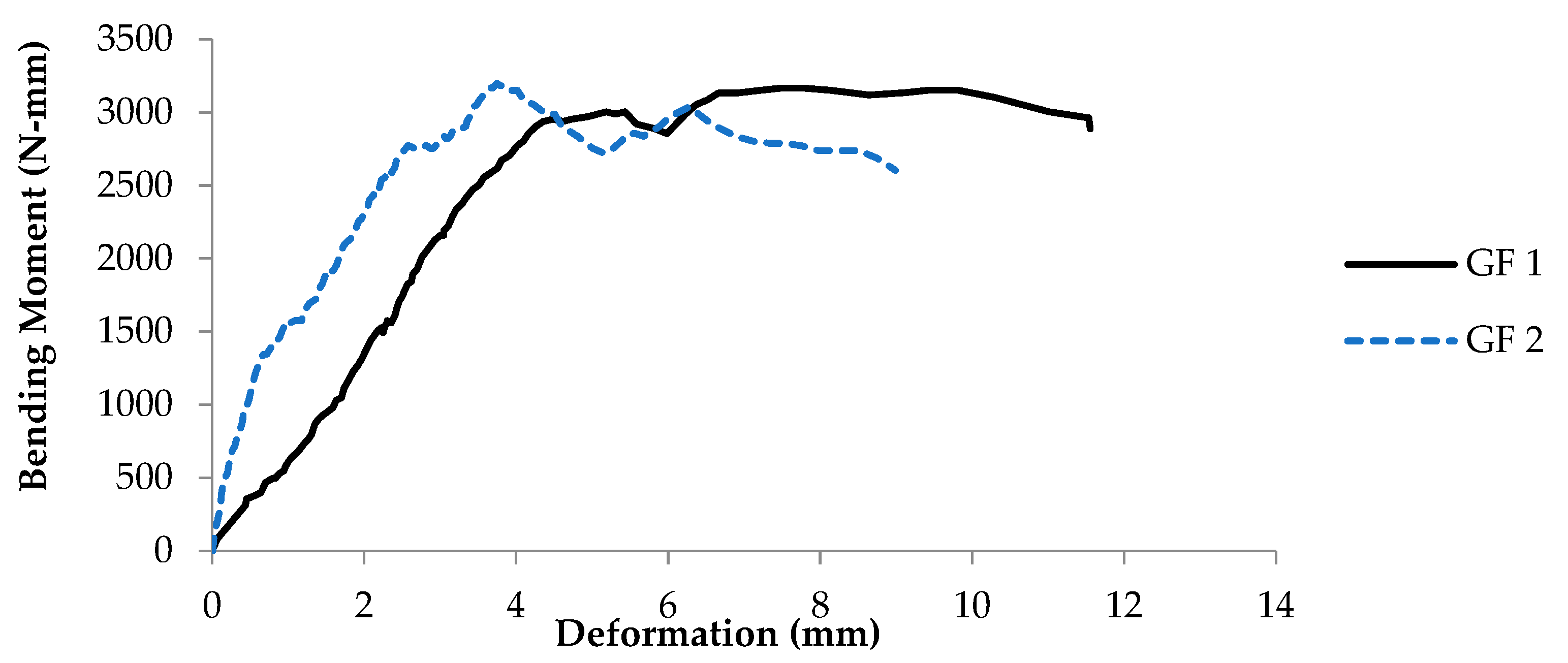
- A significant increase has been observed in the bending moment of prism utilizing glass fiber. It can be seen that the bending moment of a controlled specimen is about 490 N*mm/mm while it raised to 3183 N*mm/mm (average bending moment of two prisms) by means of glass fibers.
- The ultimate load-bearing capacity of a prism using glass fibers has been increased considerably along with the ductility and stiffness ratios. It can be observed that the ductility ratio amplified up to 5.73 times while the stiffness ratio increased up to 4.16 times with the aid of glass fibers.
- It has been observed from the failure pattern that glass fibers de-nailed firstly followed by the cracking of the brick prism.
Author Contributions
Funding
Conflicts of Interest
References
- Vishal, A.; Ali, S.M.; Kumar, M.B.; Harsha, K.; Nagarathinam, L. Comparitive Analysis on Reinforced and Unreinforced Brick Masonry Walls. Int. J. Recent Technol. Eng. 2019, 7, 677–681. [Google Scholar]
- Wu, M.; Wu, G. An analysis of rural households’ earthquake-resistant construction behavior: Evidence from pingliang and yuxi, China. Int. J. Environ. Res. Public Health 2020, 17, 9079. [Google Scholar] [CrossRef]
- Jia, S.; Cao, W.; Zhang, Y.; Yuan, Q. Analysis of the Stiffness Ratio at the Interim Layer of Frame-Supported Multi-Ribbed Lightweight Walls under Low-Reversed Cyclic Loading. Appl. Sci. 2016, 6, 21. [Google Scholar] [CrossRef]
- History.com. 2005 Kashmir Earthquake. History 2018.
- Bank, W. Pakistan 2005 Earthquake Preliminary Damage and Needs Assessment; World Bank: Bretton Woods, NH, USA, 2005. [Google Scholar]
- Calabrese, G. Conservation of historic earth buildings. Woodhead Publ. Ser. Energy 2012, 401–424. [Google Scholar] [CrossRef]
- Ingham, J.; Griffith, M.C. Damage to unreinforced masonry structures by seismic activity. Struct. Eng. 2016, 89, 2–4. [Google Scholar]
- ACT. Evaluation of Earthquake Damaged Concrete and Masonry Wall Buildings; ACT: Redwood City, CA, USA, 1998. [Google Scholar]
- Steneker, P.; Filiatrault, A.; Wiebe, L.; Konstantinidis, D. Retrofit vs. Repair: Economic Benefits and Costs of Seismic Retrofit of Non-Structural Components. In Proceedings of the 4th International Workshop on the Seismic Performance of Non-Structural Elements (SPONSE), Pavia, Italy, 22–23 May 2019; pp. 1–13. [Google Scholar]
- Kaish, A.B.M.A.; Jamil, M.; Raman, S.N.; Zain, M.F.M.; Nahar, L. Ferrocement composites for strengthening of concrete columns: A review. Constr. Build. Mater. 2018, 160, 326–340. [Google Scholar] [CrossRef]
- Fan, W.; Mao, J.; Jin, W.; Zhang, J.; Li, Q. Repair effect of cracked reinforced concrete based on electrochemical rehabilitation technology. J. Build. Eng. 2022, 61, 105211. [Google Scholar] [CrossRef]
- Júlio, E.N.B.S.; Branco, F.A.B.; Silva, V.D. Reinforced concrete jacketing–Interface influence on cyclic loading response. ACI Struct. J. 2008, 105, 471–477. [Google Scholar] [CrossRef]
- Foster, S.J. The application of steel-fibres as concrete reinforcement in Australia: From material to structure. Mater. Struct. Constr. 2009, 42, 1209–1220. [Google Scholar] [CrossRef]
- Łukasz, D. Study of impact of bed joint reinforcement on load-carrying capacity and crack resistance of masonry walls made of calcium silicate units. J. Build. Eng. 2021, 33, 101841. [Google Scholar] [CrossRef]
- Mustafaraj, E.; Yardim, Y.; Corradi, M.; Borri, A. Polypropylene as a retrofitting material for shear walls. Materials 2020, 13, 2503. [Google Scholar] [CrossRef]
- Achudhan, D.; Vandhana, S. Strengthening and Retrofitting of RC Beams Using Fiber Reinforced Polymers. Mater. Today Proc. 2019, 16, 361–366. [Google Scholar] [CrossRef]
- Pareek, K.; Ansari, M.S.; Saha, P.; Verma, S. Seismic Retrofitting of the Structure: An Overview. 2016. [Google Scholar]
- Lee, H.; Jung, W.T.; Chung, W. Post-tension near-surface mounted strengthening system for reinforced concrete beams with changes in concrete condition. Compos. Part B Eng. 2019, 161, 514–529. [Google Scholar] [CrossRef]
- Reinhorn, A.M.; Prawel, S.P.; Jia, Z.H. Experimental Study of Ferrocement As a Seismic Retrofit Material for Masonry Walls. J. Ferrocem. 1985, 15, 247–260. [Google Scholar]
- Farghaly, A.A.; Abdallah, A.M. Evaluation of Seismic Retrofitting Techniques Used in Old Reinforced. IOSR J. Eng. 2015, 4, 1–7. [Google Scholar] [CrossRef]
- Griffith, M.C.; Lam, N.T.; Wilson, L.J.; Doherty, K. Experimental Investigation of Unreinforced Brick Masonry Walls in Flexure. J. Struct. Eng. 2004, 130, 1–10. [Google Scholar] [CrossRef]
- Elgawady, M.A.; Lestuzzi, P.; Badoux, M. A review of conventional seismic retrofitting techniques for URM. In Proceedings of the 13th International Brick and Block Masonry Conference, Amsterdam, The Netherlands, July 4–7 2004; pp. 1–10. [Google Scholar]
- Kahn, L.F. Shotcrete Retrofit for Unreinforced Brick Masonry. 1982. Available online: https://smartech.gatech.edu/handle/1853/35058 (accessed on 30 August 2022).
- Saileysh Sivaraja, S.; Thandavamoorthy, T.S.; Vijayakumar, S.; Mosesaranganathan, S.; Rathnasheela, P.T.; Dasarathy, A.K. GFRP strengthening and applications of unreinforced masonry wall (UMW). Procedia Eng. 2013, 54, 428–439. [Google Scholar] [CrossRef]
- ASTMC67/C67-M18; Standard Test Methods for Sampling and Testing Brick and Structural Clay Tile. ASTM International: West Conshohocken, PA, USA, 2018.
- ASTMC78/C78-M18; Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading). ASTM International: West Conshohocken, PA, USA, 2018.
- ASTM_E519/E519-10; Standard Test Method for Diagonal Tension (Shear) in Masonry Assemblages. American Society for Testing and Materials; ASTM International: West Conshohocken, PA, USA, 2010; pp. 1–5.
- ASTM_E447-74; Standard Test Methods for Compressive Strength Of Masonry Prisms. American Society of Testing Materials; ASTM International: West Conshohocken, PA, USA, 2017.
- Khan, J.; Bhatti, N.; Ansari, A.; Khoso, S.; Wagan, F. Qualitative analysis of baked clay bricks available in Larkana region, Pakistan. Archit. Civ. Eng. Environ. 2014, 7, 41–50. [Google Scholar]
- Mohamed, N.; Farghaly, A.S.; Benmokrane, B.; Neale, K.W. Drift capacity design of shear walls reinforced with glass fiber-reinforced polymer bars. ACI Struct. J. 2014, 111, 1397–1406. [Google Scholar] [CrossRef]
- Paulay, T.; Priestly, M.J. Seismic Design of Reinforced Concrete and Masonry Buildings; John Wiley & Sons, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Muñoz, W.; Mohammad, M.; Salenikovich, A.; Quenneville, P. Determination of Yield Point and Ductility of Timber Assemblies: In Search for a Harmonised Approach. In Proceedings of the Meeting 41 of CIB-W18, St. Andrews, NB, Canada; 2008. [Google Scholar]
- Chang, L.; Messali, F.; Esposito, R. Capacity of unreinforced masonry walls in out-of-plane two-way bending: A review of analytical formulations. Structures 2020, 28, 2431–2447. [Google Scholar] [CrossRef]
- Messali, F.; Ravenshorst, G.; Esposito, R.; Rots, J. Large-Scale Testing Program for the Seismic Characterization of Dutch Masonry Walls. 2017. Available online: http://resolver.tudelft.nl/uuid:7f4baaa0-b1d4-49ad-b41c-584f324c102e (accessed on 1 August 2022).
- Kalali, A.; Kabir, M.Z. Cyclic behavior of perforated masonry walls strengthened with glass fiber reinforced polymers. Sci. Iran. 2012, 19, 151–165. [Google Scholar] [CrossRef]
- Abrams, D. Strength and behavior of unreinforced masonry elements. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992. [Google Scholar]
- Erdal, M. Improving out-of-plane strength and ductility of unreinforced masonry walls in low-rise buildings by centrally applied FRP strip. Int. J. Phys. Sci. 2010, 5, 116–131. [Google Scholar]
- Kazaz, I.; Gulkan, P.; Yakut, A. Deformation Limits for Structural Walls with Confined Boundaries Deformation Limits for Structural Walls with Confined Boundaries. Earthq. Spectra 2007, 28, 1019–1046. [Google Scholar] [CrossRef]
- ASTM_E2126-19; Standard Test Methods for Cyclic (Reversed) Load Test for Shear Resistance of Vertical Elements of the Lateral Force Resisting Systems for Buildings. American Society of Testing Materials; ASTM International: West Conshohocken, PA, USA, 2019.
- Cheah, C.B.; Ramli, M. Composites: Part B The structural behaviour of HCWA ferrocement–reinforced concrete composite slabs. Compos. Part B 2013, 51, 68–78. [Google Scholar] [CrossRef]
- Álvarez-Pérez, J.; Chávez-Gómez, J.H.; Terán-Torres, B.T.; Mesa-Lavista, M.; Balandrano-Vázquez, R. Multifactorial behavior of the elastic modulus and compressive strength in masonry prisms of hollow concrete blocks. Constr. Build. Mater. 2020, 241, 118002. [Google Scholar] [CrossRef]




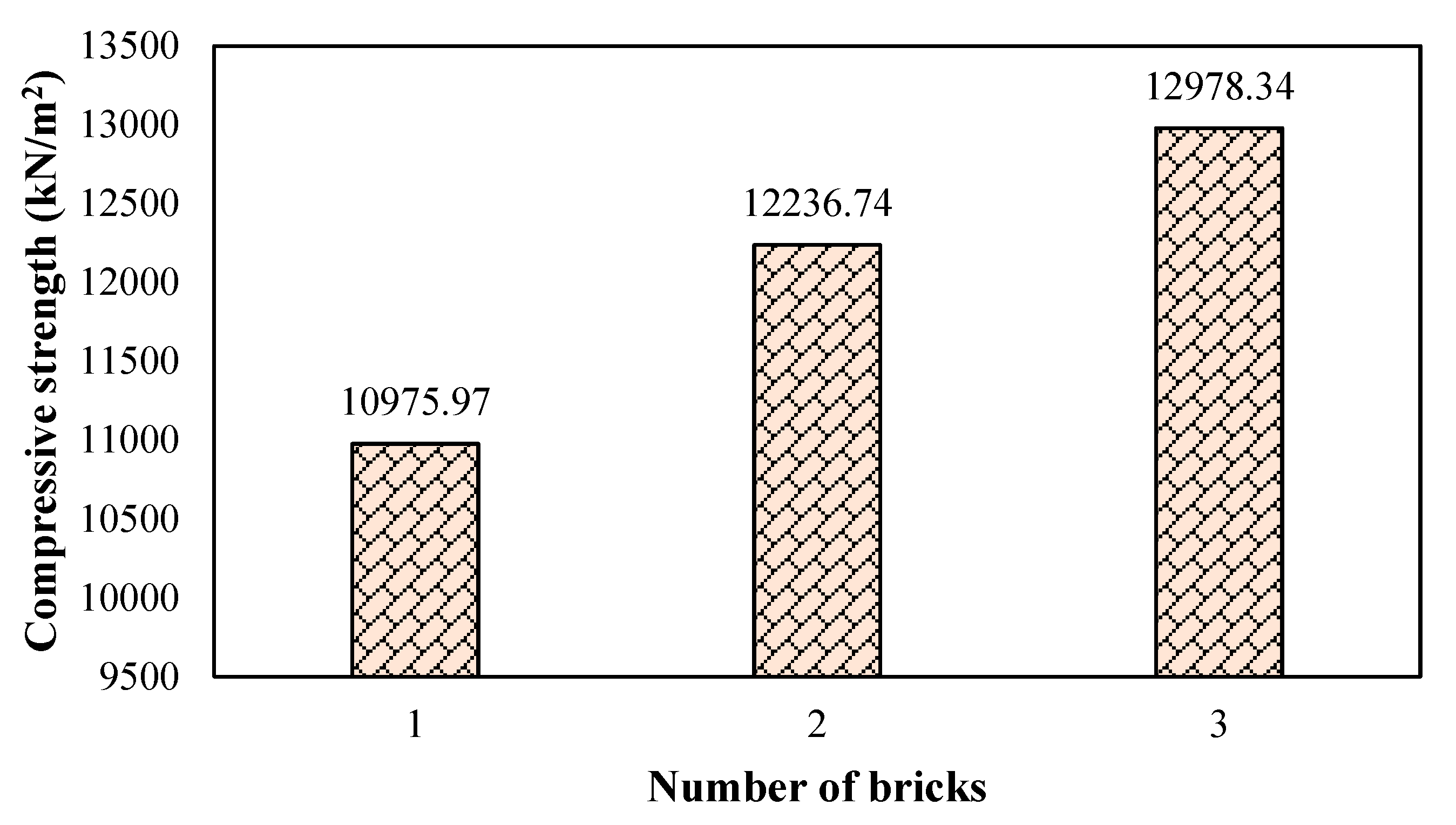

| S. No | Max Load in kN (Tons) | Loaded Area in cm (in) | Compressive Strength in kN/m2 (Psi) | Ave. Strength in kN/m2 (Psi) |
|---|---|---|---|---|
| 1 | 288.95 (29) | 21.5 × 10.2 | 10,975.97 (1591.93) | 12,064.37 (1749.79) |
| 2 | 328.81 (33) | 21.5 × 10.2 | 12,236.74 (1774.79) | |
| 3 | 348.74 (35) | 21.5 × 10.2 | 12,978.34 (1882.35) |
| Test Specimen | Pmax (N) | Pu (N) | Δy (mm) | Δu (mm) | Δmax (mm) |
|---|---|---|---|---|---|
| GF1 | 7563.34 | 7000 | 4 | 11 | 11.36 |
| GF2 | 7640 | 6250 | 1.1 | 8.98 | 9 |
| S. No | Sample | Properties | |||
|---|---|---|---|---|---|
| Max Stress MPa (psi) | Ultimate Strain (mm/mm) | Yield Strain (mm/mm) | E in MPa (psi) | ||
| 1 | CS | 1.657 (240.3) | 0.019 | 0.0015 | 151.5 (21,968) |
| 2 | GF | 2.195 (318.2) | 0.021 | 0.0069 | 266.6 (38,657) |
| 3 | FCS | 2.471 (358.4) | 0.020 | 0.0044 | 248.3 (36,013) |
| S. No | Samples | Properties | ||
|---|---|---|---|---|
| Max Stress in MPa (psi) | Max Strain (mm/mm) | G in MPa (psi) | ||
| 1 | CS | 0.1815 ± 0.167 (26.31) | 0.0013 ± 0.002 | 275 (39,875) |
| 2 | GF | 0.25 (36.25) | 0.0026 ±0.0001 | 227.3 ± 136.08 (32,967) |
| 3 | FCS | 0.224 ± 0.013 (32.55) | 0.0014 ±0.00021 | 393.86 ± 28.52 (57,110) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halim, F.; Ahmad, A.; Adil, M.; Khan, A.; Ghareeb, M.; Alzara, M.; Eldin, S.M.; Alsharari, F.; Yosri, A.M. Investigating the Retrofitting Effect of Fiber-Reinforced Plastic and Steel Mesh Casting on Unreinforced Masonry Walls. Materials 2023, 16, 257. https://doi.org/10.3390/ma16010257
Halim F, Ahmad A, Adil M, Khan A, Ghareeb M, Alzara M, Eldin SM, Alsharari F, Yosri AM. Investigating the Retrofitting Effect of Fiber-Reinforced Plastic and Steel Mesh Casting on Unreinforced Masonry Walls. Materials. 2023; 16(1):257. https://doi.org/10.3390/ma16010257
Chicago/Turabian StyleHalim, Faizan, Afnan Ahmad, Mohammad Adil, Asad Khan, Mohamed Ghareeb, Majed Alzara, Sayed M. Eldin, Fahad Alsharari, and Ahmed M. Yosri. 2023. "Investigating the Retrofitting Effect of Fiber-Reinforced Plastic and Steel Mesh Casting on Unreinforced Masonry Walls" Materials 16, no. 1: 257. https://doi.org/10.3390/ma16010257
APA StyleHalim, F., Ahmad, A., Adil, M., Khan, A., Ghareeb, M., Alzara, M., Eldin, S. M., Alsharari, F., & Yosri, A. M. (2023). Investigating the Retrofitting Effect of Fiber-Reinforced Plastic and Steel Mesh Casting on Unreinforced Masonry Walls. Materials, 16(1), 257. https://doi.org/10.3390/ma16010257










