Clinical Impact of Computational Heart Valve Models
Abstract
1. Introduction
1.1. Chordal Repair/Replacement
1.2. Heart Valve Repairs/Devices
1.3. Repair versus Replacement
1.4. Tissue Engineering
1.5. Imaging Modalities
1.6. Transcatheter Repairs
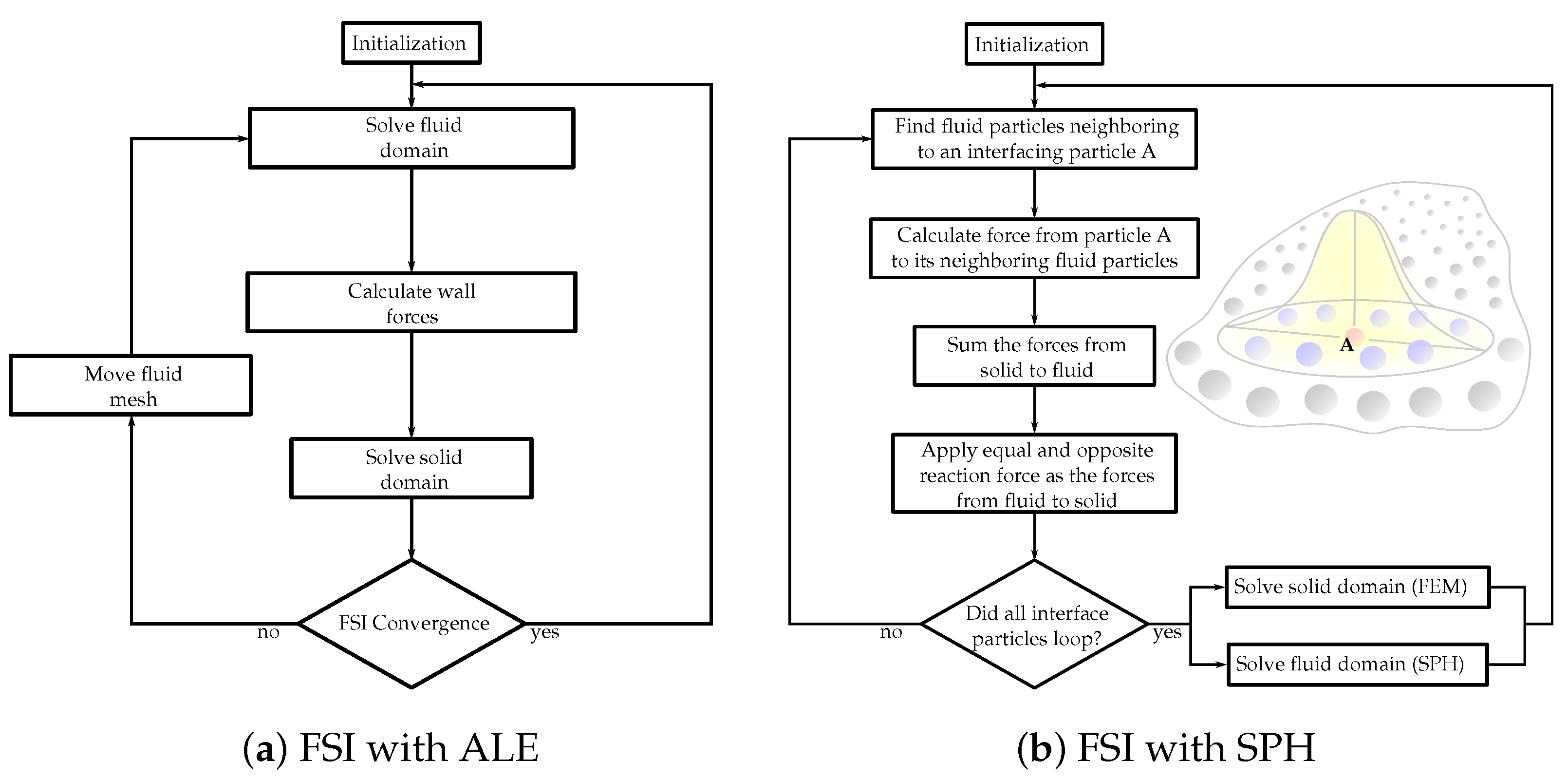
2. Computational Simulations
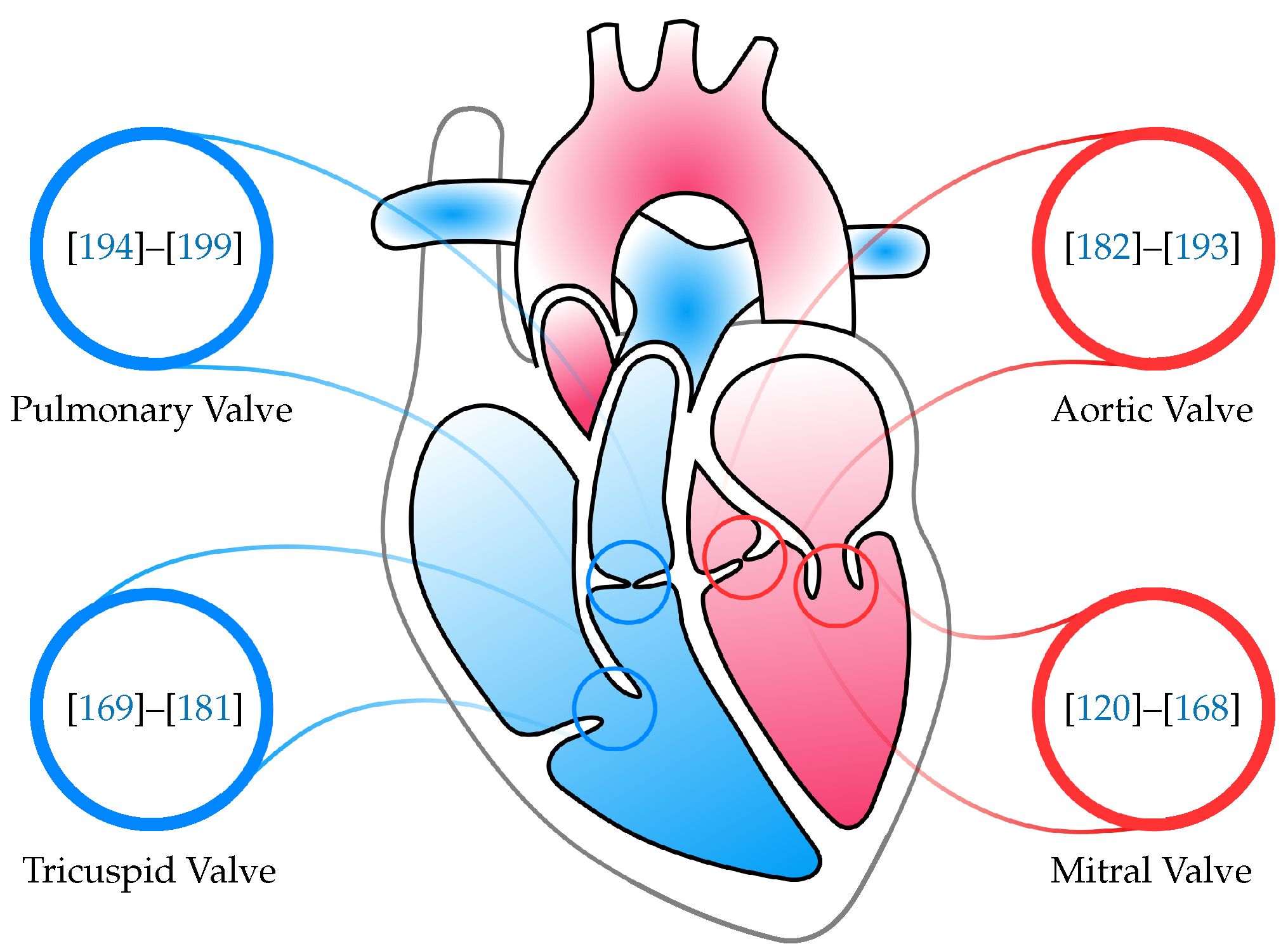
3. Mitral Valve
4. Tricuspid Valve
5. Aortic Valve
6. Pulmonary Valve
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MV | mitral vavle |
| TV | tricuspid valve |
| AV | aortic valve |
| PV | pulmonary valve |
| CFD | computational fluid dynamics |
| ISO | international organization for standardization |
| FDA | food and drug administration |
| FSI | fluid–structure interaction |
| IB | immersed boundary |
| FEM | finite-element method |
| 2D | two-dimensional |
| 3D | three-dimensional |
| CT | computed tomography |
| MRI | magnetic resonance imaging |
| ALE | arbitrary Lagrangian–Eulerian |
| SPH | smoothed-particle hydrodynamics |
| GPU | graphics processing unit |
References
- Fedele, M.; Quarteroni, A. Polygonal surface processing and mesh generation tools for the numerical simulation of the cardiac function. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3435. [Google Scholar] [CrossRef]
- Stephens, S.E.; Kammien, A.J.; Paris, J.C.; Applequist, A.P.; Ingels, N.B.; Jensen, H.K.; Rodgers, D.E.; Cole, C.R.; Wenk, J.F.; Jensen, M.O. In Vitro Mitral Valve Model with Unrestricted Ventricular Access: Using Vacuum to Close the Valve and Enable Static Trans-Mitral Pressure. J. Cardiovasc. Transl. Res. 2022, 1–10. [Google Scholar] [CrossRef]
- Atkins, S.; McNally, A.; Sucosky, P. Mechanobiology in Cardiovascular Disease Management: Potential Strategies and Current Needs. Front. Bioeng. Biotechnol. 2016, 4, 79. [Google Scholar] [CrossRef] [PubMed]
- Dasi, L.P.; Sucosky, P.; De Zelicourt, D.; Sundareswaran, K.; Jimenez, J.; Yoganathan, A.P. Advances in Cardiovascular Fluid Mechanics: Bench to Bedside. Ann. N. Y. Acad. Sci. 2009, 1161, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Addepalli, D.; Chan-Akeley, R. The Intricacies of Computational Medical Research: An Advanced Study Approach. Recent Dev. Med. Med. Res. 2021, 4, 71–83. [Google Scholar] [CrossRef]
- Wei, Z.A.; Sonntag, S.J.; Toma, M.; Singh-Gryzbon, S.; Sun, W. Computational Fluid Dynamics Assessment Associated with Transcatheter Heart Valve Prostheses: A Position Paper of the ISO Working Group. Cardiovasc. Eng. Technol. 2018, 9, 289–299. [Google Scholar] [CrossRef]
- Food and Drug Administration. Assessing the Credibility of Computational Modeling and Simulation in Medical Device Submissions, Draft Guidance for Industry and Food and Drug Administration Staff; U.S. Department of Health and Human Services Food and Drug Administration Center for Devices and Radiological Health: Rockville, MD, USA, 2022.
- Ammarullah, M.I.; Afif, I.Y.; Maula, M.I.; Winarni, T.I.; Tauviqirrahman, M.; Akbar, I.; Basri, H.; van der Heide, E.; Jamari, J. Tresca Stress Simulation of Metal-on-Metal Total Hip Arthroplasty during Normal Walking Activity. Materials 2021, 14, 7554. [Google Scholar] [CrossRef] [PubMed]
- Jamari, J.; Ammarullah, M.; Saad, A.; Syahrom, A.; Uddin, M.; van der Heide, E.; Basri, H. The Effect of Bottom Profile Dimples on the Femoral Head on Wear in Metal-on-Metal Total Hip Arthroplasty. J. Funct. Biomater. 2021, 12, 38. [Google Scholar] [CrossRef]
- Heijman, J.; Sutanto, H.; Crijns, H.J.G.M.; Nattel, S.; Trayanova, A.N. Computational models of atrial fibrillation: Achievements, challenges, and perspectives for improving clinical care. Cardiovasc. Res. 2021, 117, 1682–1699. [Google Scholar] [CrossRef]
- Holmes, J.W.; Lumens, J. Clinical Applications of Patient-Specific Models: The Case for a Simple Approach. J. Cardiovasc. Transl. Res. 2018, 11, 71–79. [Google Scholar] [CrossRef]
- Adams, D.H.; Rosenhek, R.; Falk, V. Degenerative mitral valve regurgitation: Best practice revolution. Eur. Heart J. 2010, 31, 1958–1966. [Google Scholar] [CrossRef] [PubMed]
- Boon, R.; Hazekamp, M.; Hoohenkerk, G.; Rijlaarsdam, M.; Schoof, P.; Koolbergen, D.; Heredia, L.; Dion, R. Artificial chordae for pediatric mitral and tricuspid valve repair. Eur. J. Cardio-Thorac. Surg. 2007, 32, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Bloodworth, C.H.; Einstein, D.R.; Pierce, E.L.; Cochran, R.P.; Yoganathan, A.P.; Kunzelman, K.S. High-resolution subject-specific mitral valve imaging and modeling: Experimental and computational methods. Biomech. Model. Mechanobiol. 2016, 15, 1619–1630. [Google Scholar] [CrossRef]
- Singh-Gryzbon, S.; Sadri, V.; Toma, M.; Pierce, E.L.; Wei, Z.A.; Yoganathan, A.P. Development of a Computational Method for Simulating Tricuspid Valve Dynamics. Ann. Biomed. Eng. 2019, 47, 1422–1434. [Google Scholar] [CrossRef] [PubMed]
- Watton, P.; Luo, X.; Singleton, R.; Wang, X.; Bernacca, G.; Molloy, P.; Wheatley, D. Modelling Chorded Prosthetic Mitral Valves using the Immersed Boundary Method. In Proceedings of the 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Francisco, CA, USA, 1–5 September 2004; Volume 2, pp. 3745–3748. [Google Scholar] [CrossRef]
- Ibrahim, M.; Rao, C.; Savvopoulou, M.; Casula, R.; Athanasiou, T. Outcomes of mitral valve repair using artificial chordae. Eur. J. Cardio-Thorac. Surg. 2013, 45, 593–601. [Google Scholar] [CrossRef]
- Zussa, C.; Polesel, E.; Da Col, U.; Galloni, M.; Valfré, C. Seven-year experience with chordal replacement with expanded polytetrafluoroethylene in floppy mitral valve. J. Thorac. Cardiovasc. Surg. 1994, 108, 37–41. [Google Scholar] [CrossRef]
- Toma, M.; Bloodworth, C.H.; Pierce, E.L.; Einstein, D.R.; Cochran, R.P.; Yoganathan, A.P.; Kunzelman, K.S. Fluid-Structure Interaction Analysis of Ruptured Mitral Chordae Tendineae. Ann. Biomed. Eng. 2016, 45, 619–631. [Google Scholar] [CrossRef]
- Zussa, C.; Frater, R.W.; Polesel, E.; Galloni, M.; Valfré, C. Artificial mitral valve chorde: Experimental and clinical experience. Ann. Thorac. Surg. 1990, 50, 367–373. [Google Scholar] [CrossRef]
- Lobo, F.L.; Takeda, F.R.; Brandão, C.M.D.A.; Braile, D.M.; Jatene, F.B.; Pomerantzeff, P.M.A. Study of the traction resistance of mitral valve chordae tendineae. Clinics 2006, 61, 395–400. [Google Scholar] [CrossRef][Green Version]
- Bortolotti, U.; Celiento, M.; Pratali, S.; Anastasio, G.; Pucci, A. Recurrent mitral regurgitation due to ruptured artificial chordae: Case report and review of the literature. J. Heart Valve Dis. 2012, 21, 440. [Google Scholar]
- Calafiore, A.M.; Refaie, R.; Iacò, A.L.; Asif, M.; Al Shurafa, H.S.; Al-Amri, H.; Romeo, A.; Di Mauro, M. Chordal cutting in ischemic mitral regurgitation: A propensity-matched study. J. Thorac. Cardiovasc. Surg. 2014, 148, 41–46. [Google Scholar] [CrossRef] [PubMed]
- Fayad, G.; Maréchaux, S.; Modine, T.; Azzaoui, R.; Larrue, B.; Ennezat, P.-V.; Bekhti, H.; Decoene, C.; Deklunder, G.; Le Tourneau, T.; et al. Chordal Cutting VIA Aortotomy in Ischemic Mitral Regurgitation: Surgical and Echocardiographic Study. J. Card. Surg. 2008, 23, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Fattouch, K.; Sampognaro, R.; Bianco, G.; Navarra, E.; Moscarelli, M.; Speziale, G.; Ruvolo, G. Implantation of Gore-Tex Chordae on Aortic Valve Leaflet to Treat Prolapse Using “The Chordae Technique”: Surgical Aspects and Clinical Results. Ann. Thorac. Surg. 2008, 85, 2019–2024. [Google Scholar] [CrossRef] [PubMed]
- Athanasiou, T.; Chow, A.; Rao, C.; Aziz, O.; Siannis, F.; Ali, A.; Darzi, A.; Wells, F. Preservation of the mitral valve apparatus: Evidence synthesis and critical reappraisal of surgical techniques. Eur. J. Cardio-Thorac. Surg. 2008, 33, 391–401. [Google Scholar] [CrossRef]
- A Timek, T.; Nielsen, S.L.; Green, G.; Dagum, P.; Bolger, A.F.; Daughters, G.T.; Hasenkam, J.; Ingels, N.B.; Miller, D. Influence of anterior mitral leaflet second-order chordae on leaflet dynamics and valve competence. Ann. Thorac. Surg. 2001, 72, 535–540. [Google Scholar] [CrossRef]
- Colli, A.; Manzan, E.; Rucinskas, K.; Janusauskas, V.; Zucchetta, F.; Zakarkaitė, D.; Aidietis, A.; Gerosa, G. Acute safety and efficacy of the NeoChord procedure. Interact. Cardiovasc. Thorac. Surg. 2015, 20, 575–581. [Google Scholar] [CrossRef]
- A Borger, M.; Yau, T.M.; Rao, V.; E Scully, H.; E David, T. Reoperative mitral valve replacement: Importance of preservation of the subvalvular apparatus. Ann. Thorac. Surg. 2002, 74, 1482–1487. [Google Scholar] [CrossRef]
- Smerup, M.; Funder, J.; Nyboe, C.; Høyer, C.; Pedersen, T.F.; Ribe, L.; Ringgaard, S.; Kim, W.Y.; Pedersen, E.M.; Andersen, N.T.; et al. Strut chordal-sparing mitral valve replacement preserves long-term left ventricular shape and function in pigs. J. Thorac. Cardiovasc. Surg. 2005, 130, 1675–1682. [Google Scholar] [CrossRef]
- Seeburger, J.; Falk, V.; Borger, M.; Passage, J.; Walther, T.; Doll, N.; Mohr, F.W.; Seeburger, J.; Falk, V.; Borger, M.; et al. Chordae Replacement Versus Resection for Repair of Isolated Posterior Mitral Leaflet Prolapse: À Ègalité. Ann. Thorac. Surg. 2009, 87, 1715–1720. [Google Scholar] [CrossRef]
- Daneshmand, M.A.; Milano, C.A.; Rankin, J.S.; Honeycutt, E.F.; Swaminathan, M.; Shaw, L.K.; Smith, P.K.; Glower, D.D. Mitral Valve Repair for Degenerative Disease: A 20-Year Experience. Ann. Thorac. Surg. 2009, 88, 1828–1837. [Google Scholar] [CrossRef]
- Gillinov, A.; Faber, C.; Houghtaling, P.L.; Blackstone, E.H.; Lam, B.-K.; Diaz, R.; Lytle, B.W.; Sabik, J.F.; Cosgrove, D.M. Repair versus replacement for degenerative mitral valve disease with coexisting ischemic heart disease. J. Thorac. Cardiovasc. Surg. 2003, 125, 1350–1361. [Google Scholar] [CrossRef]
- Flameng, W.; Meuris, B.; Herijgers, P.; Herregods, M.-C. Durability of mitral valve repair in Barlow disease versus fibroelastic deficiency. J. Thorac. Cardiovasc. Surg. 2008, 135, 274–282. [Google Scholar] [CrossRef] [PubMed]
- Hata, H.; Fujita, T.; Shimahara, Y.; Sato, S.; Ishibashi-Ueda, H.; Kobayashi, J. A 25-year study of chordal replacement with expanded polytetrafluoroethylene in mitral valve repair. Interact. Cardiovasc. Thorac. Surg. 2014, 20, 463–469. [Google Scholar] [CrossRef][Green Version]
- Tabata, M.; Kasegawa, H.; Fukui, T.; Shimizu, A.; Sato, Y.; Takanashi, S. Long-term outcomes of artificial chordal replacement with tourniquet technique in mitral valve repair: A single-center experience of 700 cases. J. Thorac. Cardiovasc. Surg. 2014, 148, 2033–2038. [Google Scholar] [CrossRef]
- Chiappini, B.; Sanchez, A.; Noirhomme, P.; Verhelst, R.; Rubay, J.; Poncelet, A.; Funken, J.C.; El Khoury, G. Replacement of chordae tendineae with polytetrafluoroethylene (PTFE) sutures in mitral valve repair: Early and long-term results. J. Heart Valve Dis. 2006, 15, 657. [Google Scholar] [PubMed]
- Garcia-Villarreal, O.A. eComment. Let’s get real: The problem is how to safely measure the neochordae. Interact. Cardiovasc. Thorac. Surg. 2015, 20, 469. [Google Scholar] [CrossRef][Green Version]
- Savic, V.; Pozzoli, A.; Gülme, G.; Demir, H.; Batinkov, N.; Kuwata, S.; Weber, A.; Vogel, R.; Tanner, F.; Zuber, M.; et al. Transcatheter mitral valve chord repair. Ann. Cardiothorac. Surg. 2018, 7, 731–740. [Google Scholar] [CrossRef]
- Maisano, F.; Cioni, M.; Seeburger, J.; Falk, V.; Mohr, F.W.; Mack, M.J.; Alfieri, O.; Vanermen, H. Beating-heart implantation of adjustable length mitral valve chordae: Acute and chronic experience in an animal model. Eur. J. Cardio-Thorac. Surg. 2011, 40, 840–847. [Google Scholar] [CrossRef]
- Weber, A.; Hurni, S.; Vandenberghe, S.; Wahl, A.; Aymard, T.; Vogel, R.; Carrel, T. Ideal site for ventricular anchoring of artificial chordae in mitral regurgitation. J. Thorac. Cardiovasc. Surg. 2012, 143, S78–S81. [Google Scholar] [CrossRef][Green Version]
- Jensen, H.; Jensen, M.O.; Vind-Kezunovic, S.; Vestergaard, R.; Ringgaard, S.; Smerup, M.H.; Hønge, J.L.; Hasenkam, J.M.; Nielsen, S.L. Surgical relocation of the papillary muscles in functional ischemic mitral regurgitation: What are the forces of the relocation stitches acting on the myocardium? J. Heart Valve Dis. 2013, 22, 524–531. [Google Scholar]
- Jensen, M.O.; Jensen, H.; Honge, J.L.; Hans, N.; Hasenkam, J.M.; Nielsen, S.L. External approach to in vivo force measurement on mitral valve traction suture. J. Biomech. 2012, 45, 908–912. [Google Scholar] [CrossRef] [PubMed]
- Yousefnia, M.A.; Dehestani, A.; Saidi, B.; Roshanali, F.; Mandegar, M.H.; Alaeddini, F. Papillary Muscle Repositioning in Valve Replacement for Left Ventricular Dysfunction: Ischemic Mitral Regurgitation. Ann. Thorac. Surg. 2010, 90, 497–502. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.-H.; Czer, L.S.; Soukiasian, H.J.; De Robertis, M.; Magliato, K.E.; Blanche, C.; Raissi, S.S.; Mirocha, J.; Siegel, R.J.; Kass, R.M.; et al. Ischemic Mitral Regurgitation: Revascularization Alone Versus Revascularization and Mitral Valve Repair. Ann. Thorac. Surg. 2005, 79, 1895–1901. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Einstein, D.R.; Kohli, K.; Caroll, S.L.; Iv, C.H.B.; Cochran, R.P.; Kunzelman, K.S.; Yoganathan, A.P.; Bloodworth, C. Effect of Edge-to-Edge Mitral Valve Repair on Chordal Strain: Fluid-Structure Interaction Simulations. Biology 2020, 9, 173. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, J.H.; Liou, S.W.; Padala, M.; He, Z.; Sacks, M.; Gorman, R.C.; Gorman, J.H.; Yoganathan, A.P. A saddle-shaped annulus reduces systolic strain on the central region of the mitral valve anterior leaflet. J. Thorac. Cardiovasc. Surg. 2007, 134, 1562–1568. [Google Scholar] [CrossRef]
- Sidiki, A.I.; Faybushevich, A.G.; Lishchuk, A.N.; Koltunov, A.N.; Roshchina, E.A. The Carpentier-Edwards Classic And Physio Annuloplasty Rings in Repair of Degenerative Mitral Valve Disease: A Retrospective Study. J. Saudi Heart Assoc. 2020, 32, 224–232. [Google Scholar] [CrossRef]
- Accola, K.D.; Scott, M.L.; Thompson, P.A.; Palmer, G.J.; Sand, M.E.; Ebra, G. Midterm Outcomes Using the Physio Ring in Mitral Valve Reconstruction: Experience in 492 Patients. Ann. Thorac. Surg. 2005, 79, 1276–1283. [Google Scholar] [CrossRef]
- A Tibayan, F.; Rodriguez, F.; Langer, F.; Zasio, M.K.; Bailey, L.; Liang, D.; Daughters, G.T.; Ingels, N.B.; Miller, D. Does septal-lateral annular cinching work for chronic ischemic mitral regurgitation? J. Thorac. Cardiovasc. Surg. 2004, 127, 654–663. [Google Scholar] [CrossRef][Green Version]
- 2006 WRITING COMMITTEE MEMBERS; Bonow, R.O.; Carabello, B.A.; Chatterjee, K.; De Leon, A.C.; Faxon, D.P.; Freed, M.D.; Gaasch, W.H.; Lytle, B.W.; Nishimura, R.A.; et al. 2008 Focused Update Incorporated Into the ACC/AHA 2006 Guidelines for the Management of Patients with Valvular Heart Disease. Circulation 2008, 118, e523–e661. [Google Scholar] [CrossRef]
- Romano, A.M.; Bolling, S.F. Mitral valve repair as an alternative treatment for heart failure patients. Heart Fail. Monit. 2003, 4, 7–12. [Google Scholar]
- McGee, E.C.; Gillinov, A.M.; Blackstone, E.H.; Rajeswaran, J.; Cohen, G.; Najam, F.; Shiota, T.; Sabik, J.F.; Lytle, B.W.; McCarthy, P.M.; et al. Recurrent mitral regurgitation after annuloplasty for functional ischemic mitral regurgitation. J. Thorac. Cardiovasc. Surg. 2004, 128, 916–924. [Google Scholar] [CrossRef] [PubMed]
- Hung, J.; Papakostas, L.; Tahta, S.A.; Hardy, B.G.; Bollen, B.A.; Duran, C.M.; Levine, R.A. Mechanism of Recurrent Ischemic Mitral Regurgitation After Annuloplasty. Circulation 2004, 110, II-85–II-90. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, A.; A Tahta, S.; Duran, C.M. Failure of reduction annuloplasty for functional ischemic mitral regurgitation. J. Heart Valve Dis. 2004, 13, 390–398. [Google Scholar] [PubMed]
- Gelsomino, S.; Lorusso, R.; De Cicco, G.; Capecchi, I.; Rostagno, C.; Caciolli, S.; Romagnoli, S.; Da Broi, U.; Stefàno, P.; Gensini, G.F. Five-year echocardiographic results of combined undersized mitral ring annuloplasty and coronary artery bypass grafting for chronic ischaemic mitral regurgitation. Eur. Heart J. 2007, 29, 231–240. [Google Scholar] [CrossRef]
- A Tahta, S.; Oury, J.H.; Maxwell, J.M.; Hiro, S.P.; Duran, C.M.G. Outcome after mitral valve repair for functional ischemic mitral regurgitation. J. Heart Valve Dis. 2002, 11, 11–18. [Google Scholar]
- Yousefnia, M.A.; Mandegar, M.H.; Roshanali, F.; Alaeddini, F.; Amouzadeh, F. Papillary Muscle Repositioning in Mitral Valve Replacement in Patients With Left Ventricular Dysfunction. Ann. Thorac. Surg. 2007, 83, 958–963. [Google Scholar] [CrossRef]
- Minardi, G.; Manzara, C.; Pulignano, G.; Luzi, G.; Maselli, D.; Casali, G.; Musumeci, F. Rest and Dobutamine stress echocardiography in the evaluation of mid-term results of mitral valve repair in Barlow’s disease. Cardiovasc. Ultrasound 2007, 5, 17. [Google Scholar] [CrossRef]
- Seeburger, J.; Borger, M.; Doll, N.; Walther, T.; Passage, J.; Falk, V.; Mohr, F.W. Comparison of outcomes of minimally invasive mitral valve surgery for posterior, anterior and bileaflet prolapse. Eur. J. Cardio-Thorac. Surg. 2009, 36, 532–538. [Google Scholar] [CrossRef]
- Minami, K.; Kado, H.; Sai, S.; Tatewaki, H.; Shiokawa, Y.; Nakashima, A.; Fukae, K.; Hirose, H. Midterm results of mitral valve repair with artificial chordae in children. J. Thorac. Cardiovasc. Surg. 2005, 129, 336–342. [Google Scholar] [CrossRef][Green Version]
- Croft, L.R.; Jimenez, J.H.; Gorman, R.C.; Gorman, J.H.; Yoganathan, A.P. Efficacy of the Edge-to-Edge Repair in the Setting of a Dilated Ventricle: An In Vitro Study. Ann. Thorac. Surg. 2007, 84, 1578–1584. [Google Scholar] [CrossRef]
- Espino, D.M.; Hukins, D.W.L.; Shepherd, D.E.T.; Buchan, K.G. Mitral valve repair: An in-vitro comparison of the effect of surgical repair on the pressure required to cause mitral valve regurgitation. J. Heart Valve Dis. 2006, 15, 375–381. [Google Scholar] [PubMed]
- Melillo, F.; Baldetti, L.; Beneduce, A.; Agricola, E.; Margonato, A.; Godino, C. Mitral valve surgery after a failed MitraClip procedure. Interact. Cardiovasc. Thorac. Surg. 2020, 32, 380–385. [Google Scholar] [CrossRef] [PubMed]
- Askov, J.B.; Honge, J.L.; Jensen, M.O.; Nygaard, H.; Hasenkam, J.M.; Nielsen, S.L. Significance of force transfer in mitral valve–left ventricular interaction: In vivo assessment. J. Thorac. Cardiovasc. Surg. 2013, 145, 1635–1641.e1. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Jensen, M.; Einstein, D.R.; Yoganathan, A.P.; Cochran, R.P.; Kunzelman, K.S. Fluid–Structure Interaction Analysis of Papillary Muscle Forces Using a Comprehensive Mitral Valve Model with 3D Chordal Structure. Ann. Biomed. Eng. 2015, 44, 942–953. [Google Scholar] [CrossRef]
- Dalrymple-Hay, M.J.; Bryant, M.; A Jones, R.; Langley, S.M.; A Livesey, S.; Monro, J.L. Degenerative mitral regurgitation: When should we operate? Ann. Thorac. Surg. 1998, 66, 1579–1583. [Google Scholar] [CrossRef]
- Enriquez-Sarano, M.; Akins, C.W.; Vahanian, A. Mitral regurgitation. Lancet 2009, 373, 1382–1394. [Google Scholar] [CrossRef]
- Flameng, W.; Herijgers, P.; Bogaerts, K. Recurrence of Mitral Valve Regurgitation After Mitral Valve Repair in Degenerative Valve Disease. Circulation 2003, 107, 1609–1613. [Google Scholar] [CrossRef]
- Asakai, H.; Kaneko, Y.; Kaneko, M.; Misaki, Y.; Achiwa, I.; Hirata, Y.; Kato, H. Acute Progressive Mitral Regurgitation Resulting From Chordal Rupture in Infants. Pediatr. Cardiol. 2011, 32, 634–638. [Google Scholar] [CrossRef]
- Maslow, A.D.; Poppas, A.; Apostolidou, E. Primary mitral valve regurgitation: Update and review. Glob. Cardiol. Sci. Pract. 2017, 2017, e201703. [Google Scholar] [CrossRef]
- Northrup, W.F. Mitral valve repair: We must do a better job. Curr. Cardiol. Rep. 2005, 7, 94–100. [Google Scholar] [CrossRef]
- Suri, R.M.; Schaff, H.V.; Dearani, J.A.; Sundt, T.M.; Daly, R.C.; Mullany, C.J.; Enriquez-Sarano, M.; Orszulak, T.A. Recurrent mitral regurgitation after repair: Should the mitral valve be re-repaired? J. Thorac. Cardiovasc. Surg. 2006, 132, 1390–1397. [Google Scholar] [CrossRef] [PubMed]
- Aphram, G.; De Kerchove, L.; Mastrobuoni, S.; Navarra, E.; Solari, S.; Tamer, S.; Baert, J.; Poncelet, A.; Rubay, J.; Astarci, P.; et al. Re-repair of the failed mitral valve: Insights into aetiology and surgical management. Eur. J. Cardio-Thorac. Surg. 2018, 54, 774–780. [Google Scholar] [CrossRef] [PubMed]
- Lio, A.; Miceli, A.; Varone, E.; Canarutto, D.; Di Stefano, G.; Della Pina, F.; Gilmanov, D.; Murzi, M.; Solinas, M.; Glauber, M. Mitral valve repair versus replacement in patients with ischaemic mitral regurgitation and depressed ejection fraction: Risk factors for early and mid-term mortality. Interact. Cardiovasc. Thorac. Surg. 2014, 19, 64–69. [Google Scholar] [CrossRef] [PubMed]
- Takagi, H.; Umemoto, T. Similar Survival After Repair vs Replacement for Ischemic Mitral Regurgitation. Semin. Thorac. Cardiovasc. Surg. 2016, 28, 748–756. [Google Scholar] [CrossRef]
- A Moore, R.; Gillinov, A.M.; Burns, D.J.; Pettersson, G.B.; Wierup, P. Techniques for Mitral Valve Re-repair. Oper. Tech. Thorac. Cardiovasc. Surg. 2021, 26, 42–65. [Google Scholar] [CrossRef]
- Veerappan, M.; Cheekoty, P.; Sazzad, F.; Kofidis, T. Mitral valve re-repair vs replacement following failed initial repair: A systematic review and meta-analysis. J. Cardiothorac. Surg. 2020, 15, 304. [Google Scholar] [CrossRef]
- El Oumeiri, B.; Boodhwani, M.; Glineur, D.; De Kerchove, L.; Poncelet, A.; Astarci, P.; Pasquet, A.; Vanoverschelde, J.-L.; Verhelst, R.; Rubay, J.; et al. Extending the Scope of Mitral Valve Repair in Rheumatic Disease. Ann. Thorac. Surg. 2009, 87, 1735–1740. [Google Scholar] [CrossRef]
- Sharma, A.; Agrawal, S.; Goel, S.; Borer, J.S. Surgical Treatment of Ischemic Mitral Regurgitation: Valve Repair Versus Replacement. Curr. Cardiol. Rep. 2017, 19, 3. [Google Scholar] [CrossRef]
- Soares, J.S.; Feaver, K.R.; Zhang, W.; Kamensky, D.; Aggarwal, A.; Sacks, M.S. Biomechanical Behavior of Bioprosthetic Heart Valve Heterograft Tissues: Characterization, Simulation, and Performance. Cardiovasc. Eng. Technol. 2016, 7, 309–351. [Google Scholar] [CrossRef]
- Hetzer, R.; Javier, M.F.D.M.; Wagner, F.; Loebe, M.; Delmo, E.M.J. Organ-saving surgical alternatives to treatment of heart failure. Cardiovasc. Diagn. Ther. 2021, 11, 213–225. [Google Scholar] [CrossRef]
- Winston, T.S.; Suddhapas, K.; Wang, C.; Ramos, R.; Soman, P.; Ma, Z. Serum-Free Manufacturing of Mesenchymal Stem Cell Tissue Rings Using Human-Induced Pluripotent Stem Cells. Stem Cells Int. 2019, 2019, 5654324. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.J.; Im, H.; Kim, S.H.; Park, J.W.; Jung, Y. Toward Biomimetic Scaffolds for Tissue Engineering: 3D Printing Techniques in Regenerative Medicine. Front. Bioeng. Biotechnol. 2020, 8, 586406. [Google Scholar] [CrossRef] [PubMed]
- Flanagan, T.C.; Pandit, A. Living artificial heart valve alternatives: A review. Eur. Cells Mater. 2003, 6, 28–45. [Google Scholar] [CrossRef]
- Blum, K.M.; Drews, J.D.; Breuer, C.K. Tissue-Engineered Heart Valves: A Call for Mechanistic Studies. Tissue Eng. Part B Rev. 2018, 24, 240–253. [Google Scholar] [CrossRef]
- Butcher, J.T. The root problem of heart valve engineering. Sci. Transl. Med. 2018, 10, eaat5850. [Google Scholar] [CrossRef] [PubMed]
- Emmert, M.Y.; Schmitt, B.A.; Loerakker, S.; Sanders, B.; Spriestersbach, H.; Fioretta, E.S.; Bruder, L.; Brakmann, K.; Motta, S.E.; Lintas, V.; et al. Computational modeling guides tissue-engineered heart valve design for long-term in vivo performance in a translational sheep model. Sci. Transl. Med. 2018, 10, eaan4587. [Google Scholar] [CrossRef] [PubMed]
- Zamorano, J.L.; Badano, L.; Bruce, C.; Chan, K.-L.; Gonçalves, A.; Hahn, R.T.; Keane, M.G.; La Canna, G.; Monaghan, M.J.; Nihoyannopoulos, P.; et al. EAE/ASE recommendations for the use of echocardiography in new transcatheter interventions for valvular heart disease. Eur. Heart J. 2011, 32, 2189–2214. [Google Scholar] [CrossRef]
- Shiota, T. Role of echocardiography for catheter-based management of valvular heart disease. J. Cardiol. 2017, 69, 66–73. [Google Scholar] [CrossRef]
- Zhou, L.; Wei, H.-Y.; Ge, Y.-L.; Ding, Z.-N.; Shi, H.-W. Comparison of the effective orifice area of prosthetic mitral valves using two-dimensional versus three-dimensional transesophageal echocardiography. J. Int. Med. Res. 2021, 49, 300060521997621. [Google Scholar] [CrossRef]
- Chourdakis, E.; Koniari, I.; Kounis, N.G.; Velissaris, D.; Koutsogiannis, N.; Tsigkas, G.; Hauptmann, K.E.; Sontag, B.; Hahalis, G. The role of echocardiography and CT angiography in transcatheter aortic valve implantation patients. J. Geriatr. Cardiol. 2018, 15, 86–94. [Google Scholar] [CrossRef]
- Ryan, L.P.; Jackson, B.M.; Eperjesi, T.J.; Plappert, T.J.; John-Sutton, M.S.; Gorman, R.C.; Gorman, J.H. A methodology for assessing human mitral leaflet curvature using real-time 3-dimensional echocardiography. J. Thorac. Cardiovasc. Surg. 2008, 136, 726–734. [Google Scholar] [CrossRef] [PubMed]
- Tamborini, G.; Mantegazza, V.; Garlaschè, A.; Muratori, M.; Fusini, L.; Ali, S.G.; Cefalù, C.; Italiano, G.; Gripari, P.; Maltagliati, A.; et al. Head to Head Comparison between Different 3-Dimensional Echocardiographic Rendering Tools in the Imaging of Percutaneous Edge-to-Edge Mitral Valve Repair. J. Cardiovasc. Dev. Dis. 2021, 8, 73. [Google Scholar] [CrossRef] [PubMed]
- Kaple, R.K.; Murphy, R.T.; DiPaola, L.M.; Houghtaling, P.L.; Lever, H.M.; Lytle, B.W.; Blackstone, E.H.; Smedira, N.G. Mitral Valve Abnormalities in Hypertrophic Cardiomyopathy: Echocardiographic Features and Surgical Outcomes. Ann. Thorac. Surg. 2008, 85, 1527–1535.e2. [Google Scholar] [CrossRef] [PubMed]
- Morris, M.F.; Pena, A.; Kalya, A.; Sawant, A.C.; Lotun, K.; Byrne, T.; Fang, H.K.; Pershad, A. Predicting paravalvular leak after transcatheter mitral valve replacement using commercially available software modeling. J. Cardiovasc. Comput. Tomogr. 2020, 14, 495–499. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, E.Y.; Jin, G.Y.; Choi, J.B. A Review of the Use of Cardiac Computed Tomography for Evaluating the Mitral Valve before and after Mitral Valve Repair. Korean J. Radiol. 2017, 18, 773–785. [Google Scholar] [CrossRef] [PubMed]
- Feldman, T.; Kar, S.; Elmariah, S.; Smart, S.C.; Trento, A.; Siegel, R.J.; Apruzzese, P.; Fail, P.; Rinaldi, M.J.; Smalling, R.W.; et al. Randomized Comparison of Percutaneous Repair and Surgery for Mitral Regurgitation. J. Am. Coll. Cardiol. 2015, 66, 2844–2854. [Google Scholar] [CrossRef] [PubMed]
- Joseph, K.M.; Nyman, C. Mitral Valve Annuloplasty Failure and Percutaneous Treatment Options. Curr. Cardiol. Rep. 2021, 23, 140. [Google Scholar] [CrossRef]
- Van Mieghem, N.M.; Piazza, N.; Anderson, R.H.; Tzikas, A.; Nieman, K.; De Laat, L.E.; McGhie, J.S.; Geleijnse, M.L.; Feldman, T.; Serruys, P.W.; et al. Anatomy of the Mitral Valvular Complex and Its Implications for Transcatheter Interventions for Mitral Regurgitation. J. Am. Coll. Cardiol. 2010, 56, 617–626. [Google Scholar] [CrossRef]
- Zamorano, J.L.; González-Gómez, A.; Lancellotti, P. Mitral valve anatomy: Implications for transcatheter mitral valve interventions. EuroIntervention 2014, 10, U106–U111. [Google Scholar] [CrossRef]
- Schievano, S.; Kunzelman, K.; A Nicosia, M.; Cochran, R.P.; Einstein, D.R.; Khambadkone, S.; Bonhoeffer, P. Percutaneous mitral valve dilatation: Single balloon versus double balloon. A finite element study. J. Heart Valve Dis. 2009, 18, 28–34. [Google Scholar]
- Ludwig, S.; Rübsamen, N.; Deuschl, F.; Schofer, N.; Kalbacher, D.; Schaefer, A.; Koell, B.; Westermann, D.; Reichenspurner, H.; Blankenberg, S.; et al. Screening for transcatheter mitral valve replacement: A decision tree algorithm. EuroIntervention 2020, 16, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Koell, B.; Kalbacher, D.; Lubos, E. Current devices and interventions in mitral regurgitation. Herz 2021, 46, 419–428. [Google Scholar] [CrossRef] [PubMed]
- Arnold, M.; Haug, J.; Landendinger, M. Tricuspid Annuloplasty: Transcatheter Approaches. Curr. Cardiol. Rep. 2021, 23, 139. [Google Scholar] [CrossRef] [PubMed]
- Grover, R.; Ohana, M.; Arepalli, C.D.; Sellers, S.L.; Mooney, J.; Kueh, S.-H.; Kim, U.; Blanke, P.; Leipsic, J.A. Role of MDCT Imaging in Planning Mitral Valve Intervention. Curr. Cardiol. Rep. 2018, 20, 16. [Google Scholar] [CrossRef] [PubMed]
- Kohli, K.; Wei, Z.A.; Yoganathan, A.P.; Oshinski, J.N.; Leipsic, J.; Blanke, P. Transcatheter Mitral Valve Planning and the Neo-LVOT: Utilization of Virtual Simulation Models and 3D Printing. Curr. Treat. Options Cardiovasc. Med. 2018, 20, 99. [Google Scholar] [CrossRef]
- Yoon, S.-H.; Bleiziffer, S.; Latib, A.; Eschenbach, L.; Ancona, M.; Vincent, F.; Kim, W.-K.; Unbehaum, A.; Asami, M.; Dhoble, A.; et al. Predictors of Left Ventricular Outflow Tract Obstruction After Transcatheter Mitral Valve Replacement. JACC Cardiovasc. Interv. 2019, 12, 182–193. [Google Scholar] [CrossRef]
- Ge, L.; Jones, S.C.; Sotiropoulos, F.; Healy, T.M.; Yoganathan, A.P. Numerical Simulation of Flow in Mechanical Heart Valves: Grid Resolution and the Assumption of Flow Symmetry. J. Biomech. Eng. 2003, 125, 709–718. [Google Scholar] [CrossRef]
- Toma, M.; Oshima, M.; Takagi, S. Decomposition and parallelization of strongly coupled fluid-structure interaction linear subsystems based on the Q1/P0 discretization. J. Comput. Struct. 2016, 173, 84–94. [Google Scholar] [CrossRef]
- Gao, H.; Feng, L.; Qi, N.; Berry, C.; Griffith, B.; Luo, X. A coupled mitral valve—left ventricle model with fluid–structure interaction. Med. Eng. Phys. 2017, 47, 128–136. [Google Scholar] [CrossRef]
- Feng, L.; Gao, H.; Griffith, B.; Niederer, S.A.; Luo, X. Analysis of a coupled fluid-structure interaction model of the left atrium and mitral valve. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3254. [Google Scholar] [CrossRef]
- Peskin, C.S. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977, 25, 220–252. [Google Scholar] [CrossRef]
- Tang, D.; Yang, C.; Kobayashi, S.; Zheng, J.; Vito, R.P. Effect of Stenosis Asymmetry on Blood Flow and Artery Compression: A Three-Dimensional Fluid-Structure Interaction Model. Ann. Biomed. Eng. 2003, 31, 1182–1193. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.; Fong, F.; Wang, D. Computational evaluation of smoothed particle hydrodynamics for implementing blood flow modelling through CT reconstructed arteries. J. Ray Sci. Technol. 2017, 25, 213–232. [Google Scholar]
- Nasar, A. Eulerian and Lagrangian Smoothed Particle Hydrodynamics as Models for the Interaction of Fluids and Flexible Structures in Biomedical Flows. Ph.D. Thesis, The University of Manchester (United Kingdom), PQDT-UK & Ireland, Manchester, UK, 2016. [Google Scholar]
- Hron, J.; Mádlík, M. Fluid-structure interaction with applications in biomechanics. Nonlinear Anal. Real World Appl. 2007, 8, 1431–1458. [Google Scholar] [CrossRef]
- Al-Saad, M.; Suarez, C.A.; Obeidat, A.; Bordas, S.P.A.; Kulasegaram, S. Application of Smooth Particle Hydrodynamics Method for Modelling Blood Flow with Thrombus Formation. Comput. Model. Eng. Sci. 2020, 122, 831–862. [Google Scholar] [CrossRef]
- Le, T.B.; Usta, M.; Aidun, C.; Yoganathan, A.; Sotiropoulos, F. Computational Methods for Fluid-Structure Interaction Simulation of Heart Valves in Patient-Specific Left Heart Anatomies. Fluids 2022, 7, 94. [Google Scholar] [CrossRef]
- Seo, J.H.; Vedula, V.; Abraham, T.; Lardo, A.C.; Dawoud, F.; Luo, H.; Mittal, R. Effect of the mitral valve on diastolic flow patterns. Phys. Fluids 2014, 26, 121901. [Google Scholar] [CrossRef]
- Al-Atabi, M.; Espino, D.M.; Hukins, D.W.L. Computer and Experimental Modelling of Blood Flow through the Mitral Valve of the Heart. J. Biomech. Sci. Eng. 2010, 5, 78–84. [Google Scholar] [CrossRef][Green Version]
- Domenichini, F.; Pedrizzetti, G. Asymptotic Model of Fluid–Tissue Interaction for Mitral Valve Dynamics. Cardiovasc. Eng. Technol. 2014, 6, 95–104. [Google Scholar] [CrossRef]
- Govindarajan, V.; Mousel, J.; Udaykumar, H.S.; Vigmostad, S.C.; McPherson, D.D.; Kim, H.; Chandran, K.B. Synergy between Diastolic Mitral Valve Function and Left Ventricular Flow Aids in Valve Closure and Blood Transport during Systole. Sci. Rep. 2018, 8, 6187. [Google Scholar] [CrossRef]
- Bavo, A.; Pouch, A.; Degroote, J.; Vierendeels, J.; Gorman, J.; Gorman, R.; Segers, P. Patient-specific CFD models for intraventricular flow analysis from 3D ultrasound imaging: Comparison of three clinical cases. J. Biomech. 2016, 50, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Hassani, K.; Karimi, A.; Dehghani, A.; Golpaygani, A.T.; Abdi, H.; Espino, D.M. Development of a fluid-structure interaction model to simulate mitral valve malcoaptation. Perfusion 2018, 34, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Khalafvand, S.S.; Xu, F.; Westenberg, J.; Gijsen, F.; Kenjeres, S. Intraventricular blood flow with a fully dynamic mitral valve model. Comput. Biol. Med. 2018, 104, 197–204. [Google Scholar] [CrossRef] [PubMed]
- Rego, B.V.; Khalighi, A.H.; Drach, A.; Lai, E.K.; Pouch, A.M.; Gorman, R.C.; Gorman, J.H.; Sacks, M.S. A noninvasive method for the determination of in vivo mitral valve leaflet strains. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3142. [Google Scholar] [CrossRef]
- Ross, C.J.; Hsu, M.-C.; Baumwart, R.; Mir, A.; Burkhart, H.M.; Holzapfel, G.A.; Wu, Y.; Lee, C.-H. Quantification of load-dependent changes in the collagen fiber architecture for the strut chordae tendineae-leaflet insertion of porcine atrioventricular heart valves. Biomech. Model. Mechanobiol. 2020, 20, 223–241. [Google Scholar] [CrossRef]
- Toma, M.; Einstein, D.R.; Iv, C.H.B.; Cochran, R.P.; Yoganathan, A.P.; Kunzelman, K.S. Fluid-structure interaction and structural analyses using a comprehensive mitral valve model with 3D chordal structure. Int. J. Numer. Methods Biomed. Eng. 2016, 33, e2815. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.; Caballero, A.; McKay, R.; Primiano, C.; Sun, W. Fully-coupled fluid-structure interaction simulation of the aortic and mitral valves in a realistic 3D left ventricle model. PLoS ONE 2017, 12, e0184729. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Primiano, C.; Hashim, S.; Sun, W. New insights into mitral heart valve prolapse after chordae rupture through fluid–structure interaction computational modeling. Sci. Rep. 2018, 8, 17306. [Google Scholar] [CrossRef]
- Mao, W.; Caballero, A.; Hahn, R.T.; Sun, W. Comparative quantification of primary mitral regurgitation by computer modeling and simulated echocardiography. Am. J. Physiol. Circ. Physiol. 2020, 318, H547–H557. [Google Scholar] [CrossRef]
- Biffi, B.; Gritti, M.; Grasso, A.; Milano, E.G.; Fontana, M.; Alkareef, H.; Davar, J.; Jeetley, P.; Whelan, C.; Anderson, S.; et al. A workflow for patient-specific fluid–structure interaction analysis of the mitral valve: A proof of concept on a mitral regurgitation case. Med. Eng. Phys. 2019, 74, 153–161. [Google Scholar] [CrossRef]
- Toma, M.; Einstein, D.R.; Iv, C.H.B.; Kohli, K.; Cochran, R.P.; Kunzelman, K.S.; Yoganathan, A.P. Fluid-Structure Interaction Analysis of Subject-Specific Mitral Valve Regurgitation Treatment with an Intra-Valvular Spacer. Prosthesis 2020, 2, 65–75. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Hahn, R.T.; Sun, W. A Comprehensive Engineering Analysis of Left Heart Dynamics After MitraClip in a Functional Mitral Regurgitation Patient. Front. Physiol. 2020, 11, 432. [Google Scholar] [CrossRef] [PubMed]
- Caballero, A.; Mao, W.; McKay, R.; Sun, W. Transapical mitral valve repair with neochordae implantation: FSI analysis of neochordae number and complexity of leaflet prolapse. Int. J. Numer. Methods Biomed. Eng. 2019, 36, e3297. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.; Li, K.; Sun, W. Fluid–Structure Interaction Study of Transcatheter Aortic Valve Dynamics Using Smoothed Particle Hydrodynamics. Cardiovasc. Eng. Technol. 2016, 7, 374–388. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Sun, W. The impact of balloon-expandable transcatheter aortic valve replacement on concomitant mitral regurgitation: A comprehensive computational analysis. J. R. Soc. Interface 2019, 16, 20190355. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Sun, W. The Impact of Self-Expandable Transcatheter Aortic Valve Replacement on Concomitant Functional Mitral Regurgitation: A Comprehensive Engineering Analysis. Struct. Heart 2020, 4, 179–191. [Google Scholar] [CrossRef]
- Dabiri, Y.; Yao, J.; Sack, K.; Kassab, G.S.; Guccione, J.M. Tricuspid valve regurgitation decreases after mitraclip implantation: Fluid structure interaction simulation. Mech. Res. Commun. 2019, 97, 96–100. [Google Scholar] [CrossRef]
- Durrwachter, J. Hemodynamics of the Left Ventricle: Validation of a Smoothed-Particle Hydrodynamics Fluid-Structure Interaction Model. Master’s Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2016. [Google Scholar]
- Yuan, Q.; Ye, X. A New Way to Simulate the Fluid Structure Interaction between the Bioprosthetic Heart Valve and Blood: FE-SPH Method; Mechanical Science and Engineering IV; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; Volume 472, pp. 125–130. [Google Scholar]
- Marom, G.; Mayo, R.P.; Again, N.; Raanani, E. Numerical Biomechanics Models of the Interaction Between a Novel Transcatheter Mitral Valve Device and the Subvalvular Apparatus. Innov. Technol. Tech. Cardiothorac. Vasc. Surg. 2021, 16, 327–333. [Google Scholar] [CrossRef]
- He, S.; Weston, M.W.; Lemmon, J.; Jensen, M.; Levine, R.A.; Yoganathan, A.P. Geometric distribution of chordae tendineae: An important anatomic feature in mitral valve function. J. Heart Valve Dis. 2000, 9, 495–501. [Google Scholar]
- Kunzelman, K.S.; Cochran, R.P. Mechanical properties of basal and marginal mitral valve chordae tendineae. ASAIO Trans. 1990, 36, M405–M408. [Google Scholar]
- Alharbi, Y.; Otton, J.; Muller, D.W.; Geelan-Small, P.; Lovell, N.H.; Al Abed, A.; Dokos, S. Predicting the outcome of transcatheter mitral valve implantation using image-based computational models. J. Cardiovasc. Comput. Tomogr. 2020, 14, 335–342. [Google Scholar] [CrossRef] [PubMed]
- Pasta, S.; Cannata, S.; Gentile, G.; Agnese, V.; Pilato, M.; Gandolfo, C. Simulation of left ventricular outflow tract (LVOT) obstruction in transcatheter mitral valve-in-ring replacement. Med. Eng. Phys. 2020, 82, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Fumagalli, I.; Fedele, M.; Vergara, C.; Dede’, L.; Ippolito, S.; Nicolò, F.; Antona, C.; Scrofani, R.; Quarteroni, A. An image-based computational hemodynamics study of the Systolic Anterior Motion of the mitral valve. Comput. Biol. Med. 2020, 123, 103922. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Song, H.; Yang, Y.; Wu, Z.; Hu, R.; Chen, J.; Guo, J.; Wang, Y.; Jia, D.; Cao, S.; et al. Hemodynamic testing using three-dimensional printing and computational fluid dynamics preoperatively may provide more information in mitral repair than traditional image dataset. Ann. Transl. Med. 2021, 9, 632. [Google Scholar] [CrossRef]
- Lantz, J.; Bäck, S.; Carlhäll, C.-J.; Bolger, A.; Persson, A.; Karlsson, M.; Ebbers, T. Impact of prosthetic mitral valve orientation on the ventricular flow field: Comparison using patient-specific computational fluid dynamics. J. Biomech. 2020, 116, 110209. [Google Scholar] [CrossRef]
- Galili, L.; Zeira, A.W.; Marom, G. Numerical biomechanics modelling of indirect mitral annuloplasty treatments for functional mitral regurgitation. R. Soc. Open Sci. 2022, 9, 211464. [Google Scholar] [CrossRef]
- Padala, M. Patient-specific computational biomechanical modeling to guide mitral valve repair strategy: Practicality and value? J. Thorac. Cardiovasc. Surg. 2018, 155, 606–607. [Google Scholar] [CrossRef]
- Drach, A.; Khalighi, A.H.; Sacks, M.S. A comprehensive pipeline for multi-resolution modeling of the mitral valve: Validation, computational efficiency, and predictive capability. Int. J. Numer. Methods Biomed. Eng. 2017, 34, e2921. [Google Scholar] [CrossRef]
- Khalighi, A.H.; Drach, A.; Bloodworth, C.H.; Pierce, E.L.; Yoganathan, A.P.; Gorman, R.C.; Gorman, J.H.; Sacks, M.S. Mitral Valve Chordae Tendineae: Topological and Geometrical Characterization. Ann. Biomed. Eng. 2017, 45, 378–393. [Google Scholar] [CrossRef]
- Toma, M.; Chan-Akeley, R.; Arias, J.; Kurgansky, G.; Mao, W. Fluid–Structure Interaction Analyses of Biological Systems Using Smoothed-Particle Hydrodynamics. Biology 2021, 10, 185. [Google Scholar] [CrossRef]
- Toma, M.; Chan-Akeley, R. Biofluid-Biostructure Interaction Analyses Using Comprehensive Patient-Specific Geometries. In Proceedings of the Future Technologies Conference; Springer: Cham, Switzerland, 2020; pp. 1–16. [Google Scholar] [CrossRef]
- Imanparast, A.; Fatouraee, N.; Sharif, F. The impact of valve simplifications on left ventricular hemodynamics in a three dimensional simulation based on in vivo MRI data. J. Biomech. 2016, 49, 1482–1489. [Google Scholar] [CrossRef] [PubMed]
- Villard, P.-F.; Hammer, P.E.; Perrin, D.P.; Del Nido, P.J.; Howe, R.D. Fast image-based mitral valve simulation from individualized geometry. Int. J. Med Robot. Comput. Assist. Surg. 2018, 14, e1880. [Google Scholar] [CrossRef]
- Daub, A.; Kriegseis, J.; Frohnapfel, B. Replication of left ventricular haemodynamics with a simple planar mitral valve model. Biomed. Eng. Biomed. Tech. 2020, 65, 595–603. [Google Scholar] [CrossRef] [PubMed]
- Wojtas, K.; Kozłowski, M.; Orciuch, W.; Makowski, Ł. Computational Fluid Dynamics Simulations of Mitral Paravalvular Leaks in Human Heart. Materials 2021, 14, 7354. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Kanik, J.; Mansi, T.; Voigt, I.; Sharma, P.; Ionasec, R.I.; Subrahmanyan, L.; Lin, B.A.; Sugeng, L.; Yuh, D.; et al. Towards patient-specific modeling of mitral valve repair: 3D transesophageal echocardiography-derived parameter estimation. Med Image Anal. 2017, 35, 599–609. [Google Scholar] [CrossRef]
- Tautz, L.; Neugebauer, M.; Hüllebrand, M.; Vellguth, K.; Degener, F.; Sündermann, S.; Wamala, I.; Goubergrits, L.; Kuehne, T.; Falk, V.; et al. Extraction of open-state mitral valve geometry from CT volumes. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 1741–1754. [Google Scholar] [CrossRef]
- Toma, M.; Lu, Y.; Zhou, H.; Garcia, J.D. Thresholding Segmentation Errors and Uncertainty with Patient-Specific Geometries. J. Biomed. Phys. Eng. 2021, 11, 115–122. [Google Scholar] [CrossRef]
- Bloodworth, C.H.; Pierce, E.L.; Easley, T.F.; Drach, A.; Khalighi, A.H.; Toma, M.; Jensen, M.O.; Sacks, M.S.; Yoganathan, A.P. Ex Vivo Methods for Informing Computational Models of the Mitral Valve. Ann. Biomed. Eng. 2016, 45, 496–507. [Google Scholar] [CrossRef]
- Feng, L.; Qi, N.; Gao, H.; Sun, W.; Vazquez, M.; E Griffith, B.; Luo, X. On the chordae structure and dynamic behaviour of the mitral valve. IMA J. Appl. Math. 2018, 83, 1066–1091. [Google Scholar] [CrossRef]
- Vellguth, K.; Brüning, J.; Tautz, L.; Degener, F.; Wamala, I.; Sündermann, S.; Kertzscher, U.; Kuehne, T.; Hennemuth, A.; Falk, V.; et al. User-dependent variability in mitral valve segmentation and its impact on CFD-computed hemodynamic parameters. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 1687–1696. [Google Scholar] [CrossRef]
- Gao, H.; Qi, N.; Feng, L.; Ma, X.; Danton, M.; Berry, C.; Luo, X. Modelling mitral valvular dynamics-current trend and future directions. Int. J. Numer. Methods Biomed. Eng. 2016, 33, e2858. [Google Scholar] [CrossRef] [PubMed]
- Morgan, A.E.; Pantoja, J.; Weinsaft, J.; Grossi, E.; Guccione, J.M.; Ge, L.; Ratcliffe, M. Finite Element Modeling of Mitral Valve Repair. J. Biomech. Eng. 2016, 138, 021009. [Google Scholar] [CrossRef]
- Nath, J.; Foster, E.; Heidenreich, P.A. Impact of tricuspid regurgitation on long-term survival. J. Am. Coll. Cardiol. 2004, 43, 405–409. [Google Scholar] [CrossRef]
- Utsunomiya, H.; Itabashi, Y.; Mihara, H.; Berdejo, J.; Kobayashi, S.; Siegel, R.J.; Shiota, T. Functional Tricuspid Regurgitation Caused by Chronic Atrial Fibrillation. Circ. Cardiovasc. Imaging 2017, 10, e004897. [Google Scholar] [CrossRef] [PubMed]
- van Rosendael, P.J.; Kamperidis, V.; Kong, W.K.; van Rosendael, A.R.; van der Kley, F.; Marsan, N.A.; Delgado, V.; Bax, J.J. Computed tomography for planning transcatheter tricuspid valve therapy. Eur. Heart J. 2016, 38, 665–674. [Google Scholar] [CrossRef] [PubMed]
- Baumgartner, H.; Falk, V.; Bax, J.J.; De Bonis, M.; Hamm, C.; Holm, P.J.; Iung, B.; Lancellotti, P.; Lansac, E.; Rodriguez Muñoz, D.; et al. 2017 ESC/EACTS Guidelines for the management of valvular heart disease. Eur. J. Cardio-Thorac. Surg. 2017, 52, 616–664, Correction: Eur. J. Cardio-Thorac. Surg. 2017, 52, 832. [Google Scholar] [CrossRef]
- Otto, C.M.; Nishimura, R.A.; Bonow, R.O.; Carabello, B.A.; Erwin, J.P.; Gentile, F.; Jneid, H.; Krieger, E.V.; Mack, M.; McLeod, C.; et al. 2020 ACC/AHA Guideline for the Management of Patients With Valvular Heart Disease: A Report of the American College of Cardiology/American Heart Association Joint Committee on Clinical Practice Guidelines. Circulation 2021, 143, e35–e71. [Google Scholar] [CrossRef]
- Topilsky, Y.; Khanna, A.D.; Oh, J.K.; Nishimura, R.A.; Enriquez-Sarano, M.; Jeon, Y.B.; Sundt, T.M.; Schaff, H.; Park, S.J. Preoperative Factors Associated With Adverse Outcome After Tricuspid Valve Replacement. Circulation 2011, 123, 1929–1939. [Google Scholar] [CrossRef]
- Zack, C.J.; Fender, E.A.; Chandrashekar, P.; Reddy, Y.N.; Bennett, C.E.; Stulak, J.M.; Miller, V.M.; Nishimura, R.A. National Trends and Outcomes in Isolated Tricuspid Valve Surgery. J. Am. Coll. Cardiol. 2017, 70, 2953–2960. [Google Scholar] [CrossRef]
- Pant, A.D.; Thomas, V.S.; Black, A.L.; Verba, T.; Lesicko, J.G.; Amini, R. Pressure-induced microstructural changes in porcine tricuspid valve leaflets. Acta Biomater. 2018, 67, 248–258. [Google Scholar] [CrossRef]
- Thomas, V.S.; Lai, V.; Amini, R. A computational multi-scale approach to investigate mechanically-induced changes in tricuspid valve anterior leaflet microstructure. Acta Biomater. 2019, 94, 524–535. [Google Scholar] [CrossRef] [PubMed]
- Kong, F.; Pham, T.; Martin, C.; McKay, R.; Primiano, C.; Hashim, S.; Kodali, S.; Sun, W. Finite Element Analysis of Tricuspid Valve Deformation from Multi-slice Computed Tomography Images. Ann. Biomed. Eng. 2018, 46, 1112–1127. [Google Scholar] [CrossRef] [PubMed]
- Laurence, D.W.; Johnson, E.L.; Hsu, M.; Baumwart, R.; Mir, A.; Burkhart, H.M.; Holzapfel, G.A.; Wu, Y.; Lee, C. A pilot in silico modeling-based study of the pathological effects on the biomechanical function of tricuspid valves. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3346. [Google Scholar] [CrossRef] [PubMed]
- Taramasso, M.; Pozzoli, A.; Basso, C.; Thiene, G.; Denti, P.; Kuwata, S.; Nietlispach, F.; Alfieri, O.; Hahn, R.T.; Nickenig, G.; et al. Compare and contrast tricuspid and mitral valve anatomy: Interventional perspectives for transcatheter tricuspid valve therapies. EuroIntervention 2018, 13, 1889–1898. [Google Scholar] [CrossRef]
- Jett, S.; Laurence, D.; Kunkel, R.; Babu, A.R.; Kramer, K.; Baumwart, R.; Towner, R.; Wu, Y.; Lee, C.-H. An investigation of the anisotropic mechanical properties and anatomical structure of porcine atrioventricular heart valves. J. Mech. Behav. Biomed. Mater. 2018, 87, 155–171. [Google Scholar] [CrossRef]
- Morganti, S.; Auricchio, F.; Benson, D.; Gambarin, F.I.; Hartmann, S.; Hughes, T.J.R.; Reali, A. Patient-specific isogeometric structural analysis of aortic valve closure. Comput. Methods Appl. Mech. Eng. 2015, 284, 508–520. [Google Scholar] [CrossRef]
- Marom, G. Numerical Methods for Fluid–Structure Interaction Models of Aortic Valves. Arch. Comput. Methods Eng. 2014, 22, 595–620. [Google Scholar] [CrossRef]
- Zakerzadeh, R.; Hsu, M.-C.; Sacks, M.S. Computational methods for the aortic heart valve and its replacements. Expert Rev. Med. Devices 2017, 14, 849–866. [Google Scholar] [CrossRef]
- Jhun, C.-S.; Newswanger, R.; Cysyk, J.P.; Ponnaluri, S.; Good, B.; Manning, K.B.; Rosenberg, G. Dynamics of Blood Flows in Aortic Stenosis: Mild, Moderate, and Severe. ASAIO J. 2020, 67, 666–674. [Google Scholar] [CrossRef]
- Xu, L.; Yin, L.; Liu, Y.; Liang, F. A computational study on the influence of aortic valve disease on hemodynamics in dilated aorta. Math. Biosci. Eng. 2020, 17, 606–626. [Google Scholar] [CrossRef]
- Xu, F.; Johnson, E.L.; Wang, C.; Jafari, A.; Yang, C.-H.; Sacks, M.S.; Krishnamurthy, A.; Hsu, M.-C. Computational investigation of left ventricular hemodynamics following bioprosthetic aortic and mitral valve replacement. Mech. Res. Commun. 2020, 112, 103604. [Google Scholar] [CrossRef] [PubMed]
- Su, B.; Zhong, L.; Wang, X.-K.; Zhang, J.-M.; Tan, R.S.; Allen, J.C.; Tan, S.K.; Kim, S.; Leo, H.L. Numerical simulation of patient-specific left ventricular model with both mitral and aortic valves by FSI approach. Comput. Methods Programs Biomed. 2014, 113, 474–482. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.; Su, B.; Zhang, J.-M.; Leo, H.L.; Tan, R.S. FSI simulation of intra-ventricular flow in patient-specific ventricular model with both mitral and aortic valves. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; Volume 2013, pp. 703–706. [Google Scholar] [CrossRef]
- Maragiannis, D.; Jackson, M.S.; Igo, S.R.; Schutt, R.C.; Connell, P.; Grande-Allen, J.; Barker, C.M.; Chang, S.M.; Reardon, M.J.; Zoghbi, W.A.; et al. Replicating Patient-Specific Severe Aortic Valve Stenosis With Functional 3D Modeling. Circ. Cardiovasc. Imaging 2015, 8, e003626. [Google Scholar] [CrossRef]
- de Oliveira, D.M.C.; Abdullah, N.; Green, N.C.; Espino, D.M. Biomechanical Assessment of Bicuspid Aortic Valve Phenotypes: A Fluid–Structure Interaction Modelling Approach. Cardiovasc. Eng. Technol. 2020, 11, 431–447. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Li, J.; Wang, W.; Wei, L.; Wang, S. A Fluid–Structure Interaction Study of Different Bicuspid Aortic Valve Phenotypes Throughout the Cardiac Cycle. Front. Physiol. 2021, 12, 6015. [Google Scholar] [CrossRef] [PubMed]
- Youssefi, P.; Gomez, A.; He, T.; Anderson, L.; Bunce, N.; Sharma, R.; Figueroa, C.A.; Jahangiri, M. Patient-specific computational fluid dynamics—Assessment of aortic hemodynamics in a spectrum of aortic valve pathologies. J. Thorac. Cardiovasc. Surg. 2016, 153, 8–20.e3. [Google Scholar] [CrossRef]
- Shen, X.; Bai, L.; Cai, L.; Cao, X. A geometric model for the human pulmonary valve in its fully open case. PLoS ONE 2018, 13, e0199390. [Google Scholar] [CrossRef]
- Loke, Y.-H.; Capuano, F.; Balaras, E.; Olivieri, L.J. Computational Modeling of Right Ventricular Motion and Intracardiac Flow in Repaired Tetralogy of Fallot. Cardiovasc. Eng. Technol. 2021, 13, 41–54. [Google Scholar] [CrossRef]
- Caiazzo, A.; Guibert, R.; Boudjemline, Y.; Vignon-Clementel, I.E. Blood Flow Simulations for the Design of Stented Valve Reducer in Enlarged Ventricular Outflow Tracts. Cardiovasc. Eng. Technol. 2015, 6, 485–500. [Google Scholar] [CrossRef]
- Caiazzo, A.; Guibert, R.; Vignon-Clementel, I.E. A reduced-order modeling for efficient design study of artificial valve in enlarged ventricular outflow tracts. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 1314–1318. [Google Scholar] [CrossRef]
- Berdajs, D.; Mosbahi, S.; Vos, J.; Charbonnier, D.; Hullin, R.; Von Segesser, L.K. Fluid dynamics simulation of right ventricular outflow tract oversizing. Interact. Cardiovasc. Thorac. Surg. 2015, 21, 176–182. [Google Scholar] [CrossRef] [PubMed]
- Sonntag, S.J.; Kütting, M.; Ghalati, P.F.; Kaufmann, T.; Vazquez-Jimenez, J.; Steinseifer, U.; Vodiskar, J. Effect of Pulmonary Conduit Oversizing on Hemodynamics in Children. Int. J. Artif. Organs 2015, 38, 548–556. [Google Scholar] [CrossRef] [PubMed]
- Savarese, G.; Lund, L.H. Global Public Health Burden of Heart Failure. Card. Fail. Rev. 2017, 3, 7–11. [Google Scholar] [CrossRef]
- Oveissi, F.; Naficy, S.; Lee, A.; Winlaw, D.; Dehghani, F. Materials and manufacturing perspectives in engineering heart valves: A review. Mater. Today Bio 2019, 5, 100038. [Google Scholar] [CrossRef] [PubMed]
- Arthurs, C.J.; Khlebnikov, R.; Melville, A.; Marčan, M.; Gomez, A.; Dillon-Murphy, D.; Cuomo, F.; Vieira, M.S.; Schollenberger, J.; Lynch, S.R.; et al. CRIMSON: An open-source software framework for cardiovascular integrated modelling and simulation. PLOS Comput. Biol. 2021, 17, e1008881. [Google Scholar] [CrossRef] [PubMed]
- Erdemir, A.; Guess, T.M.; Halloran, J.P.; Modenese, L.; Reinbolt, J.A.; Thelen, D.G.; Umberger, B. Commentary on the Integration of Model Sharing and Reproducibility Analysis to Scholarly Publishing Workflow in Computational Biomechanics. IEEE Trans. Biomed. Eng. 2016, 63, 2080–2085. [Google Scholar] [CrossRef]
- Toma, M.; Guru, S.; Wu, W.; Ali, M.; Ong, C. Addressing Discrepancies between Experimental and Computational Procedures. Biology 2021, 10, 536. [Google Scholar] [CrossRef]
- Campbell, K.S.; Yengo, C.M.; Lee, L.-C.; Kotter, J.; Sorrell, V.L.; Guglin, M.; Wenk, J.F. Closing the therapeutic loop. Arch. Biochem. Biophys. 2019, 663, 129–131. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.I. Rhythmic behaviors of the human heart with piecewise derivative. Math. Biosci. Eng. 2022, 19, 3091–3109. [Google Scholar] [CrossRef]
- Tiwary, B.K. Computational medicine: Quantitative modeling of complex diseases. Brief. Bioinform. 2019, 21, 429–440. [Google Scholar] [CrossRef]
- Olivier, B.G.; Swat, M.J.; Moné, M.J. Modeling and Simulation Tools: From Systems Biology to Systems Medicine. Syst. Med. 2016, 1386, 441–463. [Google Scholar] [CrossRef]
- Winslow, R.L.; Trayanova, N.; Geman, D.; Miller, M.I. Computational Medicine: Translating Models to Clinical Care. Sci. Transl. Med. 2012, 4, 158rv11. [Google Scholar] [CrossRef]
- Sakellaropoulos, T.; Hur, J.; Melas, I.N.; Guo, E.Y.; Alexopoulos, L.; Bohlooly, M.; Bai, J.P. Computational Approaches to Accelerating Novel Medicine and Better Patient Care from Bedside to Benchtop. Adv. Protein Chem. Struct. Biol. 2016, 102, 147–179. [Google Scholar] [CrossRef] [PubMed]
- Miller, D.D.; Brown, E.W. Artificial Intelligence in Medical Practice: The Question to the Answer? Am. J. Med. 2018, 131, 129–133. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.B.; Wei, W.; Weeraratne, D.; Frisse, M.E.; Misulis, K.; Rhee, K.; Zhao, J.; Snowdon, J.L. Precision Medicine, AI, and the Future of Personalized Health Care. Clin. Transl. Sci. 2020, 14, 86–93. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toma, M.; Singh-Gryzbon, S.; Frankini, E.; Wei, Z.; Yoganathan, A.P. Clinical Impact of Computational Heart Valve Models. Materials 2022, 15, 3302. https://doi.org/10.3390/ma15093302
Toma M, Singh-Gryzbon S, Frankini E, Wei Z, Yoganathan AP. Clinical Impact of Computational Heart Valve Models. Materials. 2022; 15(9):3302. https://doi.org/10.3390/ma15093302
Chicago/Turabian StyleToma, Milan, Shelly Singh-Gryzbon, Elisabeth Frankini, Zhenglun (Alan) Wei, and Ajit P. Yoganathan. 2022. "Clinical Impact of Computational Heart Valve Models" Materials 15, no. 9: 3302. https://doi.org/10.3390/ma15093302
APA StyleToma, M., Singh-Gryzbon, S., Frankini, E., Wei, Z., & Yoganathan, A. P. (2022). Clinical Impact of Computational Heart Valve Models. Materials, 15(9), 3302. https://doi.org/10.3390/ma15093302






