A New Method for the Calculation of Characteristics of Disc Springs with Trapezoidal Cross-Sections and Rounded Edges
Abstract
1. Introduction
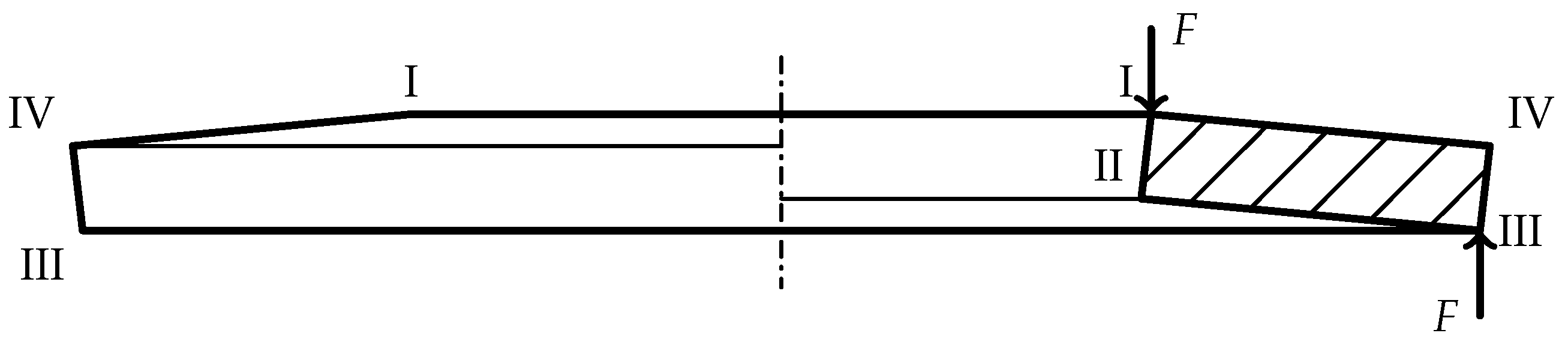
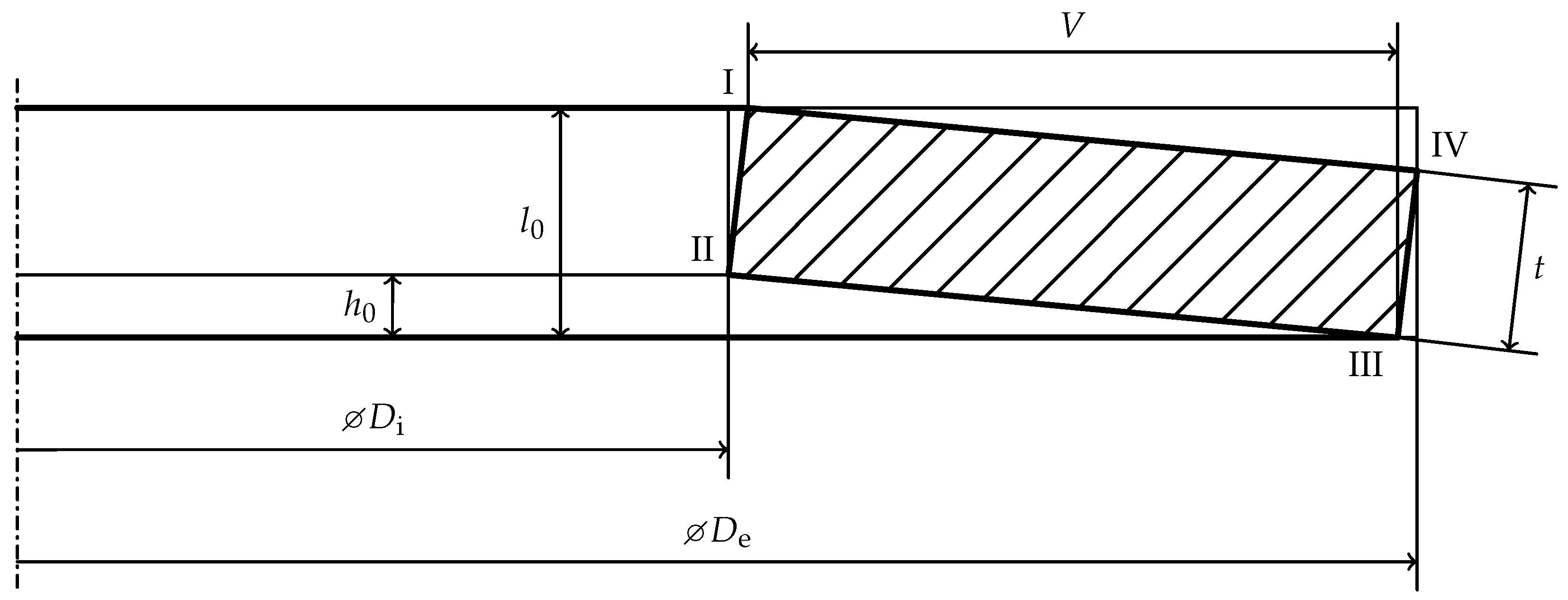
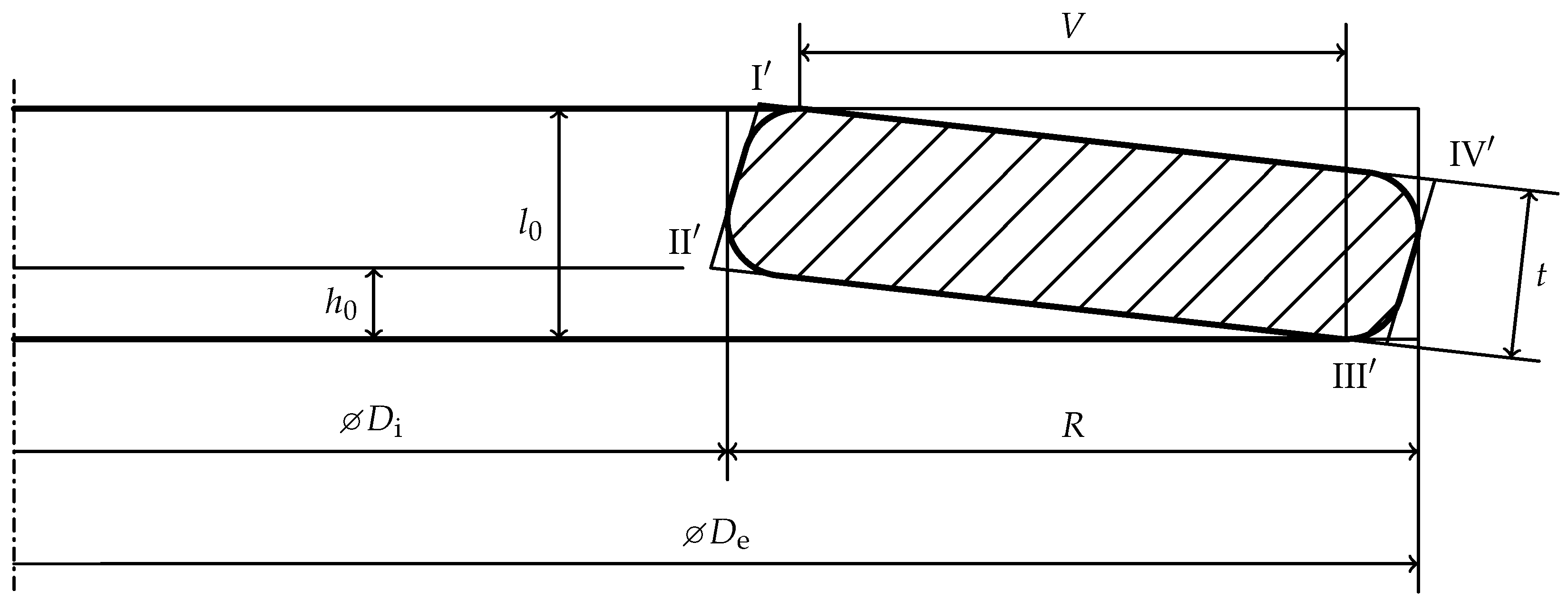
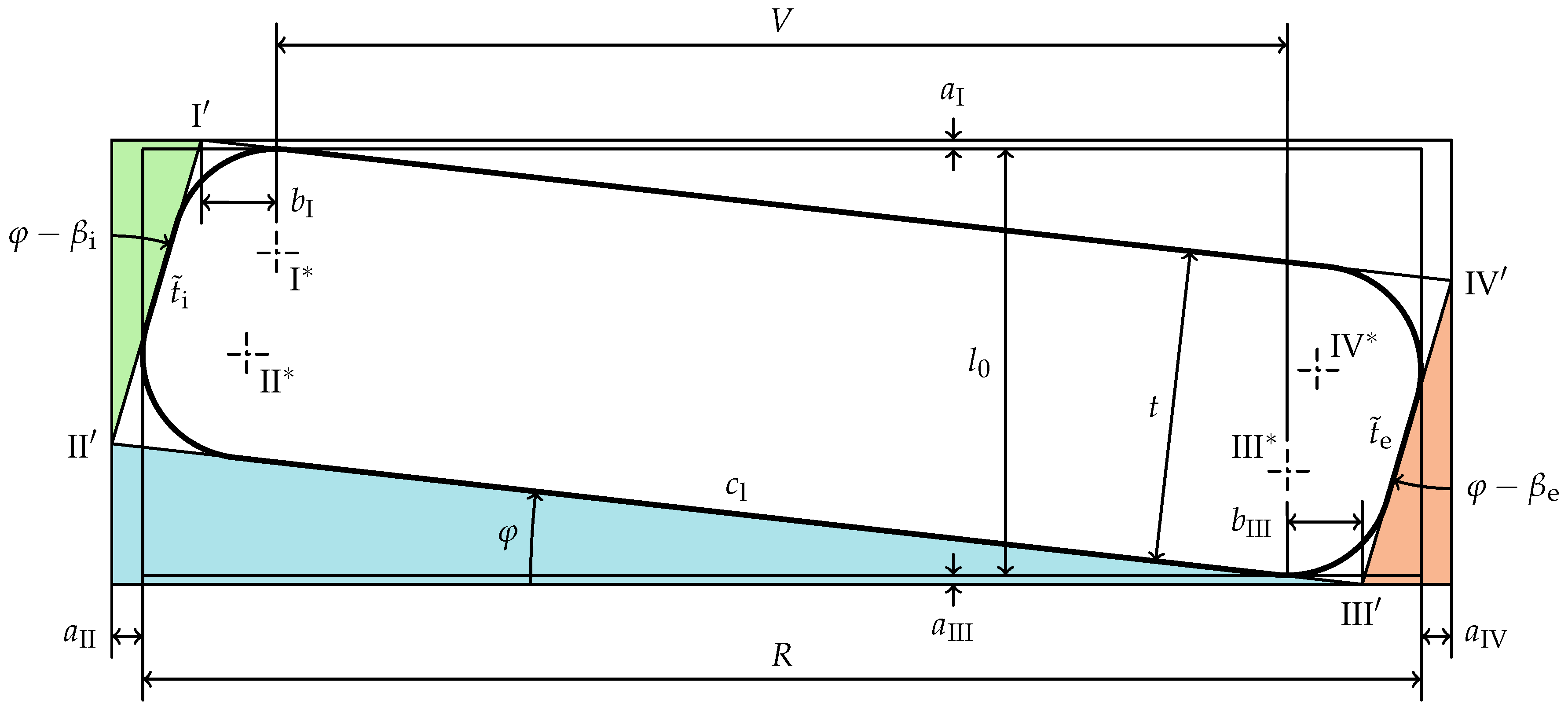
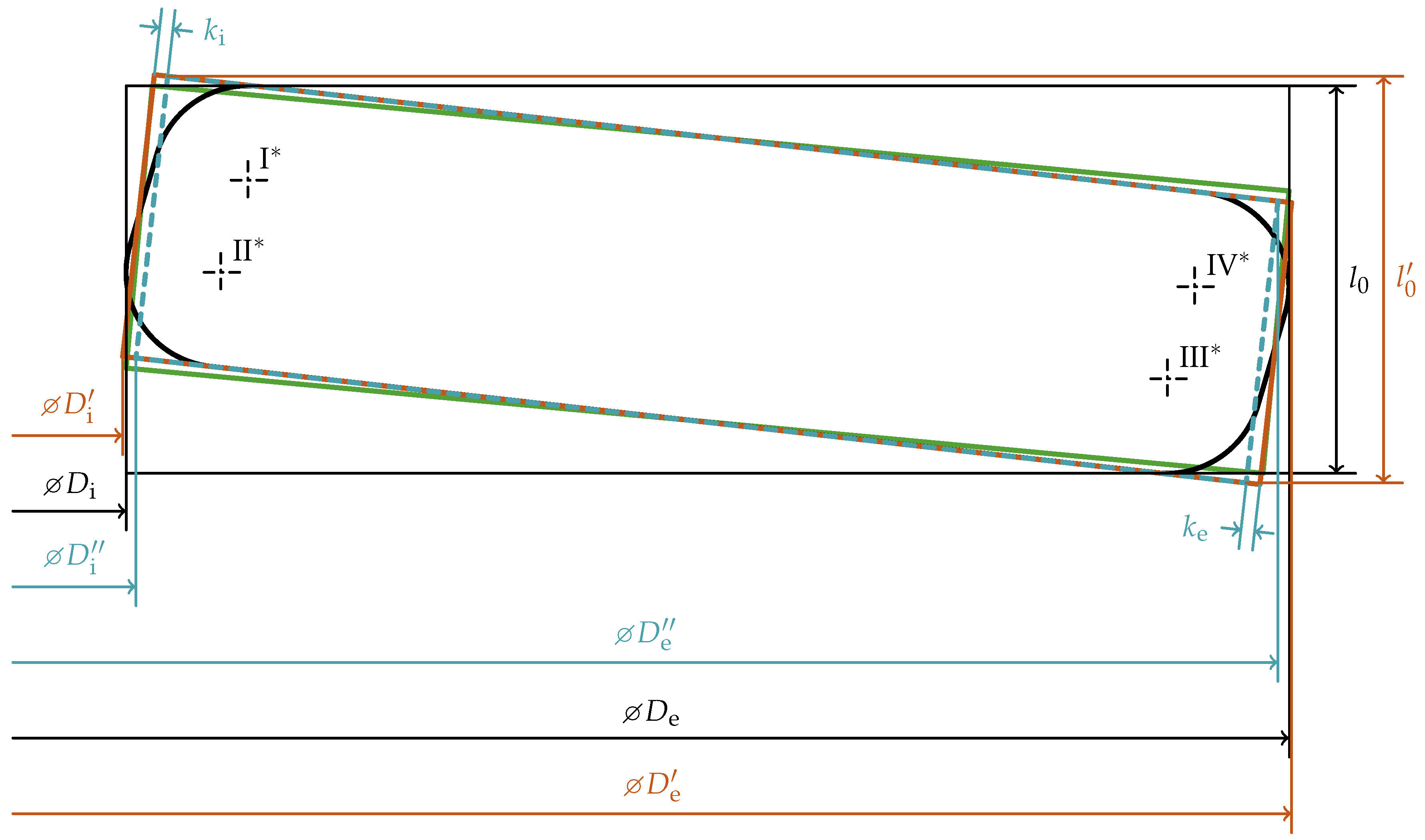
2. Idealized Geometry of Disc Springs
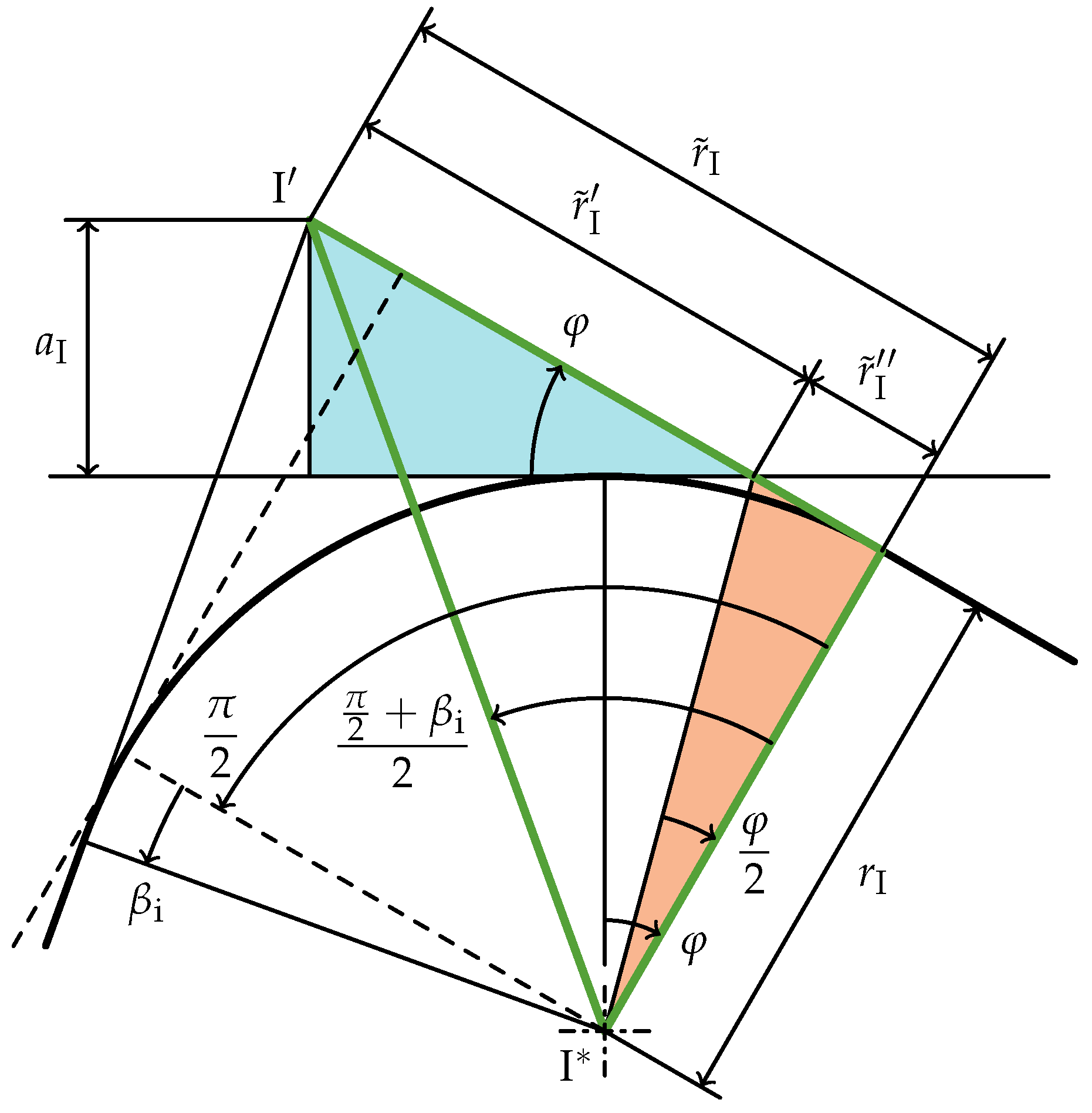
3. Calculation of Initial Slope Angle and Lever Arm
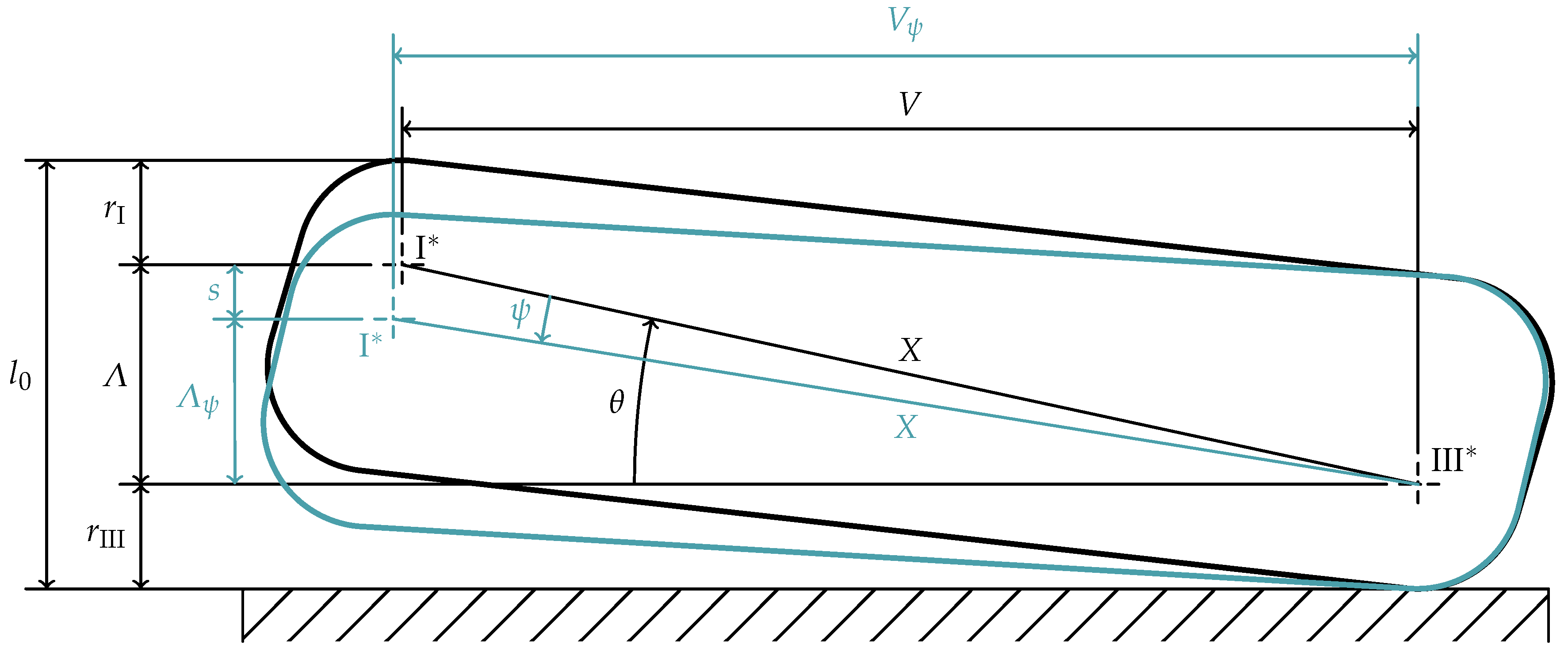
4. Calculation of Deformed Geometries of Loaded Disc Springs
5. Calculation of Spring Characteristics
5.1. Concept
5.2. Applying the Method to Almen’s Formula
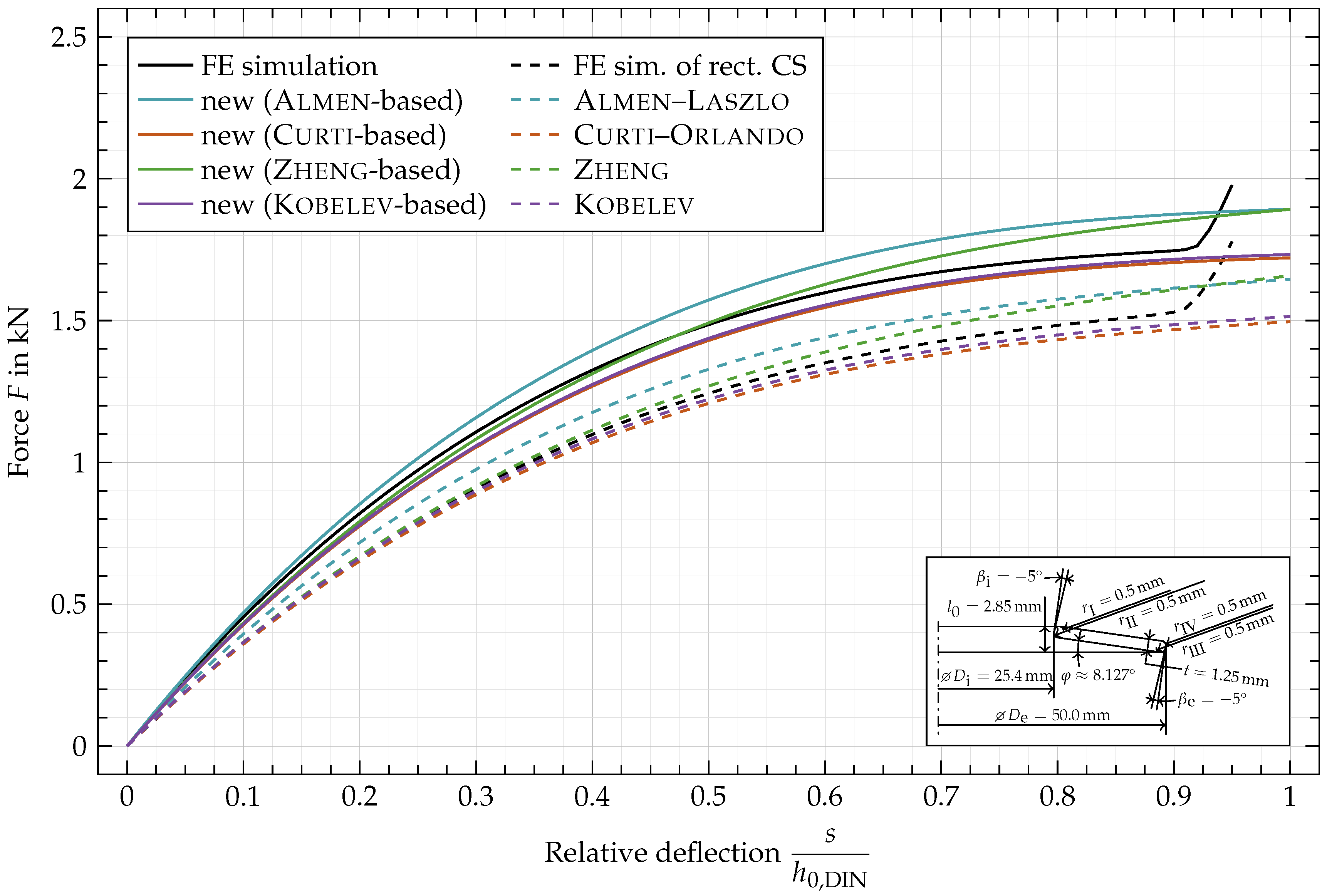
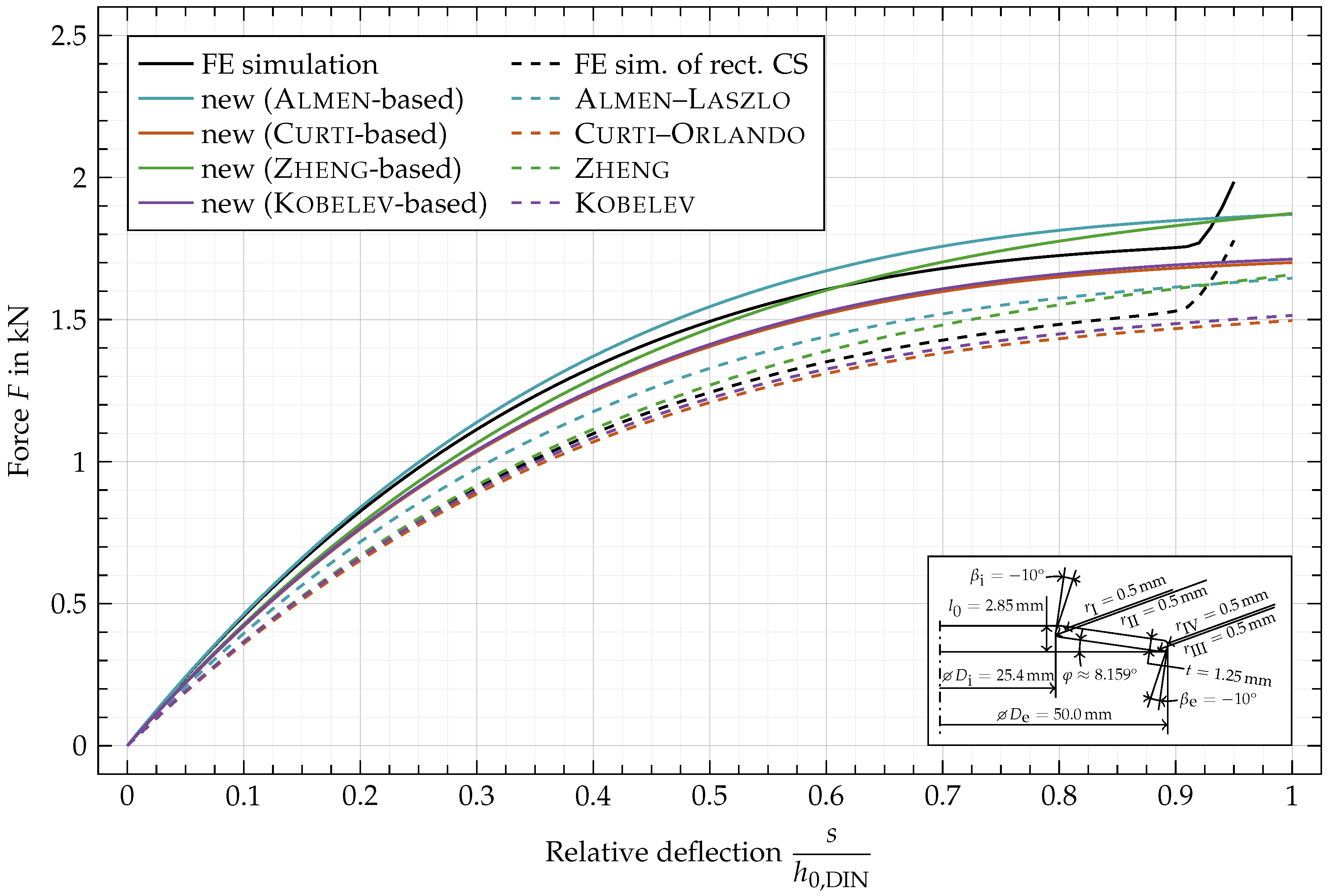
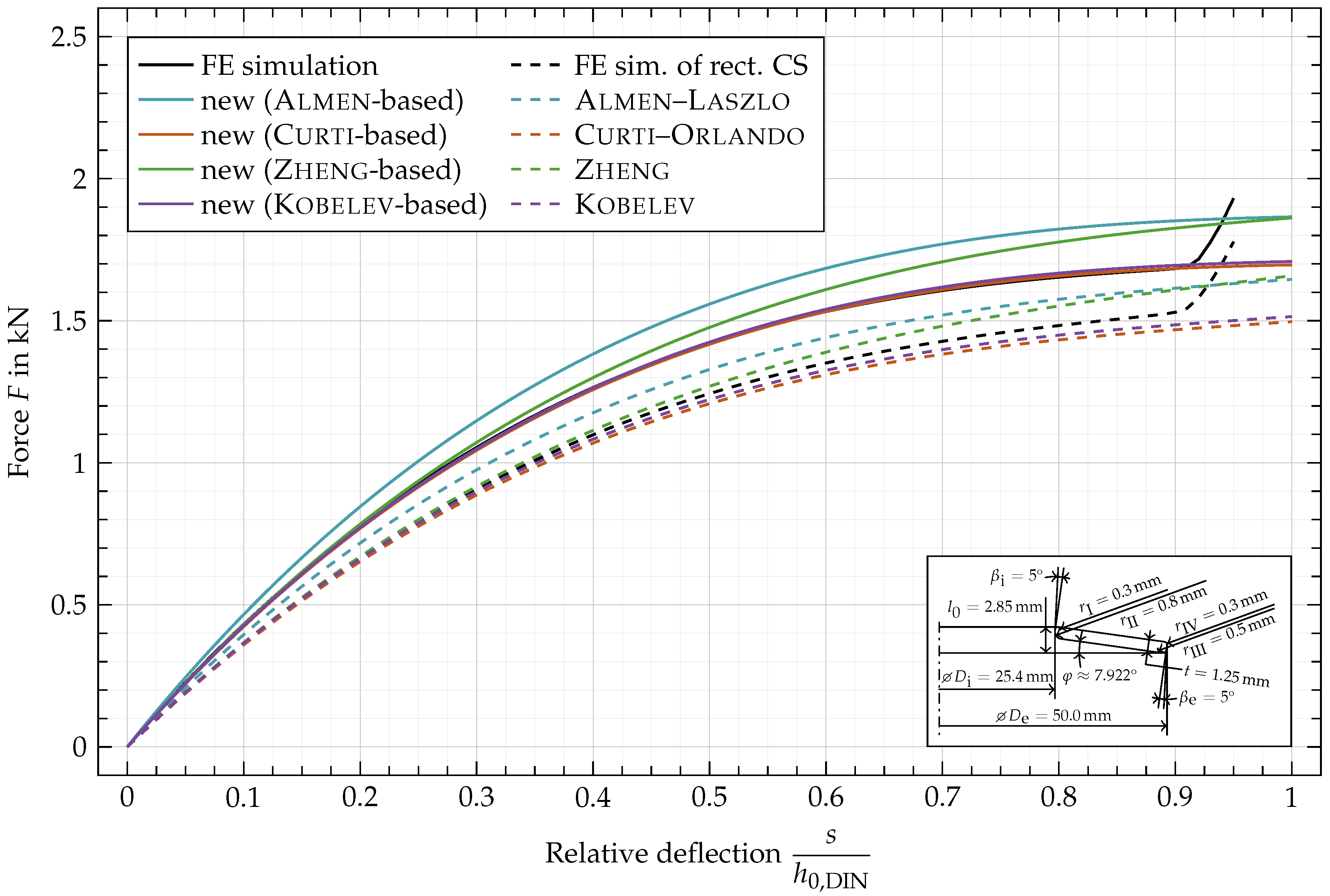
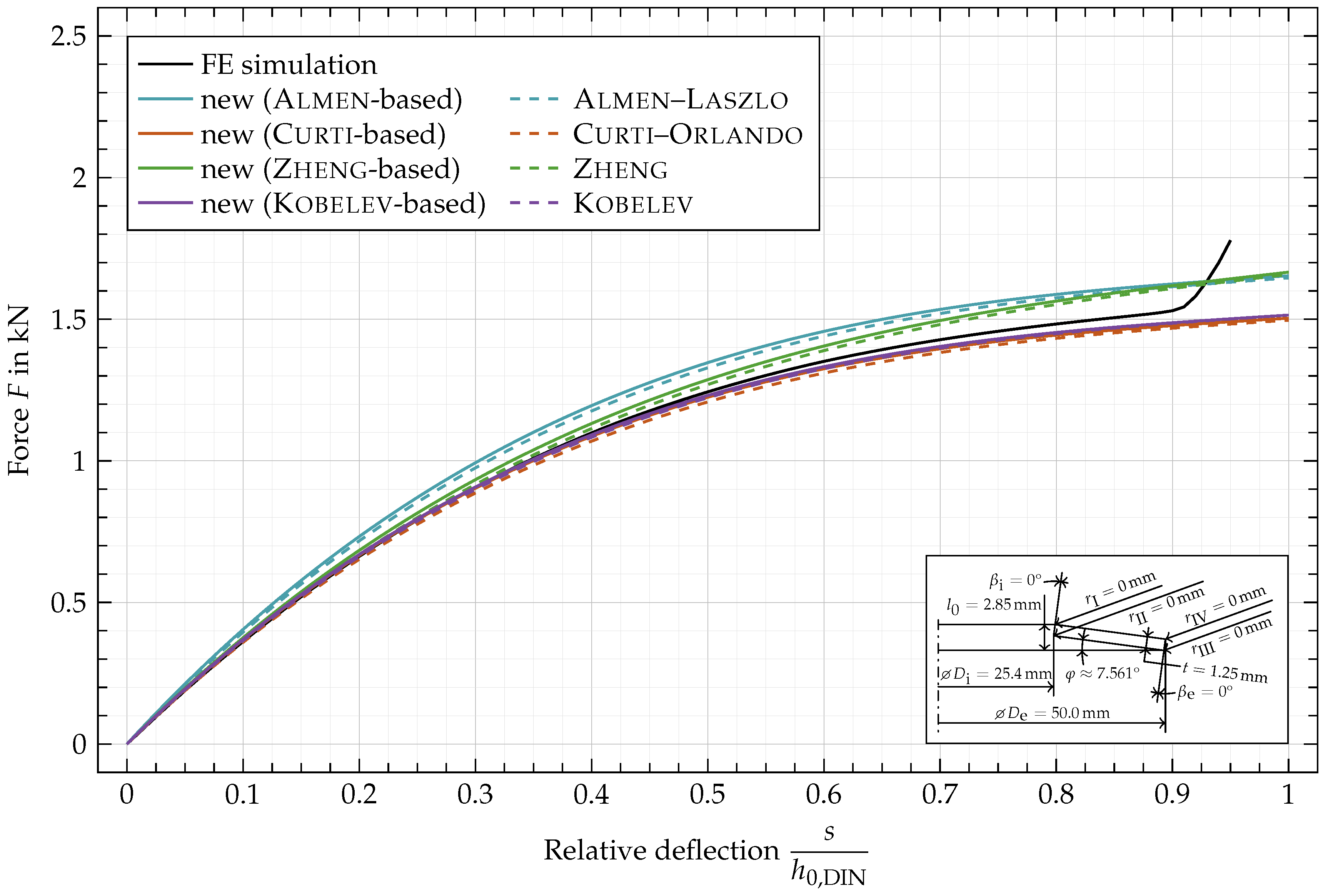
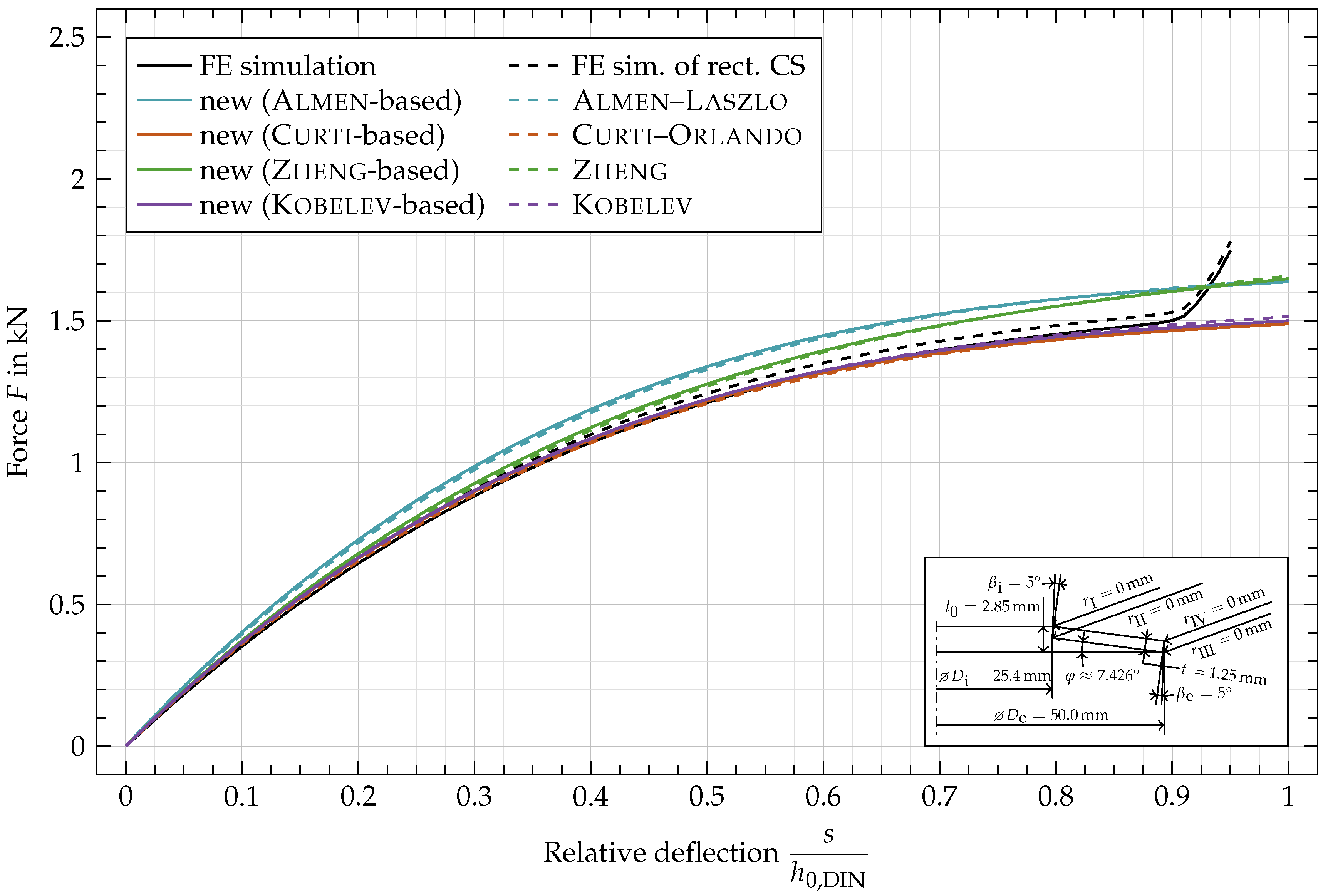
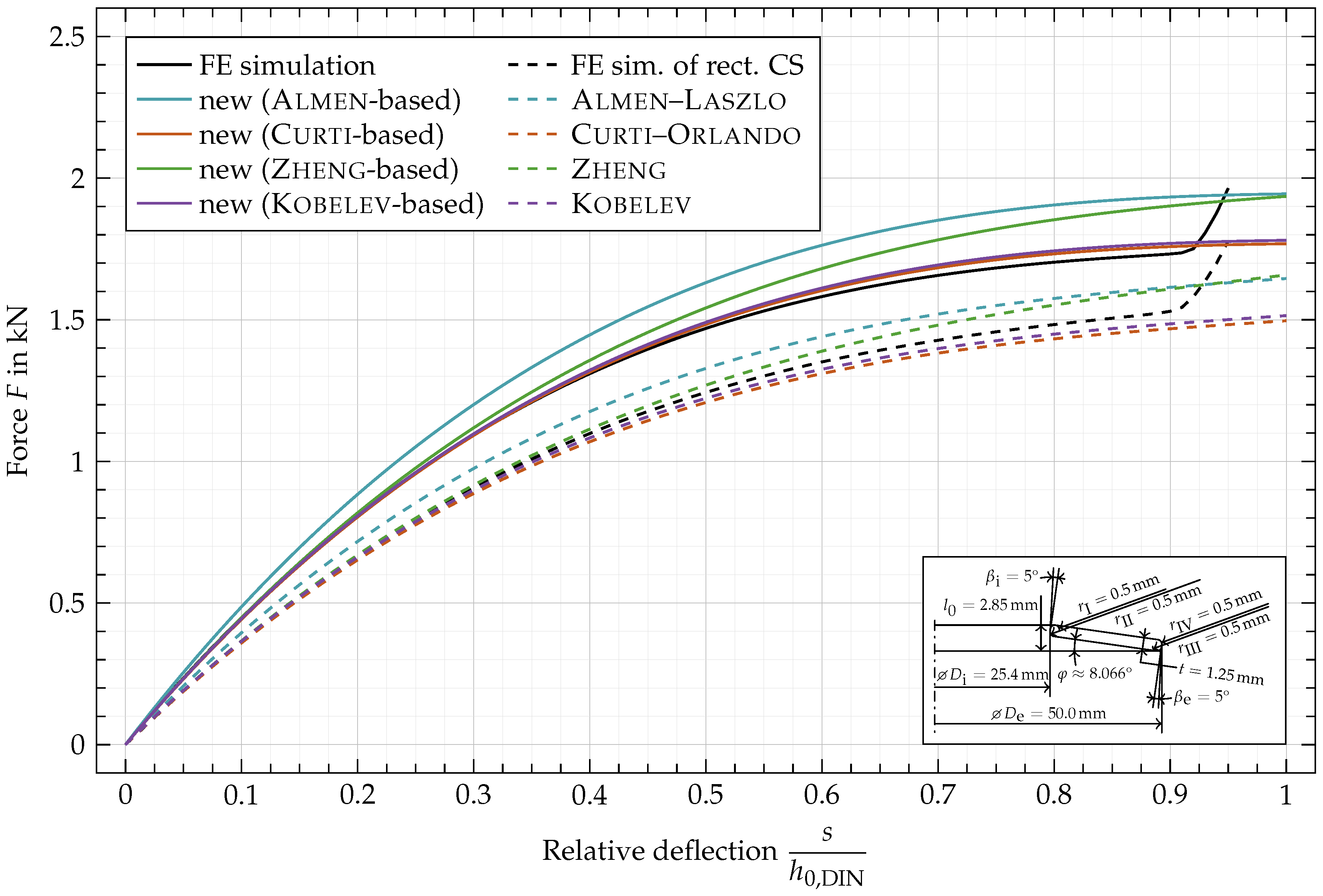
6. Results and Discussion
7. Conclusions
- A set of formulas were introduced to describe the geometric relations of the cross-section of a disc spring with non-rectangular cross-section and rounded edges. They enable the formulation of a more accurate way to compute the lever arm, taking its elongation during deflection into account.
- A method adapting characteristic calculation formulas and algorithms to non-rectangular cross-sections with rounded edges was outlined. This new adaption method can be applied to different traditional characteristic calculation algorithms designed for disc springs with a rectangular cross-section. The method was exemplarily applied to the algorithms of Almen–Laszlo, Curti–Orlando, Zheng and Kobelev to show its applicability.
- The adjusted formulas were used to calculate characteristics of different disc springs. The results were compared to those of the original formulas and those obtained by FE simulations. Provided that the original characteristics approximate those of rectangular cross-sectional disc springs well, the adjusted characteristics based on them fit well for most investigated geometries. Based on the results of exemplarily computed characteristics, we recommend the use of the proposed method, utilizing formulas introduced by Curti–Orlando or Kobelev. The relative errors made with the new method are in the same order of magnitude as those of geometries with rectangular cross-section.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of through and through
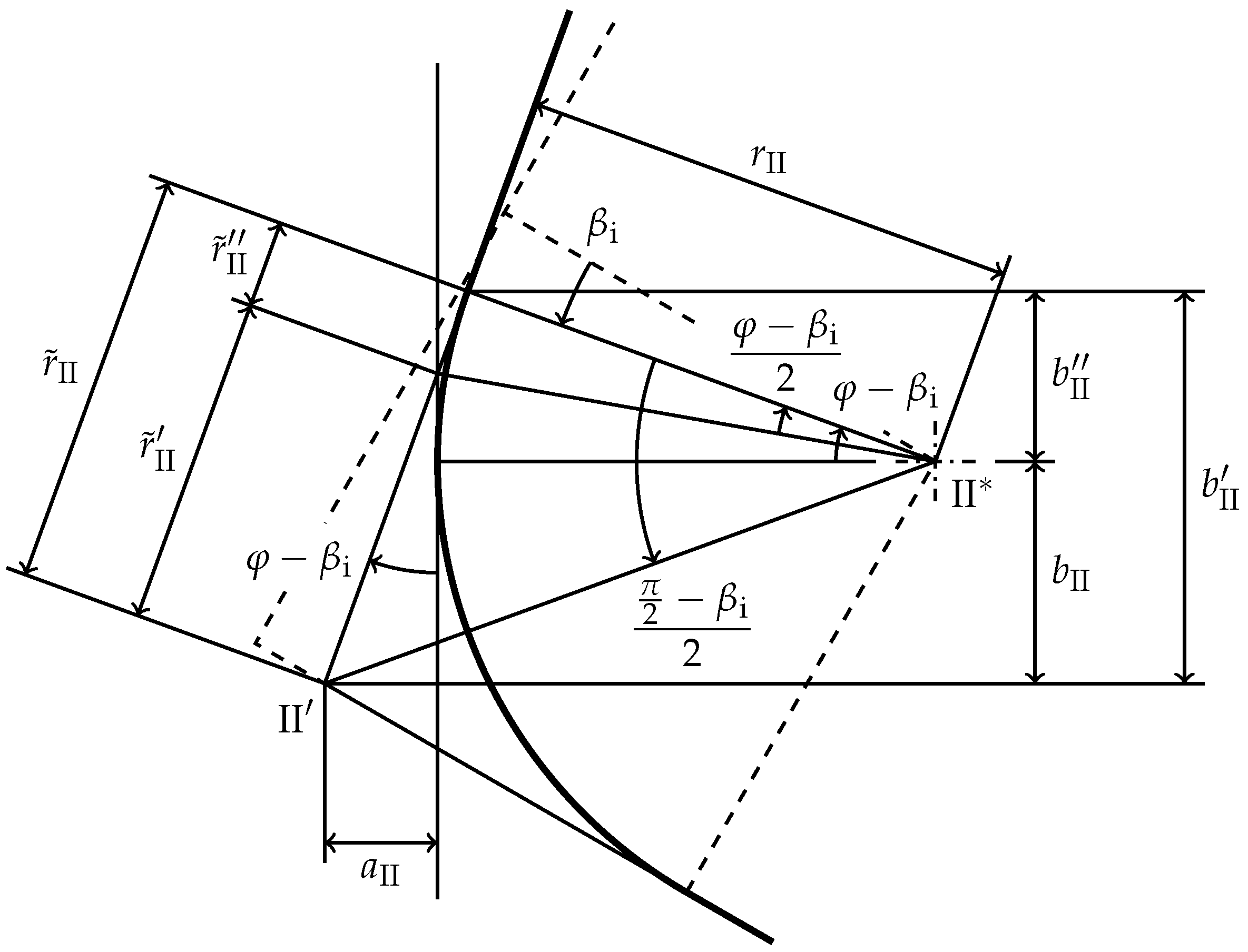
Appendix B. Full Equations
Appendix C. Force vs. Deflection Curves for Additional Geometric Variations
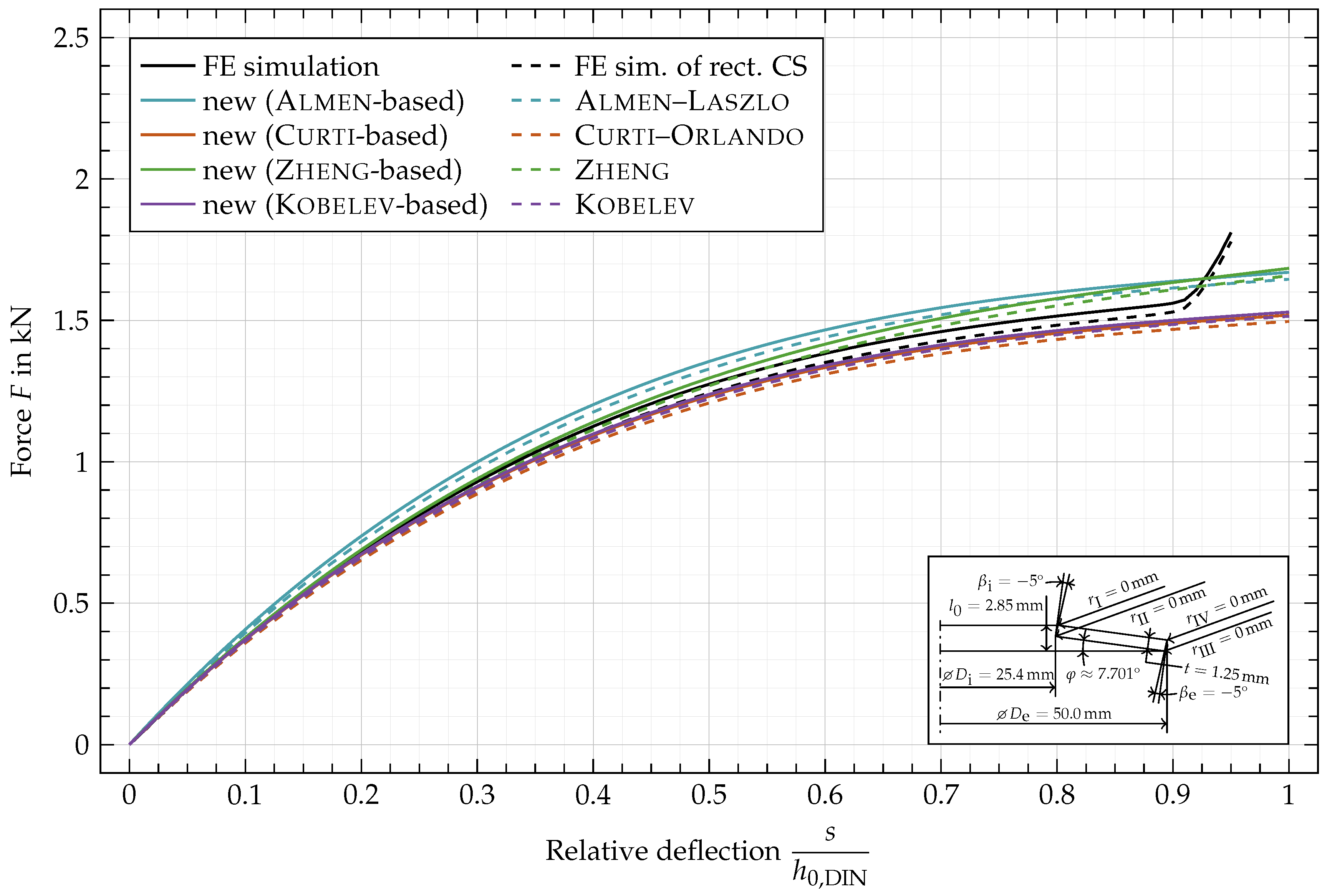
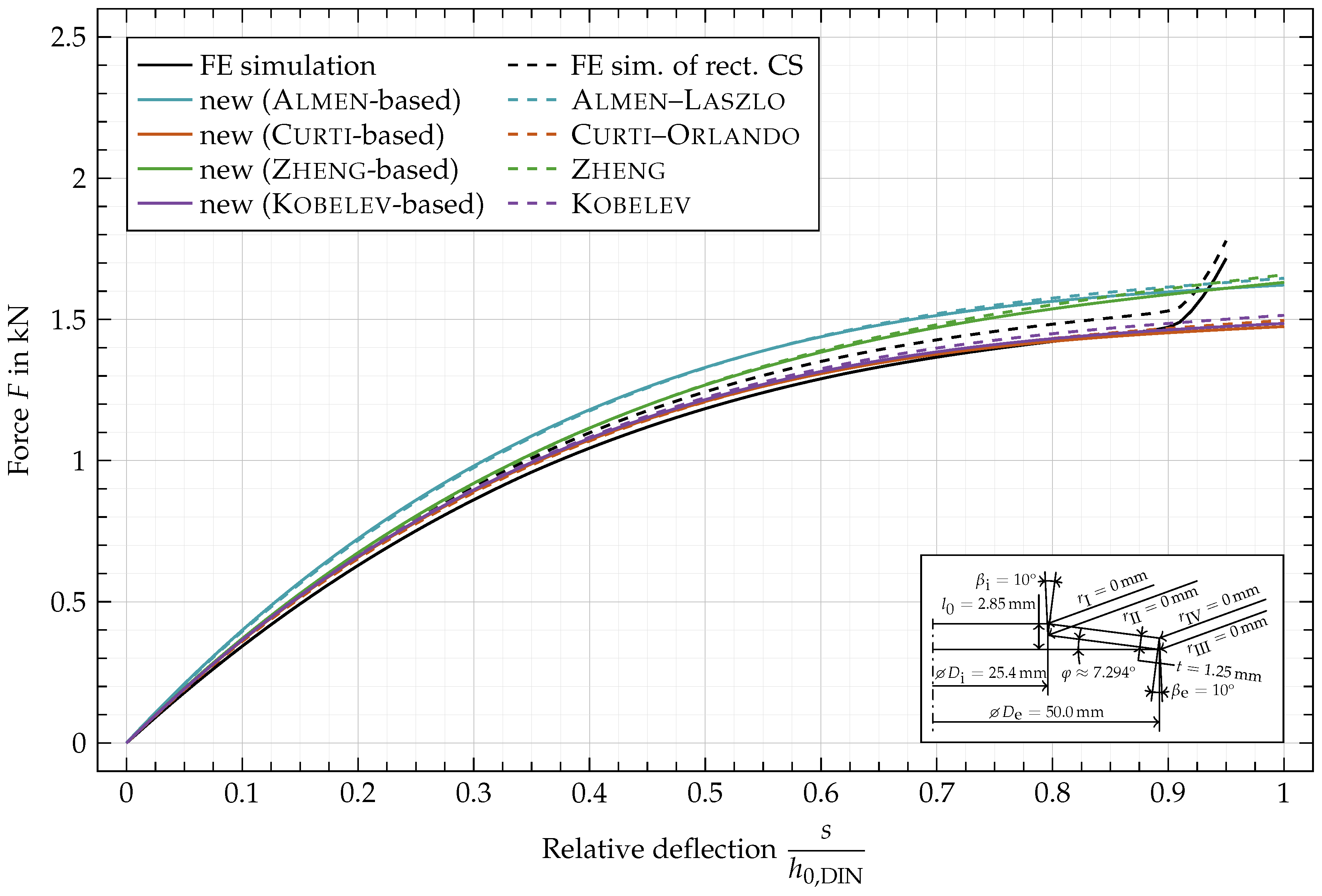
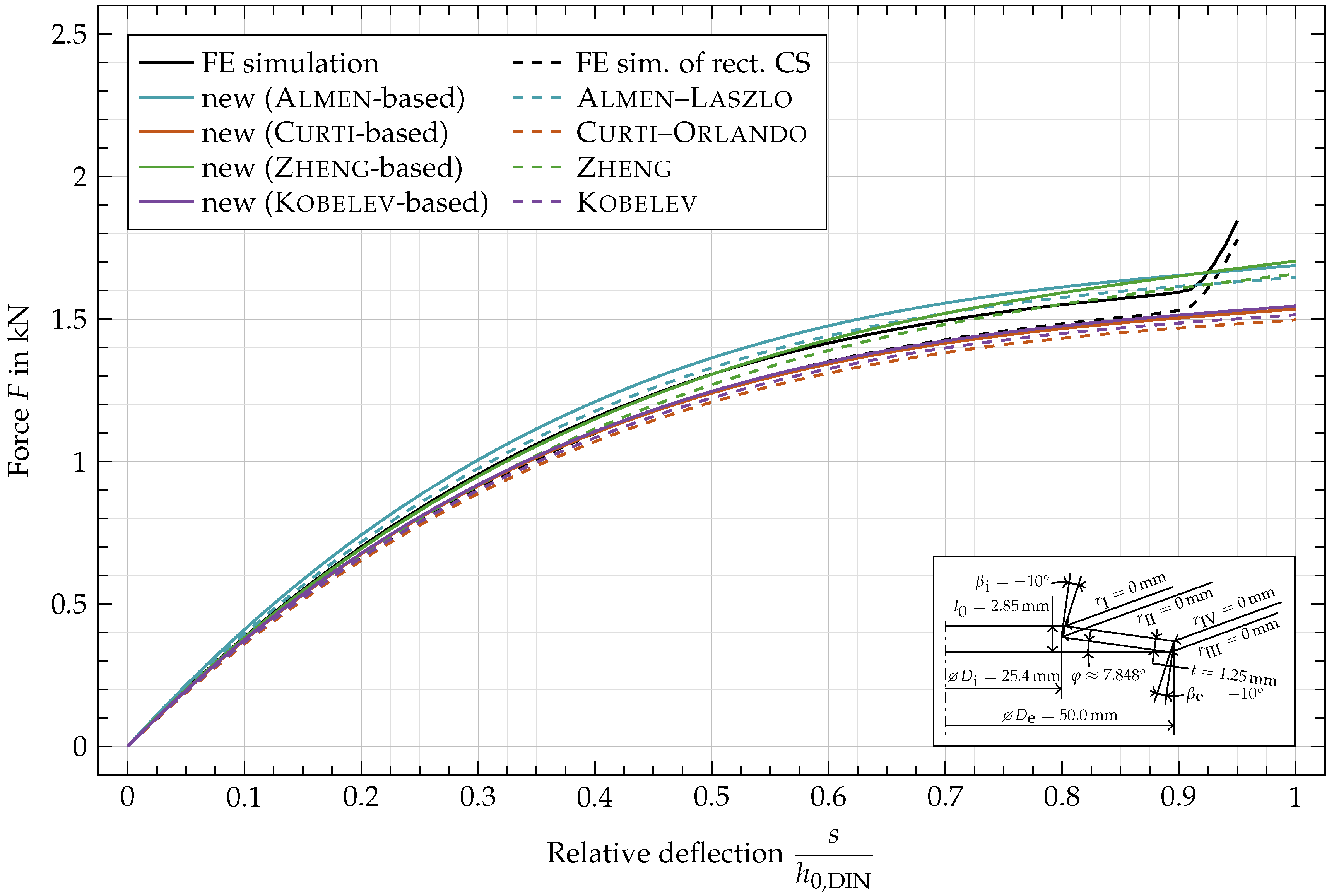

| Curti–Orlando Based | Kobelev Based | |||
|---|---|---|---|---|
| 10° | 9.64% | 4.06% | 10.18% | 4.68% |
| 5° | 7.36% | 1.73% | 17.88% | 2.35% |
| 0° | 5.09% | 4.22% | 15.58% | 3.69% |
| −5° | 3.98% | 6.37% | 13.37% | 5.87% |
| −10° | 5.41% | 8.47% | 14.82% | 8.00% |
| 5° | 1.97% | 1.43% | ||
References
- Köhler, W. Die Tellerfeder, ein Hilfsmittel zur Klärung von Grenzflächenvorgängen. Mater. Corros. 1955, 6, 389–397. [Google Scholar] [CrossRef]
- Lee, C.Y.; Chae, Y.S.; Gwon, J.D.; Nam, U.H.; Kim, T.H. Finite element analysis and optimal design of automobile clutch diaphragm spring. Trans. Korean Soc. Mech. Eng. A 2000, 24, 1616–1623. [Google Scholar]
- Chen, Y.S.; Chiu, C.C.; Cheng, Y.D. Dynamic analysis of disc spring effects on the contact pressure of the collet—Spindle interface in a high-speed spindle system. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1191–1201. [Google Scholar] [CrossRef]
- Bouzid, A.H.; Nechache, A. The modelling of bolted flange joints used with disc springs and tube spacers to reduce relaxation. Int. J. Press. Vessel. Pip. 2010, 87, 730–736. [Google Scholar] [CrossRef]
- Sfarni, S.; Bellenger, E.; Fortin, J.; Malley, M. Numerical and experimental study of automotive riveted clutch discs with contact pressure analysis for the prediction of facing wear. Finite Elem. Anal. Des. 2011, 47, 129–141. [Google Scholar] [CrossRef]
- Ha, S.H.; Seong, M.S.; Choi, S.B. Design and vibration control of military vehicle suspension system using magnetorheological damper and disc spring. Smart Mater. Struct. 2013, 22, 065006. [Google Scholar] [CrossRef]
- Castagnetti, D. A Belleville-spring-based electromagnetic energy harvester. Smart Mater. Struct. 2015, 24, 094009. [Google Scholar] [CrossRef]
- Aktir, Y.; Brunel, J.F.; Dufrenoy, P.; Mahé, H. Three-dimensional finite element model of an automotive clutch for analysis of axial vibrations. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 1324–1337. [Google Scholar] [CrossRef]
- Tsang, K.S.; Ion, W.; English, M. Investigation into the Numerical Model Behaviour of Belleville Washers in Cold Roll Forming. Key Eng. Mater. 2016, 716, 719–727. [Google Scholar] [CrossRef]
- Sgambitterra, E.; Maletta, C.; Furgiuele, F. Modeling and simulation of the thermo-mechanical response of NiTi-based Belleville springs. J. Intell. Mater. Syst. Struct. 2016, 27, 81–91. [Google Scholar] [CrossRef]
- Ramhormozian, S.; Clifton, G.C.; MacRae, G.A.; Davet, G.P. Stiffness-based approach for Belleville springs use in friction sliding structural connections. J. Constr. Steel Res. 2017, 138, 340–356. [Google Scholar] [CrossRef]
- Xu, L.; Fan, X.; Li, Z. Experimental behavior and analysis of self-centering steel brace with pre-pressed disc springs. J. Constr. Steel Res. 2017, 139, 363–373. [Google Scholar] [CrossRef]
- Krishnasamy, K.; Masse, F.; Simon, O. Fatigue analysis of Diaphragm spring in double dry clutch including manufacturing process. Procedia Eng. 2018, 213, 606–612. [Google Scholar] [CrossRef]
- Xu, L.; Fan, X.; Li, Z. Hysteretic analysis model for pre-pressed spring self-centering energy dissipation braces. J. Struct. Eng. 2018, 144, 04018073. [Google Scholar] [CrossRef]
- Xu, L.H.; Xie, X.S.; Li, Z.X. Development and experimental study of a self-centering variable damping energy dissipation brace. Eng. Struct. 2018, 160, 270–280. [Google Scholar] [CrossRef]
- Chang, Y.; Li, W.; Luo, H.; He, X.; Iannuzzo, F.; Blaabjerg, F.; Lin, W. A 3D thermal network model for monitoring imbalanced thermal distribution of press-pack IGBT modules in MMC-HVDC applications. Energies 2019, 12, 1319. [Google Scholar] [CrossRef]
- Fukasawa, T.; Okamura, S.; Somaki, T.; Miyagawa, T.; Uchita, M.; Yamamoto, T.; Watakabe, T.; Fujita, S. Research and Development of Three-Dimensional Isolation System for Sodium-Cooled Fast Reactor: Part 4—Proposal of Optimal Combination Method for Disc Spring Units and Newly Friction Model for Sliding Elements. In Pressure Vessels and Piping Conference; American Society of Mechanical Engineers: New York, NY, USA, 2019; p. V008T08A038. [Google Scholar]
- Shou, M.; Liao, C.; Zhang, H.; Xie, L. A design methodology based on full dynamic model for magnetorheological energy absorber equipped with disc springs. Smart Mater. Struct. 2019, 28, 065020. [Google Scholar] [CrossRef]
- Sapountzakis, I.E.; Tranakidis, P.G.; Antoniadis, I.A. Implementation of the KDamper concept using disc springs. J. Low Freq. Noise Vib. Act. Control 2019, 38, 168–186. [Google Scholar] [CrossRef]
- Sano, T.; Shirai, K.; Suzui, Y.; Utsumi, Y. Loading tests of a brace-type multi-unit friction damper using coned disc springs and numerical assessment of its seismic response control effects. Bull. Earthq. Eng. 2019, 17, 5365–5391. [Google Scholar] [CrossRef]
- Sun, Y.; Gong, D.; Zhou, J.; Sun, W.; Xia, Z. Low frequency vibration control of railway vehicles based on a high static low dynamic stiffness dynamic vibration absorber. Sci. China Technol. Sci. 2019, 62, 60–69. [Google Scholar] [CrossRef]
- Huang, X.; Su, Z.; Wang, S.; Wei, X.; Wang, Y.; Hua, H. High-frequency disturbance force suppression mechanism of a flywheel equipped with a flexible dynamic vibration absorber. J. Vib. Control 2020, 26, 2113–2124. [Google Scholar] [CrossRef]
- Xiao, S.J.; Xu, L.H.; Li, Z.X. Design and experimental verification of disc spring devices in self–centering reinforced concrete shear walls. Struct. Control Health Monit. 2020, 27, e2549. [Google Scholar] [CrossRef]
- Xiao, S.J.; Xu, L.H.; Li, Z.X. Development and experimental verification of self-centering shear walls with disc spring devices. Eng. Struct. 2020, 213, 110622. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, C.; Wang, Z.; Mao, K. Study on Dynamic Characteristics of the Disc Spring System in Vibration Screen. Shock Vib. 2020, 2020, 3518037. [Google Scholar] [CrossRef]
- Xu, L.H.; Xiao, S.J. A performance-based section design method of a self-centering concrete shear wall with disc spring devices. Eng. Mech. 2020, 37, 70–77. [Google Scholar]
- Menne, H.; Franck, C. Benchmarking the Suitability of a Bi-Stable Disc Spring as Novel Ultra-Fast Switchgear Actuation Principle. In 2020 CIGRE e-session. Papers and Proceedings; International Council on Large Electric Systems: Paris, France, 2020; p. A3302. [Google Scholar]
- Pal, U.; Palit, P.; Gokarn, P.; Kanrar, S.; Kumar, A. Improvement of wagon tippler disc spring life by design modification. Eng. Fail. Anal. 2021, 120, 105030. [Google Scholar] [CrossRef]
- Fang, C.; Wang, W.; Shen, D. Development and experimental study of disc spring–based self-centering devices for seismic resilience. J. Struct. Eng. 2021, 147, 04021094. [Google Scholar] [CrossRef]
- Mrázek, M.; Sedláček, F.; Skovajsa, M. Design of Composite Disc Spring for Automotive Suspension with using Numerical Simulation. Manuf. Technol. 2021, 21, 1213–2489. [Google Scholar] [CrossRef]
- Holtmann, C.; Köhler, C. (Eds.) Eddy Current and Friction Brake Fusion by a Disc-Spring to a Hybrid-Brake; International Council on Large Electric Systems (Cigré): Paris, France, 2021. [Google Scholar]
- Chen, R.; Li, X.; Xu, J.; Yang, Z.; Yang, H. Properties Analysis of Disk Spring with Effects of Asymmetric Variable Friction. Int. J. Appl. Mech. 2021, 13, 2150076. [Google Scholar] [CrossRef]
- Kumar, S. Design and Analysis of Weld Bead Cutting Tool Using FEA Technique with Experimental Verification of Cutting Force. In Advances in Mechanical Processing and Design; Springer: Singapore, 2021; pp. 581–592. [Google Scholar]
- Hong, G.; Zhongmin, D.; Yanlin, Z.; Hongbo, Y.; Xinjie, Z.; Lingzi, M.; Qi, L. Time-delayed feedback control of nonlinear dynamics in a giant magnetostrictive actuator. Nonlinear Dyn. 2022, 1–24. [Google Scholar] [CrossRef]
- DIN EN 16983:2017-09; Tellerfedern—Qualitätsanforderungen—Maße; Deutsche Fassung EN 16983:2016. DIN Deutsches Institut für Normung: Berlin, Germany, 2017.
- DIN EN 16984:2017-09; Tellerfedern—Berechnung; Deutsche Fassung EN 16984:2016. DIN Deutsches Institut für Normung: Berlin, Germany, 2017.
- Geilen, M.B.; Klein, M.; Oechsner, M. Spring_stack—Ein Modul zur numerischen Simulation von Tellerfedern und Tellerfedersäulen. In Ilmenauer Federntag 2019—Neueste Erkenntnisse zu Funktion, Berechnung, Prüfung und Gestaltung von Federn und Werkstoffen; ISLE: Ilmenau, Germany, 2019; pp. 77–86. [Google Scholar]
- Geilen, M.B.; Klein, M.; Oechsner, M. A Novel Algorithm for the Determination of Walker Damage in Loaded Disc Springs. Materials 2020, 13, 1661. [Google Scholar] [CrossRef] [PubMed]
- Almen, J.O.; Laszlo, A. The Uniform-Section Disc Spring. Trans. Am. Soc. Mech. Eng. 1936, 58, 305–314. [Google Scholar]
- Curti, G.; Orlando, M. Ein neues Berechnungsverfahren für Tellerfedern. Draht 1997, 30, 17–22. [Google Scholar]
- Zheng, E.; Jia, F.; Zhou, X. Energy-based method for nonlinear characteristics analysis of Belleville springs. Thin-Walled Struct. 2014, 79, 52–61. [Google Scholar] [CrossRef]
- Kobelev, V. Exact shell solutions for conical springs. Mech. Based Des. Struct. Mach. 2016, 44, 317–339. [Google Scholar] [CrossRef]
- Luxenburg, Y.; Givli, S. The Static Response of Axisymmetric Conical Shells Exhibiting Bistable Behavior. J. Appl. Mech. 2021, 88. [Google Scholar] [CrossRef]
- Curti, G.; Montanini, R. On the influence of friction in the calculation of conical disk springs. J. Mech. Des. 1999, 121, 622–627. [Google Scholar] [CrossRef]
- Ozaki, S.; Tsuda, K.; Tominaga, J. Analyses of static and dynamic behavior of coned disc springs: Effects of friction boundaries. Thin-Walled Struct. 2012, 59, 132–143. [Google Scholar] [CrossRef]
- Mastricola, N.P.; Dreyer, J.T.; Singh, R. Analytical and experimental characterization of nonlinear coned disk springs with focus on edge friction contribution to force-deflection hysteresis. Mech. Syst. Signal Process. 2017, 91, 215–232. [Google Scholar] [CrossRef]
- Chen, R.; Li, X.; Yang, Z.; Xu, J.; Yang, H. Nonlinear behavior of disk spring with complex contact state. Sci. Prog. 2021, 104, 00368504211052360. [Google Scholar] [CrossRef]
- Li, X.; Chen, R.; Yang, Z.; Yang, H.; Xu, J. Static behavior analysis of disc spring considering variable static friction coefficient. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 5583–5593. [Google Scholar] [CrossRef]
- Schremmer, G. Die geschlitzte Tellerfeder. Konstruktion 1972, 24, 226–229. [Google Scholar]
- Curti, G.; Orlando, M. Geschlitzte Tellerfedern. Draht 1981, 32, 608–615. [Google Scholar]
- Fawazi, N.; Lee, J.Y.; Oh, J.E. A load-displacement prediction for a bended slotted disc using the energy method. Proc. Inst. Mech. Engeneers, Part C J. Mech. Eng. Sci. 2012, 226, 2126–2137. [Google Scholar] [CrossRef]
- Wang, J.; Jian, L.; Leng, W.; She, C.; Sun, Z. An Analytical Model for the Stiffness of Slotted Disk Springs. Int. J. Appl. Mech. 2020, 12, 2050120. [Google Scholar] [CrossRef]
- La Rosa, G.; Messina, M.; Risitano, A. Stiffness of Variable Thickness Belleville Springs. J. Mech. Des. 2001, 123, 294. [Google Scholar] [CrossRef]
- Chaturvedi, R.; Trikha, M.; Simha, K.R. Theoretical and numerical analysis of stepped disk spring. Thin-Walled Struct. 2019, 136, 162–174. [Google Scholar] [CrossRef]
- Du, X.; Liao, C.; Gan, B.; Zhang, Y.; Xie, L.; Zhang, H. Analytical modeling and experimental verification for linearly gradient thickness disk springs. Thin-Walled Struct. 2021, 167, 108153. [Google Scholar] [CrossRef]
- Muhr, K.H.; Niepage, P. Zur Berechnung von Tellerfedern mit rechteckigem Querschnitt und Auflageflächen. Konstruktion 1966, 18, 24–27. [Google Scholar]
- Ferrari, G. A New Calculation Method for Belleville Disc Springs with Contact Flats and Reduced Thickness. Int. J. Manuf. Mater. Mech. Eng. 2013, 3, 63–73. [Google Scholar] [CrossRef][Green Version]
- Curti, G.; Appendino, D. Vergleich von Berechnungsverfahren für Tellerfedern. Draht 1982, 33, 38–40. [Google Scholar]
- Schiffner, K.; Dietrich, M. Numerische Simulation der Entstehung von Eigenspannungen 1. Art an Tellerfedern. ZAMM 1987, 67, 235–237. [Google Scholar]
- Wagner, W.; Wetzel, M. Berechnung von Tellerfedern mit Hilfe der Methode der Finiten Elemente. Konstruktion 1987, 39, 147–150. [Google Scholar]
- Bagavathiperumal, P.; Chandrasekaran, K.; Manivasagam, S. Elastic load-displacement predictions for coned disc springs subjected to axial loading using the finite element method. J. Strain Anal. 1991, 26, 147–152. [Google Scholar] [CrossRef]
- Curti, G.; Raffa, F.A. Material nonlinearity effects in the stress analysis of conical disk springs. J. Mech. Des. 1992, 114, 238–244. [Google Scholar] [CrossRef]
- Yahata, N.; Watanabe, M.; Ishii, N. Analysis of coned disc spring by finite element method. Jpn. Soc. Mech. Eng. 1993, 59, 260–265. [Google Scholar] [CrossRef][Green Version]
- Curti, G.; Montanini, R. Theoretical, Numerical and Experimental Analysis of Conical Disk Spring. XXV AIAS Gall. Lecce Sept. 1996, 1, 573. [Google Scholar]
- Lee, B.S. Load Characteristics and Sensitivity Analysis for an Automotive Clutch Diaphragm Spring. Trans. Korean Soc. Automot. Eng. 2006, 14, 54–59. [Google Scholar]
- Shen, W.; Fang, W. Design of a Friction Clutch Using Dual Belleville Structures. J. Mech. Des. 2007, 129, 986. [Google Scholar] [CrossRef]
- Berger, C.; Veleva, D. AVIF A 244: Experimentelle Untersuchung und numerische Simulation des Relaxationsverhaltens von Tellerfedern. In Abschlussbericht; TU Darmstadt: Darmstadt, Germany, 2010. [Google Scholar]
- Veleva, D.; Kaiser, B.; Berger, C. Experimentelle Untersuchung und numerische Simulation des Relaxationsverhaltens von Tellerfedern. In Ilmenauer Federntag 2010; ISLE: Illmenau, Germany, 2010; pp. 71–78. [Google Scholar]
- Wehmann, C.; Neidnicht, M.; Nützel, F.; Roith, B.; Rieg, F. Finite Elemente Analysen zur Berechnung von Maschinenelementen mit nichtlinearem Verhalten. In 8. Gemeinsames Kolloquium Konstruktionstechnik; Docupoint: Magdeburg, Germany, 2010; pp. 47–52. [Google Scholar]
- Karakaya, Ş. Investigation of hybrid and different cross-section composite disc springs using finite element method. Trans. Can. Soc. Mech. Eng. 2012, 36, 399–412. [Google Scholar] [CrossRef]
- Veleva, D. Experimentelle Untersuchung und numerische Simulation des Relaxationsverhaltens von Tellerfedern. Ph.D. Thesis, TU Darmstadt, Darmsatdt, Germany, 2012. [Google Scholar]
- Maletta, C.; Filice, L.; Furgiuele, F. NiTi Belleville washers: Design, manufacturing and testing. J. Intell. Mater. Syst. Struct. 2013, 24, 695–703. [Google Scholar] [CrossRef]
- Jia, F.; Zhang, F.C. A Study on the Mechanical Properties of Disc Spring Vibration Isolator with Viscous Dampers. Adv. Mater. Res. 2014, 904, 454–459. [Google Scholar] [CrossRef]
- Fang, C.; Zhou, X.; Osofero, A.I.; Shu, Z.; Corradi, M. Superelastic SMA Belleville washers for seismic resisting applications: Experimental study and modelling strategy. Smart Mater. Struct. 2016, 25, 105013. [Google Scholar] [CrossRef]
- Lonkwic, P.; Różyło, P.; Usydus, I. Numerical Analysis and Experimental Investigation of Disk Spring Configurations with Regard to Load Capacity of Safety Progressive Gears. Appl. Comput. Sci. 2016, 12, 5–16. [Google Scholar]
- Baak, N.; Garlich, M.; Schmiedt, A.; Bambach, M.; Walther, F. Characterization of residual stresses in austenitic disc springs induced by martensite formation during incremental forming using micromagnetic methods. Mater. Test. 2017, 59, 309–314. [Google Scholar] [CrossRef]
- Yubing, G.; Defeng, Z. Mechanism for the Forced Strengthening on the Diaphragm Spring’s Load-Deflection Characteristic. Int. J. Eng. Technol. 2017, 9, 287–292. [Google Scholar] [CrossRef][Green Version]
- Fang, C.; Yam, M.C.H.; Chan, T.M.; Wang, W.; Yang, X.; Lin, X. A study of hybrid self-centring connections equipped with shape memory alloy washers and bolts. Eng. Struct. 2018, 164, 155–168. [Google Scholar] [CrossRef]
- Zala, R.G.; Gawande, K.R. Disc Spring Washer: Design and Axisymmetric analysis using ANSYS. Trends Mach. Des. 2018, 4, 21–25. [Google Scholar]
- Zhu, D.; Ding, F.; Liu, H.; Zhao, S.; Liu, G. Mechanical property analysis of disc spring. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 230. [Google Scholar] [CrossRef]
- Koplin, C.; Schröder, C.; Beckert, W.; Stockmann, J.; Kailer, A. Demonstration der Zuverlässigkeit von keramischen Schraubendruck- und Tellerfedern für korrosive Umgebungen und hohe Temperaturen. In Ilmenauer Federntag 2019; ISLE: Illmenau, Germany, 2019; pp. 11–21. [Google Scholar]
- Khader, I.; Koplin, C.; Schröder, C.; Stockmann, J.; Beckert, W.; Kunz, W.; Kailer, A. Characterization of a silicon nitride ceramic material for ceramic springs. J. Eur. Ceram. Soc. 2020, 40, 3541–3554. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, C.; Wang, Z.; Mao, K.; Wang, X. A Study on the Influence of Different Constraint Modes and Number of Disc Springs on the Dynamics of Disc Spring System. Shock Vib. 2021, 2021, 8866159. [Google Scholar] [CrossRef]
- Niepage, P. Vergleich verschiedener Verfahren zur Berechnung von Tellerfedern—Teil I. Draht 1983, 34, 105–108; 255–258. [Google Scholar]
- Kobelev, V. Durability of Springs, 2nd ed.; Springer: Cham, Switzerland, 2021. [Google Scholar]


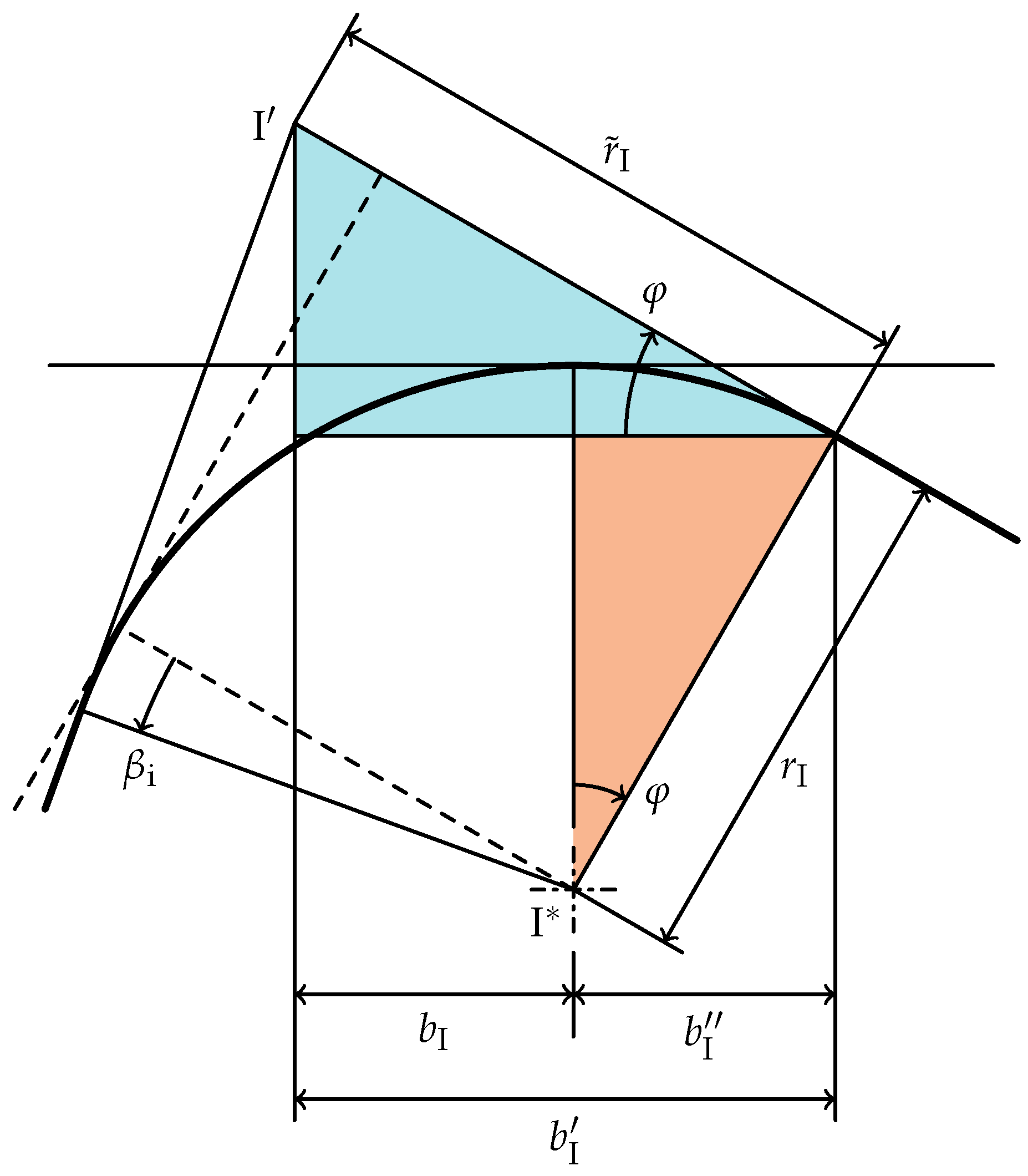

| Curti–Orlando Based | Kobelev Based | |||
|---|---|---|---|---|
| 0° | 5.09% | 4.22% | 5.58% | 3.69% |
| 5° | 7.36% | 1.73% | 7.88% | 2.35% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leininger, D.S.; Geilen, M.B.; Klein, M.; Oechsner, M. A New Method for the Calculation of Characteristics of Disc Springs with Trapezoidal Cross-Sections and Rounded Edges. Materials 2022, 15, 1954. https://doi.org/10.3390/ma15051954
Leininger DS, Geilen MB, Klein M, Oechsner M. A New Method for the Calculation of Characteristics of Disc Springs with Trapezoidal Cross-Sections and Rounded Edges. Materials. 2022; 15(5):1954. https://doi.org/10.3390/ma15051954
Chicago/Turabian StyleLeininger, Dominik Sebastian, Max Benedikt Geilen, Marcus Klein, and Matthias Oechsner. 2022. "A New Method for the Calculation of Characteristics of Disc Springs with Trapezoidal Cross-Sections and Rounded Edges" Materials 15, no. 5: 1954. https://doi.org/10.3390/ma15051954
APA StyleLeininger, D. S., Geilen, M. B., Klein, M., & Oechsner, M. (2022). A New Method for the Calculation of Characteristics of Disc Springs with Trapezoidal Cross-Sections and Rounded Edges. Materials, 15(5), 1954. https://doi.org/10.3390/ma15051954







