Evaluation of In Doped GaAs Alloys to Optimize Electronic, Thermoelectric and Mechanical Properties
Abstract
:1. Introduction
2. Method of Calculations
3. Results and Discussion
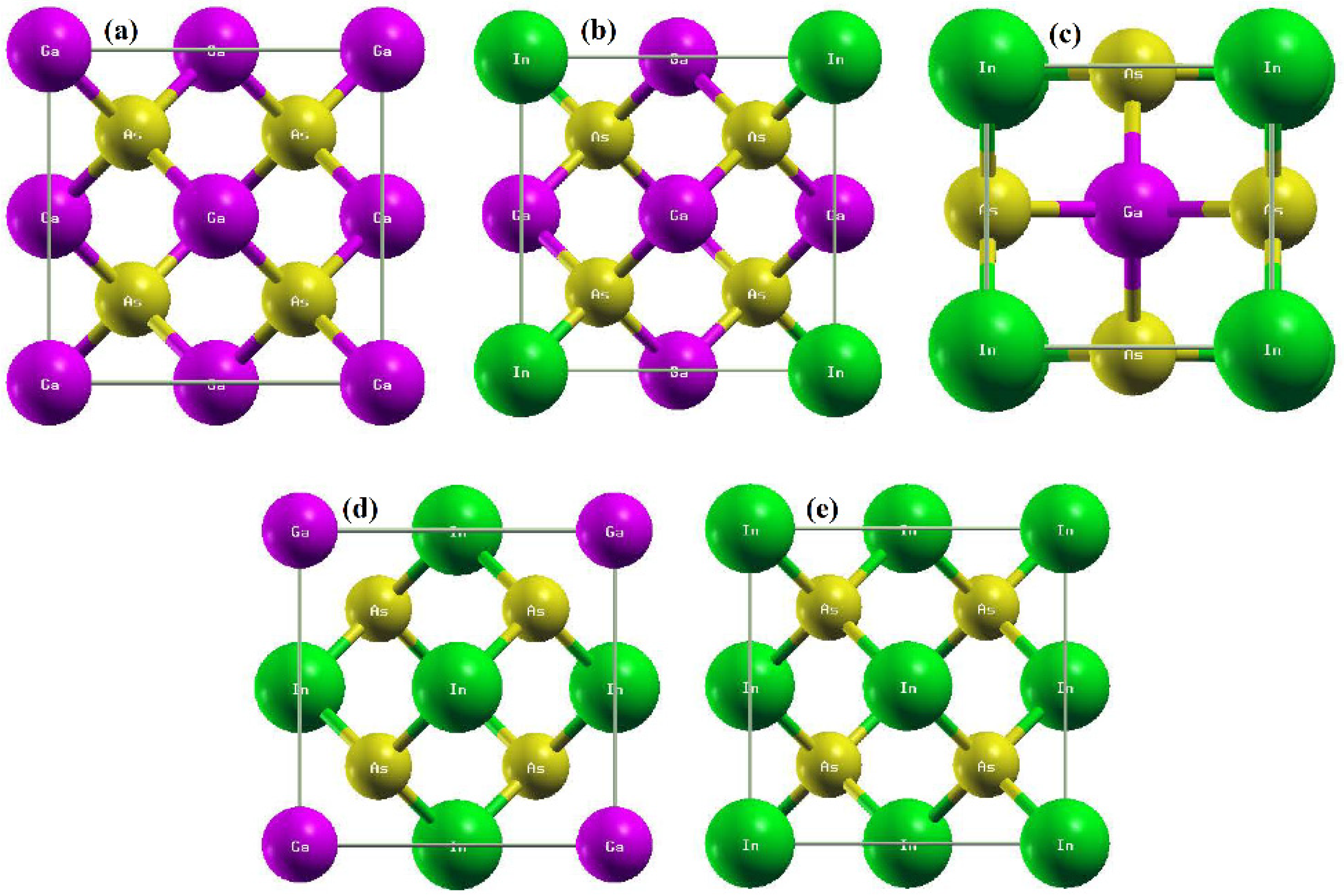
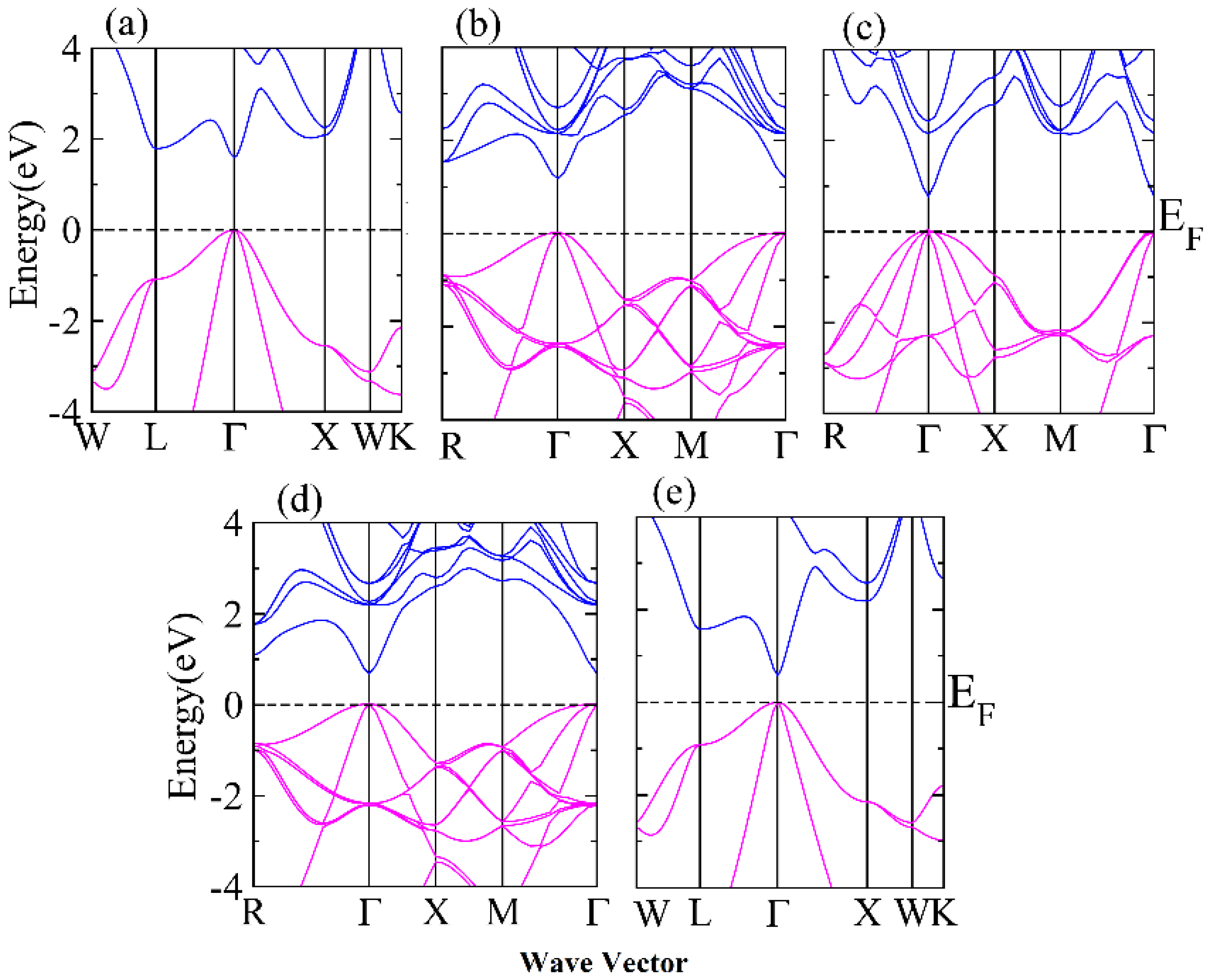
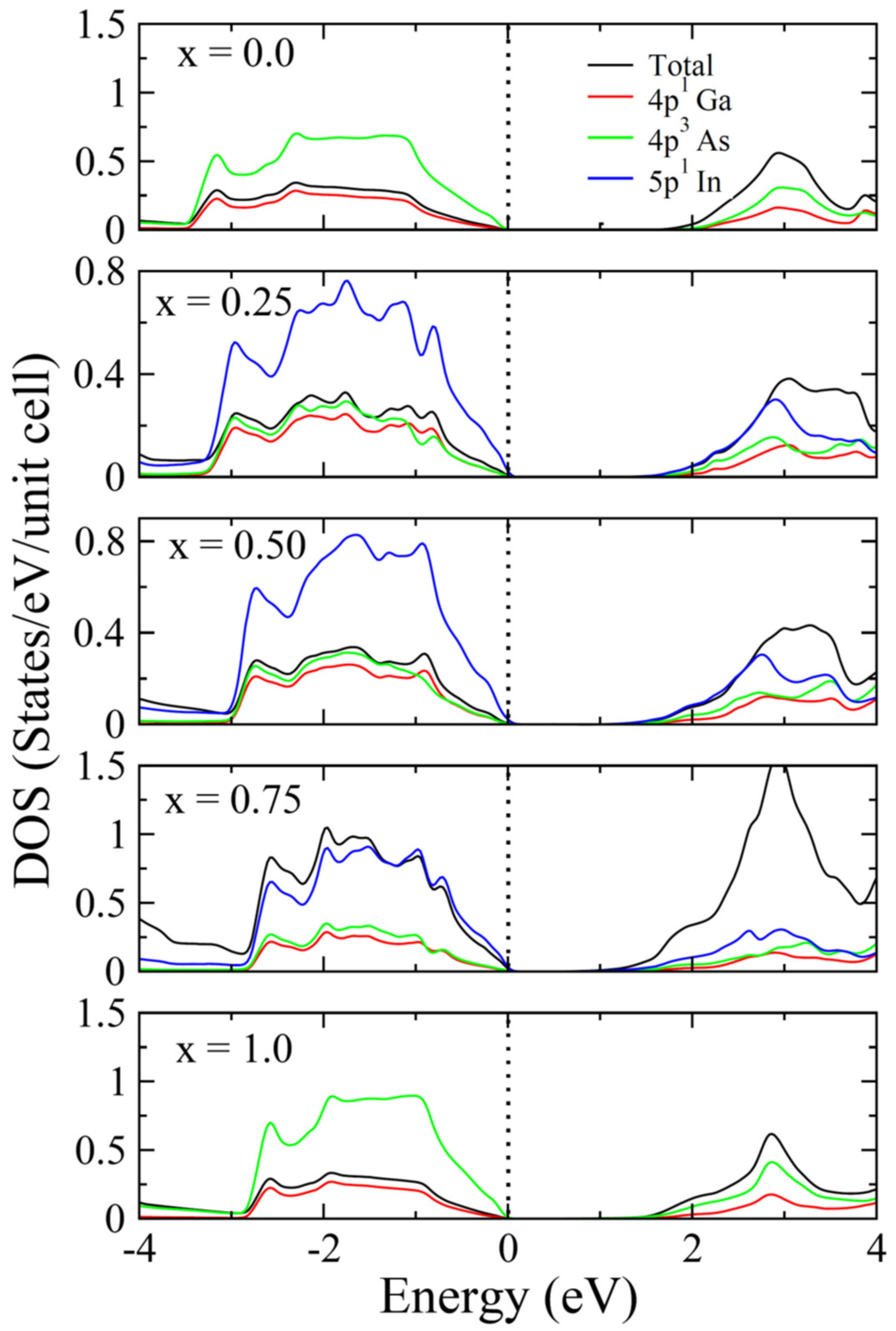
3.1. Structural and Electronic Behavior
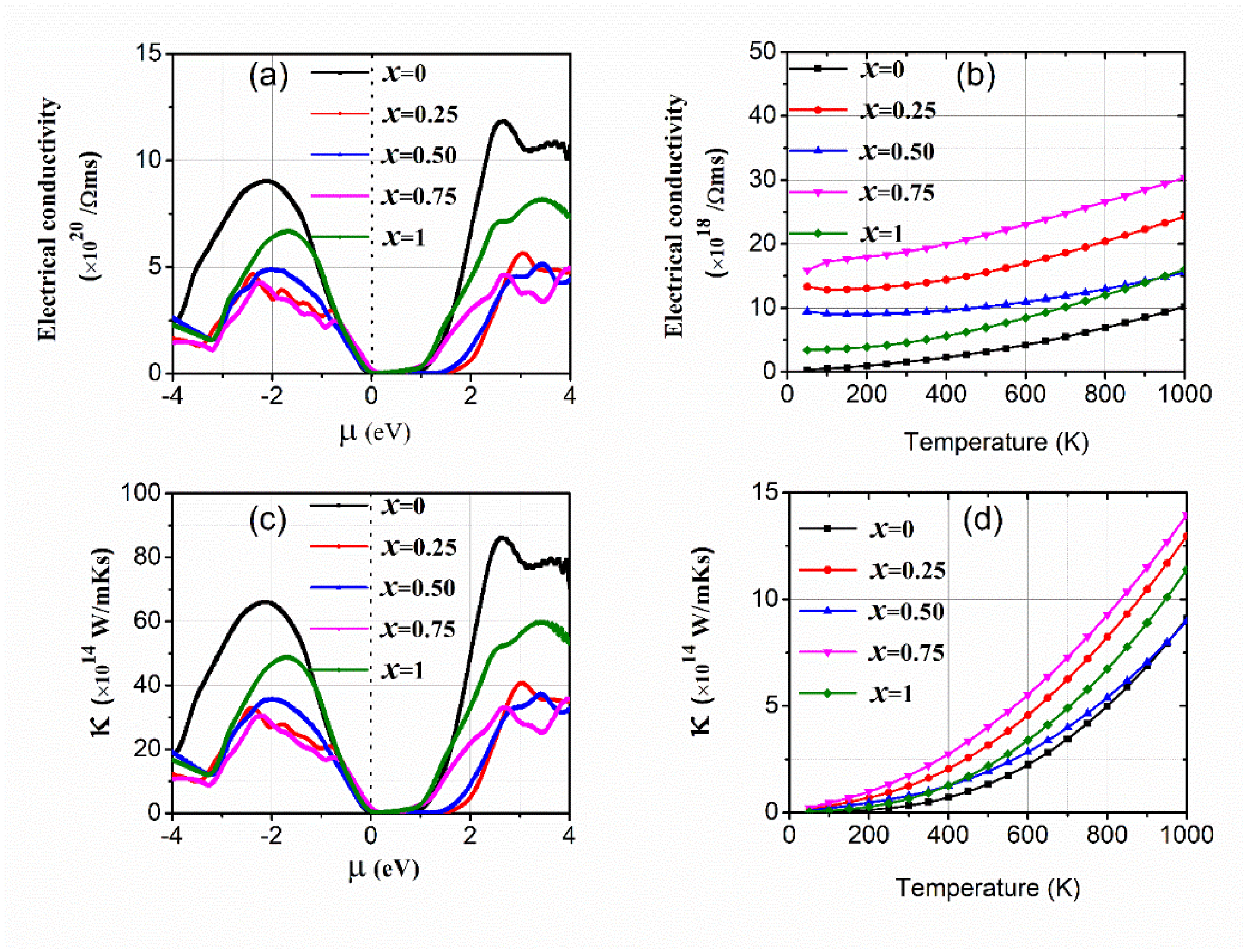
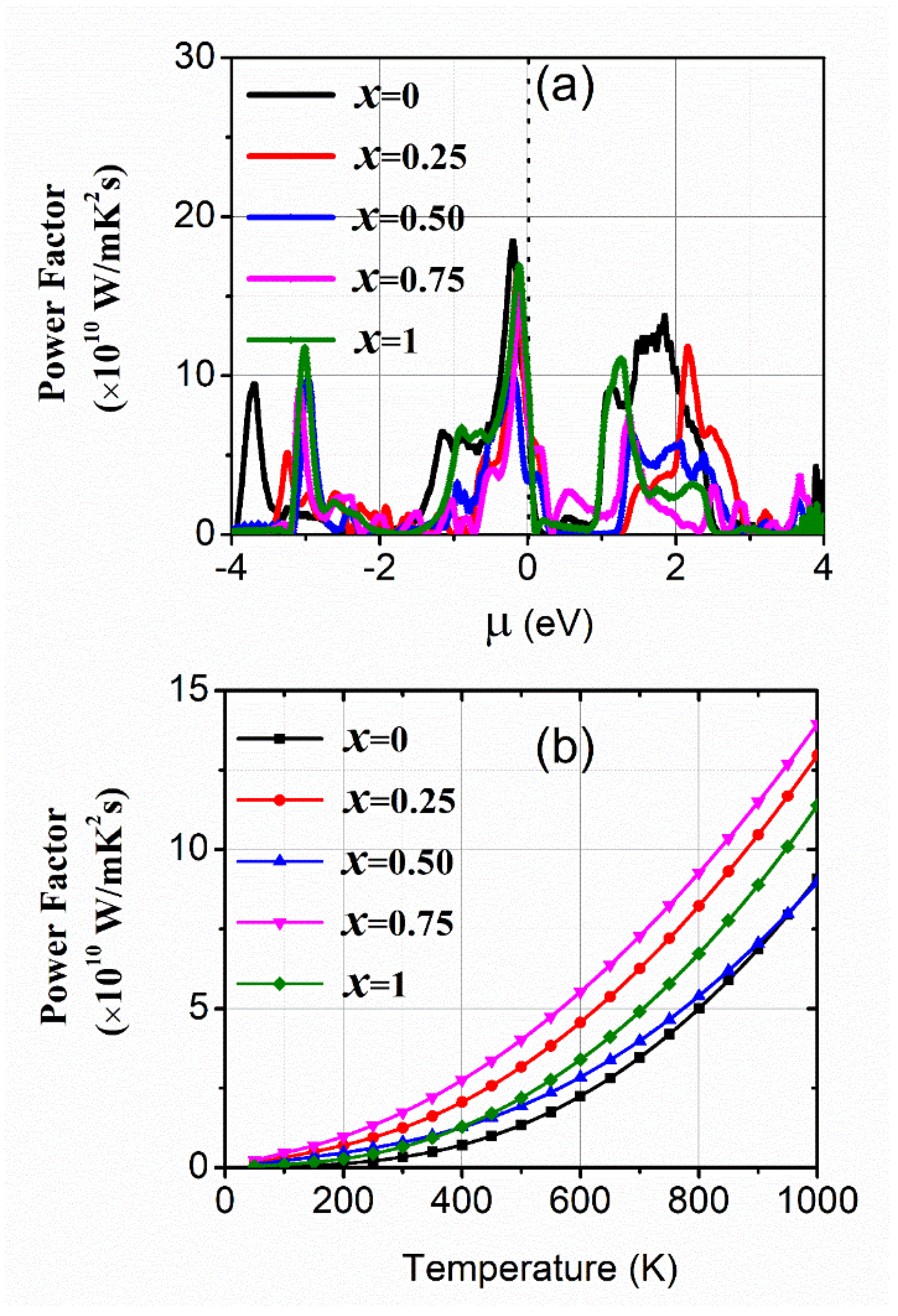
3.2. Transport Properties
3.3. Mechanical Properties
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akinlami, J.O.; Ashamu, A.O. Optical properties of GaAs. J. Semicond. 2013, 34, 032002. [Google Scholar] [CrossRef]
- Ajia, I.A.; Edwards, P.R.; Pak, Y.; Belekov, E.; Roldan, M.A.; Wei, N.; Liu, Z. Generated carrier dynamics in V-pit-enhanced InGaN/GaN light-emitting diode. ACS Photonics 2017, 5, 820–826. [Google Scholar] [CrossRef] [Green Version]
- Muhammed, M.M.; Alwadai, N.; Lopatin, S.; Kuramata, A.; Roqan, I.S. High-efficiency InGaN/GaN quantum well-based vertical light-emitting diodes fabricated on β-Ga2O3 substrate. ACS Appl. Mater. Interfaces 2017, 9, 34057–34063. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Sun, H.; Jia, I.A.A.; Roqan, I.S.; Zhang, D.; Dai, J.; Chen, C.; Feng, Z.C.; Li, X. Significant internal quantum efficiency enhancement of GaN/AlGaN multiple quantum wells emitting at ~350 nm via step quantum well structure design. J. Phys. D Appl. Phys. 2017, 50, 245101. [Google Scholar] [CrossRef]
- Alfaraj, N.; Mitra, S.; Wu, F.; Ajia, I.A.; Janjua, B.; Prabaswara, A.; Aljefri, R.A.; Sun, H. Photoinduced entropy of InGaN/GaN pin double-heterostructure nanowires. Appl. Phys. Lett. 2017, 110, 161110. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Schwingenschlögl, U.; Roqan, I.S. Vacancy complexes induce long-range ferromagnetism in GaN. J. Appl. Phys. 2015, 116, 183905. [Google Scholar] [CrossRef] [Green Version]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Tibermacine, T.; Mercizga, A. Revue des energies recoverable. Alger. Sci. J. Platf. 2009, 12, 125. [Google Scholar]
- Colombo, C.; Heiss, M.; Grätzel, M.; Morral, A.F.I. Gallium arsenide P-I-N radial structures for photovoltaic applications. Appl. Phys. Lett. 2009, 94, 173108. [Google Scholar] [CrossRef]
- Ng, K.K. Complete Guide to Semiconductor Device, 2nd ed.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Kendall, E.J.M. Transistors; Pergamon Press: New York, NY, USA, 1969. [Google Scholar]
- Liou, J.J.; Schwierz, F. RF MOSFET: Recent advances, status, and future trends. Solid-State Electron. 2003, 47, 1881. [Google Scholar] [CrossRef]
- Zhou, F.; Moore, A.L.; Bolinsson, J.; Persson, A.; Froberg, L.; Pettes, M.T.; Kong, H.; Rabenberg, L.; Caroff, P.; Stewart, D.A.; et al. Thermal conductivity of indium arsenide nanowires with wurtzite and zinc blende phases. Phys. Rev. B 2011, 83, 205416. [Google Scholar] [CrossRef] [Green Version]
- Warren, M.V.; Canniff, J.C.; Chi, H.; Morag, E.; Naab, F.; Stoica, V.A.; Clarke, R.; Uher, C.; Goldman, R.S. Influence of embedded indium nanocrystals on GaAs thermoelectric properties. J. Appl. Phys. 2013, 114, 043704. [Google Scholar] [CrossRef]
- Haq, B.U.; Ahmed, R.; Hassan, F.E.H.; Khenata, R.; Kasmin, M.K.; Goumri-Said, S. Mutual alloying of XAs (x = Ga, In, Al) materials: Tuning the optoelectronic and thermodynamic properties for solar energy applications. Sol. Energy 2014, 100, 1–8. [Google Scholar] [CrossRef]
- Rodríguez-Jiménez, J.A.; Aguilera-Granja, F.; Robles, J.; Vega, A. On the doping of the Ga12As12 cluster w ith groups p and d atomic impurities. Theor. Chem. Acc. 2021, 140, 160. [Google Scholar] [CrossRef]
- Gutsev, G.L.; Mochena, M.D.; Bauschlicher, C.W., Jr. Structure and magnetic properties of (GaAs)nMnm and (GaAs)nFem clusters. Chem. Phys. Lett. 2007, 439, 95–101. [Google Scholar] [CrossRef]
- Gutsev, G.L.; Mochena, M.D.; Saha, B.C.; Weatherford, C.A.; Derosa, P.A. Structure and properties of (GaAs)n clusters. J. Comp. Theo. Nano. 2010, 7, 254–263. [Google Scholar] [CrossRef]
- Schwarz, K.; Blaha, P.; Madsen, G.K.H. Electronic structure calculations of solids using the WIEN2k package for material sciences. Comp. Phys. Commun. 2002, 147, 71–76. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J. Wien2K Code, an Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties; Vienna University of Technology: Vienna, Austria, 2016. [Google Scholar]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [Green Version]
- Tran, F.; Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 2009, 102, 226401. [Google Scholar] [CrossRef] [Green Version]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 2006, 175, 67–71. [Google Scholar] [CrossRef] [Green Version]
- Blakemore, S.J. Semiconducting and other major properties of gallium arsenide. J. Appl. Phys. 1982, 53, R123–R181. [Google Scholar] [CrossRef]
- Levinshtein, M.E.; Rumyantsev, S.L. Handbook Series on Semiconductor Parameters; Levinshtein, M., Rumyantsev, S., Shur, M., Eds.; World Scientific: London, UK, 1996; Volume 1, pp. 77–103. [Google Scholar]
- Glazov, V.M.; Pashinkin, A.S. Thermal expansion and heat capacity of GaAs and InAs. Inorg. Mater. 2000, 36, 225–231. [Google Scholar] [CrossRef]
- Sabir, B.; Murtaza, G.; Mahmood, Q.; Ahmad, R.; Bhamu, K.C. First principles investigations of electronics, magnetic, and thermoelectric properties of rare earth based PrYO3 (Y = Cr, V) perovskites. Curr. Appl. Phys. 2017, 17, 1539–1546. [Google Scholar] [CrossRef]
- Strauch, D.; Dorner, B. Phonon dispersion in GaAs. J. Phys. Condens. Matter 1990, 2, 1457. [Google Scholar] [CrossRef]
- Dabhi, S.D.; Jha, P.K. Phonon dispersion and Raman spectra of wurtzite InAs under pressure. J. Phys. Chem. Solids 2015, 83, 70–74. [Google Scholar] [CrossRef]
- Biswas, K.; He, J.; Blum, I.D.; Wu, C.I.; Hogan, T.P.; Seidman, D.N.; Dravid, V.P.; Kanatzidis, M.G. High-performance bulk thermoelectric with all-scale hierarchical architectures. Nature 2012, 489, 414–418. [Google Scholar] [CrossRef]
- Goldsmid, H.J.; Douglas, R.W. The use of semiconductors in thermoelectric refrigeration. J. Appl. Phys. 1954, 5, 386–390. [Google Scholar]
- Tritt, T.M. Thermoelectric phenomena, materials, and applications. Rev. Mater. Res. 2011, 41, 433–448. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states. Science 2008, 321, 554–557. [Google Scholar] [CrossRef] [Green Version]
- Kawano, T.; Takahashi, J.; Okutani, T.; Yamada, T.; Yamane, H. Synthesis, crystal structures and high-temperature thermoelectric properties of spinel-type cobalt ruthenium oxides. J. Alloys Compd. 2009, 468, 447–451. [Google Scholar] [CrossRef]
- Mahmood, Q.; Ghrib, T.; Rached, A.; Laref, A.; Kamran, M.A. Probing of mechanical, optical, and thermoelectric characteristics of double perovskites Cs2GeCl/Br6 by DFT method. Mater. Sci. Semi. Proc. 2020, 112, 105009. [Google Scholar] [CrossRef]
- Khan, T.T.; Ur, S.C. Thermoelectric properties of the perovskites-type oxide SrTi1−xNbxO3 synthesized by solid-state reaction method. Electron. Mater. Lett. 2018, 14, 336–341. [Google Scholar] [CrossRef]
- Oyama, T.; Muta, H.; Uno, M.; Yamanaka, S. Thermoelectric properties of perovskites type barium molybdate. J. Alloys Compd. 2004, 372, 65–69. [Google Scholar]
- Kumar, N.R.; Radhakrishnan, R. Electronic, optical, and mechanical properties of lead-free halide double perovskites using first-principles density functional theory. Mater. Lett. 2018, 227, 289–291. [Google Scholar] [CrossRef]
- Ji, X.; Yu, Y.; Ji, J.; Long, J.; Chen, J.; Liu, D. Theoretical studies of the pressure induced phase transition and elastic properties of BeS. J. Alloys Compd. 2015, 623, 304–310. [Google Scholar] [CrossRef]
- Roknuzzaman, M.; Ostrikov, K.; Wang, H.; Du, A.; Tesfamichael, T. Towards lead-free perovskite photovoltaics and optoelectronics by ab-initio simulations. Sci. Rep. 2017, 7, 14025. [Google Scholar] [CrossRef]
- Noor, N.; Mahmood, Q.; Rashid, M.; Haq, B.U.; Laref, A. The pressure-induced mechanical and optoelectronic behavior of cubic perovskite PbSnO3 via ab-initio investigations. Ceram. Int. 2018, 44, 13750–13756. [Google Scholar] [CrossRef]
- Ciftci, Y.O.; Colakoglu, K.; Deligoz, E.; Ozissk, H. The first-principles study on the LaN. Mater. Chem. Phys. 2008, 108, 120–123. [Google Scholar] [CrossRef]
- Hao, Y.J.; Chen, X.R.; Cui, H.L.; Bai, Y.L. First-principles calculations of elastic constants of c-BN. Phys. B Condens. Matter 2006, 382, 118–122. [Google Scholar] [CrossRef]
- Singh, R.; Balasubramanian, G. Impeding phonon transport through super-lattices of organic-inorganic halide perovskites. RSC Adv. 2017, 7, 37015–37020. [Google Scholar] [CrossRef] [Green Version]
- Marathe, M.; Grunebohm, A.; Nishimatsu, T.; Entel, P.; Ederer, C. First-principles based calculation of the electrocaloric effect: A comparison of direct and indirect methods. Phys. Rev. B 2016, 93, 054110. [Google Scholar] [CrossRef] [Green Version]

| Parameter | x = 0.0 | x = 0.25 | x = 0.50 | x = 0.75 | x = 1.0 |
|---|---|---|---|---|---|
| ao | 5.66 | 5.75 | 5.90 | 5.97 | 6.09 |
| Bo | 69.34 | 66.12 | 63.56 | 60.16 | 57.84 |
| Hf | −0.36 | −0.32 | −0.27 | −0.25 | −0.23 |
| Eg | 1.55 | 1.25 | 0.90 | 0.73 | 0.57 |
| Composition | (×1018/Ωms) | (×1013 W/mKs) | Seebeck Coefficient (μV/K) | PF (×1010 W/mK2s) |
|---|---|---|---|---|
| GaAs | 1.57 | 3.32 | 223.63 | 7.30 |
| Ga0.75In0.25As | 13.58 | 12.48 | 71.47 | 6.94 |
| Ga0.50In0.50As | 9.29 | 7.90 | 60.78 | 3.42 |
| Ga0.25In0.75As | 18.80 | 17.36 | 62.70 | 8.39 |
| InAs | 4.58 | 6.50 | 148.83 | 7.50 |
| Parameters | x = 0.0 | x = 0.25 | x = 0.50 | x = 0.75 | x = 1.0 |
|---|---|---|---|---|---|
| C11 (GPa) | 99 | 91 | 83 | 77 | 71 |
| C12 (GPa) | 43 | 42 | 41 | 39 | 38 |
| C44 (GPa) | 51 | 46 | 41 | 38 | 34 |
| B (GPa) | 61 | 58 | 55 | 52 | 49 |
| G (GPa) | 41 | 36 | 31 | 26 | 25 |
| E (GPa) | 99 | 88 | 79 | 73 | 65 |
| B/G | 1.53 | 1.63 | 1.75 | 1.80 | 1.92 |
| υ | 0.23 | 0.24 | 0.25 | 0.26 | 0.28 |
| A | 1.82 | 1.90 | 1.95 | 2.0 | 2.06 |
| ξ | 0.56 | 0.58 | 0.61 | 0.63 | 0.65 |
| Vm (Km/s) | 5.06 | 5.85 | 5.66 | 5.39 | 3.74 |
| ϴD (K) | 321 | 295 | 268 | 253 | 312 |
| Tm (K) | 1138 | 1090 | 1043 | 1008 | 972 |
| Ha (GPa) | 184 | 148 | 115 | 101 | 80.2 |
| Kmin (Wm−1K−1) | 0.28 | 0.26 | 0.25 | 0.23 | 0.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhodaib, A. Evaluation of In Doped GaAs Alloys to Optimize Electronic, Thermoelectric and Mechanical Properties. Materials 2022, 15, 1781. https://doi.org/10.3390/ma15051781
Alhodaib A. Evaluation of In Doped GaAs Alloys to Optimize Electronic, Thermoelectric and Mechanical Properties. Materials. 2022; 15(5):1781. https://doi.org/10.3390/ma15051781
Chicago/Turabian StyleAlhodaib, Aiyeshah. 2022. "Evaluation of In Doped GaAs Alloys to Optimize Electronic, Thermoelectric and Mechanical Properties" Materials 15, no. 5: 1781. https://doi.org/10.3390/ma15051781
APA StyleAlhodaib, A. (2022). Evaluation of In Doped GaAs Alloys to Optimize Electronic, Thermoelectric and Mechanical Properties. Materials, 15(5), 1781. https://doi.org/10.3390/ma15051781






