Hot Deformation Behaviour and Constitutive Equation of Mg-9Gd-4Y-2Zn-0.5Zr Alloy
Abstract
:1. Introduction
2. Methods and Experimental Section
3. Results and Discussion
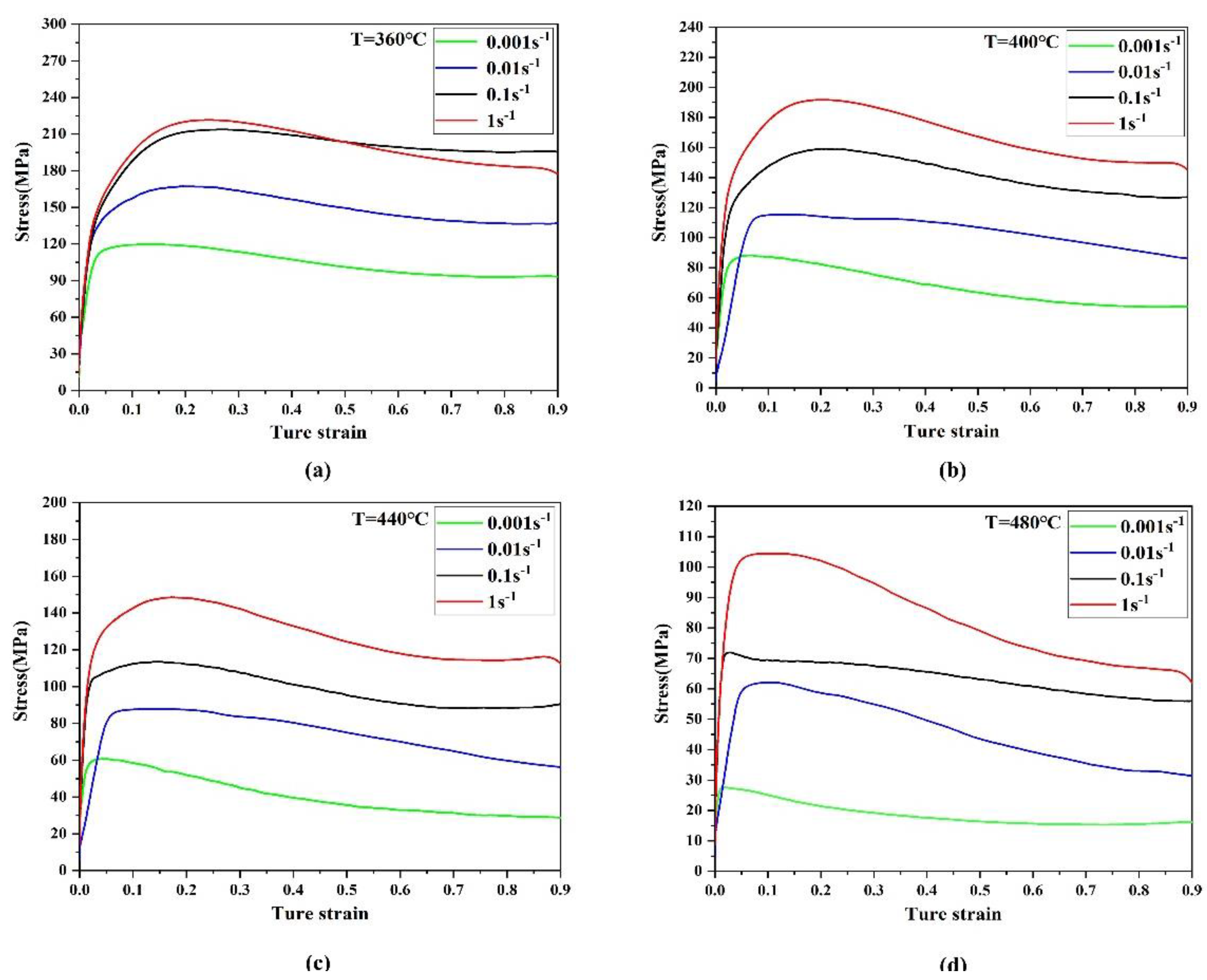
3.1. True Stress-True Strain Curve
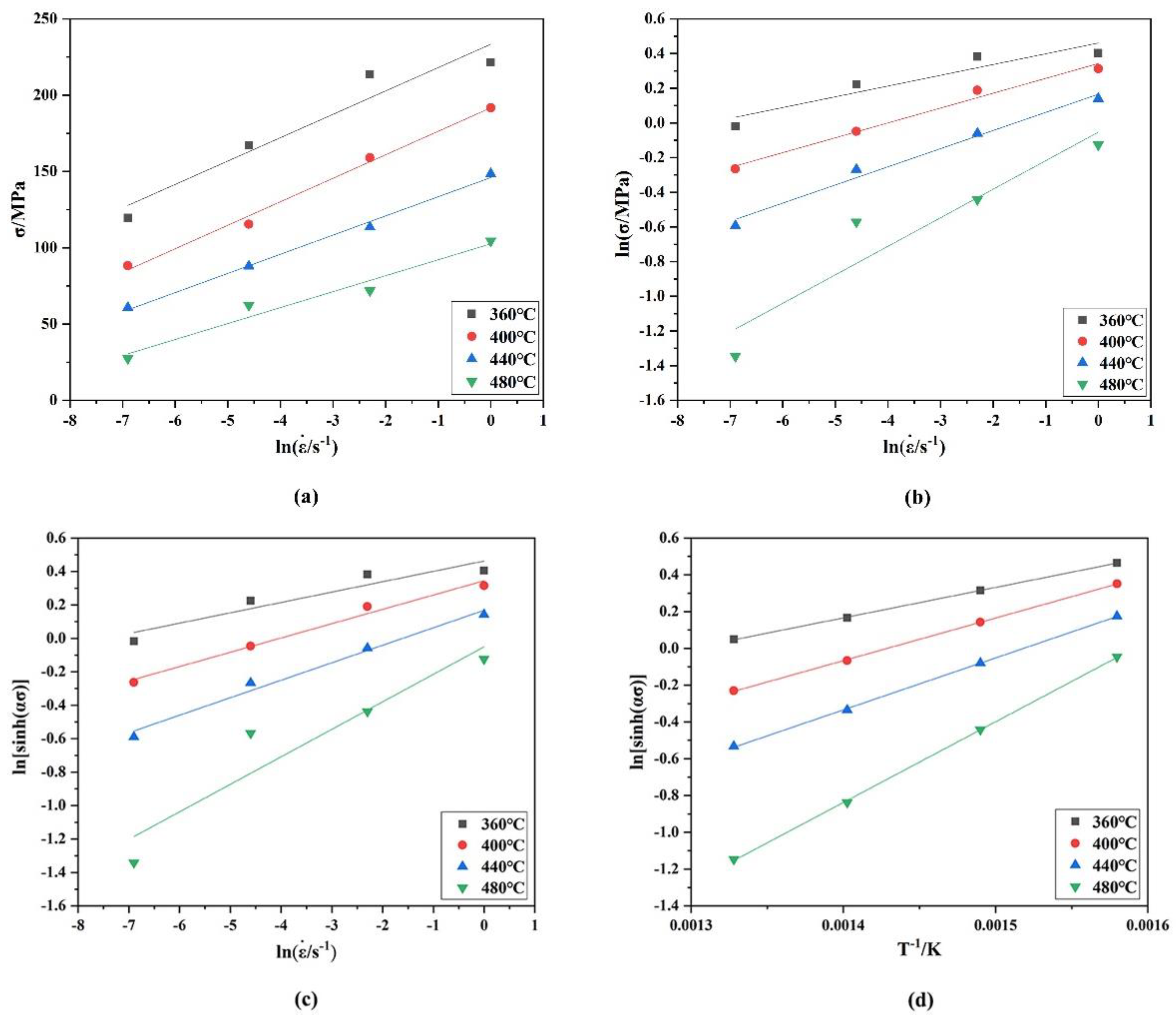
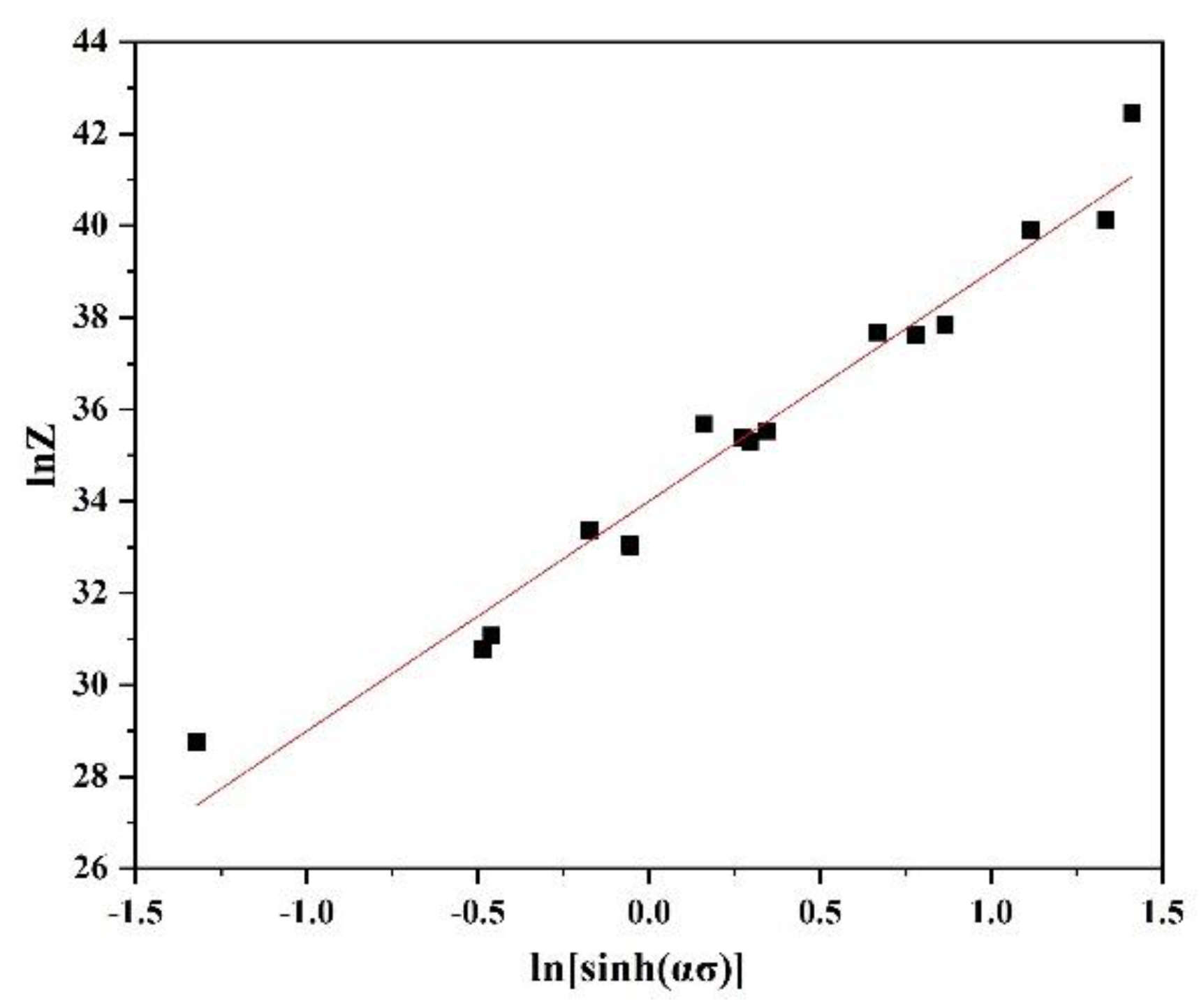
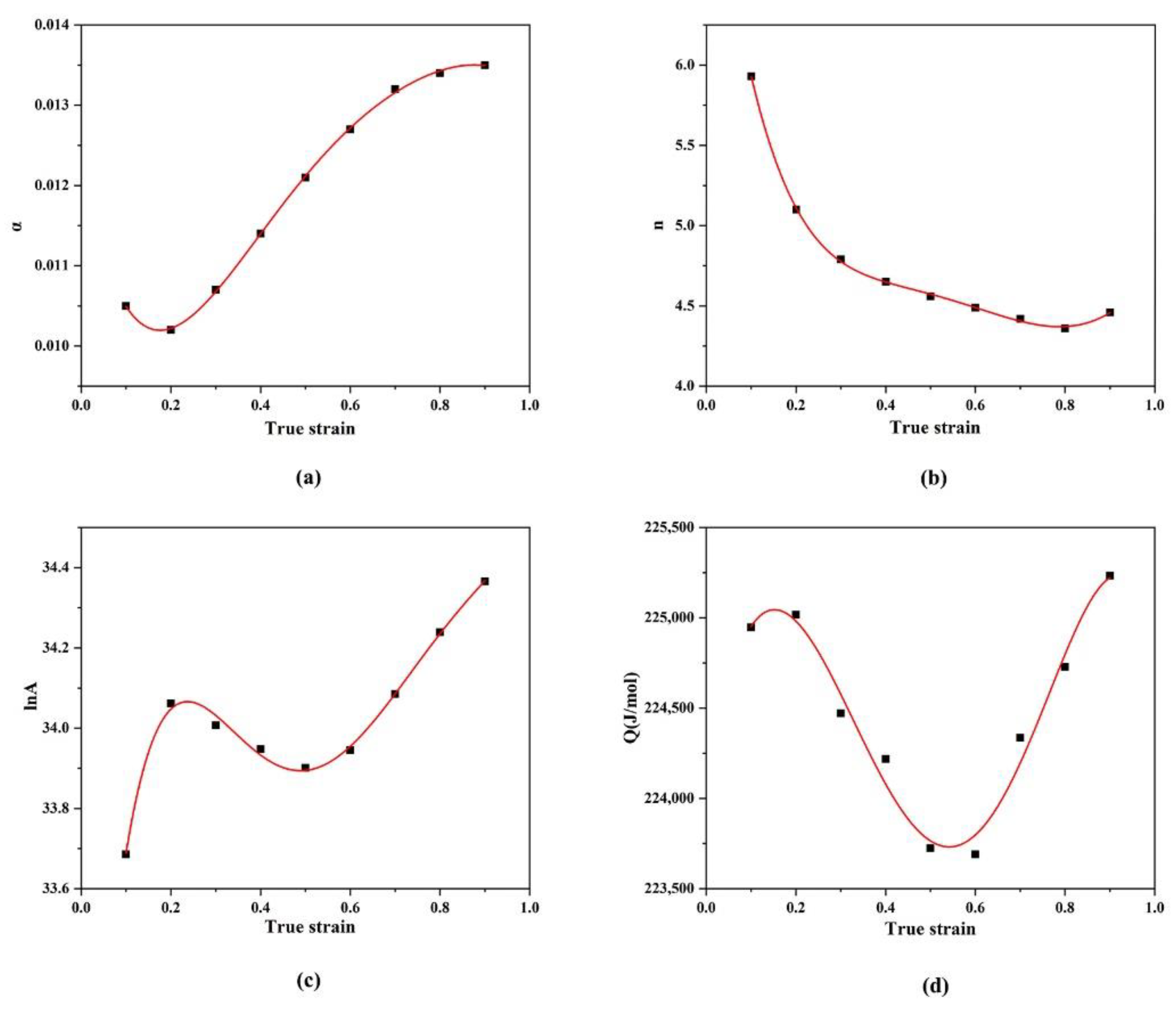
3.2. The Establishment of a Constitutive Equation
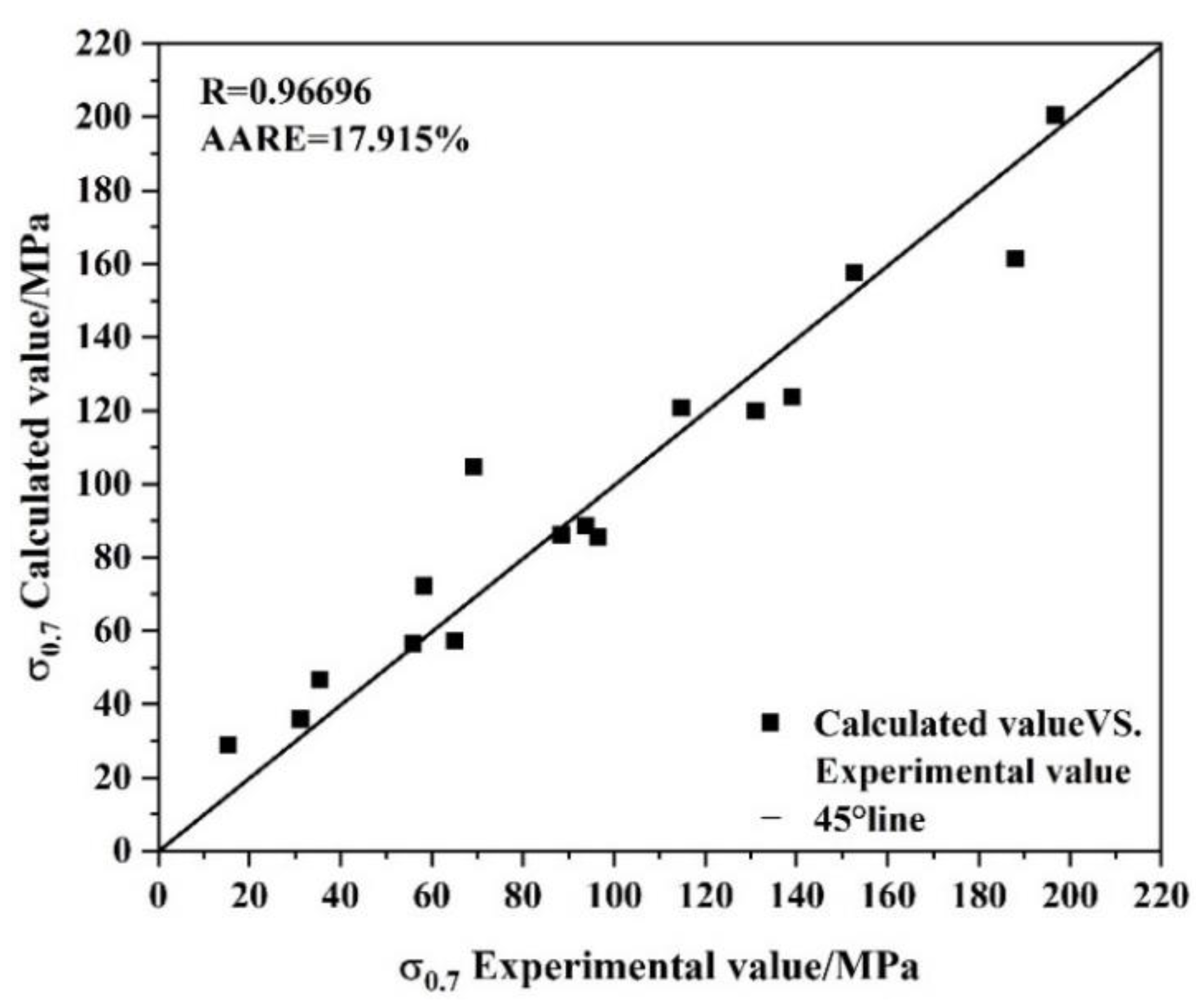
3.3. Error Analysis
3.4. Processing Map
4. Conclusions
- The effect of deformation softening can be improved by increasing deformation temperature and decreasing strain rate. The increase in deformation temperature provides more energy and higher grain boundary mobility, which lead to the nucleation and growth of dynamically recrystallized grains and reduce the flow stress level. The dislocations fully spread to achieve reorganization while the strain rate decreases, thus increasing the DRX degree and softening effect. Shear bands and microcracks occurred in the Mg-9Gd-4Y-2Zn-0.5Zr alloy deformed at the temperature of 360–400 °C and strain rate of 0.01–1 s−1.
- Strain has a great influence on material constants, and the constitutive equation constructed by polynomial fitting of material constants corresponding to different strain variables is:
- We observed an obvious effect of strain on the peak power dissipation rate coefficient and instability range. With increasing strain, the dissipation coefficient of the peak power decreased, and the instability range increased gradually. According to the analysis of the hot working diagram, the optimum hot working conditions were a temperature of 400–480 °C and a strain rate of 0.001–0.01 s−1.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, Z.; Lie, X.; Zhen, J. Microstructure evolution, texture and mechanical properties of a Mg–Gd–Y–Zn–Zr alloy fabricated by cyclic expansion extrusion with an asymmetrical extrusion cavity: The influence of passes and processing route. J. Magnes. Alloy. 2021, 9, 964–982. [Google Scholar] [CrossRef]
- Chen, X.; Ning, F.; Hou, J.; Le, Q.; Tang, Y. Dual-frequency ultrasonic treatment on microstructure and mechanical properties of ZK60 magnesium alloy. Ultrason. Sonochem. 2018, 40 Pt A, 433–441. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, J.; Song, H.; Liu, P. Research Situation on Application of Magnesium Alloys and Its Forming Technology. Hot Work. Technol. 2013, 42, 24–27. [Google Scholar]
- Polmear, I.J. Magnesium alloys and applications. Mater. Sci. Technol. 1994, 10, 1–16. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Zhao, Y. Research and future development of wrought magnesium alloy. Hot Work. Technol. 2011, 40, 54–55. [Google Scholar]
- Chen, T.; Chen, Z.Y.; Shao, J.B.; Wang, R.K.; Mao, L.H.; Liu, C.M. Evolution of LPSO phases in a Mg-Zn-Y-Gd-Zr alloy during semi-continuous casting, homogenization and hot extrusion. Mater. Des. 2018, 152, 1–9. [Google Scholar] [CrossRef]
- Chino, Y.; Mabuchi, M.; Hagiwara, S.; Iwasaki, H.; Yamamoto, A.; Tsubakino, H. Novel equilibrium two phase Mg alloy with the long-period ordered structure. Scr. Mater. 2004, 51, 711–714. [Google Scholar] [CrossRef]
- Fei, F.; Huang, S.; Meng, Z.; Hu, J.; Yang, J. A constitutive and fracture model for AZ31B magnesium alloy in the tensile state. Mater. Sci. Eng. A 2014, 594, 334–343. [Google Scholar]
- Ren, L.; Quan, G.; Zhou, M.; Guo, Y.; Jiang, Z.; Tang, Q. Effect of Y addition on the aging hardening behavior and precipitation evolution of extruded Mg-Al-Zn alloys. Mater. Sci. Eng. A 2017, 690, 195–207. [Google Scholar] [CrossRef]
- Zhao, Z.; Teng, X.; Zhou, G.; Leng, J.; Geng, J. Effect of Mg-Zn-Nd quasicrystals on corrosion resistance of AZ91 alloy. Rare Met. Mater. Eng. 2014, 43, 791–795. [Google Scholar] [CrossRef] [Green Version]
- Cui, C.; Wu, R.; Wang, H. Thermodynamic properties of rare earth elements and their application in metal matrix composites. Rare Met. Mater. Eng. 1997, 26, 53–58. [Google Scholar]
- Honma, T.; Ohkubo, T.; Hono, K.; Kamado, S. Chemistry of nanoscale precipitates in Mg–2.1Gd–0.6Y–0.2Zr (at.%) alloy investigated by the atom probe technique. Mater. Sci. Eng. A 2005, 395, 301–306. [Google Scholar] [CrossRef]
- Kawamura, Y.; Hayashi, K.; Inoue, A.; Masumoto, T. Rapidly Solidified Powder Metallurgy Mg97Zn1Y2Alloys with Excellent Tensile Yield Strength above 600 MPa. Mater. Trans. 2001, 42, 1172–1176. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Li, Y.; Zhang, K. Microstructure and hot deformation behavior of the Mg-8 wt.% Sn-1.5 wt.% Al alloy. Materials 2021, 14, 2050. [Google Scholar] [CrossRef] [PubMed]
- Bao, C.; Zhou, T.; Shi, L. Hot Deformation behavior and constitutive analysis of as-extruded Mg-6Zn-5Ca-3Ce alloy fabricated by rapid solidification. Metals 2021, 11, 480. [Google Scholar] [CrossRef]
- Wang, J.; Wang, B.; Wang, Y. Hot compression behavior and processing diagram of cast Mg-4Al-2Sn-Y-Nd magnesium alloy. Trans. Nonferrous Met. Soc. China 2014, 24, 626–631. [Google Scholar] [CrossRef]
- Hui, Y.U.; Yu, H.S.; Kim, Y.M.; You, B.S.; Min, G.H. Hot deformation behavior and processing maps of Mg-Zn-Cu-Zr magnesium alloy. Trans. Nonferr. Met. Soc. China 2013, 23, 756–764. [Google Scholar]
- Yamada, K.; Okubo, Y.; Shiono, M.; Watanabe, H.; Kamado, S.; Kojima, Y. Alloy development of high toughness Mg-Gd-Y-Zn-Zr alloys. Mater. Trans. 2006, 47, 1066–1070. [Google Scholar] [CrossRef] [Green Version]
- Yan, Z.; Zhu, J.; Zhang, Z. hot deformation behavior and processing map of A Mg-Gd-Y-Zn-Zr alloy. Mater. Tehnol. 2021, 55, 781–788. [Google Scholar] [CrossRef]
- Zhang, X.L.; Fu-Guo, L.I.; Peng, F.H.; Huang, Y.S.; Shuai, C.L. Hot workability of Ti-6Al-4V alloy based on processing map. J. Aeronaut. Mater. 2007, 27, 40–44. [Google Scholar]
- Yang, J.; Zhang, P.; Zhao, S. Hot deformation constitutive equation of TC4-DT titanium alloy. J. Plast. Eng. 2016, 23, 120–125. [Google Scholar]
- Sellars, C.M.; Whiteman, J.A. Recrystallization and grain growth in hot rolling. Met. Sci. 1979, 13, 187–194. [Google Scholar] [CrossRef]
- Zener, C.; Hollomom, J.H. Effect of strain rate upon plastic flow of steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Yu, X. Study on microstructure evolution and constitutive relation of ring rolling state Ti40 titanium alloy in thermal deformation. J. Plast. Eng. 2018, 25, 228–233. [Google Scholar]
- Wu, Y.; Liu, H.; Xu, J.; Zhang, Z.; Xue, Y. Constitutive equations and processing map for hot deformation of a Ti-6Al-4V alloy prepared with spark-plasma sintering. Mater. Tehnol. 2020, 54, 25–32. [Google Scholar] [CrossRef]
- Xiao, H. Hot deformation behaviors and processing parameters optimizing of Mg-9.5Gd-3.8Y-0.6Zr alloy. Ph.D. Thesis, Central South University, Changsha, China, 2013. [Google Scholar]



| Element | Gd | Y | Zn | Zr | Si | Cu | Mg |
|---|---|---|---|---|---|---|---|
| wt.% | 9.48 | 4.00 | 1.98 | 0.50 | <0.01 | <0.01 | Bal. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Y.; Zheng, J.; Han, R.; Jia, L.; Zhang, Z.; Xue, Y. Hot Deformation Behaviour and Constitutive Equation of Mg-9Gd-4Y-2Zn-0.5Zr Alloy. Materials 2022, 15, 1779. https://doi.org/10.3390/ma15051779
Nie Y, Zheng J, Han R, Jia L, Zhang Z, Xue Y. Hot Deformation Behaviour and Constitutive Equation of Mg-9Gd-4Y-2Zn-0.5Zr Alloy. Materials. 2022; 15(5):1779. https://doi.org/10.3390/ma15051779
Chicago/Turabian StyleNie, Yangjunfeng, Jie Zheng, Rui Han, Leichen Jia, Zhimin Zhang, and Yong Xue. 2022. "Hot Deformation Behaviour and Constitutive Equation of Mg-9Gd-4Y-2Zn-0.5Zr Alloy" Materials 15, no. 5: 1779. https://doi.org/10.3390/ma15051779
APA StyleNie, Y., Zheng, J., Han, R., Jia, L., Zhang, Z., & Xue, Y. (2022). Hot Deformation Behaviour and Constitutive Equation of Mg-9Gd-4Y-2Zn-0.5Zr Alloy. Materials, 15(5), 1779. https://doi.org/10.3390/ma15051779






