Numerical Analysis of the Mechanical Response of Two-Phase Nanocomposites Consisting of Nanoporous Gold and Polymer
Abstract
1. Introduction
2. Materials and Methods
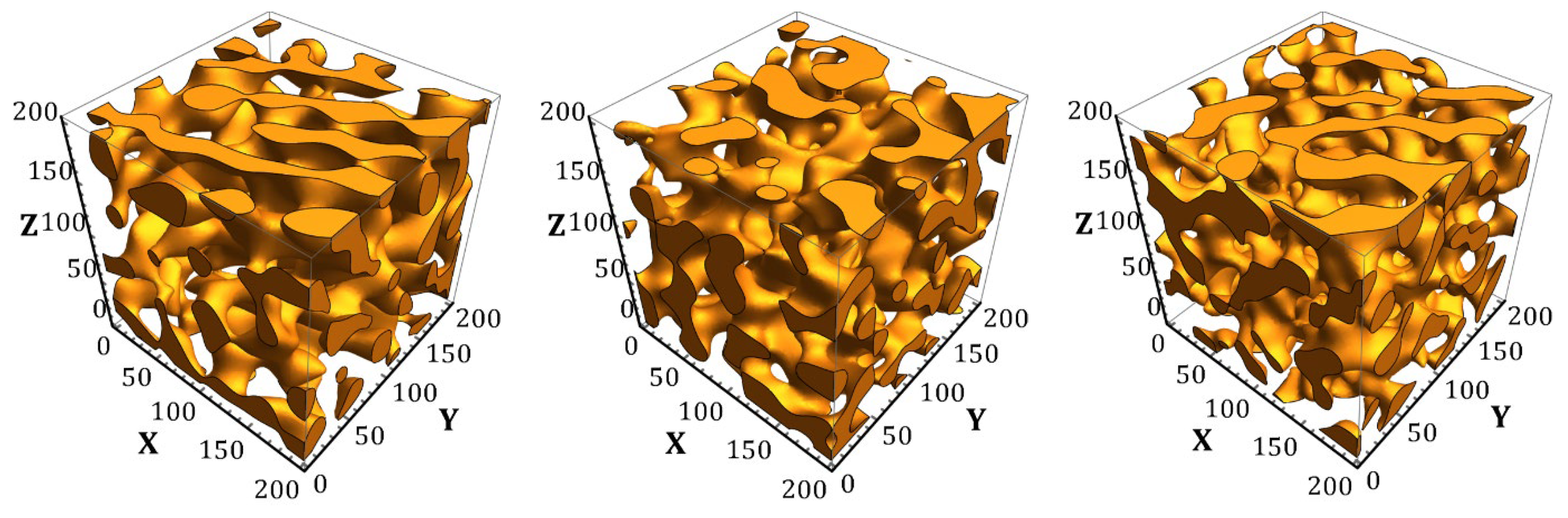
2.1. Geometry Models
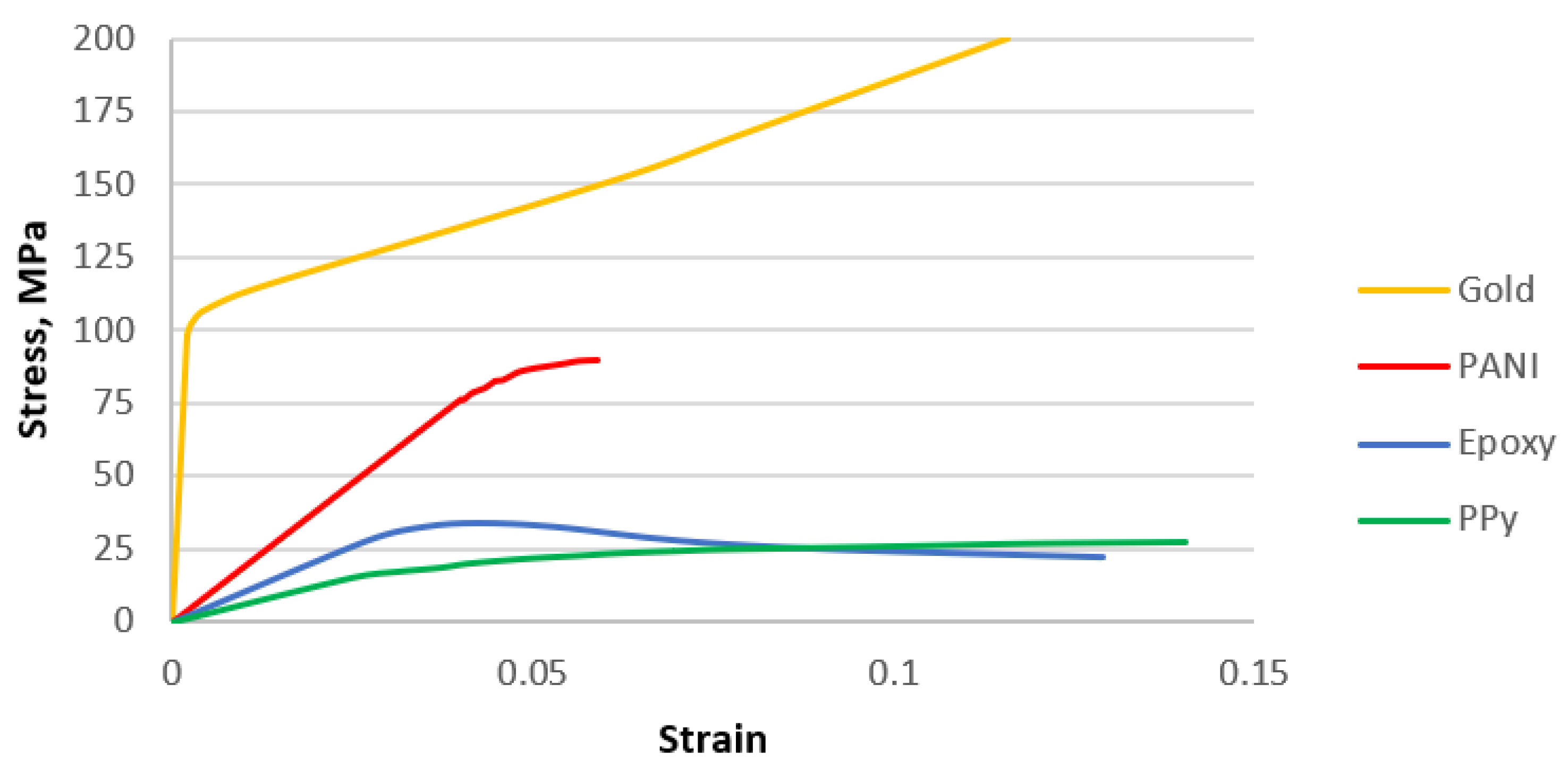
2.2. Material Models
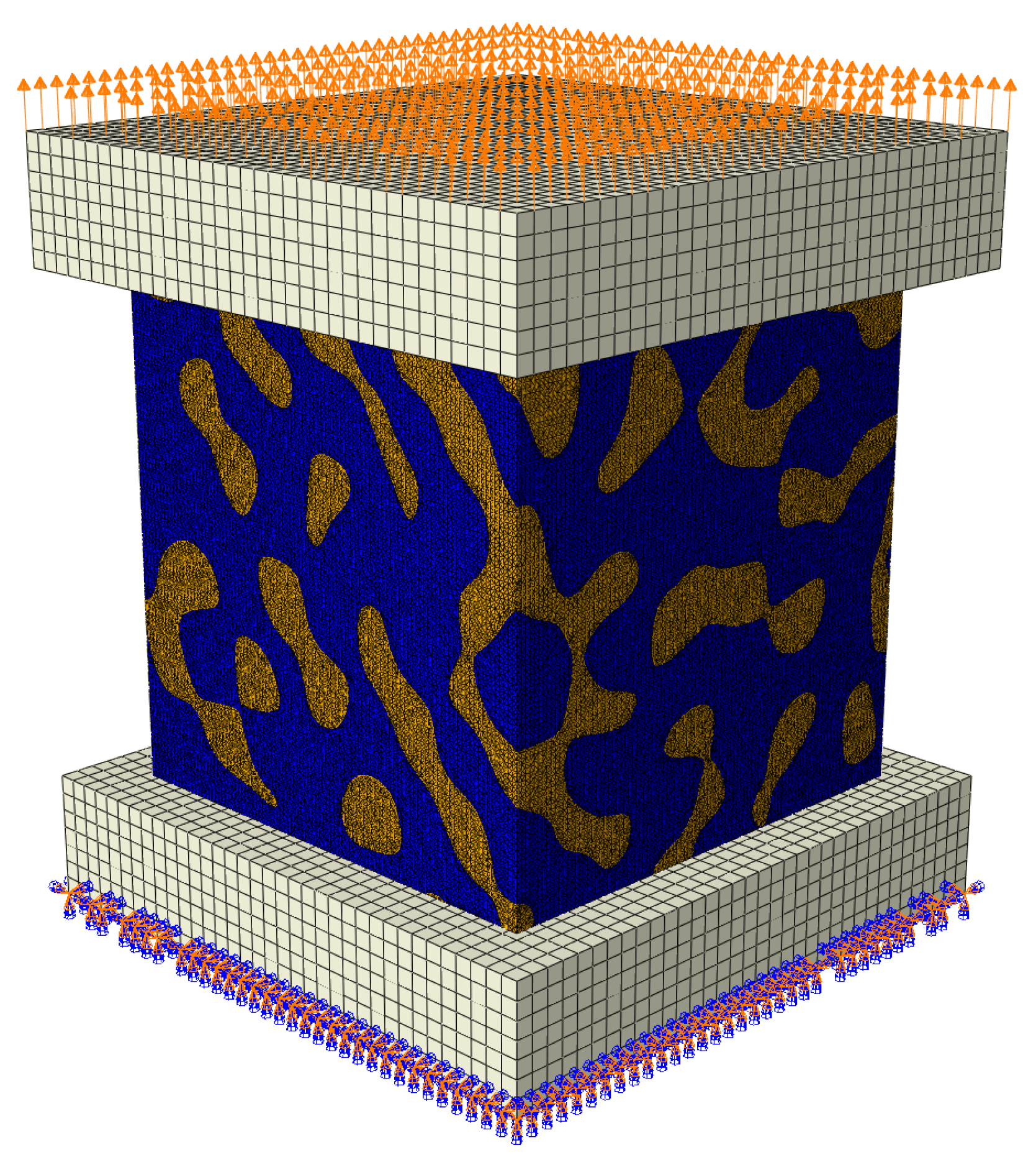
2.3. Boundary Conditions
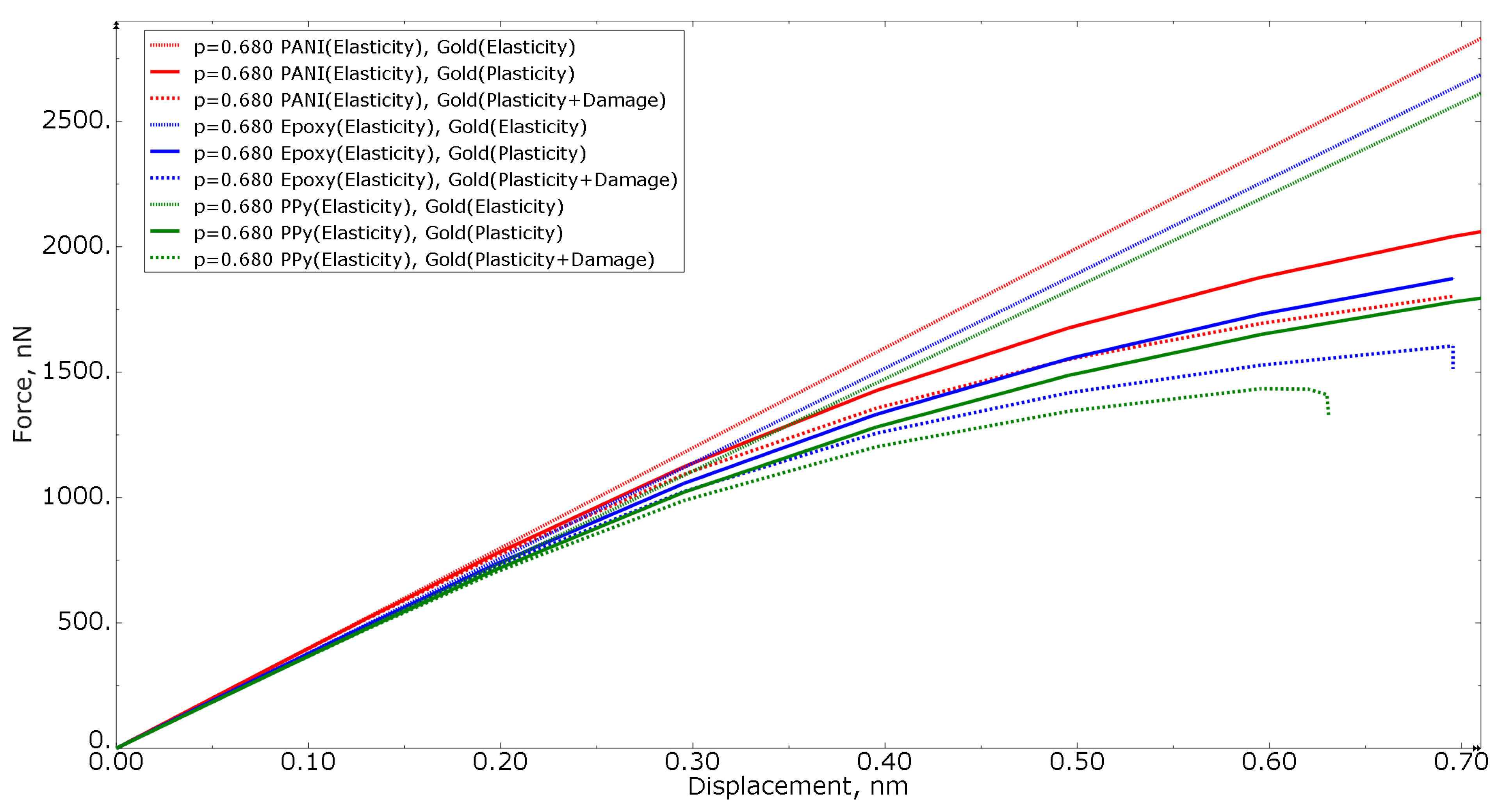
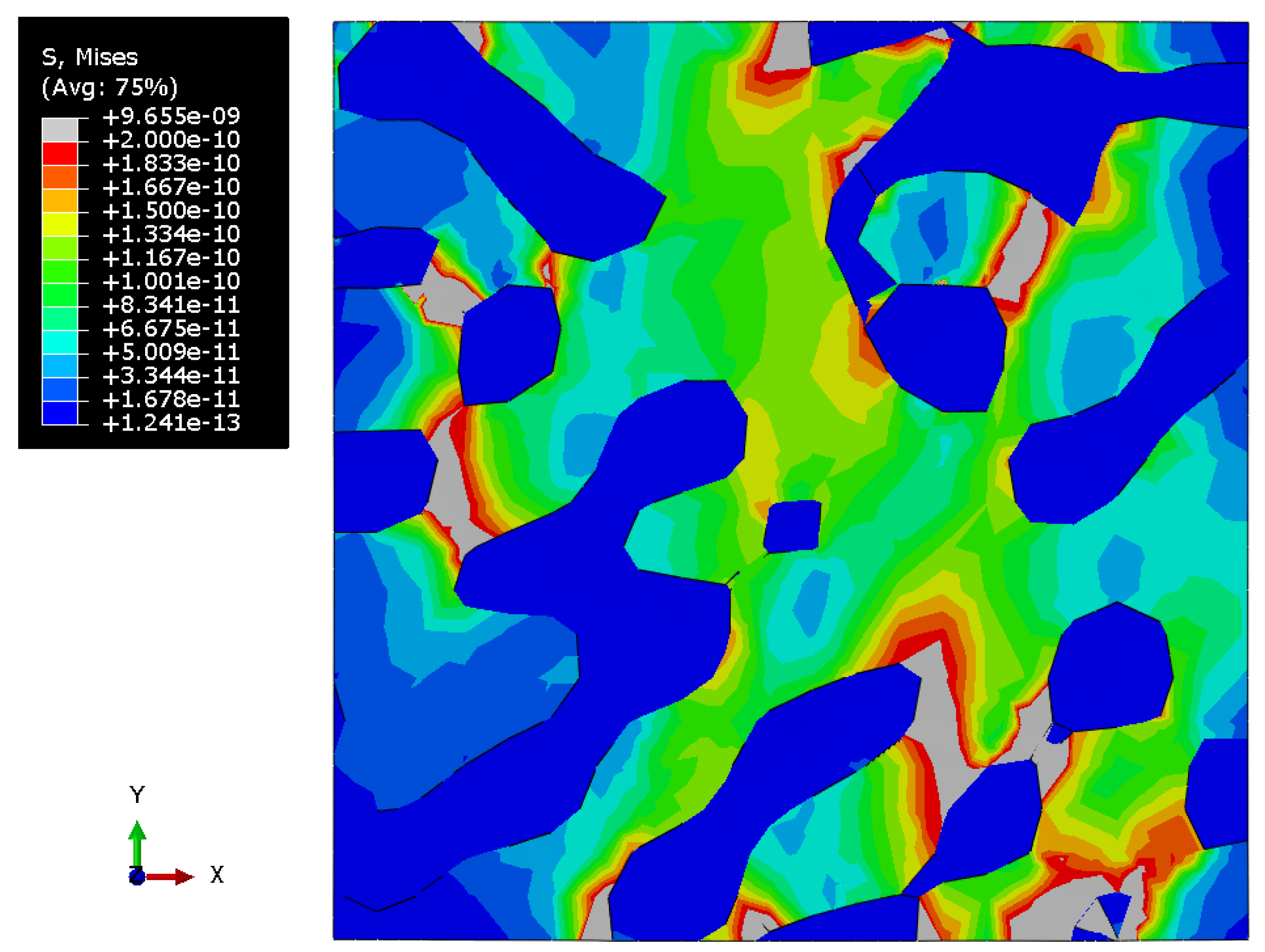
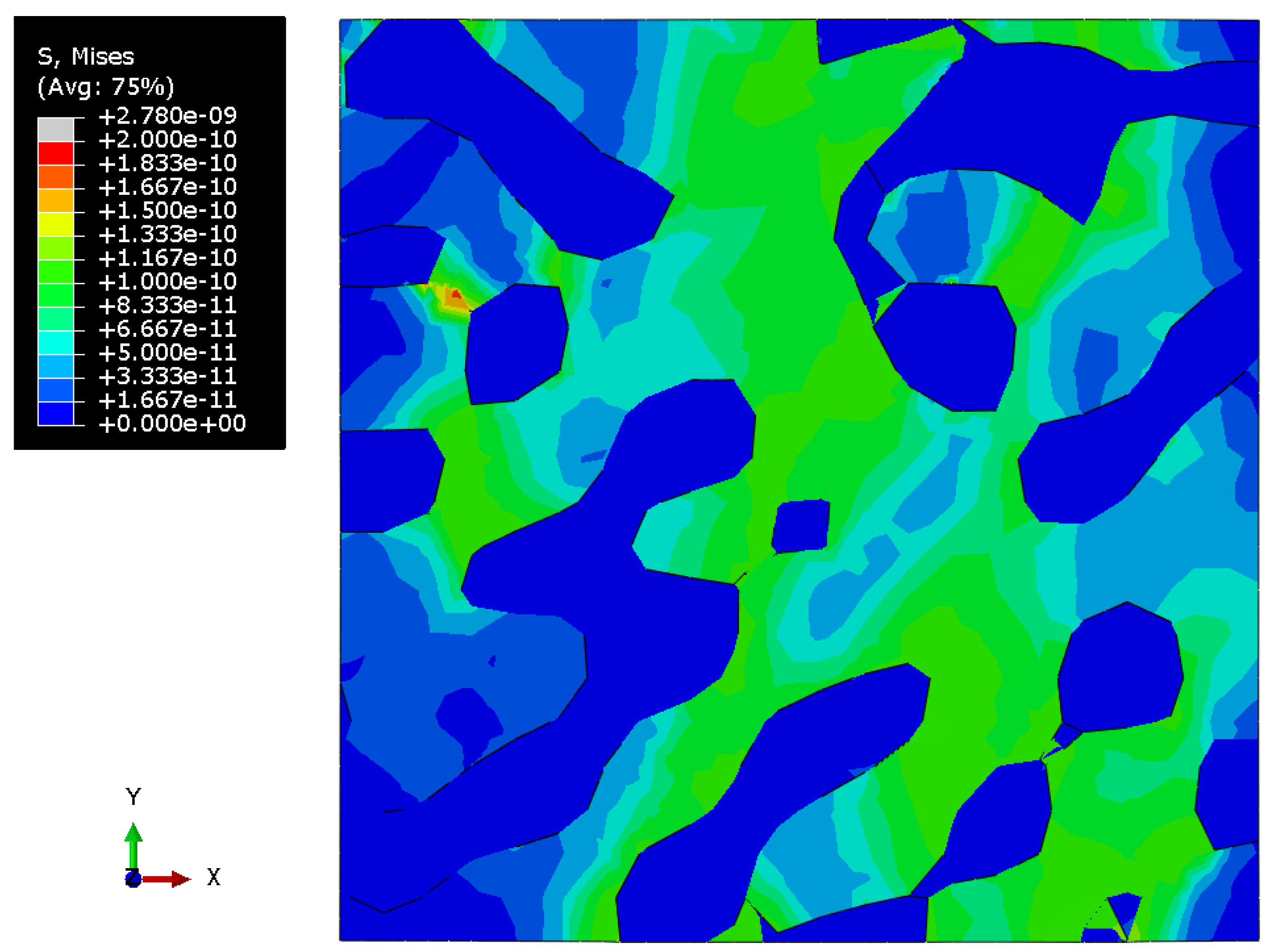
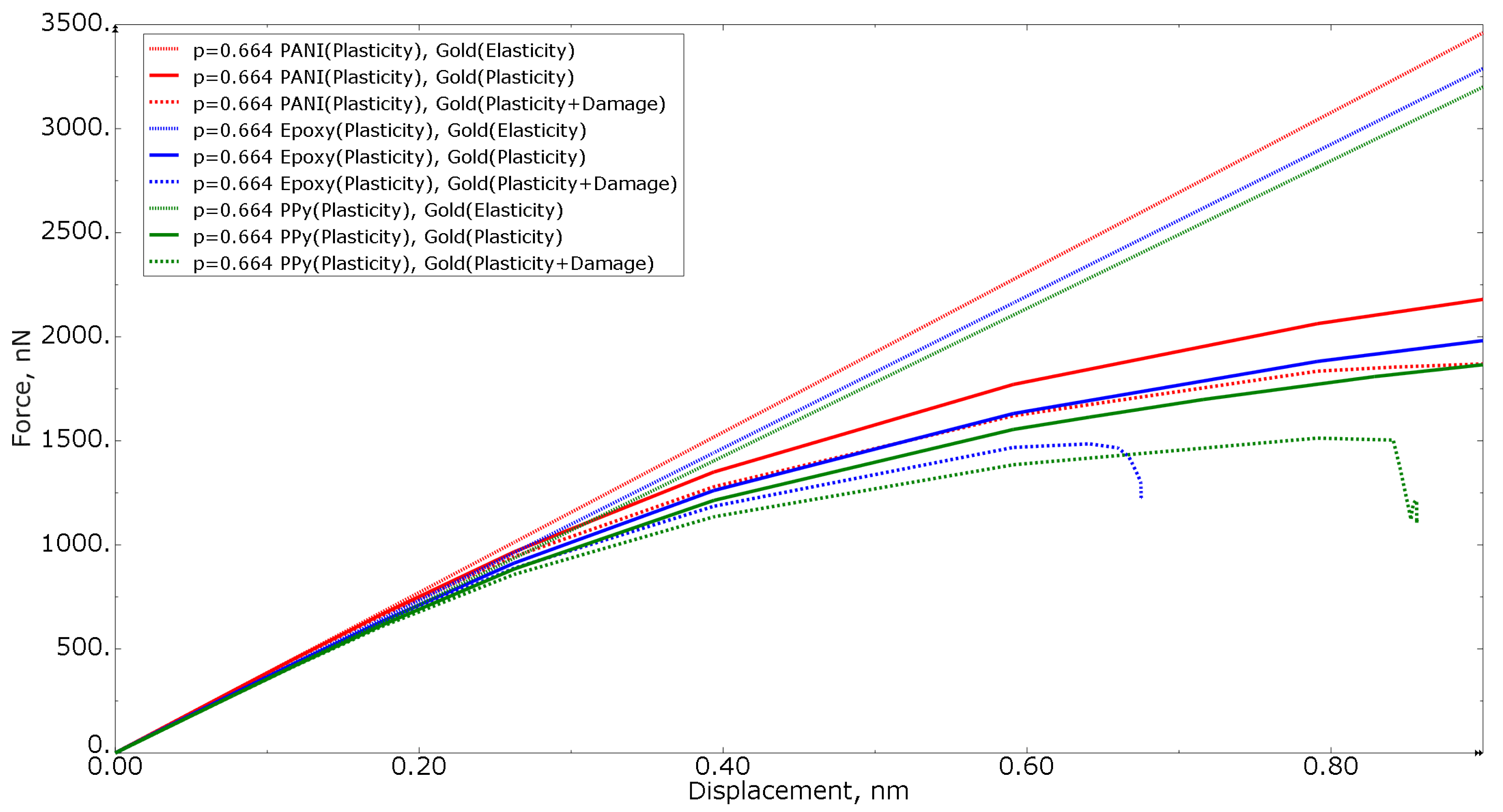
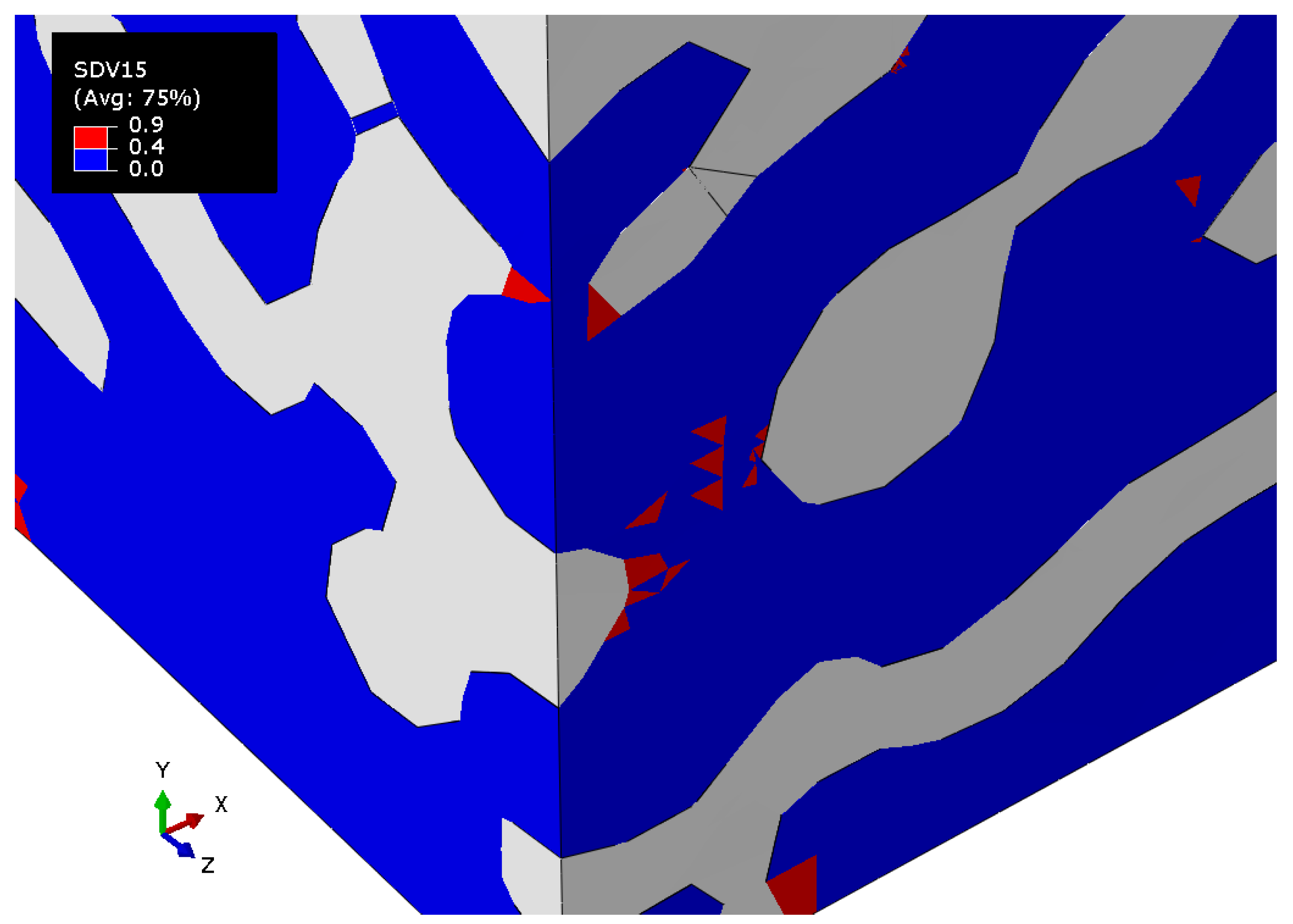
3. Results
3.1. Nanoporous Gold with Elastic Polymer
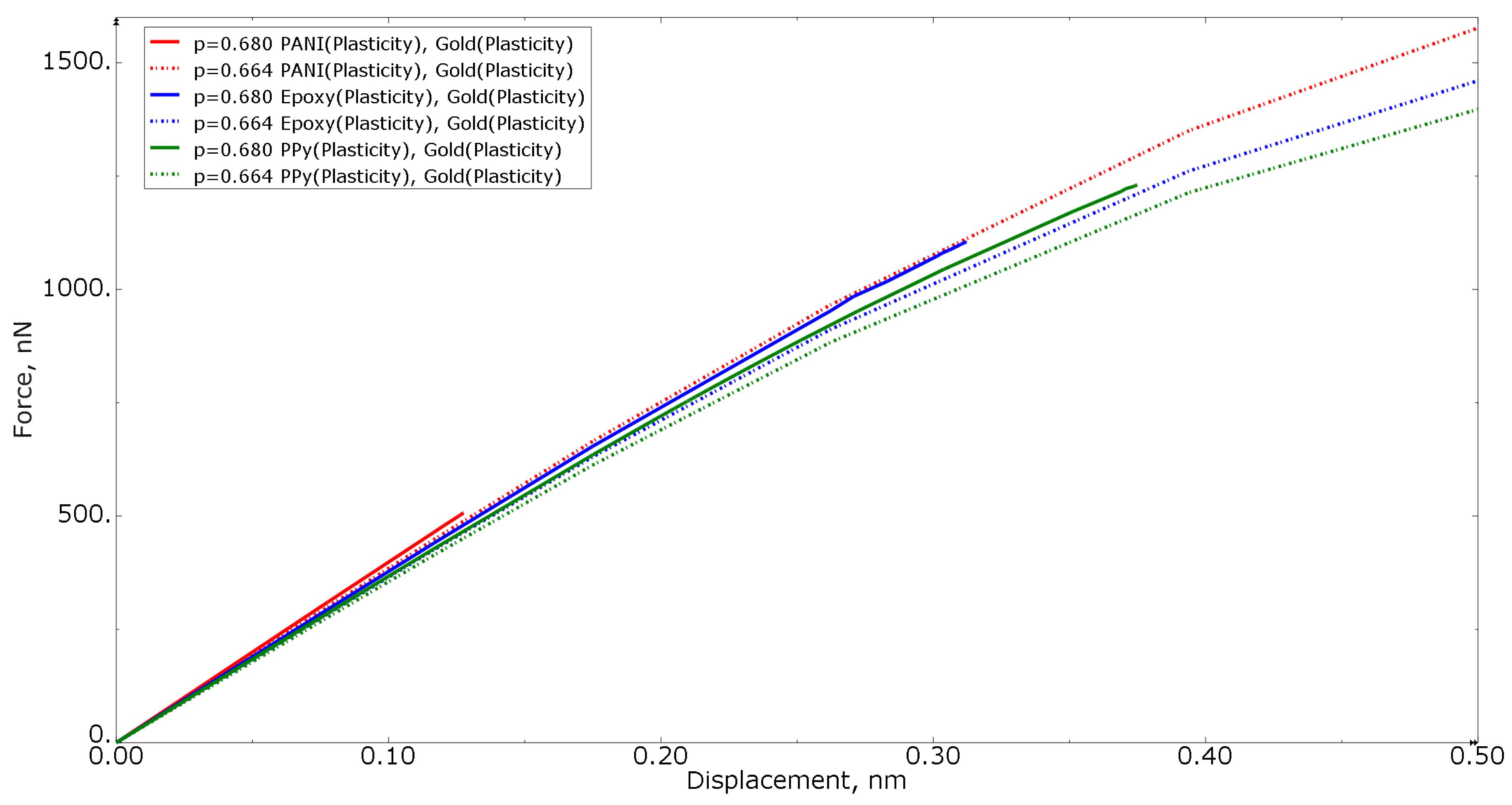
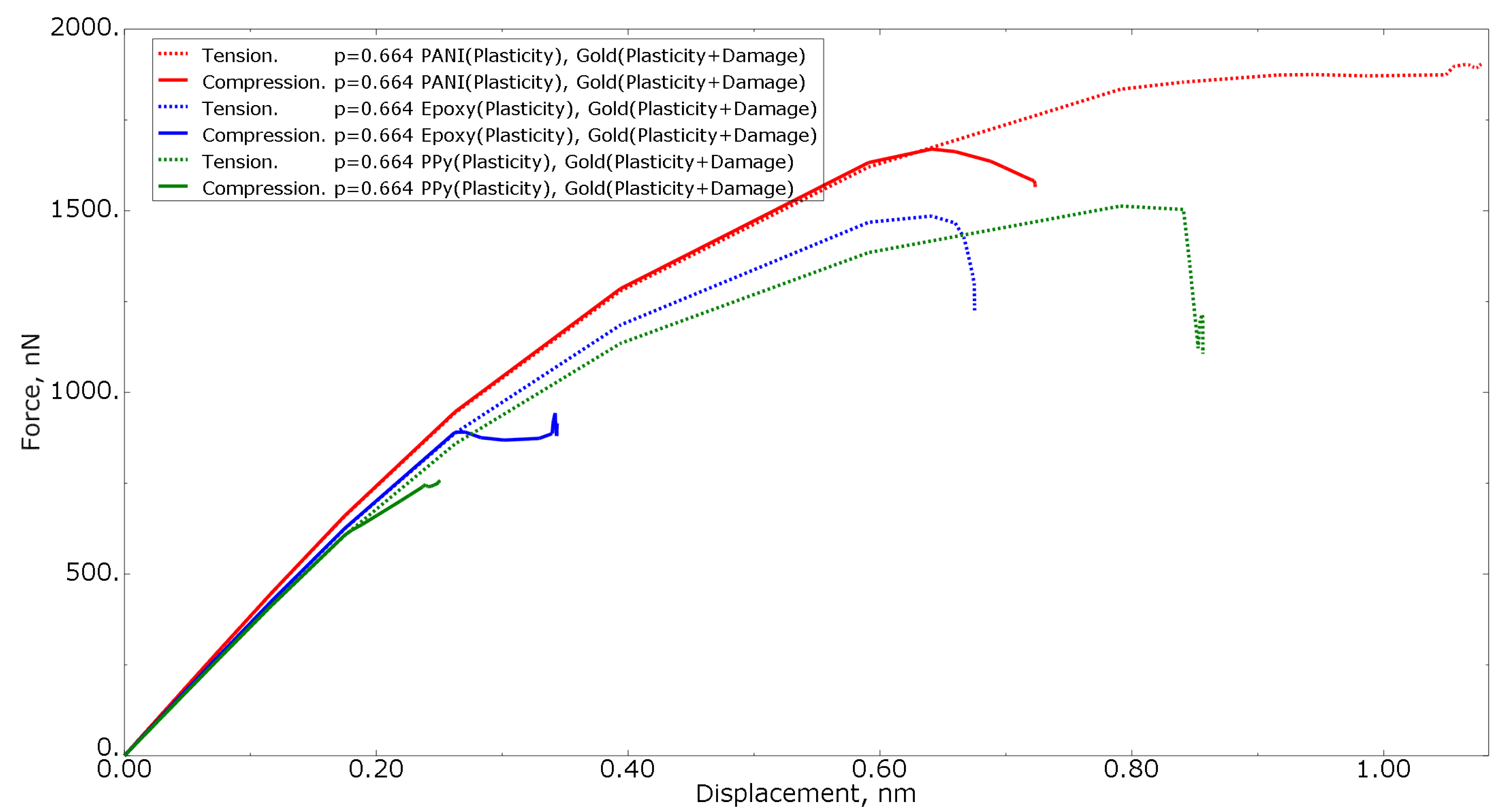
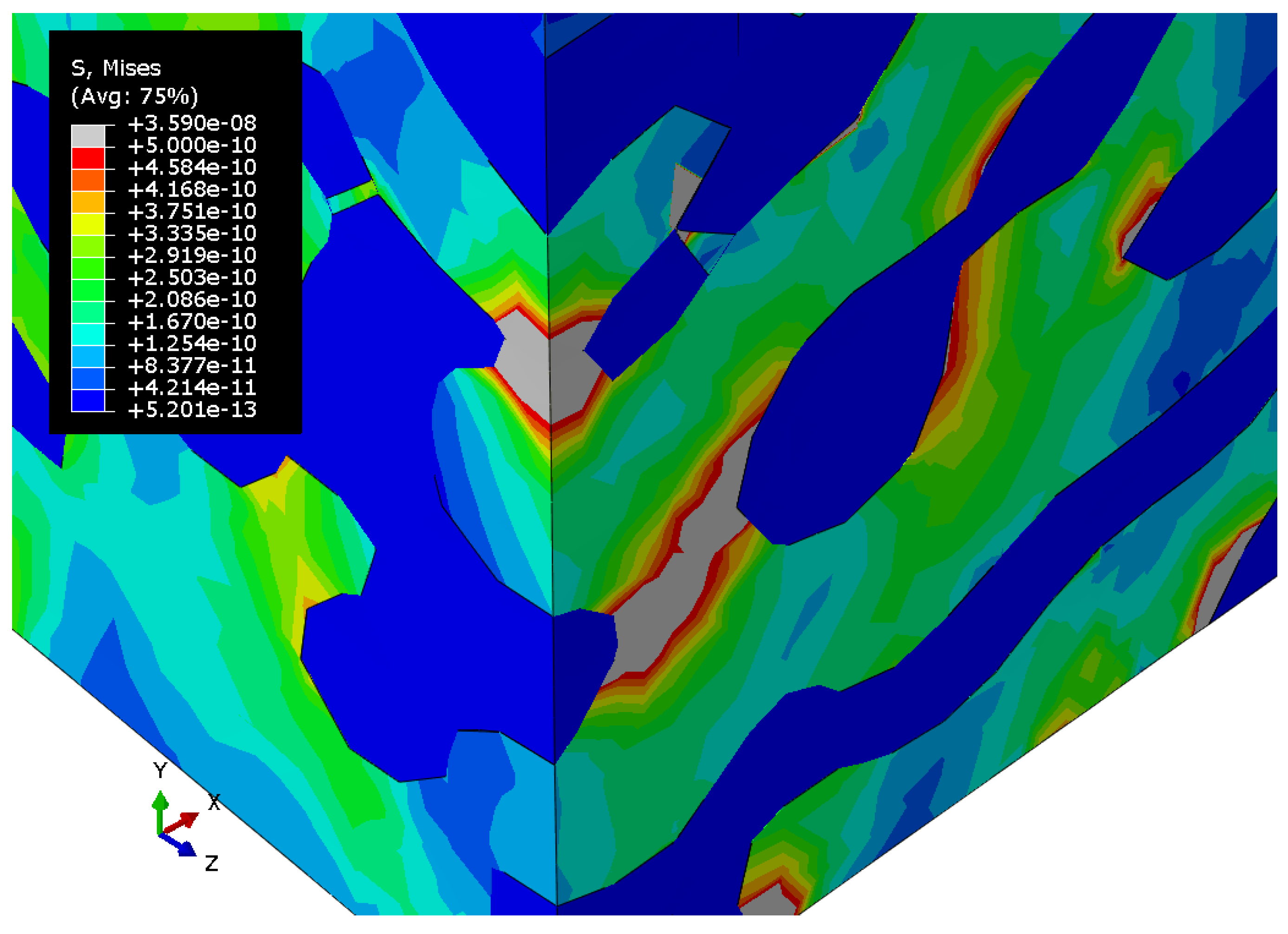
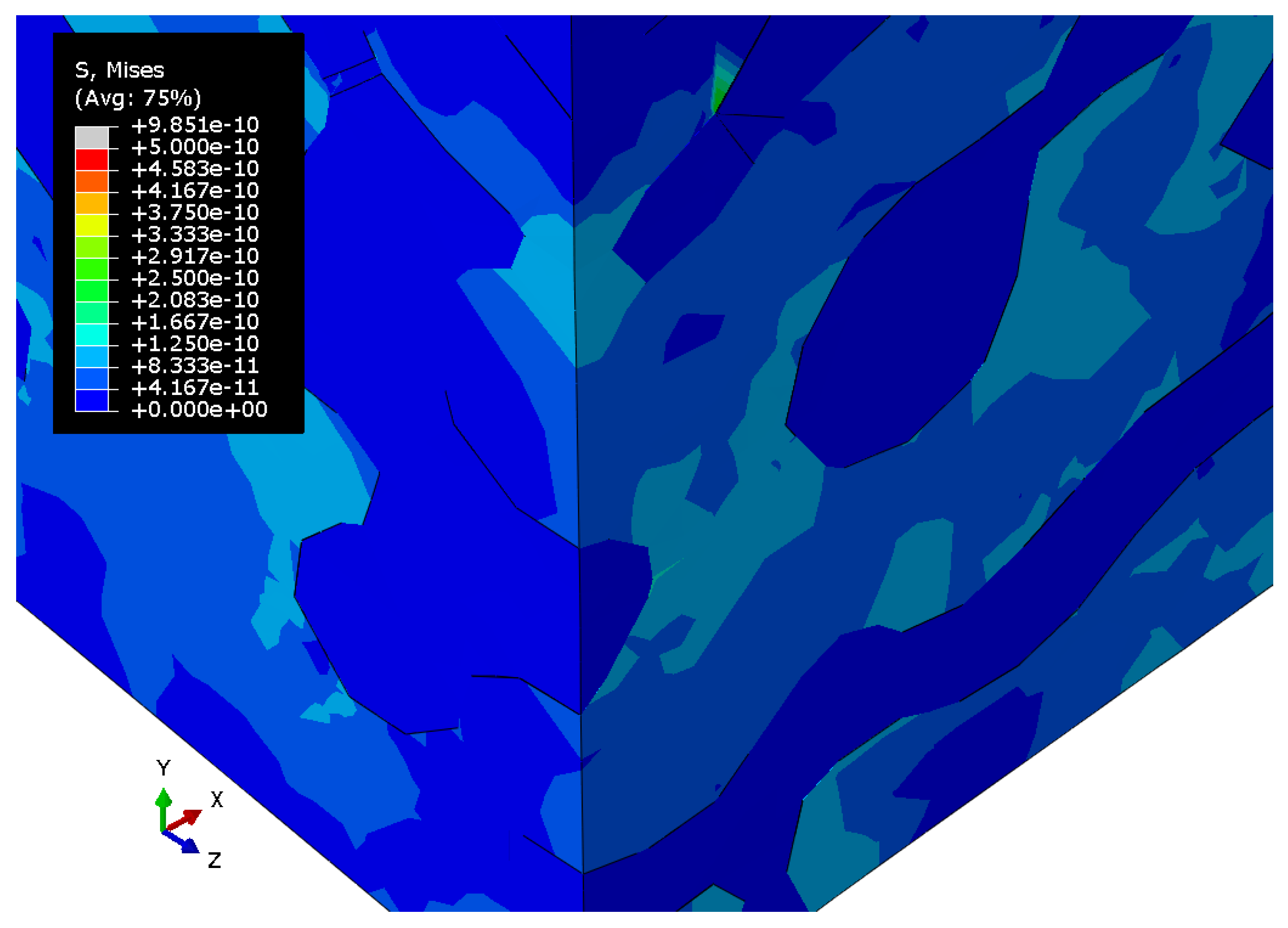
3.2. Nanoporous Gold with Elastoplastic Polymer
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Biener, J.; Hodge, A.M.; Hamza, A.V.; Hsiung, L.M.; Satcher, J.H. Nanoporous Au: A High Yield Strength Material. J. Appl. Phys. 2005, 97, 24301. [Google Scholar] [CrossRef]
- Liu, R.; Antoniou, A. A Relationship between the Geometrical Structure of a Nanoporous Metal Foam and Its Modulus. Acta Mater. 2013, 61, 2390–2402. [Google Scholar] [CrossRef]
- Detsi, E.; Vuković, Z.; Punzhin, S.; Bronsveld, P.M.; Onck, P.R.; Hosson, J.T.M. De Fine-Tuning the Feature Size of Nanoporous Silver. CrystEngComm 2012, 14, 5402–5406. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Qi, Z.; Zhang, W.; Qin, J.; Frenzel, J. Generalized Fabrication of Nanoporous Metals (Au, Pd, Pt, Ag, and Cu) through Chemical Dealloying. J. Phys. Chem. C 2009, 113, 12629–12636. [Google Scholar] [CrossRef]
- Burpo, F.J.; Nagelli, E.A.; Morris, L.A.; McClure, J.P.; Ryu, M.Y.; Palmer, J.L. Direct Solution-Based Reduction Synthesis of Au, Pd, and Pt Aerogels. J. Mater. Res. 2017, 32, 4153–4165. [Google Scholar] [CrossRef]
- Hayes, J.R.; Hodge, A.M.; Biener, J.; Hamza, A.V.; Sieradzki, K. Monolithic Nanoporous Copper by Dealloying Mn–Cu. J. Mater. Res. 2006, 21, 2611–2616. [Google Scholar] [CrossRef]
- Qiu, H.-J.; Kang, J.L.; Liu, P.; Hirata, A.; Fujita, T.; Chen, M.W. Fabrication of Large-Scale Nanoporous Nickel with a Tunable Pore Size for Energy Storage. J. Power Sources 2014, 247, 896–905. [Google Scholar] [CrossRef]
- Shi, S.; Markmann, J.; Weissmüller, J. Actuation by Hydrogen Electrosorption in Hierarchical Nanoporous Palladium. Philos. Mag. 2017, 97, 1571–1587. [Google Scholar] [CrossRef]
- Zareie Yazdan-Abad, M.; Noroozifar, M.; Modaresi Alam, A.R.; Saravani, H. Palladium Aerogel as a High-Performance Electrocatalyst for Ethanol Electro-Oxidation in Alkaline Media. J. Mater. Chem. A 2017, 5, 10244–10249. [Google Scholar] [CrossRef]
- Okulov, I.V.; Weissmüller, J.; Markmann, J. Dealloying-Based Interpenetrating-Phase Nanocomposites Matching the Elastic Behavior of Human Bone. Sci. Rep. 2017, 7, 20. [Google Scholar] [CrossRef]
- Yang, W.; Zheng, X.-G.; Wang, S.-G.; Jin, H.-J. Nanoporous Aluminum by Galvanic Replacement: Dealloying and Inward-Growth Plating. J. Electrochem. Soc. 2018, 165, C492–C496. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, M. Nanoporous Metals for Catalytic and Optical Applications. MRS Bull. 2009, 34, 569–576. [Google Scholar] [CrossRef]
- Stenner, C.; Shao, L.-H.; Mameka, N.; Weissmüller, J. Piezoelectric Gold: Strong Charge-Load Response in a Metal-Based Hybrid Nanomaterial. Adv. Funct. Mater. 2016, 26, 5174–5181. [Google Scholar] [CrossRef]
- Jiao, J.; Huber, N. Deformation Mechanisms in Nanoporous Metals: Effect of Ligament Shape and Disorder. Comput. Mater. Sci. 2017, 127, 194–203. [Google Scholar] [CrossRef][Green Version]
- Biener, J.; Hodge, A.M.; Hayes, J.R.; Volkert, C.A.; Zepeda-Ruiz, L.A.; Hamza, A.V.; Abraham, F.F. Size Effects on the Mechanical Behavior of Nanoporous Au. Nano Lett. 2006, 6, 2379–2382. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Heidelberg, A.; Boland, J.J. Mechanical Properties of Ultrahigh-Strength Gold Nanowires. Nat. Mater. 2005, 4, 525–529. [Google Scholar] [CrossRef] [PubMed]
- Volkert, C.A.; Lilleodden, E.T. Size Effects in the Deformation of Sub-Micron Au Columns. Philos. Mag. 2006, 86, 5567–5579. [Google Scholar] [CrossRef]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D Representative Volume Elements for Heterogeneous Materials: A Review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
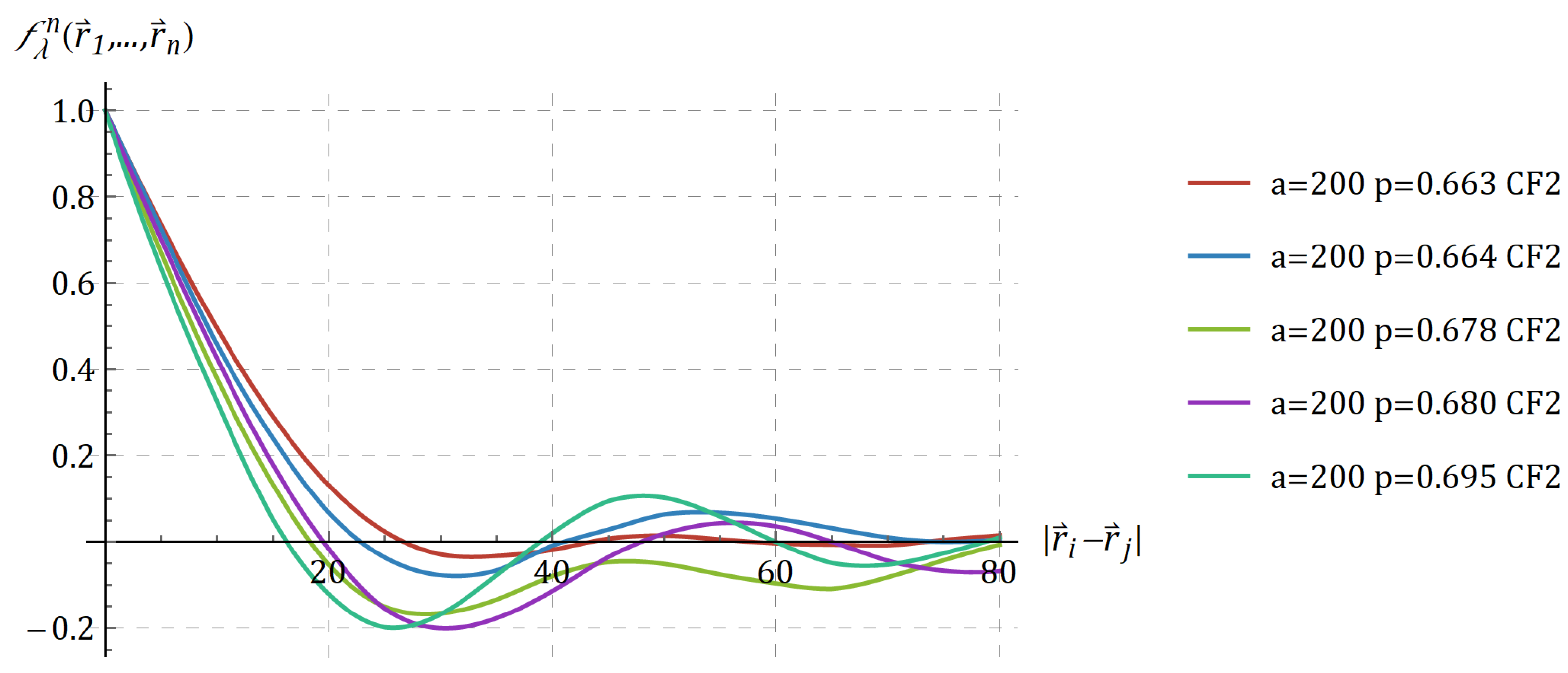
- Soyarslan, C.; Bargmann, S.; Pradas, M.; Weissmüller, J. 3D Stochastic Bicontinuous Microstructures: Generation, Topology and Elasticity. Acta Mater. 2018, 149, 326–340. [Google Scholar] [CrossRef]
- Xia, R.; Wu, R.N.; Liu, Y.L.; Sun, X.Y. The Role of Computer Simulation in Nanoporous Metals-a Review. Materials 2015, 8, 5060–5083. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Bringa, E.M.; Stukowski, A.; Rodríguez Nieva, J.F.; Tang, Y.; Meyers, M.A. Plastic Deformation of a Porous Bcc Metal Containing Nanometer Sized Voids. Comput. Mater. Sci. 2014, 88, 92–102. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Bringa, E.M.; Stukowski, A.; Rodríguez Nieva, J.F.; Bertolino, G.; Tang, Y.; Meyers, M.A. Atomistic Simulation of the Mechanical Response of a Nanoporous Body-Centered Cubic Metal. Scr. Mater. 2013, 68, 817–820. [Google Scholar] [CrossRef]
- Wang, J.; Lam, D.C.C. Model and Analysis of Size-Stiffening in Nanoporous Cellular Solids. J. Mater. Sci. 2009, 44, 985–991. [Google Scholar] [CrossRef]
- Shalimov, A.S.; Tashkinov, M.A. Finite Element Simulation of Elastoplastic Behavior of Nanoporous Metals Using Bicontinuous RVE Models. Procedia Struct. Integr. 2021, 32, 230–237. [Google Scholar] [CrossRef]
- Tashkinov, M.A.; Shalimov, A.S. Modeling of the Effect of Microscale Morphological Parameters on the Deformation Behavior of Porous Materials with a Metal Matrix. Phys. Mesomech. 2021, 24, 618–624. [Google Scholar] [CrossRef]
- Lee, D.; Wei, X.; Zhao, M.; Chen, X.; Jun, S.C.; Hone, J.; Kysar, J.W. Plastic Deformation in Nanoscale Gold Single Crystals and Open-Celled Nanoporous Gold. Model. Simul. Mater. Sci. Eng. 2007, 15, S181–S192. [Google Scholar] [CrossRef]
- Zhu, H.X.; Zhang, H.C.; You, J.F.; Kennedy, D.; Wang, Z.B.; Fan, T.X.; Zhang, D. The Elastic and Geometrical Properties of Micro- and Nano-Structured Hierarchical Random Irregular Honeycombs. J. Mater. Sci. 2014, 49, 5690–5702. [Google Scholar] [CrossRef]
- Jiao, J.; Huber, N. Effect of Nodal Mass on Macroscopic Mechanical Properties of Nanoporous Metals. Int. J. Mech. Sci. 2017, 134, 234–243. [Google Scholar] [CrossRef]
- Hu, K.; Ziehmer, M.; Wang, K.; Lilleodden, E.T. Nanoporous Gold: 3D Structural Analyses of Representative Volumes and Their Implications on Scaling Relations of Mechanical Behaviour. Philos. Mag. 2016, 96, 3322–3335. [Google Scholar] [CrossRef]
- Ngô, B.-N.D.; Roschning, B.; Albe, K.; Weissmüller, J.; Markmann, J. On the Origin of the Anomalous Compliance of Dealloying-Derived Nanoporous Gold. Scr. Mater. 2017, 130, 74–77. [Google Scholar] [CrossRef]
- Griffiths, E.; Wilmers, J.; Bargmann, S.; Reddy, B.D. Nanoporous Metal Based Composites: Giving Polymers Strength and Making Metals Move. J. Mech. Phys. Solids 2019, 137, 103848. [Google Scholar] [CrossRef]
- Wang, K.; Kobler, A.; Kübel, C.; Jelitto, H.; Schneider, G.; Weissmüller, J. Nanoporous-Gold-Based Composites: Toward Tensile Ductility. NPG Asia Mater. 2015, 7, e187. [Google Scholar] [CrossRef]
- Bargmann, S.; Soyarslan, C.; Husser, E.; Konchakova, N. Materials Based Design of Structures: Computational Modeling of the Mechanical Behavior of Gold-Polymer Nanocomposites. Mech. Mater. 2016, 94, 53–65. [Google Scholar] [CrossRef]
- Griffiths, E.; Bargmann, S.; Reddy, B.D. Elastic Behaviour at the Nanoscale of Innovative Composites of Nanoporous Gold and Polymer. Extrem. Mech. Lett. 2017, 17, 16–23. [Google Scholar] [CrossRef]
- Soyarslan, C.; Pradas, M.; Bargmann, S. Effective Elastic Properties of 3D Stochastic Bicontinuous Composites. Mech. Mater. 2019, 137, 103098. [Google Scholar] [CrossRef]
- Stine, K.J.; Jefferson, K.; Shulga, O.V. Nanoporous Gold for Enzyme Immobilization. Methods Mol. Biol. 2017, 1504, 37–60. [Google Scholar] [CrossRef]
- Tashkinov, M. Statistical Characteristics of Structural Stochastic Stress and Strain Fields in Polydisperse Heterogeneous Solid Media. Comput. Mater. Sci. 2014, 94, 44–50. [Google Scholar] [CrossRef]
- Tashkinov, M. Micro-Scale Modeling of Phase-Level Elastic Fields of SiC Reinforced Metal Matrix Multiphase Composites Using Statistical Approach. Comput. Mater. Sci. 2016, 116, 113–121. [Google Scholar] [CrossRef]
- Tashkinov, M.A.; Vildeman, V.E.; Mikhailova, N.V. Method of Successive Approximations in a Stochastic Boundary-Value Problem in the Elasticity Theory of Structurally Heterogeneous Media. Compos. Mech. Comput. Appl. 2011, 2, 21–37. [Google Scholar] [CrossRef]
- Tashkinov, M.A. Stochastic Modelling of Deformation Process in Elastoplastic Composites with Randomly Located Inclusions Using High Order Correlation Functions. PNRPU Mech. Bull. 2014, 2014, 163–185. [Google Scholar] [CrossRef]
- Tashkinov, M.A. Multipoint Stochastic Approach to Localization of Microscale Elastic Behavior of Random Heterogeneous Media. Comput. Struct. 2021, 249, 106474. [Google Scholar] [CrossRef]
- Beets, N.; Stuckner, J.; Murayama, M.; Farkas, D. Fracture in Nanoporous Gold: An Integrated Computational and Experimental Study. Acta Mater. 2020, 185, 257–270. [Google Scholar] [CrossRef]
- Jin, H.J.; Kurmanaeva, L.; Schmauch, J.; Rösner, H.; Ivanisenko, Y.; Weissmüller, J. Deforming Nanoporous Metal: Role of Lattice Coherency. Acta Mater. 2009, 57, 2665–2672. [Google Scholar] [CrossRef]
- Li, J.J.; Xian, Y.H.; Zhou, H.J.; Wu, R.N.; Hu, G.M.; Xia, R. Mechanical Properties of Nanocrystalline Nanoporous Gold Complicated by Variation of Grain and Ligament: A Molecular Dynamics Simulation. Sci. China Technol. Sci. 2018, 61, 1353–1363. [Google Scholar] [CrossRef]
- Mathesan, S.; Mordehai, D. Size-Dependent Elastic Modulus of Nanoporous Au Nanopillars. Acta Mater. 2020, 185, 441–452. [Google Scholar] [CrossRef]
- Li, J.; Tian, C.; Lu, B.; Xian, Y.; Wu, R.; Hu, G.; Xia, R. Deformation Behavior of Nanoporous Gold Based Composite in Compression: A Finite Element Analysis. Compos. Struct. 2019, 211, 229–235. [Google Scholar] [CrossRef]
- Lee, D.; Wei, X.; Chen, X.; Zhao, M.; Jun, S.C.; Hone, J.; Herbert, E.G.; Oliver, W.C.; Kysar, J.W. Microfabrication and Mechanical Properties of Nanoporous Gold at the Nanoscale. Scr. Mater. 2007, 56, 437–440. [Google Scholar] [CrossRef]
- Foroughi, J.; Ghorbani, S.R.; Peleckis, G.; Spinks, G.M.; Wallace, G.G.; Wang, X.L.; Dou, S.X. The Mechanical and the Electrical Properties of Conducting Polypyrrole Fibers. J. Appl. Phys. 2010, 107, 103712. [Google Scholar] [CrossRef]
- Wang, K.; Weissmüller, J. Composites of Nanoporous Gold and Polymer. Adv. Mater. 2013, 25, 1280–1284. [Google Scholar] [CrossRef]
- Saadattalab, V.; Shakeri, A.; Gholami, H. Effect of CNTs and Nano ZnO on Physical and Mechanical Properties of Polyaniline Composites Applicable in Energy Devices. Prog. Nat. Sci. Mater. Int. 2016, 26, 517–522. [Google Scholar] [CrossRef]
- Han, D.H.; Park, S.M. Electrochemistry of Conductive Polymers. 32. Nanoscopic Examination of Conductivities of Polyaniline Films. J. Phys. Chem. B 2004, 108, 13921–13927. [Google Scholar] [CrossRef]
- Coman, C.D. Influence of Preload on Failure Modes of Hybrid Metal-Composite Protruding Bolted Joints. INCAS Bull. 2021, 13, 29–41. [Google Scholar] [CrossRef]
- González Del Solar, G.; Martín, P.; Maldonado, N. Formulation, Implementation and Validation of a Scalar Damage Model for Brittle Materials Applied to Three-Dimensional Solid Elements. Rev. Ing. De Constr. 2018, 33, 111–122. [Google Scholar] [CrossRef]







| Parameter | Symbol | Value | Ref. |
|---|---|---|---|
| Gold | |||
| Young’s module | 48,000 MPa | [33,46] | |
| Poisson’s ratio | 0.44 | [33,46] | |
| Elastic limit | 96 MPa | [33] | |
| Ultimate strength | 190 MPa | [47] | |
| Stress−strain curve | - | - | [33] |
| Polypyrrole (PPy) | |||
| Young’s module | 600 MPa | [31] | |
| Poisson’s ratio | 0.3 | [31] | |
| Elastic limit | 15 MPa | [48] | |
| Stress−strain curve | - | - | [48] |
| Epoxy resin | |||
| Young’s module | 1038 MPa | [33,49] | |
| Poisson’s ratio | 0.35 | [33,49] | |
| Elastic limit | 28 MPa | [33,49] | |
| Stress−strain curve | - | - | [33,49] |
| Polyaniline (PANI) | |||
| Young’s module | 1910 MPa | [50] | |
| Poisson’s ratio | 0.38 | [51] | |
| Elastic limit | 76 MPa | [50] | |
| Stress−strain curve | - | - | [50] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shalimov, A.; Tashkinov, M. Numerical Analysis of the Mechanical Response of Two-Phase Nanocomposites Consisting of Nanoporous Gold and Polymer. Materials 2022, 15, 1574. https://doi.org/10.3390/ma15041574
Shalimov A, Tashkinov M. Numerical Analysis of the Mechanical Response of Two-Phase Nanocomposites Consisting of Nanoporous Gold and Polymer. Materials. 2022; 15(4):1574. https://doi.org/10.3390/ma15041574
Chicago/Turabian StyleShalimov, Aleksandr, and Mikhail Tashkinov. 2022. "Numerical Analysis of the Mechanical Response of Two-Phase Nanocomposites Consisting of Nanoporous Gold and Polymer" Materials 15, no. 4: 1574. https://doi.org/10.3390/ma15041574
APA StyleShalimov, A., & Tashkinov, M. (2022). Numerical Analysis of the Mechanical Response of Two-Phase Nanocomposites Consisting of Nanoporous Gold and Polymer. Materials, 15(4), 1574. https://doi.org/10.3390/ma15041574






