Analysis and Modeling of Stress–Strain Curves in Microalloyed Steels Based on a Dislocation Density Evolution Model
Abstract
1. Introduction
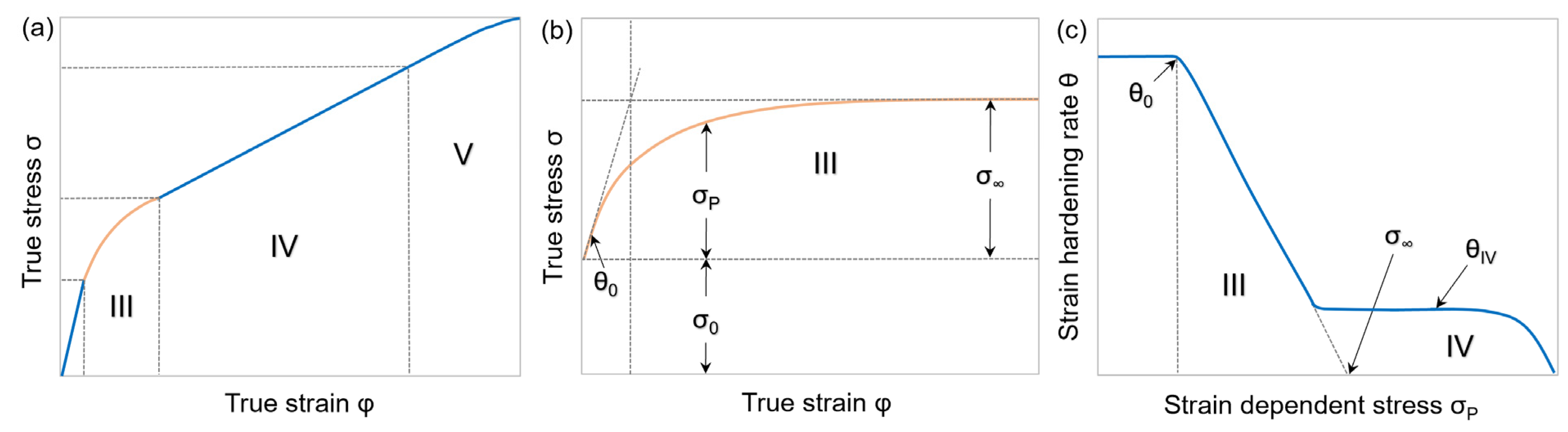
1.1. Flow Curve Characteristics
1.2. Carbonitrides in Microalloyed Steel
2. Model Approach
2.1. Dislocation Density Model
2.2. ABC-Model
2.3. MatCalc Strength Modeling
3. Materials and Methods
3.1. Simulation
3.1.1. MatCalc Parameters for the Simulation Setup
3.1.2. Preparatory Equilibrium Calculations
3.2. Experiments
4. Results and Discussion
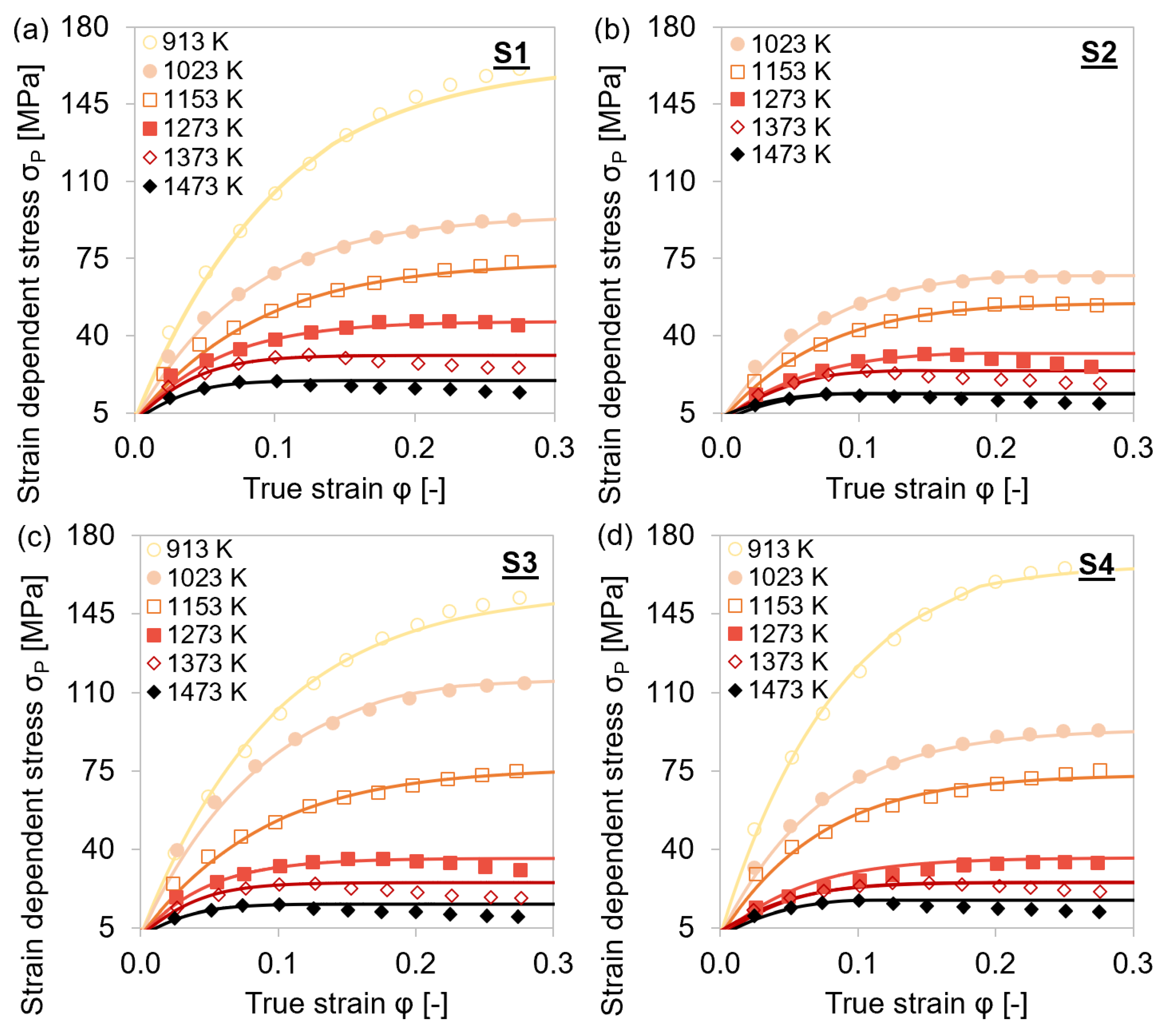
4.1. Experimental Flow Curves
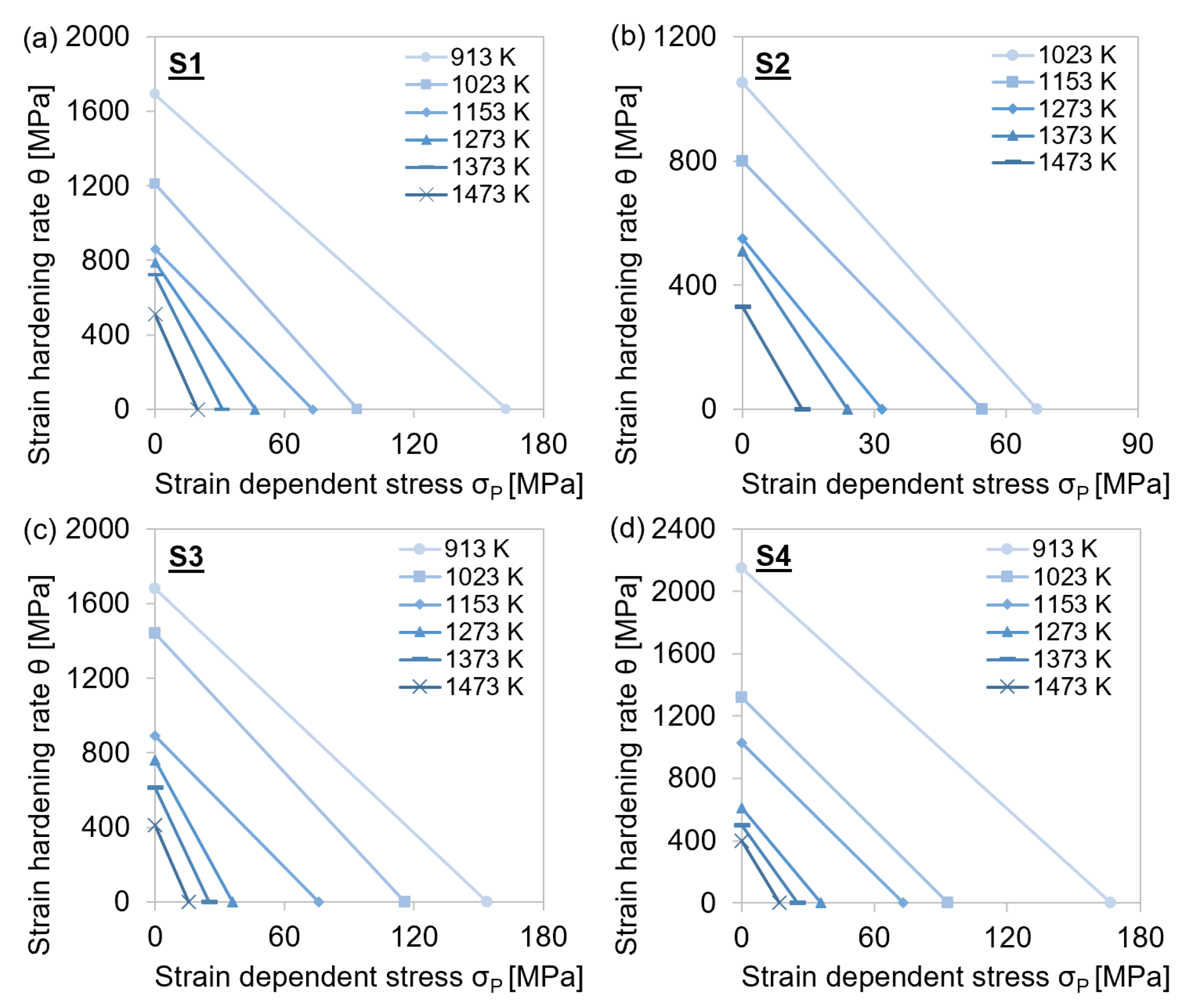
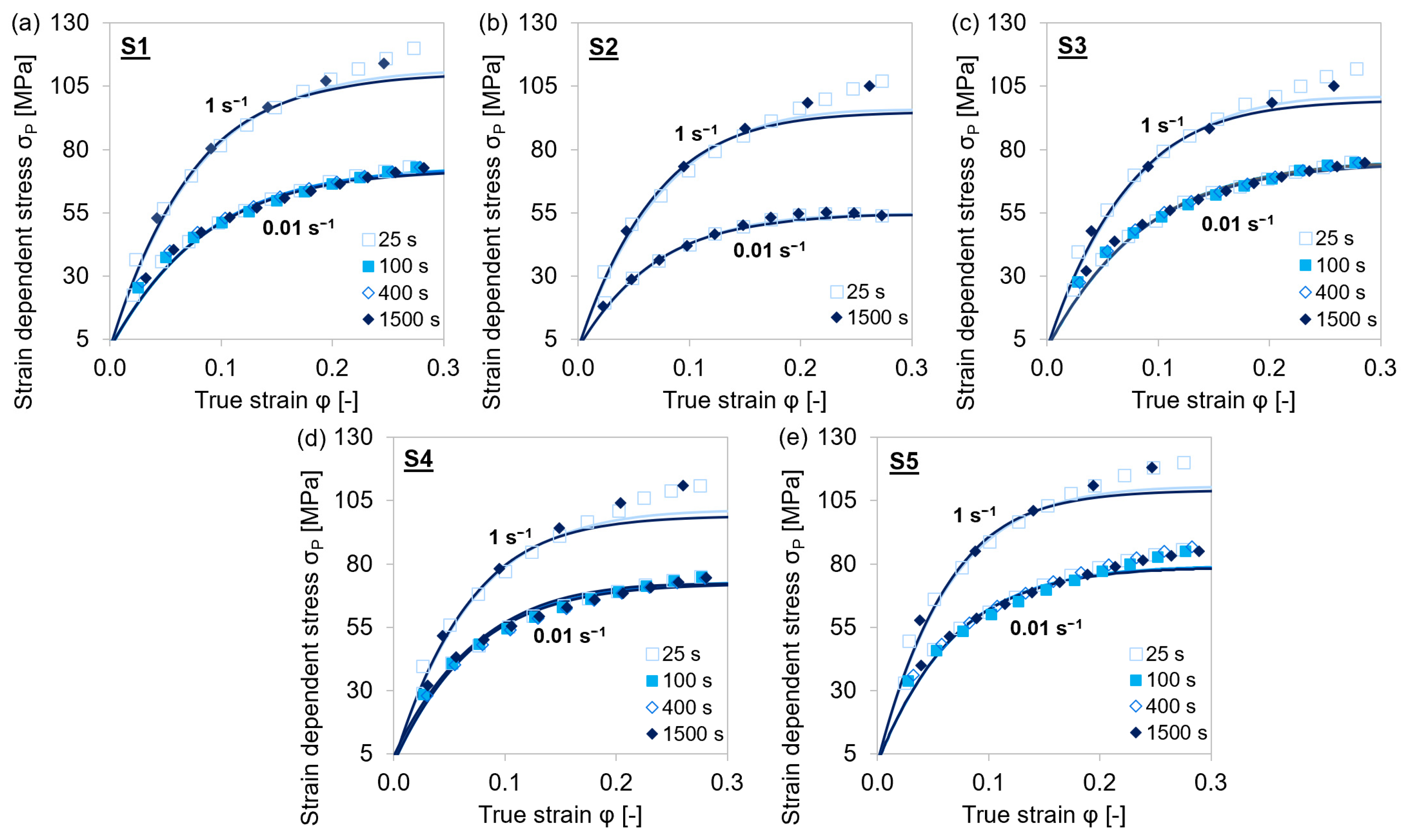
4.1.1. Steel Grades S1–S5
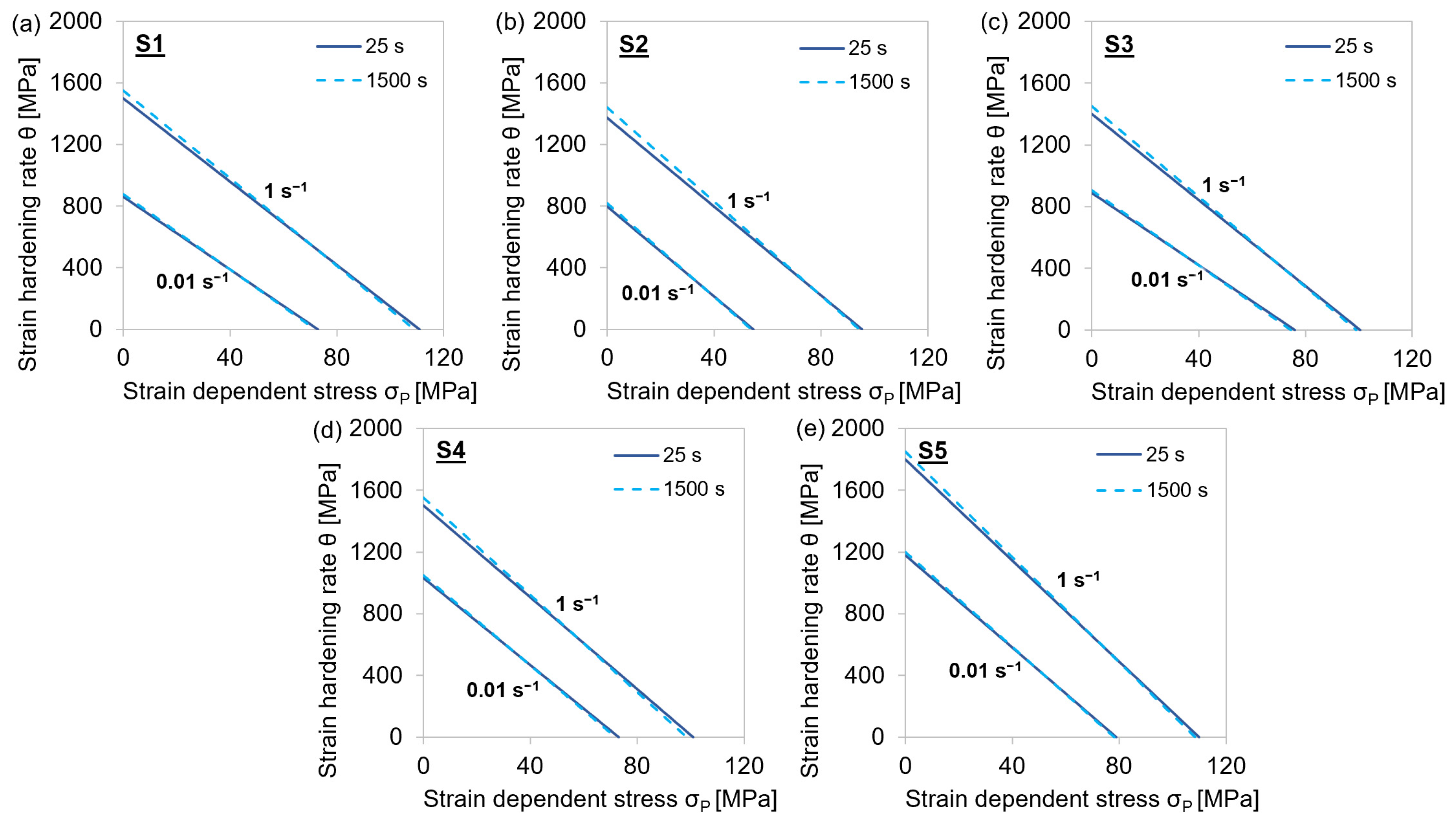
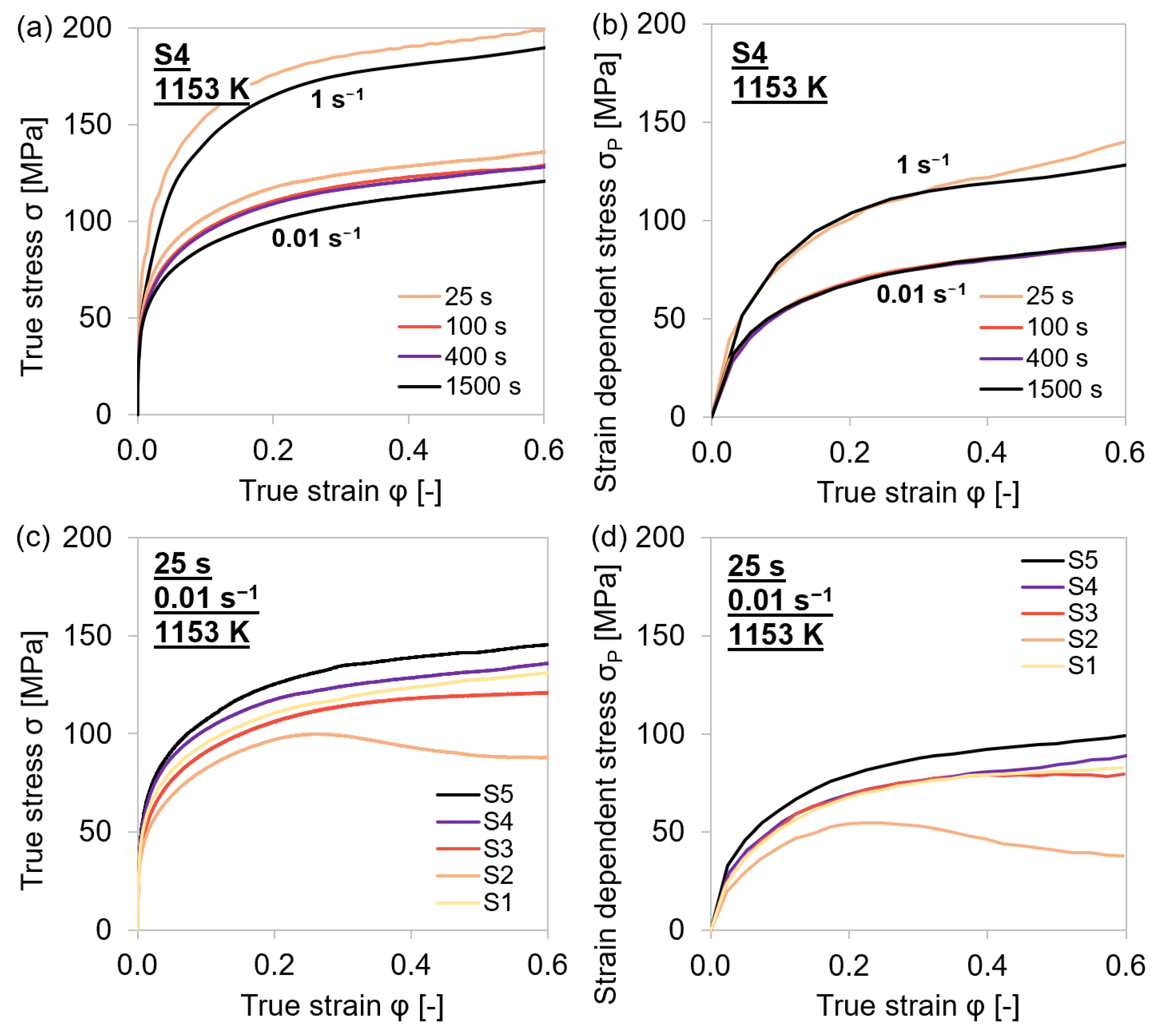
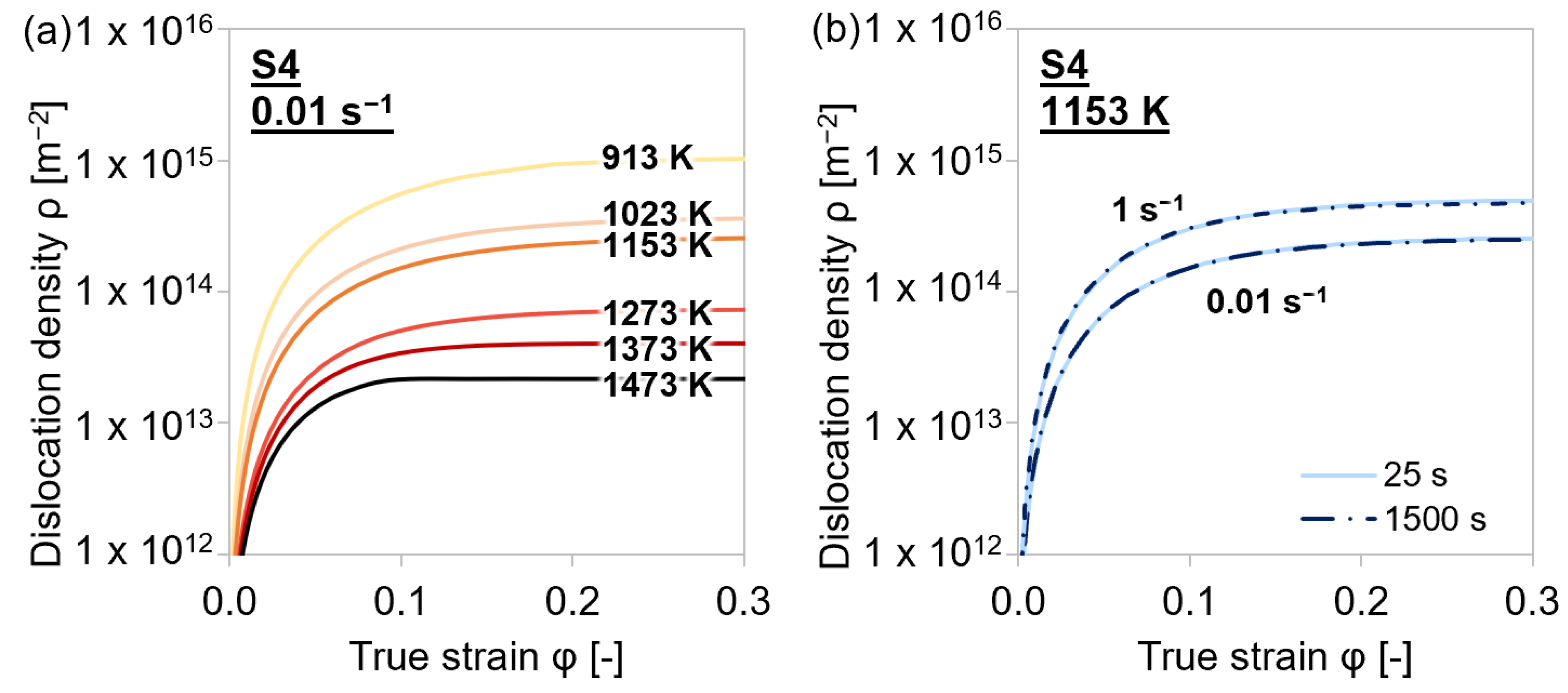
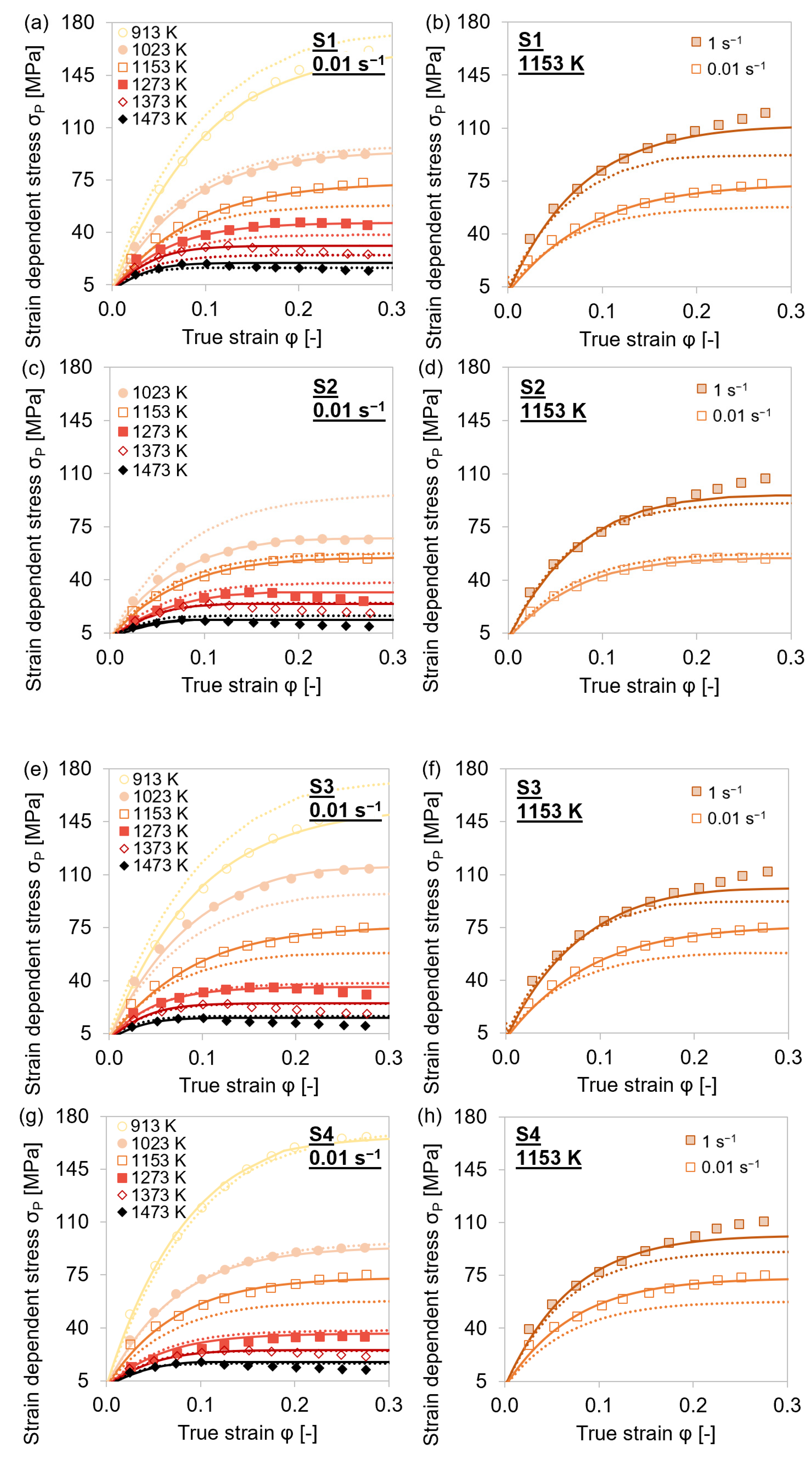
4.1.2. Variation of Test Temperatures, Intermediate Holding Times, and Strain Rates
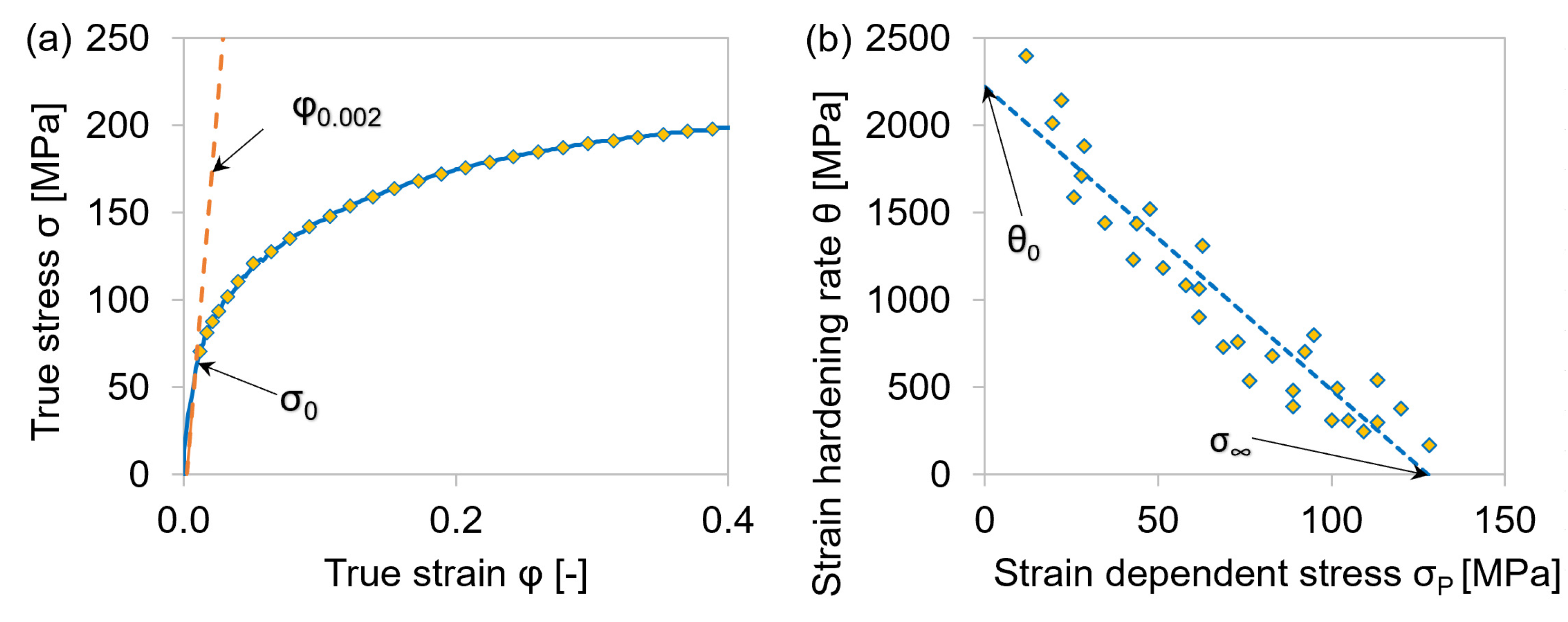
4.2. Physical Parameters σ0, σ∞, and θ0
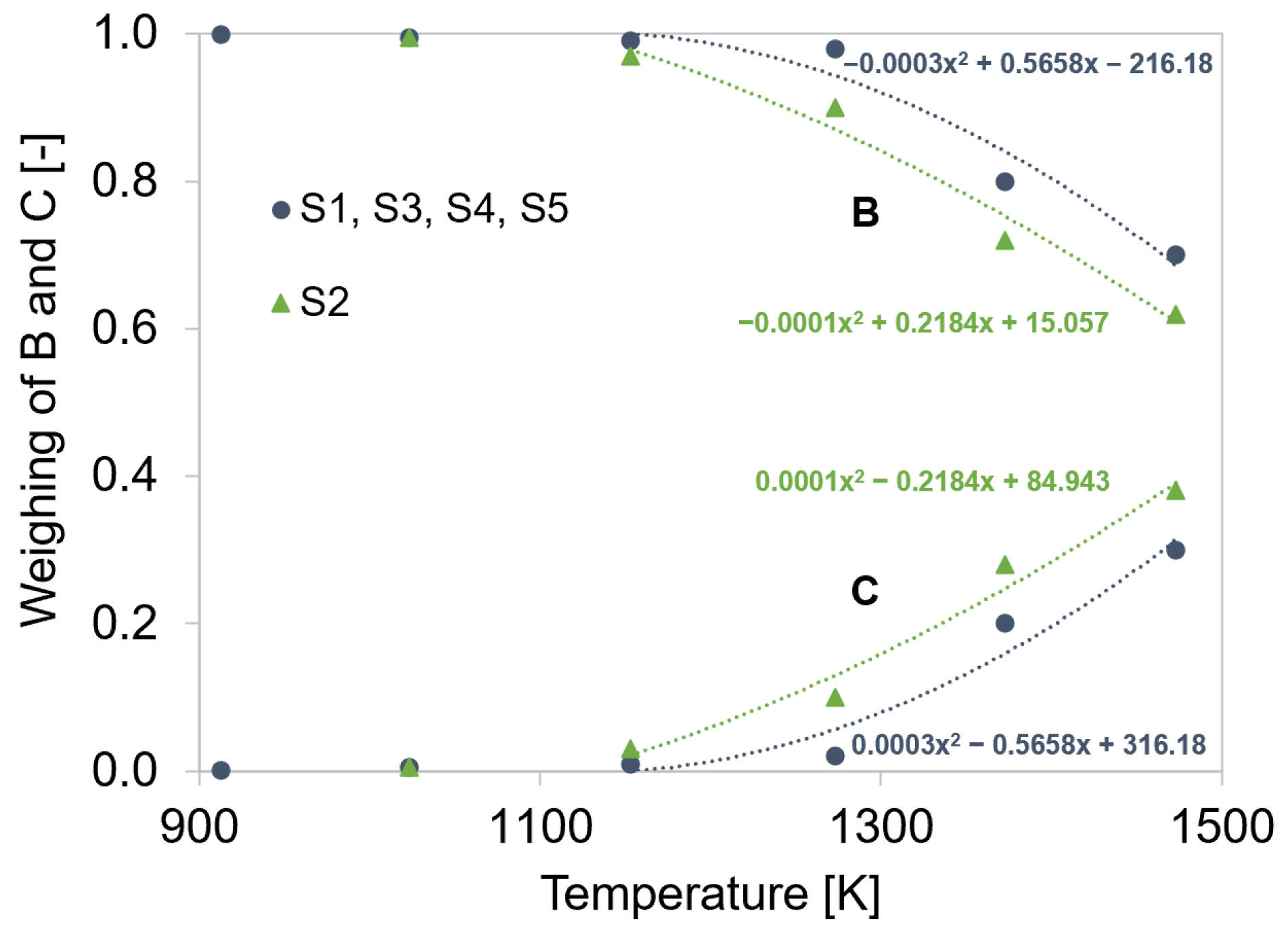
4.3. Strengthening Parameters A, B, and C
4.4. Computational Analysis of the Results
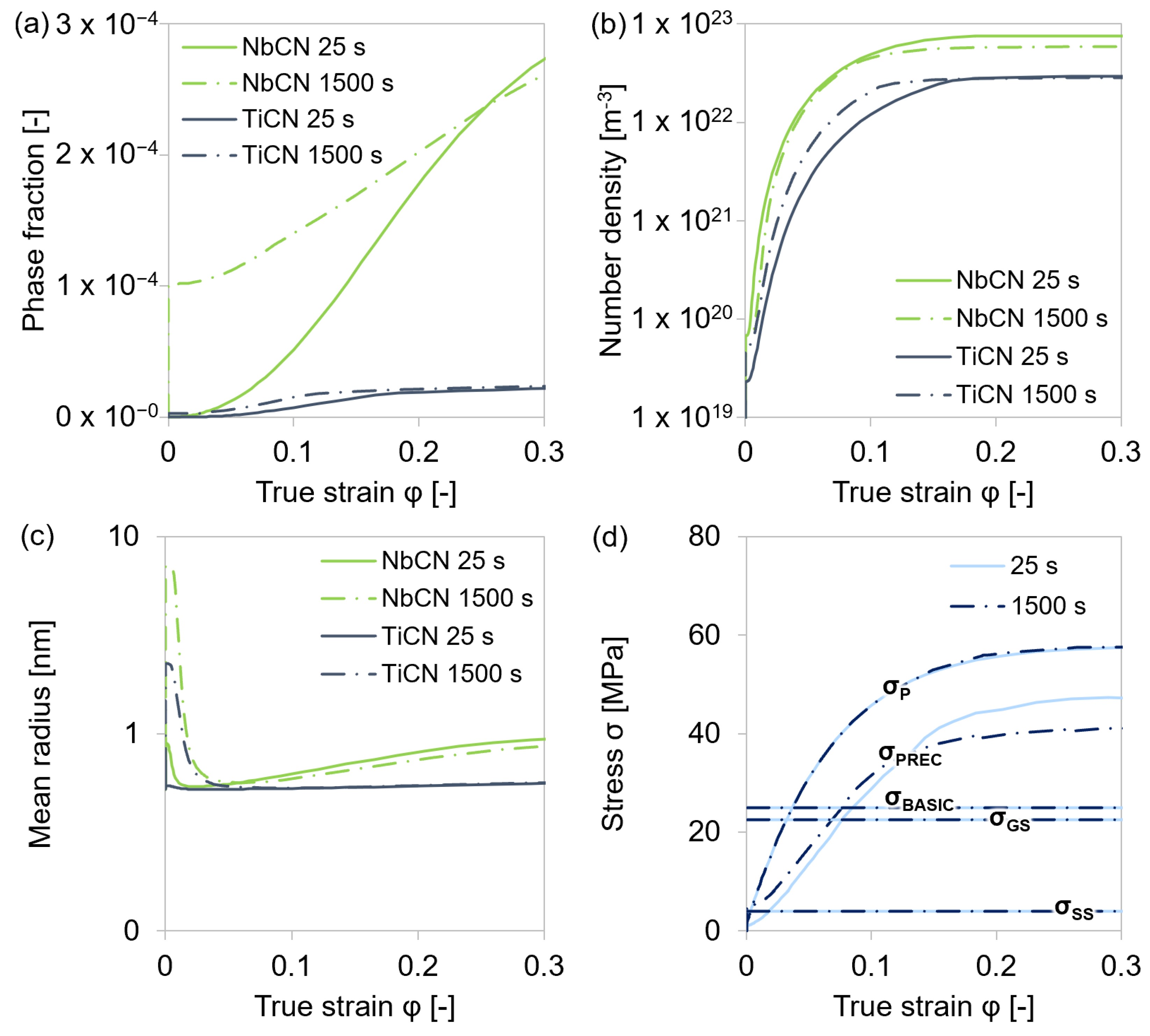
4.4.1. Dislocation Density Evolution
4.4.2. Flow Curves
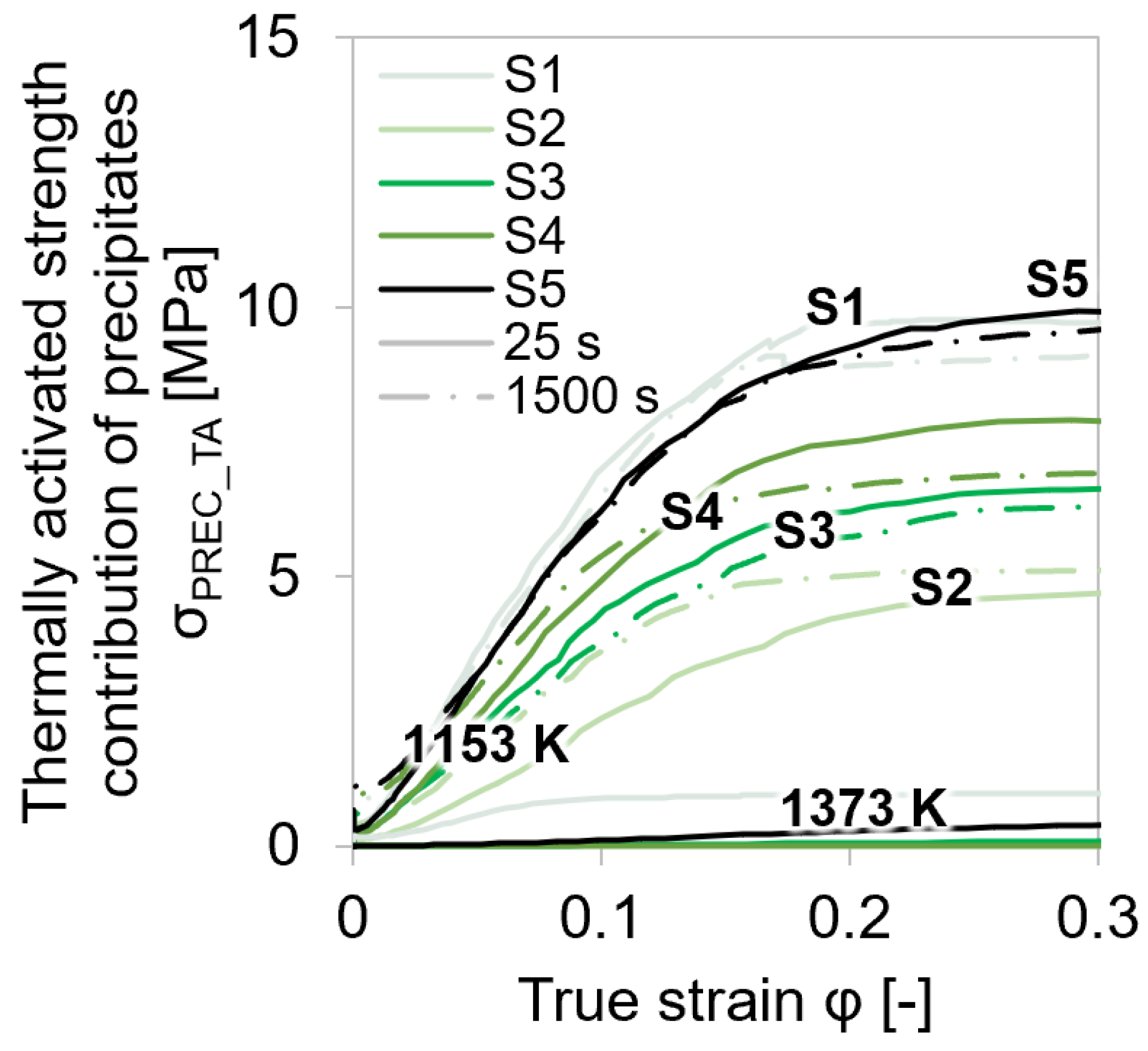
4.4.3. Impact of Microalloy Carbonitrides on Strengthening
4.5. Description of ABC Parameters by Newly Developed Equations
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Consideration of the Stiffness of the Gleeble® Device in the Calculation of the Flow Curves

Appendix B. Kocks Plots for Determination of θ0 and σ∞
References
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Li, Y.Z.; Liang, Z.Y.; Huang, M.X. Strengthening contributions of dislocations and twins in warm-rolled TWIP steels. Int. J. Plast. 2022, 150, 103198. [Google Scholar] [CrossRef]
- Baker, T.N. Microalloyed steels. Ironmak. Steelmak. 2016, 43, 264–307. [Google Scholar] [CrossRef]
- Zeng, Y.-N.; Li, J.-G.; Wang, Y.-J. Thermodynamic and Kinetic Analysis of Inhomogeneous Distribution of Solute on Precipitations in as Cast Nb–V–Ti Microalloyed Steel. In TMS 2019 148th Annual Meeting & Exhibition Supplemental Proceedings; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Carvalho Resende, T.; Bouvier, S.; Abed-Meraim, F.; Balan, T.; Sablin, S.-S. Dislocation-based model for the prediction of the behavior of b.c.c. materials—Grain size and strain path effects. Int. J. Plast. 2013, 47, 29–48. [Google Scholar] [CrossRef][Green Version]
- Graux, A.; Cazottes, S.; de Castro, D.; San Martín, D.; Capdevila, C.; Cabrera, J.M.; Molas, S.; Schreiber, S.; Mirković, D.; Danoix, F. Precipitation and grain growth modelling in Ti-Nb microalloyed steels. Materialia 2019, 5, 100233. [Google Scholar] [CrossRef]
- Zeng, R.; Huang, L.; Li, J.; Li, H.; Zhu, H.; Zhang, X. Quantification of multiple softening processes occurring during multi-stage thermoforming of high-strength steel. Int. J. Plast. 2019, 120, 64–87. [Google Scholar] [CrossRef]
- Esterl, R.; Sonnleitner, M.; Schnitzer, R. Microstructural Analysis of the Recrystallization Behavior of Low Alloyed Steels. Steel Res. Int. 2019, 90, 1800500. [Google Scholar] [CrossRef]
- Zhao, Y.; Tong, X.; Wei, X.H.; Xu, S.S.; Lan, S.; Wang, X.-L.; Zhang, Z.W. Effects of microstructure on crack resistance and low-temperature toughness of ultra-low carbon high strength steel. Int. J. Plast. 2019, 116, 203–215. [Google Scholar] [CrossRef]
- Sietsma, J. Nucleation and growth during the austenite-to-ferrite phase transformation in steels after plastic deformation. In Phase Transformations in Steels; Elsevier: Amsterdam, The Netherlands, 2012; pp. 505–526. ISBN 9781845699703. [Google Scholar]
- Nabarro, F.; Basinski, Z.S.; Holt, D.B. The plasticity of pure single crystals. Adv. Phys. 1964, 13, 193–323. [Google Scholar] [CrossRef]
- Taheri, M.; Weiland, H.; Rollett, A. A method of measuring stored energy macroscopically using statistically stored dislocations in commercial purity aluminum. Metall. Mater. Trans. A 2006, 37, 19–25. [Google Scholar] [CrossRef]
- Kalácska, S.; Groma, I.; Borbély, A.; Ispánovity, P.D. Comparison of the dislocation density obtained by HR-EBSD and X-ray profile analysis. Appl. Phys. Lett. 2017, 110, 91912. [Google Scholar] [CrossRef]
- Yadav, S.D.; El-Tahawy, M.; Kalácska, S.; Dománková, M.; Yubero, D.C.; Poletti, M.C. Characterizing dislocation configurations and their evolution during creep of a new 12% Cr steel. Mater. Charact. 2017, 134, 387–397. [Google Scholar] [CrossRef]
- Vershinina, T.; Leont'eva-Smirnova, M. Dislocation density evolution in the process of high-temperature treatment and creep of EK-181 steel. Mater. Charact. 2017, 125, 23–28. [Google Scholar] [CrossRef]
- Macchi, J.; Gaudez, S.; Geandier, G.; Teixeira, J.; Denis, S.; Bonnet, F.; Allain, S.Y.P. Dislocation densities in a low-carbon steel during martensite transformation determined by in situ high energy X-Ray diffraction. Mater. Sci. Eng. A 2021, 800, 140249. [Google Scholar] [CrossRef]
- An, D.; Zaefferer, S. Formation mechanism of dislocation patterns under low cycle fatigue of a high-manganese austenitic TRIP steel with dominating planar slip mode. Int. J. Plast. 2019, 121, 244–260. [Google Scholar] [CrossRef]
- Grilli, N.; Janssens, K.G.F.; Nellessen, J.; Sandlöbes, S.; Raabe, D. Multiple slip dislocation patterning in a dislocation-based crystal plasticity finite element method. Int. J. Plast. 2018, 100, 104–121. [Google Scholar] [CrossRef]
- León-Cázares, F.D.; Monni, F.; Jackson, T.; Galindo-Nava, E.I.; Rae, C. Stress response and microstructural evolution of nickel-based superalloys during low cycle fatigue: Physics-based modelling of cyclic hardening and softening. Int. J. Plast. 2020, 128, 102682. [Google Scholar] [CrossRef]
- Kim, S.-D.; Park, J.Y.; Park, S.-J.; Moon, J.; Ha, H.-Y.; Lee, C.-H.; Kang, J.-Y.; Shin, J.-H.; Lee, T.-H. Direct observation of dislocation plasticity in high-Mn lightweight steel by in-situ TEM. Sci. Rep. 2019, 9, 15171. [Google Scholar] [CrossRef]
- Li, Y.; Ran, G.; Guo, Y.; Sun, Z.; Liu, X.; Li, Y.; Qiu, X.; Xin, Y. The evolution of dislocation loop and its interaction with pre-existing dislocation in He+-irradiated molybdenum: In-situ TEM observation and molecular dynamics simulation. Acta Mater. 2020, 201, 462–476. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, S.; Zhang, B.; Tian, X.; Kan, Q.; Kang, G. Dislocation–grain boundary interaction-based discrete dislocation dynamics modeling and its application to bicrystals with different misorientations. Acta Mater. 2021, 202, 88–98. [Google Scholar] [CrossRef]
- Jiang, M.; Monnet, G.; Devincre, B. On the origin of the Hall–Petch law: A 3D-dislocation dynamics simulation investigation. Acta Mater. 2021, 209, 116783. [Google Scholar] [CrossRef]
- Guo, X.; Sun, C.; Wang, C.; Jiang, J.; Fu, M.W. Study of dislocation-twin boundary interaction mechanisms in plastic deformation of TWIP steel by discrete dislocation dynamics and dislocation density-based modeling. Int. J. Plast. 2021, 145, 103076. [Google Scholar] [CrossRef]
- Jiang, M.; Devincre, B.; Monnet, G. Effects of the grain size and shape on the flow stress: A dislocation dynamics study. Int. J. Plast. 2019, 113, 111–124. [Google Scholar] [CrossRef]
- Sudmanns, M.; El-Awady, J.A. The effect of local chemical ordering on dislocation activity in multi-principle element alloys: A three-dimensional discrete dislocation dynamics study. Acta Mater. 2021, 220, 117307. [Google Scholar] [CrossRef]
- Jamond, O.; Gatti, R.; Roos, A.; Devincre, B. Consistent formulation for the Discrete-Continuous Model: Improving complex dislocation dynamics simulations. Int. J. Plast. 2016, 80, 19–37. [Google Scholar] [CrossRef]
- Hunter, A.; Preston, D.L. Analytic model of dislocation density evolution in fcc polycrystals accounting for dislocation generation, storage, and dynamic recovery mechanisms. Int. J. Plast. 2022, 151, 103178. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, Q.; Eskandari Sabzi, H.; Wen, W.; Rivera-Díaz-del-Castillo, P.E. Modelling stress relaxation after hot deformation: Microstructure-property relationships in Nb-bearing steels. Int. J. Plast. 2022, 151, 103219. [Google Scholar] [CrossRef]
- Cong, T.; Li, R.; Zheng, Z.; Ma, X.; Wu, S.; Zhang, R.; Berto, F.; Sun, J.; Qian, G. Experimental and computational investigation of weathering steel Q450NQR1 under high cycle fatigue loading via crystal plasticity finite element method. Int. J. Fatigue 2022, 159, 106772. [Google Scholar] [CrossRef]
- Buzolin, R.H.; Lasnik, M.; Krumphals, A.; Poletti, M.C. A dislocation-based model for the microstructure evolution and the flow stress of a Ti5553 alloy. Int. J. Plast. 2021, 136, 102862. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, J.; Wang, Z.; Gan, B.; Zhao, J.; Kang, G.; Zhang, X. Crystal plasticity finite element analysis of gradient nanostructured TWIP steel. Int. J. Plast. 2020, 130, 102703. [Google Scholar] [CrossRef]
- Farrokh, B.; Khan, A.S. Grain size, strain rate, and temperature dependence of flow stress in ultra-fine grained and nanocrystalline Cu and Al: Synthesis, experiment, and constitutive modeling. Int. J. Plast. 2009, 25, 715–732. [Google Scholar] [CrossRef]
- Feather, W.G.; Savage, D.J.; Knezevic, M. A crystal plasticity finite element model embedding strain-rate sensitivities inherent to deformation mechanisms: Application to alloy AZ31. Int. J. Plast. 2021, 143, 103031. [Google Scholar] [CrossRef]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I.—Theoretical. Proc. R. Soc. Lond. A 1934, 145, 362–387. [Google Scholar] [CrossRef]
- Sauzay, M.; Kubin, L.P. Scaling laws for dislocation microstructures in monotonic and cyclic deformation of fcc metals. Prog. Mater. Sci. 2011, 56, 725–784. [Google Scholar] [CrossRef]
- Mughrabi, H. The α-factor in the Taylor flow-stress law in monotonic, cyclic and quasi-stationary deformations: Dependence on slip mode, dislocation arrangement and density. Curr. Opin. Solid State Mater. Sci. 2016, 20, 411–420. [Google Scholar] [CrossRef]
- Großeiber, S.; Ilie, S.; Poletti, M.C.; Harrer, B.; Degischer, H.P. Influence of Strain Rate on Hot Ductility of a V-Microalloyed Steel Slab. Steel Res. Int. 2012, 83, 445–455. [Google Scholar] [CrossRef]
- Khalifa, H.; Megahed, G.M.; El-Bitar, T.; Taha, M.A. Numerical analysis of flow behaviour, grain size prediction and experimental verification of hot rolled ultralow carbon niobium microalloyed steel. Materialwiss. Werkstofftech. 2021, 52, 725–738. [Google Scholar] [CrossRef]
- Diehl, J. Zugverformung von Kupfer Einkristallen I. Verfestigungskurven und Oberflächenerscheinungen. Z. Metallkd. 1956, 47, 331–343. [Google Scholar] [CrossRef]
- Diehl, J.; Mader, S.; Seeger, A. Gleitmechanismus und Oberflächenerscheinungen bei kubisch flächenzentrierten Metallen. Z. Metallkd. 1955, 46, 650–657. [Google Scholar] [CrossRef]
- Kocks, U.F. Laws for Work-Hardening and Low-Temperature Creep. J. Eng. Mater. Technol. 1976, 98, 76–85. [Google Scholar] [CrossRef]
- Kreyca, J.; Kozeschnik, E. Temperature-dependent strain hardening, precipitation and deformation-induced microstructure evolution in AA 6061. Mater. Sci. Eng. A 2017, 708, 411–418. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Baker, T.N. Titanium microalloyed steels. Ironmak. Steelmak. 2017, 46, 1–55. [Google Scholar] [CrossRef]
- Rainforth, W.M.; Black, M.P.; Higginson, R.L.; Palmiere, E.J.; Sellars, C.M.; Prabst, I.; Warbichler, P.; Hofer, F. Precipitation of NbC in a model austenitic steel. Acta Mater. 2002, 50, 735–747. [Google Scholar] [CrossRef]
- Karmakar, A.; Biswas, S.; Mukherjee, S.; Chakrabarti, D.; Kumar, V. Effect of composition and thermo-mechanical processing schedule on the microstructure, precipitation and strengthening of Nb-microalloyed steel. Mater. Sci. Eng. A 2017, 690, 158–169. [Google Scholar] [CrossRef]
- Hansen, S.S.; Vander Sande, J.B.; Cohen, M. Niobium carbonitride precipitation and austenite recrystallization in hot-rolled microalloyed steels. Met. Trans. A 1980, 11, 387–402. [Google Scholar] [CrossRef]
- Akhtar, M.N.; Khan, M.; Khan, S.A.; Afzal, A.; Subbiah, R.; Ahmad, S.N.; Husain, M.; Butt, M.M.; Othman, A.R.; Bakar, E.A. Determination of non-recrystallization temperature for niobium microalloyed steel. Materials 2021, 14, 2639. [Google Scholar] [CrossRef]
- Baker, T.N. Processes, microstructure and properties of vanadium microalloyed steels. Mater. Sci. Technol. 2013, 25, 1083–1107. [Google Scholar] [CrossRef]
- Ioannidou, C.; Arechabaleta, Z.; Navarro-López, A.; Rijkenberg, A.; Dalgliesh, R.M.; Kölling, S.; Bliznuk, V.; Pappas, C.; Sietsma, J.; van Well, A.A.; et al. Interaction of precipitation with austenite-to-ferrite phase transformation in vanadium micro-alloyed steels. Acta Mater. 2019, 181, 10–24. [Google Scholar] [CrossRef]
- Canelo-Yubero, D.; Kovács, Z.; Simonet Fotso, J.T.; Tolnai, D.; Schell, N.; Groma, I.; Poletti, C. In-situ characterization of continuous dynamic recrystallization during hot torsion of an Al–Si–Mg alloy. J. Alloys Compd. 2020, 822, 153282. [Google Scholar] [CrossRef]
- Barlat, F.; Glazov, M.V.; Brem, J.C.; Lege, D.J. A simple model for dislocation behavior, strain and strain rate hardening evolution in deforming aluminum alloys. Int. J. Plast. 2002, 18, 919–939. [Google Scholar] [CrossRef]
- Simar, A.; Bréchet, Y.; de Meester, B.; Denquin, A.; Gallais, C.; Pardoen, T. Integrated modeling of friction stir welding of 6xxx series Al alloys: Process, microstructure and properties. Prog. Mater. Sci. 2012, 57, 95–183. [Google Scholar] [CrossRef]
- Kreyca, J. State Parameter Based Modelling of Stress-Strain Curves in Aluminium Alloys: Dissertation; TU Wien: Wien, Austria, 2017. [Google Scholar]
- Kreyca, J.; Kozeschnik, E. State parameter-based constitutive modelling of stress strain curves in Al-Mg solid solutions. Int. J. Plast. 2018, 103, 67–80. [Google Scholar] [CrossRef]
- Sherstnev, P.; Lang, P.; Kozeschnik, E. Treatment of simultaneous deformation and solid-state precipitation in thermo-kinetic calculations: (ECCOMAS 2012). Eur. Congr. Comput. Methods Appl. Sci. Eng. 2012, 5331–5338. [Google Scholar]
- Kozeschnik, E. Mean-Field Microstructure Kinetics Modeling. Encycl.Mater. Met. Alloy. 2022, 4, 521–526. [Google Scholar] [CrossRef]
- Labusch, R. A Statistical Theory of Solid Solution Hardening. Phys. Stat. Sol. 1970, 41, 659–669. [Google Scholar] [CrossRef]
- Hall, E.O. The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. Lond. Sect. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Ahmadi, M.R.; Povoden-Karadeniz, E.; Öksüz, K.I.; Falahati, A.; Kozeschnik, E. A model for precipitation strengthening in multi-particle systems. Comput. Mater. Sci. 2014, 91, 173–186. [Google Scholar] [CrossRef]
- CDL-IPE, Inst. of Mat. Sci. and Technol., TU Wien. CDL-IPE, Thermodynamic Database with Modified Carbo-Nitride Descriptions Based on the Open-Licence Multi-Component MatCalc Database mc_fe, Version 2.060. Available online: https://www.matcalc.at/index.php/databases/open-databases (accessed on 21 January 2022).
- Inst. of Mat. Sci. and Technol., TU Wien. Open-Licence Multi-Component MatCalc Diffusion Mobilities Database mc_fe, Version 2.012. Available online: https://www.matcalc.at/index.php/databases/open-databases (accessed on 21 January 2022).
- Dutta, B.; Valdes, E.; Sellars, C.M. Mechanism and kinetics of strain induced precipitation of Nb(C, N) in austenite. Acta Metall. Mater. 1992, 40, 653–662. [Google Scholar] [CrossRef]
- Roters, F.; Raabe, D.; Gottstein, G. Work hardening in heterogeneous alloys—A microstructural approach based on three internal state variables. Acta Mater. 2000, 48, 4181–4189. [Google Scholar] [CrossRef]
- Stechauner, G.; Kozeschnik, E. Assessment of substitutional self-diffusion along short-circuit paths in Al, Fe and Ni. Calphad 2014, 47, 92–99. [Google Scholar] [CrossRef]
- Vujic, S.; Sandström, R.; Sommitsch, C. Precipitation evolution and creep strength modelling of 25Cr20NiNbN austenitic steel. Mater. High Temp. 2015, 32, 607–618. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C. Effect of grain and twin boundaries on the hardening mechanisms of twinning-induced plasticity steels. Scr. Mater. 2008, 58, 484–487. [Google Scholar] [CrossRef]
- Pitre, L.; Plimmer, M.D.; Sparasci, F.; Himbert, M.E. Determinations of the Boltzmann constant. C. R. Phys. 2019, 20, 129–139. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A.P. CALPHAD (Calculation of Phase Diagrams): A Comprehensive Guide; Elsevier: Amsterdam, The Netherlands, 1998; ISBN 0-08-0421296. [Google Scholar]
- Mishra, R.S. Dislocation-particle interaction at elevated temperatures. JOM 2009, 61, 52–55. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Y.; Niezgoda, S.R. Microstructural and micromechanical evolution during dynamic recrystallization. Int. J. Plast. 2018, 100, 52–68. [Google Scholar] [CrossRef]
- Arechabaleta, Z.; van Liempt, P.; Sietsma, J. Unravelling dislocation networks in metals. Mater. Sci. Eng. A 2018, 710, 329–333. [Google Scholar] [CrossRef]
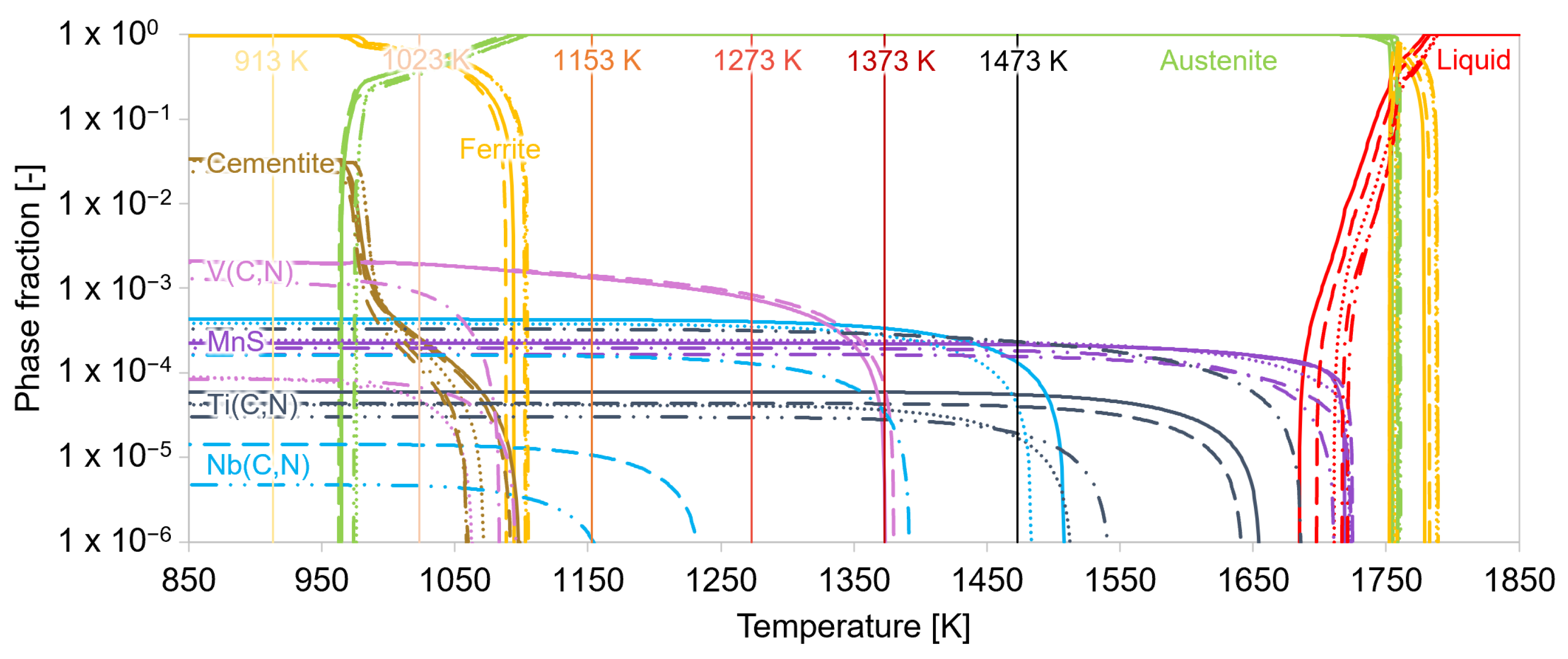
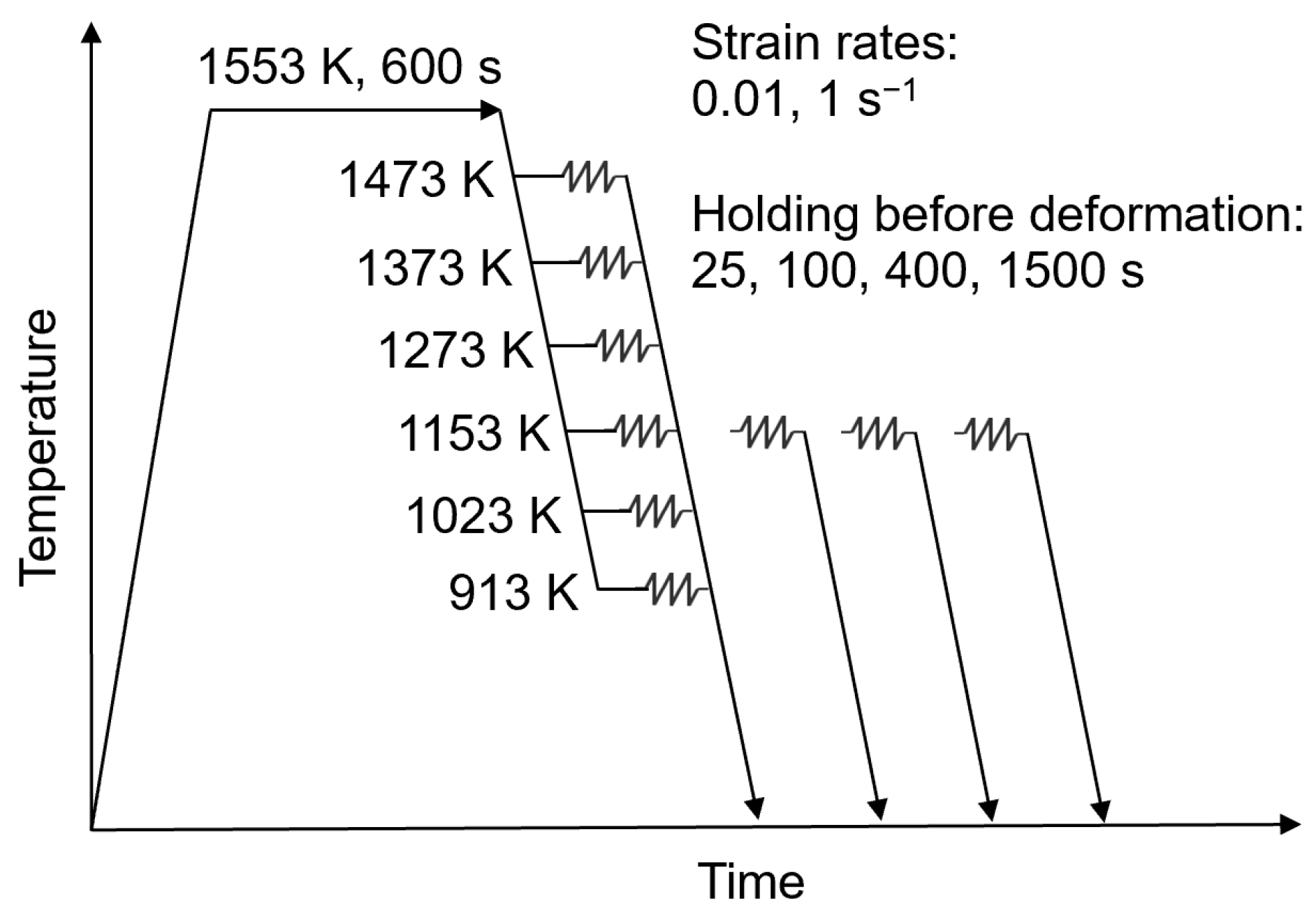


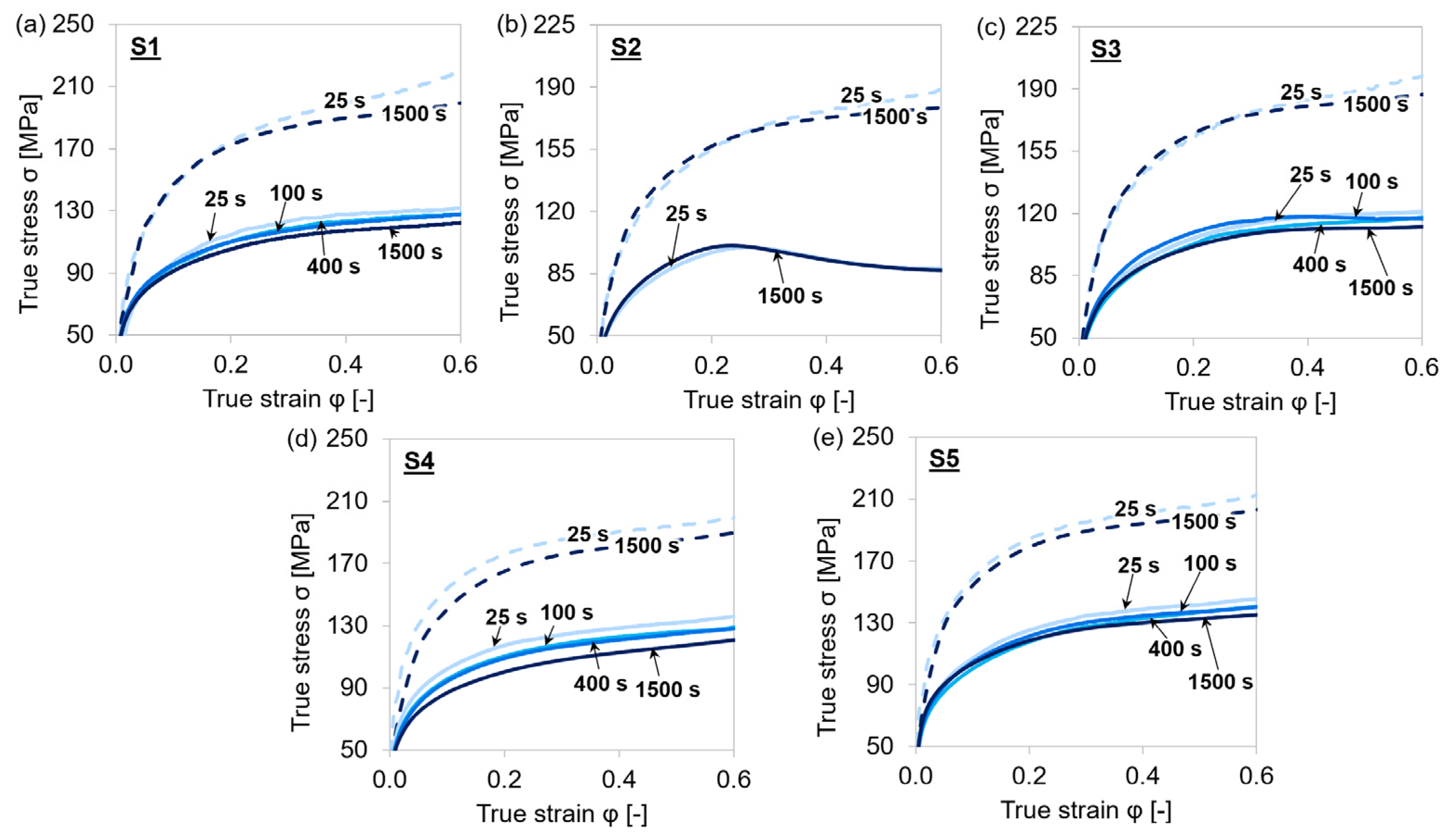
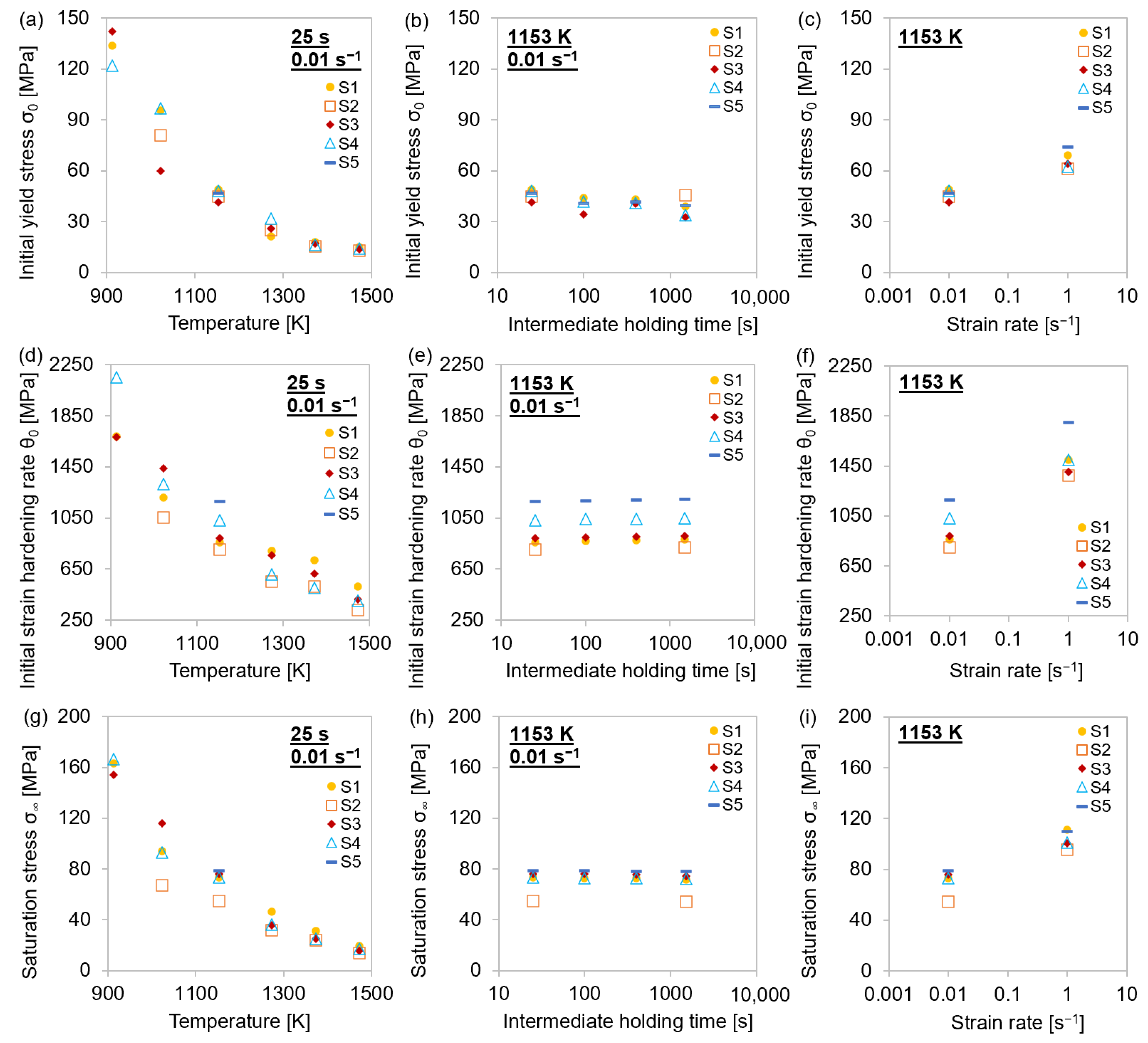

| Steel Grade | C | Mn | Ti | Nb | V | Cr |
|---|---|---|---|---|---|---|
| S1 | 0.15 | 1.27 | 0.01 | 0.01 | 0.07 | 0.20 |
| S2 | 0.18 | 0.88 | <0.01 | <0.01 | <0.01 | 0.02 |
| S3 | 0.20 | 1.40 | <0.01 | <0.01 | 0.10 | 0.02 |
| S4 | 0.18 | 0.93 | <0.01 | 0.03 | <0.01 | 0.03 |
| S5 | 0.21 | 1.45 | <0.01 | 0.04 | 0.10 | 0.03 |
| Symbol | Name | Value | Unit | Literature Source |
|---|---|---|---|---|
| ν | Poisson’s ratio | 0.30 | - | [68] |
| G | Shear modulus | MPa | MatCalc default value | |
| b | Burgers vector | 2.50∙10−10 | m | [69] |
| M | Taylor factor | 3.06 | - | [69] |
| k | Boltzmann constant | 1.38065∙10−23 | JK−1 | [70] |
| A for 913–1473 K |
| B for 913–1473 K |
| C for 1273–1473 K |
| C for 913–1273 K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobotka, E.; Kreyca, J.; Poletti, M.C.; Povoden-Karadeniz, E. Analysis and Modeling of Stress–Strain Curves in Microalloyed Steels Based on a Dislocation Density Evolution Model. Materials 2022, 15, 6824. https://doi.org/10.3390/ma15196824
Sobotka E, Kreyca J, Poletti MC, Povoden-Karadeniz E. Analysis and Modeling of Stress–Strain Curves in Microalloyed Steels Based on a Dislocation Density Evolution Model. Materials. 2022; 15(19):6824. https://doi.org/10.3390/ma15196824
Chicago/Turabian StyleSobotka, Evelyn, Johannes Kreyca, Maria Cecilia Poletti, and Erwin Povoden-Karadeniz. 2022. "Analysis and Modeling of Stress–Strain Curves in Microalloyed Steels Based on a Dislocation Density Evolution Model" Materials 15, no. 19: 6824. https://doi.org/10.3390/ma15196824
APA StyleSobotka, E., Kreyca, J., Poletti, M. C., & Povoden-Karadeniz, E. (2022). Analysis and Modeling of Stress–Strain Curves in Microalloyed Steels Based on a Dislocation Density Evolution Model. Materials, 15(19), 6824. https://doi.org/10.3390/ma15196824







