On the Single-Point Calculation of Stress–Strain Data under Large Deformations with Stress and Mixed Control
Abstract
1. Introduction
2. The Single-Point Calculator
2.1. Strain Control in the Single-Point Calculator
2.2. Stress and Mixed Control in the Single-Point Calculator
2.3. Implementation of the Single-Point Calculator
- (1)
- Divide the loading into N segments. Thus, the prescribed deformation gradient and stress increase in N steps accordingly.
- (2)
- Calculate the deformation gradient and the stress with the known tensors in the last step and the prescribed values in this step. The initial deformation gradient is set as , and the initial stress can be set as .
- (3)
- Perform the Newton iteration within one step, as shown in Algorithm 1. In the -th iteration, the increment of the deformation gradient can be solved from Equation (11). The deformation gradient is then updated:The stress is updated: . The iteration goes on until the acceptable deformation gradient and stress are found.
| Algorithm 1 Iteration in the stress and mixed control single-point calculator. |
3. Applications of the Single-Point Calculator
3.1. Application in Tests of a Single Crystal Plasticity Model
3.1.1. Constitutive Model
3.1.2. Calculation and Results
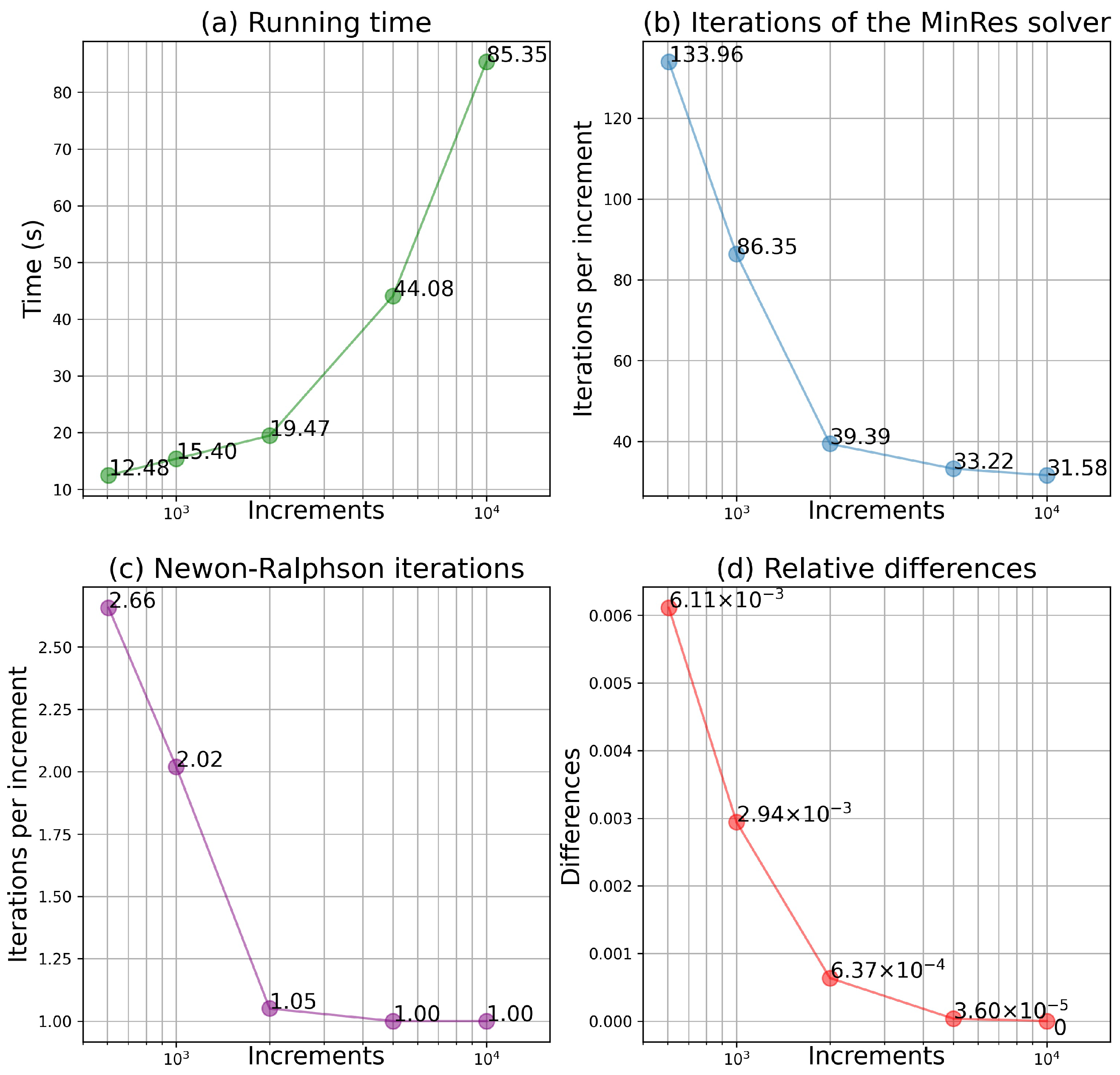
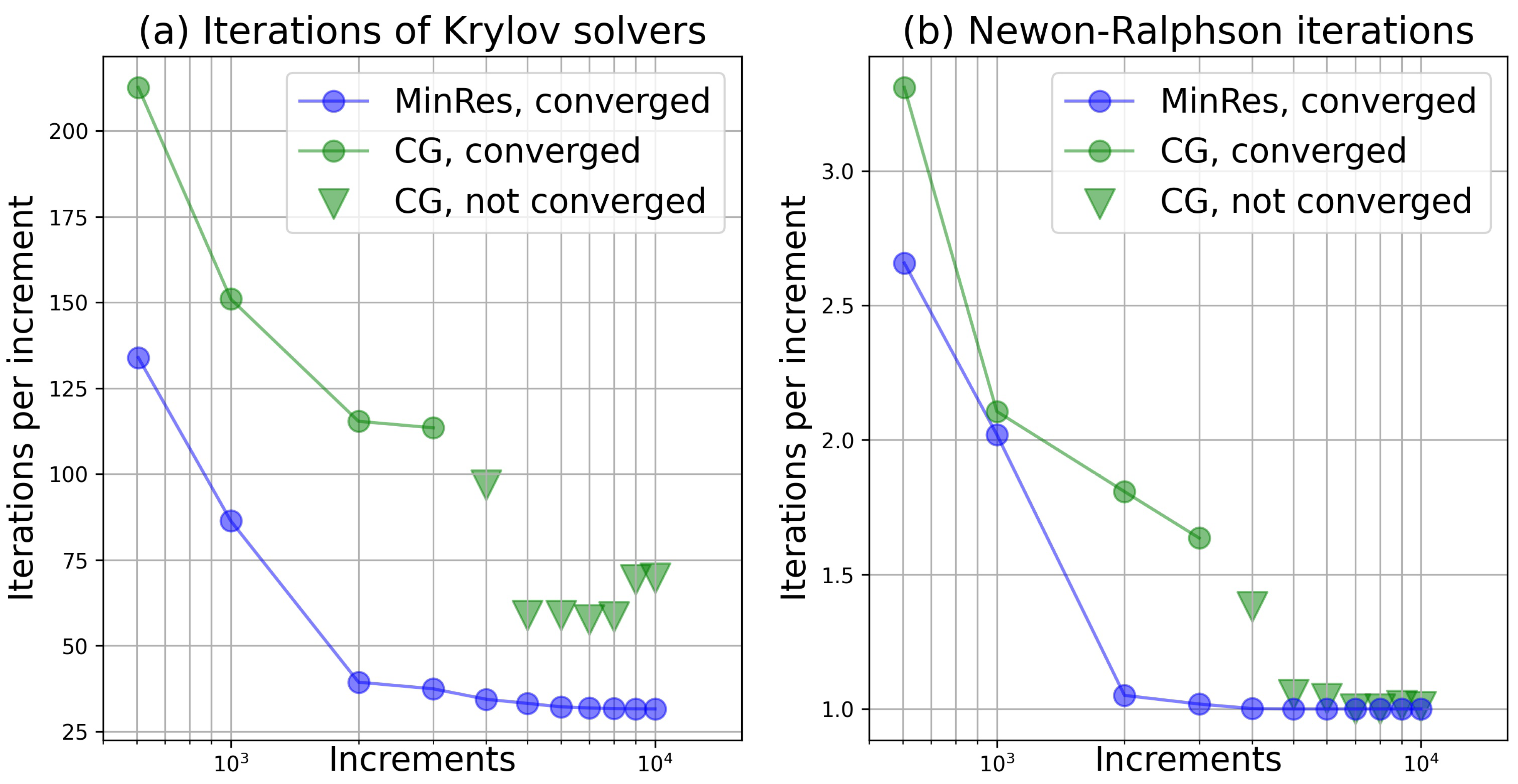
3.1.3. Performance of the Calculator
- Unified form of Equation (11) for all kinds of the stress control;
- Ability to deal with the possible singular stiffness tangent;
- Robustness, comparing to the CG solver.
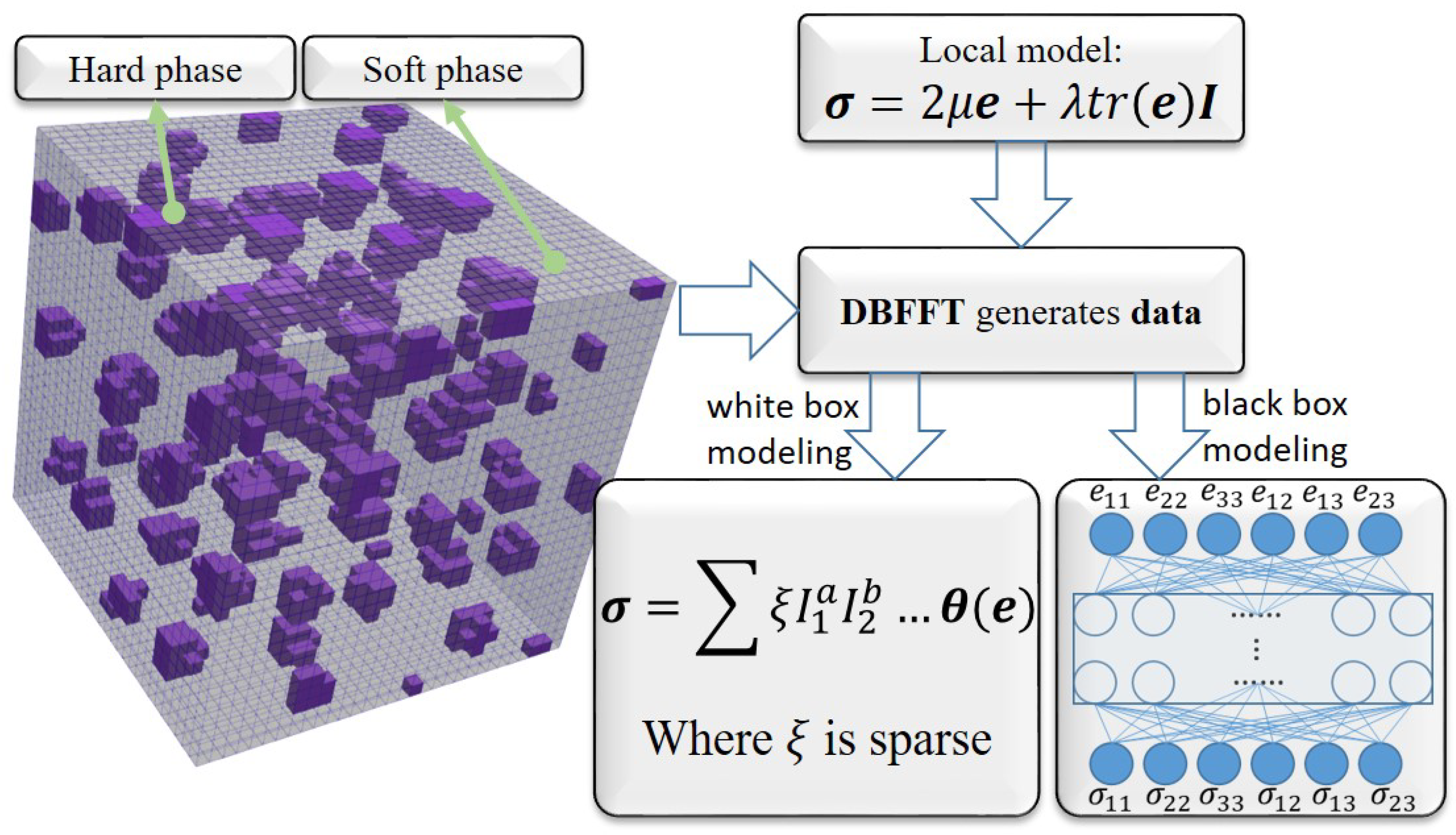
3.2. Application in Tests of an Artificial Neural Network Elasticity Model
3.2.1. Data-Driven Constitutive Models
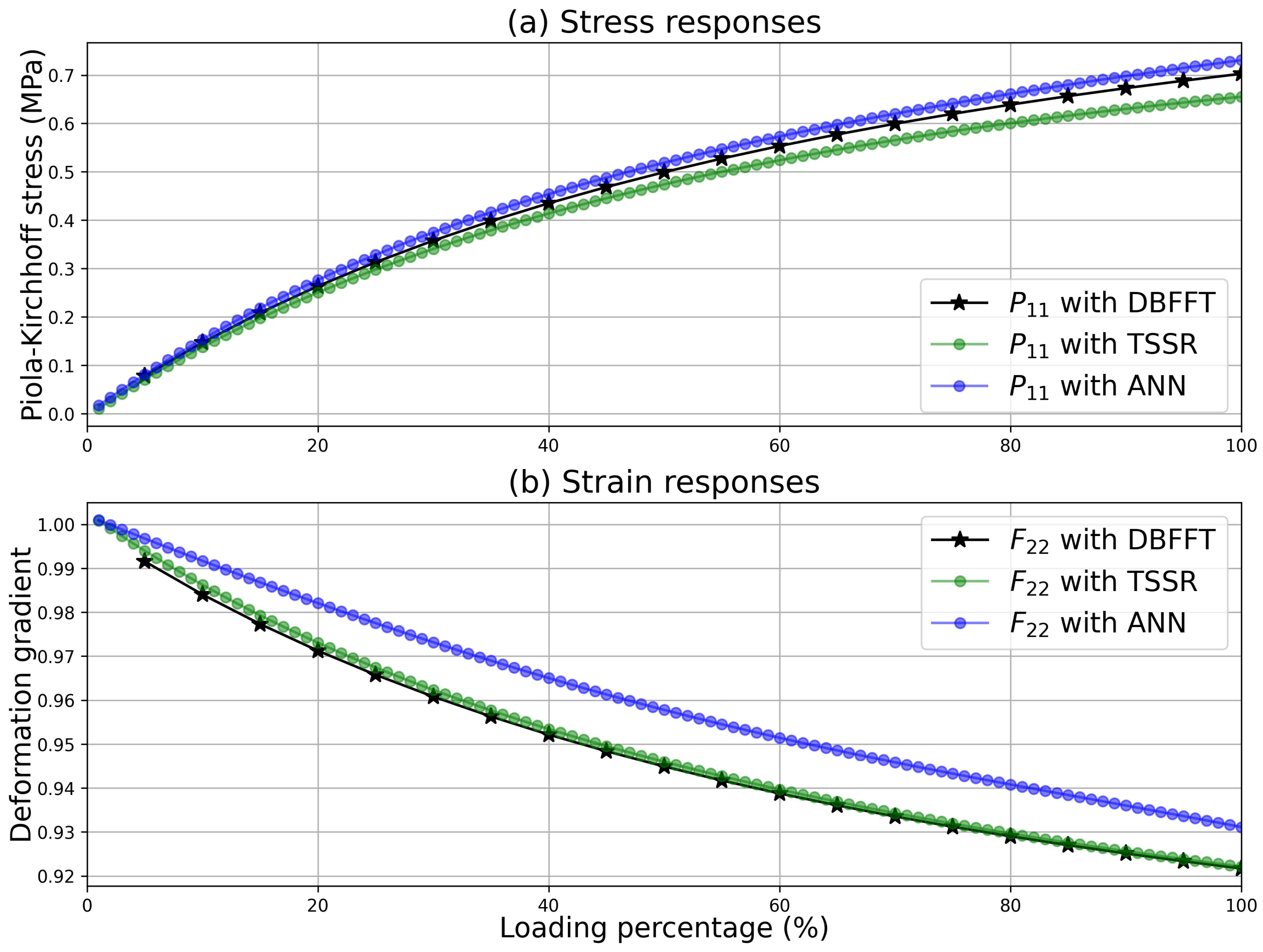
3.2.2. Calculation and Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of arteries. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1551–1597. [Google Scholar] [CrossRef]
- Cisse, C.; Zaki, W.; Zineb, T.B. A review of constitutive models and modeling techniques for shape memory alloys. Int. J. Plast. 2016, 76, 244–284. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Hossain, M. A microstructural-based approach to model magneto-viscoelastic materials at finite strains. Int. J. Solids Struct. 2021, 208–209, 119–132. [Google Scholar] [CrossRef]
- Liu, X.; Tian, S.; Tao, F.; Yu, W. A review of artificial neural networks in the constitutive modeling of composite materials. Compos. Part B Eng. 2021, 224, 109152. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.; Bieler, T.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Segurado, J.; Lebensohn, R.A.; LLorca, J. Chapter One—Computational Homogenization of Polycrystals. In Advances in Crystals and Elastic Metamaterials, Part 1; Volume 51: Advances in Applied Mechanics; Hussein, M.I., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 1–114. [Google Scholar] [CrossRef]
- de Carvalho, R.; Valente, R.A.F.; Andrade-Campos, A. On the Objective Function Evaluation in Parameter Identification of Material Constitutive Models - Single-point or FE Analysis. Int. J. Mater. Form. 2010, 3, 33–36. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 2016, 304, 81–101. [Google Scholar] [CrossRef]
- Hartmaier, A. Data-Oriented Constitutive Modeling of Plasticity in Metals. Materials 2020, 13, 1600. [Google Scholar] [CrossRef]
- Kalayci, C.B.; Karagoz, S.; Karakas, Ö. Soft computing methods for fatigue life estimation: A review of the current state and future trends. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 2763–2785. [Google Scholar] [CrossRef]
- Zhang, P.; Yin, Z.Y.; Jin, Y.F. State-of-the-Art Review of Machine Learning Applications in Constitutive Modeling of Soils. Arch. Comput. Methods Eng. 2021, 28, 3661–3686. [Google Scholar] [CrossRef]
- Logarzo, H.J.; Capuano, G.; Rimoli, J.J. Smart constitutive laws: Inelastic homogenization through machine learning. Comput. Methods Appl. Mech. Eng. 2021, 373, 113482. [Google Scholar] [CrossRef]
- Wang, M.; Chen, C.; Liu, W. Establish algebraic data-driven constitutive models for elastic solids with a tensorial sparse symbolic regression method and a hybrid feature selection technique. J. Mech. Phys. Solids 2022, 159, 104742. [Google Scholar] [CrossRef]
- Huang, Y. A User-Material Subroutine Incorporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Technical Report; Harvard University: Cambridge, MA, USA, 1991; Report Mech-178. [Google Scholar]
- Harewood, F.; McHugh, P. Comparison of the implicit and explicit finite element methods using crystal plasticity. Comput. Mater. Sci. 2007, 39, 481–494. [Google Scholar] [CrossRef]
- Yasmeen, T.; Shao, Z.; Zhao, L.; Gao, P.; Lin, J.; Jiang, J. Constitutive modeling for the simulation of the superplastic forming of TA15 titanium alloy. Int. J. Mech. Sci. 2019, 164, 105178. [Google Scholar] [CrossRef]
- Feng, Z.; Zecevic, M.; Knezevic, M.; Lebensohn, R.A. Predicting extreme anisotropy and shape variations in impact testing of tantalum single crystals. Int. J. Solids Struct. 2022, 241, 111466. [Google Scholar] [CrossRef]
- Mánik, T.; Asadkandi, H.; Holmedal, B. A robust algorithm for rate-independent crystal plasticity. Comput. Methods Appl. Mech. Eng. 2022, 393, 114831. [Google Scholar] [CrossRef]
- Rossiter, J.; Brahme, A.; Simha, M.; Inal, K.; Mishra, R. A new crystal plasticity scheme for explicit time integration codes to simulate deformation in 3D microstructures: Effects of strain path, strain rate and thermal softening on localized deformation in the aluminum alloy 5754 during simple shear. Int. J. Plast. 2010, 26, 1702–1725. [Google Scholar] [CrossRef]
- Zhang, K.; Hopperstad, O.; Holmedal, B.; Dumoulin, S. A robust and efficient substepping scheme for the explicit numerical integration of a rate-dependent crystal plasticity model. Int. J. Numer. Methods Eng. 2014, 99, 239–262. [Google Scholar] [CrossRef]
- Kohar, C.P.; Martin, É.; Connolly, D.S.; Patil, S.; Krutz, N.; Wei, D.; Inal, K. A new and efficient thermo-elasto-viscoplastic numerical implementation for implicit finite element simulations of powder metals: An application to hot isostatic pressing. Int. J. Mech. Sci. 2019, 155, 222–234. [Google Scholar] [CrossRef]
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Sample Dimensions Influence Strength and Crystal Plasticity. Science 2004, 305, 986–989. [Google Scholar] [CrossRef]
- Vondřejc, J.; Zeman, J.; Marek, I. An FFT-based Galerkin method for homogenization of periodic media. Comput. Math. Appl. 2014, 68, 156–173. [Google Scholar] [CrossRef]
- de Geus, T.; Vondřejc, J.; Zeman, J.; Peerlings, R.; Geers, M. Finite strain FFT-based non-linear solvers made simple. Comput. Methods Appl. Mech. Eng. 2017, 318, 412–430. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, K.; Chen, C. A mixed FFT-Galerkin approach for incompressible or slightly compressible hyperelastic solids under finite deformation. Comput. Methods Appl. Mech. Eng. 2022, 396, 115092. [Google Scholar] [CrossRef]
- Lucarini, S.; Segurado, J. An algorithm for stress and mixed control in Galerkin-based FFT homogenization. Int. J. Numer. Methods Eng. 2019, 119, 797–805. [Google Scholar] [CrossRef]
- Lucarini, S.; Segurado, J. DBFFT: A displacement based FFT approach for non-linear homogenization of the mechanical behavior. Int. J. Eng. Sci. 2019, 144, 103131. [Google Scholar] [CrossRef]
- Lucarini, S.; Cobian, L.; Voitus, A.; Segurado, J. Adaptation and validation of FFT methods for homogenization of lattice based materials. Comput. Methods Appl. Mech. Eng. 2022, 388, 114223. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Mozaffar, M.; Bostanabad, R.; Chen, W.; Ehmann, K.; Cao, J.; Bessa, M.A. Deep learning predicts path-dependent plasticity. Proc. Natl. Acad. Sci. USA 2019, 116, 26414–26420. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; USENIX Association: Berkeley, CA, USA, 2016. OSDI’16. pp. 265–283. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019. [Google Scholar]
- Berahas, A.S.; Byrd, R.H.; Nocedal, J. Derivative-Free Optimization of Noisy Functions via Quasi–Newton Methods. SIAM J. Optim. 2019, 29, 965–993. [Google Scholar] [CrossRef]
- Larson, J.; Menickelly, M.; Wild, S.M. Derivative-free optimization methods. Acta Numer. 2019, 28, 287–404. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Winget, J. Finite rotation effects in numerical integration of rate constitutive equations arising in large-deformation analysis. Int. J. Numer. Methods Eng. 1980, 15, 1862–1867. [Google Scholar] [CrossRef]
- Holmedal, B. Regularized Yield Surfaces for Crystal Plasticity of Metals. Crystals 2020, 10, 1076. [Google Scholar] [CrossRef]
- Scherzinger, W. A return mapping algorithm for isotropic and anisotropic plasticity models using a line search method. Comput. Methods Appl. Mech. Eng. 2017, 317, 526–553. [Google Scholar] [CrossRef]
- Lucarini, S.; Segurado, J. On the accuracy of spectral solvers for micromechanics based fatigue modeling. Comput. Mech. 2018, 63, 365–382. [Google Scholar] [CrossRef]
- Ma, R.; Truster, T.J. FFT-based homogenization of hypoelastic plasticity at finite strains. Comput. Methods Appl. Mech. Eng. 2019, 349, 499–521. [Google Scholar] [CrossRef]
- Tinzefte, A.; Menach, Y.L.; Piriou, F. Iterative Solvers for Singular Symmetric Linear Systems in Low Frequency Electromagnetics. IEEE Trans. Magn. 2009, 45, 1428–1431. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Ratku, A.; Neumann, D. Derivatives of feed-forward neural networks and their application in real-time market risk management. OR Spectr. 2022, 44, 947–965. [Google Scholar] [CrossRef]
- Rodini, S. Analytical derivatives of neural networks. Comput. Phys. Commun. 2022, 270, 108169. [Google Scholar] [CrossRef]
- Im, S.; Kim, H.; Kim, W.; Cho, M. Neural network constitutive model for crystal structures. Comput. Mech. 2020, 67, 185–206. [Google Scholar] [CrossRef]
- Gu, Q.; Pan, J.; Liu, Y.; Fu, M.; Zhang, J. An Effective Tangent Stiffness of Train–Track–Bridge Systems Based on Artificial Neural Network. Appl. Sci. 2022, 12, 2735. [Google Scholar] [CrossRef]


| Cubic Elasticity Modulus | Hardening Parameters | Euler Angles | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (GPa) | (GPa) | (GPa) | (MPa) | (MPa) | () | () | () | n | |
| 106.75 | 60.41 | 28.34 | 10.0 | 63.0 | 0.1 | 128.0 | 40.0 | 37.0 | 100 |
| Soft Matrix Phase | Hard Particle Phase | ||
|---|---|---|---|
| (MPa) | (MPa) | (MPa) | (MPa) |
| 1.5 | 1.0 | 7.5 | 5.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Chen, C. On the Single-Point Calculation of Stress–Strain Data under Large Deformations with Stress and Mixed Control. Materials 2022, 15, 6644. https://doi.org/10.3390/ma15196644
Wang M, Chen C. On the Single-Point Calculation of Stress–Strain Data under Large Deformations with Stress and Mixed Control. Materials. 2022; 15(19):6644. https://doi.org/10.3390/ma15196644
Chicago/Turabian StyleWang, Mingchuan, and Cai Chen. 2022. "On the Single-Point Calculation of Stress–Strain Data under Large Deformations with Stress and Mixed Control" Materials 15, no. 19: 6644. https://doi.org/10.3390/ma15196644
APA StyleWang, M., & Chen, C. (2022). On the Single-Point Calculation of Stress–Strain Data under Large Deformations with Stress and Mixed Control. Materials, 15(19), 6644. https://doi.org/10.3390/ma15196644







