Blast Resistance of Reinforced Concrete Slabs Based on Residual Load-Bearing Capacity
Abstract
:1. Introduction
2. Experimental Study
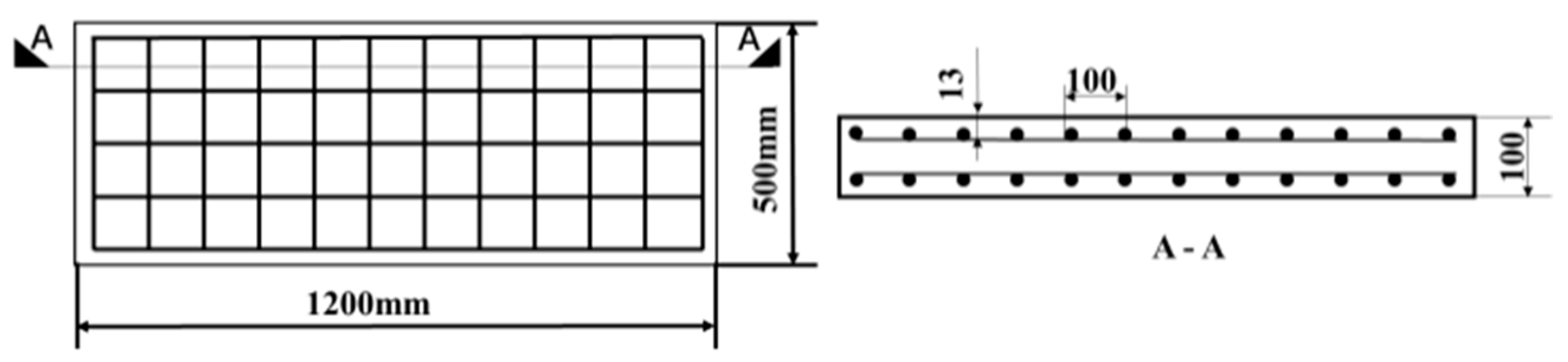
2.1. Test Specimen Design
2.2. Experimental Results and Analysis
2.2.1. Blast-Load Measurement
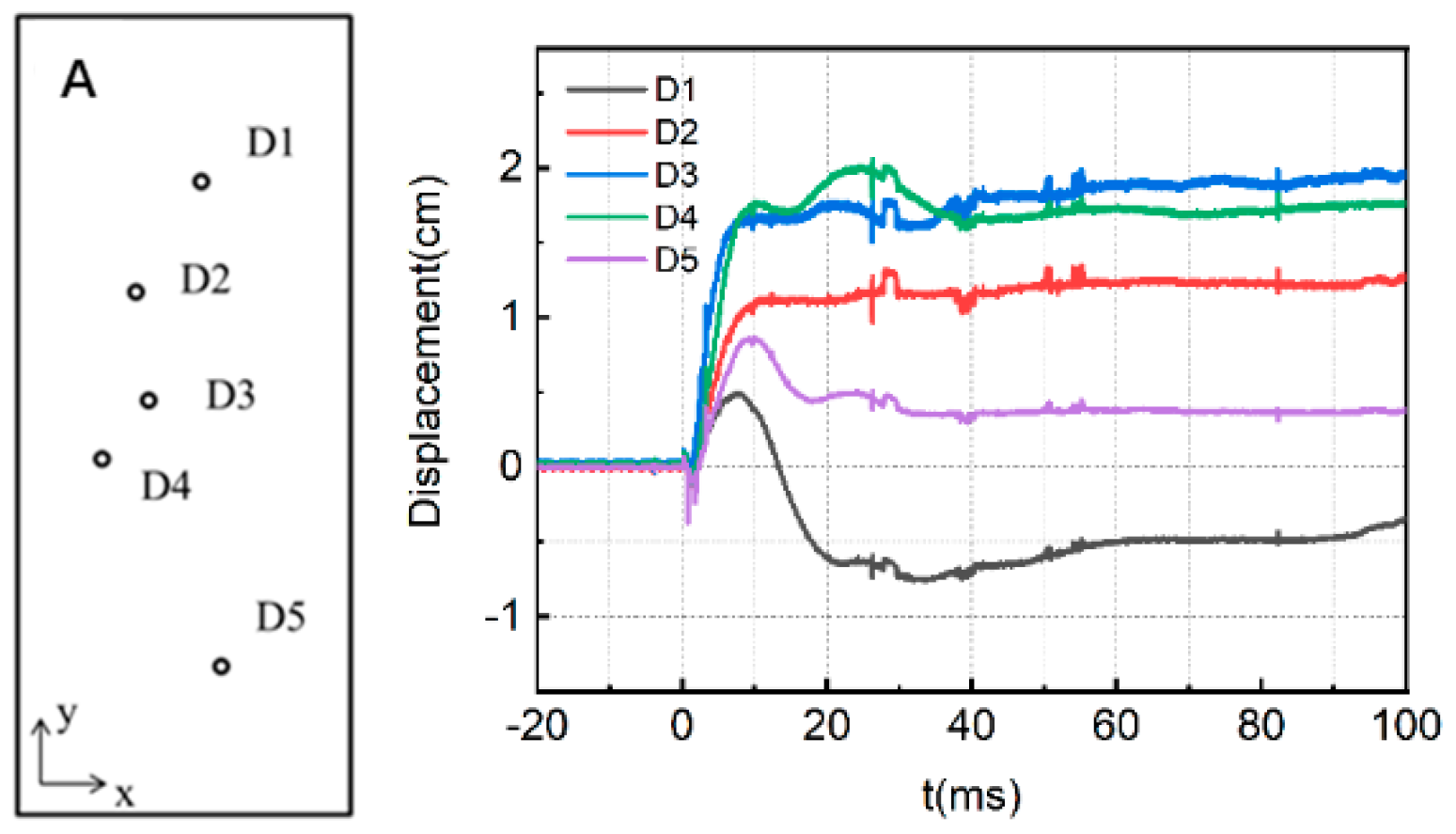
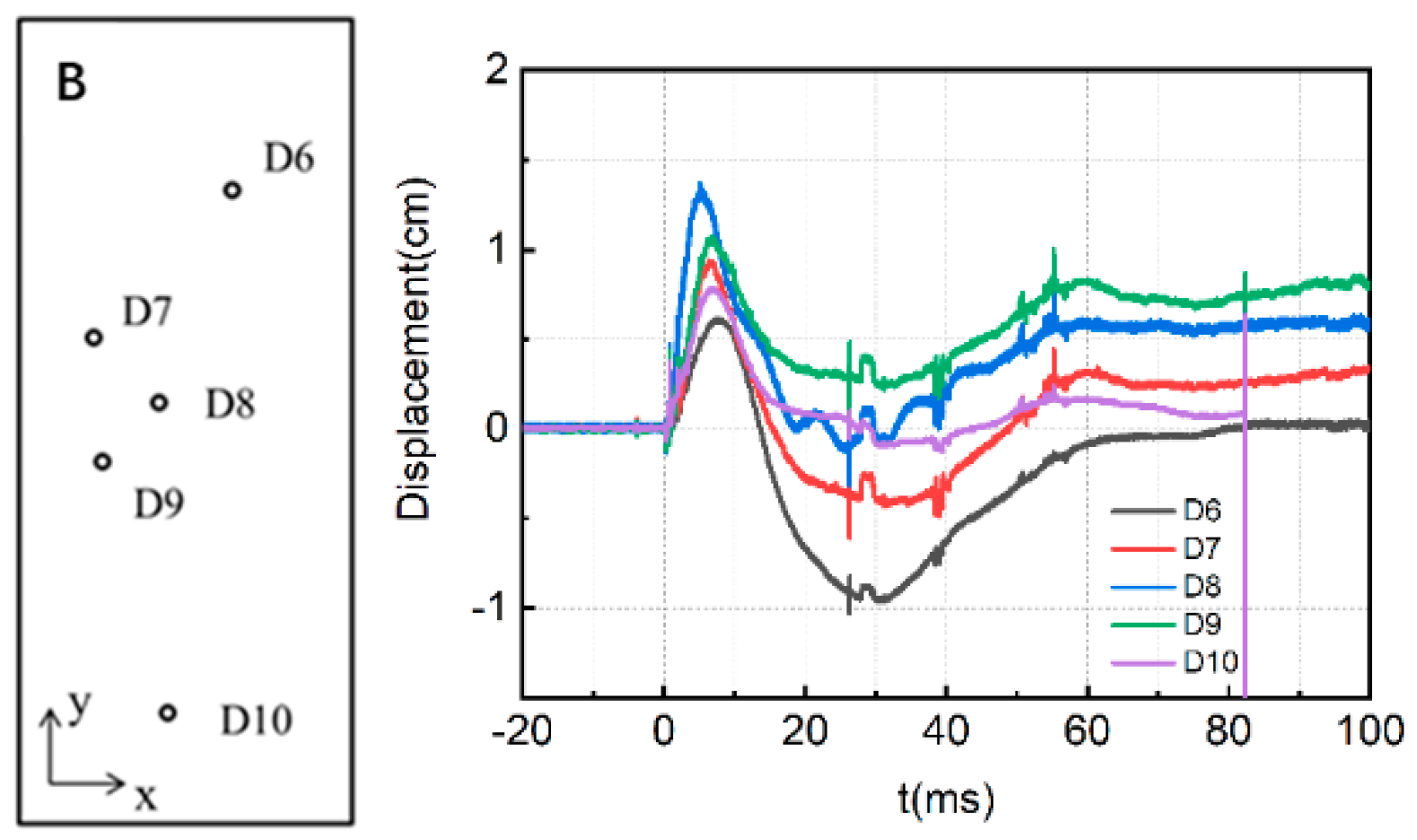
2.2.2. Displacement Response-Time History
2.2.3. Comparison of Damage Modes
3. Numerical Simulation
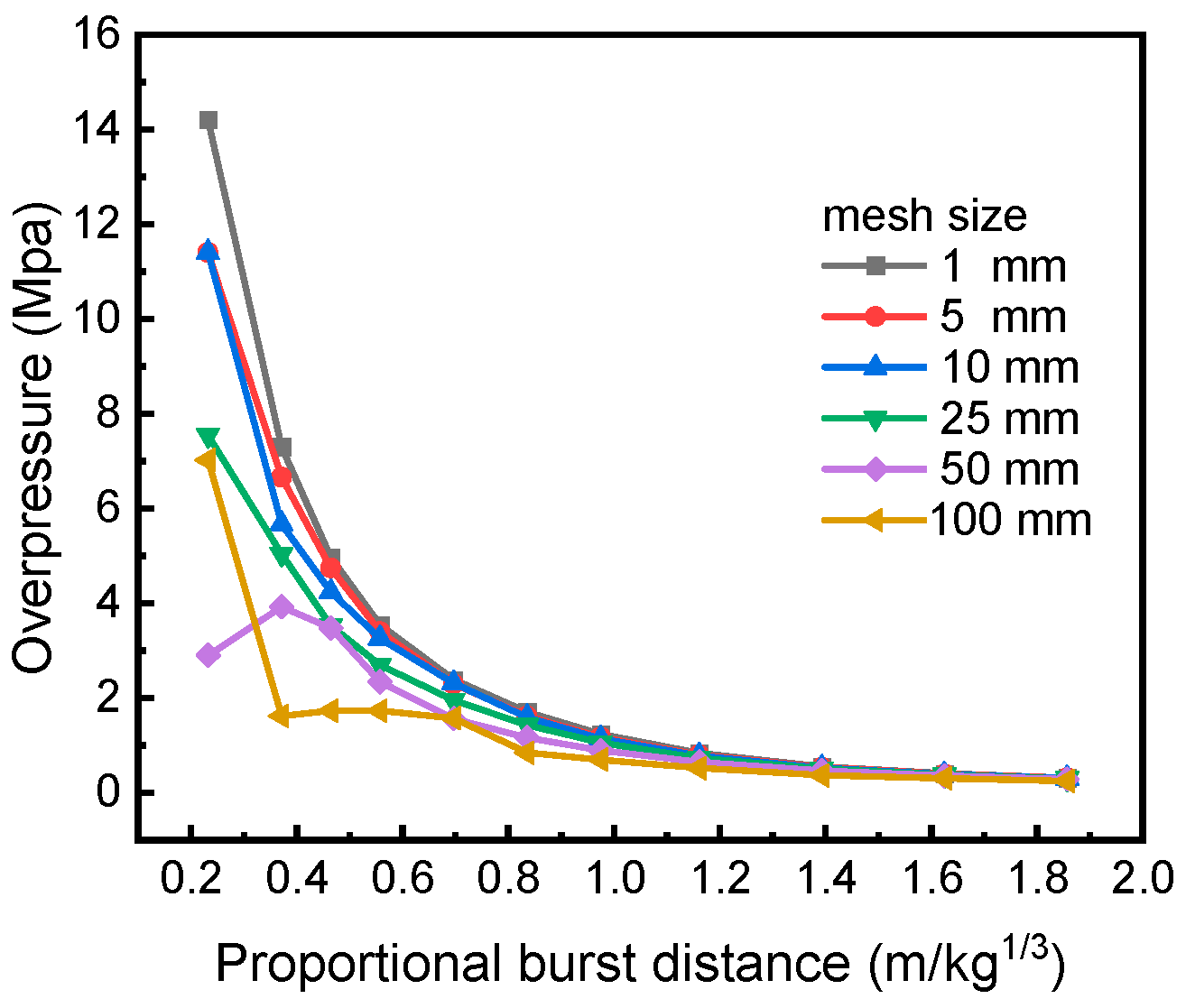
3.1. Finite Element Model
3.2. Material Model
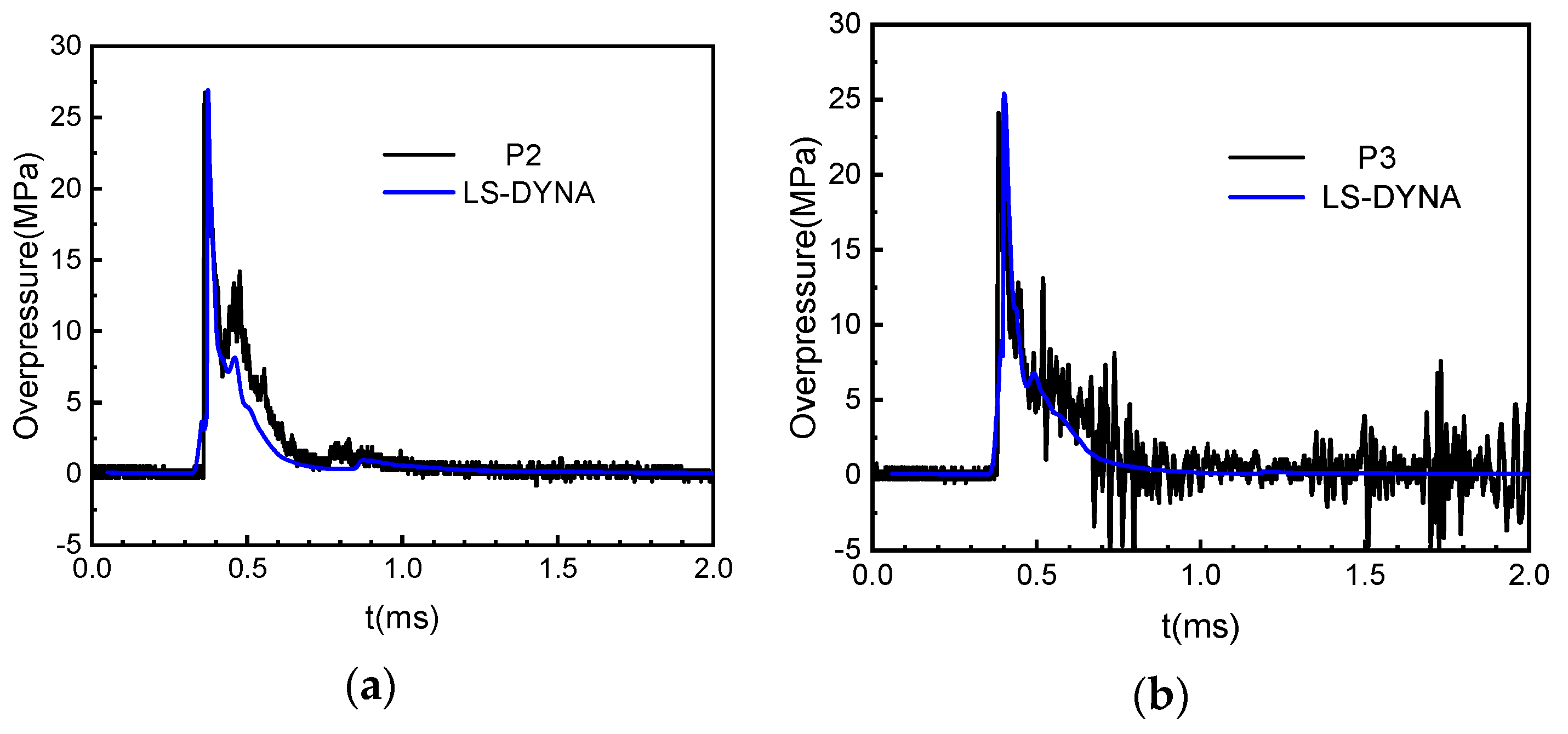
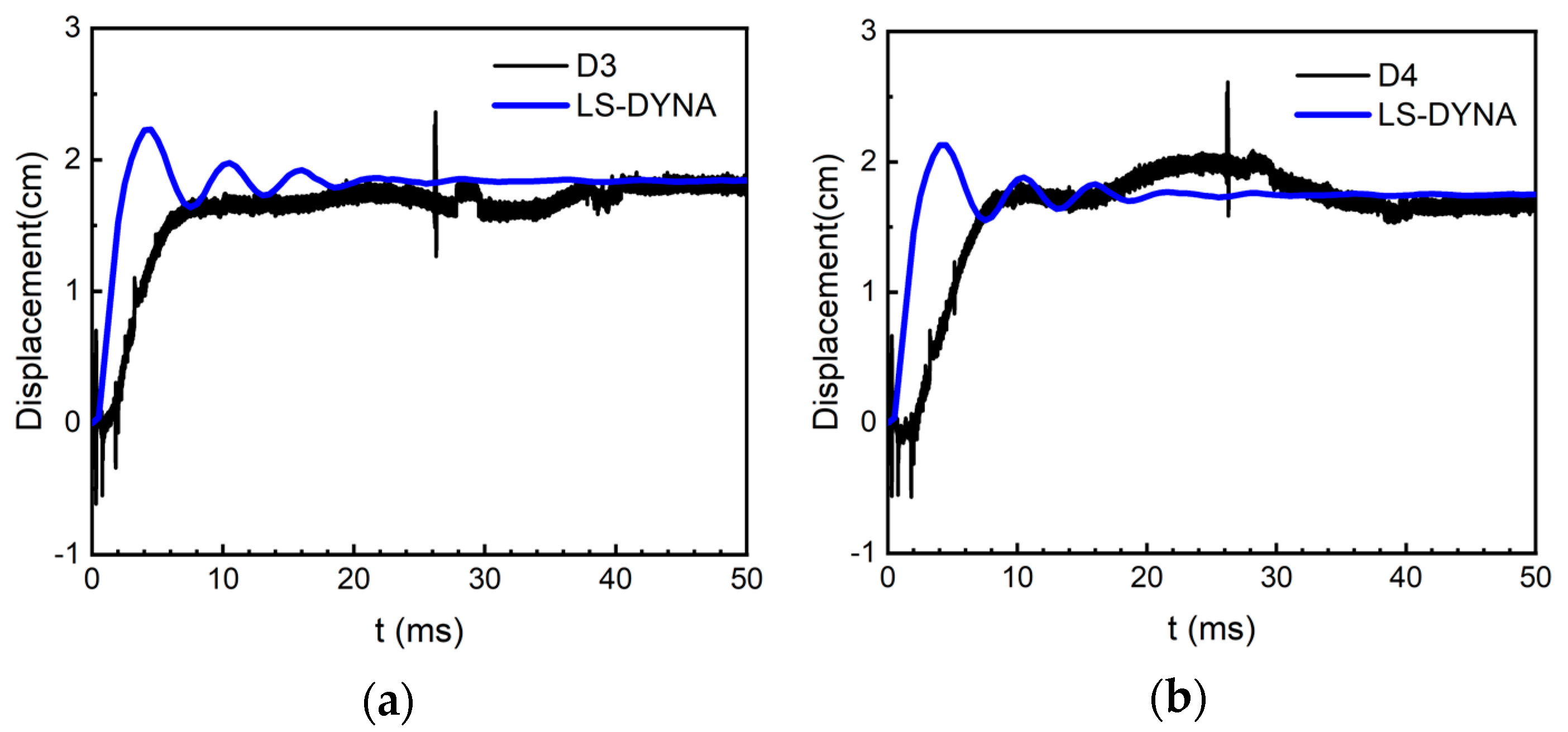
3.3. Finite Element Model Verification
3.4. Analysis of Finite Element Calculation Results
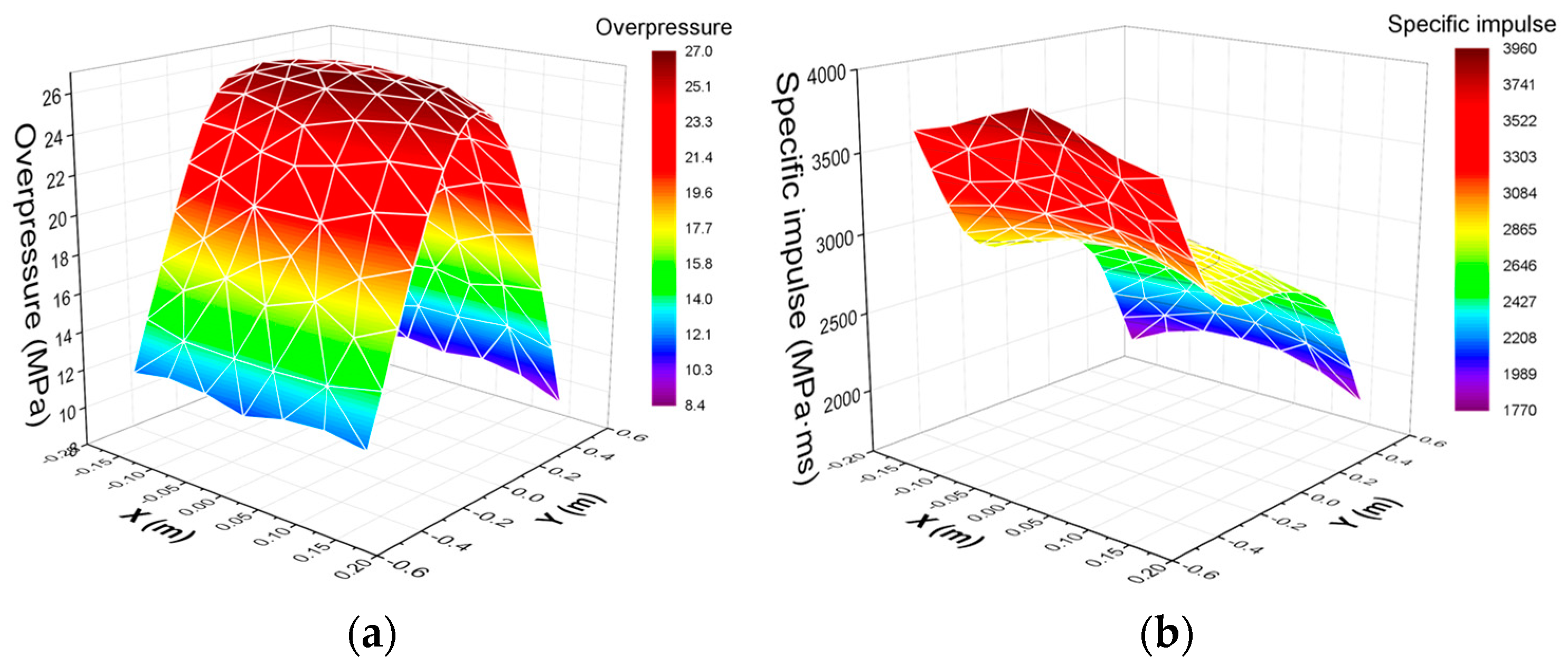
3.4.1. Explosion Load Analysis
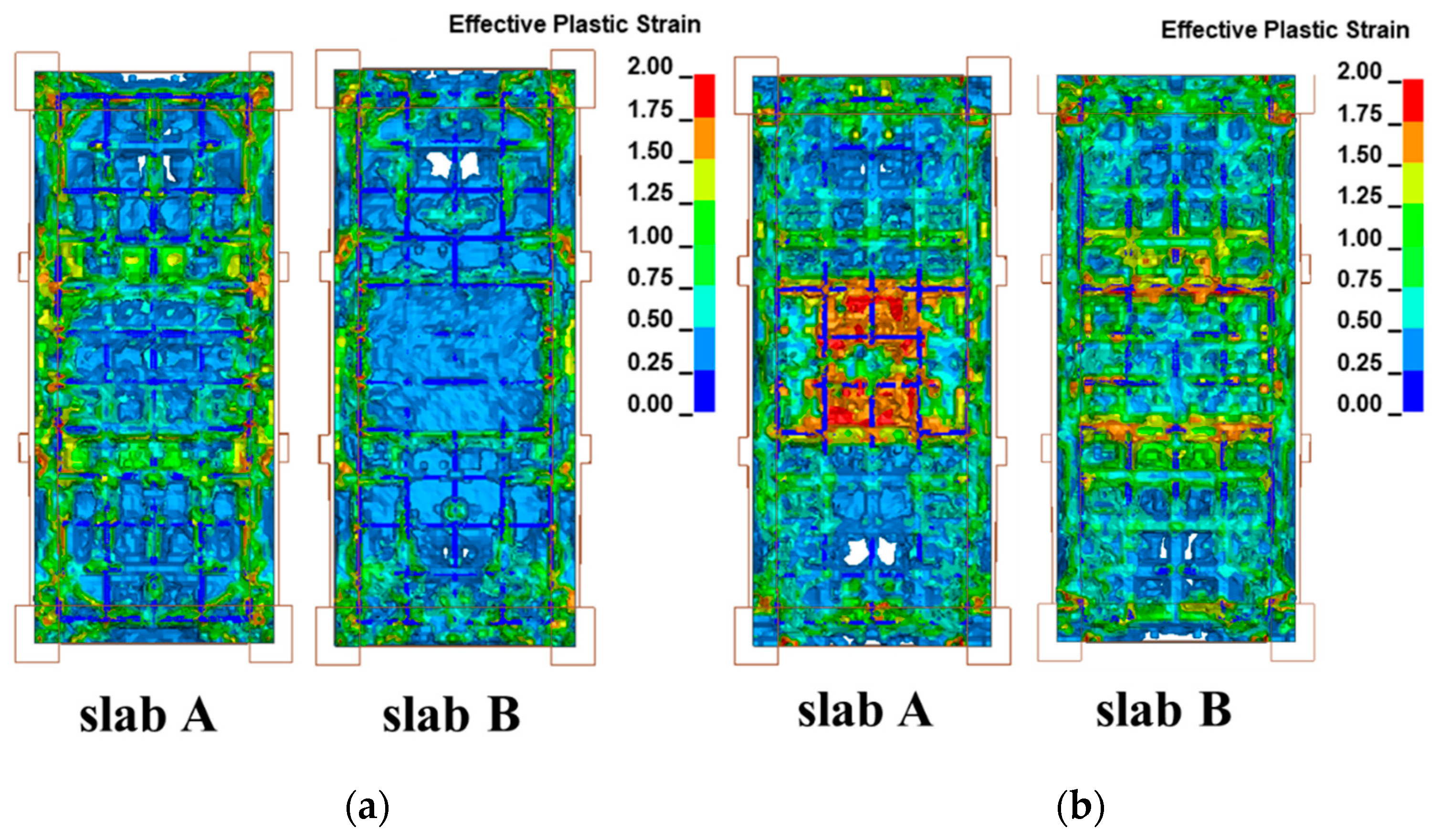
3.4.2. Damage Analysis of RC Slab
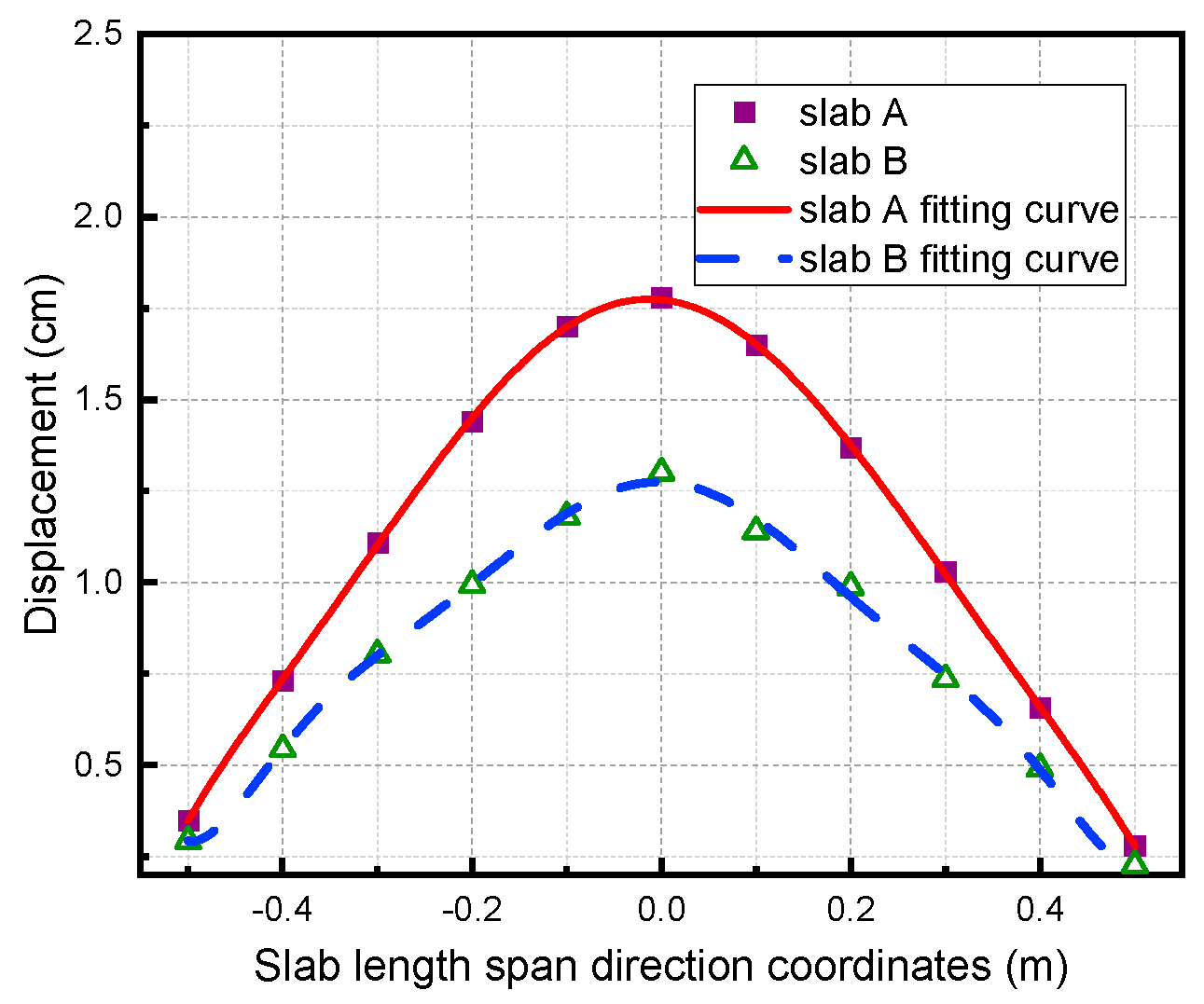
3.4.3. Residual Displacement Analysis
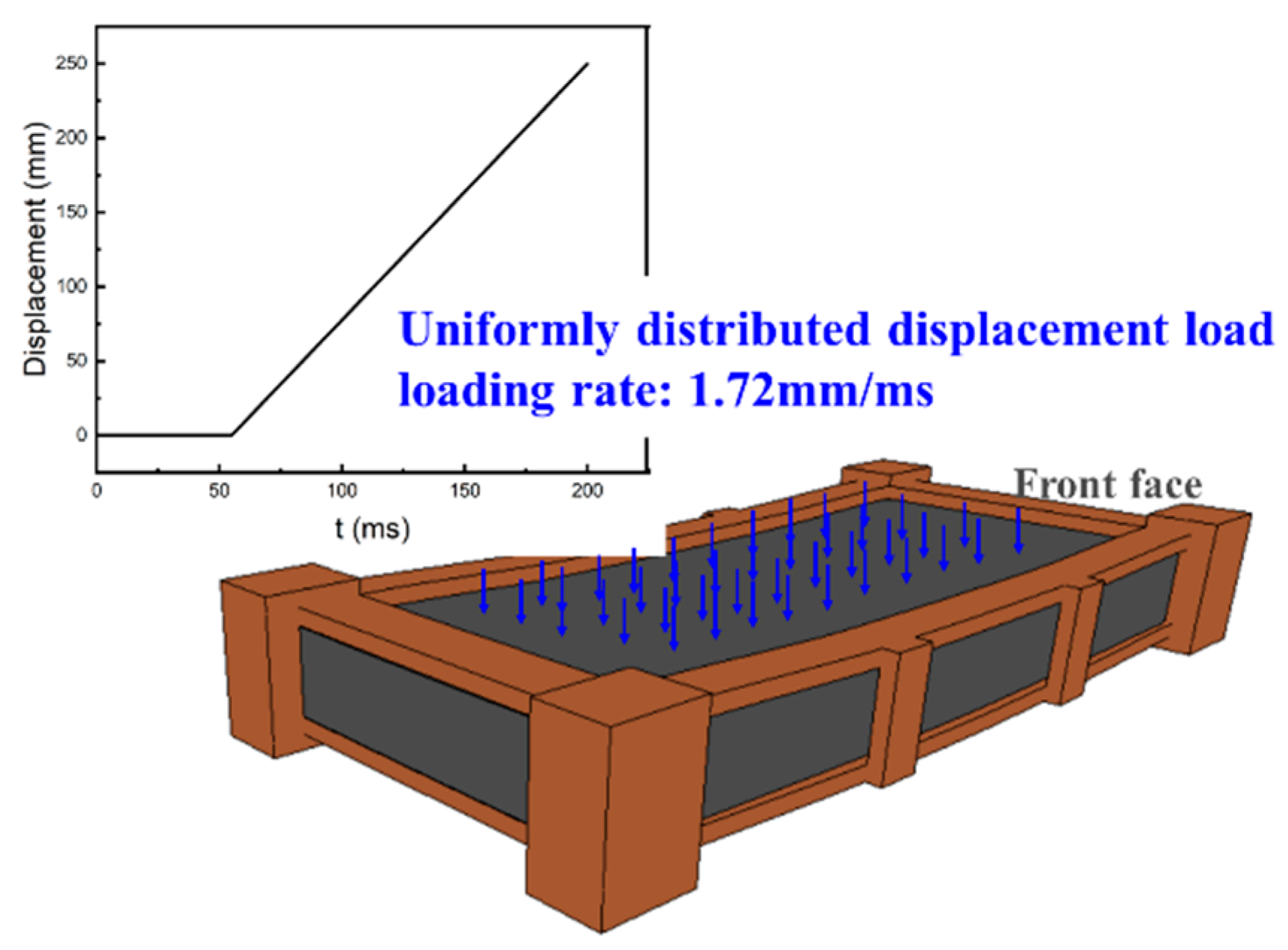
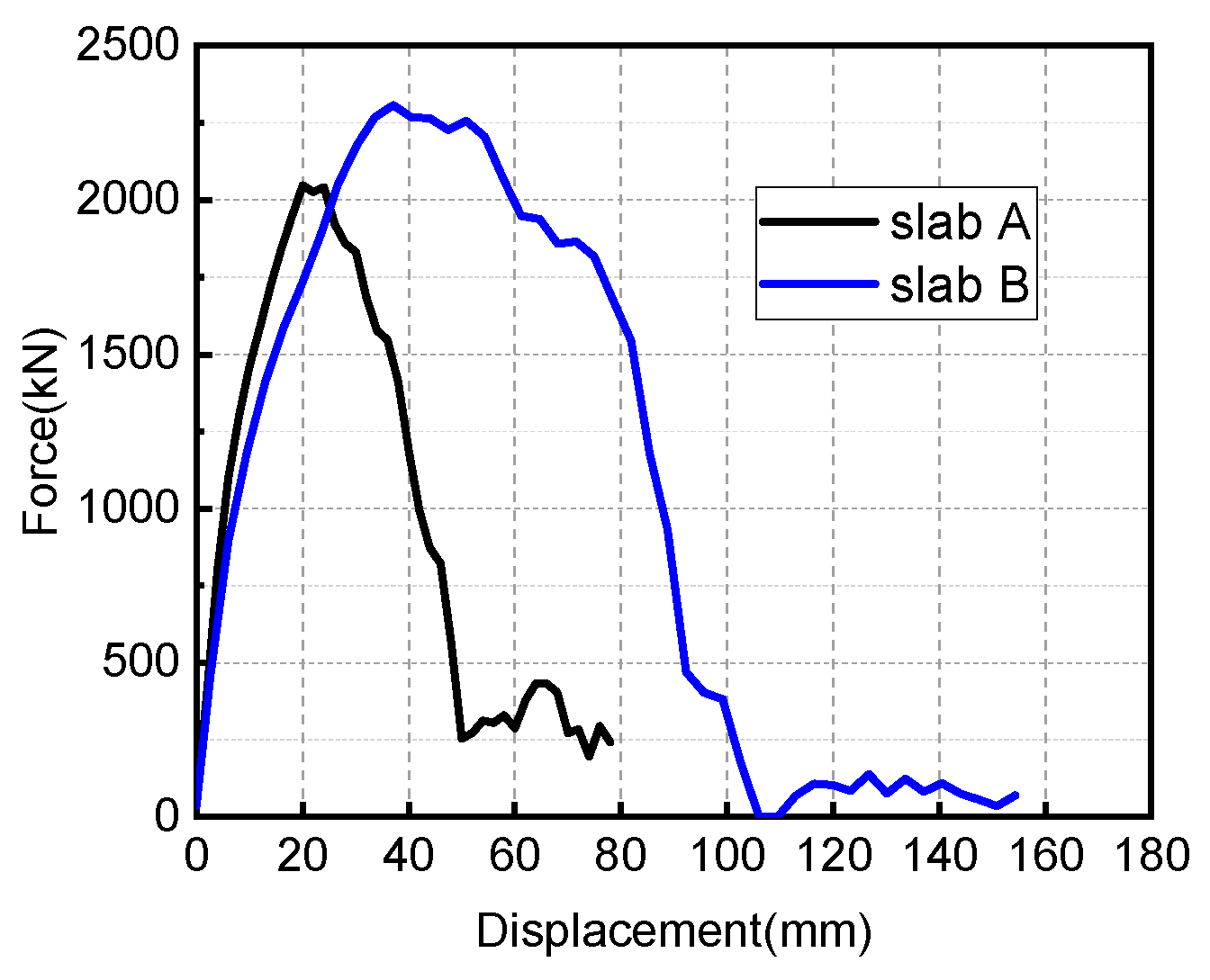
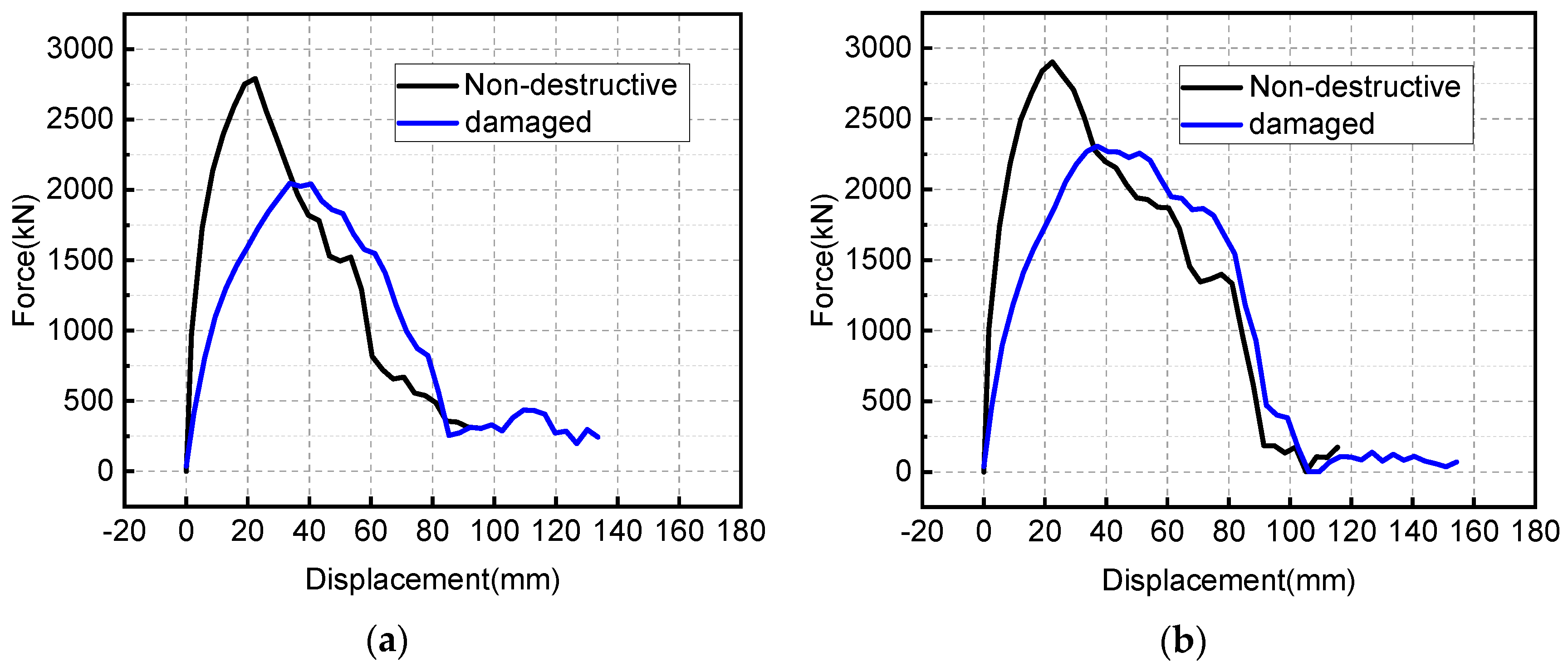
3.4.4. Residual Bearing Capacity Analysis
4. Conclusions
- The load distribution in the RC slabs under close-in blast loading was extremely uneven. The peak overpressure on the impact surface of the slabs was large in the center along the long-span direction and gradually decreased at both ends. The specific impulse was gradually reduced along the long-span direction. The impulse near the ground was about two times that at the top.
- The damage distribution of the two RC slabs with different reinforcement ratios was similar, but the degree of damage differed markedly. A large rectangular plastic strain zone appeared in the center of the back surface of the slab with a low reinforcement ratio, several plastic strands along the short-span direction could be observed, and the concrete in some areas almost completely failed, and the damage range and degree are significantly higher than those of the slab with a high reinforcement ratio.
- Compared with the undamaged slabs, the shape of the resistance curves of the damaged RC slabs saw significant changes, and their load-bearing capacity and bending stiffness were irreversibly degraded. Increasing the reinforcement ratio can not only inhibit the crack extension and reduce the residual displacement of components, but also reduce the decrease of bearing capacity after damage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Hao, H. Numerical study of concrete spall damage to blast loads. Int. J. Impact Eng. 2014, 68, 41–55. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Cui, J. Experimental studies on fragments of reinforced concrete slabs under close-in explosions. Int. J. Impact Eng. 2020, 144, 103630. [Google Scholar] [CrossRef]
- Wu, C.; Nurwidayati, R.; Oehlers, D.J. Fragmentation from spallation of RC slabs due to airblast loads. Int. J. Impact Eng. 2009, 36, 1371–1376. [Google Scholar] [CrossRef]
- Kumar, V.; Kartik, K.V.; Iqbal, M.A. Experimental and numerical investigation of reinforced concrete slabs under blast loading. Eng. Struct. 2020, 206, 110125. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Hao, H. Investigation of ultra-high performance concrete slab and normal strength concrete slab under contact explosion. Eng. Struct. 2015, 102, 395–408. [Google Scholar] [CrossRef]
- Yao, S.; Zhang, D.; Chen, X.; Lu, F.; Wang, W. Experimental and numerical study on the dynamic response of RC slabs under blast loading. Eng. Fail. Anal. 2016, 66, 120–129. [Google Scholar] [CrossRef]
- Lan, S.; Lok, T.-S.; Heng, L. Composite structural panels subjected to explosive loading. Constr. Build. Mater. 2005, 19, 387–395. [Google Scholar] [CrossRef]
- Huff, W.L. Collapse Strength of a Two-Way-Reinforced Concrete Slab Contained within a Steel Frame Structure; Final Report; US Army Engineer Waterways Experiment Station: Vicksburg, MI, USA, 1975. [Google Scholar]
- Wang, W.; Zhang, D.; Lu, F.; Wang, S.-C.; Tang, F. Experimental study on scaling the explosion resistance of a one-way square reinforced concrete slab under a close-in blast loading. Int. J. Impact Eng. 2012, 49, 158–164. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, D.; Lu, F.; Wang, S.-C.; Tang, F. Experimental study and numerical simulation of the damage mode of a square reinforced concrete slab under close-in explosion. Eng. Fail. Anal. 2013, 27, 41–51. [Google Scholar] [CrossRef]
- Lu, B. Improving the blast resistance capacity of RC slabs with innovative composite materials. Compos. Part B Eng. 2007, 38, 523–534. [Google Scholar]
- Schenker, A.; Anteby, I.; Gal, E.; Kivity, Y.; Nizri, E.; Sadot, O.; Michaelis, R.; Levintant, O.; Ben-Dor, G. Full-scale field tests of concrete slabs subjected to blast loads. Int. J. Impact Eng. 2008, 35, 184–198. [Google Scholar] [CrossRef]
- Thiagarajan, G.; Kadambi, A.V.; Robert, S.; Johnson, C.F. Experimental and finite element analysis of doubly reinforced concrete slabs subjected to blast loads. Int. J. Impact Eng. 2015, 75, 162–173. [Google Scholar] [CrossRef]
- Wu, C.; Oehlers, D.J.; Rebentrost, M.; Leach, J.; Whittaker, A.S. Blast testing of ultra-high performance fibre and FRP-retrofitted concrete slabs. Eng. Struct. 2009, 31, 2060–2069. [Google Scholar] [CrossRef]
- Abedini, M.; Mutalib, A.A.; Raman, S.N.; Alipour, R.; Akhlaghi, E. Pressure–Impulse (P–I) Diagrams for Reinforced Concrete (RC) Structures: A Review. Arch. Comput. Methods Eng. 2018, 26, 733–767. [Google Scholar] [CrossRef]
- Krauthammer, T.; Astarlioglu, S.; Blasko, J.; Soh, T.B.; Ng, P.H. Pressure–Impulse diagrams for the behavior assessment of structural components. Int. J. Impact Eng. 2008, 35, 771–783. [Google Scholar] [CrossRef]
- Li, Q.M.; Meng, H. Pulse loading shape effects on pressure–impulse diagram of an elastic–plastic, single-degree-of-freedom structural model. Int. J. Mech. Sci. 2002, 44, 1985–1998. [Google Scholar] [CrossRef]
- Li, Q.M.; Meng, H. Pressure-Impulse Diagram for Blast Loads Based on Dimensional Analysis and Single-Degree-of-Freedom Model. J. Eng. Mech. 2002, 128, 87–92. [Google Scholar] [CrossRef]
- Low, H.Y.; Hao, H. Reliability analysis of reinforced concrete slabs under explosive loading. Struct. Saf. 2001, 23, 157–178. [Google Scholar] [CrossRef]
- Low, H.Y.; Hao, H. Reliability analysis of direct shear and flexural failure modes of RC slabs under explosive loading. Eng. Struct. 2002, 24, 189–198. [Google Scholar] [CrossRef]
- Xu, J.; Wu, C.; Li, Z.-X. Analysis of direct shear failure mode for RC slabs under external explosive loading. Int. J. Impact Eng. 2014, 69, 136–148. [Google Scholar] [CrossRef]
- Anas, S.M.; Alam, M.; Umair, M. Experimental and numerical investigations on performance of reinforced concrete slabs under explosive-induced air-blast loading: A state-of-the-art review. Structures 2021, 31, 428–461. [Google Scholar] [CrossRef]
- Tai, Y.S.; Chu, T.L.; Hu, H.T.; Wu, J.Y. Dynamic response of a reinforced concrete slab subjected to air blast load. Theor. Appl. Fract. Mech. 2011, 56, 140–147. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Q.; Lu, X.; Wang, J. Numerical study on dynamic behaviors of NRC slabs in containment dome subjected to close-in blast loading. Thin Walled Struct. 2019, 135, 269–284. [Google Scholar] [CrossRef]
- Xin, C.; Wang, J.; Yu, D.; Li, T.; Song, J. Empirical Formula and Numerical Simulation of TNT Explosion Shock Wave in Free Air. Missiles Space Veh. 2018, 3, 98–102. [Google Scholar] [CrossRef]
- Hallquist, J. LS-DYNA Keyword User’s Manual, Version: 970; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2003. [Google Scholar]
- Zhao, C.; Wang, Q.; Wang, J.; Zhang, Z. Blast Resistance of Containment Dome Reinforced Concrete Slab in NPP under Close-in Explosion. Chin. J. High Press. Phys. 2019, 33, 143–155. [Google Scholar] [CrossRef]

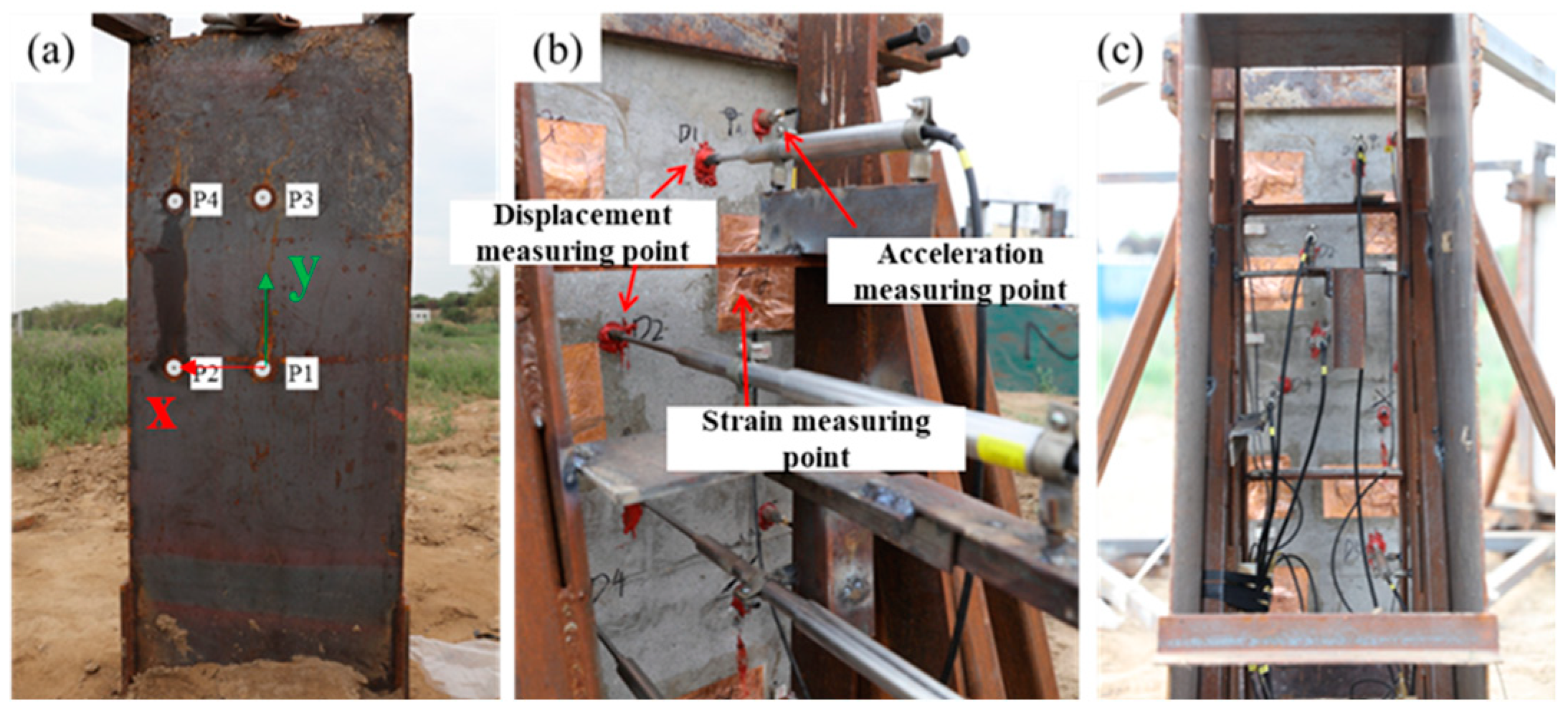
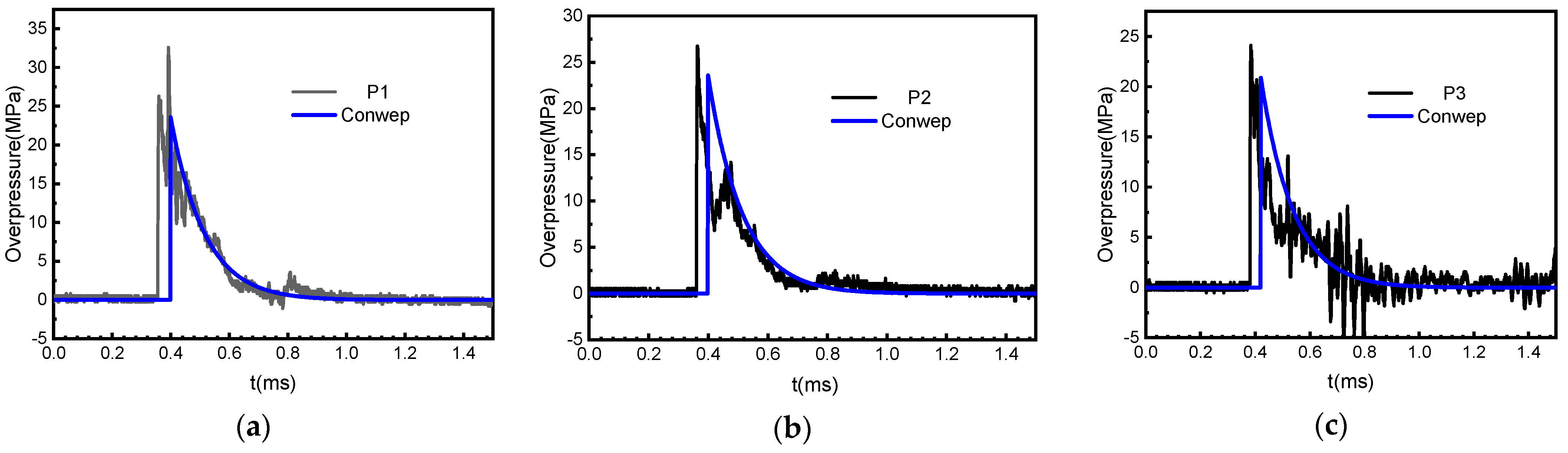


| Measuring Point | X/m | Y/m | Distance from Explosion Source/m | Scaled Distance/m/kg1/3 | Angle of Incidence/° |
|---|---|---|---|---|---|
| P1 | 0 | 0 | 1.2 | 0.557 | 90 |
| P2 | 0.16 | 0 | 1.211 | 0.562 | 82.4 |
| P3 | 0 | 0.3 | 1.237 | 0.574 | 75.96 |
| P4 | 0.16 | 0.3 | 1.247 | 0.579 | 74.18 |
| Measuring Point | Scaled Distance/m/kg1/3 | Peak Positive Pressure/MPa | Shock Wave Arrival Time/ms | Specific Impulse/MPa × ms | Angle of Incidence/° |
|---|---|---|---|---|---|
| P1 | 0.557 | 32.32 | 0.36 | 3.35 | 90 |
| P2 | 0.562 | 26.47 | 0.363 | 3.02 | 82.4 |
| P3 | 0.574 | 23.58 | 0.38 | 2.93 | 75.96 |
| Displacement Measuring Point | D1 | D2 | D3 | D4 | D5 |
|---|---|---|---|---|---|
| Peak displacement/cm | 0.51 | 1.18 | 1.97 | 1.98 | 0.89 |
| Residual displacement/cm | −0.37 | 1.18 | 1.97 | 1.73 | 0.38 |
| Displacement Measuring Point | D6 | D7 | D8 | D9 | D10 |
|---|---|---|---|---|---|
| Peak displacement/cm | 0.67 | 0.92 | 1.41 | 1.09 | 0.79 |
| Residual displacement/cm | 0.03 | 0.31 | 0.58 | 0.80 | 0.08 |
| Parameter | ρ/kg·m−3 | E/GPa | Vs | σy/MPa | Et/GPa | C/s−1 | Ps | Fs |
|---|---|---|---|---|---|---|---|---|
| HRB400 | 7850 | 210 | 0.28 | 400 | 2.1 | 40 | 5 | 0.2 |
| HPB235 | 235 | |||||||
| Clamp | 300 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Cheng, S.; Liao, Z.; Yin, W.; Liu, K.; Ma, L.; Wang, T.; Zhang, D. Blast Resistance of Reinforced Concrete Slabs Based on Residual Load-Bearing Capacity. Materials 2022, 15, 6449. https://doi.org/10.3390/ma15186449
Wang L, Cheng S, Liao Z, Yin W, Liu K, Ma L, Wang T, Zhang D. Blast Resistance of Reinforced Concrete Slabs Based on Residual Load-Bearing Capacity. Materials. 2022; 15(18):6449. https://doi.org/10.3390/ma15186449
Chicago/Turabian StyleWang, Lijun, Shuai Cheng, Zhen Liao, Wenjun Yin, Kai Liu, Long Ma, Tao Wang, and Dezhi Zhang. 2022. "Blast Resistance of Reinforced Concrete Slabs Based on Residual Load-Bearing Capacity" Materials 15, no. 18: 6449. https://doi.org/10.3390/ma15186449
APA StyleWang, L., Cheng, S., Liao, Z., Yin, W., Liu, K., Ma, L., Wang, T., & Zhang, D. (2022). Blast Resistance of Reinforced Concrete Slabs Based on Residual Load-Bearing Capacity. Materials, 15(18), 6449. https://doi.org/10.3390/ma15186449





