Optimal Design of Acoustic Metamaterial of Multiple Parallel Hexagonal Helmholtz Resonators by Combination of Finite Element Simulation and Cuckoo Search Algorithm
Abstract
:1. Introduction
2. Initial Structural Design
2.1. Design Objective
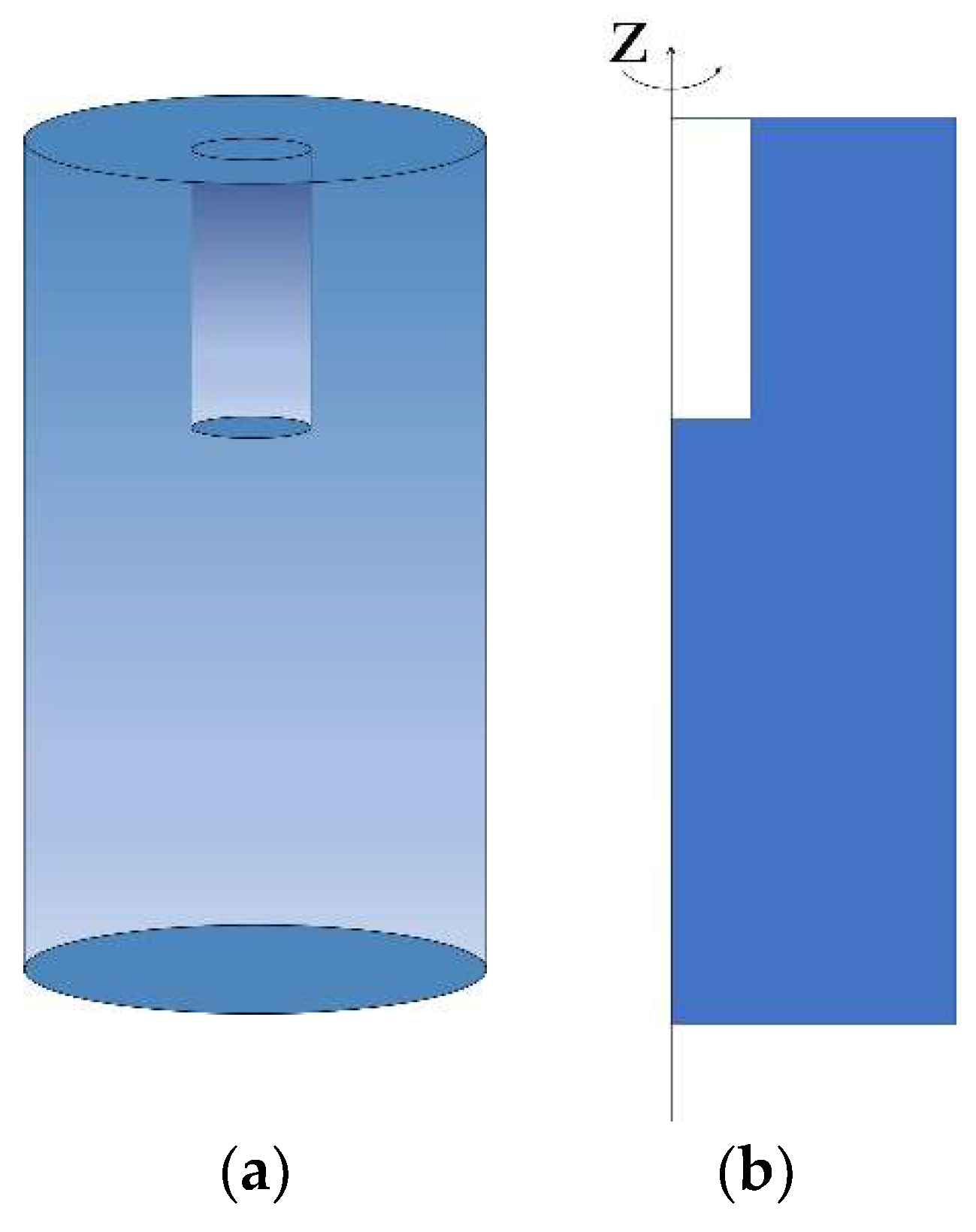
2.2. Geometric Parameters Design
3. Optimization of Acoustic Metamaterial
3.1. Establishment of Finite Element Simulation Model
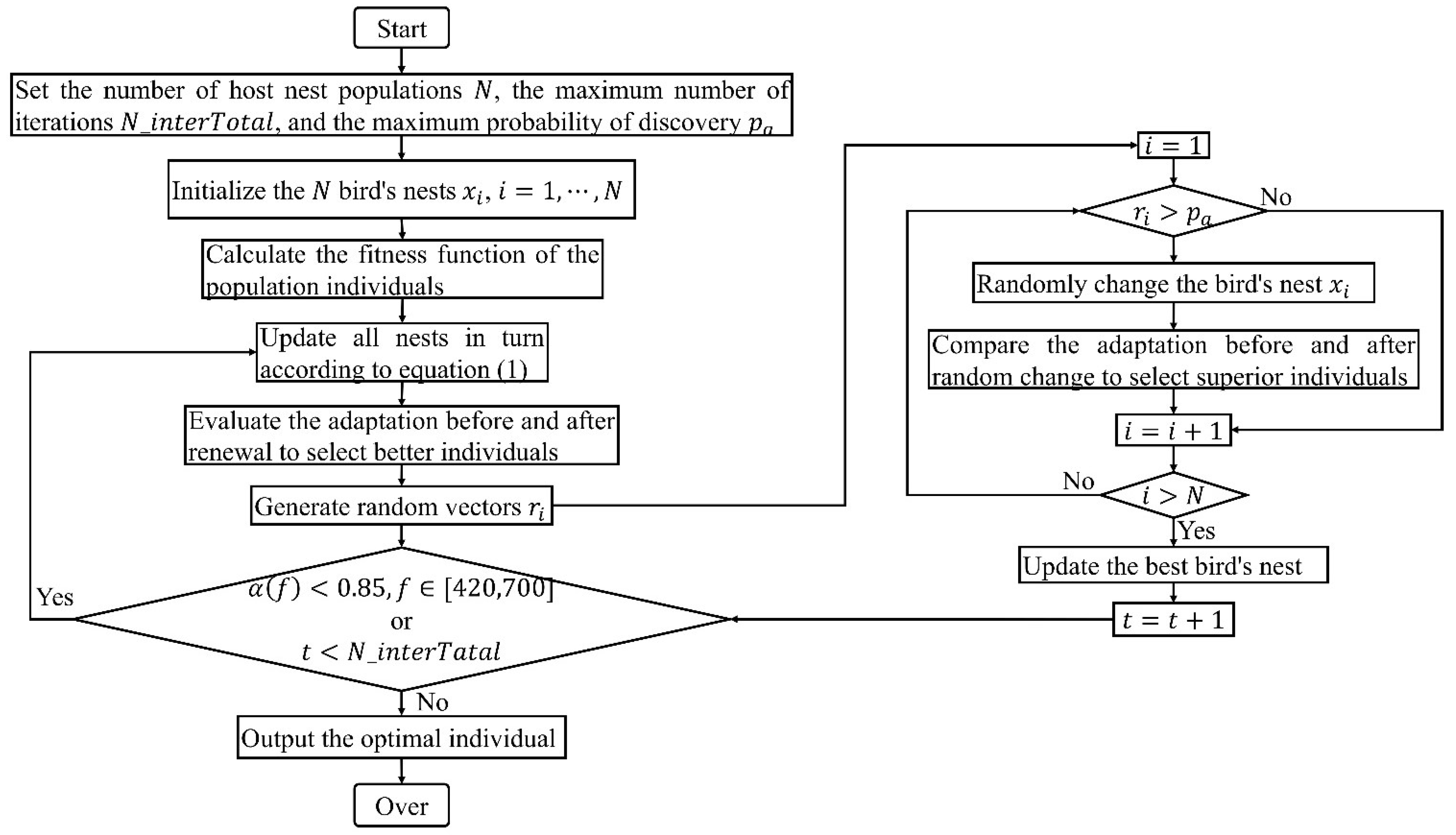
3.2. Optimization Algorithm
- (1)
- Set the initial parameters for the algorithm. In the current optimization process, the number of host nest populations was set as , the maximum number of iterations was , and the maximum probability of discovery was .
- (2)
- Calculate the fitness function of the population individual. In this research, sound absorption performance within the target frequency range of the acoustic metamaterial of multiple parallel hexagonal Helmholtz resonators was the research object and the depth of neck of each resonator was the optimization parameter. To ensure that the resulted absorption curve could maintain a high absorption coefficient in the target frequency range, the fitness value function was chosen as the total amount of sound energy absorbed at the target frequency range, as shown in Equation (1).
- (3)
- Update all nests according to Equation (3).
- (4)
- For all nests , a random number is generated and compared to the probability . If , then is randomly changed, otherwise there will be no change. The adaptation of the nests before and after the random change was evaluated, retaining the nest with better adaptation as the final . Afterwards, the return step (2) was iterated.
- (5)
- When all the absorption coefficients at the target frequency range were above 0.85, or it had reached the maximum number of iterations, the iteration ended, and the current optimal individual was output.
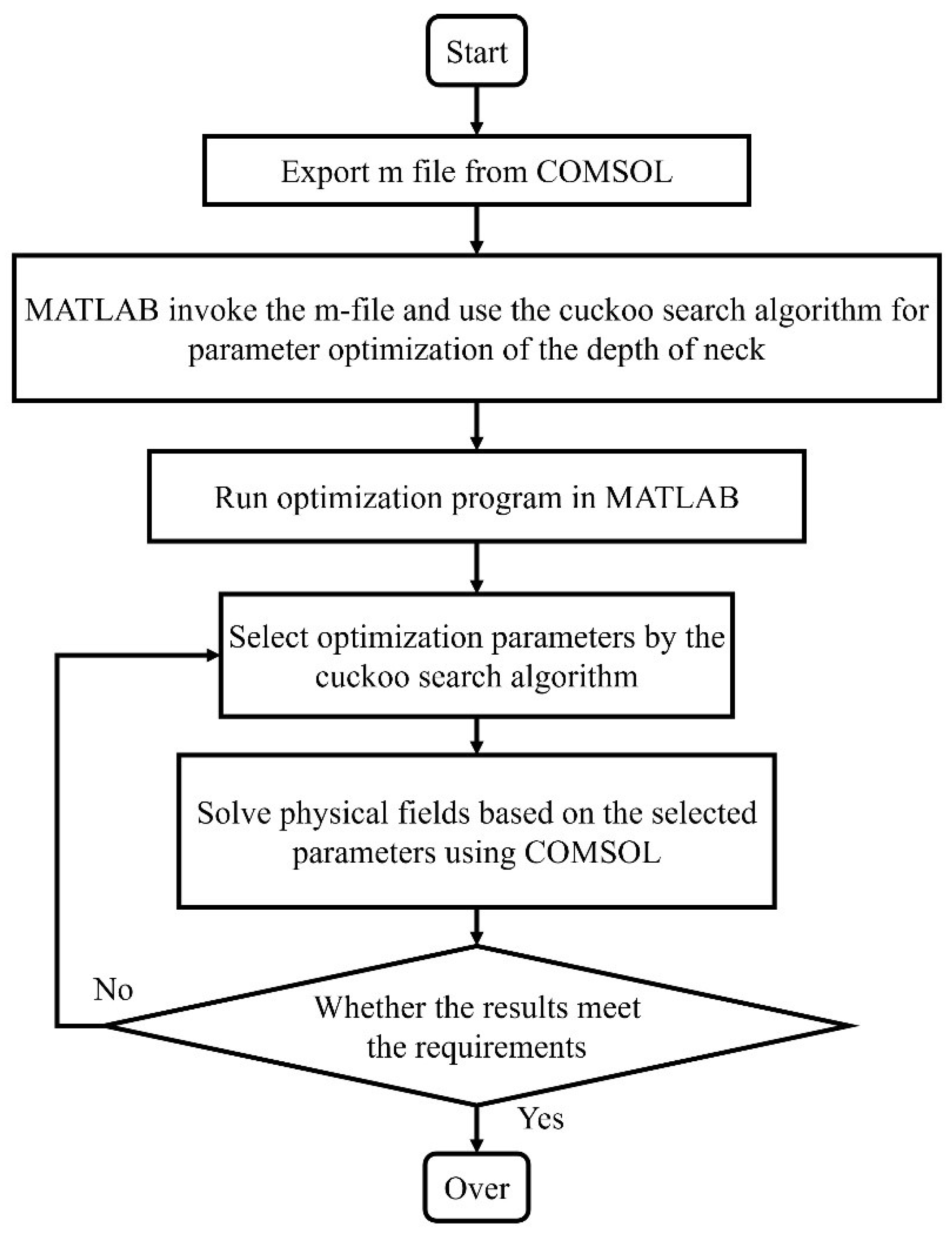
3.3. Interactive Operations with MATLAB and COMSOL
4. Results and Discussion
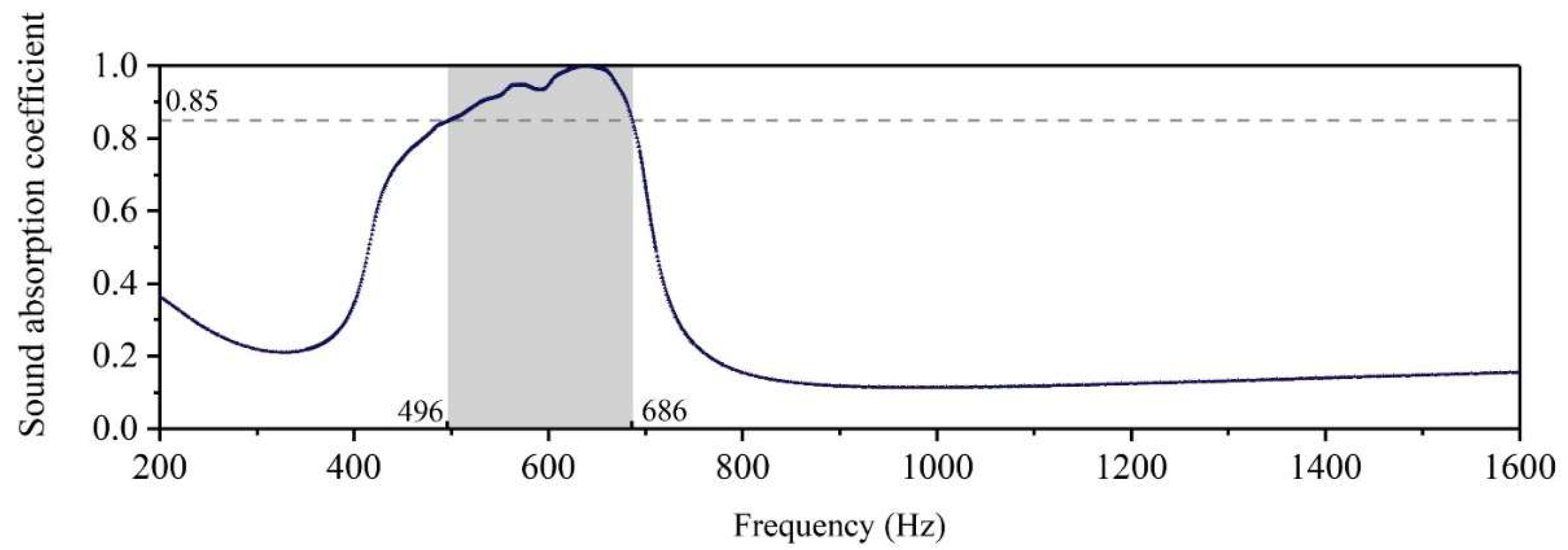
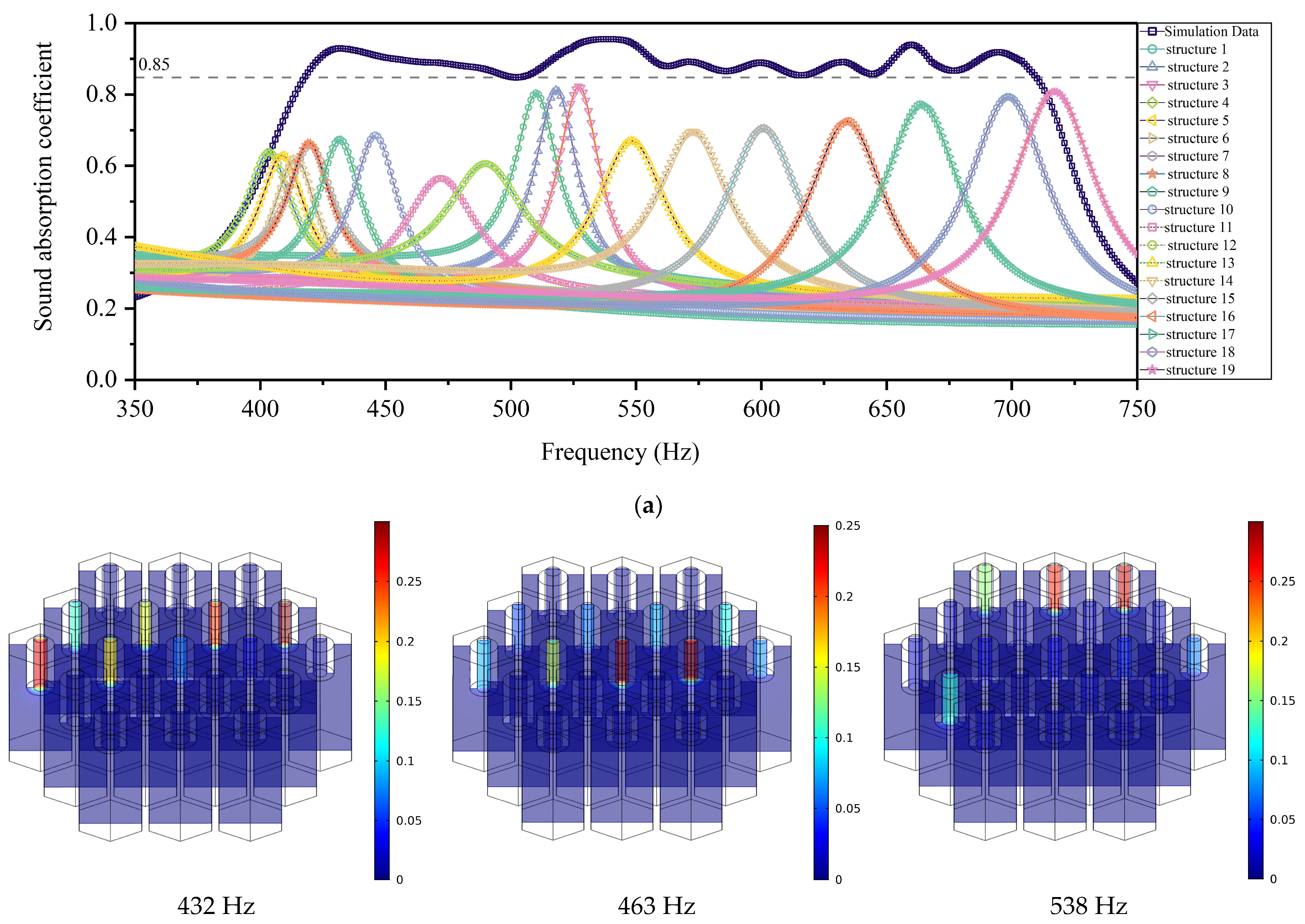
4.1. Optimization Results
4.2. Theoretical Analysis
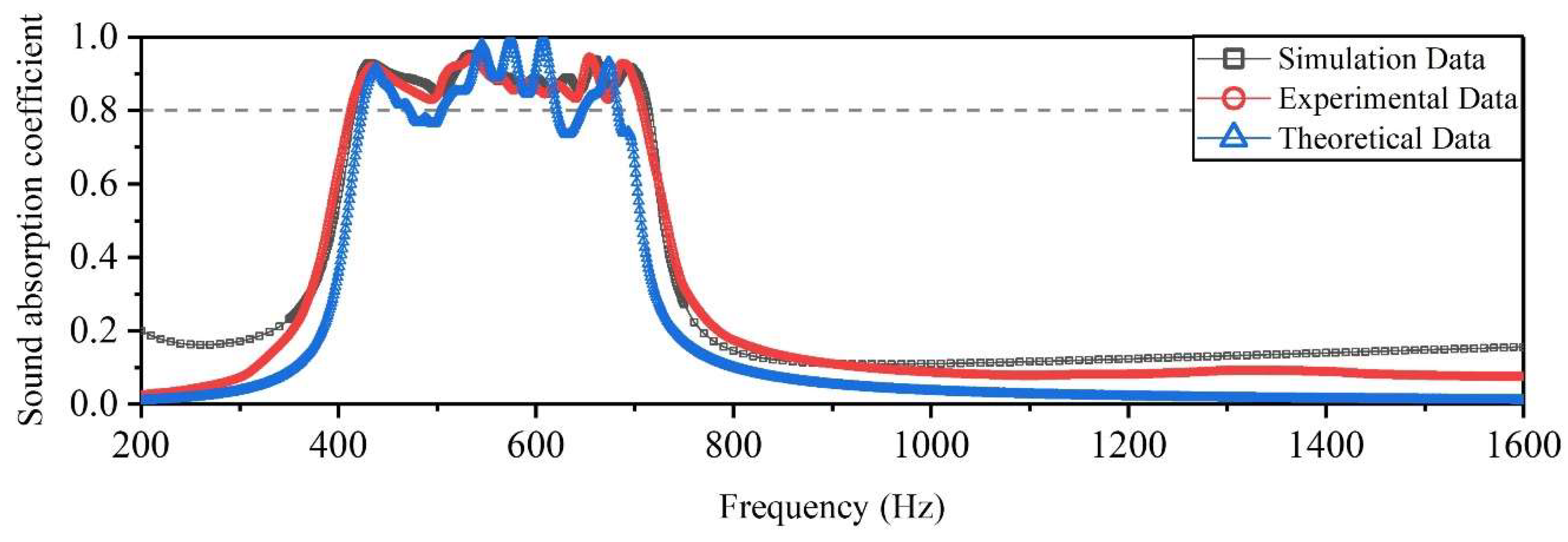
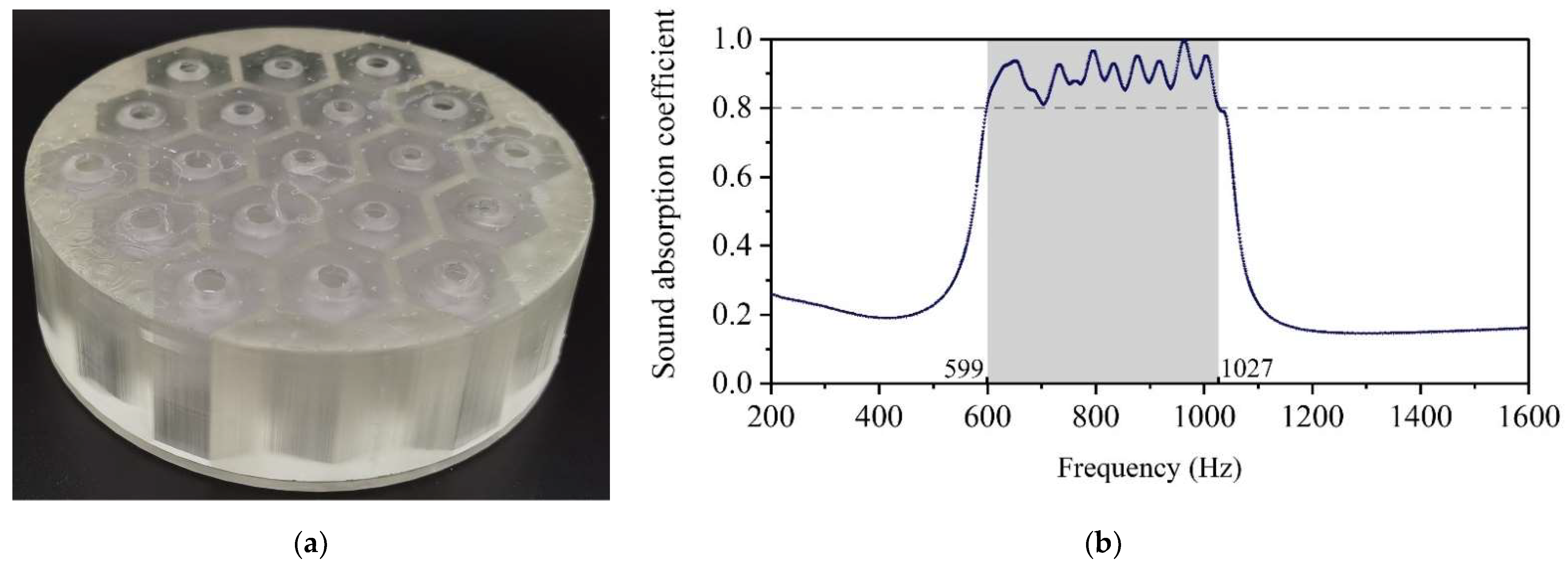
4.3. Experimental Validation
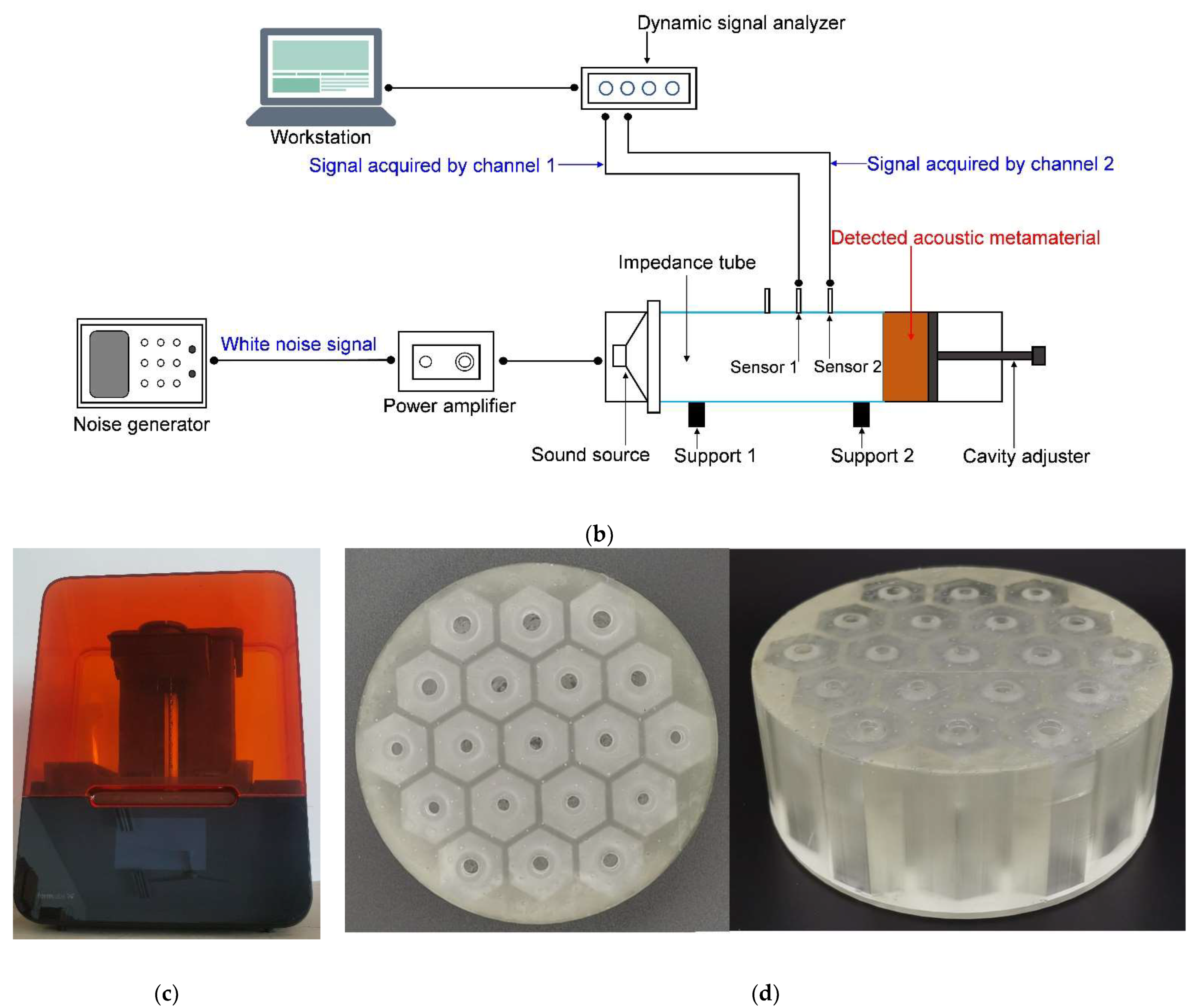
4.3.1. Methodology
4.3.2. Experimental Results
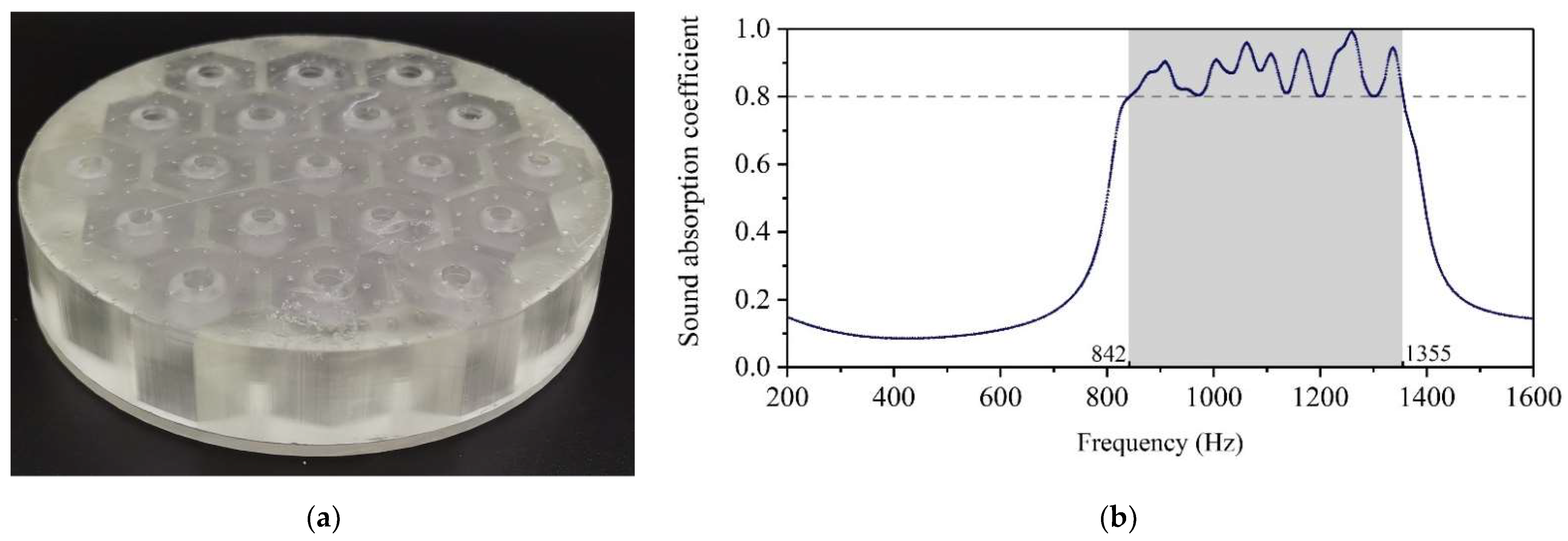
4.4. Applicability of the Optimal Design
5. Conclusions
- (1)
- For the problem of low frequency broadband noise in the workshop and the narrow absorption bandwidth of a single Helmholtz resonator, the acoustic metamaterial of multiple parallel hexagonal Helmholtz resonators was designed and optimized. Its effective absorption capacity was verified by experimental validation. Therefore, the proposed acoustic metamaterial could attenuate the noise with a broad frequency range, which was also beneficial in practical engineering applications.
- (2)
- A joint simulation method incorporating the finite element simulation and cuckoo search algorithm was employed for optimization of the proposed acoustic metamaterial to achieve broadband sound absorption effect at the low frequency range in this research. Compared with the optimization method based on theoretical models, the design method proposed in this research could obtain more accurate optimization results, which satisfied the requirements of certain practical conditions.
- (3)
- The optimal design method proposed in this research could be applied to the absorption needs for different conditions, which also proved its feasibility and practicality. It presented a novel method for the development and application of acoustic metamaterial, which would be favorable to promote its practical applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liao, G.X.; Luan, C.C.; Wang, Z.W.; Liu, J.P.; Yao, X.H.; Fu, J.Z. Acoustic wave filtering strategy based on gradient acoustic metamaterial absorbers. J. Phys. D Appl. Phys. 2021, 54, 335301. [Google Scholar] [CrossRef]
- Yang, X.C.; Shen, X.M.; Bai, P.F.; He, X.H.; Zhang, X.N.; Li, Z.Z.; Chen, L.; Yin, Q. Preparation and characterization of gradient compressed porous metal for high-efficiency and thin–thickness acoustic absorber. Materials 2019, 12, 1413. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.C.; Shen, X.M.; Duan, H.Q.; Yang, F.; Zhang, X.N.; Pan, M.; Yin, Q. Improving and Optimizing Sound Absorption Performance of Polyurethane Foam by Prepositive Microperforated Polymethyl Methacrylate Panel. Appl. Sci. 2020, 10, 2103. [Google Scholar] [CrossRef]
- Dong, C.L.; Dong, Y.B.; Wang, Y.; Shi, J.B.; Zhai, S.L.; Zhao, X.P. Acoustic metamaterial absorbers and metasurfaces composed of meta–atoms and meta–molecules. J. Phys. D Appl. Phys. 2022, 55, 253002. [Google Scholar] [CrossRef]
- Xu, Y.C.; Wu, J.H.; Cai, Y.Q.; Ma, F.Y. Acoustic bi–anisotropy in asymmetric acoustic metamaterials. Appl. Phys. Express 2020, 13, 106503. [Google Scholar] [CrossRef]
- Cai, Z.R.; Zhao, S.D.; Huang, Z.D.; Li, Z.; Su, M.; Zhang, Z.Y.; Zhao, Z.P.; Hu, X.T.; Wang, Y.S.; Song, Y.L. Bubble Architectures for Locally Resonant Acoustic Metamaterials. Adv. Funct. Mater. 2019, 29, 1906984. [Google Scholar] [CrossRef]
- Liu, H.X.; Wu, J.H.; Ma, F.Y. High–efficiency sound absorption by a nested and ventilated metasurface based on multi–slit synergetic resonance. J. Phys. D Appl. Phys. 2021, 54, 205304. [Google Scholar] [CrossRef]
- Jimenez, N.; Huang, W.; Romero–Garcia, V.; Pagneux, V.; Groby, J.P. Ultra–thin metamaterial for perfect and quasi–omnidirectional sound absorption. Appl. Phys. Lett. 2016, 109, 121902. [Google Scholar] [CrossRef]
- Zhang, L.; Xin, F.X. Perfect low–frequency sound absorption of rough neck embedded Helmholtz resonators. J. Acoust. Soc. Am. 2022, 151, 1191–1199. [Google Scholar] [CrossRef]
- Sharafkhani, N. A Helmholtz Resonator–Based Acoustic Metamaterial for Power Transformer Noise Control. Acoust. Aust. 2021, 50, 71–77. [Google Scholar] [CrossRef]
- Ismail, A.Y.; Kim, J.; Chang, S.M.; Koo, B. Sound transmission loss of a Helmholtz Resonator-based acoustic metasurface. Appl. Acoust. 2022, 188, 108569. [Google Scholar] [CrossRef]
- Zhu, J.Z.; Qu, Y.G.; Gao, H.; Meng, G. Nonlinear sound absorption of Helmholtz resonators with serrated necks under high-amplitude sound wave excitation. J. Sound Vib. 2022, 537, 117197. [Google Scholar] [CrossRef]
- Gao, Y.X.; Lin, Y.P.; Zhu, Y.F.; Liang, B.; Yang, J.; Yang, J.; Cheng, J.C. Broadband thin sound absorber based on hybrid labyrinthine metastructures with optimally designed parameters. Sci. Rep. 2020, 10, 10705. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.L.; Wu, J.W.; Chen, J.; Xiong, Y.; Mao, Q.B.; Zhang, X. Optimization design and analysis of honeycomb micro–perforated plate broadband sound absorber. Appl. Acoust. 2022, 186, 108487. [Google Scholar] [CrossRef]
- Gao, N.S.; Wang, B.Z.; Lu, K.; Hou, H. Teaching–learning–based optimization of an ultra–broadband parallel sound absorber—ScienceDirect. Appl. Acoust. 2021, 178, 107969. [Google Scholar] [CrossRef]
- Romero-García, V.; Theocharis, G.; Richoux, O.; Merkel, A.; Tournat, V.; Pagneux, V. Perfect and broadband acoustic absorption by critically coupled sub-wavelength resonators. Sci. Rep. 2016, 6, 19519. [Google Scholar] [CrossRef]
- Herrero-Durá, I.; Cebrecos, A.; Picó, R.; Romero-García, V.; García-Raffi, L.M.; Sánchez-Morcillo, V.J. Sound Absorption and Diffusion by 2D Arrays of Helmholtz Resonators. Appl. Sci. 2020, 10, 1690. [Google Scholar] [CrossRef]
- Shen, J.H.; Lee, H.P.; Yan, X. Sound absorption performance and mechanism of flexible PVA microperforated membrane. Appl. Acoust. 2021, 185, 108402. [Google Scholar] [CrossRef]
- Xu, Z.B.; Wang, B.C.; Zhang, S.M.; Chen, R.J. Design and acoustical performance investigation of sound absorption structure based on plastic micro–capillary films. Appl. Acoust. 2015, 89, 152–158. [Google Scholar] [CrossRef]
- Yang, X.C.; Yang, F.; Shen, X.M.; Wang, E.S.; Zhang, X.N.; Shen, C.; Peng, W.Q. Development of Adjustable Parallel Helmholtz Acoustic Metamaterial for Broad Low-Frequency Sound Absorption Band. Materials 2022, 15, 5938. [Google Scholar] [CrossRef]
- Wen, J.; Zhao, H.; Lv, L.M.; Yuan, B.; Wang, G.; Wen, X.S. Effects of locally resonant modes on underwater sound absorption in viscoelastic materials. J. Acoust. Soc. Am. 2011, 130, 1201. [Google Scholar] [CrossRef] [PubMed]
- Ye, C.Z.; Liu, X.W.; Xin, F.X.; Lu, T.J. Influence of hole shape on sound absorption of underwater anechoic layers. J. Sound Vib. 2018, 426, 54–74. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, M.; Li, C.; Ren, L.; Wang, P.Y.; Li, J.W.; Yang, W.D.; Pan, Y. Simulation study on characteristics of acoustic metamaterial absorbers based on Mie and Helmholtz resonance for low–frequency acoustic wave control. J. Phys. D Appl. Phys. 2021, 54, 385501. [Google Scholar] [CrossRef]
- Cai, X.J.; Niu, Y.; Geng, S.J.; Zhang, J.J.; Cui, Z.H.; Li, J.W.; Chen, J.J. An under-sampled software defect prediction method based on hybrid multi-objective cuckoo search. Concurr.-Comp. Pract. Exp. 2020, 32, e5478. [Google Scholar] [CrossRef]
- Jain, A.; Chaudhari, N. A novel cuckoo search technique for solving discrete optimization problems. Int. J. Syst. Assur. Eng. 2018, 9, 972–986. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search: Recent advances and applications. Neural Comput. Appl. 2014, 24, 169–174. [Google Scholar] [CrossRef]
- Qi, X.B.; Yuan, Z.H.; Song, Y. An integrated cuckoo search optimizer for single and multi–objective optimization problems. PeerJ Comput. Sci. 2021, 7, e370. [Google Scholar] [CrossRef]
- Yang, X.C.; Bai, P.F.; Shen, X.M.; To, S.; Chen, L.; Zhang, X.N.; Yin, Q. Optimal design and experimental validation of sound absorbing multilayer microperforated panel with constraint conditions. Appl. Acoust. 2019, 146, 334–344. [Google Scholar] [CrossRef]
- Jha, K.; Gupta, A.; Alabdulatif, A.; Tanwar, S.; Safirescu, C.O.; Mihaltan, T.C. CSVAG: Optimizing Vertical Handoff Using Hybrid Cuckoo Search and Genetic Algorithm-Based Approaches. Sustainability 2022, 14, 8547. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Le, B. Optimization of electric distribution network configuration for power loss reduction based on enhanced binary cuckoo search algorithm. Comput. Electr. Eng. 2020, 90, 106893. [Google Scholar] [CrossRef]
- Yang, F.; Shen, X.M.; Bai, P.F.; Zhang, X.N.; Li, Z.Z.; Yin, Q. Optimization and Validation of Sound Absorption Performance of 10-Layer Gradient Compressed Porous Metal. Metals 2019, 9, 588. [Google Scholar] [CrossRef]
- Sicuaio, T.; Niyomubyeyi, O.; Shyndyapin, A.; Pilesjö, P.; Mansourian, A. Multi-Objective Optimization Using Evolutionary Cuckoo Search Algorithm for Evacuation Planning. Geomatics 2022, 2, 53–75. [Google Scholar] [CrossRef]
- Bergin, M.; Myles, T.A.; Radic, A.; Hatchwell, C.J.; Lambrick, S.M.; Ward, D.J.; Eder, S.D.; Fahy, A.; Barr, M.; Dastoor, P.C. Complex optical elements for scanning helium microscopy through 3D printing. J. Phys. D Appl. Phys. 2022, 55, 095305. [Google Scholar] [CrossRef]
- Zhu, J.; Lao, C.S.; Chen, T.N.; Li, J.S. 3D–printed woodpile structure for integral imaging and invisibility cloaking. Mater. Des. 2020, 191, 108618. [Google Scholar] [CrossRef]
- Nowoświat, A.; Olechowska, M. Experimental Validation of the Model of Reverberation Time Prediction in a Room. Buildings 2022, 12, 347. [Google Scholar] [CrossRef]
- Quan, H.Y.; Zhang, T.; Xu, H.; Luo, S.; Nie, J.; Zhu, X.Q. Photo–curing 3D printing technique and its challenges. Bioact. Mater. 2020, 5, 110–115. [Google Scholar] [CrossRef]
- Grieder, S.; Zhilyaev, I.; Küng, M.; Brauner, C.; Akermann, M.; Bosshard, J.; Inderkum, P.; Francisco, J.; Willemin, Y.; Eichenhofer, M. Consolidation of Additive Manufactured Continuous Carbon Fiber Reinforced Polyamide 12 Composites and the Development of Process-Related Numerical Simulation Methods. Polymers 2022, 14, 3429. [Google Scholar] [CrossRef]
- Shinde, V.V.; Celestine, A.D.; Beckingham, L.E.; Beckingham, B.S. Stereolithography 3D Printing of Microcapsule Catalyst–Based Self–Healing Composites. ACS Appl. Polym. Mater. 2020, 2, 5048–5057. [Google Scholar] [CrossRef]
- Huang, S.B.; Fang, X.S.; Wang, X.; Assouar, B.; Cheng, Q.; Li, Y. Acoustic perfect absorbers via Helmholtz resonators with embedded apertures. J. Acoust. Soc. Am. 2019, 145, 254–262. [Google Scholar] [CrossRef]
- Guo, J.W.; Fang, Y.; Jiang, Z.Y.; Zhang, X. An investigation on noise attenuation by acoustic liner constructed by Helmholtz resonators with extended necks. J. Acoust. Soc. Am. 2021, 149, 70–81. [Google Scholar] [CrossRef]
- Duan, H.Q.; Shen, X.M.; Wang, E.S.; Yang, F.; Zhang, X.N.; Yin, Q. Acoustic multi-layer Helmholtz resonance metamaterials with multiple adjustable absorption peaks. Appl. Phys. Lett. 2021, 118, 241904. [Google Scholar] [CrossRef]




| Group | Serial Number | Thickness/mm | Diameter of Micropore/mm | Depth of Neck/mm |
|---|---|---|---|---|
| I | 1 | 40 | 4.47 | 13.0 |
| 2 | 12.1 | |||
| 3 | 11.2 | |||
| II | 4 | 3.54 | 14.7 | |
| 5 | 13.4 | |||
| 6 | 12.3 | |||
| 7 | 11.3 | |||
| III | 8 | 3.75 | 12.1 | |
| 9 | 11.2 | |||
| 10 | 10.3 | |||
| 11 | 9.5 | |||
| 12 | 8.8 | |||
| IV | 13 | 4.74 | 12.3 | |
| 14 | 11.4 | |||
| 15 | 10.7 | |||
| 16 | 10.0 | |||
| V | 17 | 5.16 | 11.8 | |
| 18 | 11.0 | |||
| 19 | 10.3 |
| Group | Serial Number | Thickness/mm | Diameter of Micropore/mm | Depth of Neck/mm |
|---|---|---|---|---|
| I | 1 | 40 | 4.47 | 15.7 |
| 2 | 15.2 | |||
| 3 | 14.4 | |||
| II | 4 | 3.54 | 15.9 | |
| 5 | 15.2 | |||
| 6 | 14.7 | |||
| 7 | 14.3 | |||
| III | 8 | 3.75 | 16.7 | |
| 9 | 15.3 | |||
| 10 | 14.1 | |||
| 11 | 13.1 | |||
| 12 | 11.8 | |||
| IV | 13 | 4.74 | 16.2 | |
| 14 | 14.5 | |||
| 15 | 12.6 | |||
| 16 | 10.9 | |||
| V | 17 | 5.16 | 12.0 | |
| 18 | 10.3 | |||
| 19 | 9.5 |
| Group | Serial Number | Thickness/mm | Diameter of Micropore/mm | Depth of Neck/mm |
|---|---|---|---|---|
| I | 1 | 20 | 4.47 | 8.8 |
| 2 | 8.2 | |||
| 3 | 7.3 | |||
| II | 4 | 3.54 | 8.1 | |
| 5 | 7.6 | |||
| 6 | 6.8 | |||
| 7 | 6.1 | |||
| III | 8 | 3.75 | 9.1 | |
| 9 | 8.2 | |||
| 10 | 7.1 | |||
| 11 | 6.3 | |||
| 12 | 5.1 | |||
| IV | 13 | 4.74 | 9.0 | |
| 14 | 7.6 | |||
| 15 | 6.4 | |||
| 16 | 5.3 | |||
| V | 17 | 5.16 | 6.2 | |
| 18 | 5.0 | |||
| 19 | 4.5 |
| Group | Serial Number | Thickness/mm | Diameter of Micropore/mm | Depth of Neck/mm |
|---|---|---|---|---|
| I | 1 | 30 | 4.47 | 10.3 |
| 2 | 9.1 | |||
| 3 | 8.0 | |||
| II | 4 | 3.54 | 9.8 | |
| 5 | 9.0 | |||
| 6 | 8.4 | |||
| 7 | 7.7 | |||
| III | 8 | 3.75 | 10.8 | |
| 9 | 9.9 | |||
| 10 | 8.6 | |||
| 11 | 7.6 | |||
| 12 | 6.5 | |||
| IV | 13 | 4.74 | 9.5 | |
| 14 | 8.2 | |||
| 15 | 7.0 | |||
| 16 | 5.9 | |||
| V | 17 | 5.16 | 6.4 | |
| 18 | 5.4 | |||
| 19 | 4.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Wang, E.; Shen, X.; Zhang, X.; Yin, Q.; Wang, X.; Yang, X.; Shen, C.; Peng, W. Optimal Design of Acoustic Metamaterial of Multiple Parallel Hexagonal Helmholtz Resonators by Combination of Finite Element Simulation and Cuckoo Search Algorithm. Materials 2022, 15, 6450. https://doi.org/10.3390/ma15186450
Yang F, Wang E, Shen X, Zhang X, Yin Q, Wang X, Yang X, Shen C, Peng W. Optimal Design of Acoustic Metamaterial of Multiple Parallel Hexagonal Helmholtz Resonators by Combination of Finite Element Simulation and Cuckoo Search Algorithm. Materials. 2022; 15(18):6450. https://doi.org/10.3390/ma15186450
Chicago/Turabian StyleYang, Fei, Enshuai Wang, Xinmin Shen, Xiaonan Zhang, Qin Yin, Xinqing Wang, Xiaocui Yang, Cheng Shen, and Wenqiang Peng. 2022. "Optimal Design of Acoustic Metamaterial of Multiple Parallel Hexagonal Helmholtz Resonators by Combination of Finite Element Simulation and Cuckoo Search Algorithm" Materials 15, no. 18: 6450. https://doi.org/10.3390/ma15186450
APA StyleYang, F., Wang, E., Shen, X., Zhang, X., Yin, Q., Wang, X., Yang, X., Shen, C., & Peng, W. (2022). Optimal Design of Acoustic Metamaterial of Multiple Parallel Hexagonal Helmholtz Resonators by Combination of Finite Element Simulation and Cuckoo Search Algorithm. Materials, 15(18), 6450. https://doi.org/10.3390/ma15186450








