A Dual-Input Neural Network for Online State-of-Charge Estimation of the Lithium-Ion Battery throughout Its Lifetime
Abstract
:1. Introduction
2. Methodology
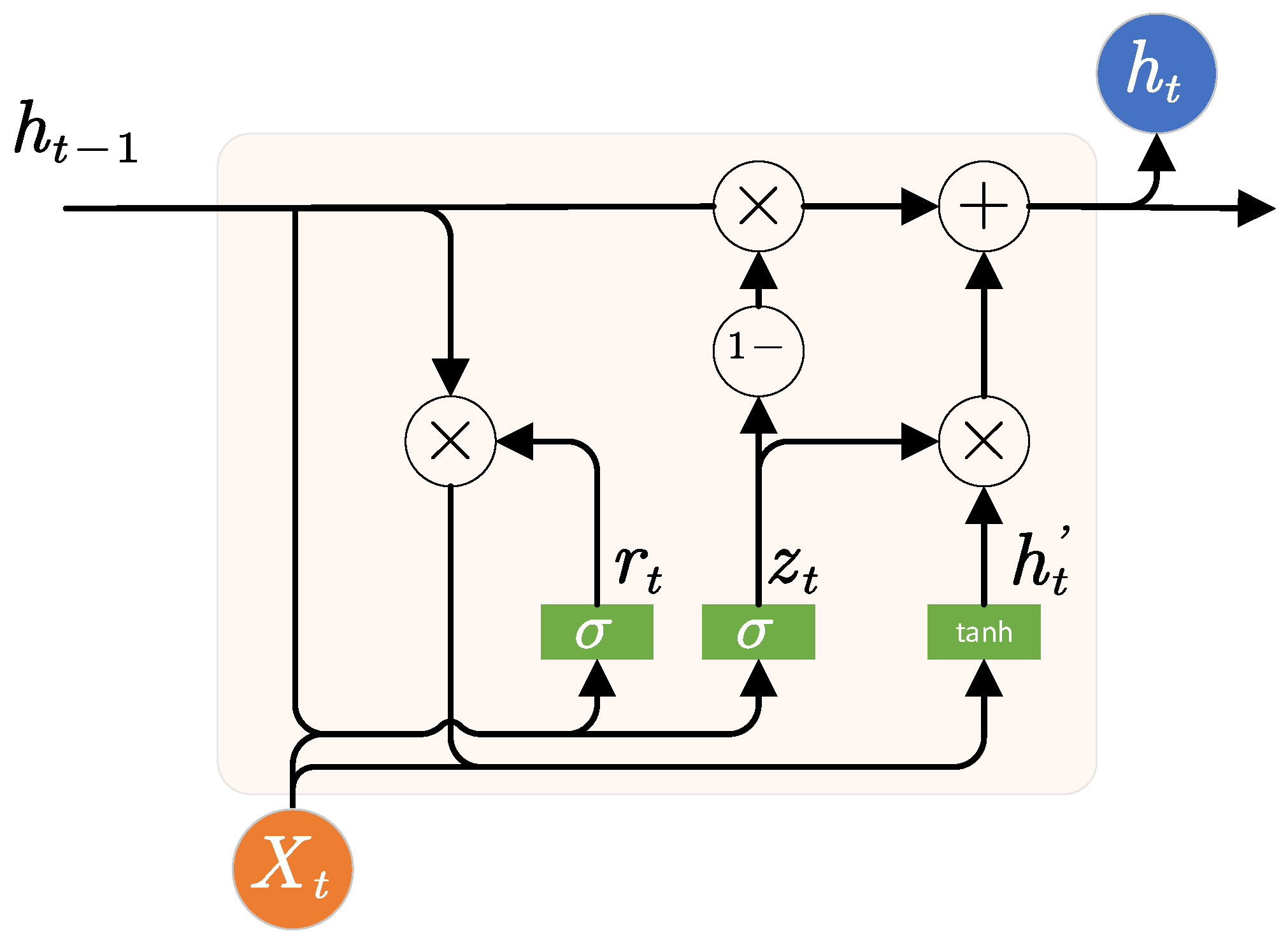
2.1. DIGF Network
2.2. SOC Estimation Procedure
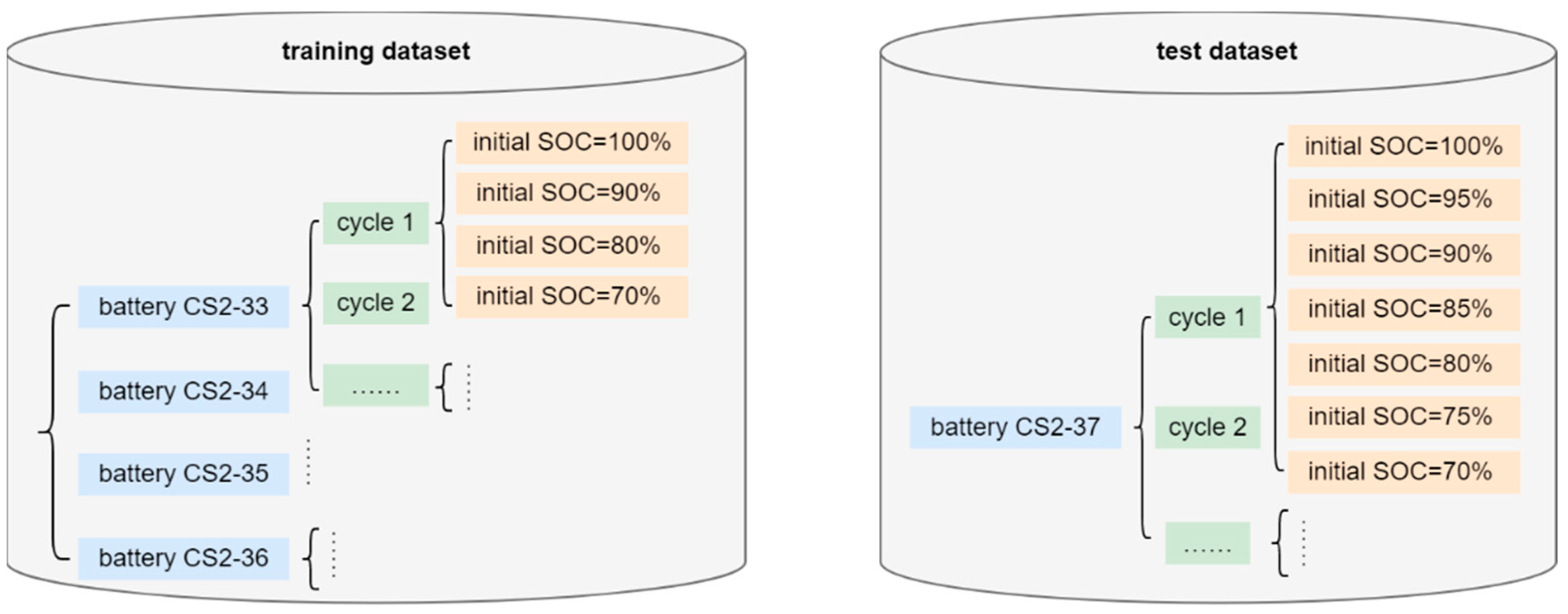
2.2.1. Data Preprocessing
2.2.2. DIGF Network Training
2.2.3. SOC Estimation
3. Experimental Data
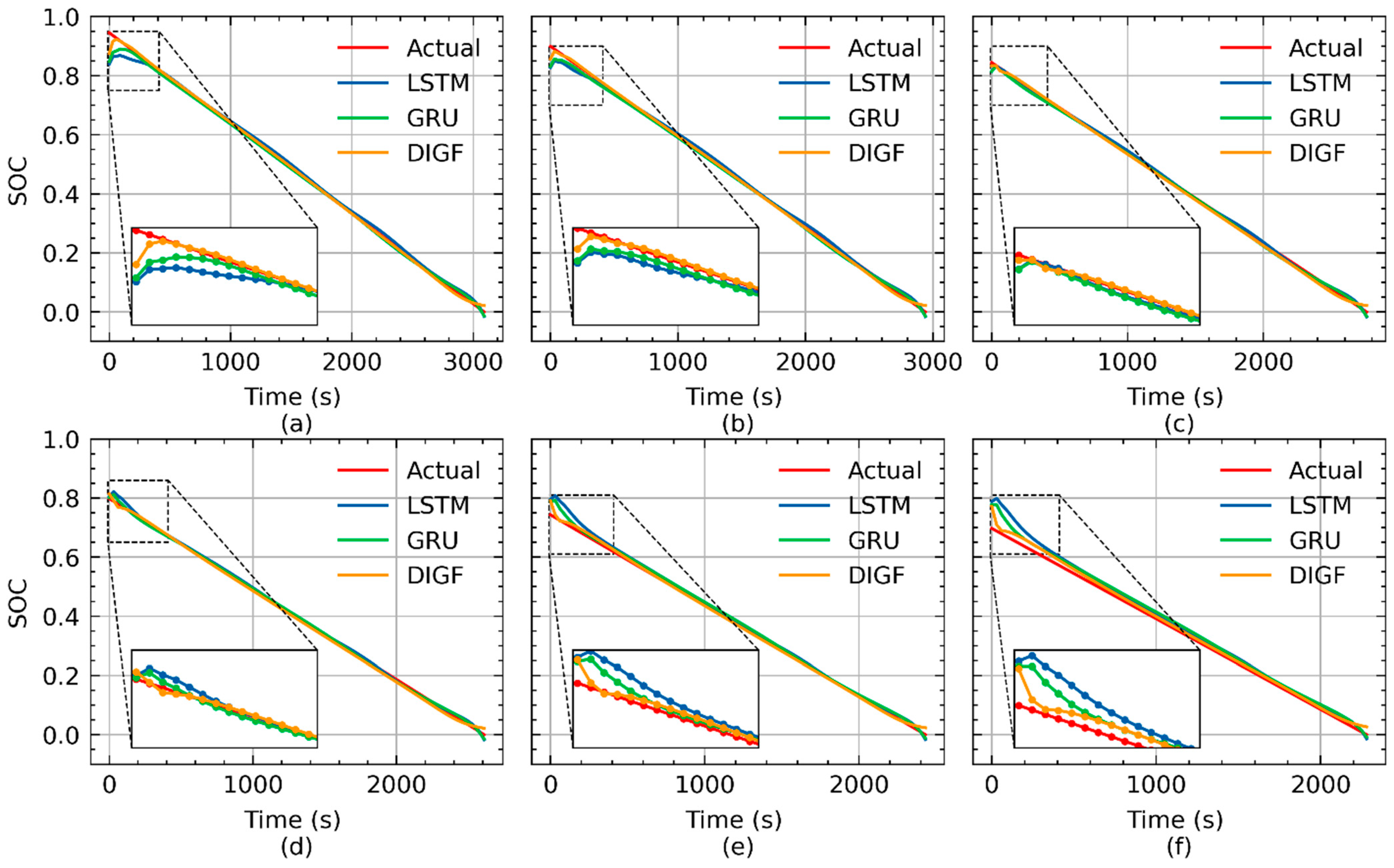
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SOC | state-of-charge |
| RNN | recurrent neural network |
| GRU | gated recurring unit |
| FC | fully connected |
| DIGF | dual-input neural network combining GRU layers and FC layers |
| SOH | state of health |
| EV | electric vehicles |
| AHI | ampere-hour integral |
| OCV | open-circuit voltage |
| ECM | equivalent circuit model |
| LSTM | long short-term memory |
| RMSE | root mean square error |
| CC–CV | constant current–constant voltage |
| T | Timestep |
| input of RNN | |
| output of RNN | |
| number of features in the RNN input | |
| number of features in the RNN output | |
| output of update gate | |
| output of reset gate | |
| candidate state | |
| parameters of update gate in GRU | |
| parameters of reset gate in GRU | |
| parameters of candidate state in GRU | |
| sigmoid function | |
| hyperbolic tangent function | |
| input of FC layer | |
| parameters of FC layer | |
| number of features in the input of FC layer | |
| number of features in the output of FC layer | |
| output of FC layer | |
| index of cycle | |
| voltage measurement of battery | |
| current measurements of battery | |
| input 1 of DIGF network | |
| input 2 of DIGF network | |
| function of GRU layer in the DIGF network | |
| function of FC layer in the DIGF network | |
| output of layer 1, layer 2, layer 3, layer 4 in DIGF network | |
| battery’s rated capacity | |
| interpolation interval | |
| number of interpolation samples | |
| unnormalized current/voltage in the training dataset | |
| unnormalized voltage/current in the training or testing datasets | |
| normalized voltage/current in the training or testing datasets | |
| index of iteration during training process | |
| all parameters of DIGF network | |
| loss function | |
| decay rates of Adam optimizer | |
| learning rate of Adam optimizer | |
| constant term of Adam optimizer | |
| M | number of samples in the training dataset |
| experimental SOC | |
| estimated SOC | |
| total number of the estimated SOCs in cycle | |
| duration of the discharge cycle | |
References
- Cheng, X.; Zhang, R.; Zhao, C.; Wei, F.; Zhang, J.; Zhang, Q. A Review of Solid Electrolyte Interphases on Lithium Metal Anode. Adv. Sci. 2016, 3, 1500213. [Google Scholar]
- Xia, Q.; Yang, D.; Wang, Z.; Ren, Y.; Sun, B.; Feng, Q.; Qian, C. Multiphysical Modeling for Life Analysis of Lithium-Ion Battery Pack in Electric Vehicles. Renew. Sustain. Energy Rev. 2020, 131, 109993. [Google Scholar]
- Horiba, T.; Maeshima, T.; Matsumura, T.; Koseki, M.; Arai, J.; Muranaka, Y. Applications of High Power Density Lithium Ion Batteries. J. Power Sources 2005, 146, 107–110. [Google Scholar]
- Whittingham, M.S. Ultimate Limits to Intercalation Reactions for Lithium Batteries. Chem. Rev. 2014, 114, 11414–11443. [Google Scholar]
- Mu, H.; Xiong, R. Modeling, Evaluation, and State Estimation for Batteries. In Modeling, Dynamics and Control of Electrified Vehicles; Woodhead Publishing: Cambridge, UK, 2018; pp. 1–38. [Google Scholar]
- Ng, M.-F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the State of Charge and Health of Batteries Using Data-Driven Machine Learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC Estimation for Lithium-Ion Batteries: Review and Future Challenges. Electronics 2017, 6, 102. [Google Scholar]
- How, D.N.; Hannan, M.; Lipu, M.H.; Ker, P.J. State of Charge Estimation for Lithium-Ion Batteries Using Model-Based and Data-Driven Methods: A Review. IEEE Access 2019, 7, 136116–136136. [Google Scholar]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the Art of Lithium-Ion Battery SOC Estimation for Electrical Vehicles. Energies 2018, 11, 1820. [Google Scholar]
- Ng, K.; Moo, C.; Chen, Y.; Hsieh, Y. Enhanced Coulomb Counting Method for Estimating State-of-Charge and State-of-Health of Lithium-Ion Batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Li, Z.; Lu, L.; Ouyang, M. Comparison of Methods for Improving SOC Estimation Accuracy through an Ampere-Hour Integeration Approach. J. Tsinghua Univ. Sci. Technol. 2010, 8, 1293–1301. [Google Scholar]
- Yang, W.; Zhu, S.; Chen, Y.; Zhu, J.; Xue, L.; Center, M. SOC Estimation of Lithium-Ion Battery Based on Improved Ampere-Hour Integral Method. Chin. J. Power Sources 2018, 42, 183–184. [Google Scholar]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online Model-Based Estimation of State-of-Charge and Open-Circuit Voltage of Lithium-Ion Batteries in Electric Vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P.C. A Generalized SOC-OCV Model for Lithium-Ion Batteries and the SOC Estimation for LNMCO Battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of Charge Estimation of Lithium-Ion Batteries Using the Open-Circuit Voltage at Various Ambient Temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L. Characteristics Analysis of Open Circuit Voltage of Aged LiFePO4 Battery for Electric Vehicle. Chin. J. Power Sources 2015, 39, 1876–1878. [Google Scholar]
- Di Domenico, D.; Fiengo, G.; Stefanopoulou, A. Lithium-Ion Battery State of Charge Estimation with a Kalman Filter Based on a Electrochemical Model. In Proceedings of the 2008 IEEE International Conference on Control Applications, San Antonio, TX, USA, 3–5 September 2008; pp. 702–707. [Google Scholar]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive Unscented Kalman Filtering for State of Charge Estimation of a Lithium-Ion Battery for Electric Vehicles. Energy 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, Z. A Method for State-of-Charge Estimation of LiFePO4 Batteries at Dynamic Currents and Temperatures Using Particle Filter. J. Power Sources 2015, 279, 306–311. [Google Scholar] [CrossRef]
- Kim, I. The Novel State of Charge Estimation Method for Lithium Battery Using Sliding Mode Observer. J. Power Sources 2006, 163, 584–590. [Google Scholar] [CrossRef]
- Li, W.; Liang, L.; Liu, W.; Wu, X. State of Charge Estimation of Lithium-Ion Batteries Using a Discrete-Time Nonlinear Observer. IEEE Trans. Ind. Electron. 2017, 64, 8557–8565. [Google Scholar] [CrossRef]
- Sun, L.; Li, G.; You, F. Combined Internal Resistance and State-of-Charge Estimation of Lithium-Ion Battery Based on Extended State Observer. Renew. Sustain. Energy Rev. 2020, 131, 109994. [Google Scholar] [CrossRef]
- Álvarez Antón, J.C.; García Nieto, P.J.; Blanco Viejo, C.; Vilán Vilán, J.A. Support Vector Machines Used to Estimate the Battery State of Charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Sahinoglu, G.O.; Pajovic, M.; Sahinoglu, Z.; Wang, Y.; Orlik, P.V.; Wada, T. Battery State-of-Charge Estimation Based on Regular/Recurrent Gaussian Process Regression. IEEE Trans. Ind. Electron. 2017, 65, 4311–4321. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Che, Y.; Xu, L.; Guo, W. Data-Driven State of Charge Estimation for Lithium-Ion Battery Packs Based on Gaussian Process Regression. Energy 2020, 205, 118000. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-Charge Estimation of Li-Ion Batteries Using Deep Neural Networks: A Machine Learning Approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, S.; Li, W.; Miao, Q. State-of-Charge Estimation of Lithium-Ion Batteries Using LSTM and UKF. Energy 2020, 201, 117664. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-Charge Estimation of Lithium-Ion Batteries Based on Gated Recurrent Neural Network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Khalid, A.; Sarwat, A.I. Fast Charging Li-Ion Battery Capacity Fade Prognostic Modeling Using Correlated Parameters’ Decomposition and Recurrent Wavelet Neural Network. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021; pp. 27–32. [Google Scholar]
- Khalid, A.; Sarwat, A.I. Unified Univariate-Neural Network Models for Lithium-Ion Battery State-of-Charge Forecasting Using Minimized Akaike Information Criterion Algorithm. IEEE Access 2021, 9, 39154–39170. [Google Scholar] [CrossRef]
- Khalid, A.; Sundararajan, A.; Sarwat, A.I. A Multi-Step Predictive Model to Estimate Li-Ion State of Charge for Higher C-Rates. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Tu, J.V. Advantages and Disadvantages of Using Artificial Neural Networks versus Logistic Regression for Predicting Medical Outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, F.; Du, C.; Kang, J.; Turkson, R.F. Evaluating the Degradation Mechanism and State of Health of LiFePO4 Lithium-Ion Batteries in Real-World Plug-in Hybrid Electric Vehicles Application for Different Ageing Paths. Energies 2017, 10, 110. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A Critical Review of Recurrent Neural Networks for Sequence Learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl.—Based Syst. 2011, 6, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Qian, C.; Xu, B.; Chang, L.; Sun, B.; Feng, Q.; Yang, D.; Ren, Y.; Wang, Z. Convolutional Neural Network Based Capacity Estimation Using Random Segments of the Charging Curves for Lithium-Ion Batteries. Energy 2021, 227, 120333. [Google Scholar] [CrossRef]
- Shanker, M.; Hu, M.Y.; Hung, M.S. Effect of Data Standardization on Neural Network Training. Omega 1996, 24, 385–397. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Kang, L.; Zhao, X.; Ma, J. A New Neural Network Model for the State-of-Charge Estimation in the Battery Degradation Process. Appl. Energy 2014, 121, 20–27. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.; Pecht, M. An Ensemble Model for Predicting the Remaining Useful Performance of Lithium-Ion Batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- Williard, N.; He, W.; Osterman, M.; Pecht, M. Comparative Analysis of Features for Determining State of Health in Lithium-Ion Batteries. Int. J. Progn. Health Manag. 2013, 4, 14–20. [Google Scholar] [CrossRef]
- Farmann, A.; Waag, W.; Marongiu, A.; Sauer, D.U. Critical Review of On-Board Capacity Estimation Techniques for Lithium-Ion Batteries in Electric and Hybrid Electric Vehicles. J. Power Sources 2015, 281, 114–130. [Google Scholar] [CrossRef]
- Smart, J.; Schey, S. Battery Electric Vehicle Driving and Charging Behavior Observed Early in The EV Project. SAE Int. J. Altern. Powertrains 2012, 1, 27–33. [Google Scholar] [CrossRef] [Green Version]

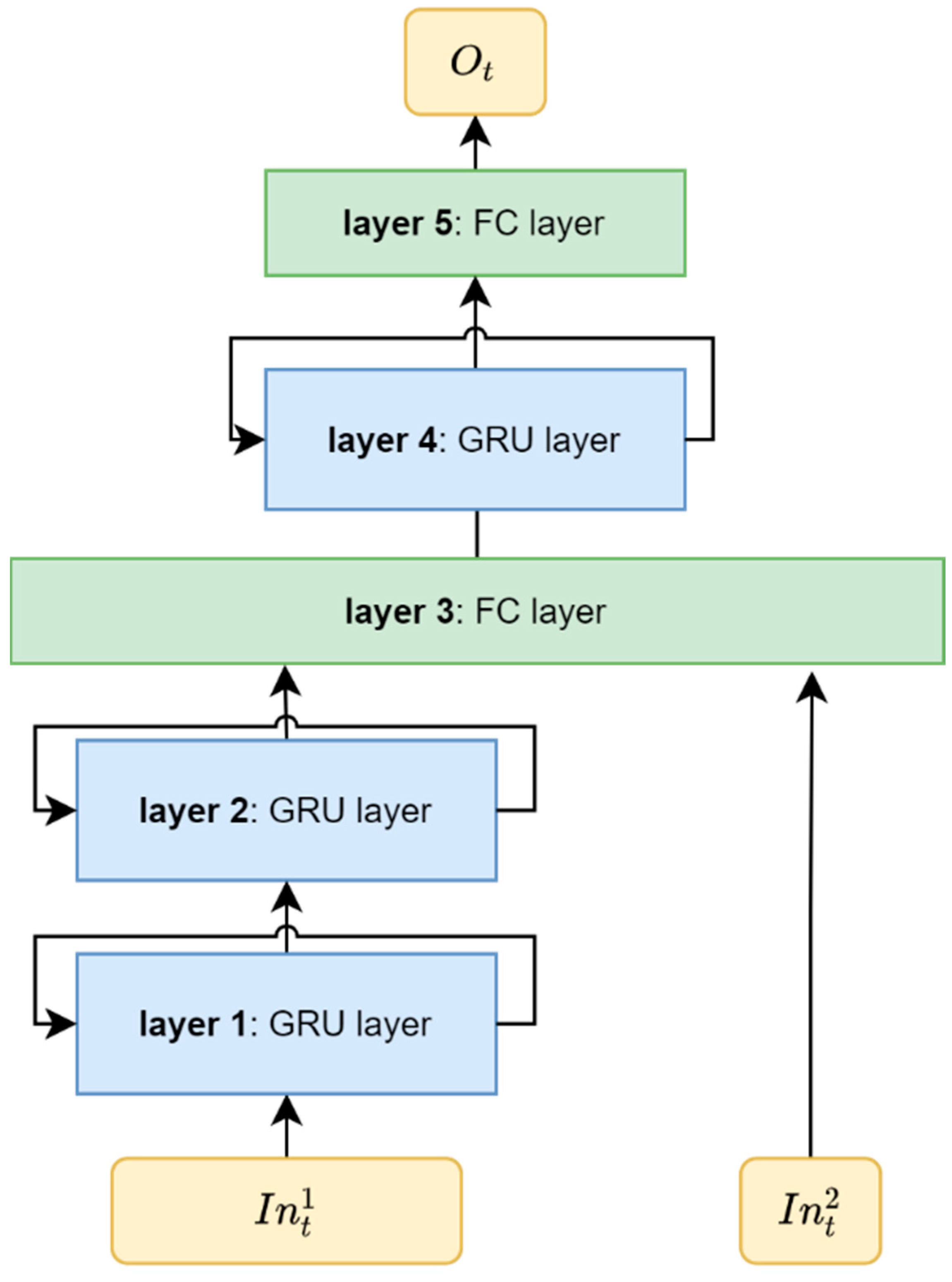



| Hyperparameter | Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 |
|---|---|---|---|---|---|
| μ | 50 | 50 | - | - | - |
| β | - | - | 50 | 50 | 1 |
| Specification | CS2-33 | CS2-34 | CS2-35 | CS2-36 | CS2-37 |
|---|---|---|---|---|---|
| Cell Chemistry | LiCoO2 cathode | ||||
| Weight (w/o safety circuit) | 21.1 g | ||||
| Dimensions | 5.4 × 33.6 × 50.6 mm | ||||
| Rated capacity (Ah) | 1.1 | 1.1 | 1.1 | 1.1 | 1.1 |
| Constant charge current (A) | 0.55 | 0.55 | 0.55 | 0.55 | 0.55 |
| Maximum charge voltage (V) | 4.2 | 4.2 | 4.2 | 4.2 | 4.2 |
| End-of-charge current (A) | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| Discharge cut-off voltage (V) | 2.7 | 2.7 | 2.7 | 2.7 | 2.7 |
| Discharge current (A) | 0.55 | 0.55 | 1.1 | 1.1 | 1.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, C.; Xu, B.; Xia, Q.; Ren, Y.; Yang, D.; Wang, Z. A Dual-Input Neural Network for Online State-of-Charge Estimation of the Lithium-Ion Battery throughout Its Lifetime. Materials 2022, 15, 5933. https://doi.org/10.3390/ma15175933
Qian C, Xu B, Xia Q, Ren Y, Yang D, Wang Z. A Dual-Input Neural Network for Online State-of-Charge Estimation of the Lithium-Ion Battery throughout Its Lifetime. Materials. 2022; 15(17):5933. https://doi.org/10.3390/ma15175933
Chicago/Turabian StyleQian, Cheng, Binghui Xu, Quan Xia, Yi Ren, Dezhen Yang, and Zili Wang. 2022. "A Dual-Input Neural Network for Online State-of-Charge Estimation of the Lithium-Ion Battery throughout Its Lifetime" Materials 15, no. 17: 5933. https://doi.org/10.3390/ma15175933
APA StyleQian, C., Xu, B., Xia, Q., Ren, Y., Yang, D., & Wang, Z. (2022). A Dual-Input Neural Network for Online State-of-Charge Estimation of the Lithium-Ion Battery throughout Its Lifetime. Materials, 15(17), 5933. https://doi.org/10.3390/ma15175933









