2D Digital Reconstruction of Asphalt Concrete Microstructure for Numerical Modeling Purposes
Abstract
:1. Introduction
1.1. Asphalt Concrete Microstructure Characterization
1.2. Numerical Representation of AC Microstructure
2. Materials and Methods
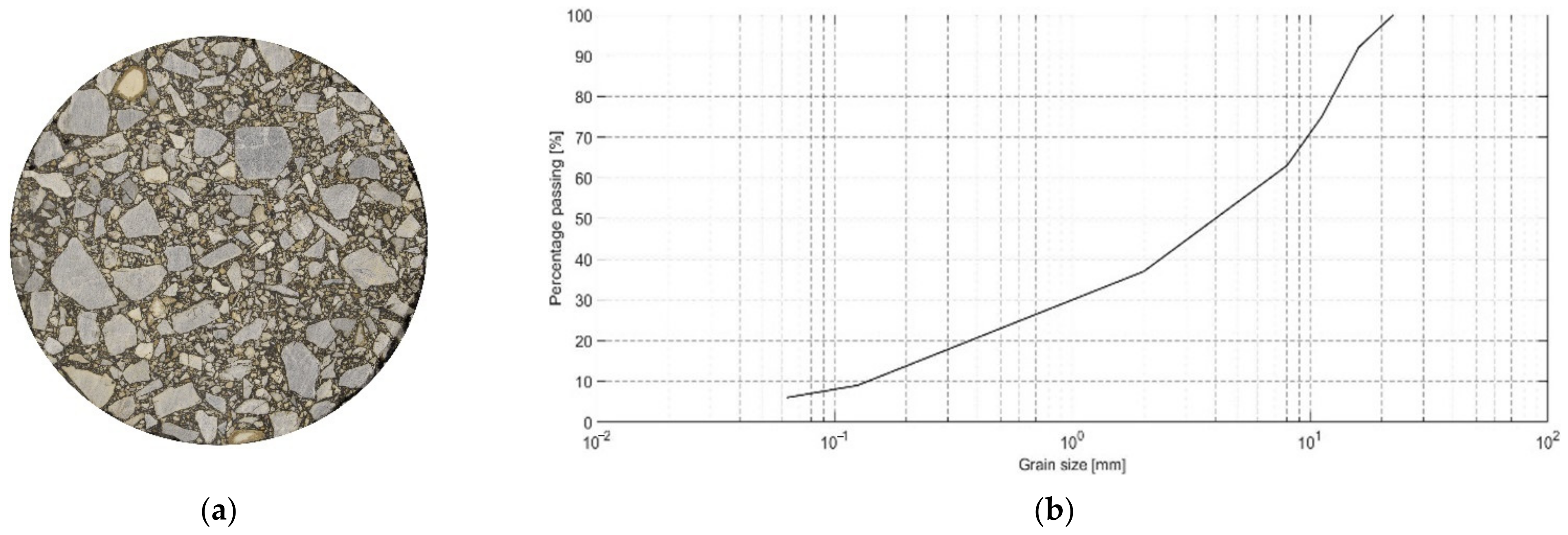
2.1. Samples and Images Preparation
2.2. Image Processing
2.2.1. Conversion RGB to Grayscale Image
2.2.2. Image Binarization
2.2.3. Enhanced Binarization
- An image is processed as described in Section 2.2.1 and Section 2.2.2 using the human visual inspection to control the process;
- A small number of inclusions is manually reconstructed;
- Those manually reconstructed inclusions are used as references;
- A threshold value described in Section 2.2.2 is iteratively updated to provide the improved agreement between the reference inclusion shapes and those reconstructed by the algorithm. So far, we have used the area of the inclusion as the quantity to be compared.
2.3. Controlled Geometry Simplification
2.3.1. Reference AC Microstructure
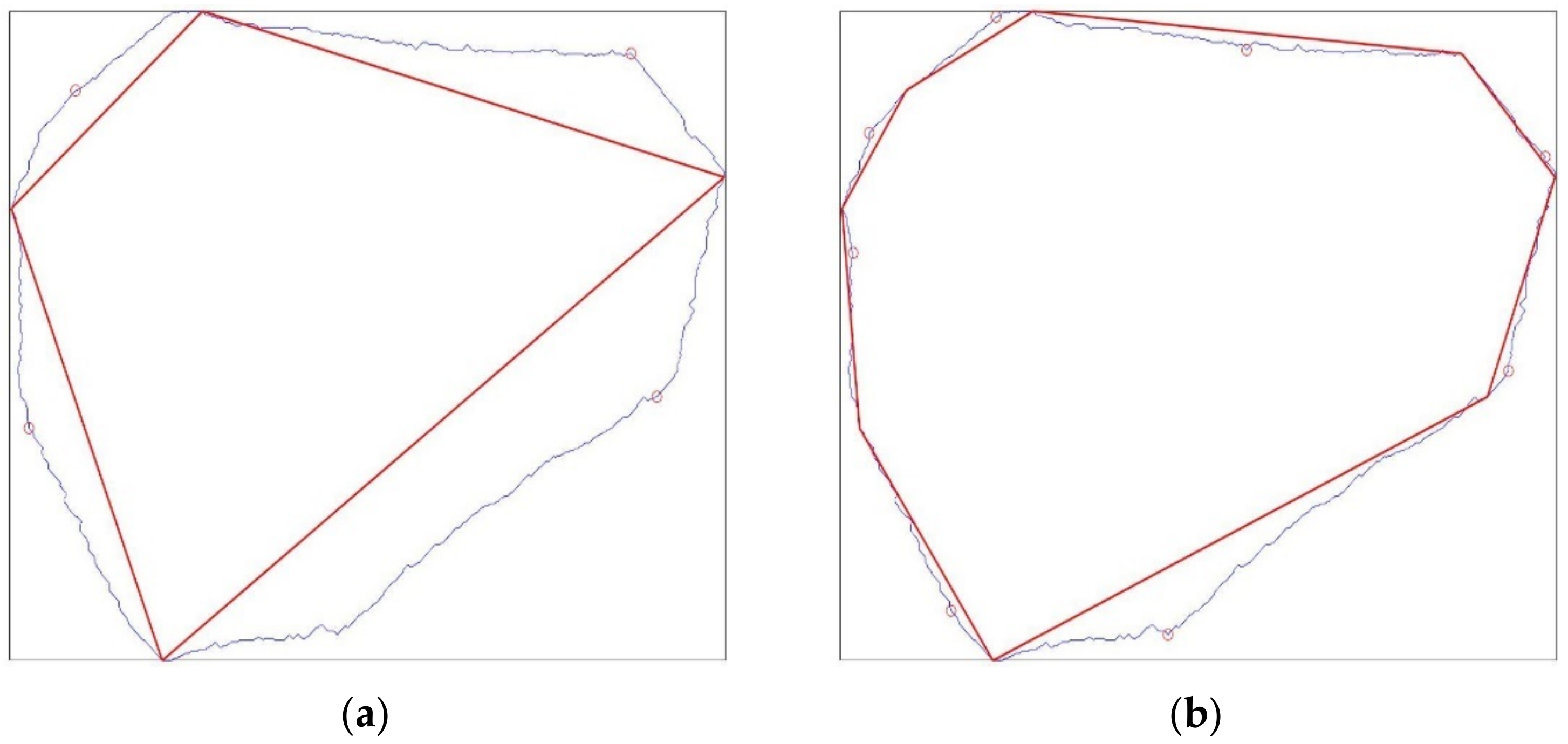
2.3.2. Shortest Edge Elimination
- Reduce the initial number of vertices by simple removal of their specified percentage (10%, 20%, etc.). The vertices are removed with regular interval, i.e., the 1st, 11th, 21st, etc. (when the percentage equal to 10% is specified). This simplification is justified by the high resolution of the processed image.
- Remove iteratively the shortest edge along the inclusion boundary.
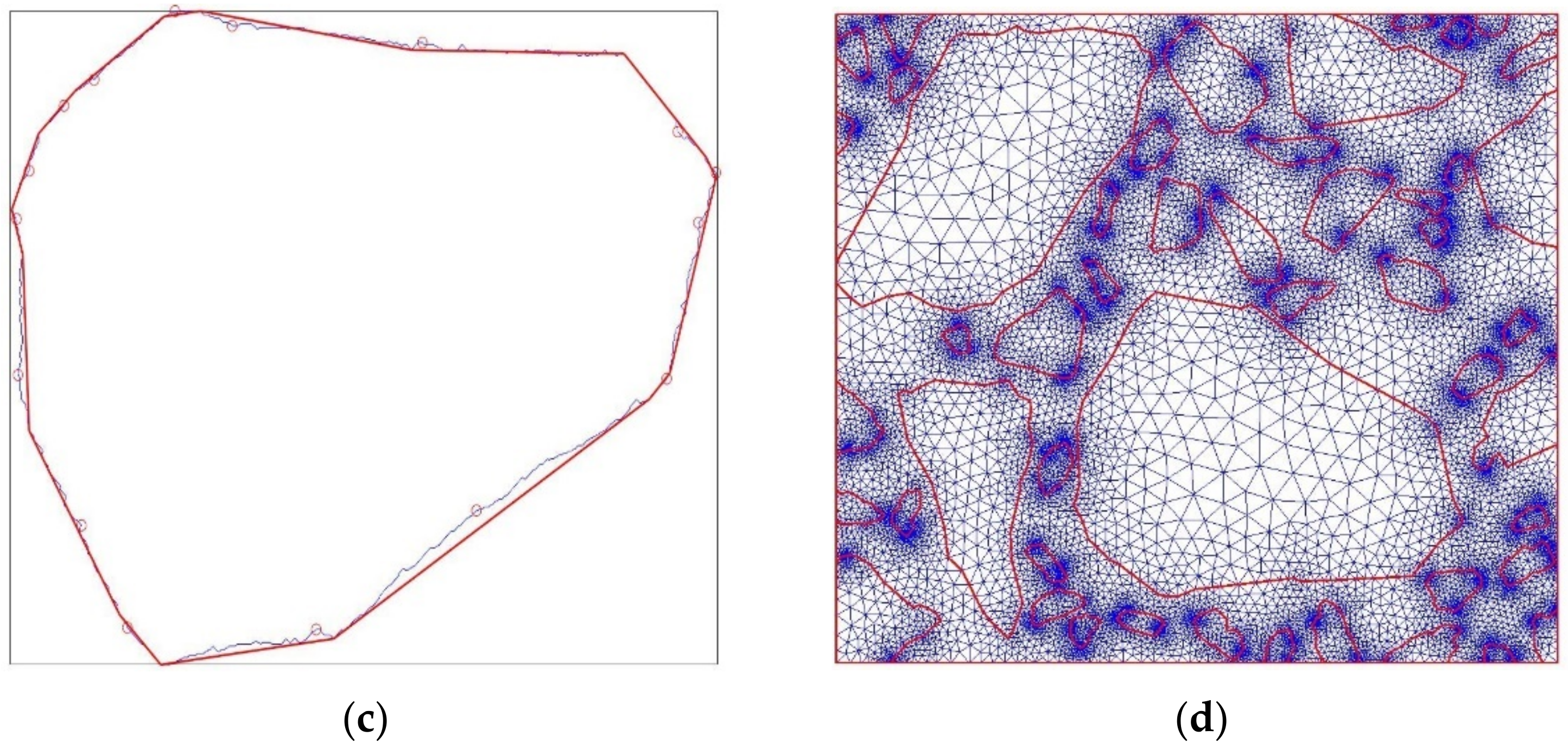
2.3.3. Local Geometry Enhancement
- Find the extreme (outermost) pixels along the inclusion boundary in all four directions, i.e., top, bottom, left and right (see Figure 8a). In the case of multiple values, we selected higher (for left and right extrema) and located more to the left pixels (for top and bottom extrema). Typically, a quadrilateral is generated.
- Iteratively, we looped over all the approximated geometry edges. The inclusion boundary pixel along the respective segment (see Figure 8b,d) with the largest distance from the approximated edge was searched. Consequently, a new vertex for the approximated geometry was added and the number of its edges increases. At this step, one can introduce additional requirements on the newly created edges. For instance, a minimum edge length can be verified before the current edge splitting.
2.3.4. Convex Subdomain Approach
3. Results
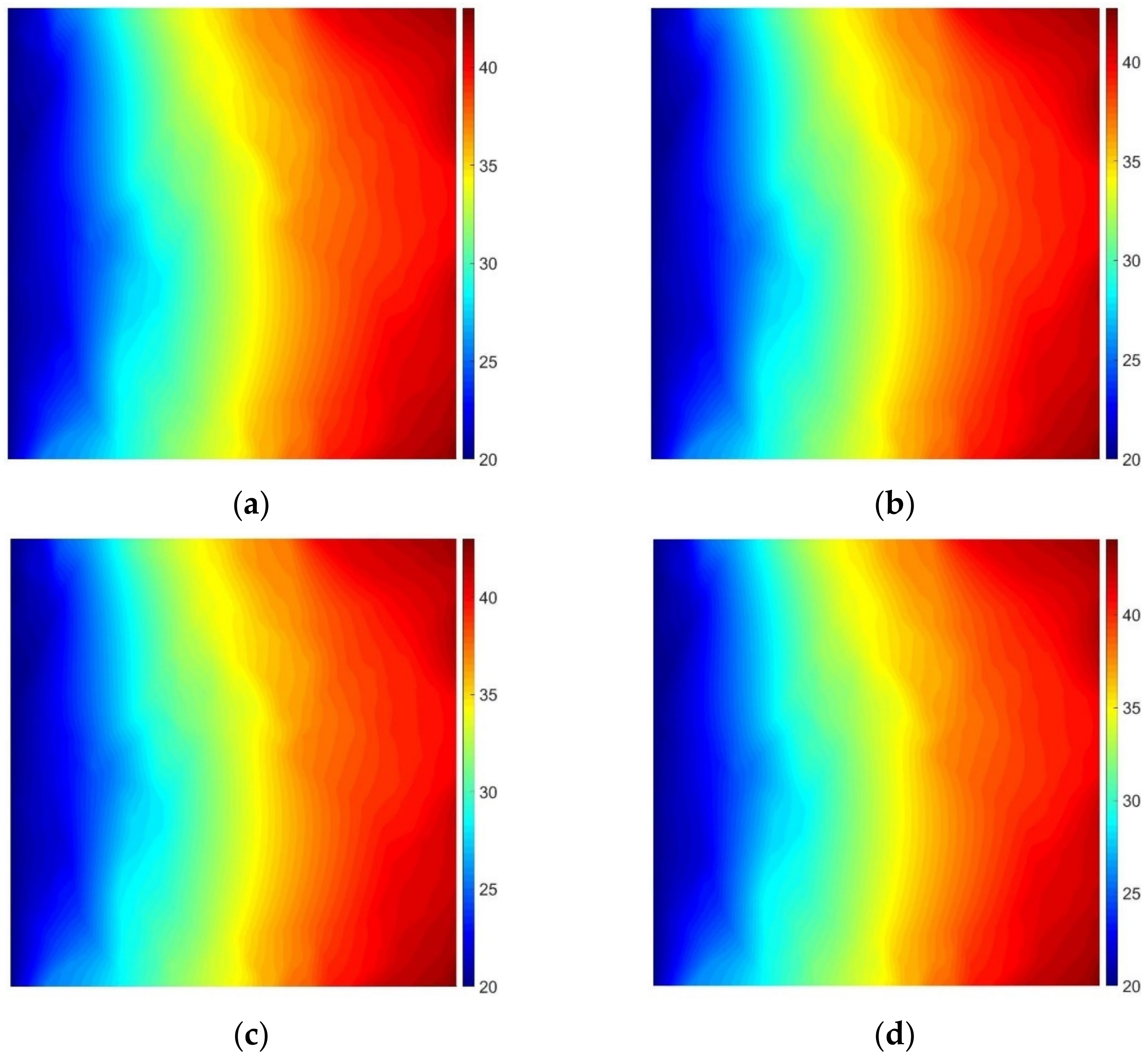
3.1. Heat Flow Problem
- in Figure 6b, which was generated on the basis of the initial microstructure geometry without any simplification,
- in Figure 7b, which was generated using the shortest edge elimination algorithm with the percentage of eliminated boundary pixels equal to about 90%,
- in Figure 8d, which was obtained after 2 local geometry enhancements, and
- in Figure 9e, after geometry correction.
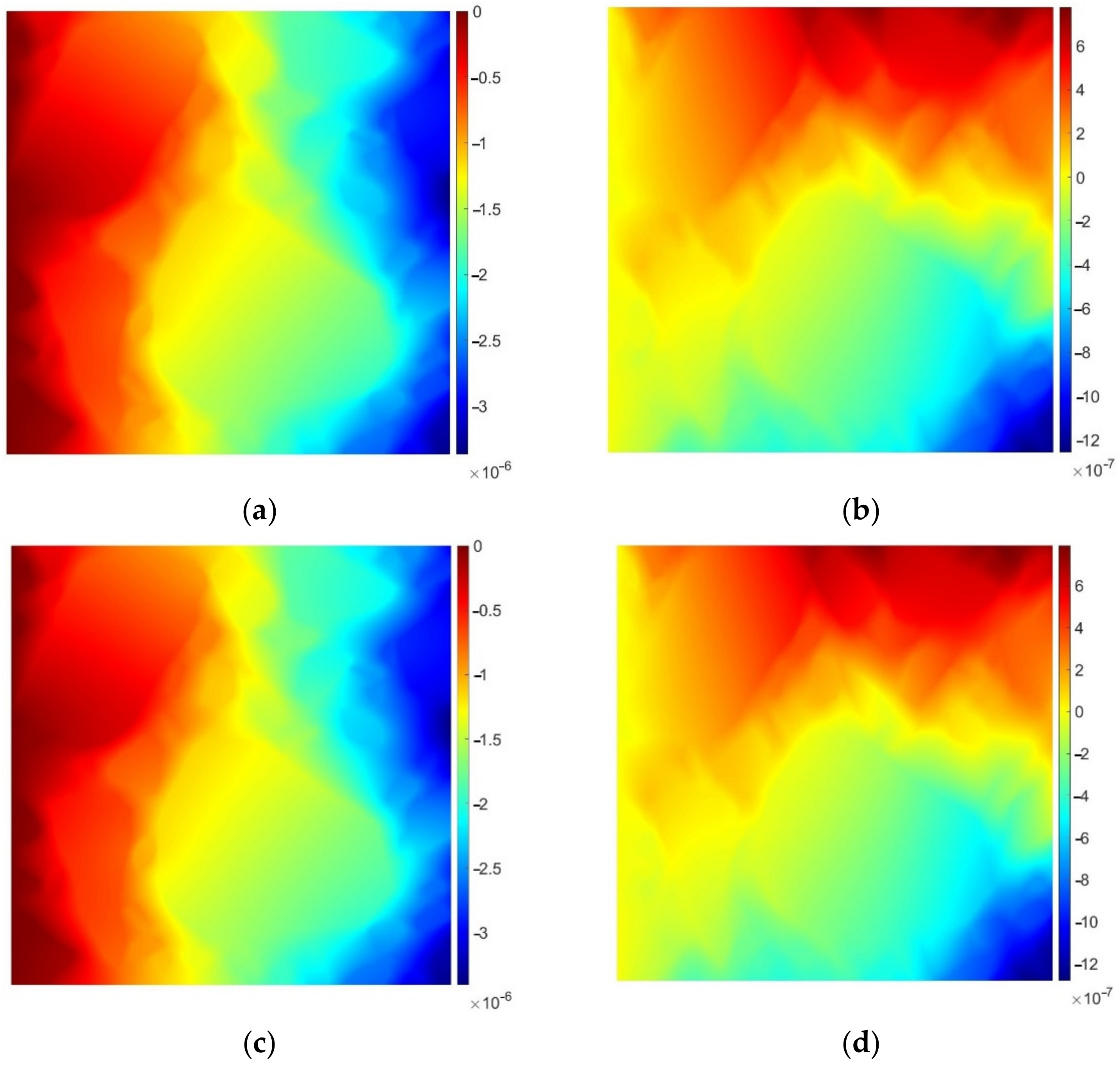
3.2. Linear Elasticity (Plane Strain) Problem
3.3. Discussion
4. Conclusions
- Image processing can be used in order to reconstruct the AC microstructure geometry.
- The initial inclusion boundaries can be effectively simplified using the algorithms presented in this paper.
- A large NDOF reduction can be obtained due to the user-controlled microstructure geometry simplification with a small solution error introduced.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, Y.-R.; Souza, F.V.; Teixeira, J.E. A two-way coupled multiscale model for predicting damage-associated performance of asphaltic roadways. Comput. Mech. 2013, 51, 187–201. [Google Scholar] [CrossRef]
- Kim, Y.-R. Modeling of Asphalt Concrete, 1st ed.; McGraw Hill: New York, NY, USA, 2009. [Google Scholar]
- Islam, M.-R.; Tarefder, R.-A. Pavement Design: Materials, Analysis, and Highways; McGraw Hill: New York, NY, USA, 2020. [Google Scholar]
- Liu, Y. Discrete Element Methods for Asphalt Concrete: Development and Application of User-Defined Microstructural Models and a Viscoelastic Micromechanical Model. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2011. [Google Scholar]
- Wollny, I.; Hartung, F.; Kaliske, M.; Liu, P.; Oeser, M.; Wang, D.; Falla, G.C.; Leischner, S.; Wellner, F. Coupling of microstructural and macrostructural computational approaches for asphalt pavements under rolling tire load. Comput. Aided. Civ. Inf. 2020, 35, 1178–1193. [Google Scholar] [CrossRef]
- Neumann, J.; Simon, J.-W.; Mollenhauer, K.; Reese, S. A framework for 3D synthetic mesoscale models of hot mix asphalt for the finite element method. Build. Mater. 2017, 148, 857–873. [Google Scholar] [CrossRef]
- Wimmer, J.; Stier, B.; Simon, J.W.; Reese, S. Computational homogenisation from a 3D finite element model of asphalt concrete-linear elastic computations. Finite Elem. Anal. Des. 2016, 110, 43–57. [Google Scholar] [CrossRef]
- Onifade, I.; Jelagin, D.; Birgisson, B.; Kringos, N. Towards asphalt mixture morphology evaluation with the virtual specimen approach. Road Mater. Pavement Des. 2015, 17, 579–599. [Google Scholar] [CrossRef]
- Fakhari Tehrani, F.; Absi, J.; Allou, F.; Petit, C. Heterogeneous numerical modeling of asphalt concrete through use of a biphasic approach: Porous matrix/inclusions. Comput. Mater. Sci. 2013, 69, 186–196. [Google Scholar] [CrossRef]
- Sepehr, K.; Svec, O.J.; Yue, Z.Q.; El Hussein, H.M. Finite element modelling of asphalt concrete microstructure. WIT Trans. Eng. Sci. 1994, 6, 225–232. [Google Scholar] [CrossRef]
- Mo, L.; Huurman, M.; Wu, S.; Molenaar, A. 2D and 3D meso-scale finite element models for ravelling analysis of porous asphalt concrete. Finite Elem. Anal. Des. 2008, 44, 186–196. [Google Scholar] [CrossRef]
- Mitra, K.; Das, A.; Basu, S. Mechanical behavior of asphalt mix: An experimental and numerical study. Constr. Build. Mater. 2012, 27, 545–552. [Google Scholar] [CrossRef]
- Sadd, M.H.; Dai, Q.; Parameswaran, V.; Shukla, A. Microstructural Simulation of Asphalt Materials: Modeling and Experimental Studies. J. Mater. Civ. Eng. 2004, 16, 107–115. [Google Scholar] [CrossRef]
- Huang, W.; Wang, H.; Yin, Y.; Zhang, X.; Yuan, J. Microstructural Modeling of Rheological Mechanical Response for Asphalt Mixture Using an Image-Based Finite Element Approach. Materials 2019, 12, 2041. [Google Scholar] [CrossRef]
- Schüller, T.; Jänicke, R.; Steeb, H. Nonlinear modeling and computational homogenization of asphalt concrete on the basis of XRCT scans. Constr. Build. Mater. 2016, 109, 96–108. [Google Scholar] [CrossRef]
- Nejad, F.M.; Motekhases, F.Z.; Zakeri, H.; Mehrabi, A. An Image Processing Approach to Asphalt Concrete Feature Extraction. J. Ind. Intell. Inf. 2015, 3, 54–60. [Google Scholar] [CrossRef]
- Liu, P.; Hu, J.; Wang, D.; Oeser, M.; Alber, S.; Ressel, W.; Fala, G. Modelling and evaluation of aggregate morphology on asphalt compression behavior. Constr. Build. Mater. 2017, 133, 196–208. [Google Scholar] [CrossRef]
- Ziaei-Rad, V.; Nouri, N.; Ziaei-Rad, S.; Abtahi, M. A numerical study on mechanical performance of asphalt mixture using a meso-scale finite element model. Finite Elem. Anal. Des. 2012, 57, 81–91. [Google Scholar] [CrossRef]
- You, T.; Al-Rub, R.; Darabi, M.; Masad, E.; Little, D. A thermo-viscoelastic–viscoplastic–viscodamage constitutive model for asphaltic materials. Int. J. Solids Struct. 2011, 1, 191–207. [Google Scholar] [CrossRef]
- Qu, X.; Wang, D.; Wang, L.; Huang, Y.; Hou, Y.; Oeser, M. The State-of-the-Art Review on Molecular Dynamics Simulation of Asphalt Binder. Adv. Civ. Eng. 2018, 2018, 4546191. [Google Scholar] [CrossRef]
- Aigner, E.; Lackner, R.; Pichler, C. Multiscale prediction of viscoelastic properties of asphalt concrete. J. Mater. Civ. Eng. 2009, 21, 771–780. [Google Scholar] [CrossRef]
- Feyel, F.; Chaboche, L. FE2 multiscale approach for modelling the elasto-viscoplastic behaviour of long fibre SiC/Ti composite materials. Comput. Methods Appl. Mech. Eng. 2000, 183, 309–330. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Jaworska, I. An effective contour plotting method for presentation of the postprocessed results. Comput. Vis. Graph. Comput. Imaging Vis. 2006, 32, 1112–1117. [Google Scholar]
- Preparata, F.P.; Shamos, M.I. Computational Geometry; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Klimczak, M.; Cecot, W. MsFEM upscaling for coupled thermo-mechanical problem. In Lecture Notes in Computer Science, Computational Science, Proceedings of the International Conference on Computational Science, Krakow, Poland, 16–18 June 2021; Maciej, P., Kranzlmüller, D., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume 12746, pp. 562–575. [Google Scholar]






| Algorithm | NDOF | Maximum Temperature [°C] | NDOF Reduction [%] | Relative Error [%] |
|---|---|---|---|---|
| Reference Solution | 110,557 | 43.03 | - | - |
| Shortest Edge Elimination | 5524 | 42.72 | 95.00 | 0.72 |
| Local Geometry Enhancement | 10,445 | 43.01 | 90.55 | 0.05 |
| Convex Subdomain Approach | 16,251 | 44.09 | 85.30 | 2.46 |
| Algorithm | NDOF | Maximum Displacement Magnitude [m] | NDOF Reduction [%] | Relative Error [%] |
|---|---|---|---|---|
| Reference Solution | 221,114 | 3.37 × 10−6 | - | - |
| Shortest Edge Elimination | 11,048 | 3.41 × 10−6 | 95.00 | 1.19 |
| Local Geometry Enhancement | 20,890 | 3.36 × 10−6 | 90.55 | 0.30 |
| Convex Subdomain Approach | 32,502 | 3.24 × 10−6 | 85.30 | 3.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimczak, M.; Jaworska, I.; Tekieli, M. 2D Digital Reconstruction of Asphalt Concrete Microstructure for Numerical Modeling Purposes. Materials 2022, 15, 5553. https://doi.org/10.3390/ma15165553
Klimczak M, Jaworska I, Tekieli M. 2D Digital Reconstruction of Asphalt Concrete Microstructure for Numerical Modeling Purposes. Materials. 2022; 15(16):5553. https://doi.org/10.3390/ma15165553
Chicago/Turabian StyleKlimczak, Marek, Irena Jaworska, and Marcin Tekieli. 2022. "2D Digital Reconstruction of Asphalt Concrete Microstructure for Numerical Modeling Purposes" Materials 15, no. 16: 5553. https://doi.org/10.3390/ma15165553
APA StyleKlimczak, M., Jaworska, I., & Tekieli, M. (2022). 2D Digital Reconstruction of Asphalt Concrete Microstructure for Numerical Modeling Purposes. Materials, 15(16), 5553. https://doi.org/10.3390/ma15165553






