A Hybrid Level Set Method for the Topology Optimization of Functionally Graded Structures
Abstract
:1. Introduction
2. Geometric Modeling Based on HLSM
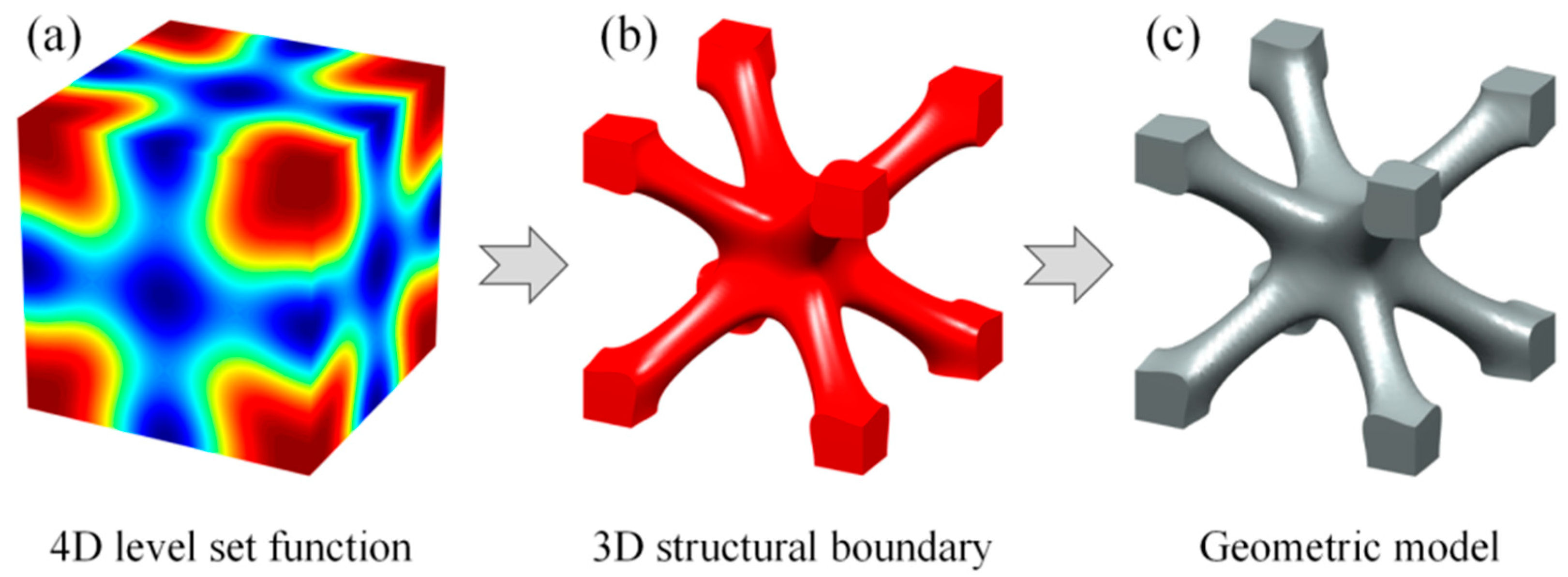
2.1. Level Set Modeling
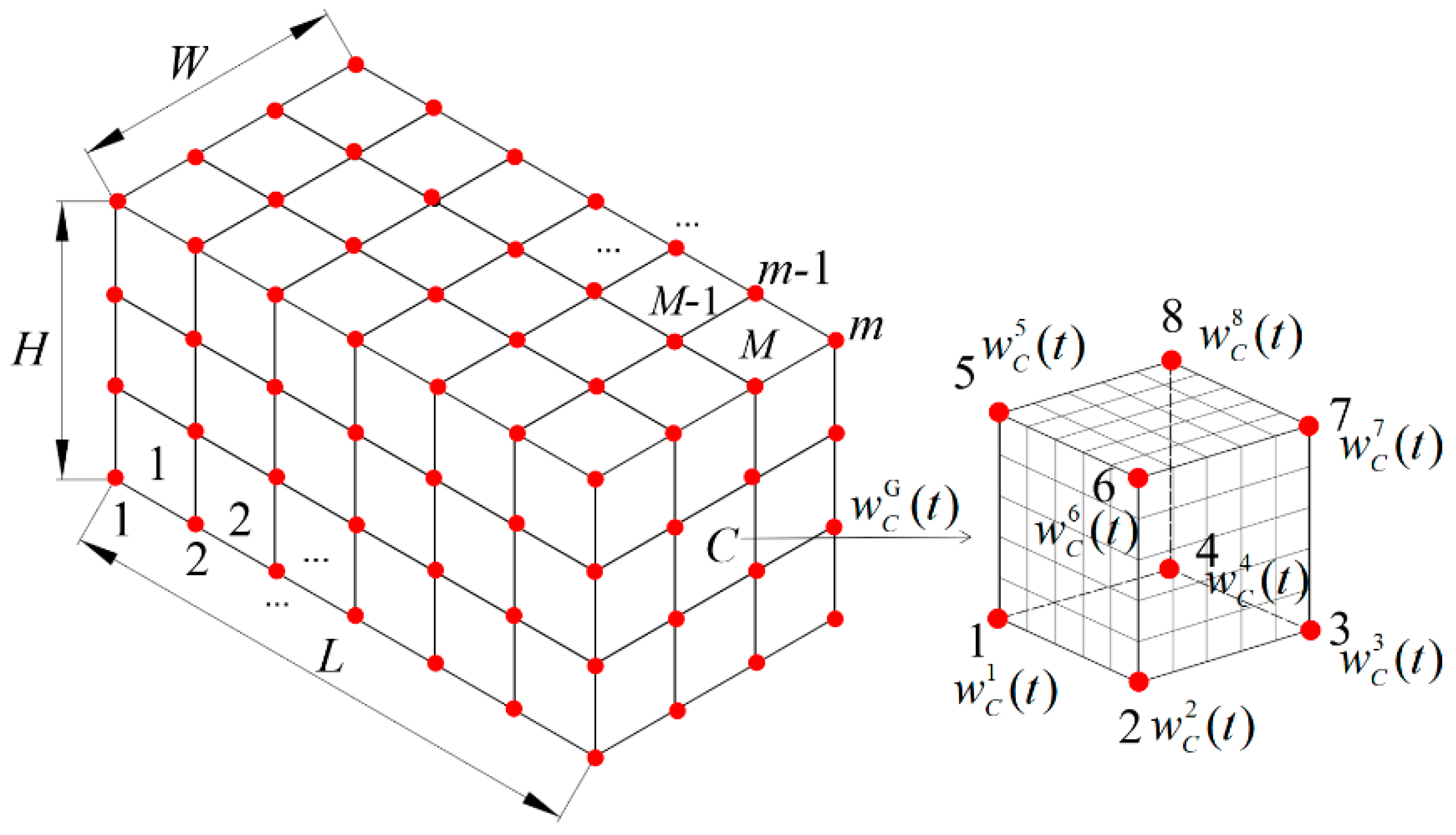
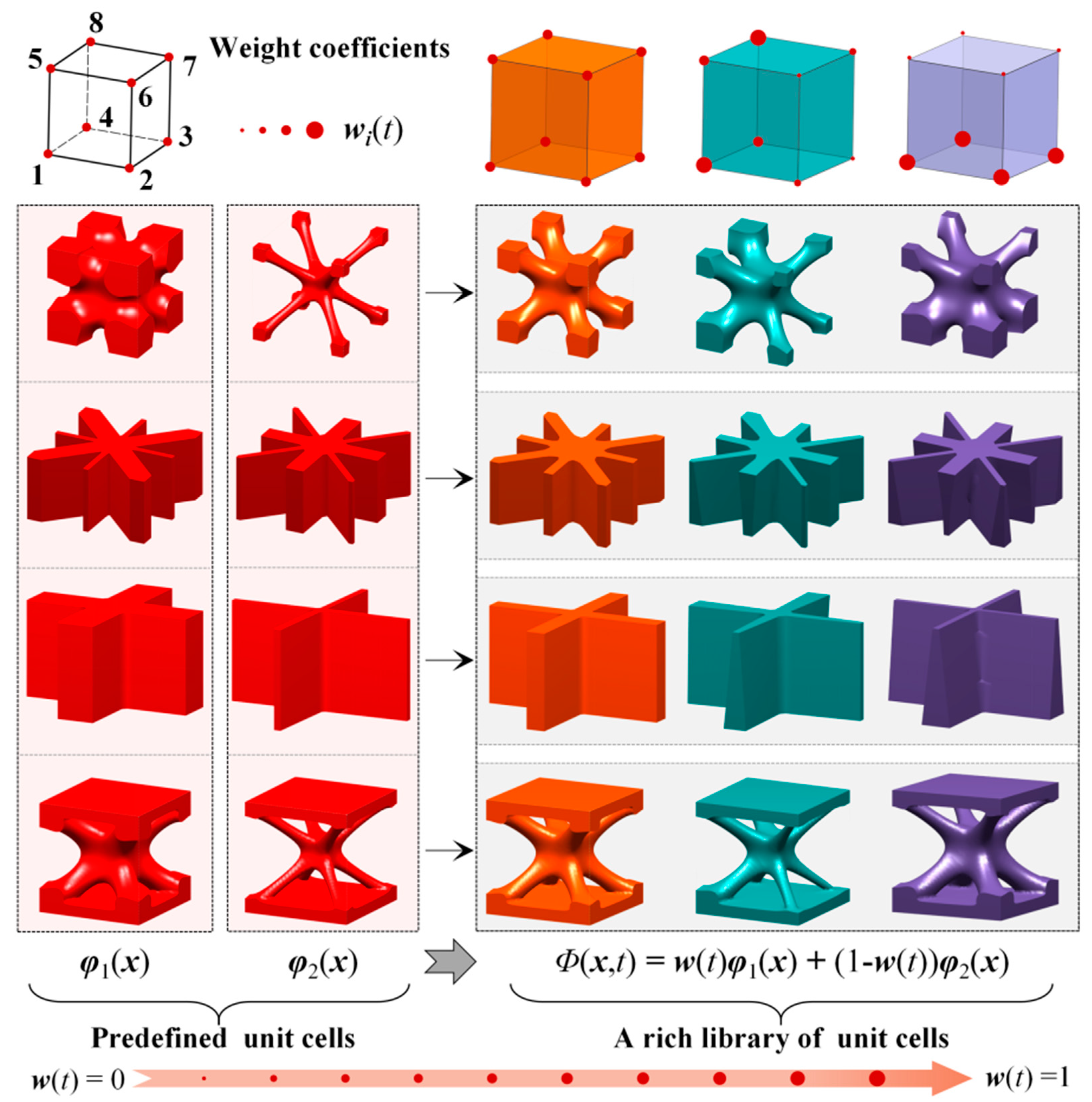
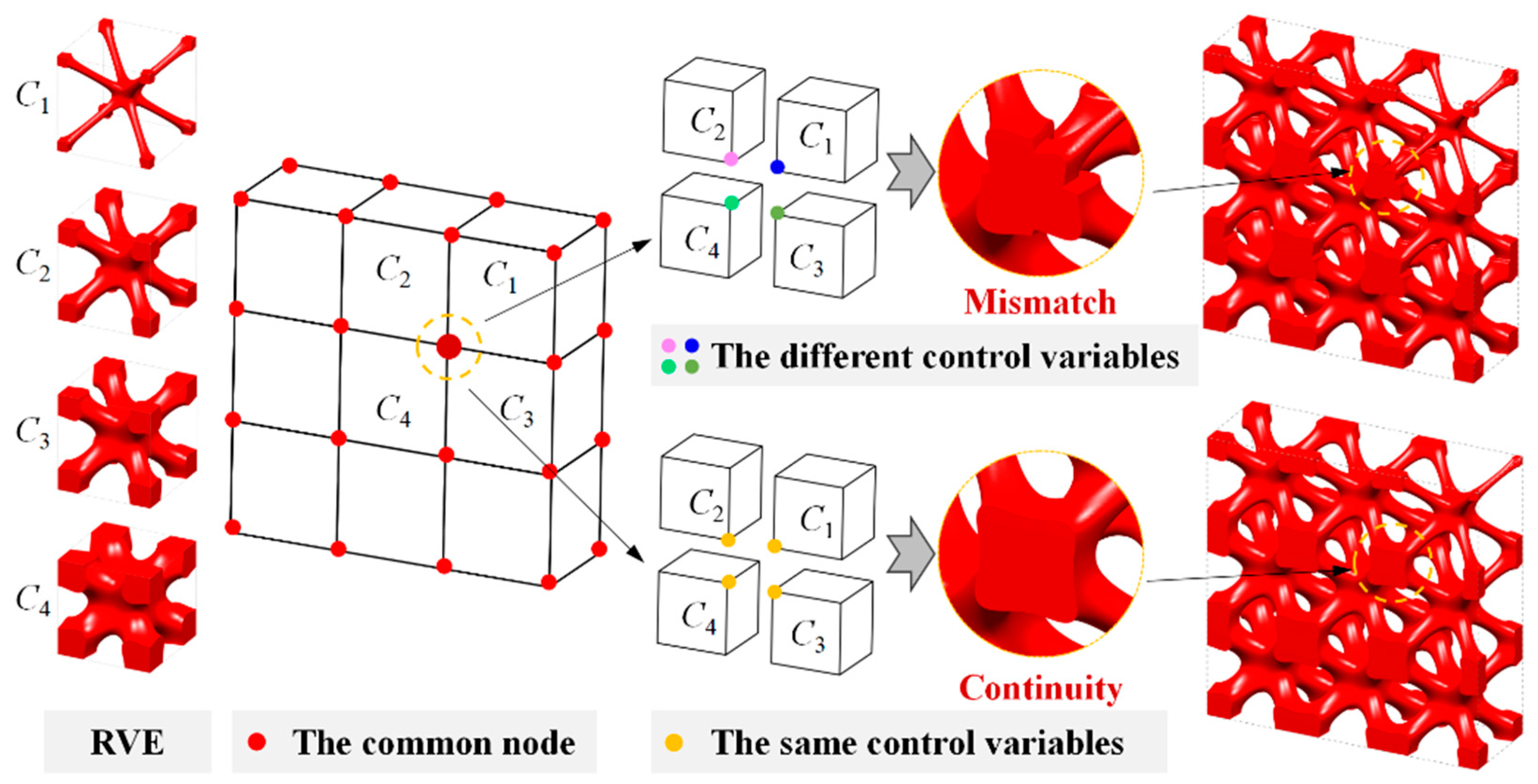
2.2. Hybrid Level Set Function
3. Topology Optimization Model and Sensitivity Analysis
3.1. Topology Optimization Model
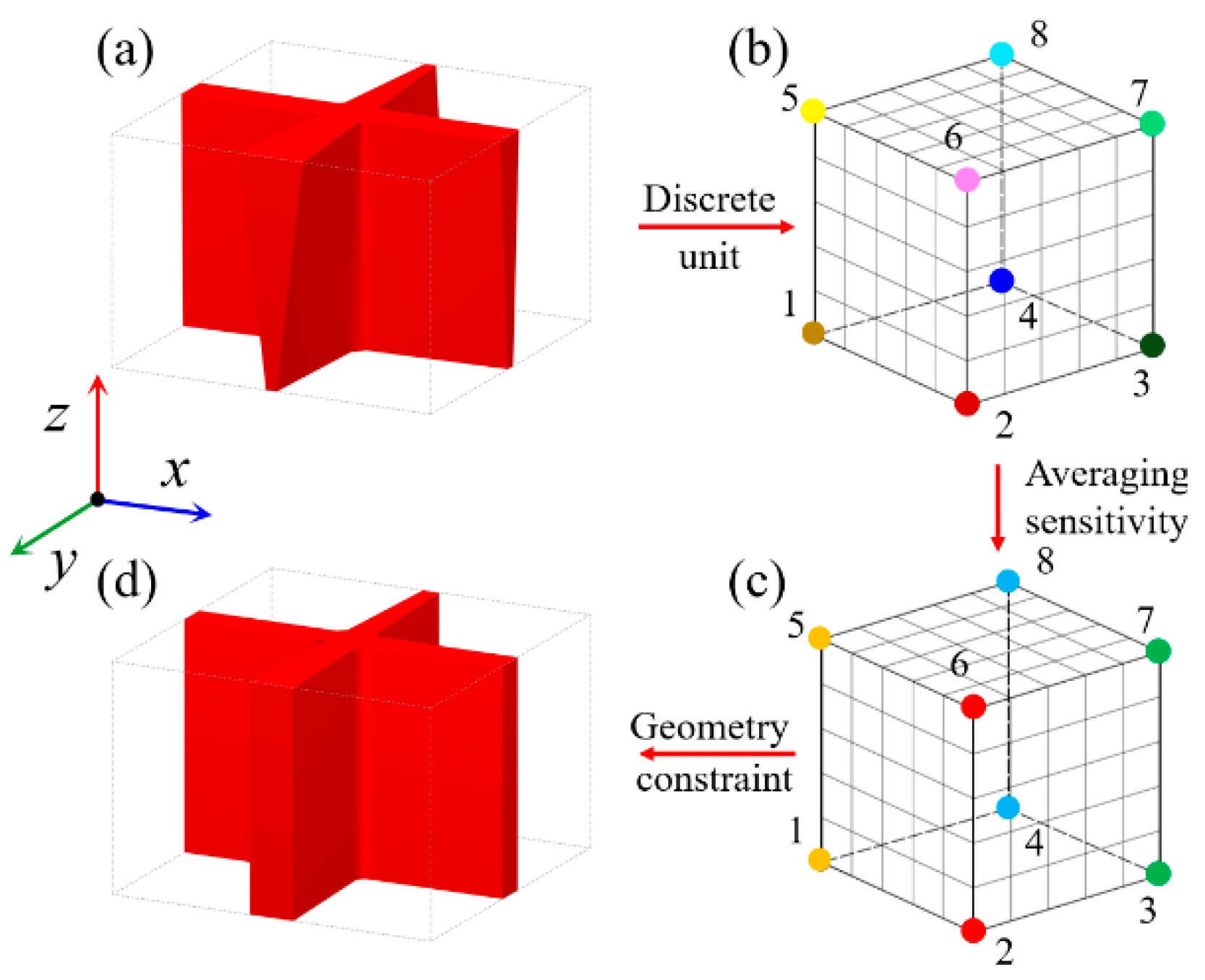
3.2. Sensitivity Analysis
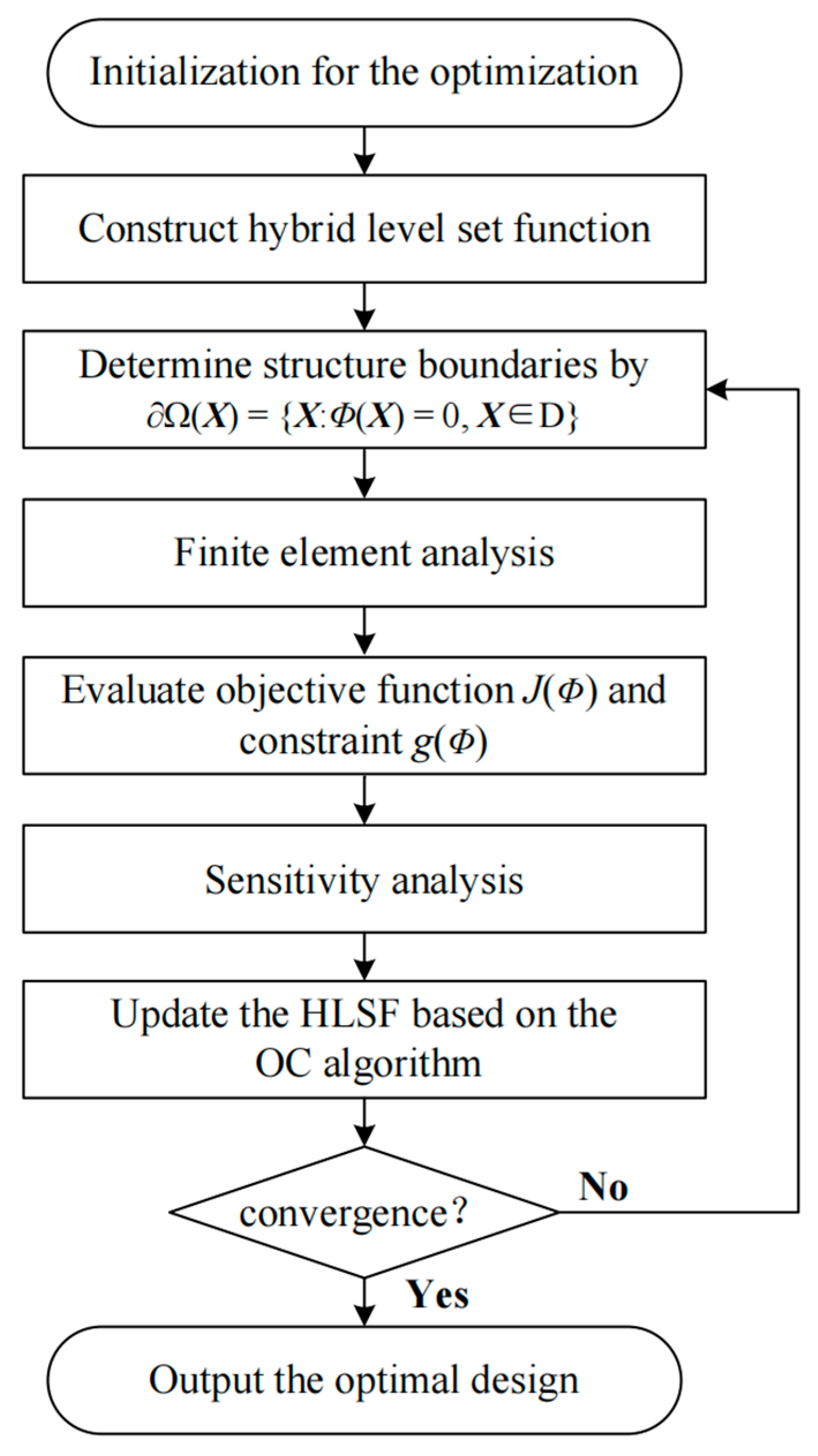
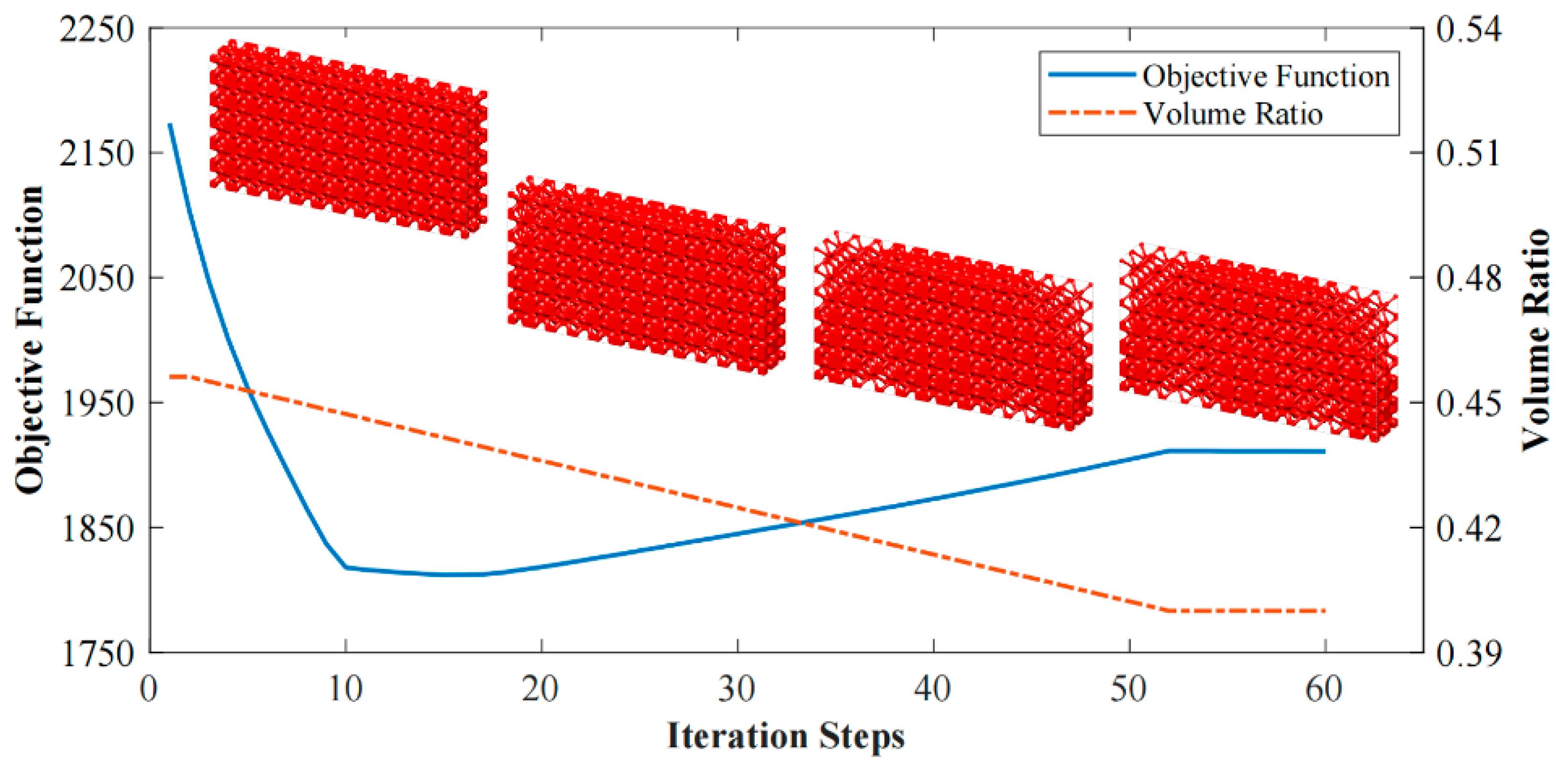
4. Numerical Implementation
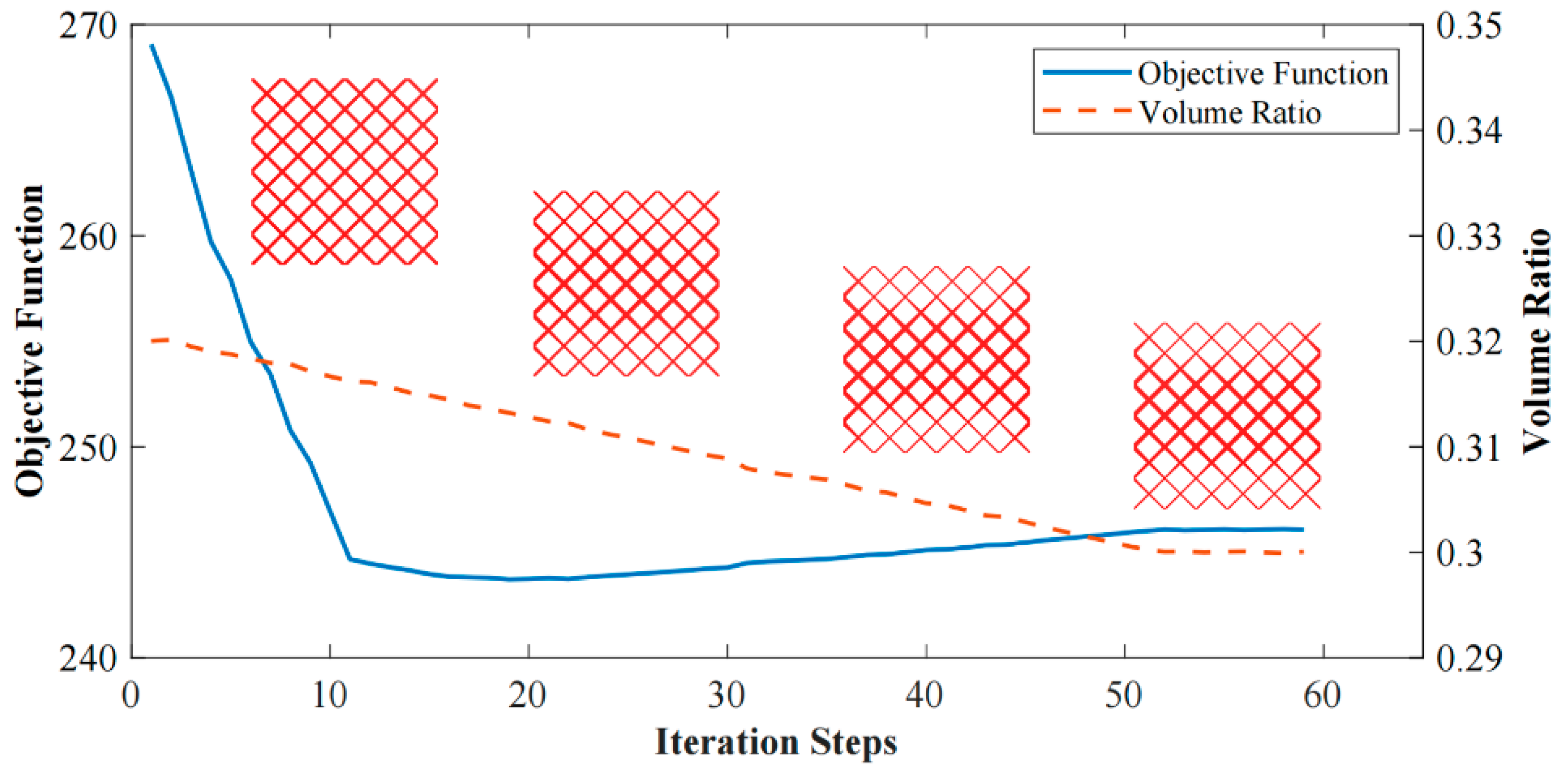
5. Numerical Examples
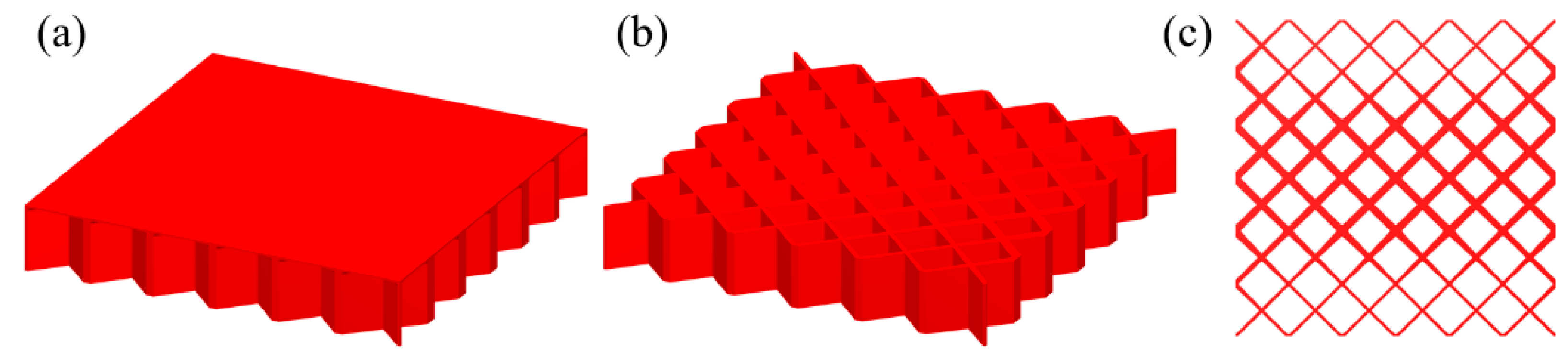
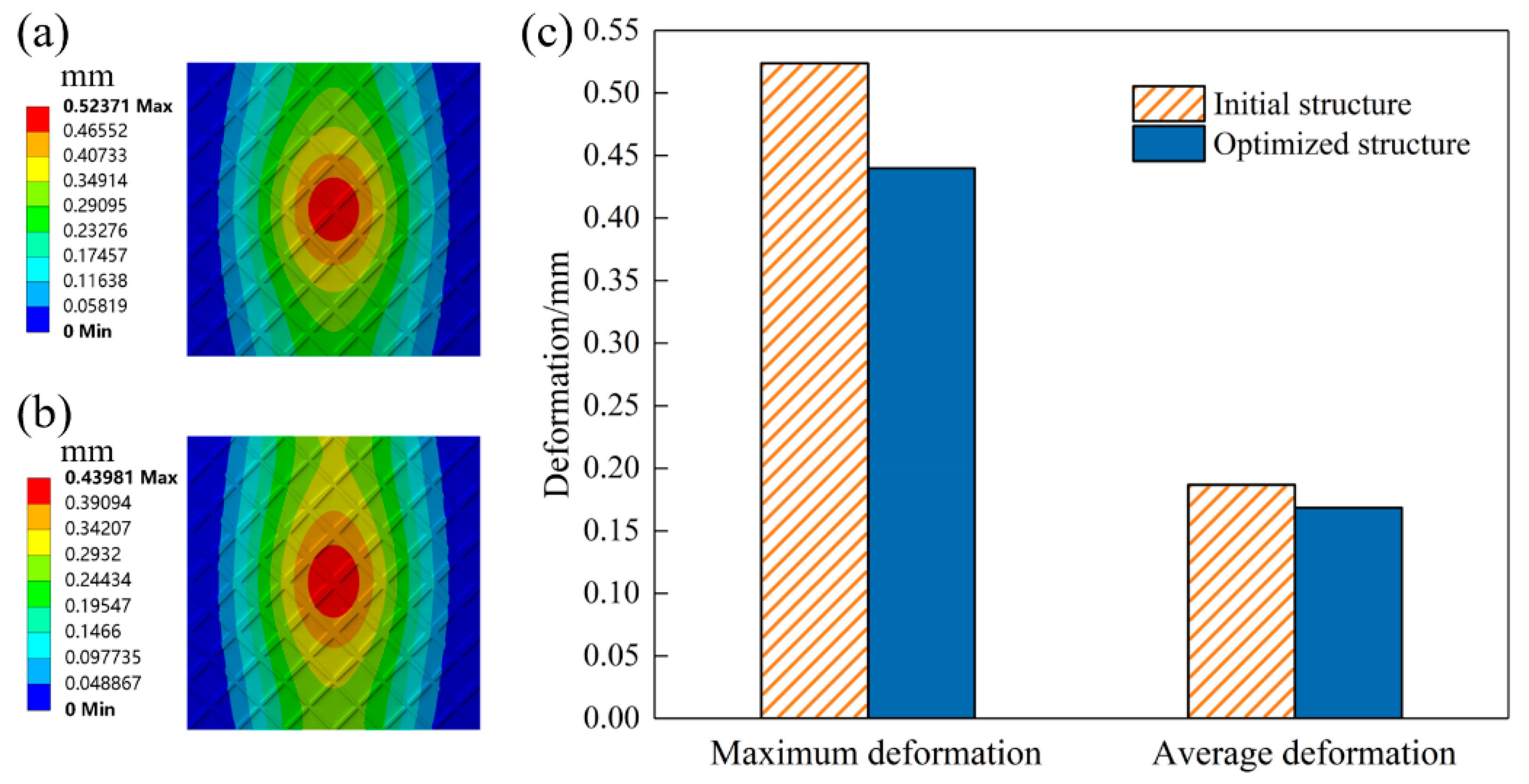
5.1. Thin-Walled Stiffened Structures
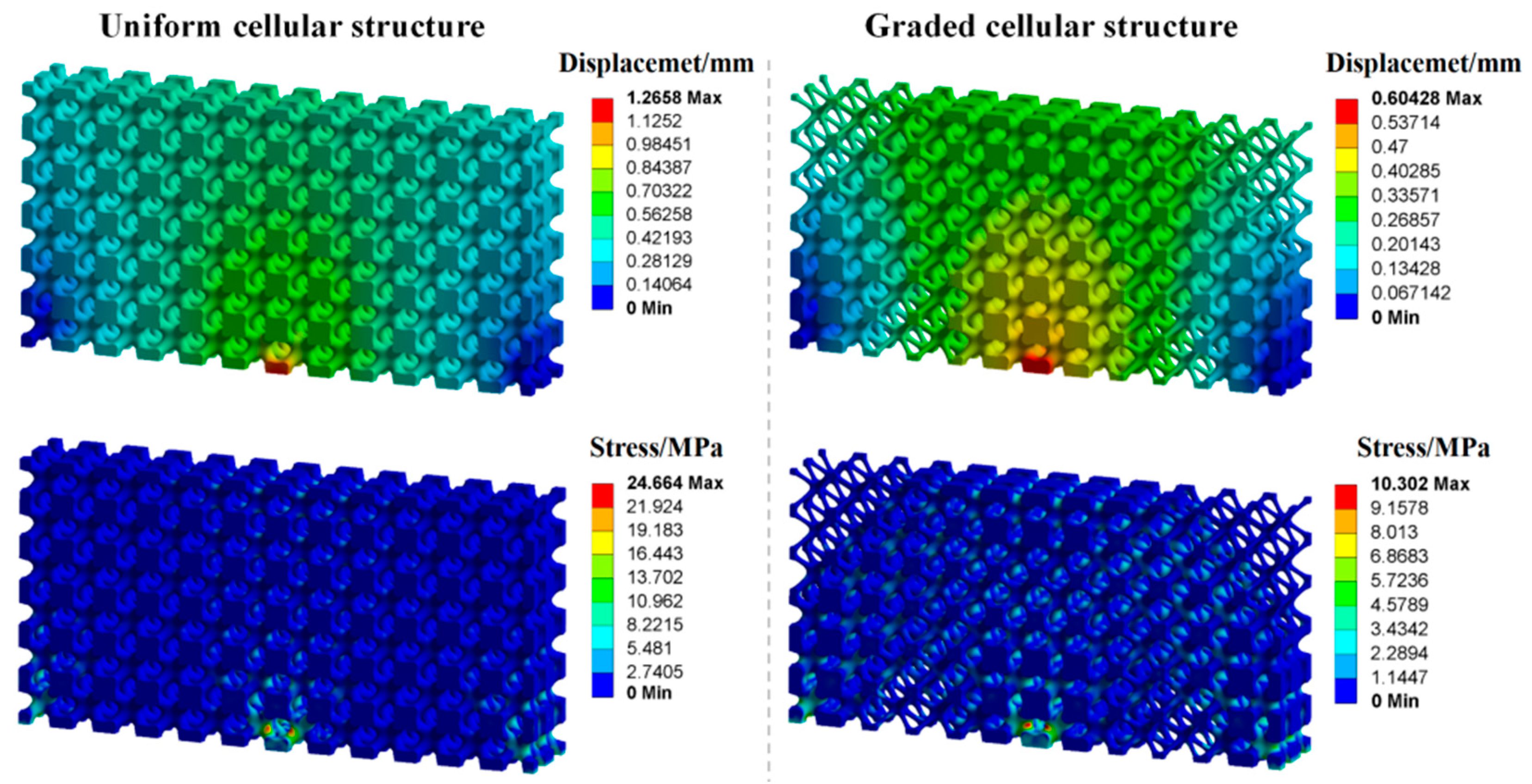
5.2. Functionally Graded Cellular Structures
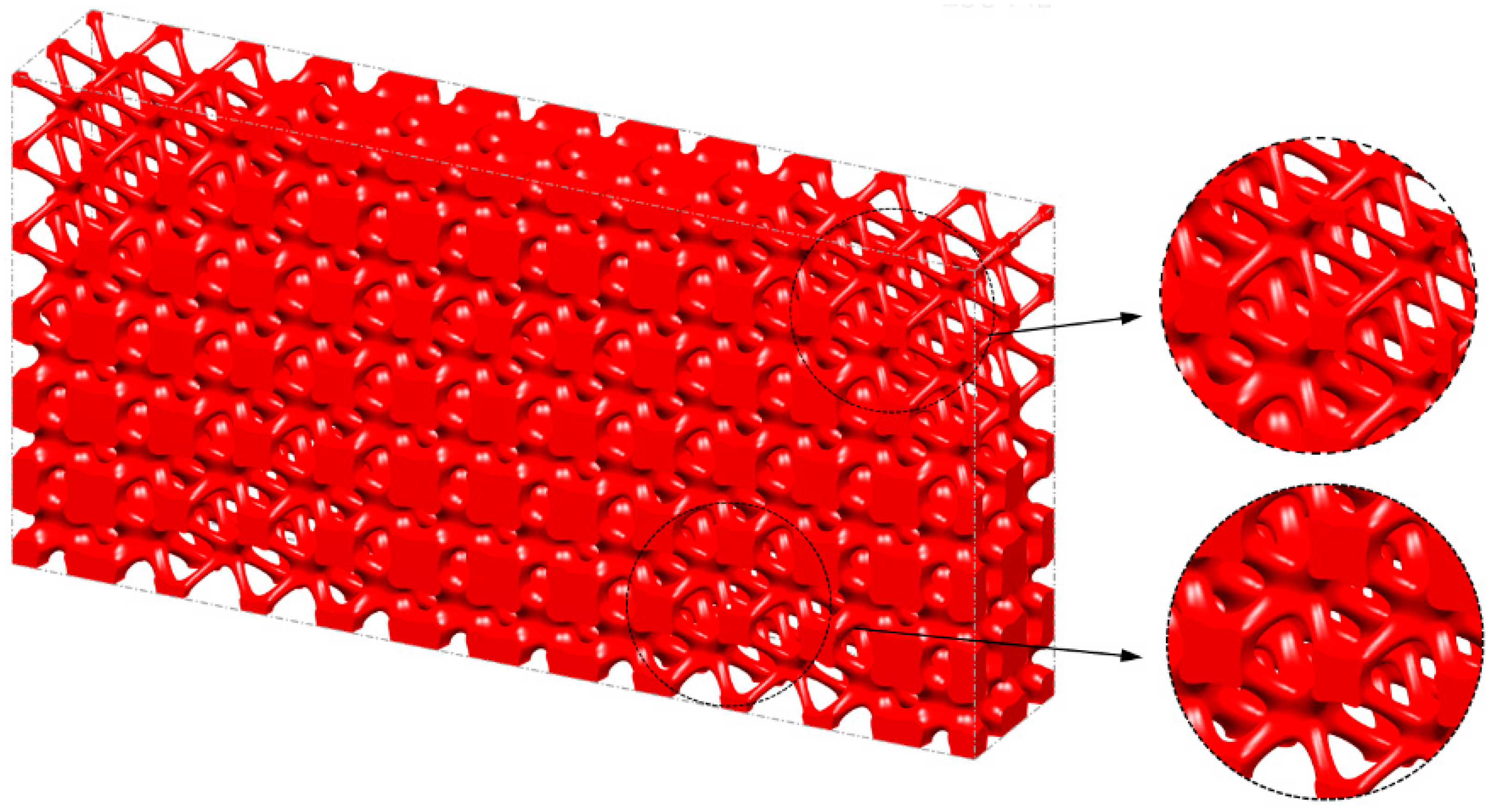
5.2.1. Graded Cellular Structure
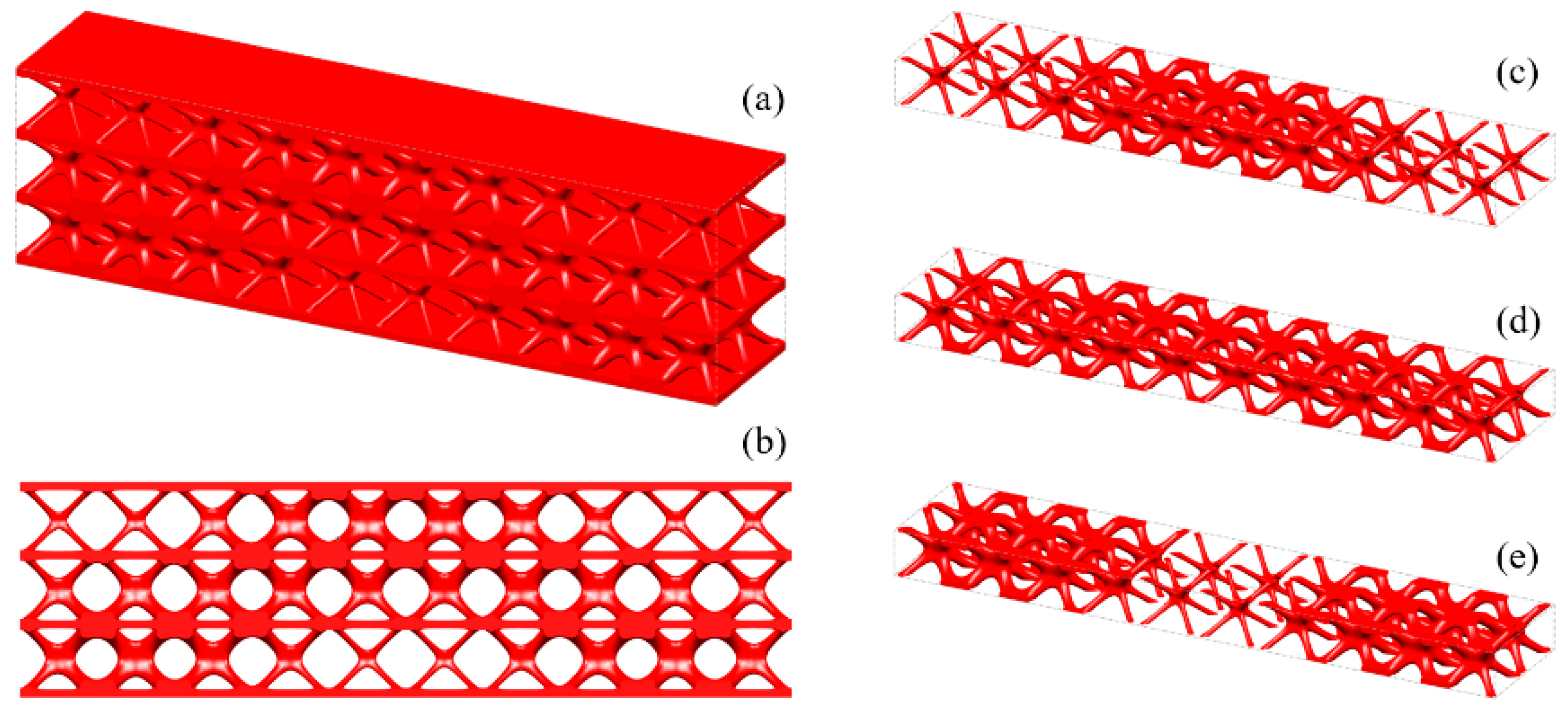
5.2.2. Lattice Sandwich Structure
6. AM and Experimental Validation
6.1. Geometric Modeling and AM Process
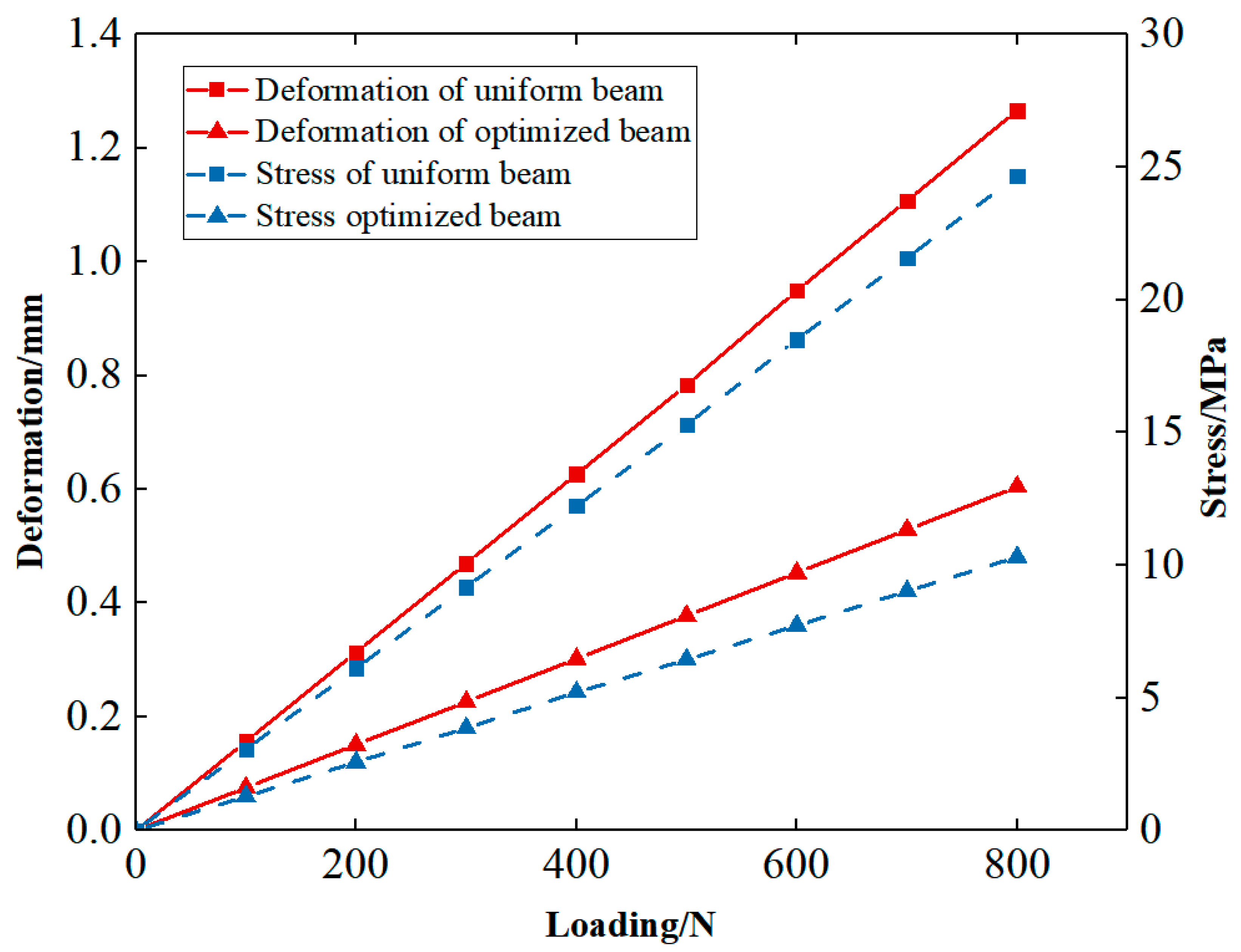
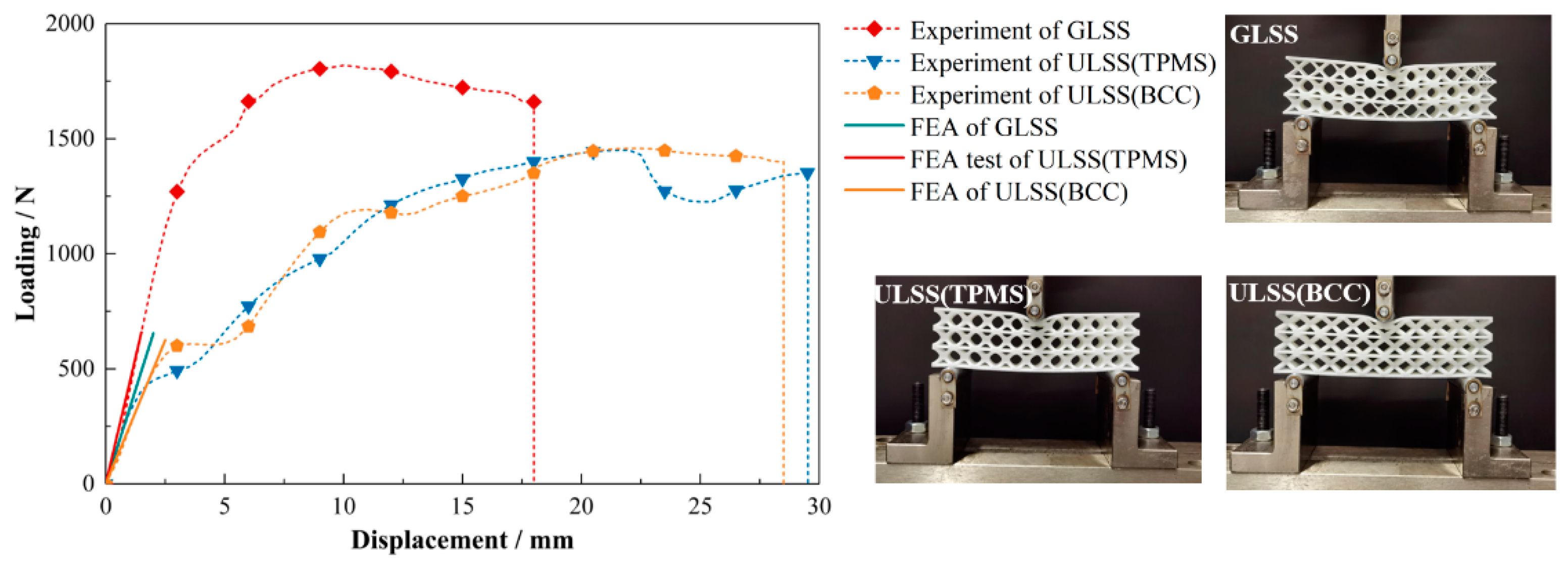
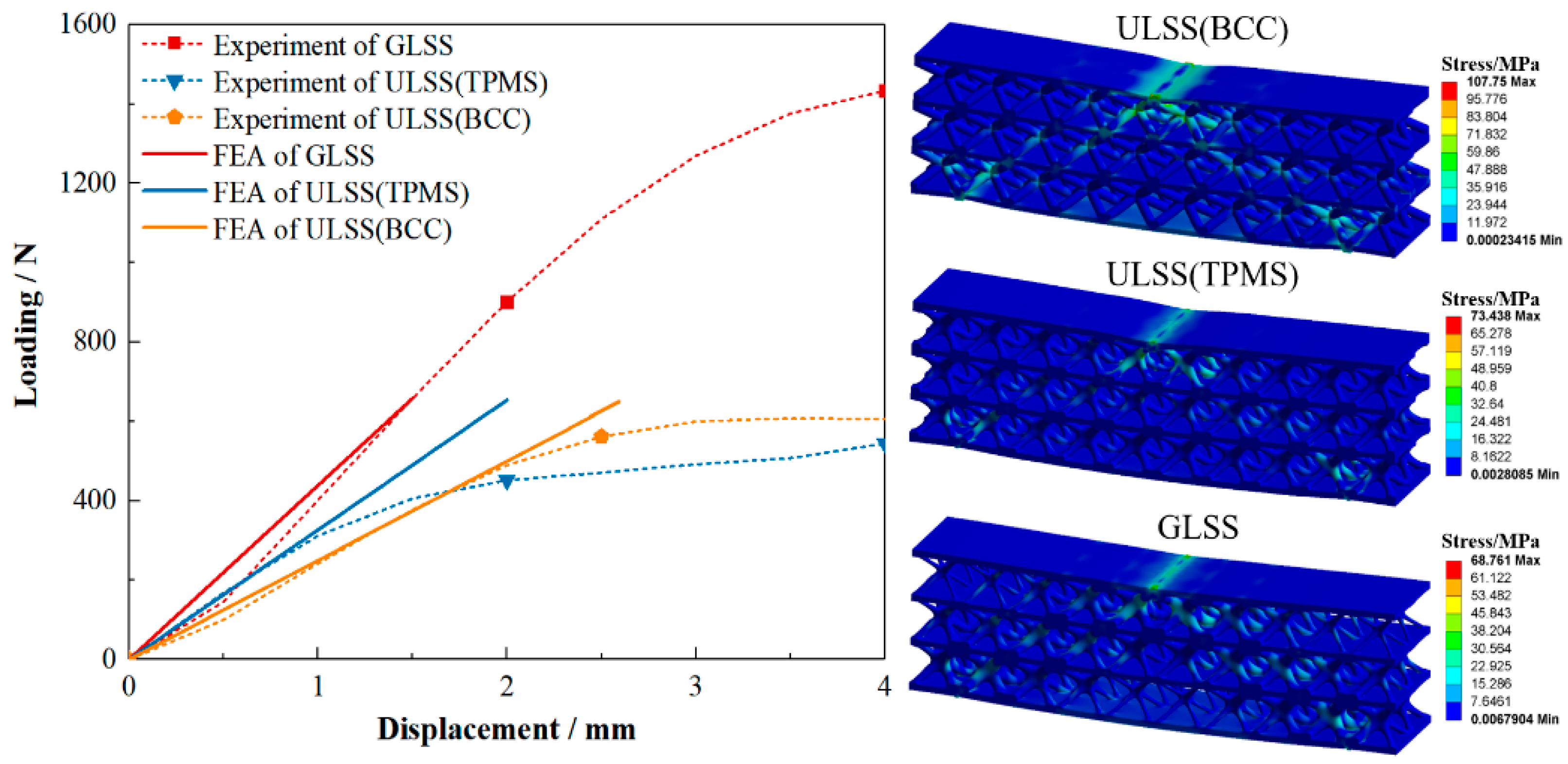
6.2. Mechanical Test
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, F.; Jiang, X.; Wang, L. Engineering lattice metamaterials for extreme property, programmability, and multifunctionality. J. Appl. Phys. 2020, 127, 150901. [Google Scholar] [CrossRef] [Green Version]
- Rahman, H.; Yarali, E.; Zolfagharian, A.; Serjouei, A.; Bodaghi, M. Energy Absorption and Mechanical Performance of Functionally Graded Soft–Hard Lattice Structures. Materials 2021, 14, 1366. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, X.; Zhang, H. A review on functionally graded structures and materials for energy absorption. Eng. Struct. 2018, 171, 309–325. [Google Scholar] [CrossRef]
- Liu, J.J.; Ou, H.H.; He, J.J.; Wen, G.G. Topological Design of a Lightweight Sandwich Aircraft Spoiler. Materials 2019, 12, 3225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jansen, M.; Pierard, O. A hybrid density/level set formulation for topology optimization of functionally graded lattice structures. Comput. Struct. 2020, 231, 106205. [Google Scholar] [CrossRef]
- Choi, Y.; Ahn, J.; Jo, C.; Chang, D. Prismatic pressure vessel with stiffened-plate structures for fuel storage in LNG-fueled ship. Ocean Eng. 2020, 196, 106829. [Google Scholar] [CrossRef]
- Wang, Y.; Arabnejad, S.; Tanzer, M.; Pasini, D. Hip Implant Design with Three-Dimensional Porous Architecture of Optimized Graded Density. J. Mech. Design 2018, 140, 111406. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Luo, Z.; Gao, L.; Qin, Q. Topology optimization for concurrent design of structures with multi-patch microstructures by level sets. Comput. Methods Appl. Mech. 2018, 331, 536–561. [Google Scholar] [CrossRef] [Green Version]
- Bendsøe, M.P.; Sigmund, O.; SpringerLink, O.S. Topology Optimization: Theory, Methods, and Applications; Springer: New York, NY, USA; Berlin, Germany, 2004. [Google Scholar]
- Liu, S.; Li, Q.; Chen, W.; Hu, R.; Tong, L. H-DGTP—A Heaviside-function based directional growth topology parameterization for design optimization of stiffener layout and height of thin-walled structures. Struct. Multidiscip. Optim. 2015, 52, 903–913. [Google Scholar] [CrossRef]
- Lam, Y.C.; Santhikumar, S. Automated rib location and optimization for plate structures. Struct. Multidiscip. Optim. 2003, 25, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Chung, J.; Lee, K. Optimal design of rib structures using the topology optimization technique. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1997, 211, 425–437. [Google Scholar] [CrossRef]
- Park, K.S.; Chang, S.Y.; Youn, S.K. Topology optimization of the primary mirror of a multi-spectral camera. Struct. Multidiscip. Optim. 2003, 25, 46–53. [Google Scholar] [CrossRef]
- Locatelli, D.; Mulani, S.B.; Kapania, R.K. Wing-Box Weight Optimization Using Curvilinear Spars and Ribs (SpaRibs). J. Aircraft 2011, 48, 1671–1684. [Google Scholar] [CrossRef]
- Ding, X.; Ji, X.; Ma, M.; Hou, J. Key techniques and applications of adaptive growth method for stiffener layout design of plates and shells. Chin. J. Mech. Eng. 2013, 26, 1138–1148. [Google Scholar] [CrossRef]
- Hu, T.; Ding, X.; Shen, L.; Zhang, H. Improved adaptive growth method of stiffeners for three-dimensional box structures with respect to natural frequencies. Comput. Struct. 2020, 239, 106330. [Google Scholar] [CrossRef]
- Wang, B.; Tian, K.; Zhou, C.; Hao, P.; Zheng, Y.; Ma, Y.; Wang, J. Grid-pattern optimization framework of novel hierarchical stiffened shells allowing for imperfection sensitivity. Aerosp. Sci. Technol. 2017, 62, 114–121. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, J.; Wu, M.; Hou, J.; Zhou, H.; Meng, L.; Li, C.; Zhang, W. Multi-scale design and optimization for solid-lattice hybrid structures and their application to aerospace vehicle components. Chinese J. Aeronaut. 2021, 34, 386–398. [Google Scholar] [CrossRef]
- Zong, H.; Liu, H.; Ma, Q.; Tian, Y.; Zhou, M.; Wang, M.Y. VCUT level set method for topology optimization of functionally graded cellular structures. Comput. Method. Appl. Mech. 2019, 354, 487–505. [Google Scholar] [CrossRef]
- Mahmoud, D.; Elbestawi, M. Lattice Structures and Functionally Graded Materials Applications in Additive Manufacturing of Orthopedic Implants: A Review. J. Manuf. Mater. Processing 2017, 1, 13. [Google Scholar] [CrossRef]
- Wadley, H.N. Multifunctional periodic cellular metals. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 31–68. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Gu, X.; Zhu, J.; Zhou, H.; Li, S.; Zhang, W. Concurrent design of hierarchical structures with three-dimensional parameterized lattice microstructures for additive manufacturing. Struct. Multidiscip. Optim. 2020, 61, 869–894. [Google Scholar] [CrossRef]
- Li, D.; Dai, N.; Tang, Y.; Dong, G.; Zhao, Y.F. Design and Optimization of Graded Cellular Structures with Triply Periodic Level Surface-Based Topological Shapes. J. Mech. Design 2019, 141, 071402. [Google Scholar] [CrossRef] [Green Version]
- Strek, T.; Jopek, H.; Maruszewski, B.T.; Nienartowicz, M. Computational analysis of sandwich-structured composites with an auxetic phase. Phys. Status Solidi 2014, 251, 354–366. [Google Scholar] [CrossRef]
- Li, H.; Luo, Z.; Gao, L.; Walker, P. Topology optimization for functionally graded cellular composites with metamaterials by level sets. Comput. Method. Appl. Mech. 2018, 328, 340–364. [Google Scholar] [CrossRef] [Green Version]
- Xiao, M.; Liu, X.; Zhang, Y.; Gao, L.; Gao, J.; Chu, S. Design of graded lattice sandwich structures by multiscale topology optimization. Comput. Method. Appl. Mech. 2021, 384, 113949. [Google Scholar] [CrossRef]
- Radman, A.; Huang, X.; Xie, Y.M. Topology optimization of functionally graded cellular materials. J. Mater. Sci. 2013, 48, 1503–1510. [Google Scholar] [CrossRef]
- Xia, L.; Breitkopf, P. Concurrent topology optimization design of material and structure within FE2 nonlinear multiscale analysis framework. Comput. Method. Appl. Mech. 2014, 278, 524–542. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. Optimal design of periodic structures using evolutionary topology optimization. Struct. Multidiscip. Optim. 2008, 36, 597–606. [Google Scholar] [CrossRef]
- Rodrigues, H.; Guedes, J.M.; Bendsoe, M.P. Hierarchical optimization of material and structure. Struct. Multidiscip. Optim. 2002, 24, 1–10. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Method. Appl. Mech. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, S. Scale-related topology optimization of cellular materials and structures. Int. J. Numer. Meth. Eng. 2006, 68, 993–1011. [Google Scholar] [CrossRef]
- Wu, J.; Wang, W.; Gao, X. Design and Optimization of Conforming Lattice Structures. IEEE Trans. Vis. Comput. Graph. 2021, 27, 43–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef] [Green Version]
- van Dijk, N.P.; Maute, K.; Langelaar, M.; van Keulen, F. Level-set methods for structural topology optimization: A review. Struct. Multidiscip. Optim. 2013, 48, 437–472. [Google Scholar] [CrossRef]
- Han, L.; Che, S. An Overview of Materials with Triply Periodic Minimal Surfaces and Related Geometry: From Biological Structures to Self-Assembled Systems. Adv. Mater. 2018, 30, 1705708. [Google Scholar] [CrossRef]
- Feng, J.; Fu, J.; Yao, X.; He, Y. Triply periodic minimal surface (TPMS) porous structures: From multi-scale design, precise additive manufacturing to multidisciplinary applications. Int. J. Extrem. Manuf. 2022, 4, 022001. [Google Scholar] [CrossRef]
- Yamasaki, S.; Nomura, T.; Kawamoto, A.; Sato, K.; Izui, K.; Nishiwaki, S. A level set based topology optimization method using the discretized signed distance function as the design variables. Struct. Multidiscip. Optim. 2010, 41, 685–698. [Google Scholar] [CrossRef]
- Liu, H.; Zong, H.; Shi, T.; Xia, Q. M-VCUT level set method for optimizing cellular structures. Comput. Method. Appl. Mech. 2020, 367, 113154. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization. Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Allaire, G.; Jouve, F.; Toader, A. Structural optimization using sensitivity analysis and a level-set method. J. Comput. Phys. 2004, 194, 363–393. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.; Rozvany, G.I.N. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization. Comput. Method. Appl. Mech. 1991, 89, 309–336. [Google Scholar] [CrossRef]
- Vogiatzis, P.; Chen, S.; Wang, X.; Li, T.; Wang, L. Topology optimization of multi-material negative Poisson’s ratio metamaterials using a reconciled level set method. Comput. Aided Design 2017, 83, 15–32. [Google Scholar] [CrossRef] [Green Version]
- Fu, J.; Li, H.; Gao, L.; Xiao, M. Design of shell-infill structures by a multiscale level set topology optimization method. Comput. Struct. 2019, 212, 162–172. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Model Size | Material Properties | Loading | ||||
|---|---|---|---|---|---|---|
| W | L | H1 | H2 | Elastic Modulus | Poisson Ratio | Concentrated Load |
| 180 mm | 180 mm | 2 mm | 5 mm | 2 × 105 MPa | 0.3 | 1000 N |
| Pre-Defined Unit Cells | Topological Configuration | Uniform Structure | Optimized TWSS |
|---|---|---|---|
 |  | 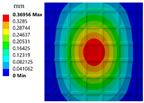 |  |
| Volume fractions: 0.15, 0.4 | μ = 0.3, J = 229 | MD: 0.37 mm AD: 0.12 mm | MD: 0.31 mm AD: 0.09 mm |
 |  |  | 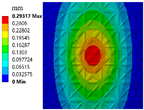 |
| Volume fractions: 0.4, 0.5 | μ = 0.45, J = 215 | MD: 0.32 mm AD: 0.11 mm | MD: 0.29 mm AD: 0.09 mm |
| Pre-Defined Unit Cells | 3D Michell Beams | 3D Cantilever Beams |
|---|---|---|
 |  |  |
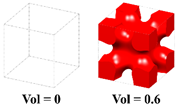 |  |  |
 |  | 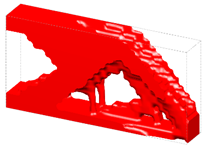 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, J.; Shu, Z.; Gao, L.; Zhou, X. A Hybrid Level Set Method for the Topology Optimization of Functionally Graded Structures. Materials 2022, 15, 4483. https://doi.org/10.3390/ma15134483
Fu J, Shu Z, Gao L, Zhou X. A Hybrid Level Set Method for the Topology Optimization of Functionally Graded Structures. Materials. 2022; 15(13):4483. https://doi.org/10.3390/ma15134483
Chicago/Turabian StyleFu, Junjian, Zhengtao Shu, Liang Gao, and Xiangman Zhou. 2022. "A Hybrid Level Set Method for the Topology Optimization of Functionally Graded Structures" Materials 15, no. 13: 4483. https://doi.org/10.3390/ma15134483
APA StyleFu, J., Shu, Z., Gao, L., & Zhou, X. (2022). A Hybrid Level Set Method for the Topology Optimization of Functionally Graded Structures. Materials, 15(13), 4483. https://doi.org/10.3390/ma15134483






