Random Material Property Fields of 3D Concrete Microstructures Based on CT Image Reconstruction
Abstract
1. Introduction
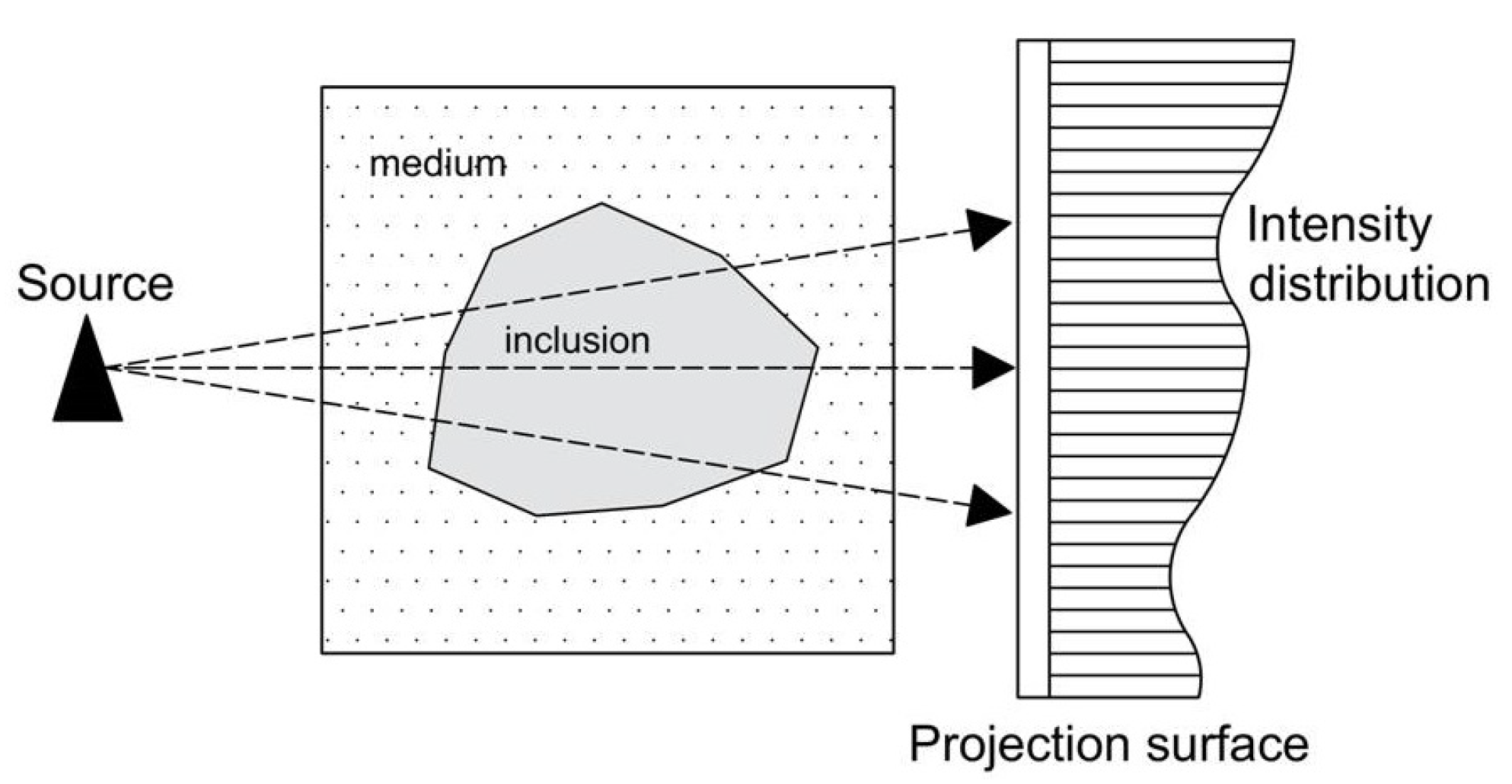
2. Reconstruction of Concrete Microstructure Based on CT Images
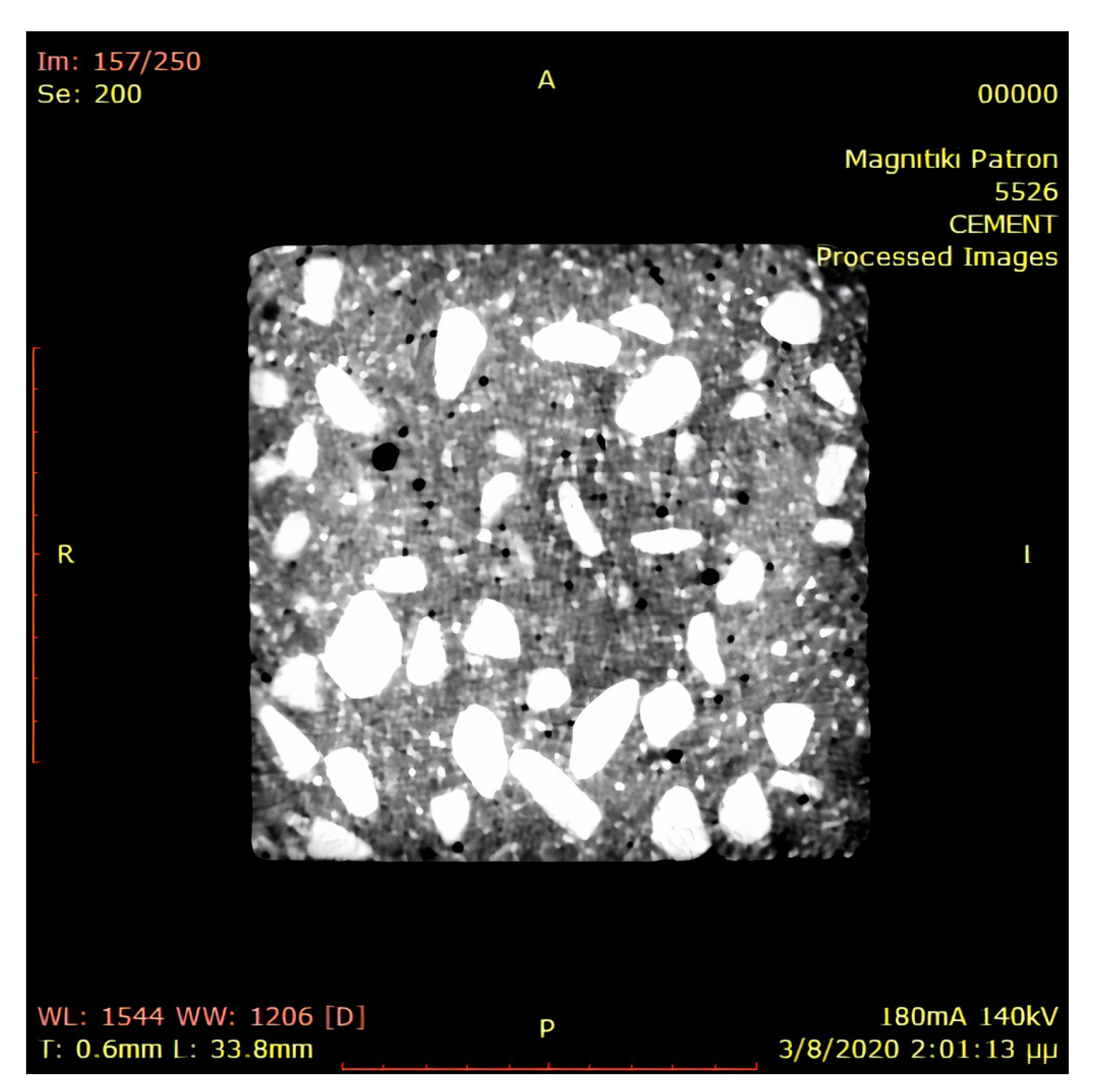
2.1. CT Images
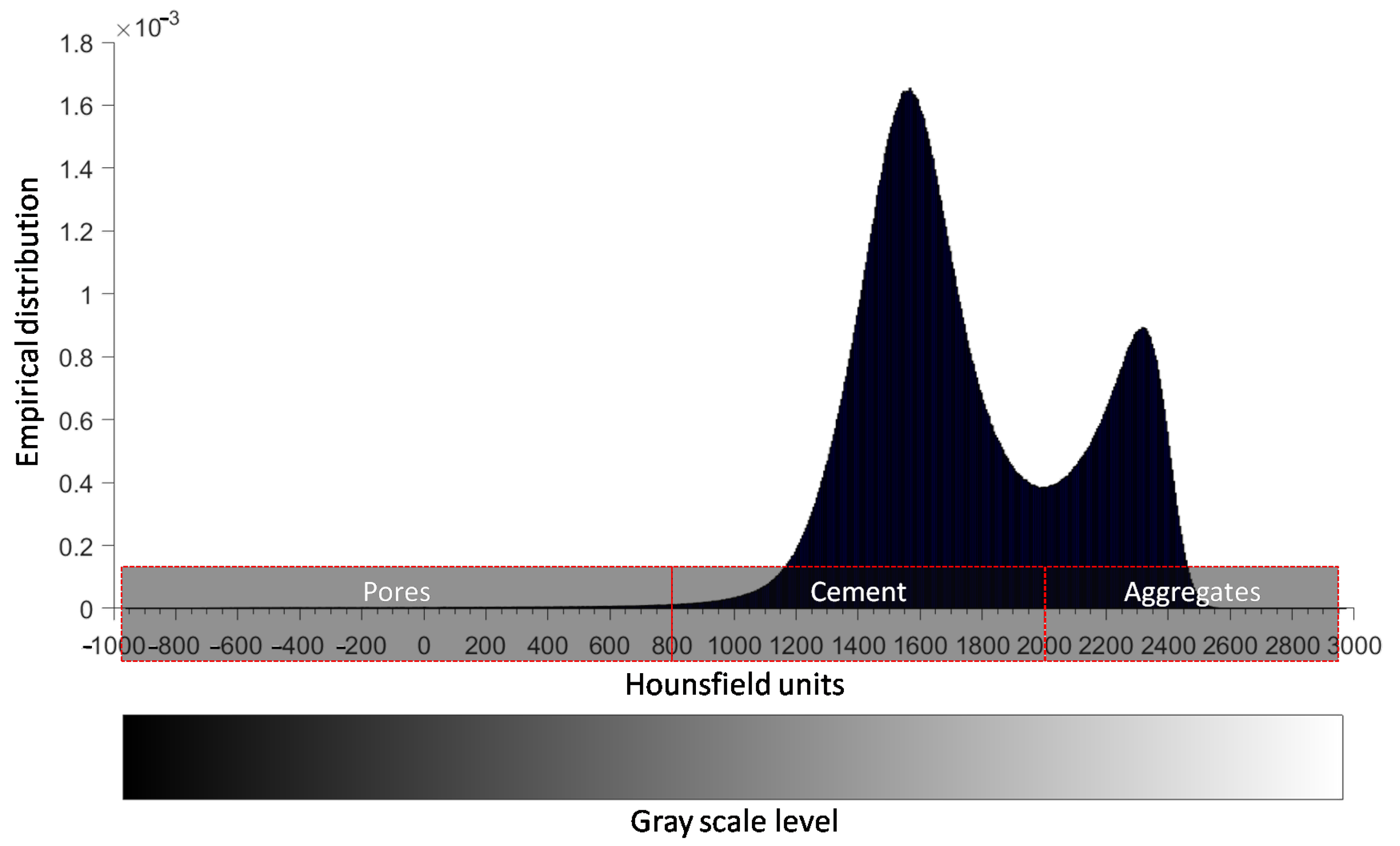
2.2. Reconstruction of Concrete Microstructure
3. Computational Homogenization
Computation of the Random Apparent Elasticity Tensor of 3D Concrete Microstructures
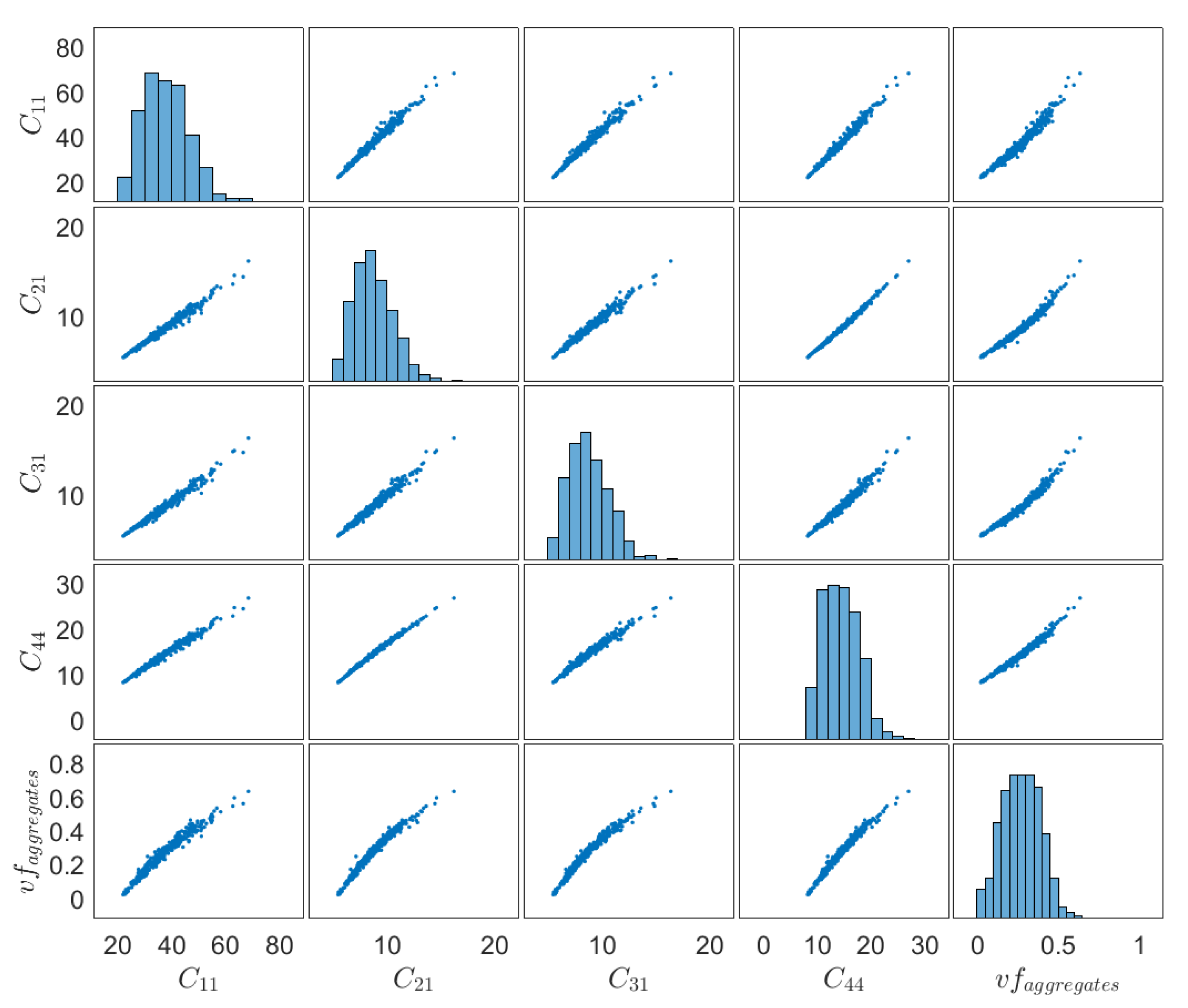
4. Numerical Results and Discussion
5. Conclusions
- In this paper, the random spatially varying apparent elasticity tensor of 3D concrete microstructures has been computed using CT images of a cubic specimen for the reconstruction of concrete microstructure and computational homogenization.
- A complete probabilistic description of the spatial variation of the elastic properties of concrete has been achieved through computation of the respective mesoscale random fields. In this way, it was possible to assess the effect of randomness in microstructure on the mechanical behavior of concrete based on the statistical characteristics (empirical distribution and correlation functions) of the random fields.
- A moderate to large variability of the local volume fraction of the constituents (pores, cement paste and aggregates) has been observed depending on the scale factor considered.
- This was reflected on the moderate to high COV of the apparent axial and shear stiffness, meaning that microstructural uncertainty can lead to substantial random spatial variation of the mechanical properties of concrete.
- The computed random material property fields can be used for the stochastic FE analysis of concrete structures.
- The consideration of the interfacial transition zone (ITZ) between cement paste and aggregates and the determination of random fracture properties could constitute the subject of future research.
Author Contributions
Funding

Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Material spatial randomness: From statistical to representative volume element. Probabilistic Eng. Mech. 2006, 21, 112–132. [Google Scholar] [CrossRef]
- Savvas, D.; Stefanou, G.; Papadrakakis, M. Determination of RVE size for random composites with local volume fraction variation. Comput. Methods Appl. Mech. Eng. 2016, 305, 340–358. [Google Scholar] [CrossRef]
- Savvas, D.; Stefanou, G. Determination of random material properties of graphene sheets with different types of defects. Compos. Part B Eng. 2018, 143, 47–54. [Google Scholar] [CrossRef]
- Liu, T.; Qin, S.; Zou, D.; Song, W.; Teng, J. Mesoscopic modeling method of concrete based on statistical analysis of CT images. Constr. Build. Mater. 2018, 192, 429–441. [Google Scholar] [CrossRef]
- Chung, S.Y.; Kim, J.S.; Stephan, D.; Han, T.S. Overview of the use of micro-computed tomography (micro-CT) to investigate the relation between the material characteristics and properties of cement-based materials. Constr. Build. Mater. 2019, 229, 116843. [Google Scholar] [CrossRef]
- Grigoriu, M.; Garboczi, E.; Kafali, C. Spherical harmonic-based random fields for aggregates used in concrete. Powder Technol. 2006, 166, 123–138. [Google Scholar] [CrossRef]
- Huang, J.; Peng, Q. A fast algorithm for multifield representation and multiscale simulation of high-quality 3D stochastic aggregate microstructures by concurrent coupling of stationary Gaussian and fractional Brownian random fields. Int. J. Numer. Methods Eng. 2018, 115, 328–357. [Google Scholar] [CrossRef]
- Constantinides, G.; Ulm, F.J. The effect of two types of CSH on the elasticity of cement-based materials: Results from nanoindentation and micromechanical modeling. Cem. Concr. Res. 2004, 34, 67–80. [Google Scholar] [CrossRef]
- Wriggers, P.; Moftah, S. Mesoscale models for concrete: Homogenisation and damage behaviour. Finite Elem. Anal. Des. 2006, 42, 623–636. [Google Scholar] [CrossRef]
- Huang, Y.; Yan, D.; Yang, Z.; Liu, G. 2D and 3D homogenization and fracture analysis of concrete based on in-situ X-ray Computed Tomography images and Monte Carlo simulations. Eng. Fract. Mech. 2016, 163, 37–54. [Google Scholar] [CrossRef]
- Tal, D.; Fish, J. Stochastic multiscale modeling and simulation framework for concrete. Cem. Concr. Compos. 2018, 90, 61–81. [Google Scholar] [CrossRef]
- Dubey, V.; Noshadravan, A. A probabilistic upscaling of microstructural randomness in modeling mesoscale elastic properties of concrete. Comput. Struct. 2020, 237, 106272. [Google Scholar] [CrossRef]
- Herman, G.T. Fundamentals of Computerized Tomography: Image Reconstruction from Projections; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Daigle, M.; Fratta, D.; Wang, L. Ultrasonic and X-ray tomographic imaging of highly contrasting inclusions in concrete specimens. Site Charact. Model. 2005, GSP 138, 1–12. [Google Scholar]
- Balázs, G.L.; Lublóy, É.; Földes, T. Evaluation of concrete elements with X-ray computed tomography. J. Mater. Civ. Eng. 2018, 30, 06018010. [Google Scholar] [CrossRef]
- Baxter, S.; Hossain, M.I.; Graham, L. Micromechanics based random material property fields for particulate reinforced composites. Int. J. Solids Struct. 2001, 38, 9209–9220. [Google Scholar] [CrossRef]
- Magnitiki Patron S.A. Available online: https://www.magnitikipatron.com (accessed on 15 February 2021).
- RadiAnt DICOM Viewer. Available online: https://www.radiantviewer.com (accessed on 15 February 2021).
- Hashin, Z. Analysis of composite materials: A survey. J. Appl. Mech. 1983, 50, 481–505. [Google Scholar] [CrossRef]
- Chwał, M.; Muc, A. Design of reinforcement in nano-and microcomposites. Materials 2019, 12, 1474. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Zeman, J.; Sejnoha, M. From random microstructures to representative volume elements. Model. Simul. Mater. Sci. Eng. 2007, 15, 325–335. [Google Scholar] [CrossRef]
- Zohdi, T.I.; Wriggers, P. An Introduction to Computational Micromechanics, 2nd ed.; Lecture Notes in Applied and Computational Mechanics; Springer: Heidelberg, Germany, 2008; Volume 20. [Google Scholar]
- Wimmer, J.; Stier, B.; Simon, J.W.; Reese, S. Computational homogenisation from a 3D finite element model of asphalt concrete–linear elastic computations. Finite Elem. Anal. Des. 2016, 110, 43–57. [Google Scholar] [CrossRef]
- Savvas, D.; Stefanou, G.; Papadopoulos, V.; Papadrakakis, M. Effect of waviness and orientation of carbon nanotubes on random apparent material properties and RVE size of CNT reinforced composites. Compos. Struct. 2016, 152, 870–882. [Google Scholar] [CrossRef]
- Reccia, E.; De Bellis, M.L.; Trovalusci, P.; Masiani, R. Sensitivity to material contrast in homogenization of random particle composites as micropolar continua. Compos. Part Eng. 2018, 136, 39–45. [Google Scholar] [CrossRef]
- Hazanov, S.; Huet, C. Order relationships for boundary conditions effect in heterogeneous bodies smaller than the representative volume. J. Mech. Phys. Solids 1994, 42, 1995–2011. [Google Scholar] [CrossRef]
- Miehe, C.; Koch, A. Computational micro-to-macro transitions of discretized microstructures undergoing small strains. Arch. Appl. Mech. 2002, 72, 300–317. [Google Scholar] [CrossRef]
- Stefanou, G. The stochastic finite element method: Past, present and future. Comput. Methods Appl. Mech. Eng. 2009, 198, 1031–1051. [Google Scholar] [CrossRef]
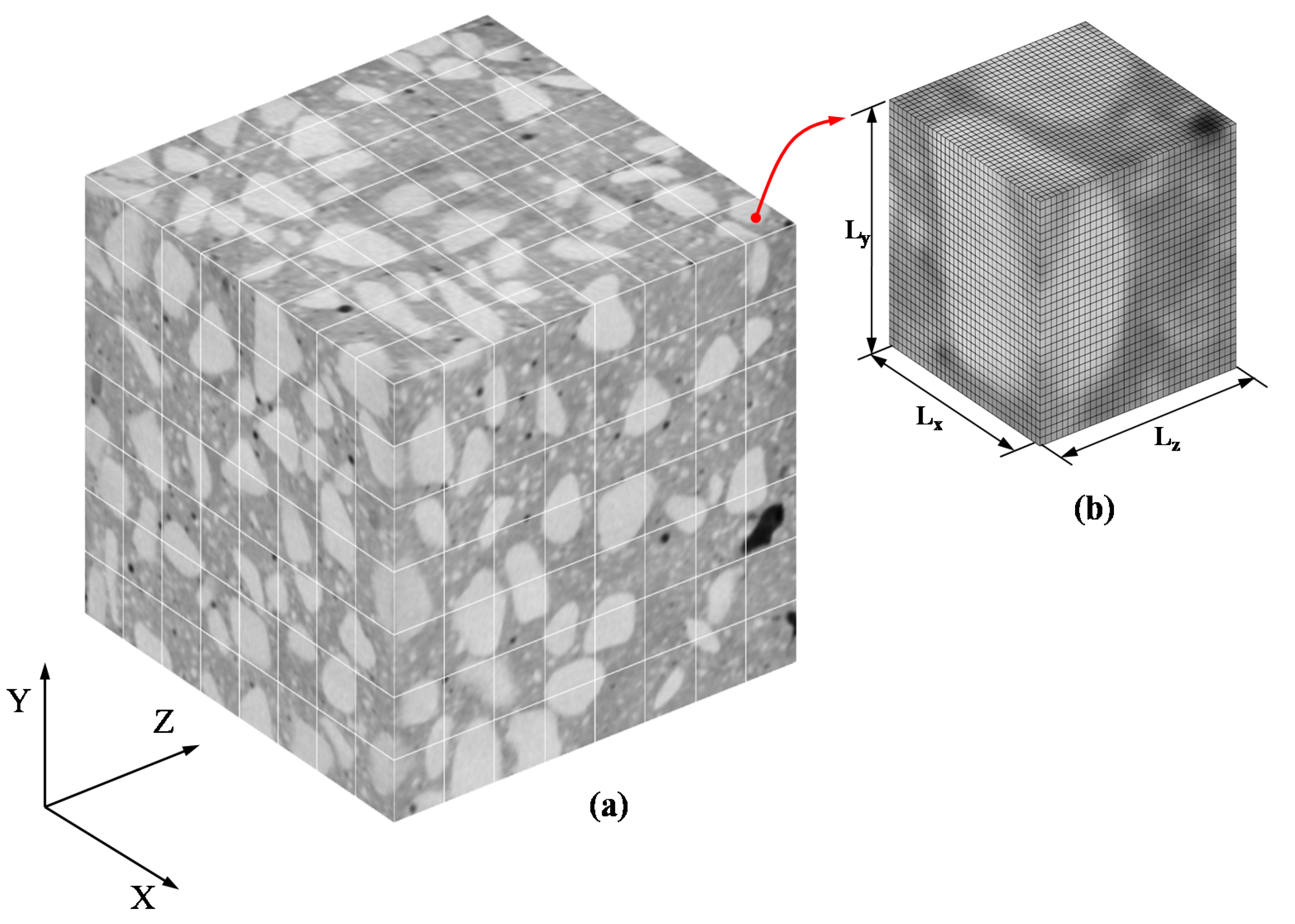
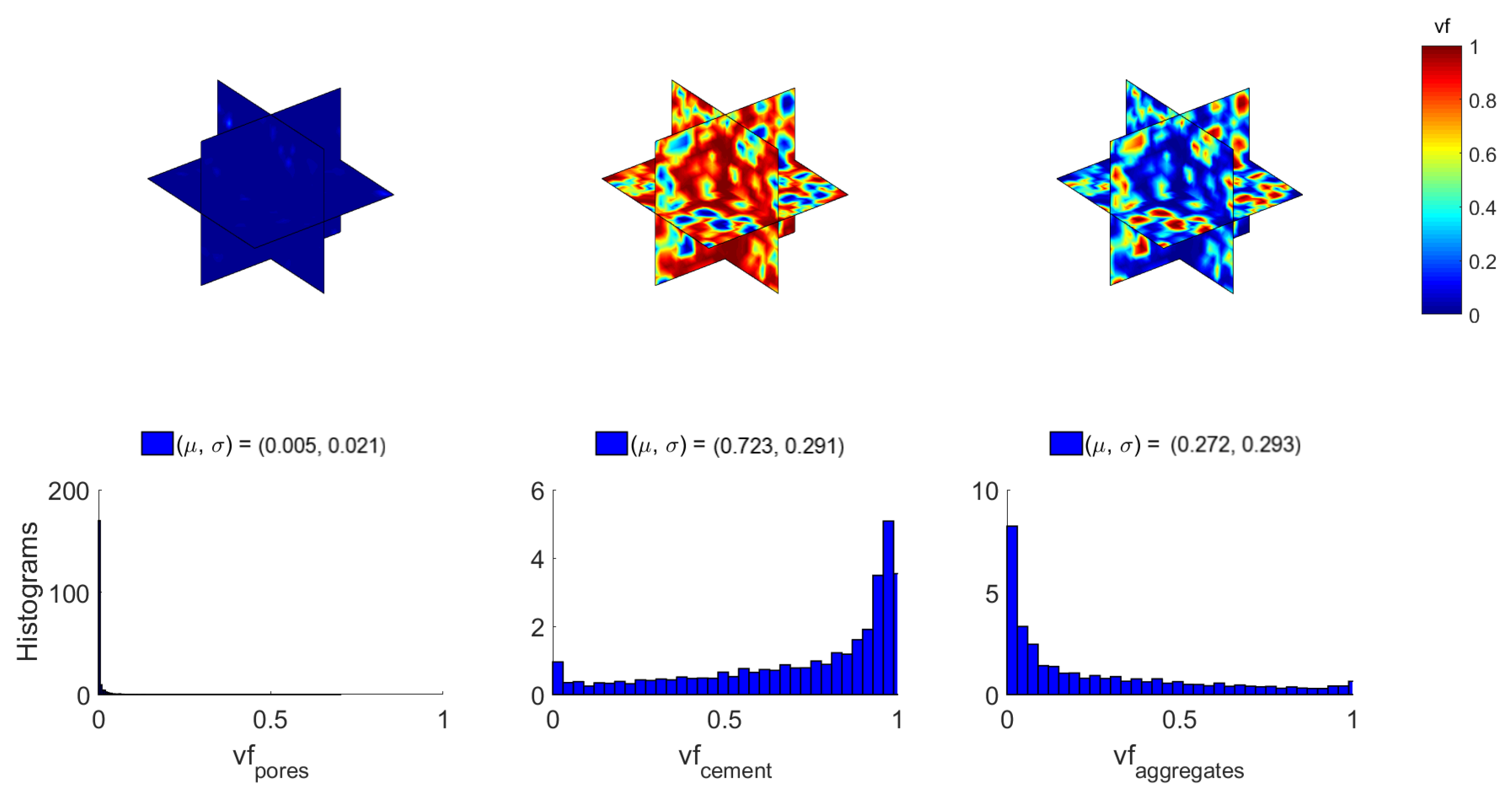
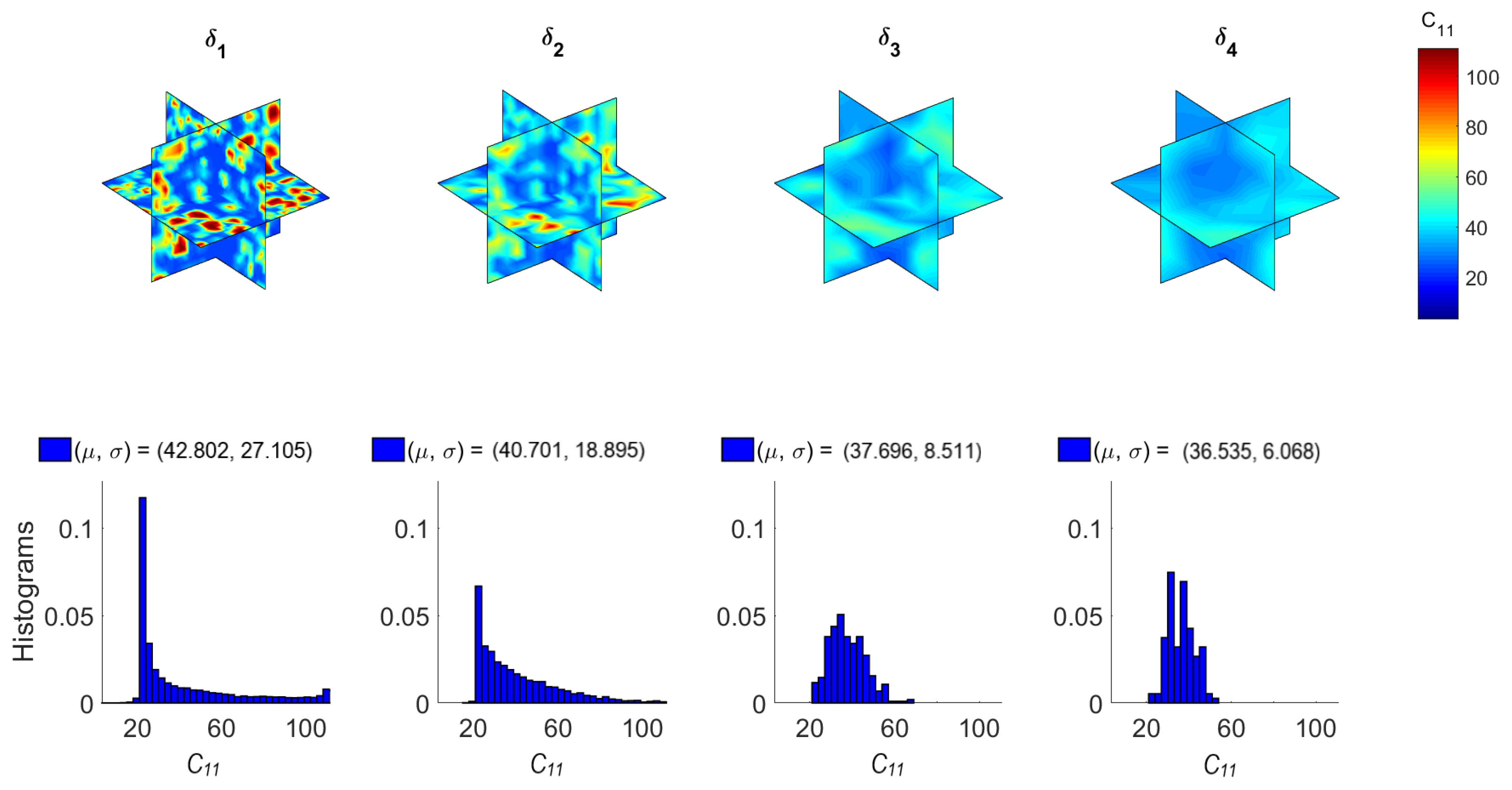


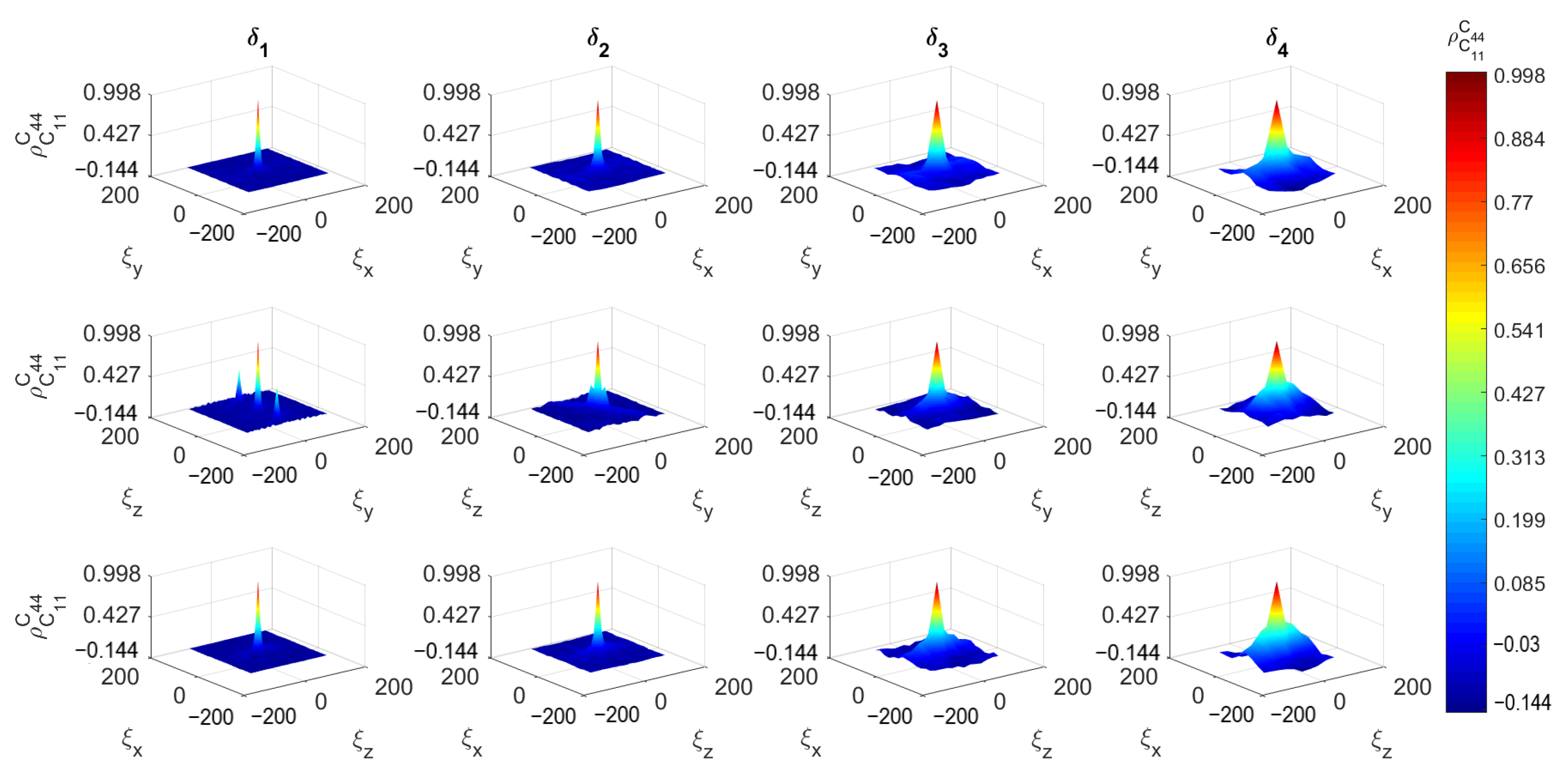
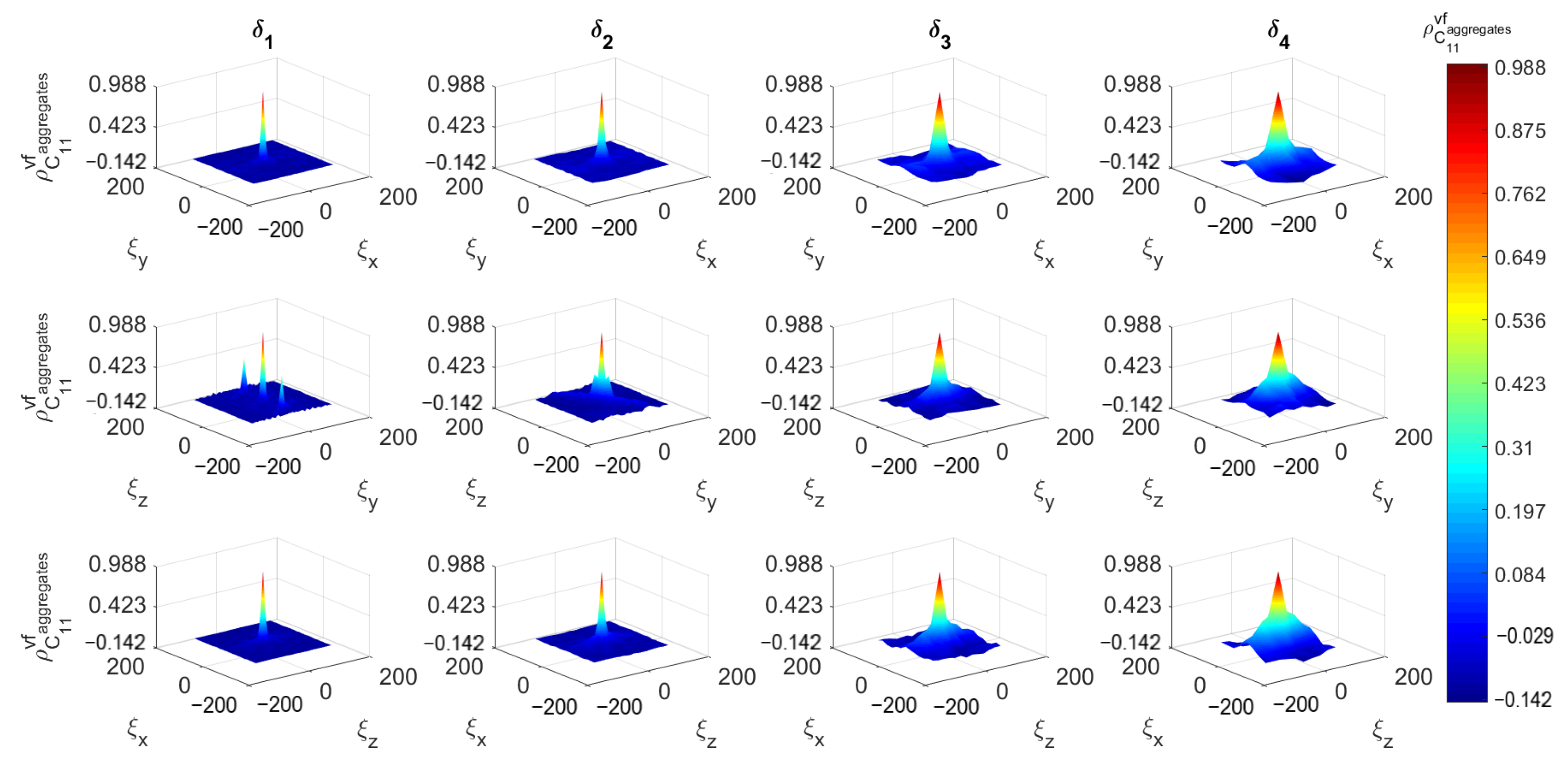
| (mm) | No. SVEs | |
|---|---|---|
| 16,464 | ||
| 2940 | ||
| 343 | ||
| 125 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stefanou, G.; Savvas, D.; Metsis, P. Random Material Property Fields of 3D Concrete Microstructures Based on CT Image Reconstruction. Materials 2021, 14, 1423. https://doi.org/10.3390/ma14061423
Stefanou G, Savvas D, Metsis P. Random Material Property Fields of 3D Concrete Microstructures Based on CT Image Reconstruction. Materials. 2021; 14(6):1423. https://doi.org/10.3390/ma14061423
Chicago/Turabian StyleStefanou, George, Dimitrios Savvas, and Panagiotis Metsis. 2021. "Random Material Property Fields of 3D Concrete Microstructures Based on CT Image Reconstruction" Materials 14, no. 6: 1423. https://doi.org/10.3390/ma14061423
APA StyleStefanou, G., Savvas, D., & Metsis, P. (2021). Random Material Property Fields of 3D Concrete Microstructures Based on CT Image Reconstruction. Materials, 14(6), 1423. https://doi.org/10.3390/ma14061423






