Superconducting Properties and Electron Scattering Mechanisms in a Nb Film with a Single Weak-Link Excavated by Focused Ion Beam
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Sample Characterization
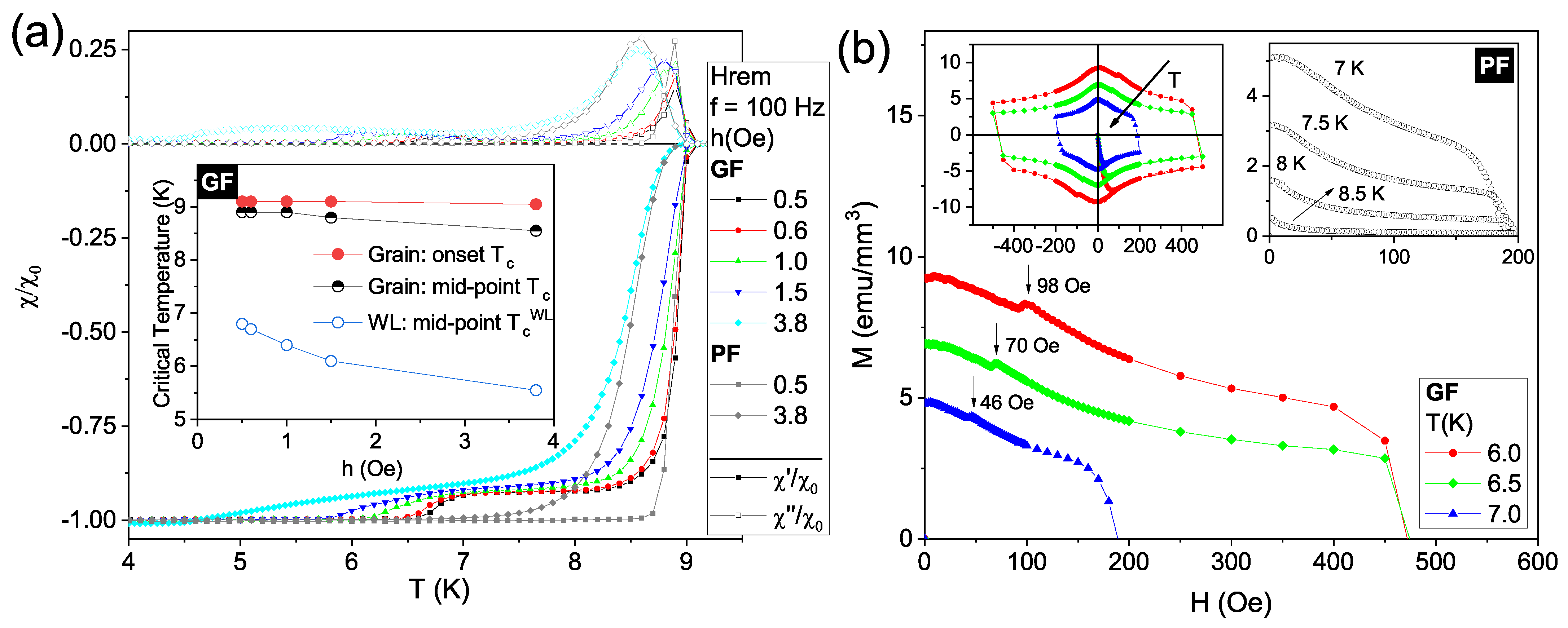
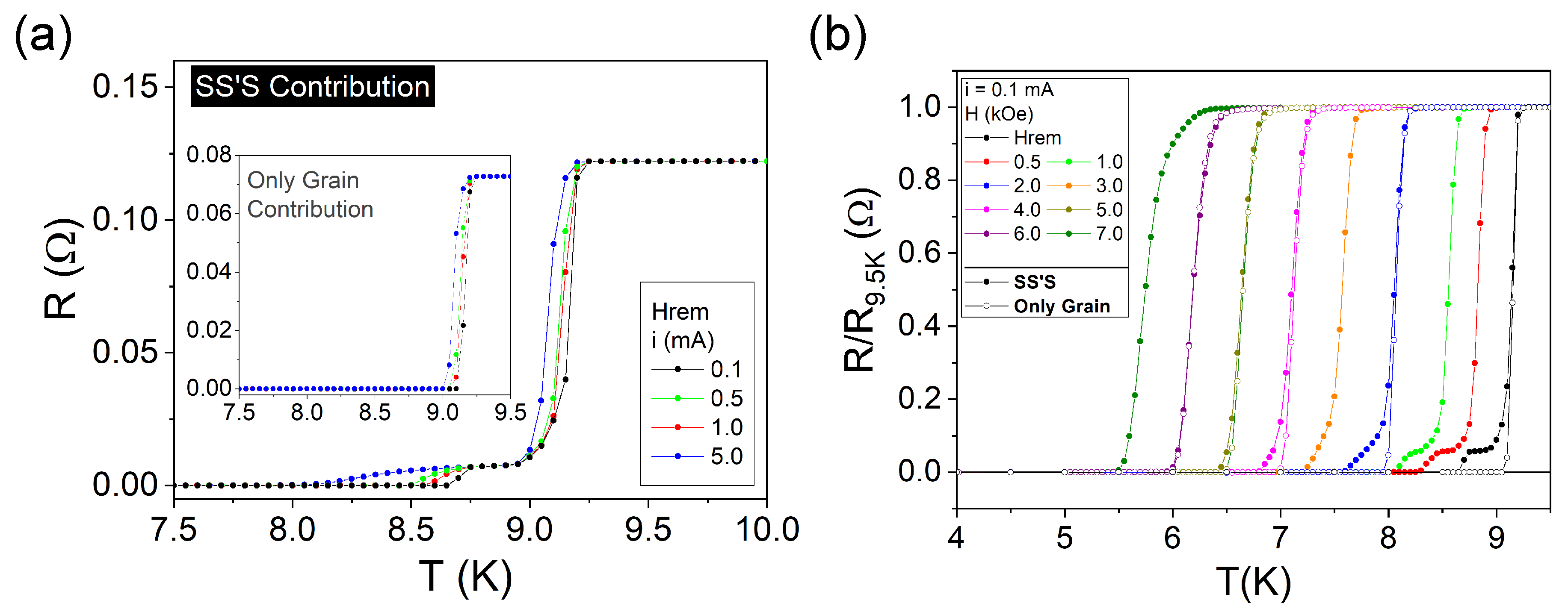
3.2. Superconducting Properties
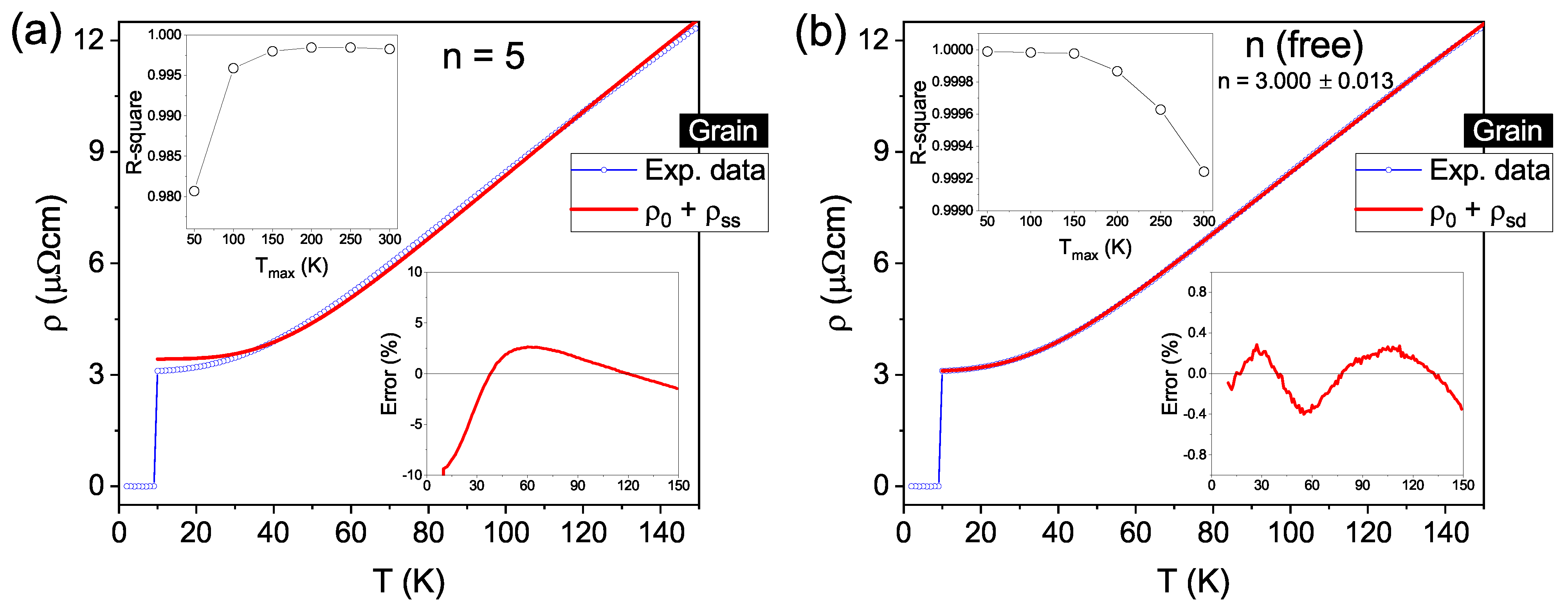
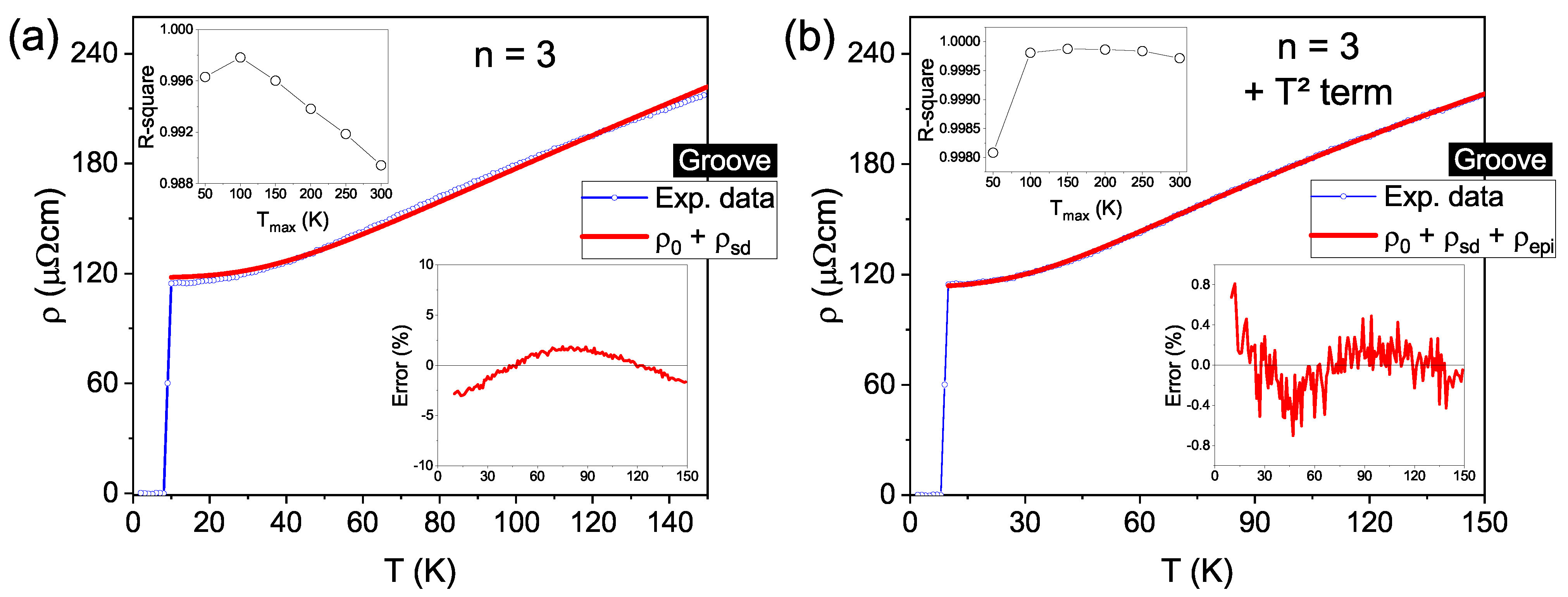
3.3. Normal State Properties
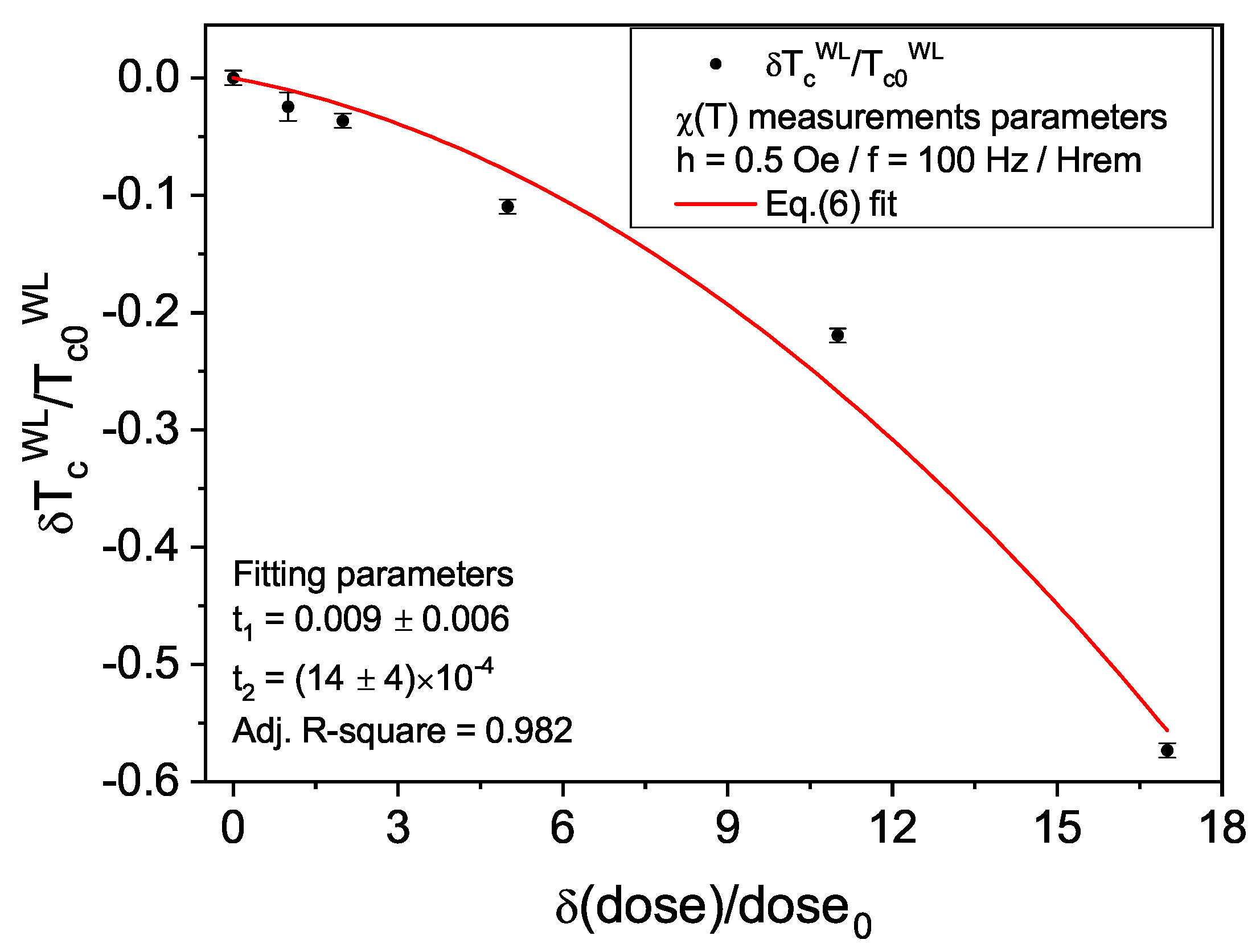
3.4. The Evolution of the Critical Temperature with Disorder
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| FIB | Focused ion beam |
| MO | Magneto-optical |
| AFM | Atomic force microscopy |
| EDS | Energy Dispersive X-ray Spectrometry |
| SEM | Scanning Electron Microscope |
| GF | Grooved Film |
| PF | Plain Film |
| S | Plain region of Grooved Film |
| S′ | Groove region of Grooved Film |
| Superconducting critical temperature | |
| WL | Weak-link |
| Weak-link critical temperature | |
| Remnant DC magnetic field | |
| h | Applied excitation field amplitude |
| T | Temperature |
| Temperature-dependent resistivity | |
| n | Power-law exponent in |
| () | Cross-section area of the grain (groove) |
| () | Length of the grain (groove) |
| Residual resistivity | |
| Groove resistivity | |
| Grain resistivity | |
| Electron-phonon-impurity resistivity contribution | |
| interband scattering resistivity contribution | |
| intraband scattering resistivity contribution | |
| Resistivity at 10 K | |
| Resistivity at 300 K | |
| Voltage measured between electrodes 2 and 3 (plain region) | |
| Voltage measured between electrodes 3 and 4 (SS′S contribution) | |
| B | Electron-phonon-impurity coefficient |
| Debye temperature | |
| Upper limit of temperature to fit | |
| Temperature-dependent AC susceptibility | |
| Real part of | |
| Imaginary part of | |
| f | Frequency |
| R | Resistance |
| Residual resistivity ratio | |
| l | Mean free path |
| Coherence length | |
| Penetration depth | |
| Upper critical field |
References
- Lubberts, G. Transport critical current density and electrical characterization of patterned high-Tc superconducting thin films prepared by metallo-organic decomposition. J. Appl. Phys. 1990, 68, 688–694. [Google Scholar] [CrossRef]
- Harada, K.; Kamimura, O.; Kasai, H.; Matsuda, T.; Tonomura, A.; Moshchalkov, V.V. Direct observation of vortex dynamics in superconducting films with regular arrays of defects. Science 1996, 274, 1167–1170. [Google Scholar] [CrossRef]
- Welp, U.; Xiao, Z.L.; Jiang, J.S.; Vlasko-Vlasov, V.K.; Bader, S.D.; Crabtree, G.W.; Liang, J.; Chik, H.; Xu, J.M. Superconducting transition and vortex pinning in Nb films patterned with nanoscale hole arrays. Phys. Rev. B 2002, 66, 212507. [Google Scholar] [CrossRef]
- Shaw, G.; Mandal, P.; Bag, B.; Banerjee, S.; Tamegai, T.; Suderow, H. Properties of nanopatterned pins generated in a superconductor with FIB. Appl. Surf. Sci. 2012, 258, 4199–4202. [Google Scholar] [CrossRef]
- Latimer, M.L.; Berdiyorov, G.R.; Xiao, Z.L.; Peeters, F.M.; Kwok, W.K. Realization of artificial ice systems for magnetic vortices in a superconducting MoGe thin film with patterned nanostructures. Phys. Rev. Lett. 2013, 111, 067001. [Google Scholar] [CrossRef] [PubMed]
- Golod, T.; Iovan, A.; Krasnov, V.M. Single Abrikosov vortices as quantized information bits. Nat. Commun. 2015, 6, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Brisbois, J.; Adami, O.A.; Avila, J.I.; Motta, M.; Ortiz, W.A.; Nguyen, N.D.; Vanderbemden, P.; Vanderheyden, B.; Kramer, R.B.G.; Silhanek, A.V. Magnetic flux penetration in Nb superconducting films with lithographically defined microindentations. Phys. Rev. B 2016, 93, 054521. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Huth, M.; Shklovskij, V.A.; Vovk, R.V. Mobile fluxons as coherent probes of periodic pinning in superconductors. Sci. Rep. 2017, 7, 13740. [Google Scholar] [CrossRef] [PubMed]
- Kalcheim, Y.; Katzir, E.; Zeides, F.; Katz, N.; Paltiel, Y.; Millo, O. Dynamic Control of the Vortex Pinning Potential in a Superconductor Using Current Injection through Nanoscale Patterns. Nano Lett. 2017, 17, 2934–2939. [Google Scholar] [CrossRef]
- Golod, T.; Kapran, O.M.; Krasnov, V.M. Planar superconductor-ferromagnet-superconductor Josephson junctions as scanning-probe sensors. Phys. Rev. Appl. 2019, 11, 014062. [Google Scholar] [CrossRef]
- Trabaldo, E.; Ruffieux, S.; Andersson, E.; Arpaia, R.; Montemurro, D.; Schneiderman, J.F.; Kalaboukhov, A.; Winkler, D.; Lombardi, F.; Bauch, T. Properties of grooved Dayem bridge based YBa2Cu3O7-δ superconducting quantum interference devices and magnetometers. Appl. Phys. Lett. 2020, 116, 132601. [Google Scholar] [CrossRef]
- Singh, G.; Lesne, E.; Winkler, D.; Claeson, T.; Bauch, T.; Lombardi, F.; Caviglia, A.D.; Kalaboukhov, A. Nanopatterning of weak links in superconducting oxide interfaces. Nanomaterials 2021, 11, 398. [Google Scholar] [CrossRef] [PubMed]
- Golod, T.; Hovhannisyan, R.A.; Kapran, O.M.; Dremov, V.V.; Stolyarov, V.S.; Krasnov, V.M. Reconfigurable Josephson Phase Shifter. Nano Let. 2021, 12, 5240–5246. [Google Scholar] [CrossRef]
- McCarthy, J.; Pei, Z.; Becker, M.; Atteridge, D. FIB micromachined submicron thickness cantilevers for the study of thin film properties. Thin Solid Films 2000, 358, 146–151. [Google Scholar] [CrossRef]
- Volkert, C.A.; Minor, A.M. Focused ion beam microscopy and micromachining. MRS Bull. 2007, 32, 389–399. [Google Scholar] [CrossRef]
- Wu, C.H.; Jhan, F.J.; Chen, J.H.; Jeng, J.T. High-Tc Josephson junctions fabricated by focused ion beam direct milling. Supercond. Sci. Technol. 2012, 26, 025010. [Google Scholar] [CrossRef]
- Pautrat, A.; Scola, J.; Goupil, C.; Simon, C.; Villard, C.; Domengès, B.; Simon, Y.; Guilpin, C.; Méchin, L. Quantitative analysis of the critical current due to vortex pinning by surface corrugation. Phys. Rev. B 2004, 69, 224504. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V.; Begun, E.; Huth, M.; Shklovskij, V.A. Electrical transport and pinning properties of Nb thin films patterned with focused ion beam-milled washboard nanostructures. New J. Phys. 2012, 14, 113027. [Google Scholar] [CrossRef]
- Cybart, S.A.; Cho, E.Y.; Wong, T.J.; Wehlin, B.H.; Ma, M.K.; Huynh, C.; Dynes, R.C. Nano josephson superconducting tunnel junctions in YBa2Cu3O7-δ directly patterned with a focused helium ion beam. Nat. Nanotechnol. 2015, 10, 598–602. [Google Scholar] [CrossRef]
- Dobrovolskiy, O.V. Abrikosov fluxonics in washboard nanolandscapes. Physica C 2017, 533, 80–90. [Google Scholar] [CrossRef]
- Mayer, J.; Giannuzzi, L.A.; Kamino, T.; Michael, J. TEM sample preparation and FIB-induced damage. MRS Bull. 2007, 32, 400–407. [Google Scholar] [CrossRef]
- De Leo, N.; Fretto, M.; Lacquaniti, V.; Cassiago, C.; D’Ortenzi, L.; Boarino, L.; Maggi, S. Thickness modulated niobium nanoconstrictions by focused ion beam and anodization. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Singh, M.; Chaujar, R.; Husale, S.; Grover, S.; Shah, A.P.; Deshmukh, M.M.; Gupta, A.; Singh, V.N.; Ojha, V.N.; Aswal, D.K.; et al. Influence of fabrication processes on transport properties of superconducting niobium nitride nanowires. Curr. Sci. 2018, 114, 1443–1450. [Google Scholar] [CrossRef]
- Datesman, A.M.; Schultz, J.C.; Cecil, T.W.; Lyons, C.M.; Lichtenberger, A.W. Gallium ion implantation into niobium thin films using a focused-ion beam. IEEE Trans. Appl. Supercond. 2005, 15, 3524–3527. [Google Scholar] [CrossRef]
- Heim, G.; Kay, E. Ion implantation during film growth and its effect on the superconducting properties of niobium. J. Appl. Phys. 1975, 46, 4006–4012. [Google Scholar] [CrossRef]
- Linker, G. Superconducting properties and structure of ion bombarded Nb layers. Radiation Effects 1980, 47, 225–228. [Google Scholar] [CrossRef]
- Camerlingo, C.; Scardi, P.; Tosello, C.; Vaglio, R. Disorder effects in ion-implanted niobium thin films. Phys. Rev. B 1985, 31, 3121. [Google Scholar] [CrossRef]
- Ziman, J. Electrons and Phonons: The Theory of Transport Phenomena in Solids; International Series of Monographs on Physics; OUP: Oxford, UK, 2001. [Google Scholar]
- Grüneisen, E. Die Abhängigkeit des elektrischen Widerstandes reiner Metalle von der Temperatur. Ann. Phys. 1933, 408, 530–540. [Google Scholar] [CrossRef]
- Mott, N.F. A discussion of the transition metals on the basis of quantum mechanics. Proc. Phys. Soc. 1935, 47, 571. [Google Scholar] [CrossRef]
- Wilson, A.H. The electrical conductivity of the transition metals. Proc. R. Soc. A 1938, 167, 580–593. [Google Scholar] [CrossRef]
- Webb, G.W. Low-Temperature Electrical Resistivity of Pure Niobium. Phys. Rev. 1969, 181, 1127–1135. [Google Scholar] [CrossRef]
- Lee, P.A.; Ramakrishnan, T.V. Disordered electronic systems. Rev. Mod. Phys. 1985, 57, 287. [Google Scholar] [CrossRef]
- MacDonald, A.H. Electron-Phonon Enhancement of Electron-Electron Scattering in Al. Phys. Rev. Lett. 1980, 44, 489–493. [Google Scholar] [CrossRef]
- Reizer, M.Y.; Sergeev, A. The effect of the electron-phonon interaction of the conductivity of impure metals. Sov. Phys. JETP 1987, 65, 1291–1298. [Google Scholar]
- Altshuler, B.; Aronov, A. Electron–Electron Interaction In Disordered Conductors. In Electron–Electron Interactions in Disordered Systems; Modern Problems in Condensed Matter Sciences; Efros, A., Pollak, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1985; Volume 10, pp. 1–153. [Google Scholar]
- ElMassalami, M.; Neto, M.B.S. Superconductivity, Fermi-liquid transport, and universal kinematic scaling relation for metallic thin films with stabilized defect complexes. Phys. Rev. B 2021, 104, 014520. [Google Scholar] [CrossRef]
- Likharev, K.K. Superconducting weak links. Rev. Mod. Phys. 1979, 51, 101–159. [Google Scholar] [CrossRef]
- Caffer, A.M.; Chaves, D.A.D.; Pessoa, A.L.; Carvalho, C.L.; Ortiz, W.A.; Zadorosny, R.; Motta, M. Optimum heat treatment to enhance the weak-link response of Y123 nanowires prepared by Solution Blow Spinning. Supercond. Sci. Technol. 2021, 34, 025009. [Google Scholar] [CrossRef]
- Babcock, S.E.; Vargas, J.L. The nature of grain boundaries in the high-Tc superconductors. Annu. Rev. Mater. Sci. 1995, 25, 193–222. [Google Scholar] [CrossRef]
- Ortiz, W.A.; Lisboa-Filho, P.N.; Passos, W.A.C.; Araujo-Moreira, F.M. Field-induced networks of weak-links: An experimental demonstration that the paramagnetic Meissner effect is inherent to granularity. Physica C 2001, 361, 267–273. [Google Scholar] [CrossRef]
- Clem, J.R. Granular and superconducting-glass properties of the high-temperature superconductors. Physica C 1988, 153, 50–55. [Google Scholar] [CrossRef]
- Clarke, J.; Braginski, A.I. The SQUID handbook: Applications of SQUIDs and SQUID Systems; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Halbritter, J. RF residual losses, surface impedance, and granularity in superconducting cuprates. J. Appl. Phys. 1990, 68, 6315–6326. [Google Scholar] [CrossRef]
- Tafuri, F.; Kirtley, J.R. Weak links in high critical temperature superconductors. Rep. Prog. Phys. 2005, 68, 2573. [Google Scholar] [CrossRef]
- Graser, S.; Hirschfeld, P.J.; Kopp, T.; Gutser, R.; Andersen, B.M.; Mannhart, J. How grain boundaries limit supercurrents in high-temperature superconductors. Nat. Phys. 2010, 6, 609–614. [Google Scholar] [CrossRef]
- Wang, G.; Raine, M.J.; Hampshire, D.P. How resistive must grain boundaries in polycrystalline superconductors be, to limit Jc? Supercond. Sci. Technol. 2017, 30, 104001. [Google Scholar] [CrossRef]
- Dimos, D.; Chaudhari, P.; Mannhart, J. Superconducting transport properties of grain boundaries in YBa2Cu3O7 bicrystals. Phys. Rev. B 1990, 41, 4038. [Google Scholar] [CrossRef] [PubMed]
- Polyanskii, A.A.; Gurevich, A.; Pashitski, A.E.; Heinig, N.F.; Redwing, R.D.; Nordman, J.E.; Larbalestier, D.C. Magneto-optical study of flux penetration and critical current densities in [001] tilt YBa2Cu3O7-δ thin-film bicrystals. Phys. Rev. B 1996, 53, 8687. [Google Scholar] [CrossRef] [PubMed]
- Arrington, C.H., III; Deaver, B.S., Jr. Superconducting weak links formed by ion implantation. Appl. Phys. Lett. 1975, 26, 204–206. [Google Scholar] [CrossRef]
- Goldfarb, R.B.; Lelental, M.; Thompson, C.A. Alternating-Field Susceptometry and Magnetic Susceptibility of Superconductors. In Magnetic Susceptibility of Superconductors and Other Spin Systems; Hein, R.A., Francavilla, T.L., Liebenberg, D.H., Eds.; Springer: Boston, MA, USA, 1991; pp. 49–80. [Google Scholar]
- Gömöry, F. Characterization of high-temperature superconductors by AC susceptibility measurements. Supercond. Sci. Technol. 1997, 10, 523–542. [Google Scholar] [CrossRef]
- Brandt, E.H. Ac response of thin-film superconductors at various temperatures and magnetic fields. Philos. Mag. B 2000, 80, 835–845. [Google Scholar] [CrossRef][Green Version]
- Jooss, C.; Albrecht, J.; Kuhn, H.; Leonhardt, S.; Kronmüller, H. Magneto-optical studies of current distributions in high-Tc superconductors. Rep. Prog. Phys. 2002, 65, 651. [Google Scholar] [CrossRef]
- Colauto, F.; Motta, M.; Ortiz, W.A. Controlling magnetic flux penetration in low-Tc superconducting films and hybrids. Supercond. Sci. Technol. 2020, 34, 013002. [Google Scholar] [CrossRef]
- Palau, A.; Puig, T.; Obradors, X.; Jooss, C. Simultaneous determination of grain and grain-boundary critical currents in YBa2Cu3O7-coated conductors by magnetic measurements. Phys. Rev. B 2007, 75, 054517. [Google Scholar] [CrossRef]
- Chen, D.X.; Sanchez, A.; Puig, T.; Martinez, L.; Muñoz, J. AC susceptibility of grains and matrix for high-Tc superconductors. Physica C 1990, 168, 652–667. [Google Scholar] [CrossRef]
- Navau, C.; Sanchez, A.; Del-Valle, N.; Chen, D.X. Alternating current susceptibility calculations for thin-film superconductors with regions of different critical-current densities. J. Appl. Phys. 2008, 103, 113907. [Google Scholar] [CrossRef]
- Chen, D.X.; Goldfarb, R.B. Kim model for magnetization of type-II superconductors. J. Appl. Phys. 1989, 66, 2489–2500. [Google Scholar] [CrossRef]
- Johansen, T.H.; Bratsberg, H. Critical-state magnetization of type-II superconductors in rectangular slab and cylinder geometries. J. Appl. Phys. 1995, 77, 3945–3952. [Google Scholar] [CrossRef]
- Däumling, M.; Walker, E.; Flükiger, R. Effect of sample shape on the low-field peak in the magnetization of YBa2Cu3O7-δ. Phys. Rev. B 1994, 50, 13024. [Google Scholar] [CrossRef] [PubMed]
- Shantsev, D.V.; Koblischka, M.R.; Galperin, Y.M.; Johansen, T.H.; Půst, L.; Jirsa, M. Central peak position in magnetization loops of high-Tc superconductors. Phys. Rev. Lett. 1999, 82, 2947. [Google Scholar] [CrossRef]
- Palau, A.; Puig, T.; Obradors, X.; Pardo, E.; Navau, C.; Sanchez, A.; Usoskin, A.; Freyhardt, H.C.; Fernandez, L.; Holzapfel, B.; et al. Simultaneous inductive determination of grain and intergrain critical current densities of YBa2Cu3O7-x coated conductors. Appl. Phys. Lett. 2004, 84, 230–232. [Google Scholar] [CrossRef]
- Poole, C.P.; Farach, H.A.; Creswick, R.J.; Prozorov, R. Superconductivity, 2nd ed.; Academic Press: Amsterdam, The Netherlands, 2007; p. 670. [Google Scholar]
- Altshuler, E.; Johansen, T.H. Colloquium: Experiments in vortex avalanches. Rev. Mod. Phys. 2004, 76, 471–487. [Google Scholar] [CrossRef]
- Andreone, A.; Cassinese, A.; Iavarone, M.; Vaglio, R.; Kulik, I.I.; Palmieri, V. Relation between normal-state and superconductive properties of niobium sputtered films. Phys. Rev. B 1995, 52, 4473. [Google Scholar] [CrossRef]
- Jiang, Q.D.; Xie, Y.L.; Zhang, W.B.; Gu, H.; Ye, Z.Y.; Wu, K.; Zhang, J.L.; Li, C.Y.; Yin, D.L. Superconductivity and transport properties in ultrathin epitaxial single-crystal niobium films. J. Phys. Condens. Matter 1990, 2, 3567. [Google Scholar] [CrossRef]
- Mayadas, A.F.; Laibowitz, R.B.; Cuomo, J.J. Electrical Characteristics of rf-Sputtered Single-Crystal Niobium Films. J. Appl. Phys. 1972, 43, 1287–1289. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; Dover Books on Physics; Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Maxfield, B.W.; McLean, W.L. Superconducting penetration depth of niobium. Phys. Rev. 1965, 139, A1515. [Google Scholar] [CrossRef]
- Gubin, A.I.; Il’in, K.S.; Vitusevich, S.A.; Siegel, M.; Klein, N. Dependence of magnetic penetration depth on the thickness of superconducting Nb thin films. Phys. Rev. B 2005, 72, 064503. [Google Scholar] [CrossRef]
- Allen, P.B. Boltzmann theory and resistivity of metals. In Quantum Theory of Real Materials; Chelikowsky, J.R., Louie, S.G., Eds.; Kluwer International Series In Engineering And Computer Science; Kluwer Academic Publishers Group: Boston, MA, USA, 1996; pp. 219–250. [Google Scholar]
- Allen, P.B.; Butler, W.H. Electrical conduction in metals. Phys. Today 1978, 31, 44–49. [Google Scholar] [CrossRef]
- James, A.M.; Lord, M.P. MacMillan’s Chemical and Physical Data; MacMillan Press: Basingstoke, UK, 1992. [Google Scholar]
- Colquitt, L. Electrical and Thermal Resistivities of the Nonmagnetic Transition Metals with a Two-Band Model. J. Appl. Phys. 1965, 36, 2454–2458. [Google Scholar] [CrossRef]
- Ptitsina, N.G.; Chulkova, G.M.; Il’in, K.S.; Sergeev, A.V.; Pochinkov, F.S.; Gershenzon, E.M.; Gershenson, M.E. Electron-phonon interaction in disordered metal films: The resistivity and electron dephasing rate. Phys. Rev. B 1997, 56, 10089–10096. [Google Scholar] [CrossRef]
- Echternach, P.M.; Gershenson, M.E.; Bozler, H.M. Evidence of interference between electron-phonon and electron-impurity scattering on the conductivity of thin metal films. Phys. Rev. B 1993, 47, 13659–13663. [Google Scholar] [CrossRef]
- Ptitsina, N.G.; Chulkova, G.M.; Gershenzon, E.M.; Gershenzon, M.E. Influence of the interference of electron-phonon and electron-impurity scattering on the conductivity of unordered Nb films. Sov. Phys. JETP 1995, 80, 960–964. [Google Scholar]
- Chulcova, G.M.; Ptitsina, N.G.; Gershenzon, E.M.; Gershenzon, M.E.; Sergeev, A.V. Effect of the interference between electron-phonon and electron-impurity (boundary) scattering on resistivity Nb, Al, Be films. Czech. J. Phys. 1996, 46, 2489–2490. [Google Scholar] [CrossRef]
- Bauriedl, W.; Heim, G.; Buckel, W. Irradiation effect on Tc of indium. Phys. Lett. A 1976, 57, 282–284. [Google Scholar] [CrossRef]
- Bernas, H.; Nedellec, P. Structural and electronic properties of ion implanted superconductors. Nucl. Instrum. Methods 1981, 182–183, 845–864. [Google Scholar] [CrossRef]
- Linker, G. Amorphization of niobium layers by phosphorus ion implantation. Nucl. Instrum. Methods Phys. Res. 1983, 209–210, 969–974. [Google Scholar] [CrossRef]
- Linker, G. Amorphization of niobium films by boron ion implantation. Mater. Sci. Eng. 1985, 69, 105–110. [Google Scholar] [CrossRef]
- Kasaei, L.; Manichev, V.; Li, M.; Feldman, L.C.; Gustafsson, T.; Collantes, Y.; Hellstrom, E.; Demir, M.; Acharya, N.; Bhattarai, P.; et al. Normal-state and superconducting properties of Co-doped BaFe2As2 and MgB2 thin films after focused helium ion beam irradiation. Supercond. Sci. Technol. 2019, 32, 095009. [Google Scholar] [CrossRef]
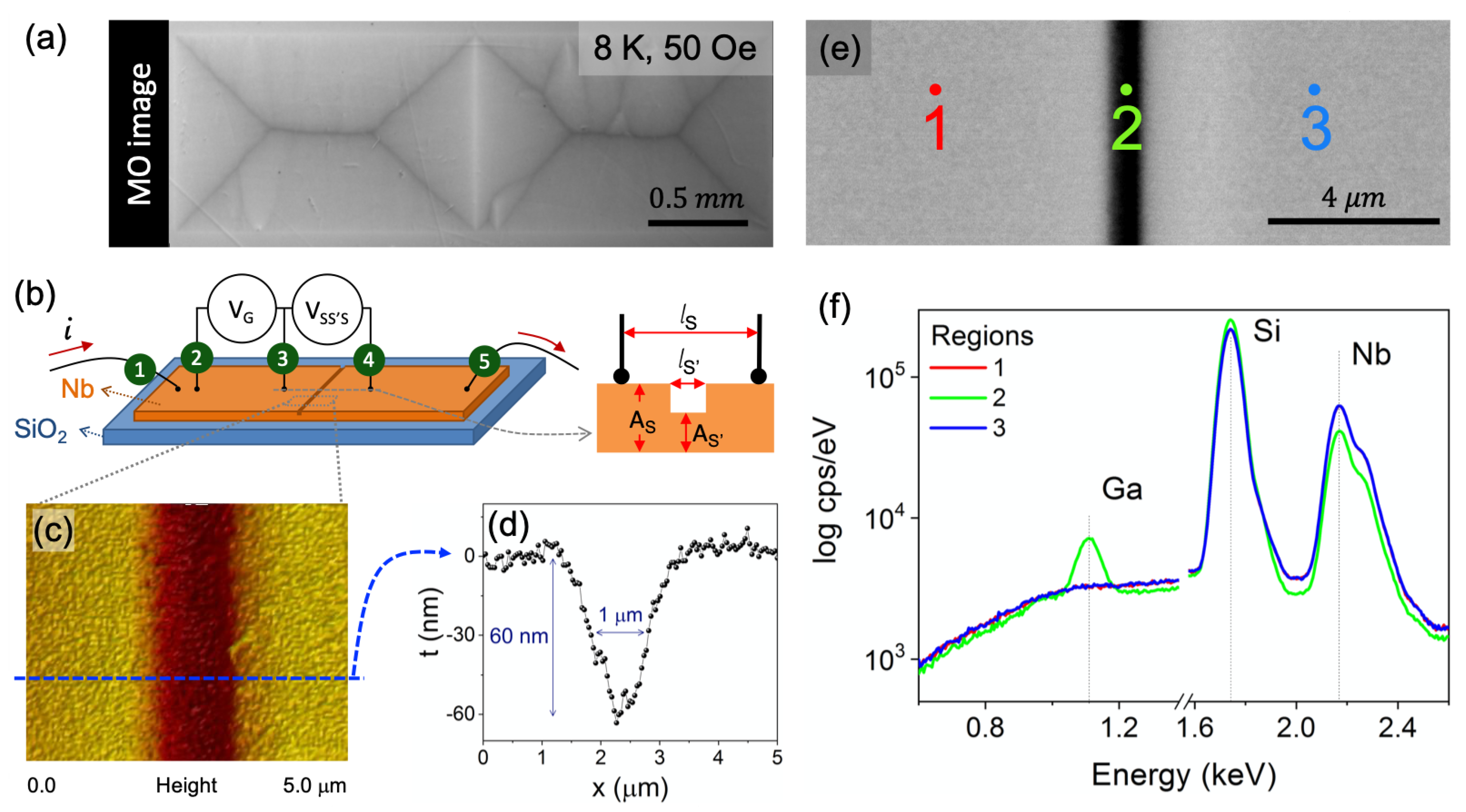
| Parameters | Grain | Weak-Link |
|---|---|---|
| [cm] | 22.48 | 302.49 |
| [cm] | 3.11 | 114.62 |
| RRR | 7.23 | 2.64 |
| [K] | ||
| l [nm] | ||
| [nm] | ||
| [nm] |
| Contribution | n | (cm) | B ( K) | (cm) | Adj. R-Square | |
|---|---|---|---|---|---|---|
| Grain | 5 | 3.426 ± 0.018 | - | 80.5 ± 0.3 | 0.99799 | |
| Grain | 3.000 ± 0.013 | 3.095 ± 0.004 | - | 39.21 ± 0.25 | 0.99998 | |
| Groove | 3 | 117.8 ± 0.3 | - | 437 ± 2 | 0.99601 | |
| Groove | 3 | 113.30 ± 0.09 | 3.93 ± 0.06 | 307 ± 2 | 0.99988 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valerio-Cuadros, M.I.; Chaves, D.A.D.; Colauto, F.; Oliveira, A.A.M.d.; Andrade, A.M.H.d.; Johansen, T.H.; Ortiz, W.A.; Motta, M. Superconducting Properties and Electron Scattering Mechanisms in a Nb Film with a Single Weak-Link Excavated by Focused Ion Beam. Materials 2021, 14, 7274. https://doi.org/10.3390/ma14237274
Valerio-Cuadros MI, Chaves DAD, Colauto F, Oliveira AAMd, Andrade AMHd, Johansen TH, Ortiz WA, Motta M. Superconducting Properties and Electron Scattering Mechanisms in a Nb Film with a Single Weak-Link Excavated by Focused Ion Beam. Materials. 2021; 14(23):7274. https://doi.org/10.3390/ma14237274
Chicago/Turabian StyleValerio-Cuadros, Marlon Ivan, Davi Araujo Dalbuquerque Chaves, Fabiano Colauto, Ana Augusta Mendonça de Oliveira, Antônio Marcos Helgueira de Andrade, Tom Henning Johansen, Wilson Aires Ortiz, and Maycon Motta. 2021. "Superconducting Properties and Electron Scattering Mechanisms in a Nb Film with a Single Weak-Link Excavated by Focused Ion Beam" Materials 14, no. 23: 7274. https://doi.org/10.3390/ma14237274
APA StyleValerio-Cuadros, M. I., Chaves, D. A. D., Colauto, F., Oliveira, A. A. M. d., Andrade, A. M. H. d., Johansen, T. H., Ortiz, W. A., & Motta, M. (2021). Superconducting Properties and Electron Scattering Mechanisms in a Nb Film with a Single Weak-Link Excavated by Focused Ion Beam. Materials, 14(23), 7274. https://doi.org/10.3390/ma14237274








