Drag Voltages in a Superconductor/Insulator/Ferromagnet Trilayer
Abstract
:1. Introduction
2. Theory
3. Experiments
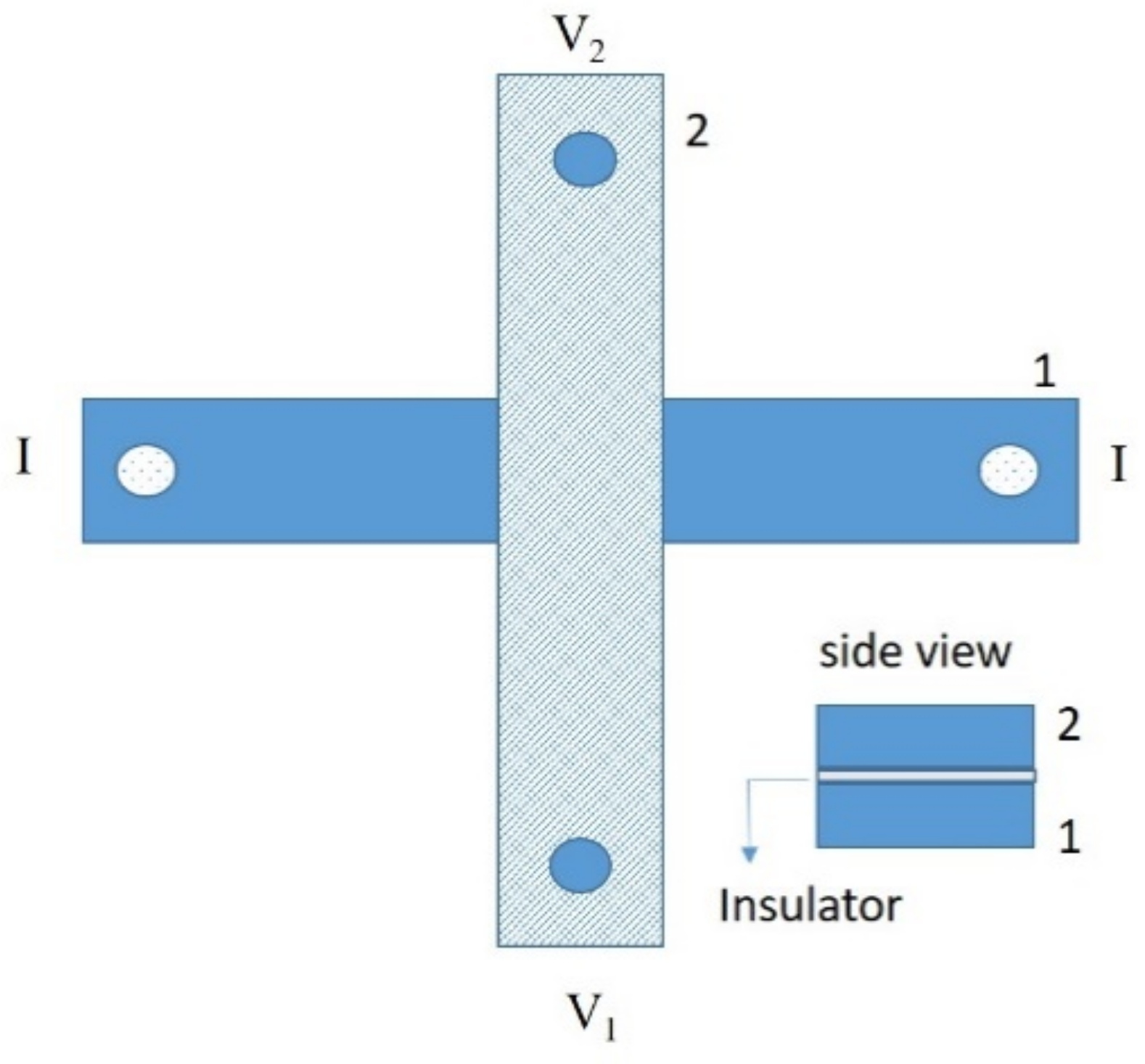
3.1. Sample Fabrication
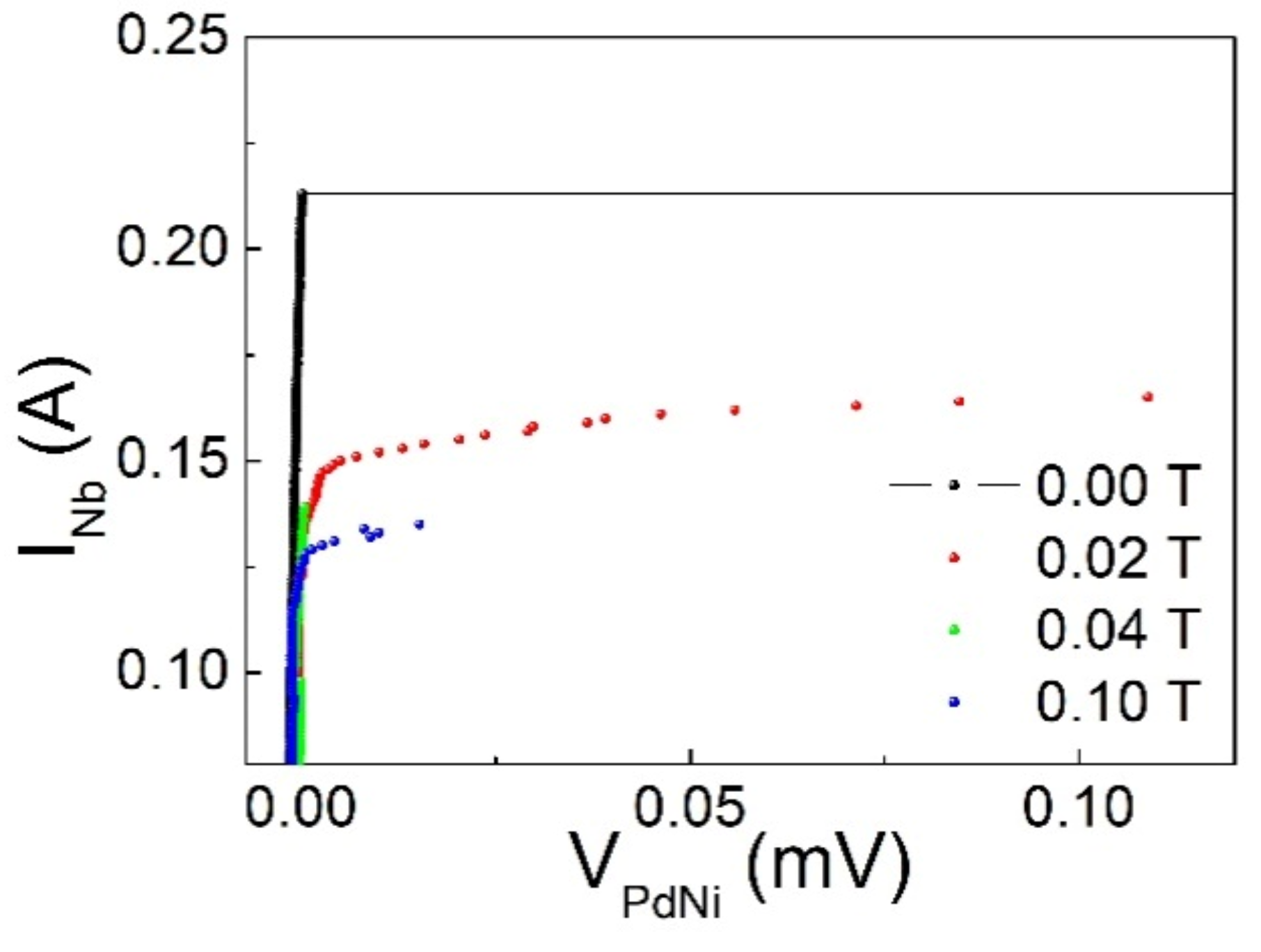
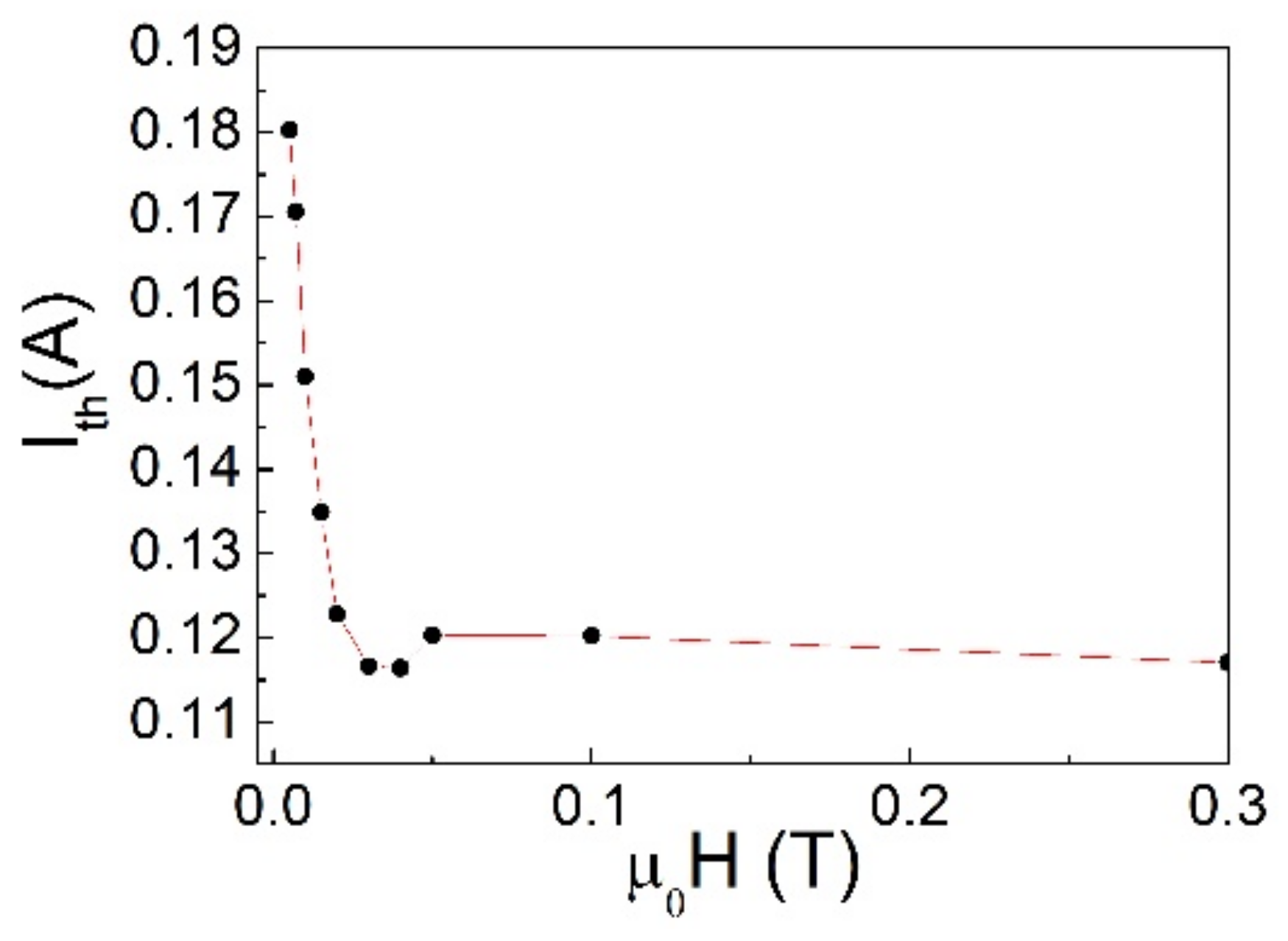
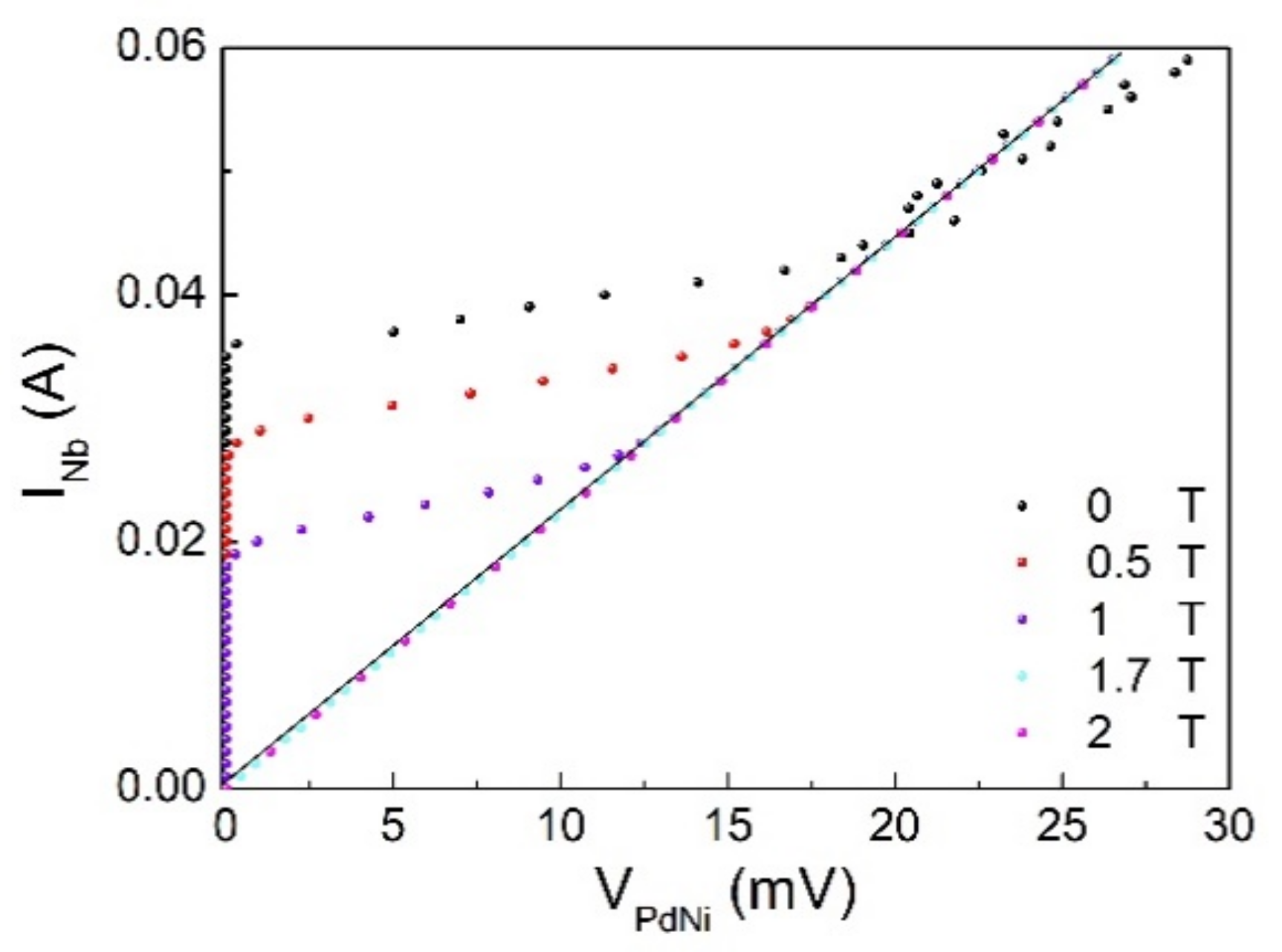
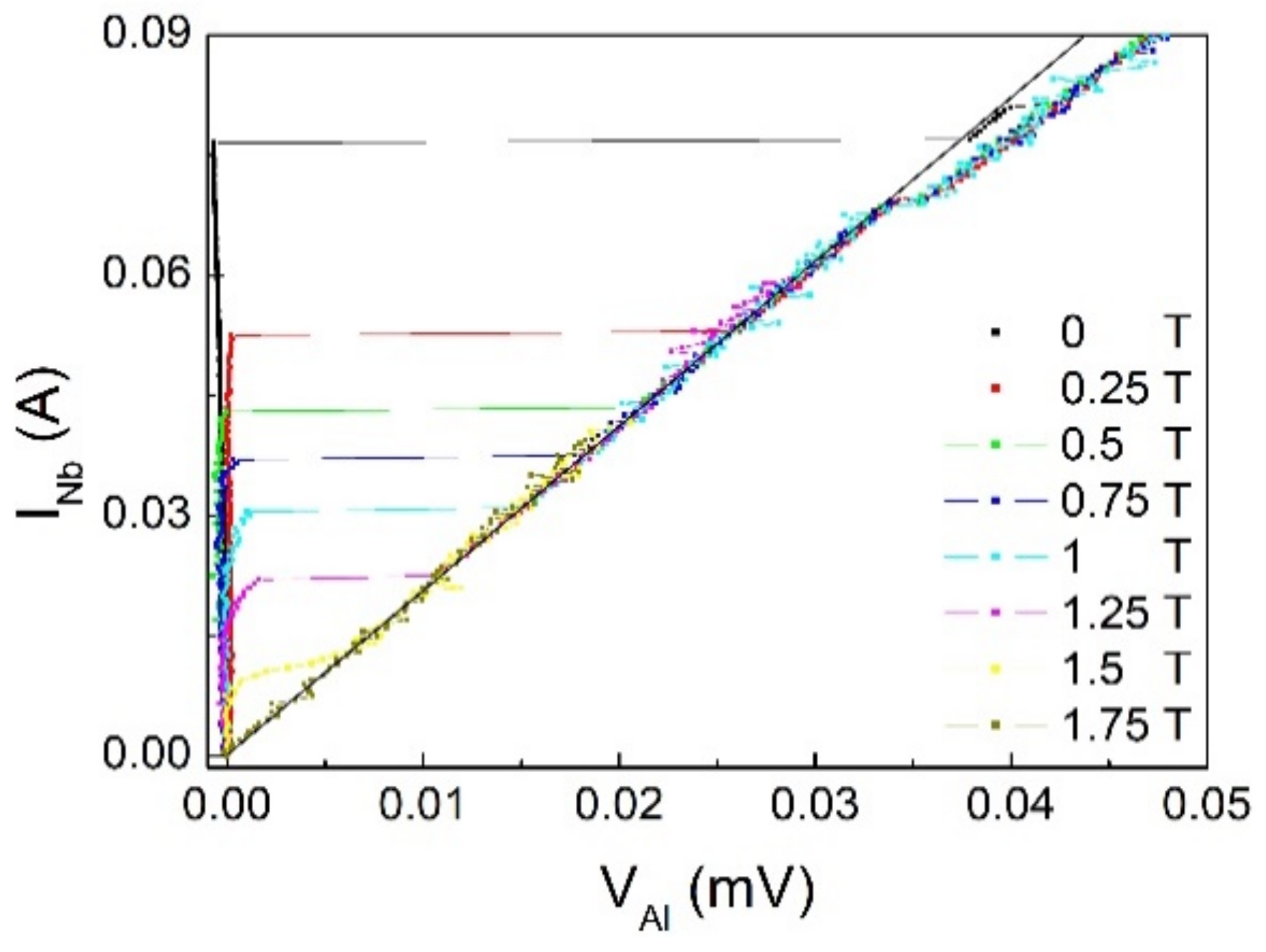
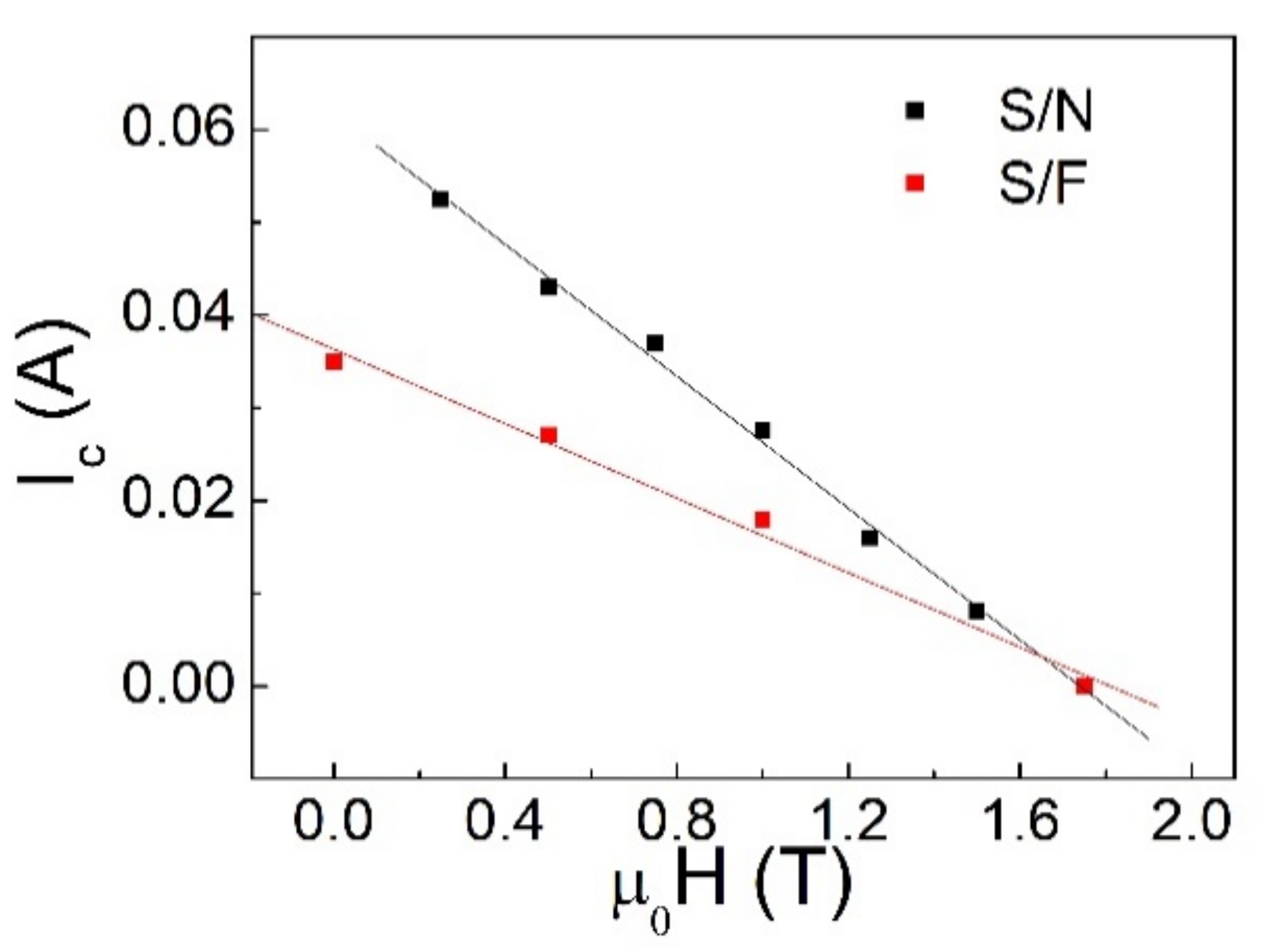
3.2. Results
4. Comments and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Price, P.J. Hot electron effects in heterolayers. Physica 1983, 117–118B+C, 750. [Google Scholar]
- Gramila, T.J.; Eisenstein, J.P.; MacDonald, A.H.; Pfeiffer, L.N.; West, K.W. Mutual friction between parallel two-dimensional electron systems. Phys. Rev. Lett. 1991, 66, 1216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jauno, P.; Smith, H. Coulomb drag between parallel two-dimensional electron systems. Phys. Rev. B 1993, 47, 4420. [Google Scholar]
- Rojo, G. Electron-drag effects in coupled electron systems. J. Phys. Cond. Matt. 1999, 11, R31. [Google Scholar] [CrossRef]
- Yang, K. Hall drag in correlated double-layer quantum Hall systems. Phys. Rev. B 1998, 58, R4246. [Google Scholar] [CrossRef] [Green Version]
- Oreg, Y.; Kamenev, A. Coulomb drag in systems with tunneling bridges. Phys. Rev. Lett. 1998, 80, 2421. [Google Scholar] [CrossRef] [Green Version]
- Oreg, Y.; Halperin, B.I. Longitudinal drag and Hall drag in a bilayer system with pinholes. Phys. Rev. B 1999, 60, 5679. [Google Scholar] [CrossRef] [Green Version]
- D’Amico, I.; Vignale, G. Theory of spin Coulomb drag in spin-polarized transport. Phys. Rev. B 2000, 62, 4853. [Google Scholar] [CrossRef] [Green Version]
- Price, S.; Savchenko, A.K.; Narozhny, B.N.; Allison, G.; Ritchie, D.A. Giant fluctuations of coulomb drag in a bilayer system. Science 2007, 316, 99–102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, X.; Bazàn, G.; Bernstein, G. Observation of supercurrent drag between normal metal and superconducting films. Phys. Rev. Lett. 1995, 74, 4051. [Google Scholar] [CrossRef] [PubMed]
- Giordano, N.; Monnier, J.D. Cross-talk effects in superconductor–insulator–normal-metal trilayers. Phys. Rev. B 1994, 50, 9363. [Google Scholar] [CrossRef] [PubMed]
- Vignale, G. Observing the spin Coulomb drag in spin-valve devices. Phys. Rev. B 2005, 71, 125103. [Google Scholar] [CrossRef] [Green Version]
- Žutić, I.; Fabian, J.; Sarma, S.D. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323. [Google Scholar] [CrossRef] [Green Version]
- Buzdin, A.I. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 2005, 77, 935. [Google Scholar] [CrossRef] [Green Version]
- Linder, J.; Robinson, J.W. Superconducting spintronics. Nat. Phys. 2015, 11, 307. [Google Scholar] [CrossRef]
- Ryazanov, V.V.; Oboznov, V.A.; Rusanov, A.Y.; Veretennikov, A.V.; Golubov, A.A.; Aarts, J. Coupling of two superconductors through a ferromagnet: Evidence for a π junction. Physical review letters. Phys. Rev. Lett. 2001, 86, 2427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kontos, T.; Aprili, M.; Lesueur, J.; Genêt, F.; Stephanidis, B.; Boursier, R. Josephson junction through a thin ferromagnetic layer: Negative coupling. Phys. Rev. Lett. 2002, 89, 137007. [Google Scholar] [CrossRef]
- Frolov, S.M.; van Harlingen, D.J.; Oboznov, V.A.; Bolginov, V.V.; Ryazanov, V.V. Measurement of the current-phase relation of superconductor/ferromagnet/superconductor π Josephson junctions. Phys. Rev. B 2004, 70, 144505. [Google Scholar] [CrossRef]
- Gu, J.Y.; You, C.Y.; Jiang, J.S.; Pearson, J.; Bazaliy, Y.B.; Bader, S.D. Magnetization-Orientation Dependence of the Superconducting Transition Temperature in the Ferromagnet-Superconductor-Ferromagnet System: CuNi/Nb/CuNi. Phys. Rev. Lett. 2002, 89, 267001. [Google Scholar] [CrossRef]
- Cuoco, M.; Saldarriaga, W.; Polcari, A.; Guarino, A.; Moran, O.; Baca, E.; Vecchione, A.; Romano, P. Nonlocal voltage effects in La2/3Ca1/3MnO3/La1/3Ca2/3MnO3/YBa2Cu3O7 trilayers. Phys. Rev. B 2009, 79, 014523. [Google Scholar] [CrossRef]
- Miccoli, I.; Edler, F.; Pfnür, H.; Tegenkamp, C. The 100th anniversary of the four-point probe technique: The role of probe geometries in isotropic and anisotropic systems. J. Phys. Condens. Matter 2015, 27, 223201. [Google Scholar] [CrossRef]
- Narozhny, N.; Levchenko, A. Coulomb drag. Rev. Mod. Phys. 2016, 88, 025003. [Google Scholar] [CrossRef] [Green Version]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Sounders College: Philadelphia, PA, USA, 1976. [Google Scholar]
- Eisenstein, J.P. Evidence for spontaneous interlayer phase coherence in a bilayer quantum Hall exciton condensate. Solid State Commun. 2003, 127, 123–130. [Google Scholar] [CrossRef]
- Eisenstein, J.P. Exciton condensation in bilayer quantum hall systems. Annu. Rev. Condens. Matter Phys. 2014, 5, 159–181. [Google Scholar] [CrossRef] [Green Version]
- Kellogg; Spielman, I.B.; Eisenstein, J.P.; Pfeiffer, L.N.; West, K.W. Observation of quantized Hall drag in a strongly correlated bilayer electron system. Physical review letters. Phys. Rev. Lett. 2002, 88, 126804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, L.H.; Zhang, R.X.; Zhang, F.C.; Wu, C. Interacting topological mirror excitonic insulator in one dimension. Phys. Rev. B 2020, 102, 235115. [Google Scholar] [CrossRef]
- Sun, Z.; Millis, A.J. Topological charge pumping in excitonic insulators. Phys. Rev. Lett. 2021, 126, 027601. [Google Scholar] [CrossRef]
- Liu, Z.R.; Hu, L.H.; Chen, C.Z.; Zhou, B.; Xu, D.H. Topological excitonic corner states and nodal phase in bilayer quantum spin Hall insulators. Phys. Rev. B 2021, 103, L201115. [Google Scholar] [CrossRef]
- Rabinovich, S.; Bobkova, I.V.; Bobkov, A.M. Electrical response of superconductor/ferromagnet/topological-insulator/superconductor junctions to magnetic texture dynamics. Phys. Rev. B 2020, 101, 054517. [Google Scholar] [CrossRef] [Green Version]
- Bakurskiy, S.V.; Neilo, A.A.; Klenov, N.V.; Soloviev, I.I.; Golubov, A.A.; Kupriyanov, M.Y. Density of states and current-voltage characteristics in SIsFS junctions. Supercond. Sci. Technol. 2021, 34, 085007. [Google Scholar] [CrossRef]
- Cirillo, C.; Ilyina, E.A.; Attanasio, C. Static and dynamic properties of the vortex lattice in superconductor/weak ferromagnet bilayers. Supercond. Sci. Technol. 2011, 24, 024017. [Google Scholar] [CrossRef]
- Leo, A.; Grimaldi, G.; Martucciello, N.; Avitabile, F.; Pace, S.; Nigro, A.; Romano, P. A Study of Ultra-Thin Superconducting Films at High Bias Currents in Different Cooling Environments. J. Supercond. Novel Magn. 2020, 33, 1911–1916. [Google Scholar] [CrossRef]
- Grimaldi, G.; Leo, A.; Cirillo, C.; Attanasio, C.; Nigro, A.; Pace, S. Magnetic field and temperature dependence of the critical vortex velocity in type-II superconducting films. J. Phys. Condens. Matter 2009, 21, 254207. [Google Scholar] [CrossRef]
- Cirillo, C.; Pagliarulo, V.; Myoren, H.; Bonavolonta, C.; Parlato, L.; Pepe, G.P.; Attanasio, C. Quasiparticle energy relaxation times in NbN/CuNi nanostripes from critical velocity measurements. Phys. Rev. B 2011, 84, 054536. [Google Scholar] [CrossRef]
- Grimaldi, G.; Leo, A.; Nigro, A.; Pace, S.; Cirillo, C.; Attanasio, C. Thickness dependence of vortex critical velocity in wide Nb films. Physica C 2008, 468, 765. [Google Scholar] [CrossRef]
- Takahashi, S.; Maekawa, S. Hall effect induced by a spin-polarized current in superconductors. Phys. Rev. Lett. 2002, 88, 116601. [Google Scholar] [CrossRef]
- Machon, P.; Eschrig, M.; Belzig, W. Giant thermoelectric effects in a proximity-coupled superconductor–ferromagnet device. New J. Phys. 2014, 16, 073002. [Google Scholar] [CrossRef]
| Substrate | dNb(nm) | dAl(nm) | dAlOx(nm) | dPdNi(nm) | |
|---|---|---|---|---|---|
| Nb/Al1−xOx/Pd0.84Ni0.16 | Si | 73 | - | 4.5 | 50 |
| Nb/Pd0.84Ni0.16 | glass | 100 | - | - | 100 |
| Nb/Al | Si | 73 | 50 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romano, P.; Polcari, A.; Cirillo, C.; Attanasio, C. Drag Voltages in a Superconductor/Insulator/Ferromagnet Trilayer. Materials 2021, 14, 7575. https://doi.org/10.3390/ma14247575
Romano P, Polcari A, Cirillo C, Attanasio C. Drag Voltages in a Superconductor/Insulator/Ferromagnet Trilayer. Materials. 2021; 14(24):7575. https://doi.org/10.3390/ma14247575
Chicago/Turabian StyleRomano, Paola, Albino Polcari, Carla Cirillo, and Carmine Attanasio. 2021. "Drag Voltages in a Superconductor/Insulator/Ferromagnet Trilayer" Materials 14, no. 24: 7575. https://doi.org/10.3390/ma14247575
APA StyleRomano, P., Polcari, A., Cirillo, C., & Attanasio, C. (2021). Drag Voltages in a Superconductor/Insulator/Ferromagnet Trilayer. Materials, 14(24), 7575. https://doi.org/10.3390/ma14247575








