Next Article in Journal
Energy Absorbing Properties Analysis of Layers Structure of Titanium Alloy Ti6Al4V during Dynamic Impact Loading Tests
Next Article in Special Issue
Integration of Fuzzy AHP and Fuzzy TOPSIS Methods for Wire Electric Discharge Machining of Titanium (Ti6Al4V) Alloy Using RSM
Previous Article in Journal
Friction and Wear Performance Evaluation of Bio-Lubricants and DLC Coatings on Cam/Tappet Interface of Internal Combustion Engines
Previous Article in Special Issue
Corrosion Resistance and Surface Bioactivity of Ti6Al4V Alloy after Finish Turning under Ecological Cutting Conditions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 14
Issue 23
10.3390/ma14237207
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study of a Multicriterion Decision-Making Approach to the MQL Turning of AISI 304 Steel Using Hybrid Nanocutting Fluid

by
Vineet Dubey
1,*,
Anuj Kumar Sharma
1,
Prameet Vats
1,
Danil Yurievich Pimenov
2,
Khaled Giasin
3 and
Daniel Chuchala
4
1
Centre for Advanced Studies, Dr. A.P.J Abdul Kalam Technical University, Lucknow 226031, India
2
Department of Automated Mechanical Engineering, South Ural State University, Lenin Prosp. 76, 454080 Chelyabinsk, Russia
3
School of Mechanical and Design Engineering, University of Portsmouth, Portsmouth PO1 3DJ, UK
4
Faculty of Mechanical Engineering and Ship Technology, Gdańsk University of Technology, 80-233 Gdańsk, Poland
*
Author to whom correspondence should be addressed.
Materials 2021, 14(23), 7207; https://doi.org/10.3390/ma14237207
Submission received: 31 October 2021 / Revised: 22 November 2021 / Accepted: 23 November 2021 / Published: 26 November 2021
(This article belongs to the Special Issue Additive and Subtractive Manufacturing of Advanced Materials: Applications, Future Trends and Perspectives of Industry 4.0)
Browse Figures
Versions Notes

Abstract

:
The enormous use of cutting fluid in machining leads to an increase in machining costs, along with different health hazards. Cutting fluid can be used efficiently using the MQL (minimum quantity lubrication) method, which aids in improving the machining performance. This paper contains multiple responses, namely, force, surface roughness, and temperature, so there arises a need for a multicriteria optimization technique. Therefore, in this paper, multiobjective optimization based on ratio analysis (MOORA), VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR), and technique for order of preference by similarity to ideal solution (TOPSIS) are used to solve different multiobjective problems, and response surface methodology is also used for optimization and to validate the results obtained by multicriterion decision-making technique (MCDM) techniques. The design of the experiment is based on the Box–Behnken technique, which used four input parameters: feed rate, depth of cut, cutting speed, and nanofluid concentration, respectively. The experiments were performed on AISI 304 steel in turning with minimum quantity lubrication (MQL) and found that the use of hybrid nanofluid (Alumina–Graphene) reduces response parameters by approximately 13% in forces, 31% in surface roughness, and 14% in temperature, as compared to Alumina nanofluid. The response parameters are analyzed using analysis of variance (ANOVA), where the depth of cut and feed rate showed a major impact on response parameters. After using all three MCDM techniques, it was found that, at fixed weight factor with each MCDM technique, a similar process parameter was achieved (velocity of 90 m/min, feed of 0.08 mm/min, depth of cut of 0.6 mm, and nanoparticle concentration of 1.5%, respectively) for optimum response. The above stated multicriterion techniques employed in this work aid decision makers in selecting optimum parameters depending upon the desired targets. Thus, this work is a novel approach to studying the effectiveness of hybrid nanofluids in the machining of AISI 304 steel using MCDM techniques.

1. Introduction

Machining is a material removal process, in which undesired material is removed from the workpiece to give it a final shape. Different machining operations, such as turning, milling, grinding, and drilling, etc., are used in the manufacturing industry for metal cutting processes. The machining process aims to provide dimensional accuracy to the workpiece. Turning is one of the most widely used metal removal processes, used generally for cylindrical parts. To attain enhanced productivity, the wear of the tool and the obtained surface roughness of the workpiece must be minimal. At the interface of the cutting tool and workpiece, a large amount of heat is generated because of friction. This heat results in temperature generation, affecting tool life and the surface quality of the workpiece. Among the different varieties of steel alloys, the turning of AISI 304 steel is widely used in industries because of its diverse applications. There are a few challenges in the machining of AISI 304 steel alloy, as it possesses lower thermal conductivity along with the tendency of work hardening [1]. Thus, while machining AISI 304 steel, issues of rapid tool wear and increased cutting force are encountered, along with an increased cutting temperature [2]. For overcoming this temperature, cutting fluid is applied at the machining zone. The traditional approach to the application of cutting fluid is effective, but when used to an excess degree, it can cause a detrimental effect on human health as well as the environment.
To limit the use of traditional cutting fluid, the novel hybrid technique of minimum quantity lubrication (MQL) can be employed in the vicinity of the machining zone [3]. In this technique, the cutting fluid is engaged in the form of a spray, by applying pressurized air [4]. Hegab and Kishawy [5] used alumina and multiwalled carbon nanotube to investigate their effect on the energy consumption and the surface finish generated in the MQL assisted turning of Inconel 718. The carbon nanotube gave a better result than alumina and it was revealed that the weight % of the nanoparticle had a significant effect on the response parameters. The enhanced tribological and heat transfer properties of the nanoparticles added in the cutting fluid led to the improvement in surface characteristics by improving the interface bond between the Inconel surface and the cutting tool used. Sen et al. [6] performed a milling operation using a hybrid mixture of palm and castor oil with a mist lubrication technique. The reduction in surface roughness, by 16.14%, and 7.97% reduction in specific cutting energy, is reported. Duc et al. [7] performed hard turning on 90CrSi steel with minimum quantity lubrication. Alumina and molybdenum disulphide nanofluids are utilized for cutting fluid. A reduction in cutting force with an increase in thrust force is reported using MoS2 nanofluid. The use of both the nanoparticles in the MQL technique led to the improved performance of the carbide insert, due to the rise in the property of the base fluid in terms of thermal conductivity and lubrication. Bai et al. [8] studied the effect of different fluids using the minimum quantity lubrication technique on the response parameters. As per the authors, MQL or near dry machining is a suitable alternative for flood cooling in reducing environmental hazards, as well as production costs. The use of nanofluids as a coolant is seen as an emerging concept for machining purposes, as they possess enhanced heat transfer capabilities [9]. Do and Hsu [10] performed machining on AISI H13 and analysed the surface roughness using MQL. Higher cutting speed and low depth of cut resulted in improved surface finish using MQL. Dubey et al. [11] reviewed different methods of temperature measurement while machining. Prediction of temperature using thermocouples was found to be suitable. In another work, Dubey et al. [12] studied the effect of different cooling mechanisms on turning. Among various techniques, MQL was reported to be the most efficient lubrication method. Gupta et al. [13] optimized machining parameters in the turning of titanium alloy under the mist lubrication technique. The result revealed lower cutting force, using graphite nanofluids as it formed lower droplets because of a lower viscosity than the other two nanofluids, and resulted in deeper penetration at the machining zone. In the case of tool wear, graphite nanofluids also outperformed, as they possess better thermal conductivity than the other two and aided in dissipating heat and retaining the cutting tool hardness. Saini et al. [14] experimented on AISI-4340 steel under MQL conditions using different carbide inserts. The application of MQL resulted in a decrease in temperature of the chip–tool interface, thus maintaining the sharpness of the cutting edges of the tool. Singh et al. [15] investigated surface finish, cutting force, and tool wear on the turning of titanium alloy. The results revealed an enhancement in surface finish, by 15%, and a reduction in cutting force by using the near dry machining technique. Qu et al. [16] studied the machining of a ceramic matrix composite, with dry, flood, and minimum quantity lubrication. The improved surface finish obtained using nanofluids assisted MQL, along with less consumption of the cutting fluid in comparison to other lubrication techniques.
With the advancement in studies of nanofluids as lubricants in machining operation, researchers are now focussing on using hybrid nanofluids for enhanced heat transfer characteristics [17]. Babar and Ali [18] reviewed the synthesis and thermophysical properties of hybrid nanofluids. It was suggested that hybrid nanofluids possess superior thermal characteristics over mono nanofluids because mono nanofluid forms clusters, thus increasing the diameter of the particles and, thus, leading to an increase in pumping power and viscosity. The thermophysical characteristic of nanofluids (viscosity, specific heat, viscosity, and density) is improved by enhancing the nanoparticle concentration. Kumar et al. [19] studied the tribological behaviour of nanofluid on different categories of steel. It was revealed that the introduction of nanofluid aided in minimizing wear. Jamil et al. [20] used combinations of alumina and carbon nanotube particles for the hybrid nanofluids machining of titanium alloy with MQL. The obtained result was compared with cryogenic cooling and an improvement in tool life by 23% was observed. A reduction of 11.8% was suggested by the authors in cutting temperature using cryogenic cooling, in comparison to MQL. Zhang et al. [21] compared the effect of hybrid nanofluid with single nanofluid on response parameters while machining on nickel alloy. The application of alumina and silicon carbide hybrid nanofluids resulted in a reduction of cutting forces and surface roughness, respectively, as both the nanofluids gave a synergistic effect and improved the grinding performance. Gugulothu and Pasam [22] investigated the performance of carbon nanotube and molybdenum disulphide nanoparticle enriched cutting fluid for turning 1040 steel. An increase in thermal conductivity is noticed by increasing the particle size, while a decrease in viscosity is encountered when rising in temperature. A reduction in surface roughness, by 28.53% and 18.3%, is reported when compared with dry machining and traditional cutting fluid. Kumar et al. [23] performed machining on silicon nitride and compared the result with mono and hybrid nanofluids. The cutting force and surface roughness were reduced by 27% and 41%. Abbas et al. [24] optimized the turning parameters using Edgeworth–Pareto method for achieving minimum turning time. The obtained surface finish reported is 0.8µm. In another study, Abbas et al. [25] performed a sustainability assessment related to power consumption and surface characteristics in the machining of AISI 1045 steel. The use of alumina nanoparticles in mist lubrication significantly improved the surface characteristic and minimized the power consumption. The effect on response parameters can be attributed to the alumina nanofluid’s spraying ability, enhanced sliding behaviour, less friction, and seizure characteristic at the tool–workpiece contact. Alajmi and Almeshal [26] used artificial intelligence to optimize surface roughness in the turning of AISI 304 steel. It was revealed that ANFIS-QPSO resulted in a more accurate prediction of surface roughness. Su et al. [27] a used multiobjective criterion for optimising machining parameters of AISI 304 steel. The reduction in surface roughness and specific energy consumption was reported to be 66.90% and 81.46%. Khan et al. [28] performed a grinding operation on D2 steel using an alumina wheel, and compared dry machining with MQL grinding. The effectiveness of heat dissipation and the penetration property of the cutting fluid using MQL gave better results. Li et al. [29] investigated tool wear and surface topography in the turning of austenitic steel. Response surface methodology was used as the optimization technique. The effective cutting parameters obtained were 120 mm/min cutting speed and 0.18 feed rate along with 0.42 mm depth of cut.
From the literature, it is evident that the machining of AISI 304 steel has been attempted by different researchers using nanofluids in improving the machining performances in terms of reduced cutting force, tooltip temperature, and surface roughness. The optimization of the process parameters is performed using Taguchi, grey relational analysis, genetic algorithm, and response surface methodology, but very little work is reported on an analysis of optimal parameters using multicriterion decision making (MCDM) techniques using minimum quantity lubrication. In the present work, alumina and graphene nanoparticles are hybridized in different volumetric concentrations. The performance of the hybrid nanofluids is analyzed in terms of cutting forces, surface roughness, and nodal temperature for the MQL turning of AISI 304 steel. The study aims to analyze the synergistic effect of the hybrid nanofluids on the response parameters for the MQL turning of steel, and suggest the optimum parameter and cutting fluid that can be used by researchers and industries while machining steel. The results obtained are further compared with that of alumina particle nanofluid. Furthermore, the selection of the optimized machining level parameter and their respective ranking is ascertained using three MCDM techniques, namely, MOORA (Multiobjective Optimization Method by Ratio Analysis), VIKOR (VlseKriterijumska Optimizacija I Kompromisno Resenje), and TOPSIS (technique for order performance by similarity to ideal solution).

2. Materials and Methods

The experiment was performed using a conventional lathe Duo machine (Duo Machine Corps, Rajkot, India). Turning was carried on an AISI 304 steel workpiece of 60 mm diameter, whose chemical composition is mentioned in Table 1. WIDIA’s tungsten carbide inserts (CNMG 120408) of grade TN 2000 and corner radius of 0.8 were used as a cutting tool material which is clamped mechanically on WIDIA’s tool holder. The experimental response, such as cutting force, was measured by using a piezoelectric Kistler dynamometer (9257B). It consists of a charge amplifier of Type 5697A1, comprising hardware for the data acquisition and the DynoWare software (3.1.2.0) for operating and storing the value of average cutting force. Turning operation was performed for 250 mm length of cylindrical workpiece and the average value of cutting force was recorded. Mitutoyo surface roughness tester (SJ210) was used for average surface roughness measurement (Ra). It consists of a probe comprising of the diamond tip of a 2 µm radius that traverses on the workpiece. The cut off length is 0.08 mm and measuring speed is 0.25 mm/s, and the retraction speed of the probe is 1mm/s. The temperature measurement was performed using a K-type thermocouple, whose one end is clamped in a carbide insert, while the other end is attached to National Instrument’s data acquisition system, which recorded the cutting temperature. The cutting fluid used for machining is biodegradable oil based, which is enriched with water based alumina nanofluid and alumina–graphene hybrid nanofluid. The selection of nanofluids is carried out to analyze the synergistic effect of alumina (high conductivity) and graphene (high thermal conductivity along with lubricity) on turning in MQL environment. The combined properties of both nanoparticles are essential for any cutting fluid used in machining. The samples of mono and hybrid nanofluids were prepared in a volumetric ratio of 90:10 in three varying volumetric concentrations of 0.5%, 1%, and 1.5%, respectively. For the discharge of the cutting fluid, a minimum quantity lubrication setup was used. The experiments were repeated thrice and the average value was taken of the responses for better accuracy. The experimental setup is shown in Figure 1.
Design of experiment is made by using MINITAB-19 and for statistical analysis response surface methodology’s Box–Behnken design was used, with four factors at three different levels where the factors are, namely, depth of cut, feed rate, cutting velocity, and nanofluid concentration, which is shown in Table 2. Due to 4 factors with 3 levels, the design contains 27 possible combinations to perform experiments. Table 3 contains all 27 combinations which give the most effective results of response parameters.
Optimization is very important in a production system because it helps to achieve good product quality at minimum cost. In this paper, there are three response parameters, and optimizing them individually may take a significant amount of time, effort and increase process complexity. Therefore, this paper deals with four optimization techniques to obtain a better result.

2.1. Response Surface Methodology

Response surface methodology is a collection of statistical and mathematical techniques which are useful for the modeling and analysis of a problem in which the response of interest is influenced by multiple variables and the objective is to optimize the response. Response surface methodology is used for surface analysis of response parameters; along with that, problems formulation and process optimization can also be performed using RSM [30].

2.2. Multicriterion Decision Making

Multicriteria decision making is mainly aimed at the optimization of conflicting responses, but in this paper, it is utilized for optimizing multiple criteria of nonconflicting nature. It is very useful when the number of response parameters is large in the count, because it calculates the optimized results for two responses and more than two responses in the same number of steps. The methodology used in these techniques is shown in Figure 2. Here, the goal is to mainly check the reliability of three MCDM techniques (MOORA, VIKOR, TOSIS) for nonconflicting responses [31,32].

2.2.1. Multiobjective Optimization Based on Ratio Analysis (MOORA)

MOORA is a simpler and popular MCDM technique; it is used to simultaneously optimize two or more than two conflicting/nonconflicting response parameters [33,34]. It is mainly used for the quantitative attribute.

2.2.2. VIKOR

The VIKOR method is a multicriteria decision making (MCDM) or multicriteria decision analysis method. It was originally developed by Serafim Opricovic (1979-80) to solve decision problems with conflicting and noncommensurable (different units) criteria. It is used to simultaneously optimize two or more two responses. The decision maker desires to have a solution that is nearest to the ideal, whereas the alternatives are evaluated as per the established criteria. VIKOR ranks alternatives and determines the solution, named compromise, that is the closest to the ideal [35].

2.2.3. TOPSIS

TOPSIS is an MCDM technique. It is also used to calculate the optimized value when responses are large in number. It is a technique for order of preference by similarity to the ideal solution. It was developed by Ching-Lai Hwang and Yoon in 1981 and, further, it was developed by Yoon in 1981 and Harang in 1993 [36].

3. Results

In this paper, there are three major responses, namely, force, surface roughness, and temperature. All the three selected response parameters come under the nonbeneficial category; therefore, all of them should be at their minimum. To minimize them, proper lubrication and cooling are required at the machining interface. Therefore, in the present paper, mono and hybrid nanofluids with an MQL setup is used for cooling and lubrication purpose. As per the experimental results, it is found that the response parameters give more promising results, as they aided in reducing cutting forces, tool temperature, and surface roughness with hybrid nanofluids, as compared to single nanofluids alone, as shown in Table 4.

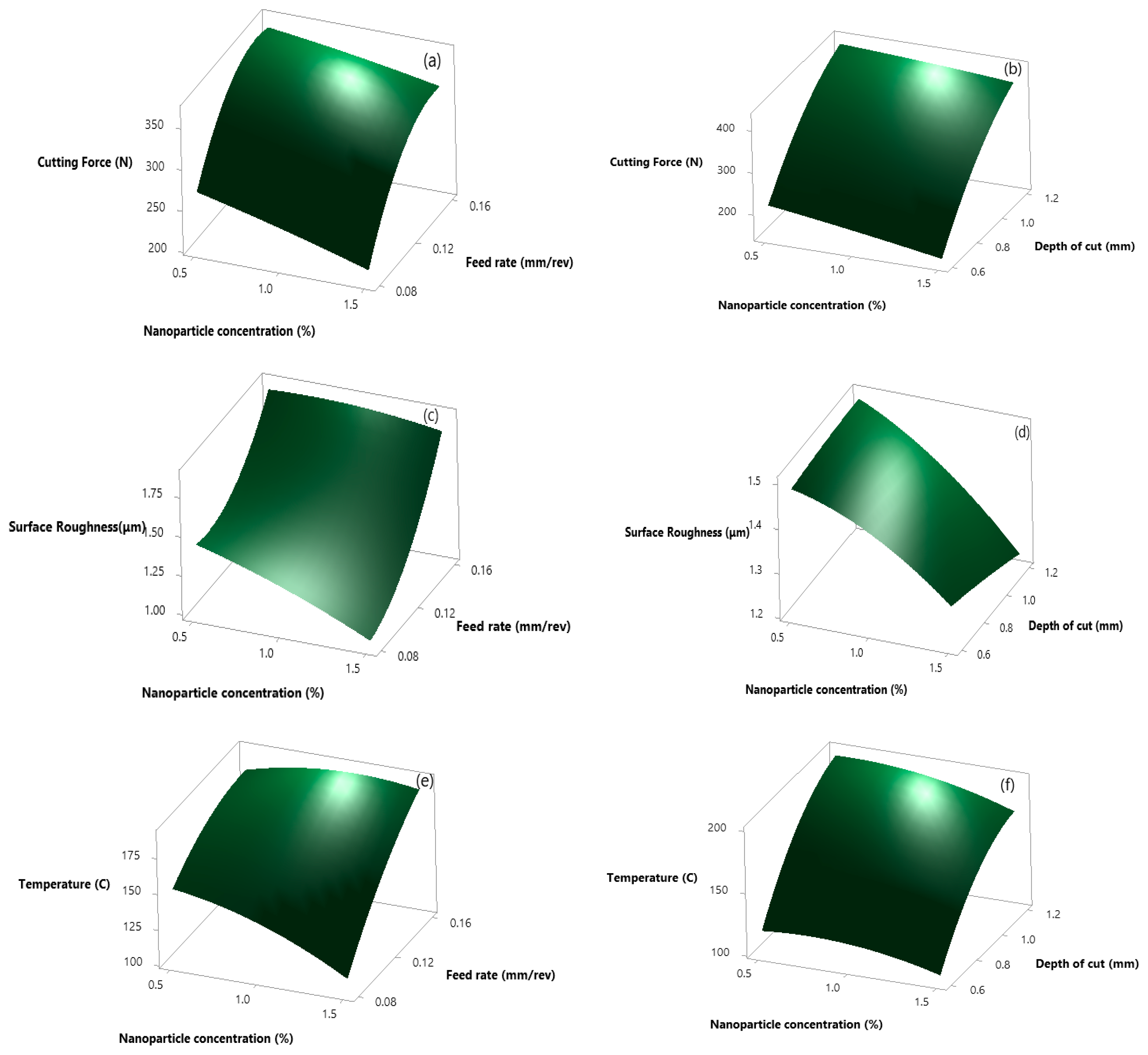
3.1. Response Surface Methodology

RSM is used as a multipurpose technique: it can help to create mathematical model to predict the response and it can also help to analyze the surface response through the response surface curve for better understanding the effect of a process parameter on a response parameter; it also helps in the analysis of variance of process parameters and it can also calculate the optimized parameter. In this paper, a second degree model is used for performing data analysis and to determine the significance of the model’s parameters, calculation of mean response, and to arrive at optimum operating conditions on the control variables that helps to achieve a maximum or a minimum response over a certain region of interest. Therefore, after getting response parameters (Table 4), the quadratic model has been developed for the analysis of variance to check the stability and significance of the response, as well as process parameters [37]. The mathematical model for response parameters is discussed in the equations given below:
For alumina
Cutting Force = −370 − 1.86vc + 3378 fo + 874 ap − 49 np% − 0.0055 vc * vc − 13159 fo * fo − 418 ap * ap − 12.0 np%*np% + 5.5 vc * fo + 2.13 vc * ap − 0.067 vc *np%+ 931 fo * ap + 354 fo *np% − 13.9ap*np%.
Surface Roughness = 2.34 + 0.0069 vc − 23.52 fo + 1.68 ap − 0.306 np% − 0.000001 vc * vc + 143.7 fo * fo − 0.169 ap * ap − 0.138 np%*np% − 0.0275 vc * fo − 0.00796 vc * ap − 0.00317 vc *np%− 4.02 fo * ap + 6.38 fo *np% − 0.234 ap *np%
Temperature = −95 − 2.01 vc + 2248 fo + 433 ap − 108.6 np%− 0.00094 vc * vc − 3501 fo * fo − 212.1 ap * ap − 16.6 np%*np% − 4.79 vc * fo + 1.896 vc * ap + 1.357 vc *np% − 532 fo * ap + 153 fo *np% − 17.5 ap *np%
For alumina–graphene
Cutting Force = −350 − 2.27 vc + 5998 fo + 646 ap − 146 np%+ 0.0044 vc * vc − 22338 fo * fo − 351 ap * ap − 7.6 np%*np% − 7.6 vc * fo + 1.76 vc * ap + 0.32 vc *np% + 1223 fo * ap + 292 fo *np%+ 59 ap *np%
Surface Roughness = 1.20 + 0.01201 vc − 14.02 fo + 0.988 ap − 0.023 np% − 0.000020 vc * vc + 97.6 fo * fo − 0.038 ap * ap − 0.120 np%*np% − 0.0399 vc * fo − 0.00541 vc * ap − 0.00415 vc *np% − 2.75 fo * ap + 4.39 fo *np%− 0.143 ap *np%
Temperature = 47 − 3.66 vc + 1187 Feed + 399 ap − 134.9 np%+ 0.00684 vc * vc − 4758 Feed*Feed − 171.3 ap * ap − 26.7 np%*np% + 4.54 vc *Feed + 1.171 vc * ap + 1.230 vc *np%− 459 Feed* ap + 615 Feed*np% − 15.2 ap *np%
The above mentioned regression model helps to predict the response parameters, i.e., cutting force, temperature, roughness. Now, the analysis of variance is required to analyze the significance and influence of the process parameters and their factors on response parameters. ANOVA was carried out at a 95% confidence level, which means the p-value of the factors must be less than 0.05 to satisfy the condition of a significant factor criteria. The coefficient of determinant, i.e., R2 and adjusted R2, is also one of the parameters to show the significance of experimental results. A regression model helps to calculate the coefficient of the determinant, and it should be more the 80% because, for the experimental results, 80% is an acceptable limit [38]. The ANOVA analysis, describing the p-value and percentage contribution of the response parameters in alumina and alumina–graphene enriched cutting fluid, is given in Table 5 and Table 6.
In Table A1, the analysis of the variance for force has been carried out to analyze the significance of the process parameters and their impact on the response parameter i.e., force. Table A1 signifies that depth of cut has a major impression on cutting force, approximately 65.2841%, which is the highest among all of the process parameters and their factors. As discussed above, parameters having a p-value <0.05 are significant; therefore, velocity, feed, depth of cut, np% and velocity*velocity, velocity* depth of cut, feed*np% are the significant parameters for cutting force. The coefficient of determinant is also used to show the significance and accuracy of experimental results: if R2 and adjusted R2 is greater than 90% the output is acceptable. In the case of cutting force, R2 is 96.25% and adjusted R2 is 91.87%. In Table A2, the analysis of the variance for roughness has been carried out, to analyze the significance of the process parameters and their impact on response parameter i.e., surface roughness. Table 5 signifies that the feed rate makes a major impression on surface roughness, approximately 62.38%, which is the highest among all of the process parameters and their factors. The coefficient of determinant is also used to show the significance and accuracy of experimental results: if R2 and adjusted R2 is greater than 90% the output is acceptable. In the case of surface roughness, R2 is 95.76% and adjusted R2 is 90.81%. In Table A3, ANOVA signifies that depth of cut makes a major impression on tool temperature, approximately 55.53%, which is the highest among all of the process parameters and their factors. The coefficient of determinant also use to show the significance and accuracy of experimental results, so, in the case of tool temperature, R2 is 95.52% and adjusted R2 is 90.29%.
In Table A4, an analysis of the variance for cutting force has been carried out to analyze the significance of the process parameter and their impact on cutting force. Table A4 signifies that depth of cut makes a major impression on cutting force, it contributes approximately 68.977% which is the highest among all the process parameters and their factors. The coefficient of determinant is also used to show the significance and accuracy of experimental results: if R2 and adjusted R2 is greater than 90% the output is acceptable. In the case of surface roughness, R2 is 94.96% and adjusted R2 is 89.09%. In the case of Table A5, the feed rate shows the major impact on surface roughness. It contributes approximately 57.547%, which is the highest among all the process parameters and their factors; while the coefficient of the determinant of experimental calculated R2 as 95.60% and adjusted R2 as 90.47%. In Table A6, ANOVA signifies that the depth of cut makes a major impression on tool temperature, approximately 48.52%, which is the highest among all of the process parameters and their factors. The coefficient of determinant is also used to show the significance and accuracy of experimental results, so, in the case of tool temperature, R2 is 93.53%and adjusted R2 is 85.99%%.
As ANOVA signifies the impact of process parameters on response parameters, similarly, the response surface curve shows the variation in response parameters by varying input. Figure 3 represents the response surface curve at variable feed, depth of cut, and nanofluid concentration for Al2O3 nanoparticles. Figure 3a,b shows variation in forces, with 0.08 feed rate, 1.5% nanofluid concentration and 0.6 depth of cut force as minimum. The reduction in cutting force can be attributed to the rolling effect produced by the spherical size of alumina, which possesses high strength, hardness and delivers enough abrasive resistance in the process of friction and aids in minimizing the frictional coefficient in the zone of contact [39]. Figure 3c,d explains variation in surface roughness, at maximum nanofluid concentration and minimum feed rate, depth of cut surface roughness is minimum as alumina resulted in minimizing the adhesion between the tool insert and workpiece and forming a tribo film, thus resulting in improved surface quality [40]. Similarly, Figure 3e,f, shows the responses plot for temperature, and, in both cases, at maximum nanofluid concentration and minimum feed rate responses are minimum.
As discussed in the case of alumina nanofluid, similar results are shown in the case of hybrid nanofluid (alumina–graphene). Figure 4 shows the variation in responses (force, surface roughness, and temperature) by varying input parameters. Figure 4a, b shows the response surface curve for cutting force, at the minimum value of feed rate, depth of cut, and maximum nanofluid concentration. The reduction in cutting force is more in the case of alumina–graphene hybrid nanofluids machining as compared to alumina nanofluids due to the exfoliation of the sheet like structure of graphene because of the shearing action produced by the chip on the tool rake face. In Figure 4c–f, surface roughness and temperature, at a 0.08 feed rate, 1.5% nanofluid concentration, and 0.6 depth of cut force is minimum. After analyzing both the figures, force, surface roughness, and temperature increase, while the increase in depth of cut and feed at minimum nanofluid concentration and decreases with a decrease in depth of cut and feed at maximum concentration [37].

3.2. MOORA Analysis for Mono and Hybrid Nanofluid

MOORA is used for selecting the best optimum parameters. Table A7 and Table A8 contain the decision matrix, normalized decision matrix, and assessed value for alumina and alumina–graphene based nanofluid results. The decision matrix contains all the response parameters, such as force, surface roughness, and temperature. Normalization of the matrix is performed to convert them into dimensionless quantities. After normalization of the decision matrix, it will be further multiplied with the weight factor and convert the matrix into the weighted normalized matrix; after that, assessment values (Bi) for the considered alternatives were determined and ranking them in descending order, the maximum value is ranked as the best (rank 1) and the minimum is ranked as the worst (rank27) [41,42]. The combined analysis of different MCDM techniques and the respective ranks obtained from the decision-making criteria used in mono and hybrid nanofluid cutting fluid based machining is mentioned in Table 7 and Table 8.

3.3. VIKOR Analysis for Mono and Hybrid Nanofluid

VIKOR is a multicriteria optimization technique used for selecting the best optimum parameters in a conflicting and nonconflicting response. Table A9 and Table A10 contain the decision matrix, normalized decision matrix, and VIKOR index for alumina and alumina–graphene based nanofluid results. The decision matrix contains all the response parameters, such as force, surface roughness, and temperature. Normalization of the matrix is performed to convert them into dimensionless quantities. After normalization of the decision matrix, it will be further multiplied with the weight factor and convert the matrix into the weighted normalized matrix, at the end, the VIKOR index was determined and they were ranked in ascending order: the minimum VIKOR index value is ranked as the best (rank 1) and the maximum VIKOR index is ranked as the worst (rank27) [43,44,45].

3.4. TOPSIS Analysis for Mono and Hybrid Nanofluid

TOPSIS analysis is used to predict ideal solutions in multiresponse parameters. Table A11 and Table A12 contain the decision matrix, normalized decision matrix, and relative ideal solution for alumina and alumina–graphene based nanofluid results. Decision matrices contain response parameters such as force, roughness, and temperature. After forming a decision matrix, normalization of the matrix is required to convert them into dimensionless quantities. Afterward, the weighted normalized matrix has been formed by multiplying the weight factor with the normalized matrix. Next, the positive ideal solution (s+) and negative ideal solutions (s−) were calculated. Ranking of the ideal solution has been assigned by arranging them in descending order [46,47,48,49].
The optimum results obtained from all four techniques are summarized in Table 9. In all four techniques, RSM gives the minimum optimized results, whereas the rest of the three techniques give similar optimum results. RSM gives the optimum output value for the new input parameters, which are different from the input parameters mentioned in the design of the experiment; whereas the MCDM techniques give ideal results from the 27 experimentals used in this paper [50,51].

4. Conclusions

The methodology used in this paper, of using multicriterion decision-making techniques in selecting the optimum parameters while performing turning operations with mono and hybrid nanofluids enriched with cutting fluid, is novel in this field. As nanofluids are very costly, their use in an efficient manner needs to be studied. The present study can help researchers and industries in choosing the optimum parameters while machining AISI 304 steel, which has wide applications. As per the experimental results, hybrid nanofluids seem to be more effective than a single nanofluid. This paper deals with three response parameters—force, surface roughness, and temperature—all of which are nonbeneficial; therefore, they should have the minimum value. After comparing the results, the following conclusions are made and summarized below:
  • The use of hybrid nanofluid (alumina–graphene) resulted in an average reduction of response parameters by approximately 13% in cutting forces, 31% in surface roughness, and 14% in temperature, when compared to alumina nanofluid.
  • It can be seen that the use of nanoparticle concentration in a lesser amount resulted in better surface characteristics and resulted in the lowering of cutting forces.
  • Analysis of variance revealed the influence of input parameters on the response parameters. In both the cases, i.e., single and hybrid nanofluid, depth of cut showed a major impact while calculating force and temperature. The contribution of the depth of cut is approximately 65.81% and 57.63% in the case of single nanofluid while in the case of hybrid the % contributions are 68.38% and 51.14%, respectively. However, in the case of surface roughness, the most influenced parameter is the feed rate: its contributions in the cases of single and hybrid nanofluid are 63.18% and 58.47%, respectively.
  • Response surface methodology is used for optimizing the response. As per RSM, the best process parameters for optimum response in the case of Al2O3 are 86.667 m/min velocity, 0.08 mm/min feed rate, 0.6 mm depth of cut, and at 1.5% of nanoparticle concentration. In the case of alumina–graphene, the suitable parameters for optimum results are 110.909 m/min velocity, 0.08 mm/min feed rate, 0.6484 mm depth of cut, and a nanoparticle concentration of 1.5%, respectively.
  • The multicriteria decision-making techniques are used, such as MOORA, VIKOR, and TOPSIS for nonconflicting, nonbeneficial responses at 0.5 weight factor. According to the MCDM techniques, the best input parameter for optimum response is at 90 m/min velocity, 0.6 mm depth of cut, 0.08 mm/min feed rate, and 1% nanoparticle concentration.
  • All three MCDM techniques showed similar responses, at a constant or fixed weight factor of 0.5.
The present paper discusses machining performance using hybrid nanofluids. Here, graphene was used for developing hybrid nanofluids. Though it gave desirable results when compared to alumina, it is costly, so there is a need to find a cheaper alternative for graphene for hybridization, so that machining cost can be minimized. Moreover, in this research, both the nanoparticles (alumina–graphene) were mixed in a fixed mixing ratio of 90:10. There is a need to use different mixing ratios and further optimize the mixing ratio so that the optimum value can be obtained. In the future, further research can be performed on the optimization of MQL parameters. Furthermore, work on the hybridization of MCDM techniques can also be done. The thermal modeling of the cutting tool in multiphase using hybrid nanofluids is yet to be explored.

Author Contributions

Conceptualization, V.D. and A.K.S.; methodology, V.D.; software, V.D. and A.K.S.; validation, A.K.S., V.D. and P.V.; formal analysis, V.D.; investigation, V.D.; resources, A.K.S. and V.D.; data curation, V.D. and A.K.S.; writing—original draft preparation, V.D.; writing—review and editing, V.D., A.K.S., D.Y.P., K.G. and D.C.; visualization, V.D. and A.K.S.; supervision, A.K.S.; project administration, A.K.S. and V.D.; funding acquisition, D.Y.P., K.G. and D.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

FcCutting force
VcCutting speed
apDepth of cut
np%Nanofluid concentration
foFeed rate
BiAssignment value
RiRelation closeness
QiVIKOR index
uUtility
rRegret
s+Separation from best solution
s−Separation from worst solution
MQLMinimum quality lubrication
MOORAMultiobjective optimization on the basis of ratio analysis
VIKORVIšekriterijumsko KOmpromisno Rangiranje
TOPSISTechnique for order of preferences by similarity to the ideal solution
MCDMMulticriteria decision making
RSMResponse surface methodology

Appendix A

Table
Table A1. Analysis of variance for cutting force using alumina.
Table A1. Analysis of variance for cutting force using alumina.
SourceDFAdj SSAdj MSF-Valuep-Value%
Contribution		Remark
Model14271,91219,42232.210.000
Linear4260,30665,076107.910.000
Vc1125012502.070.1750.44779
fo169,69369,693115.560.00024.96624significant
ap1182,240182,240302.190.00065.28413significant
np%17122712211.810.0052.551326significant
Square4923623093.830.031
Vc * Vc 11301300.220.6510.04657
fo * fo 1236423643.920.0710.84686significant
ap * ap 17564756412.540.0042.709664significant
np%*np%148480.080.7820.017195
2-Way Interaction623703950.650.687
Vc* fo11731730.290.6020.061974
Vc * ap1147514752.450.1440.528392
Vc *np%1440.010.9360.001433
fo * ap15005000.830.3810.179116
fo *np%12012010.330.5750.072005
ap *np%118180.030.8680.006448
Error127237603 2.592522
Lack-of-Fit1065986602.070.3702.363612
Pure Error2639319 0.22891
Total26279,149 100
Table
Table A2. Analysis of variance of surface roughness using alumina.
Table A2. Analysis of variance of surface roughness using alumina.
SourceDFAdj SSAdj MSF-Valuep-Value%
Contribution		Remark
Model143.757740.2684121.990.000
Linear43.252670.8131766.610.000
Vc10.518840.5188442.500.00013.28918significant
fo12.435652.43565199.520.00062.3849significant
ap10.004090.004090.330.5740.104758
np%10.294090.2940924.090.0007.532599significant
Square40.391760.097948.020.002
Vc * Vc 10.000010.000010.000.9810.000256
fo * fo 10.282010.2820123.100.0007.223191significant
ap * ap 10.001240.001240.100.7550.03176
np%*np%10.006380.006380.520.4840.163413
2-Way Interaction60.113310.018891.550.245
Vc* fo10.004340.004340.360.5620.111161
Vc * ap10.020550.020551.680.2190.526352
Vc *np%10.009040.009040.740.4060.231544
fo * ap10.009310.009310.760.4000.238459
fo *np%10.065140.065145.340.0391.668447
ap *np%10.004930.004930.400.5370.126273
Error120.146490.01221 3.752084
Lack-of-Fit100.144210.0144212.630.0763.693686
Pure Error20.002280.00114 0.058398
Total263.90423 100
Table
Table A3. Analysis of variance of temperature using alumina.
Table A3. Analysis of variance of temperature using alumina.
SourceDFAdj SSAdj MSF-Valuep-Value%
Contribution		Remark
Model1436,667.42619.119.340.000
Linear431,351.57837.957.880.000
Vc11061.51061.57.840.0162.772098significant
fo18140.18140.160.120.00021.2578significant
ap121,264.321,264.3157.040.00055.53153significant
np%1885.6885.66.540.0252.312737significant
Square42134.3533.63.940.029
Vc * Vc 13.83.80.030.8690.009924
fo * fo 1167.3167.31.240.2880.436902
ap * ap 11943.31943.314.350.0035.074911significant
np%*np%192.192.10.680.4260.240518
2-Way Interaction63181.6530.33.920.021
Vc* fo1132.1132.10.980.3430.344978
Vc * ap11165.01165.08.600.0133.042387significant
Vc *np%11656.11656.112.230.0044.32489significant
fo * ap1163.3163.31.210.2940.426456
fo *np%137.537.50.280.6080.097931
ap *np%127.627.60.200.6600.072077
Error121624.9135.4 4.243412
Lack-of-Fit101551.4155.14.230.2064.051467
Pure Error273.436.7 0.191683
Total2638,292.3 100
Table
Table A4. Analysis of variance for force using alumina–graphene.
Table A4. Analysis of variance for force using alumina–graphene.
SourceDFAdj SSAdj MSF-Valuep-Value%
Contribution		Remark
Model14214,02215,28716.170.000
Linear4198,61449,65452.510.000
Vc1262326232.770.1221.163
fo134,62234,62236.610.00015.362significant
ap1155,455155,455164.390.00068.977significant
np%1591559156.250.0282.624significant
Square412,66731673.350.046
Vc * Vc 184840.090.7710.037
fo * fo 1681368137.200.0203.0230significant
ap * ap 1531253125.620.0352.357significant
np%*np%119190.020.8880.0084
2-Way Interaction627414570.480.809
Vc* fo13363360.350.5620.149
Vc * ap19999991.060.3240.443
Vc *np%190900.100.7630.039
fo * ap18618610.910.3590.382
fo *np%11371370.140.7100.060
ap *np%13183180.340.5730.141
Error1211,348946 5.035
Lack-of-Fit1011,222112217.880.0544.979
Pure Error212663 0.055
Total26225,370 100
Table
Table A5. Analysis of variance of surface roughness using alumina–graphene.
Table A5. Analysis of variance of surface roughness using alumina–graphene.
SourceDFAdj SSAdj MSF-Valuep-Value%
Contribution		Remark
Model141.898930.1356418.630.000
Linear41.637370.4093456.240.000
Vc10.323640.3236444.460.00016.293significant
fo11.143061.14306157.040.00057.547significant
ap10.001880.001880.260.6210.094
np%10.168800.1688023.190.0008.498significant
Square40.190340.047586.540.005
Vc * Vc 10.001800.001800.250.6280.0906
fo * fo 10.129940.1299417.850.0016.5418significant
ap * ap 10.000060.000060.010.9270.0030
np%*np%10.004770.004770.660.4340.240
2-Way Interaction60.071220.011871.630.2223.585
Vc* fo10.009180.009181.260.2830.462
Vc * ap10.009500.009501.300.2760.478
Vc *np%10.015520.015522.130.1700.781
fo * ap10.004360.004360.600.4540.219
fo *np%10.030840.030844.240.0621.552
ap *np%10.001830.001830.250.6250.092
Error120.087340.00728 4.397
Lack-of-Fit100.086060.0086113.340.0724.332
Pure Error20.001290.00064 0.064
Total261.98628 100
Table
Table A6. Analysis of variance of temperature using alumina–graphene.
Table A6. Analysis of variance of temperature using alumina–graphene.
SourceDFAdj SSAdj MSF-Valuep-Value%
Contribution		Remark
Model1432,997.82357.012.400.000
Linear428,041.77010.436.880.000
Vc11746.01746.09.180.0104.949significant
fo18247.78247.743.390.00023.378significant
ap117,118.417,118.490.050.00048.522significant
np%1929.6929.64.890.0472.6349significant
Square42285.2571.33.010.062
Vc * Vc 1201.8201.81.060.3230.572
fo * fo 1309.2309.21.630.2260.876
ap * ap 11267.81267.86.670.0243.593significant
np%*np%1238.0238.01.250.2850.674
2-Way Interaction62671.0445.22.340.099
Vc* fo1118.9118.90.630.4440.337
Vc * ap1444.5444.52.340.1521.259
Vc *np%11360.81360.87.160.0203.857significant
fo * ap1121.3121.30.640.4400.343
fo *np%1604.7604.73.180.1001.7140
ap *np%120.820.80.110.7470.0589
Error122281.2190.1 6.4661
Lack-of-Fit102226.7222.78.160.1146.3116
Pure Error254.627.3 0.1547
Total2635,279.0 100
Table
Table A7. MOORA analysis for alumina.
Table A7. MOORA analysis for alumina.
Decision MatrixNormalizing Matrix
Cutting Force
(N)		Surface Rough
Ness
(µm)		Temperature
(°C)		 BRank
511.45682.63064238.7170.27190.23760.2433−0.376427
461.0752.29599195.5520.24510.20740.1993−0.325919
304.05941.426832198.82720.16170.12890.2026−0.24669
247.8412.15581149.86450.13180.19470.1527−0.23968
374.39742.051186197.34110.19900.18520.2011−0.292715
427.32592.360216216.51330.22720.21320.2207−0.330521
464.47951.767456242.05620.24690.15960.2467−0.326620
250.76421.627584190.16160.13330.14700.1938−0.23717
363.3421.717272193.60790.19320.15510.1973−0.272813
270.59311.893312155.1810.14390.17100.1582−0.23656
360.64162.016965192.67460.19170.18220.1964−0.285114
409.76011.924486196.38890.21780.17380.2002−0.295916
447.63681.830473211.64540.23800.16530.2157−0.309518
396.09151.983618204.69360.21060.17910.2086−0.299217
437.96752.946243215.54250.23280.26610.2197−0.359326
174.44231.914002128.10410.09270.17290.1306−0.19812
220.72512.050069143.72650.11730.18510.1465−0.22455
142.74041.65594783.773850.07590.14950.0854−0.15541
299.39172.214356170.13350.15920.20000.1734−0.266311
260.64971.569603158.50220.13860.14180.1615−0.22094
325.6482.052732137.56020.17310.18540.1402−0.249410
469.72632.047881224.67520.24970.18490.2290−0.331822
207.00411.973061141.20010.11010.17820.1439−0.21613
246.15142.76224154.440.13090.24950.1574−0.268912
425.76692.531105214.13870.22640.22860.2182−0.336623
436.18392.665395213.52290.23190.24070.2176−0.345124
444.45712.54873227.53970.23630.23020.2319−0.349225
Table
Table A8. MOORA analysis for alumina–graphene.
Table A8. MOORA analysis for alumina–graphene.
Decision MatrixNormalizing Matrix
Cutting Force
(N)		Surface Rough
Ness
(µm)		Temperature
(°C)		 BRank
466.9821.833206.2950.28330.23860.2409−0.381427
416.0101.601185.7310.25240.20830.2168−0.338824
275.5660.881184.5490.16720.11460.2155−0.24868
218.8821.505129.4790.13280.19590.1512−0.23996
341.8411.431170.5090.20740.18620.1991−0.296416
428.1871.643187.0830.25980.21390.2184−0.346026
420.2141.231209.1470.25490.16020.2442−0.329621
245.7001.131173.6710.14910.14720.2028−0.24959
322.8661.193167.2940.19590.15520.1953−0.273213
251.7891.318134.0840.15280.17160.1565−0.24047
329.2831.410166.5040.19980.18350.1944−0.288914
381.8231.338169.7410.23160.17410.1982−0.302017
408.7181.281182.9150.24800.16670.2136−0.314118
327.1951.381176.8620.19850.17970.2065−0.292315
352.9062.061168.3710.21410.26830.1966−0.339525
159.8591.330110.7310.09700.17310.1293−0.19973
185.9991.431124.1990.11280.18630.1450−0.22215
117.9171.15172.4280.07150.14980.0846−0.15301
247.3241.542147.0020.15000.20070.1716−0.261211
215.3191.09098.3960.13060.14180.1149−0.19372
302.9671.436128.1140.18380.18680.1496−0.260110
388.0411.426194.1900.23540.18560.2267−0.323919
171.0101.371122.0440.10370.17850.1425−0.21244
203.3451.924133.4580.12340.25040.1558−0.264812
351.7211.763185.0770.21340.22940.2161−0.329520
360.3431.864184.5020.21860.24260.2154−0.338323
310.1811.683229.7700.18820.21900.2683−0.337722
Table
Table A9. VIKOR analysis for alumina.
Table A9. VIKOR analysis for alumina.
Decision MatrixNormalizing Matrix
Cutting Force
(N)		Surface Rough
Ness
(µm)		Temperature
(°C)		 urQRank
511.45682.63064238.7170.27190.23760.2433−0.5797−0.19321.000027
461.0752.29599195.5520.24510.20740.1993−0.5798−0.19320.776321
304.05941.426832198.82720.16170.12890.2026−0.5800−0.19330.423210
247.8412.15581149.86450.13180.19470.1527−0.5800−0.19330.37509
374.39742.051186197.34110.19900.18520.2011−0.5799−0.19330.521414
427.32592.360216216.51330.22720.21320.2207−0.5798−0.19330.713419
464.47951.767456242.05620.24690.15960.2467−0.5798−0.19320.785322
250.76421.627584190.16160.13330.14700.1938−0.5800−0.19330.36568
363.3421.717272193.60790.19320.15510.1973−0.5800−0.19330.460812
270.59311.893312155.1810.14390.17100.1582−0.5801−0.19330.27115
360.64162.016965192.67460.19170.18220.1964−0.5799−0.19330.484813
409.76011.924486196.38890.21780.17380.2002−0.5799−0.19330.597016
447.63681.830473211.64540.23800.16530.2157−0.5799−0.19320.710018
396.09151.983618204.69360.21060.17910.2086−0.5799−0.19330.574715
437.96752.946243215.54250.23280.26610.2197−0.5797−0.19320.937526
174.44231.914002128.10410.09270.17290.1306−0.5802−0.19330.19182
220.72512.050069143.72650.11730.18510.1465−0.5801−0.19330.30176
142.74041.65594783.773850.07590.14950.0854−0.5803−0.19340.00001
299.39172.214356170.13350.15920.20000.1734−0.5800−0.19330.456911
260.64971.569603158.50220.13860.14180.1615−0.5801−0.19330.19723
325.6482.052732137.56020.17310.18540.1402−0.5800−0.19330.35907
469.72632.047881224.67520.24970.18490.2290−0.5798−0.19320.808525
207.00411.973061141.20010.11010.17820.1439−0.5801−0.19330.25434
246.15142.76224154.440.13090.24950.1574−0.5800−0.19320.665017
425.76692.531105214.13870.22640.22860.2182−0.5798−0.19330.732920
436.18392.665395213.52290.23190.24070.2176−0.5798−0.19320.801724
444.45712.54873227.53970.23630.23020.2319−0.5797−0.19320.792923
Table
Table A10. VIKOR analysis for alumina–graphene.
Table A10. VIKOR analysis for alumina–graphene.
Decision MatrixNormalizing Matrix
Cutting Force
(N)		Surface Rough
Ness
(µm)		Temperature
(°C)		 urQRank
466.9821.833206.2950.28330.23860.2409−0.5797−0.19321.000027
416.0101.601185.7310.25240.20830.2168−0.5798−0.19320.797523
275.5660.881184.5490.16720.11460.2155−0.5800−0.19330.469812
218.8821.505129.4790.13280.19590.1512−0.5800−0.19330.38167
341.8411.431170.5090.20740.18620.1991−0.5799−0.19330.545615
428.1871.643187.0830.25980.21390.2184−0.5798−0.19320.839524
420.2141.231209.1470.25490.16020.2442−0.5798−0.19320.786522
245.7001.131173.6710.14910.14720.2028−0.5800−0.19330.42689
322.8661.193167.2940.19590.15520.1953−0.5800−0.19330.454311
251.7891.318134.0840.15280.17160.1565−0.5800−0.19330.29665
329.2831.410166.5040.19980.18350.1944−0.5799−0.19330.502313
381.8231.338169.7410.23160.17410.1982−0.5799−0.19320.643617
408.7181.281182.9150.24800.16670.2136−0.5798−0.19320.727820
327.1951.381176.8620.19850.17970.2065−0.5799−0.19330.533714
352.9062.061168.3710.21410.26830.1966−0.5798−0.19320.855126
159.8591.330110.7310.09700.17310.1293−0.5802−0.19330.21313
185.9991.431124.1990.11280.18630.1450−0.5801−0.19330.30836
117.9171.15172.4280.07150.14980.0846−0.5803−0.19340.00001
247.3241.542147.0020.15000.20070.1716−0.5800−0.19330.445010
215.3191.09098.3960.13060.14180.1149−0.5802−0.19340.08912
302.9671.436128.1140.18380.18680.1496−0.5800−0.19330.39378
388.0411.426194.1900.23540.18560.2267−0.5798−0.19320.704919
171.0101.371122.0440.10370.17850.1425−0.5801−0.19330.25974
203.3451.924133.4580.12340.25040.1558−0.5800−0.19320.628516
351.7211.763185.0770.21340.22940.2161−0.5798−0.19330.696018
360.3431.864184.5020.21860.24260.2154−0.5798−0.19320.762021
310.1811.683229.7700.18820.21900.2683−0.5798−0.19320.851325
Table
Table A11. TOPSIS analysis for alumina.
Table A11. TOPSIS analysis for alumina.
Decision MatrixNormalizing Matrix
Cutting Force
(N)		Surface Rough
Ness
(µm)		Temperature
(°C)		 S+S−RiRank
511.45682.63064238.7170.27190.23760.24330.13710.01440.09527
461.0752.29599195.5520.24510.20740.19930.10930.04000.26821
304.05941.426832198.82720.16170.12890.20260.07260.09070.55510
247.8412.15581149.86450.13180.19470.15270.05480.09160.6267
374.39742.051186197.34110.19900.18520.20110.08910.05900.39815
427.32592.360216216.51330.22720.21320.22070.10990.03700.25222
464.47951.767456242.05620.24690.15960.24670.11860.05470.31619
250.76421.627584190.16160.13330.14700.19380.06200.09510.6058
363.3421.717272193.60790.19320.15510.19730.08210.07240.46813
270.59311.893312155.1810.14390.17100.15820.05410.09120.6286
360.64162.016965192.67460.19170.18220.19640.08450.06330.42814
409.76011.924486196.38890.21780.17380.20020.09400.05830.38316
447.63681.830473211.64540.23800.16530.21570.10560.05540.34418
396.09151.983618204.69360.21060.17910.20860.09470.05650.37417
437.96752.946243215.54250.23280.26610.21970.12400.02380.16126
174.44231.914002128.10410.09270.17290.13060.03260.11650.7812
220.72512.050069143.72650.11730.18510.14650.04640.10060.6844
142.74041.65594783.773850.07590.14950.08540.01030.13970.9311
299.39172.214356170.13350.15920.20000.17340.07030.07490.51612
260.64971.569603158.50220.13860.14180.16150.04970.10060.6695
325.6482.052732137.56020.17310.18540.14020.06260.08310.5709
469.72632.047881224.67520.24970.18490.22900.11620.04300.27020
207.00411.973061141.20010.11010.17820.14390.04190.10550.7163
246.15142.76224154.440.13090.24950.15740.07540.08390.52711
425.76692.531105214.13870.22640.22860.21820.11210.03280.22623
436.18392.665395213.52290.23190.24070.21760.11650.02780.19324
444.45712.54873227.53970.23630.23020.23190.11990.02630.18025
Table
Table A12. TOPSIS analysis for alumina–graphene.
Table A12. TOPSIS analysis for alumina–graphene.
Decision MatrixNormalizing Matrix
Cutting
Force
(N)		Surface Rough
Ness
(µm)		Temperature
(°C)		 S+S−RiRank
466.9821.833206.2950.28330.23860.24090.14550.02020.12227
416.0101.601185.7310.25240.20830.21680.12140.04240.25925
275.5660.881184.5490.16720.11460.21550.08110.09980.5529
218.8821.505129.4790.13280.19590.15120.06080.10200.6266
341.8411.431170.5090.20740.18620.19910.09580.06570.40716
428.1871.643187.0830.25980.21390.21840.12570.03870.23526
420.2141.231209.1470.25490.16020.24420.12370.05720.31619
245.7001.131173.6710.14910.14720.20280.07250.09610.5708
322.8661.193167.2940.19590.15520.19530.08570.08020.48413
251.7891.318134.0840.15280.17160.15650.06130.09860.6177
329.2831.410166.5040.19980.18350.19440.09120.07000.43414
381.8231.338169.7410.23160.17410.19820.10260.06410.38517
408.7181.281182.9150.24800.16670.21360.11230.06030.34918
327.1951.381176.8620.19850.17970.20650.09380.06870.42315
352.9062.061168.3710.21410.26830.19660.11880.04980.29523
159.8591.330110.7310.09700.17310.12930.03900.12560.7633
185.9991.431124.1990.11280.18630.14500.05120.11290.6885
117.9171.15172.4280.07150.14980.08460.01760.15220.8961
247.3241.542147.0020.15000.20070.17160.07270.08900.55010
215.3191.09098.3960.13060.14180.11490.03590.12530.7772
302.9671.436128.1140.18380.18680.14960.07420.08750.54112
388.0411.426194.1900.23540.18560.22670.11410.05210.31320
171.0101.371122.0440.10370.17850.14250.04600.11840.7204
203.3451.924133.4580.12340.25040.15580.08090.09820.54811
351.7211.763185.0770.21340.22940.21610.11250.04770.29822
360.3431.864184.5020.21860.24260.21540.11740.04370.27124
310.1811.683229.7700.18820.21900.26830.12070.05360.30721

References

  1. Touggui, Y.; Uysal, A.; Emiroglu, U.; Belhadi, S.; Temmar, M. Evaluation of MQL Performances Using Various Nanofluids in Turning of AISI 304 Stainless Steel. Int. J. Adv. Manuf. Technol. 2021, 115, 3983–3997. [Google Scholar] [CrossRef]
  2. Liu, N.; Zou, X.; Yuan, J.; Jiang, H.; Zhang, Y.; Chen, Y. Optimization of MQL Turning Process Considering the Distribution and Control of Cutting Fluid Mist Particles. Int. J. Adv. Manuf. Technol. 2021, 116, 1233–1246. [Google Scholar] [CrossRef]
  3. Mia, M.; Gupta, M.K.; Singh, G.; Królczyk, G.; Pimenov, D.Y. An Approach to Cleaner Production for Machining Hardened Steel Using Different Cooling-Lubrication Conditions. J. Clean. Prod. 2018, 187, 1069–1081. [Google Scholar] [CrossRef]
  4. Gupta, M.K.; Khan, A.M.; Song, Q.; Liu, Z.; Khalid, Q.S.; Jamil, M.; Kuntoğlu, M.; Usca, Ü.A.; Sarıkaya, M.; Pimenov, D.Y. A Review on Conventional and Advanced Minimum Quantity Lubrication Approaches on Performance Measures of Grinding Process. Int. J. Adv. Manuf. Technol. 2021, 117, 729–750. [Google Scholar] [CrossRef]
  5. Hegab, H.; Kishawy, H. Towards Sustainable Machining of Inconel 718 Using Nano-Fluid Minimum Quantity Lubrication. J. Manuf. Mater. Process. 2018, 2, 50. [Google Scholar] [CrossRef] [Green Version]
  6. Sen, B.; Gupta, M.K.; Mia, M.; Pimenov, D.Y.; Mikolajczyk, T. Performance Assessment of Minimum Quantity Castor-Palm Oil Mixtures in Hard-Milling Operation. Materials 2021, 14, 198. [Google Scholar] [CrossRef] [PubMed]
  7. Duc, T.M.; Long, T.T.; Chien, T.Q. Performance Evaluation of MQL Parameters Using Al2O3 and MoS2 Nanofluids in Hard Turning 90CrSi Steel. Lubricants 2019, 7, 40. [Google Scholar] [CrossRef] [Green Version]
  8. Bai, X.; Li, C.; Dong, L.; Yin, Q. Experimental Evaluation of the Lubrication Performances of Different Nanofluids for Minimum Quantity Lubrication (MQL) in Milling Ti-6Al-4V. Int. J. Adv. Manuf. Technol. 2019, 101, 2621–2632. [Google Scholar] [CrossRef]
  9. Das, A.; Das, S.R.; Patel, S.K.; Biswal, B.B. Effect of MQL and Nanofluid on the Machinability Aspects of Hardened Alloy Steel. Mach. Sci. Technol. 2020, 24, 291–320. [Google Scholar] [CrossRef]
  10. Do, T.-V.; Hsu, Q.-C. Optimization of Minimum Quantity Lubricant Conditions and Cutting Parameters in Hard Milling of AISI H13 Steel. Appl. Sci. 2016, 6, 83. [Google Scholar] [CrossRef]
  11. Dubey, V.; Sharma, A.K.; Singh, R.K. A Technological Review on Temperature Measurement Techniques in Various Machining Processes. In Lecture Notes in Mechanical Engineering; Springer: Singapore, 2021; pp. 55–67. [Google Scholar] [CrossRef]
  12. Dubey, V.; Sharma, A.K.; Singh, R.K. Study of Various Cooling Methodology Used in Machining Processes. Mater. Today Proc. 2020, 21, 1572–1576. [Google Scholar] [CrossRef]
  13. Gupta, M.K.; Sood, P.K.; Sharma, V.S. Optimization of Machining Parameters and Cutting Fluids during Nano-Fluid Based Minimum Quantity Lubrication Turning of Titanium Alloy by Using Evolutionary Techniques. J. Clean. Prod. 2016, 135, 1276–1288. [Google Scholar] [CrossRef]
  14. Saini, A.; Dhiman, S.; Sharma, R.; Setia, S. Experimental Estimation and Optimization of Process Parameters under Minimum Quantity Lubrication and Dry Turning of AISI-4340 with Different Carbide Inserts. J. Mech. Sci. Technol. 2014, 28, 2307–2318. [Google Scholar] [CrossRef]
  15. Singh, G.; Pruncu, C.I.; Gupta, M.K.; Mia, M.; Khan, A.M.; Jamil, M.; Pimenov, D.Y.; Sen, B.; Sharma, V.S. Investigations of Machining Characteristics in the Upgraded MQL-Assisted Turning of Pure Titanium Alloys Using Evolutionary Algorithms. Materials 2019, 12, 999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  16. Qu, S.; Gong, Y.; Yang, Y.; Wang, W.; Liang, C.; Han, B. An Investigation of Carbon Nanofluid Minimum Quantity Lubrication for Grinding Unidirectional Carbon Fibre-Reinforced Ceramic Matrix Composites. J. Clean. Prod. 2020, 249, 119353. [Google Scholar] [CrossRef]
  17. Sarkar, J.; Ghosh, P.; Adil, A. A Review on Hybrid Nanofluids: Recent Research, Development and Applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
  18. Babar, H.; Ali, H.M. Towards Hybrid Nanofluids: Preparation, Thermophysical Properties, Applications, and Challenges. J. Mol. Liq. 2019, 281, 598–633. [Google Scholar] [CrossRef]
  19. Pandey, K.; Dubey, V.; Sharma, A.K.; Mital, A. State of Art on Tribological Behaviour of Nanoparticle Enriched Cutting Fluid. In Materials Today: Proceedings; Elsevier Ltd.: Amsterdam, The Netherlands, 2019; Volume 26, pp. 2586–2589. [Google Scholar] [CrossRef]
  20. Jamil, M.; Khan, A.M.; Hegab, H.; Gong, L.; Mia, M.; Gupta, M.K.; He, N. Effects of Hybrid Al2O3-CNT Nanofluids and Cryogenic Cooling on Machining of Ti–6Al–4V. Int. J. Adv. Manuf. Technol. 2019, 102, 3895–3909. [Google Scholar] [CrossRef]
  21. Zhang, X.; Li, C.; Zhang, Y.; Jia, D.; Li, B.; Wang, Y.; Yang, M.; Hou, Y.; Zhang, X. Performances of Al2O3/SiC Hybrid Nanofluids in Minimum-Quantity Lubrication Grinding. Int. J. Adv. Manuf. Technol. 2016, 86, 3427–3441. [Google Scholar] [CrossRef]
  22. Gugulothu, S.; Pasam, V.K. Experimental Investigation to Study the Performance of CNT/MoS2 Hybrid Nanofluid in Turning of AISI 1040 Stee. Aust. J. Mech. Eng. 2020, 1–11. [Google Scholar] [CrossRef]
  23. Kumar, A.; Ghosh, S.; Aravindan, S. Experimental Investigations on Surface Grinding of Silicon Nitride Subjected to Mono and Hybrid Nanofluids. Ceram. Int. 2019, 45, 17447–17466. [Google Scholar] [CrossRef]
  24. Abbas, A.T.; Pimenov, D.Y.; Erdakov, I.N.; Mikolajczyk, T.; El Danaf, E.A.; Taha, M.A. Minimization of Turning Time for High-Strength Steel with a given Surface Roughness Using the Edgeworth–Pareto Optimization Method. Int. J. Adv. Manuf. Technol. 2017, 93, 2375–2392. [Google Scholar] [CrossRef]
  25. Abbas, A.T.; Gupta, M.K.; Soliman, M.S.; Mia, M.; Hegab, H.; Luqman, M.; Pimenov, D.Y. Sustainability Assessment Associated with Surface Roughness and Power Consumption Characteristics in Nanofluid MQL-Assisted Turning of AISI 1045 Steel. Int. J. Adv. Manuf. Technol. 2019, 105, 1311–1327. [Google Scholar] [CrossRef]
  26. Alajmi, M.S.; Almeshal, A.M. Prediction and Optimization of Surface Roughness in a Turning Process Using the ANFIS-QPSO Method. Materials 2020, 13, 2986. [Google Scholar] [CrossRef]
  27. Su, Y.; Zhao, G.; Zhao, Y.; Meng, J.; Li, C. Multi-Objective Optimization of Cutting Parameters in Turning AISI 304 Austenitic Stainless Steel. Metals 2020, 10, 217. [Google Scholar] [CrossRef] [Green Version]
  28. Khan, A.M.; Jamil, M.; Mia, M.; Pimenov, D.Y.; Gasiyarov, V.R.; Gupta, M.K.; He, N. Multi-Objective Optimization for Grinding of AISI D2 Steel with Al2O3 Wheel under MQL. Materials 2018, 11, 2269. [Google Scholar] [CrossRef] [Green Version]
  29. Li, X.; Liu, Z.; Liang, X. Tool Wear, Surface Topography, and Multi-Objective Optimization of Cutting Parameters during Machining AISI 304 Austenitic Stainless Steel Flange. Metals 2019, 9, 972. [Google Scholar] [CrossRef] [Green Version]
  30. Kilickap, E.; Yardimeden, A.; Çelik, Y.H. Mathematical Modelling and Optimization of Cutting Force, Tool Wear and Surface Roughness by Using Artificial Neural Network and Response Surface Methodology in Milling of Ti-6242S. Appl. Sci. 2017, 7, 1064. [Google Scholar] [CrossRef] [Green Version]
  31. Lukic, D.; Cep, R.; Vukman, J.; Antic, A.; Djurdjev, M.; Milosevic, M. Multi-Criteria Selection of the Optimal Parameters for High-Speed Machining of Aluminum Alloy Al7075 Thin-Walled Parts. Metals 2020, 10, 1570. [Google Scholar] [CrossRef]
  32. Prasad, S.; Ravindranath, D.K.; Devakumar, D.M.L.S. Experimental Study and Optimization in Modified Air Abrasive Jet Machining on Nickel-233 Alloy Using MCDM Techniques. Manuf. Technol. 2019, 19, 1010–1019. [Google Scholar] [CrossRef]
  33. Majumder, H.; Saha, A. Application of MCDM Based Hybrid Optimization Tool during Turning of ASTM A588. Decis. Sci. Lett. 2018, 7, 143–156. [Google Scholar] [CrossRef]
  34. Khan, A.; Maity, K. Parametric Optimization of Some Non-Conventional Machining Processes Using Moora Method. Int. J. Eng. Res. Africa 2016, 20, 19–40. [Google Scholar] [CrossRef]
  35. Khan, A.; Maity, K. Estimation of Optimal Cutting Conditions during Machining of CP-Ti Grade 2 in Fuzzy–VIKOR Context. Grey Syst. Theory Appl. 2020, 10, 293–310. [Google Scholar] [CrossRef]
  36. Khan, A.; Maity, K. Application of MCDM-Based TOPSIS Method for the Optimization of Multi Quality Characteristics of Modern Manufacturing Processes. Int. J. Eng. Res. Africa 2016, 23, 33–51. [Google Scholar] [CrossRef]
  37. Sidhu, S.S.; Yazdani, M. Comparative Analysis of MCDM Techniques for EDM of SiC/A359 Composite. Arab. J. Sci. Eng. 2018, 43, 1093–1102. [Google Scholar] [CrossRef]
  38. Yuvaraj, N.; Pradeep Kumar, M. Multiresponse Optimization of Abrasive Water Jet Cutting Process Parameters Using TOPSIS Approach. Mater. Manuf. Process. 2015, 30, 882–889. [Google Scholar] [CrossRef]
  39. Sharma, A.K.; Tiwari, A.K.; Dixit, A.R. Progress of Nanofluid Application in Machining: A Review. Materials and Manufacturing Processes 2015, 7, 30. [Google Scholar] [CrossRef]
  40. Sen, B.; Mia, M.; Gupta, M.K.; Rahman, M.A.; Mandal, U.K.; Mondal, S.P. Influence of Al2O3 and Palm Oil–Mixed Nano-Fluid on Machining Performances of Inconel-690: IF-THEN Rules–Based FIS Model in Eco-Benign Milling. Int. J. Adv. Manuf. Technol. 2019, 3389–3403. [Google Scholar] [CrossRef]
  41. Majumder, H.; Maity, K. Optimization of Machining Condition in WEDM for Titanium Grade 6 Using MOORA Coupled with PCA–A Multivariate Hybrid Approach. J. Adv. Manuf. Syst. 2017, 16, 81–99. [Google Scholar] [CrossRef]
  42. Abhang, L.B.; Iqbal, M.; Hameedullah, M. Optimization of Machining Process Parameters Using Moora Method. Defect Diffus. Forum 2020, 402, 81–89. [Google Scholar] [CrossRef]
  43. Gangil, M.; Pradhan, M.K. Optimization the Machining Parameters by Using VIKOR Method during EDM Process of Titanium Alloy. Mater. Today Proc. 2018, 5, 7486–7495. [Google Scholar] [CrossRef]
  44. Bhuyan, R.K.; Routara, B.C. Optimization the Machining Parameters by Using VIKOR and Entropy Weight Method during EDM Process of Al–18% SiCp Metal Matrix Composite. Decis. Sci. Lett. 2016, 5, 269–282. [Google Scholar] [CrossRef]
  45. Kakaravada, I.; Mahamani, A.; Pandurangadu, V. Optimization of Machining Parameters Using Entropy-VIKOR Method in Drilling of A356-TiB2/TiC in-Situ Composites. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 390. [Google Scholar] [CrossRef]
  46. Thirumalai, R.; Seenivasan, M.; Panneerselvam, K. Experimental Investigation and Multi Response Optimization of Turning Process Parameters for Inconel 718 Using TOPSIS Approach. Mater. Today Proc. 2021, 45, 467–472. [Google Scholar] [CrossRef]
  47. Rajamanickam, S.; Prasanna, J.; Chandrasekhara Sastry, C. Analysis of High Aspect Ratio Small Holes in Rapid Electrical Discharge Machining of Superalloys Using Taguchi and TOPSIS. J. Brazilian Soc. Mech. Sci. Eng. 2020, 42, 1–13. [Google Scholar] [CrossRef]
  48. Singaravel, B.; Selvaraj, T. Optimizacija Parametara Obrade u Postupcima Tokarenja Primjenom Kombinacije TOPSIS i AHP Metode. Teh. Vjesn. 2015, 22, 1475–1480. [Google Scholar] [CrossRef] [Green Version]
  49. Chodha, V.; Dubey, R.; Kumar, R.; Singh, S.; Kaur, S. Selection of Industrial Arc Welding Robot with TOPSIS and Entropy MCDM Techniques. Materials Today: Proceedings; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
  50. Ic, Y.T.; Saraloğlu Güler, E.; Cabbaroğlu, C.; Dilan Yüksel, E.; Maide Sağlam, H. Optimisation of Cutting Parameters for Minimizing Carbon Emission and Maximising Cutting Quality in Turning Process. Int. J. Prod. Res. 2018, 56, 4035–4055. [Google Scholar] [CrossRef]
  51. Wang, H.; Sun, J.; Li, J.; Lu, L.; Li, N. Evaluation of Cutting Force and Cutting Temperature in Milling Carbon Fiber-Reinforced Polymer Composites. Int. J. Adv. Manuf. Technol. 2016, 82, 1517–1525. [Google Scholar] [CrossRef]
Materials 14 07207 g001 550
Figure 1. Experimental setup for MQL turning of AISI304 steel.
Figure 1. Experimental setup for MQL turning of AISI304 steel.
Materials 14 07207 g001
Materials 14 07207 g002 550
Figure 2. Methodology of different MCDM techniques.
Figure 2. Methodology of different MCDM techniques.
Materials 14 07207 g002
Materials 14 07207 g003 550
Figure 3. Response surface plot for alumina nanofluid for cutting force. (a) np% Vs fo; (b) np% Vs ap; for surface roughness (c) np% Vs fo; (d) np% Vs ap and for cutting temperature (e) np% Vs fo; (f) np% Vs ap.
Figure 3. Response surface plot for alumina nanofluid for cutting force. (a) np% Vs fo; (b) np% Vs ap; for surface roughness (c) np% Vs fo; (d) np% Vs ap and for cutting temperature (e) np% Vs fo; (f) np% Vs ap.
Materials 14 07207 g003
Materials 14 07207 g004 550
Figure 4. Response surface plot for alumina-graphene nanofluids for cutting force. (a) np% Vs fo; (b) np% Vs ap; for surface roughness (c) np% Vs fo; (d) np% Vs ap and for cutting temperature (e) np% Vs fo; (f) np% Vs ap.
Figure 4. Response surface plot for alumina-graphene nanofluids for cutting force. (a) np% Vs fo; (b) np% Vs ap; for surface roughness (c) np% Vs fo; (d) np% Vs ap and for cutting temperature (e) np% Vs fo; (f) np% Vs ap.
Materials 14 07207 g004
Table
Table 1. Chemical constituents of AISI 304 steel.
Table 1. Chemical constituents of AISI 304 steel.
ElementsSPCMoCuSiMnNiCrFe
Weight %0.020.0270.0650.130.140.31.788.118.271.2
Table
Table 2. Input parameters used in the current study.
Table 2. Input parameters used in the current study.
Levels/Factors−101
Depth of cut (mm)0.60.91.2
Feed rate (mm/rev)0.080.120.16
Cutting speed (m/min)6090120
Nanofluid concentration (wt.%)0.51.01.5
Table
Table 3. Design of Experiment.
Table 3. Design of Experiment.
S.No.Cutting Speed
(m/min)		Feed Rate
(mm/rev)		Depth of Cut
(mm)		Nanoparticle Concentration
(%)
1900.161.21.0
2600.121.21.0
31200.120.91.5
4600.120.61.0
5900.120.91.0
6600.120.90.5
71200.121.21.0
81200.080.91.0
9900.081.21.0
10600.080.91.0
11900.120.91.0
121200.120.90.5
13900.121.21.5
14900.120.91.0
15600.160.91.0
161200.120.61.0
17900.120.60.5
18900.080.61.0
19900.080.90.5
20900.080.91.5
21600.120.91.5
22900.121.20.5
23900.120.61.5
24900.160.61.0
25900.160.91.5
26900.160.90.5
271200.160.91.0
Table
Table 4. Response parameter in turning of AISI 304 steel.
Table 4. Response parameter in turning of AISI 304 steel.
Alumina Alumina-Graphene
S. No.Cutting Force
(N)		Surface Roughness
(µm)		Temperature
(°C)		Cutting Force
(N)		Surface Roughness
(µm)		Temperature
(°C)
1511.452.630238.71466.981.833206.29
2461.072.295195.55416.001.600185.73
3304.051.426198.82275.560.880184.54
4247.842.155149.86218.881.505129.47
5374.392.051197.34341.841.431170.50
6427.322.360216.51428.181.643187.08
7464.471.767242.05420.211.230209.14
8250.761.627190.16245.691.131173.67
9363.341.717193.60322.861.192167.29
10270.591.893155.18251.781.318134.08
11360.642.016192.67329.281.410166.50
12409.761.924196.38381.821.337169.74
13447.631.830211.64408.711.280182.91
14396.091.983204.69327.191.380176.86
15437.962.946215.54352.902.061168.37
16174.441.914128.10159.851.330110.73
17220.722.050143.72185.991.431124.19
18142.741.65583.77117.911.15172.427
19299.392.214170.13247.321.542147.00
20260.641.569158.50215.311.08998.395
21325.642.052137.56302.961.435128.11
22469.722.047224.67388.041.426194.18
23207.001.973141.20171.011.371122.04
24246.152.762154.44203.341.924133.45
25425.762.531214.13351.721.763185.07
26436.182.665213.52360.341.864184.50
27444.452.548227.53310.181.682229.77
Table
Table 5. ANOVA analysis of MQL machining with alumina nanofluid.
Table 5. ANOVA analysis of MQL machining with alumina nanofluid.
Cutting Force (N)Surface Roughness (μm)Temperature (°C)
Sourcep-Value%
Contribution		p-Value%
Contribution		p-Value%
Contribution
Model0.000 0.000 0.000
Linear0.000 0.000 0.000
Vc0.1750.447790.00013.289180.0162.772098
fo0.00024.966240.00062.38490.00021.2578
ap0.00065.284130.5740.1047580.00055.53153
np%0.0052.5513260.0007.5325990.0252.312737
Square0.031 0.002 0.029
Vc * Vc 0.6510.046570.9810.0002560.8690.009924
fo * fo 0.0710.846860.0007.2231910.2880.436902
ap * ap 0.0042.7096640.7550.031760.0035.074911
np%*np%0.7820.0171950.4840.1634130.4260.240518
2-Way Interaction0.687 0.245 0.021
Vc* fo0.6020.0619740.5620.1111610.3430.344978
Vc * ap0.1440.5283920.2190.5263520.0133.042387
Vc *np%0.9360.0014330.4060.2315440.0044.32489
fo * ap0.3810.1791160.4000.2384590.2940.426456
fo *np%0.5750.0720050.0391.6684470.6080.097931
ap *np%0.8680.0064480.5370.1262730.6600.072077
Error 2.592522 3.752084 4.243412
Lack-of-Fit0.3702.3636120.0763.6936860.2064.051467
Pure Error 0.22891 0.058398 0.191683
Total 100 100 100
Table
Table 6. ANOVA analysis of MQL machining with alumina–graphene hybrid nanofluid.
Table 6. ANOVA analysis of MQL machining with alumina–graphene hybrid nanofluid.
Cutting Force (N)Surface Roughness (μm)Temperature (°C)
Sourcep-Value%
Contribution		p-Value%
Contribution		p-Value%
Contribution
Model0.000 0.000 0.000
Linear0.000 0.000 0.000
Vc0.1221.1630.00016.2930.0162.772098
fo0.00015.3620.00057.5470.00021.2578
ap0.00068.9770.6210.0940.00055.53153
np%0.0282.6240.0008.4980.0252.312737
Square0.046 0.005 0.029
Vc * Vc 0.7710.0370.6280.09060.8690.009924
fo * fo 0.0203.02300.0016.54180.2880.436902
ap * ap 0.0352.3570.9270.00300.0035.074911
np%*np%0.8880.00840.4340.2400.4260.240518
2-Way Interaction0.809 0.2223.5850.021
Vc* fo0.5620.1490.2830.4620.3430.344978
Vc * ap0.3240.4430.2760.4780.0133.042387
Vc *np%0.7630.0390.1700.7810.0044.32489
fo * ap0.3590.3820.4540.2190.2940.426456
fo *np%0.7100.0600.0621.5520.6080.097931
ap *np%0.5730.1410.6250.0920.6600.072077
Error 5.035 4.397 4.243412
Lack-of-Fit0.0544.9790.0724.3320.2064.051467
Pure Error 0.055 0.064 0.191683
Total 100 100 100
Table
Table 7. Analysis of MCDM techniques in alumina enriched nanofluid.
Table 7. Analysis of MCDM techniques in alumina enriched nanofluid.
Response ParametersRanks by Different MCDM Techniques
Cutting Force
(N)		Surface Roughness
(µm)		Temperature
(°C)		MOORAVIKORTOPSIS
511.452.630238.71272727
461.072.295195.55192121
304.051.426198.8291010
247.842.155149.86897
374.392.051197.34151415
427.322.360216.51211922
464.471.767242.05202219
250.761.627190.16788
363.341.717193.60131213
270.591.893155.18656
360.642.016192.67141314
409.761.924196.38161616
447.631.830211.64181818
396.091.983204.69171517
437.962.946215.54262626
174.441.914128.10222
220.722.050143.72564
142.741.65583.77111
299.392.214170.13111112
260.641.569158.50435
325.642.052137.561079
469.722.047224.67222520
207.001.973141.20343
246.152.762154.44121711
425.762.531214.13232023
436.182.665213.52242424
444.452.548227.53252325
Table
Table 8. Analysis of MCDM techniques in alumina–graphene nanofluid.
Table 8. Analysis of MCDM techniques in alumina–graphene nanofluid.
Response Parameters with (Alumina-Graphene)Rank by Different MCDM Techniques
Cutting Force
(N)		Surface Roughness
(µm)		Temperature
(°C)		MOORAVIKORTOPSIS
466.981.833206.29272727
416.011.601185.73242325
275.560.881184.548129
218.881.505129.47676
341.841.431170.50161516
428.181.643187.08262426
420.211.231209.14212219
245.701.131173.67998
322.861.193167.29131113
251.781.318134.08757
329.281.410166.50141314
381.821.338169.74171717
408.711.281182.91182018
327.191.381176.86151415
352.902.061168.37252623
159.851.330110.73333
185.991.431124.19565
117.911.15172.42111
247.321.542147.00111010
215.311.09098.39222
302.961.436128.1110812
388.041.426194.19191920
171.011.371122.04444
203.341.924133.45121611
351.721.763185.07201822
360.341.864184.50232124
310.181.683229.77222521
Table
Table 9. The optimum results through RSM, MOORA, VIKOR, and TOPSIS.
Table 9. The optimum results through RSM, MOORA, VIKOR, and TOPSIS.
Parameters/TechniqueCutting Speed
(mm/min)		Feed Rate
(mm/rev)		Depth of Cut
(mm)		Np%CuttingForce
(N)		Surface Roughness
(μm)		Temperature
(°C)
RSMAlumina86.6670.080.61.5101.7561.4847583.77
Alumina-Graphene110.9090.080.64841.592.6570.9118678.766
MOORAAlumina900.080.61.0142.74041.65594783.77385
Alumina-Graphene900.080.61.0117.9171.15172.428
VIKORAlumina900.080.61.0142.74041.65594783.77385
Alumina-Graphene900.080.61.0117.9171.15172.428
TOPSISAlumina900.080.61.0142.74041.65594783.77385
Alumina-Graphene900.080.61.0117.9171.15172.428
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Dubey, V.; Sharma, A.K.; Vats, P.; Pimenov, D.Y.; Giasin, K.; Chuchala, D. Study of a Multicriterion Decision-Making Approach to the MQL Turning of AISI 304 Steel Using Hybrid Nanocutting Fluid. Materials 2021, 14, 7207. https://doi.org/10.3390/ma14237207

AMA Style

Dubey V, Sharma AK, Vats P, Pimenov DY, Giasin K, Chuchala D. Study of a Multicriterion Decision-Making Approach to the MQL Turning of AISI 304 Steel Using Hybrid Nanocutting Fluid. Materials. 2021; 14(23):7207. https://doi.org/10.3390/ma14237207

Chicago/Turabian Style

Dubey, Vineet, Anuj Kumar Sharma, Prameet Vats, Danil Yurievich Pimenov, Khaled Giasin, and Daniel Chuchala. 2021. "Study of a Multicriterion Decision-Making Approach to the MQL Turning of AISI 304 Steel Using Hybrid Nanocutting Fluid" Materials 14, no. 23: 7207. https://doi.org/10.3390/ma14237207

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop