A Plane Stress Failure Criterion for Inorganically-Bound Core Materials
Abstract
1. Introduction
1.1. Fracture Strength of Inorganically-Bound Core Materials
1.2. Failure Criteria
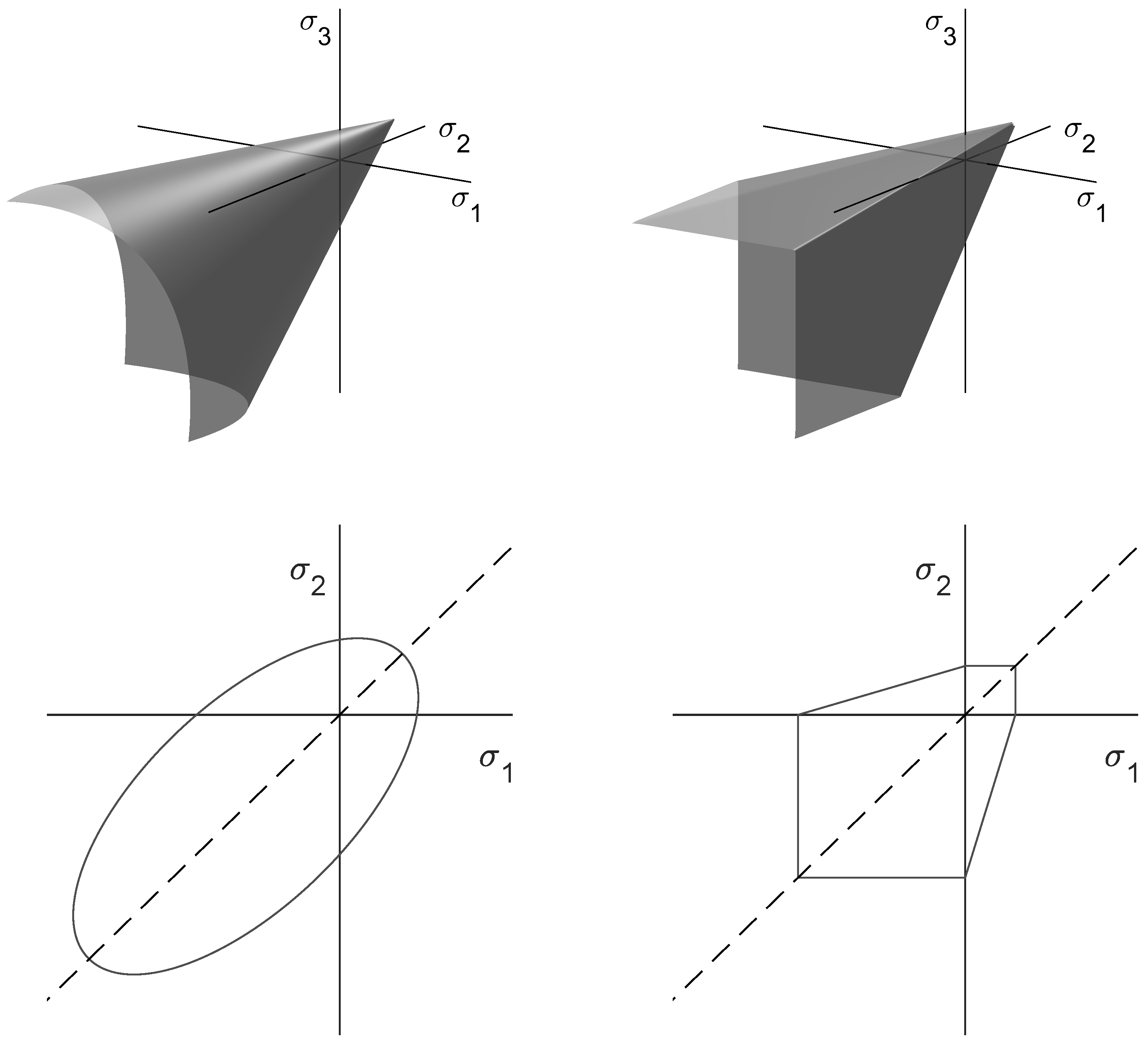
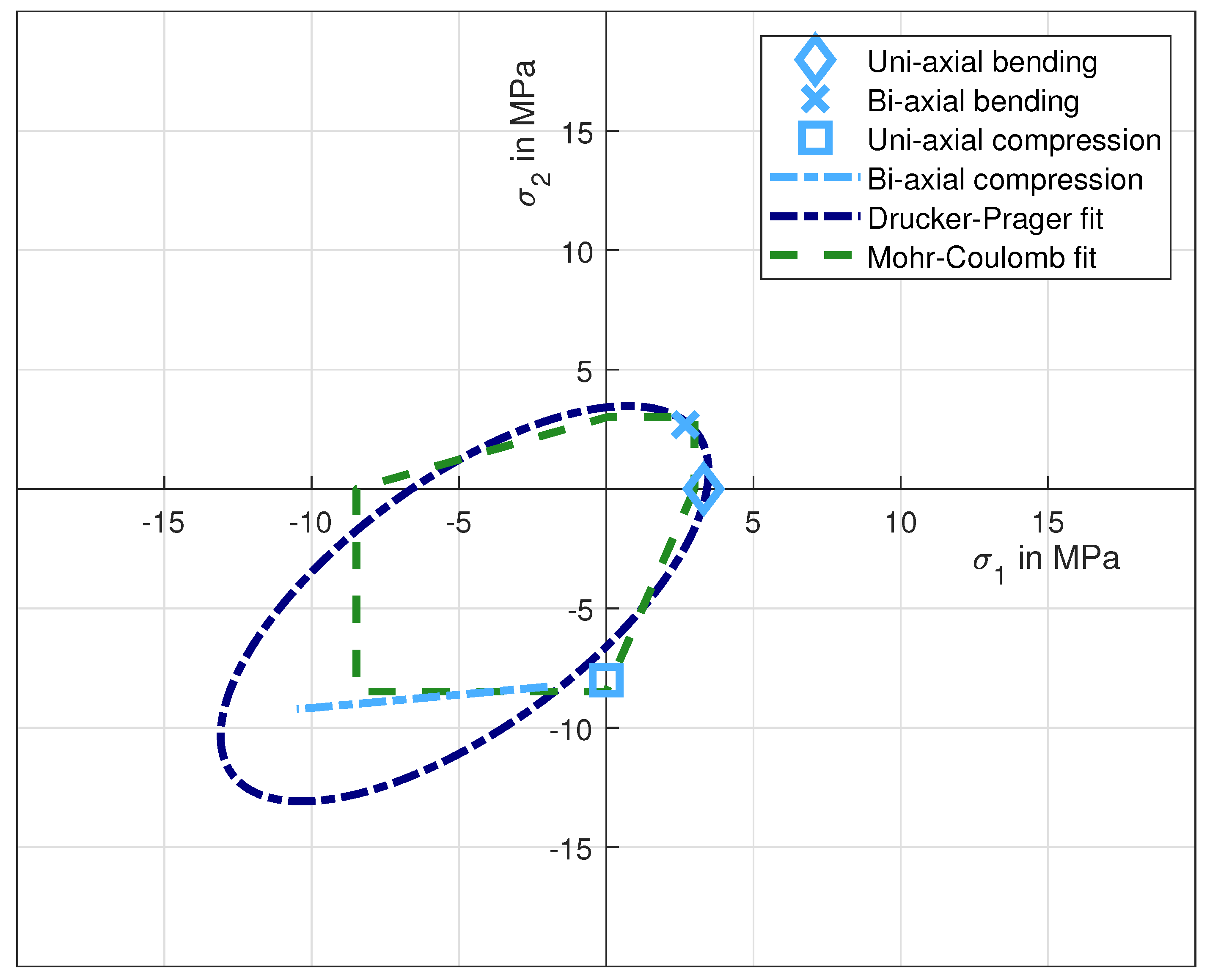
1.2.1. Drucker-Prager Failure Criterion
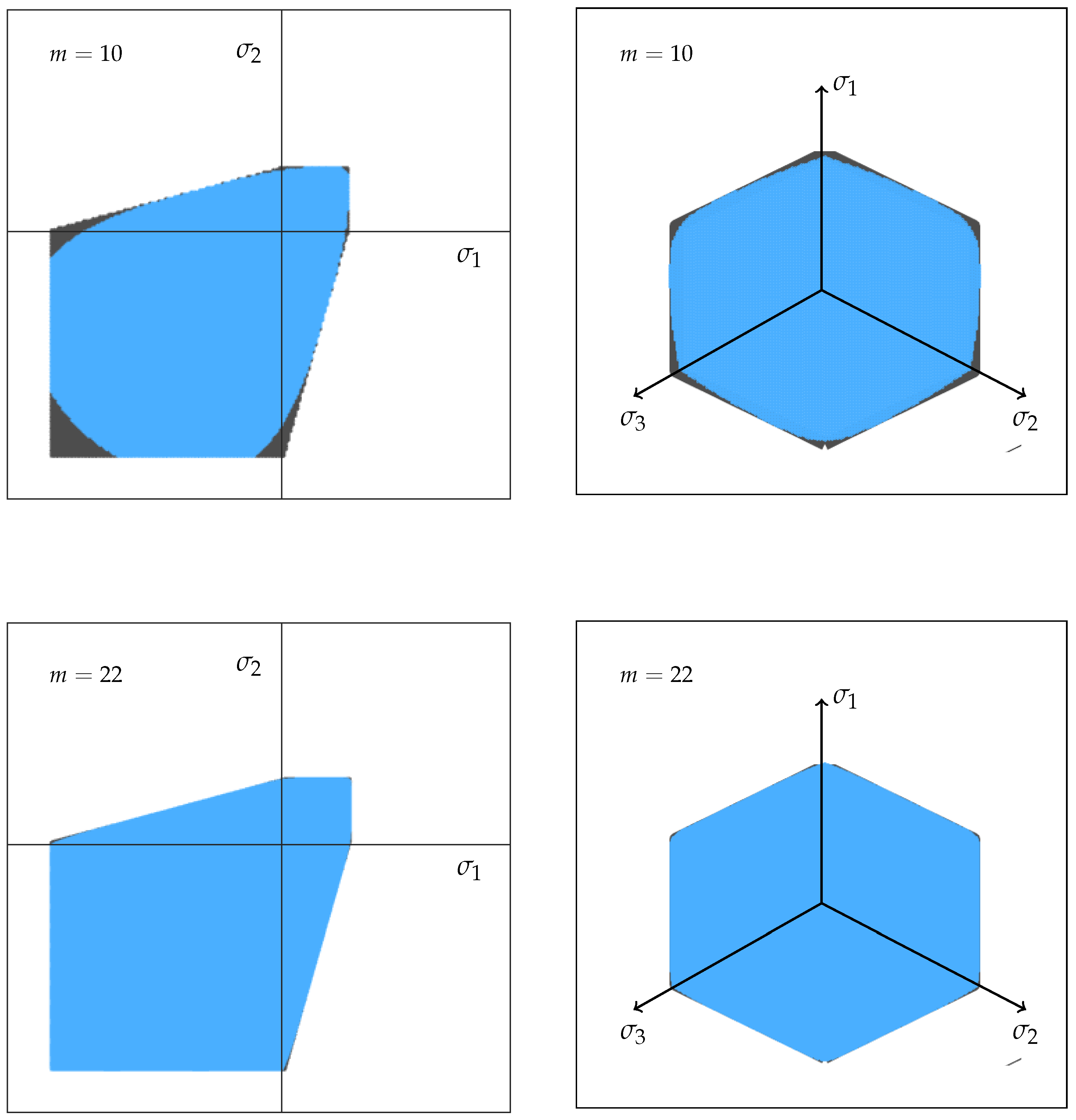
1.2.2. Mohr-Coulomb Failure Criterion
2. Materials and Methods
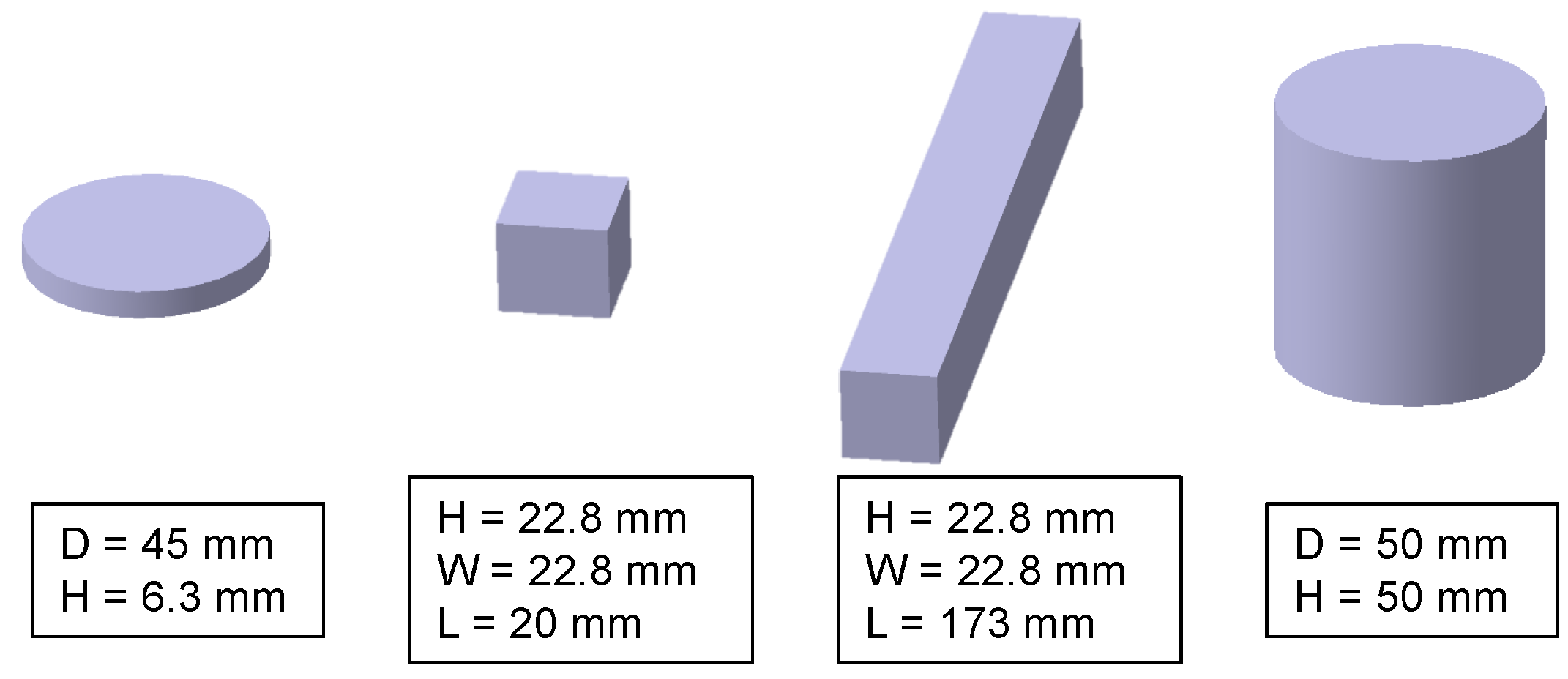
2.1. Specimens
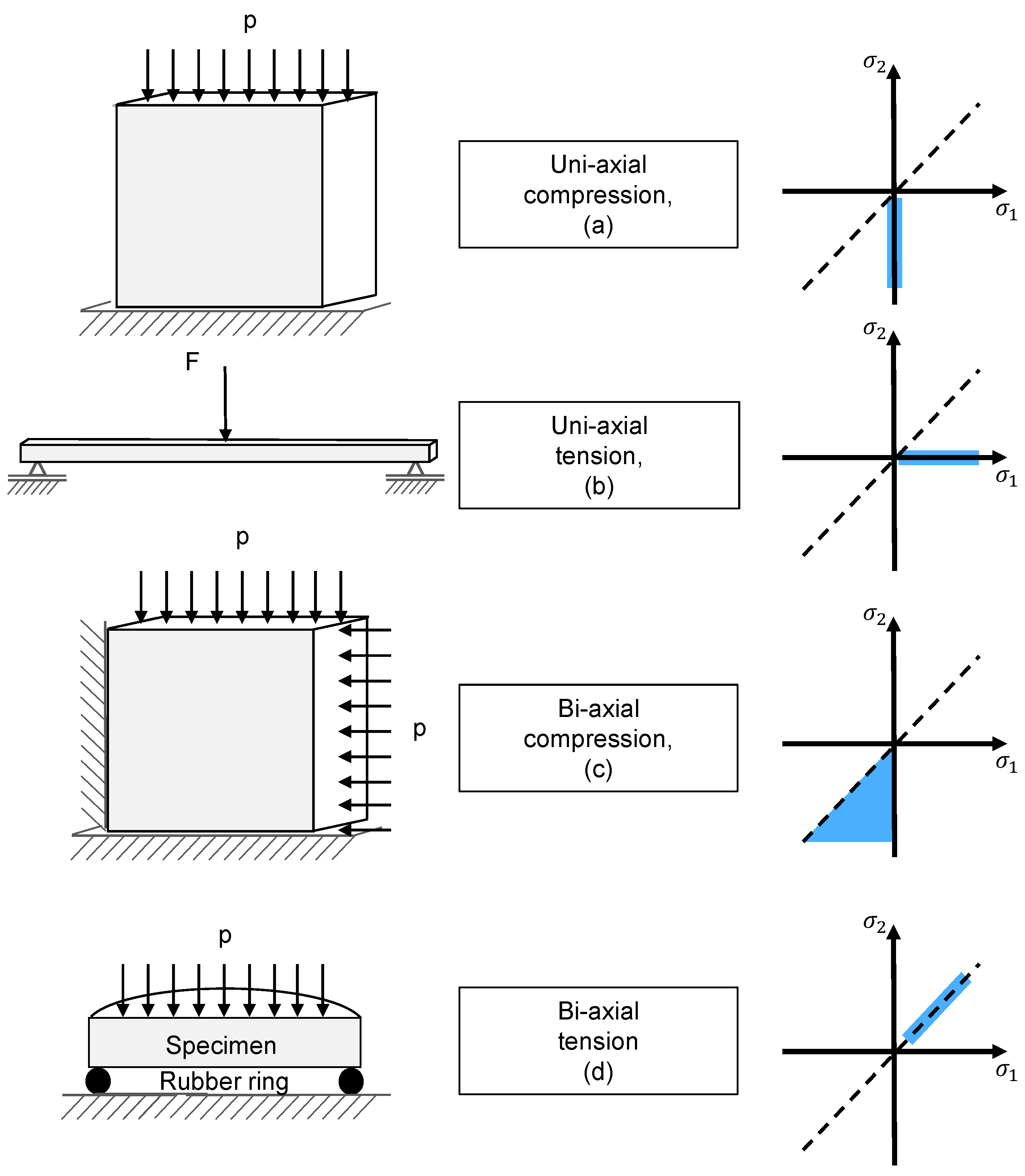
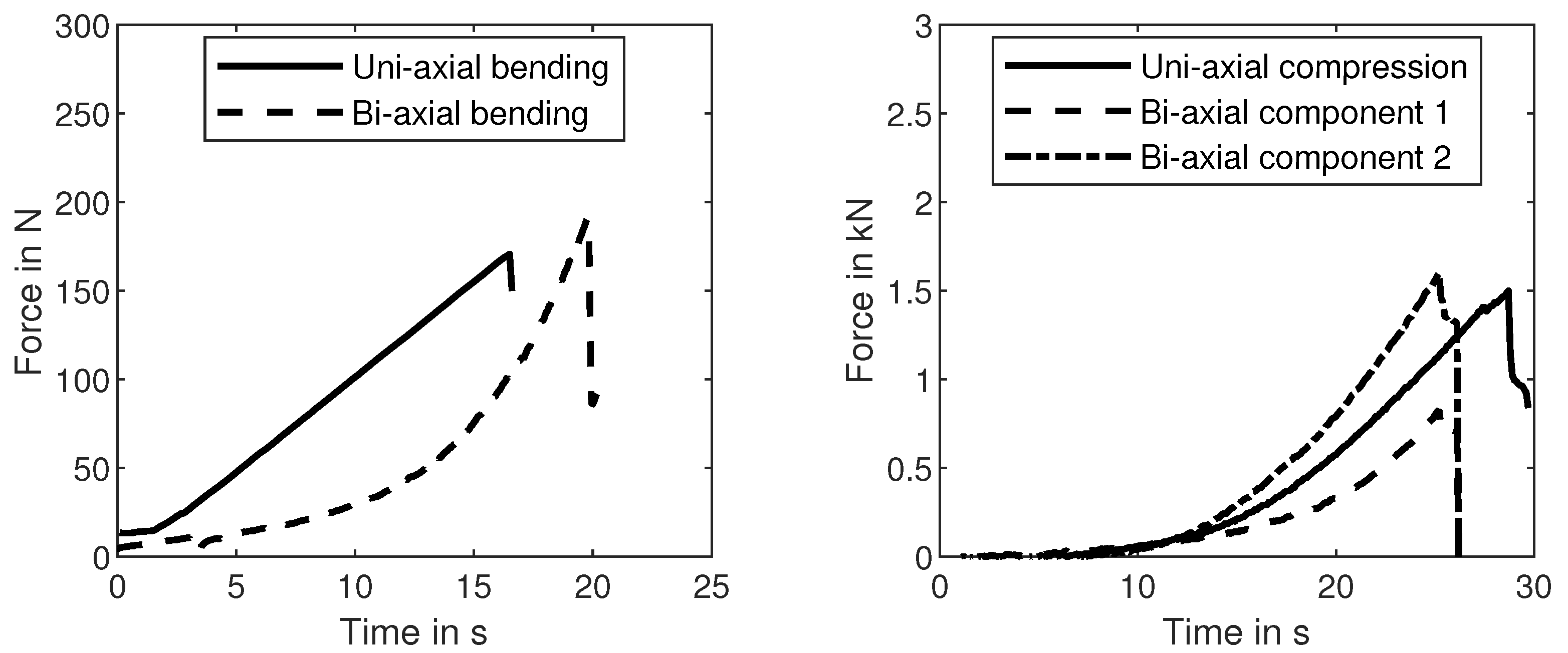
2.2. Uni-Axial Compression Experiment
2.3. Uni-Axial Tension Experiment
2.4. Bi-Axial Compression Experiment
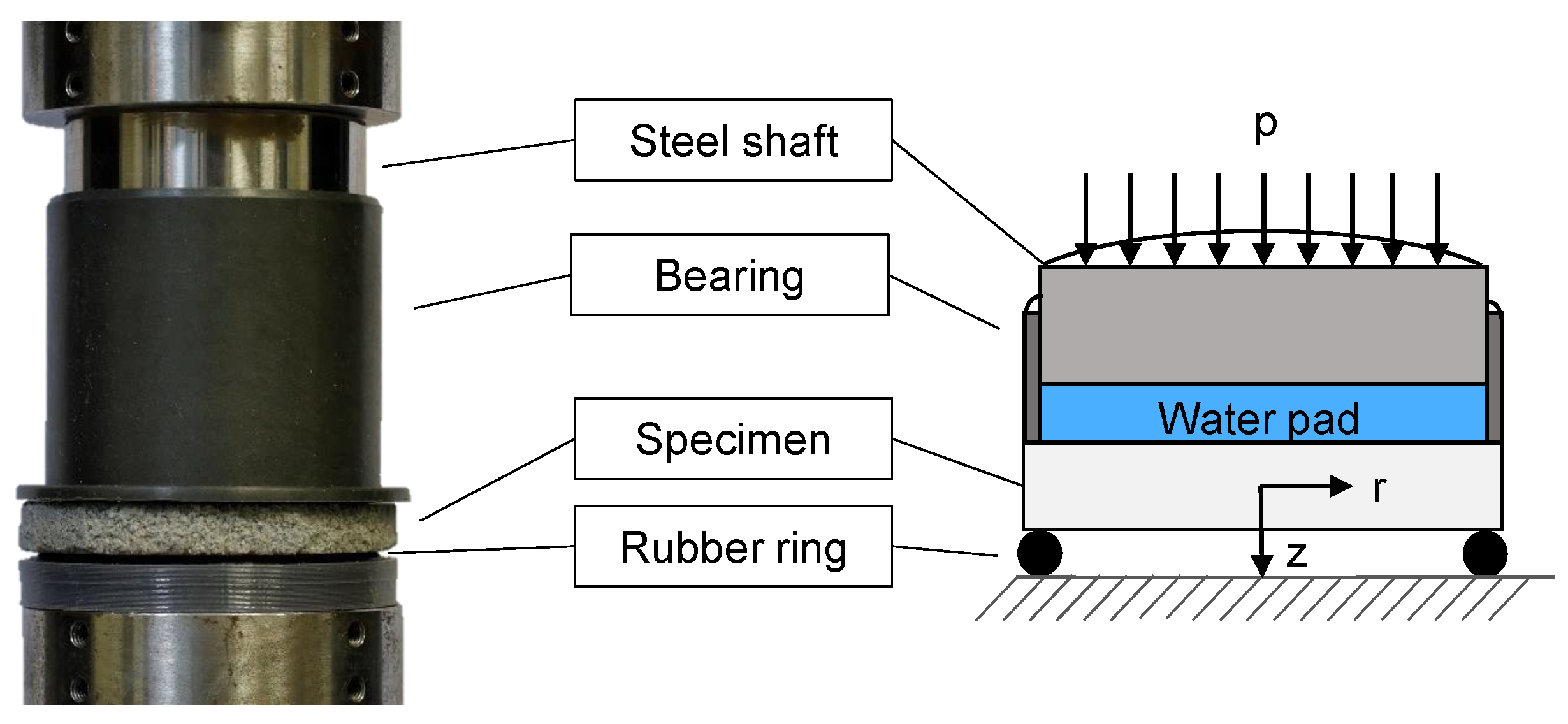
2.5. Bi-Axial Tension Experiment
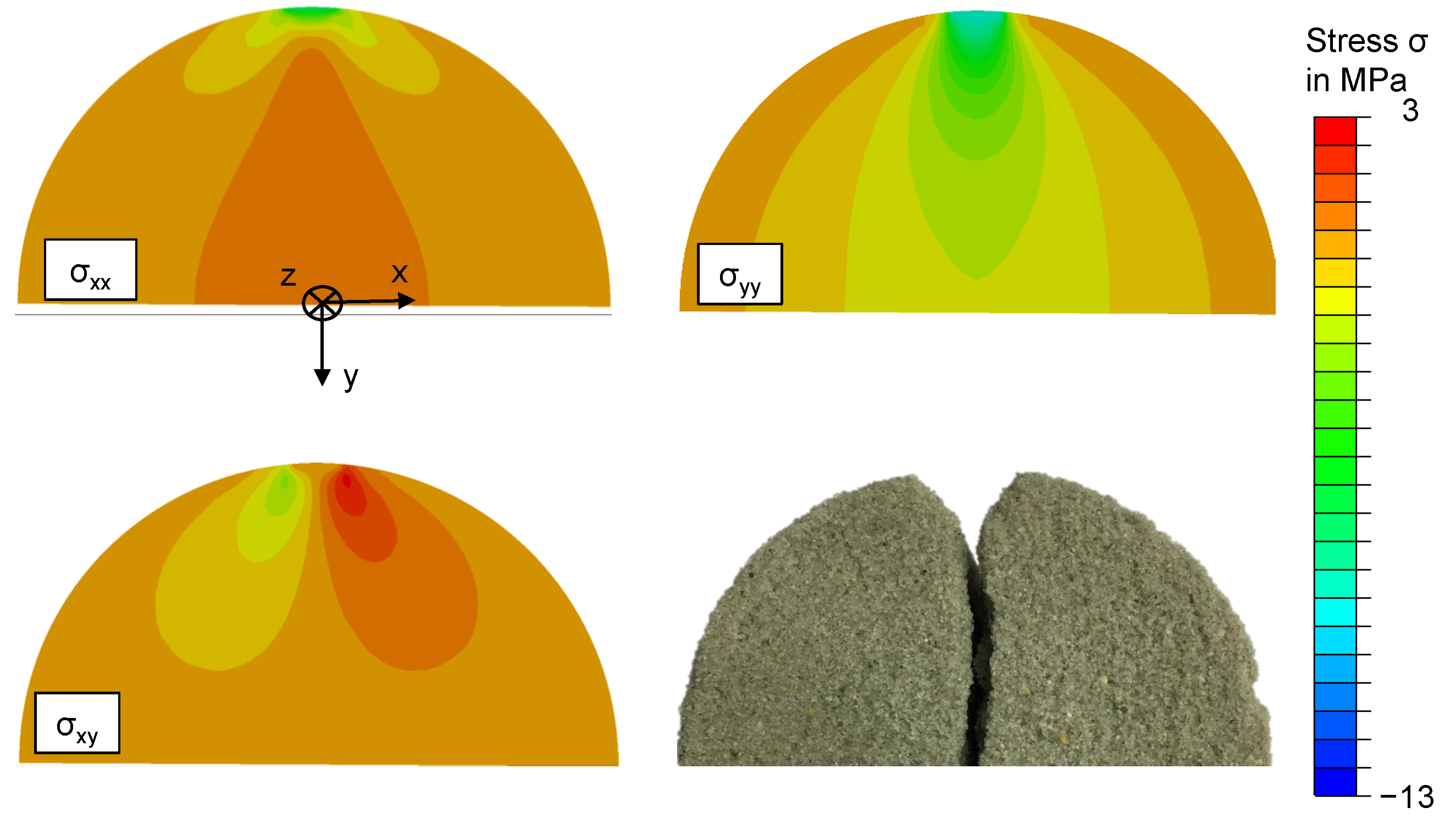
2.6. Validation Experiment
3. Experimental Results
3.1. Uni-Axial Results
3.2. Bi-Axial Compression Experiment
3.3. Bi-Axial Tension Results
3.4. Optimisation of Model Parameters
4. Mohr-Coulomb Failure Criterion Based on Weakest-Link Theory
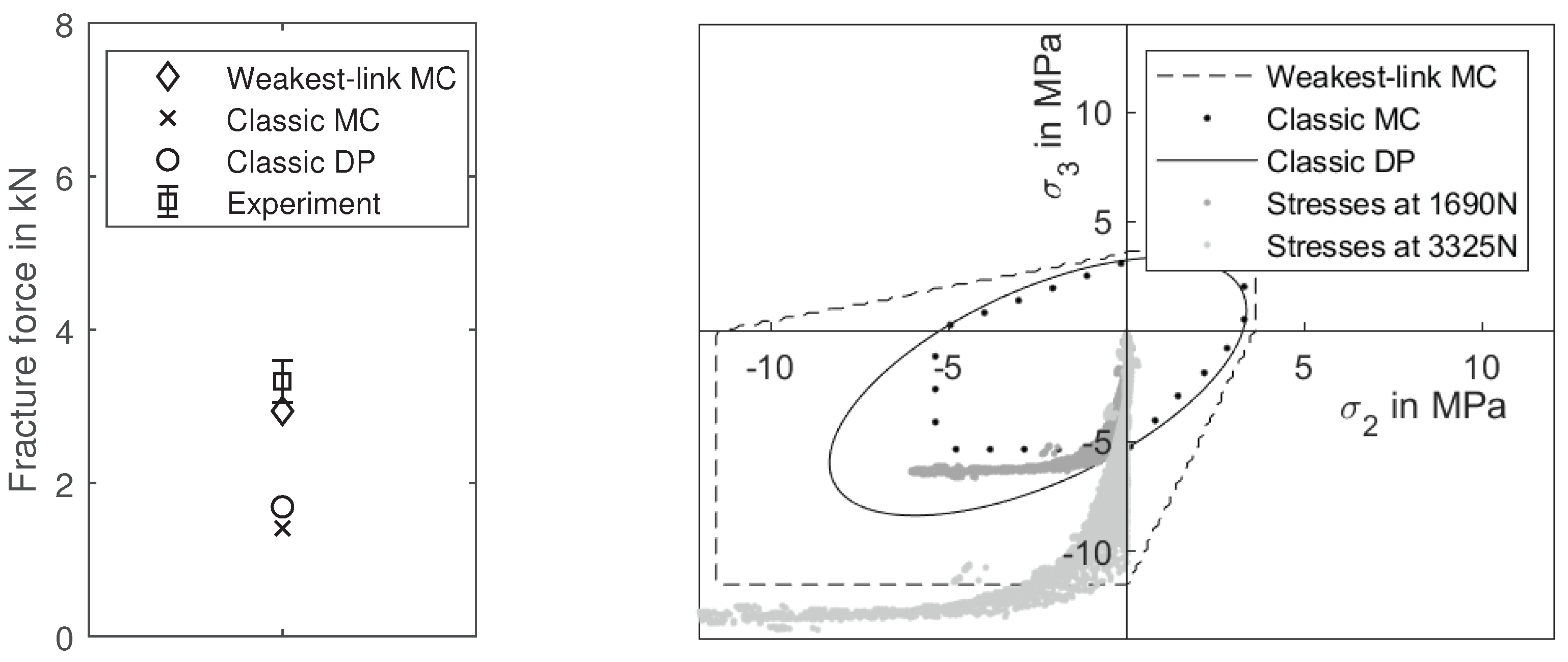
5. Validation
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 3PB | three-point-bending |
| FEM | Finite element method |
| IOB | inorganically-bound |
| PTFE | Polytetrafluorethylen |
| PIA | principle of independent action |
References
- Bührig-Polaczek, A.; Träger, H. Foundry Technology. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley: Chichester, UK, 2010; Volume 1, p. 271. [Google Scholar]
- Stauder, B.J.; Harmuth, H.; Schumacher, P. De-agglomeration rate of silicate bonded sand cores during core removal. J. Mater. Process. Technol. 2018, 252, 652–658. [Google Scholar] [CrossRef]
- Polzin, H. Inorganic Binders: For Mould and Core Production in the Foundry; Fachverlag Schiele & Schön: Berlin, Germany, 2014. [Google Scholar]
- Conev, M.; Vasková, I.; Hrubovčáková, M.; Hajdúch, P. Decoring Behaviour of Chosen Moulding Materials with Alkali Silicate Based Inorganic Binders. Arch. Metall. Mater. 2017, 62, 703–706. [Google Scholar] [CrossRef]
- Lechner, P.; Fuchs, G.; Hartmann, C.; Steinlehner, F.; Ettemeyer, F.; Volk, W. Acoustical and Optical Determination of Mechanical Properties of Inorganically-Bound Foundry Core Materials. Materials 2020, 13, 2531. [Google Scholar] [CrossRef] [PubMed]
- Wadhwa, R.S. Handling Hazardous Part Variety: Metalcasting as a Case Point. Procedia CIRP 2014, 17, 535–540. [Google Scholar] [CrossRef]
- Wadhwa, R.S. Flexible Manufacturability and Handling Automation in Metalcasting SMEs. Int. J. Met. 2012, 6, 15–24. [Google Scholar] [CrossRef]
- Muschna, M. 2020. Available online: http://www.mgm-foundry.de/de/produkte/kernhandling-systeme/ (accessed on 22 December 2020).
- Stauder, B.J.; Kerber, H.; Schumacher, P. Foundry sand core property assessment by 3-point bending test evaluation. J. Mater. Process. Technol. 2016, 237, 188–196. [Google Scholar] [CrossRef]
- Griebel, B.; Brecheisen, D.; Ramakrishnan, R.; Volk, W. Optical Measurement Techniques Determine Young’s Modulus of Sand Core Materials. Int. J. Met. 2016, 10, 524–530. [Google Scholar] [CrossRef]
- Izdebska-Szanda, I.; Baliński, A.; Angrecki, M. Evaluation of Reclamability of Molding Sands with New Inorganic Binders. Arch. Foundry Eng. 2012, 12, 161. [Google Scholar] [CrossRef]
- Popoola, A.; Fayomi, O. Accessing the performance of binders on core strength in metal casting. Int. J. Phys. Sci. 2011, 6. [Google Scholar] [CrossRef]
- Brück, S.; Ratke, L. RF-Aerogels: A New Binding Material for Foundry Application. J. Sol-Gel Sci. Technol. 2003, 26, 663–666. [Google Scholar] [CrossRef]
- Danzer, R.; Börger, A.; Supancic, P.; Ruiz Villanueva, M.A. Ein einfacher Festigkeitsversuch für Scheiben aus spröden Werkstoffen. Mater. Und Werkst. 2003, 34, 490–498. [Google Scholar] [CrossRef]
- Shetty, D.K.; Rosenfield, A.R.; McGuire, P.; Bansal, G.K.; Duckworth, W.H. Biaxial flexure tests for ceramics. Am. Ceram. Soc. Bull. 1980, 59, 1193–1197. [Google Scholar]
- Börger, A.; Supancic, P.; Danzer, R. The ball on three balls test for strength testing of brittle discs: Stress distribution in the disc. J. Eur. Ceram. Soc. 2002, 22, 1425–1436. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Griebel, B.; Volk, W.; Günther, D.; Günther, J. 3D Printing of Inorganic Sand Moulds for Casting Applications. Adv. Mater. Res. 2014, 1018, 441–449. [Google Scholar] [CrossRef]
- Ehlers, W.; Volk, W. On shear band localization phenomena of liquid-saturated granular elastoplastic porous solid materials accounting for fluid viscosity and micropolar solid rotations. Mech. Cohesive-Frict. Mater. 1997, 2, 301–320. [Google Scholar] [CrossRef]
- Lagioia, R.; Panteghini, A. On the existence of a unique class of yield and failure criteria comprising Tresca, von Mises, Drucker–Prager, Mohr–Coulomb, Galileo–Rankine, Matsuoka–Nakai and Lade–Duncan. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150713. [Google Scholar] [CrossRef]
- Mises, R. Mechanik der festen Körper im plastisch-deformablen Zustand. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen 1913, 1, 582–592. [Google Scholar]
- Sloan, S.W.; Booker, J.R. Removal of singularities in tresca and mohr-coulomb yield functions. Commun. Appl. Numer. Methods 1986, 2, 173–179. [Google Scholar] [CrossRef]
- Benz, T.; Schwab, R. A quantitative comparison of six rock failure criteria. Int. J. Rock Mech. Min. Sci. 2008, 45, 1176–1186. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil mechanics and plastic analysis or limit design. Q. Appl. Math. 1952, 10, 157–162. [Google Scholar] [CrossRef]
- Galles, D.; Beckermann, C. Effect of sand dilation on core expansion during steel casting. IOP Conf. Ser. Mater. Sci. Eng. 2015, 84, 012022. [Google Scholar] [CrossRef]
- Thorborg, J.; Kumar, S.; Wagner, I.; Sturm, J.C. The virtual core-modelling and optimization of core manufacturing and application. IOP Conf. Ser. Mater. Sci. Eng. 2020, 861, 012004. [Google Scholar] [CrossRef]
- Stauder, B.J.; Berbic, M.; Schumacher, P. Mohr-Coulomb failure criterion from unidirectional mechanical testing of sand cores after thermal exposure. J. Mater. Process. Technol. 2019, 274, 116274. [Google Scholar] [CrossRef]
- Liu, M.; Gao, Y.; Liu, H. A nonlinear Drucker–Prager and Matsuoka–Nakai unified failure criterion for geomaterials with separated stress invariants. Int. J. Rock Mech. Min. Sci. 2012, 50, 1–10. [Google Scholar] [CrossRef]
- Menetrey, P.; Willam, K.J. Triaxial Failure Criterion for Concrete and Its Generalisation. ACI Struct. J. 1995, 92, 311–318. [Google Scholar]
- Červenka, J.; Papanikolaou, V.K. Three dimensional combined fracture–plastic material model for concrete. Int. J. Plast. 2008, 24, 2192–2220. [Google Scholar] [CrossRef]
- Sucharda, O. Identification of Fracture Mechanic Properties of Concrete and Analysis of Shear Capacity of Reinforced Concrete Beams without Transverse Reinforcement. Materials 2020, 13, 2788. [Google Scholar] [CrossRef]
- Lechner, P.; Stahl, J.; Ettemeyer, F.; Himmel, B.; Tananau-Blumenschein, B.; Volk, W. Fracture Statistics for Inorganically-Bound Core Materials. Materials 2018, 11, 2306. [Google Scholar] [CrossRef]
- Li, D.; Wong, L.N.Y. The Brazilian Disc Test for Rock Mechanics Applications: Review and New Insights. Rock Mech. Rock Eng. 2013, 46, 269–287. [Google Scholar] [CrossRef]
- Magnus, K.; Müller-Slany, H.H. Grundlagen der technischen Mechanik, 7th ed.; Studium, Vieweg + Teubner: Wiesbaden, Germany, 2009. [Google Scholar]
- Hill, R.C. A theory of the plastic bulging of a metal diaphragm by lateral pressure. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1950, 41, 1133–1142. [Google Scholar] [CrossRef]
- Hake, E.; Meskouris, K. Statik der Flächentragwerke: Einführung mit vielen durchgerechneten Beispielen, 2nd ed.; Korrigierte, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Bennett, J. A Weibull Brittle Material Failure Model for the ABAQUS Computer Program; Technical report; Los Alamos National Laboratory: Los Alamos, NM, USA, 1991. [Google Scholar]
- Weibull, W. A Statistical Theory of the Strength of Materials; Swedish Institute for Engineering Research: Stockholm, Sweden, 1939. [Google Scholar]






| Experiment | Stress Component | Sample Size | Scale Parameter | Shape Parameter | Mean | Standard Deviation |
|---|---|---|---|---|---|---|
| Uni-axial bending | 8 | MPa | 36 | MPa | MPa | |
| Uni-axial compression | 10 | MPa | 11 | MPa | MPa | |
| Bi-axial bending | / | 12 | MPa | 19 | MPa | MPa |
| Bi-axial compression | 23 | MPa | 9.2 | MPa | MPa | |
| Brazilian test | - | 5 | kN | 14 | kN | kN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lechner, P.; Hartmann, C.; Ettemeyer, F.; Volk, W. A Plane Stress Failure Criterion for Inorganically-Bound Core Materials. Materials 2021, 14, 247. https://doi.org/10.3390/ma14020247
Lechner P, Hartmann C, Ettemeyer F, Volk W. A Plane Stress Failure Criterion for Inorganically-Bound Core Materials. Materials. 2021; 14(2):247. https://doi.org/10.3390/ma14020247
Chicago/Turabian StyleLechner, Philipp, Christoph Hartmann, Florian Ettemeyer, and Wolfram Volk. 2021. "A Plane Stress Failure Criterion for Inorganically-Bound Core Materials" Materials 14, no. 2: 247. https://doi.org/10.3390/ma14020247
APA StyleLechner, P., Hartmann, C., Ettemeyer, F., & Volk, W. (2021). A Plane Stress Failure Criterion for Inorganically-Bound Core Materials. Materials, 14(2), 247. https://doi.org/10.3390/ma14020247





