1. Introduction
The emergence and growth of additive manufacturing (AM) has allowed for the use of more complex freeform designs. One promising area of study is cellular lattice structures, which use newer design methodologies. Lattice structures can reduce the amount of material and thus the weight of parts, while maintaining a reasonable strength. Lattice structures can also be used to support complex overhangs, which improves manufacturability [
1]. Beyond that, lattice structures show a lot of promise in the biomedical field, e.g., lightweight orthopaedic implants can be fabricated, and the bone in-growth characteristics can be optimized for specific locations within the body [
2]. The applications of metallic-AM lattices are widespread, but their manufacturability is limited to a handful or processes. Over the past 30 years, metal-AM has been a topic of interest for many researchers. More specifically, the use of metallic-AM for lightweight cellular structures has been heavily iterated [
3]. The result is a vast trove of knowledge regarding materials, parameters, and design methodologies for metallic-AM of cellular lattice structures. However, metallic-AM has some limitations. According to Aboulkair et al. [
4], one of the most common defects in selective laser melting (SLM)—a very common metallic-AM process, irrespective of the material, is porosity. Maconachie et al. [
5] also mentioned that SLM fabrication of lattice structures is understood to result in manufacturing defects. Moreover, due to the high cost associated with the process, it cannot be used for mass manufacturing of complex parts.
Rapid-investment casting (RIC) is a process used for manufacturing lattice structures. RIC is based on the investment casting (IC), but it relies on AM for pattern making. This allows for RIC to take advantage of the design freedom of AM to produce complex parts. RIC has similar capabilities as metallic-AM. Both metallic-AM and RIC have their respective uses and place in the AM space, but RIC performs better in some applications. For example, RIC does not require sintering, which often leads to considerable shrinkage. More importantly, complex patterns for RIC can be made at a low cost using plastic AM, which opens a door for mass customization of metal parts. To the best of our knowledge, little research has been done to advance the design methodology for RIC of lattice structures when compared to its metallic-AM counterpart. Some of the limited research that has been done includes using fused filament fabrication (FFF) to produce low-cost patterns [
6], studying the effect of cross-sectional shape of struts on mechanical properties [
7], and finding the optimal filling direction for honeycomb structures [
8]. Lattice topology is defined as how the materials and voids are distributed within the unit cell. However, there is no current overarching analysis of the effect that lattice topology has on casting performance and what topological features play the most extensive role in minimizing casting defects. This analysis is required to avoid casting defects in lattice structures, so that they can be faithfully applied to metal parts. Since this paper only focuses on the strut-based lattices, the connectivity and dimension of the struts are used to control the lattice topology.
Given that RIC is a hybrid manufacturing method with both additive and solidification processes, its design considerations stem from both methods. To correctly print a pattern, design for AM needs to be applied. Considerations include print direction, support location, and overhang angle. The quality of the printed pattern depends heavily on the chosen AM method, the topology of the pattern and supports, and the material and process parameters. Design for IC has its own set of considerations: feeding direction, gating/feeding system, and pattern topology. The IC performance depends heavily on the topology of the pattern/gating system and its inherent mold flow. When it comes to the design of lattice structures for RIC, lattice topology is one of the most critical factors that affects printability, castability, and mechanical properties. Different design objectives may have contradicting requirements on the topology, and the research question here is: what lattice topological features have the most significant impact on the overall performance in RIC, and how to improve them? By answering the research question, this paper aims to develop a design methodology for RIC lattice structures. The goal of the design methodology would be to minimize casting defects related to the lattice topology. In this paper, we find a few features, including the relative strut size, joint number, joint valence, and strut angle, significantly affect the casting performance. These features are evaluated using a variety of lattice topologies and structures. Since design for RIC is a multi-objective optimization, we select only the lattice structures with excellent printability, i.e., self-supported and open-celled, and focus on improving the castability without sacrificing mechanical performance. To answer the research question, the lattices will undergo mold flow and mechanical simulation to determine which features are more critical to casting performance. The casting results will be evaluated and compared with the theoretical results to establish design guidelines for RIC lattice structures. These design guidelines are then used to create new designs with casting performance in mind. Finally, a larger scale sample of the best performing design will undergo microscopic void and grain structure analysis to verify the simulation results further. The main objective of this work is to expand the limited research on lattice design for RIC as there is no overarching analysis on the effect of lattice topology on casting performance. The contributions of this paper include:
A methodology to study the RIC performance of lattice structures is presented to test our hypothesis on the lattice topological features.
The features are compared and analyzed with the test results, and a set of design guidelines for RIC is created.
Based on the analysis, new lattice structures are designed and tested for RIC performance.
The paper is organized as follows. The rest of this section briefly reviews the related works.
Section 2 details the equipment, materials and methodology used.
Section 3 describes the theoretical and experimental results of the study.
Section 4 evaluates the results and establishes an order of importance to the topological lattice features for casting performance. Finally, the paper concludes in
Section 5.
Literature Review
Investment casting (IC) was described as taking advantage of a fluid’s ability to assume the shape of its container [
9]. IC design is principal to good mold flow [
10,
11,
12]. The most important factor affecting casting defect occurrence, is the quality of the gating system [
13]. For example the use of a novel parabolic conical-helical sprue can reduce surface turbulence in metal during mold filling [
14]. Less turbulence is important to achieve quality castings. Poor gating system design could also lead to rough surface finish and accuracy, and a design where the size of sprue and runner is unbalanced will produce unstable molten metal flow [
15]. Computing and data-driven methods can be used for gating and feeding system design in IC. These methods showed that the gating system’s diameter is most influential on the volume of average shrinkage porosity [
16]. Current research is focused on using design optimization in the hopes of reducing the likelihood of casting defects. RIC has similar gating and feeding system design considerations as IC but with the added AM design considerations [
17]. These principles can be combined to cast a structurally optimized metal component [
18]. The dimensional accuracy of the cast part using RIC is highly pattern dependent [
19,
20]. Ishida et al. [
21] tested the ability of different manufacturing methods to create dimensionally accurate full dental crowns, and they showed that all the methods had their respective drawbacks. The RIC processes, mainly using Stereolithography (SLA) can be found in a review [
22].
Presently, the use of lattice structures is desirable because AM has allowed for the fabrication of topologies with great geometrical complexity that was previously unachievable using traditional fabrication techniques [
23]. Advancements in lattice structure design and manufacturing include the casting of ordered porous lattice structures with controllable properties [
24]. Currently, properties such as high specific stiffness or very high specific strength can only be achieved using geometric methods such as lattice structures. The use of complex lattice structures to achieve specific properties has become more common. For example, Li et al. [
25] presented a novel optimization strategy for designing functionally graded cellular structures with desired mechanical properties. Beyond that, lattice structures can be designed using programmable joints resulting in lattices with both stretch- and bending-dominated behavior [
26]. These lattice structures with controllable properties can be used in complex applications such as metallic bone design [
27]. Current design and manufacturing methods allow for lattices with tailored mechanical properties. This can be achieved by varying the unit cell topology, relative density, and base material. However, there is no existing study on the casting performance of these complex lattices.
4. Discussion
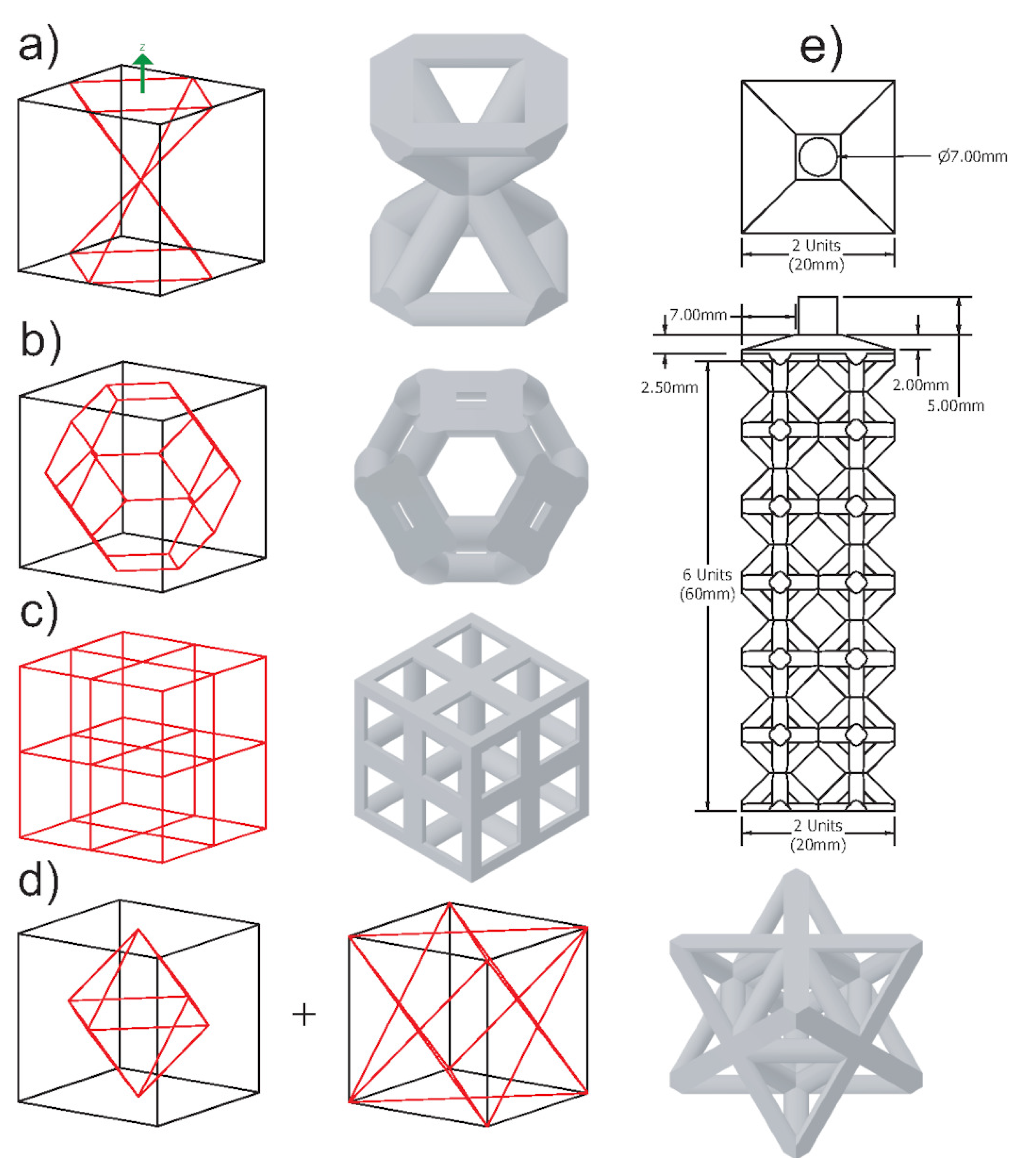
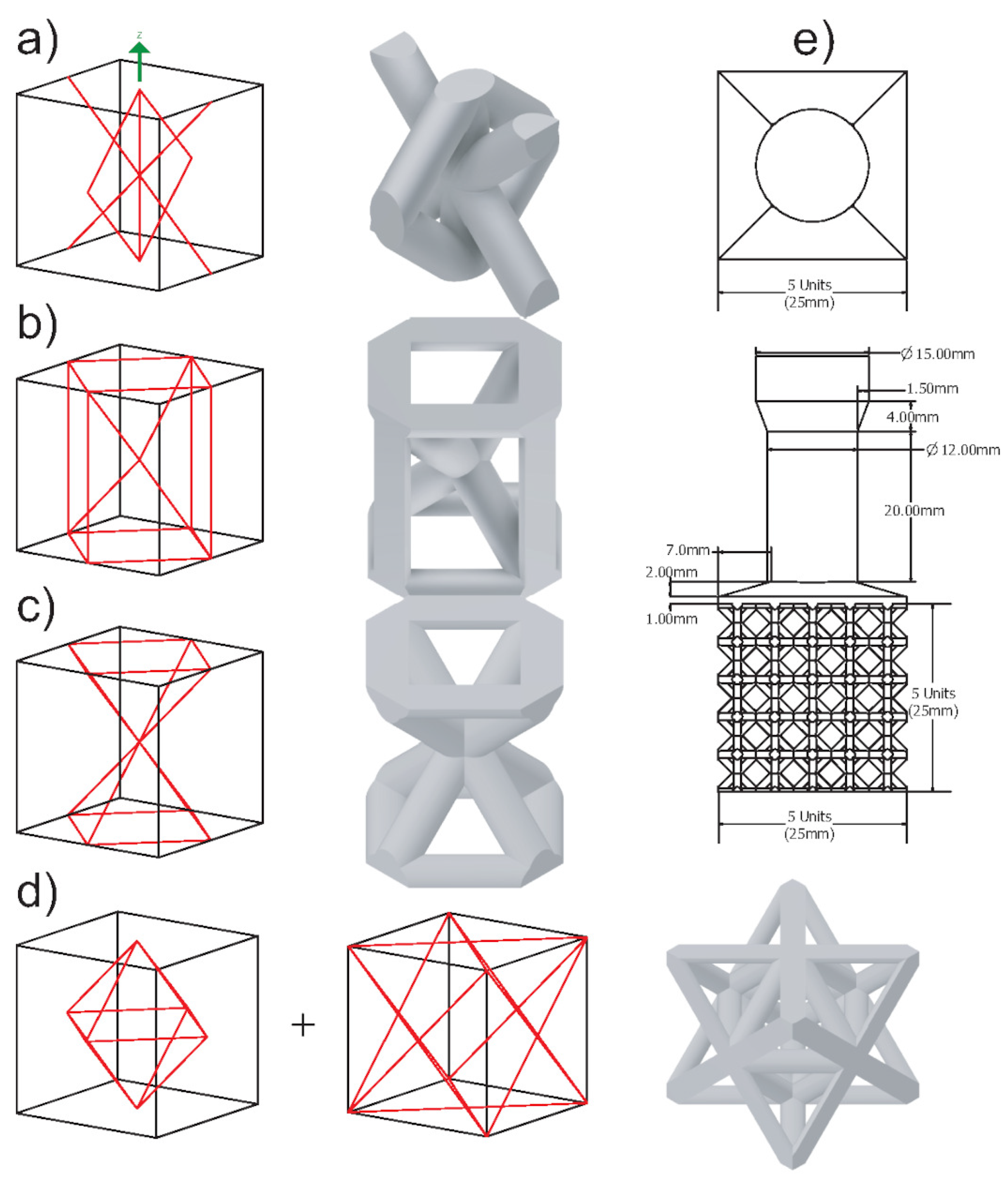
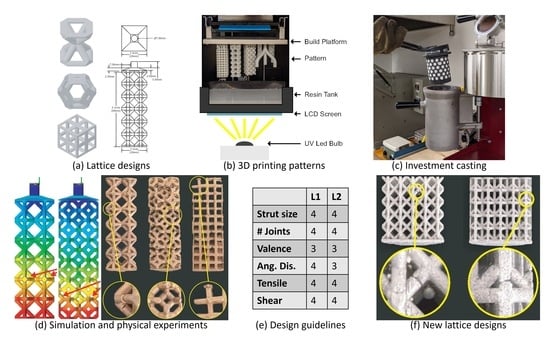
From all the results: mold flow, the two casting experiments, and the FEA, we have narrowed down the factors that significantly affect casting performance. The features that play a role in the success of the cast lattice topologies are relative strut size, number of joints, joint valence, and strut angle distribution. The casting experiments’ results and the overall performance of each lattice topology can be explained using these features. The relative strut size is the strut size divided by the unit cell width, which is a property that will remain the same regardless of unit cell width. The number of joints refers to the total number of points within the cell where struts connect. Joint valence refers to how many struts connect at a given joint. The above features are listed in
Table 7 for each lattice topology tested. Strut length can be measured for different strut angles and divided by the total to determine the strut angle distribution (see
Figure 14).
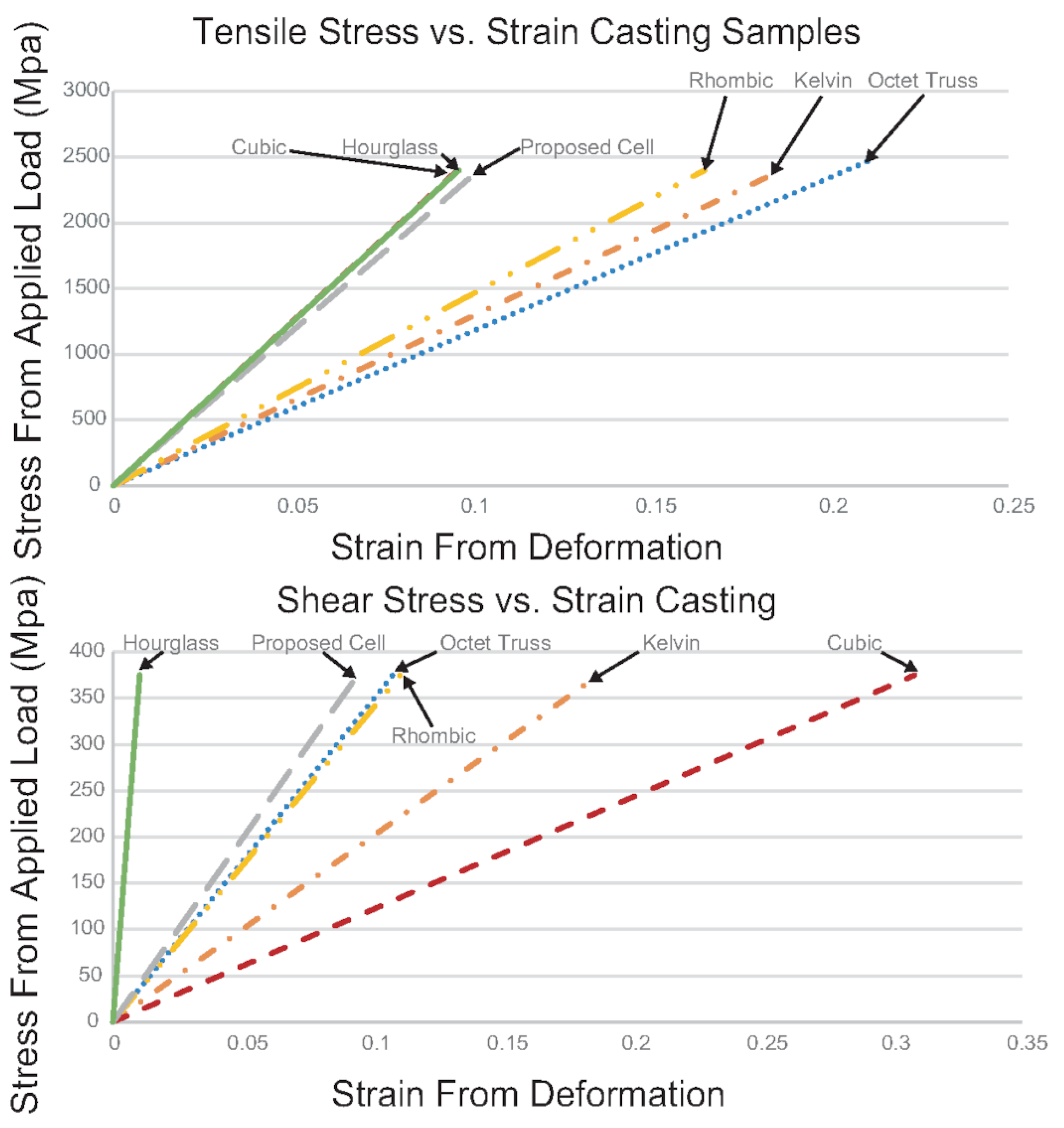
When analyzing the casting and mold flow results, the effect of relative strut size can be seen most significantly in the cubic and octet-truss topologies. The two structures have lower relative strut sizes of 0.16 and 0.14 when compared to the more successful proposed and hourglass topologies of 0.22 and 0.20 (see
Table 7). Lower relative strut sizes result in slower filling times which often results in premature melt solidification. Therefore, it is clear that the relative strut size plays the largest role in the success of a lattice structure casting. This ratio gives an idea of the negative effect that adding more struts for rigidity has on the strut size and in turn the metal flow. It allows us to determine which structures create an efficient short path for the metal to flow through.
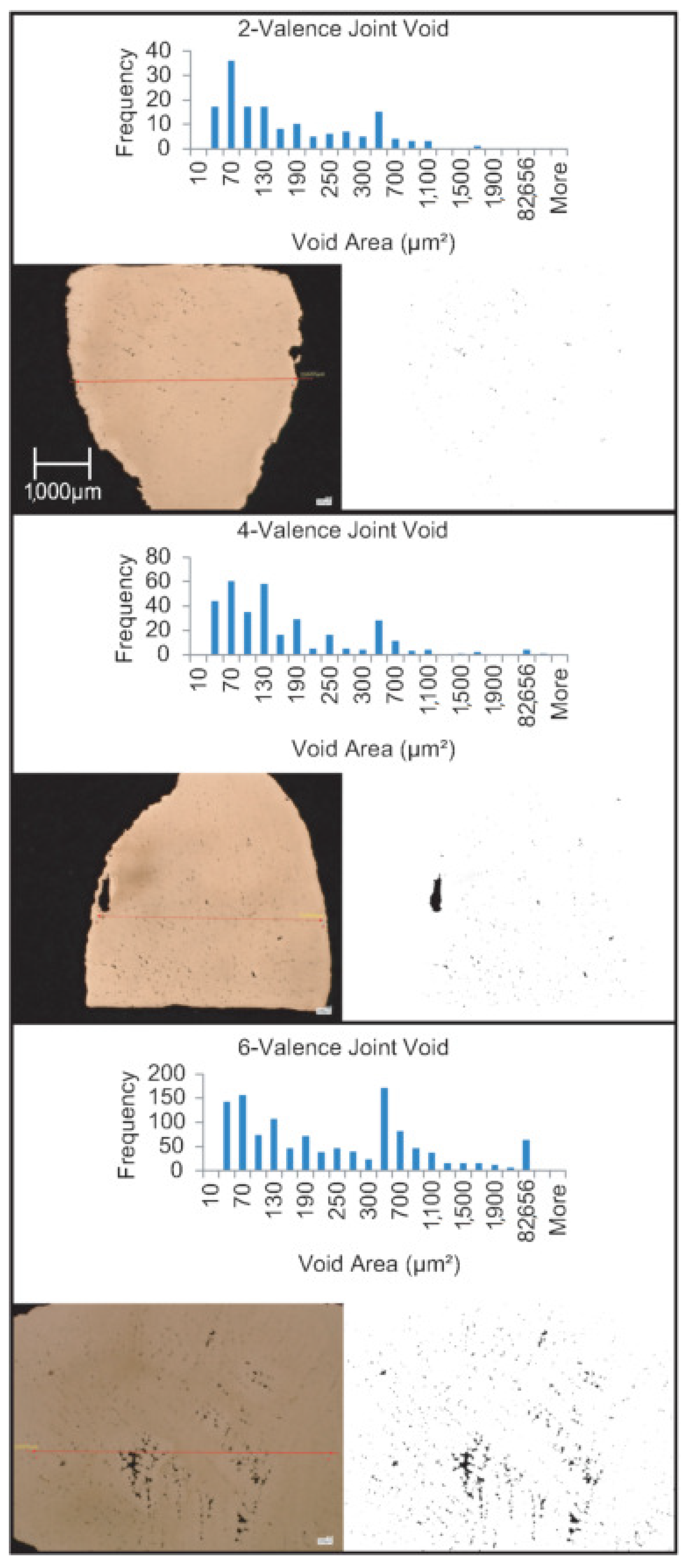
Next in the level of importance is the number of joints. From the mold flow and experimental castings, it is clear that the topologies with the highest number of joints performed very poorly. The effect can be seen in the cubic (27), kelvin cell (24) and octet-truss (14) topologies. The remaining three topologies with a joint number of 9 all performed well. To add a level of granularity to the analysis, these three topologies can be further classified based on their joint valence. The proposed structure performed better than the other two due to its low joint valence (4.58), this trend continues for the hourglass (5.74) and then the rhombic (8). This behavior can be further supported by the void analysis results. A higher void ratio can be observed as the joint valence is increased from 2 to 4 to 6.
Finally, the effect of strut angle can definitely be seen in the casting results and the mold flow results, with defects often occurring at vertical or horizontal struts. Regardless, strut angle seems to have the smallest effect on the performance. The hourglass topology illustrates this as it was the second-best performant but it has a balance of vertical, diagonal, and horizontal struts. This topology would have performed worse due to its horizontal and vertical struts if strut angle had more of an impact on the performance. From the FEA results, the presence of horizontal, diagonal, and vertical struts is important for mechanical strength under tensile and shear. Some of the structures were tested by Després et al. [
29]. They observed similar behavior as was observed in our FEA results. The diagonal struts contribute to the shear performance whereas the vertical struts contribute to the bending, tension and compression performance.
Overall, looking at a balance of casting performance and mechanical strength, it appears that the best way to improve casting performance is optimizing for relative strut size, number of joints, and joint valence. Mechanical performance can be achieved through strut angle distribution.
Design Guidelines
To better establish and understand the design guidelines for RIC, the performance grading of all the topologies can be seen in
Table 8. The topologies are graded from 1 to 4, where 4 is the best and 1 is the worst performance. This table also includes the tensile and shear performance for reference. The topological features are listed in decreasing order of casting performance from left to right. The two topologies (proposed and hourglass) performed the best experimentally, as shown in the table. They scored at least 3 across the board and scored 4 in the most important categories (relative strut size, number of joints, and joint valence). The mechanical performance was also 4 due to the angle distribution, which includes vertical, horizontal, and diagonal struts [
29]. In addition, the number of joints and joint valence affect mechanical strength. This effect was observed in the FEA results and is supported by Li et al. [
30]. The authors stated that lattice cells’ deformation mode changes from bending-dominated to stretch-dominated with the increase of the joint valence. Stretch-dominated is the more rigid one of the two behaviors. Although rigidity can be achieved without a high number of joints and joint valence, as Maxwell’s criterion of rigidity is limited as demonstrated by Chen et al. [
31]: if FEA shows a rigid lattice, then the net lattice is rigid.
From these findings and analyzes, a set of design guidelines for RIC can be drawn. On top of the design considerations for IC (e.g., minimum strut size of 1 mm) and DLP AM (e.g., open-celled). The design guidelines for RIC in order of importance are as follows:
The relative strut size should be kept below 0.2.
The number of joints should be kept below 9.
The max and mean joint valence of 8 or less is recommended.
For mechanical performance, the strut angle distribution should include vertical, diagonal, and horizontal struts.
Let it be noted that a similar condition as in this paper should be met for faithful use of the design guidelines. Besides the machines and materials used, they include straight and circular cross-sectioned struts, cubic packing strategy, and the size of unit cell ranging from 5 mm to 10 mm. By far from what has been tested, the proposed, hourglass and rhombic topologies meet all these criteria and achieve good casting and mechanical performance.
5. Conclusions
In summary, it is clear that as with other metallic-AM processes, RIC can take full advantage of AM’s unprecedented design freedom. RIC was successfully used to create a variety of lattice structures. These structures were used to determine the topological lattice features critical to casting performance. From those results, a methodology to study the performance of RIC lattice structures has been established. In this methodology, topological features are compared and analyzed using the test results. This analysis results in a set of design guidelines for RIC. The features established to affect casting performance in descending order of importance are relative strut size, number of joints, joint valence, and strut angle distribution. Without controlling these features, hot spots, porosity and premature solidification can occur. All four proposed topological lattice features directly affect a lattice’s feed paths and flow velocity/connectivity. Although the design guidelines share the same logic as the ones for general casting, they differ in that they are specifically tailored towards optimizing cellular structures. Cellular structures by nature have a high potential for flow restriction or high connectivity. For this reason, more targeted design guidelines than the general casting ones are needed. The features deemed to have the most significant effect on tensile and shear mechanical performance are strut angle distribution, number of joints, and joint valence. With the design methodology, the proposed cell and hourglass topologies were created. These lattice topologies had the best overall casting and mechanical performance of all the tested lattices. The limitations of the current work include testing only strut-based lattice topologies. Future work could expand beyond this. Future work could also further refine the design methodology and automate the design process using software-driven methods.