Topological Atomic Chains on 2D Hybrid Structure
Abstract
1. Introduction
2. Model and Theoretical Description
3. Results and Discussions
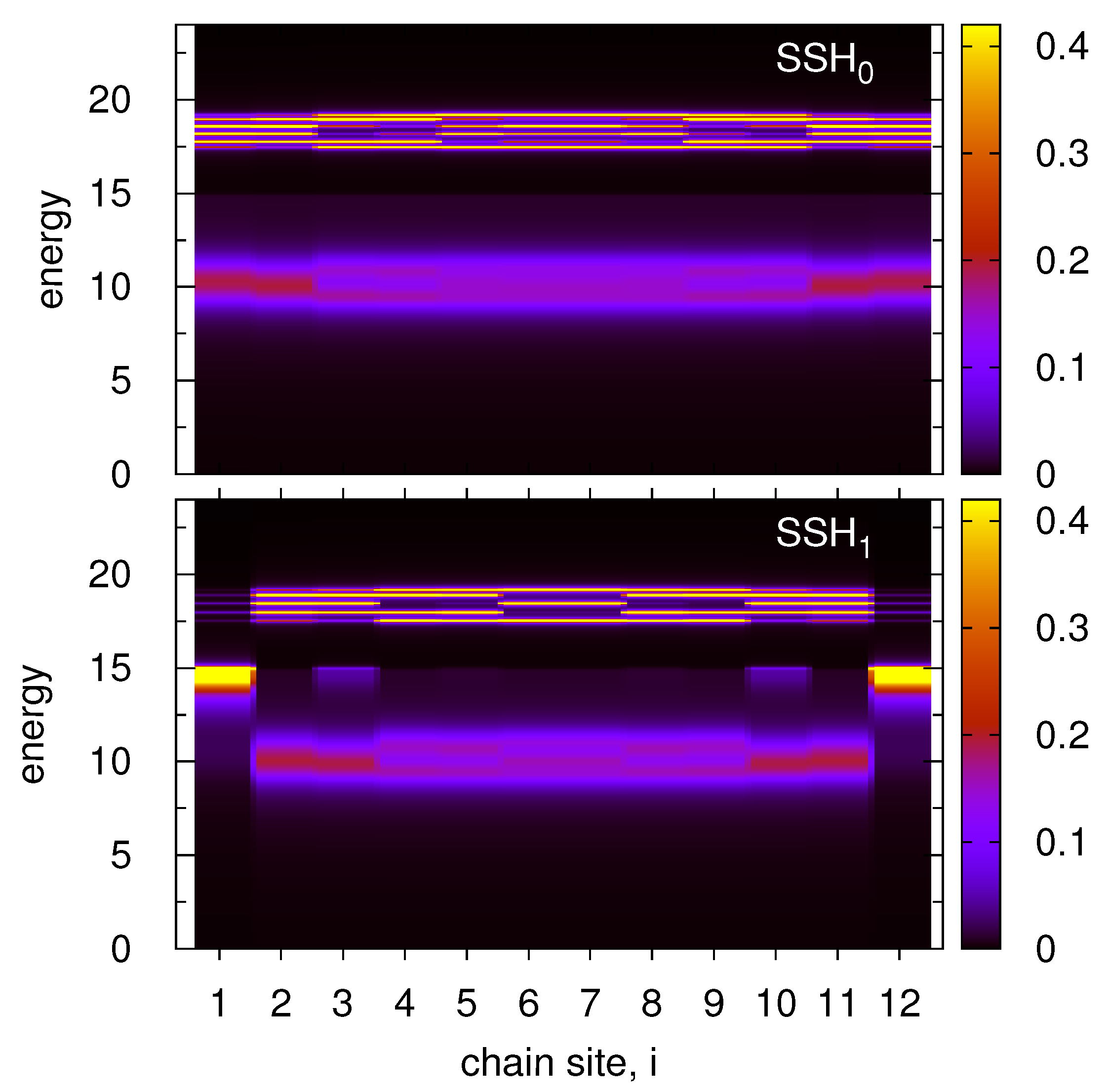
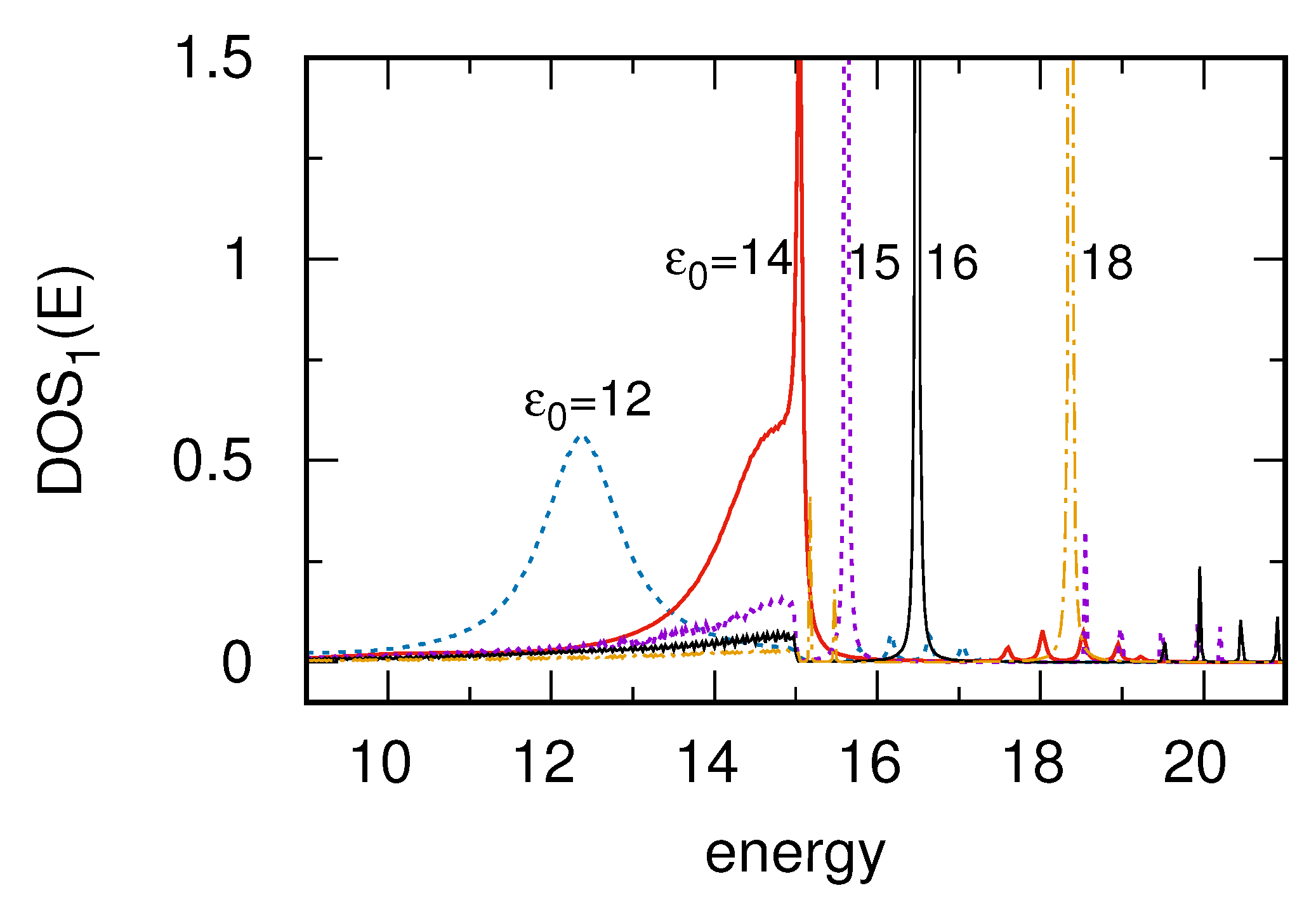
3.1. Straight SSH Atomic Chain
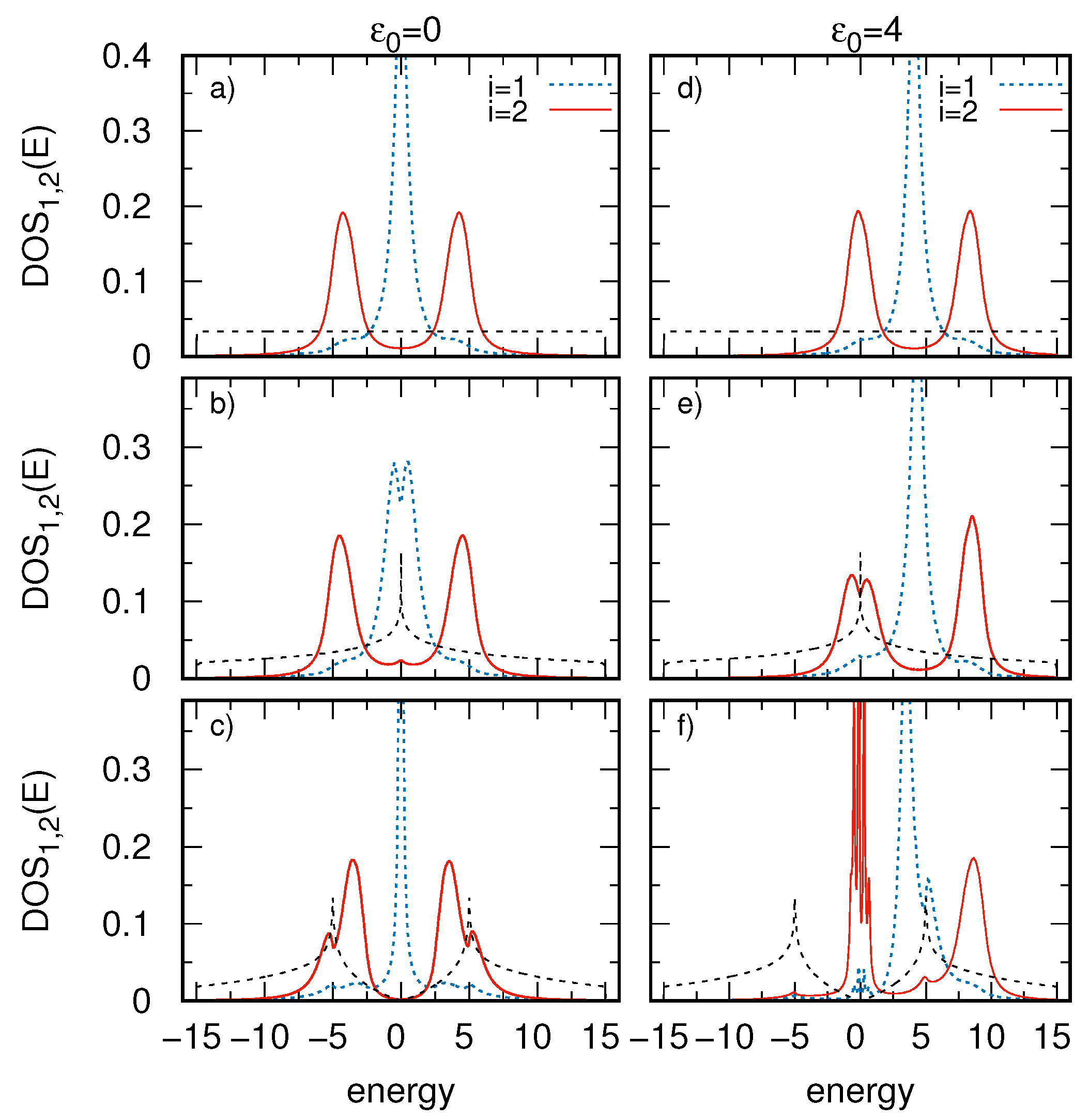
3.2. Boundary Effects in Chain DOS
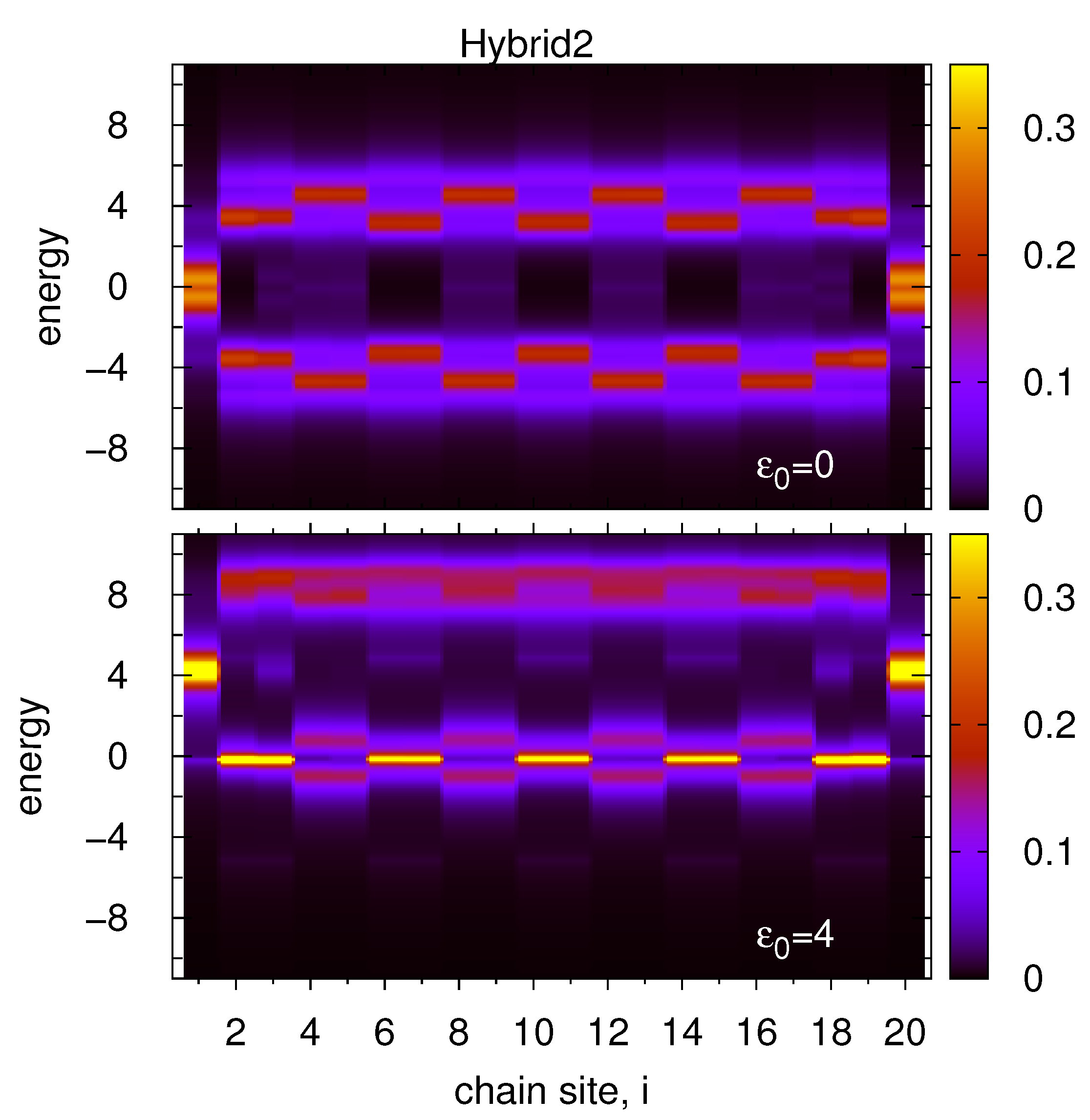
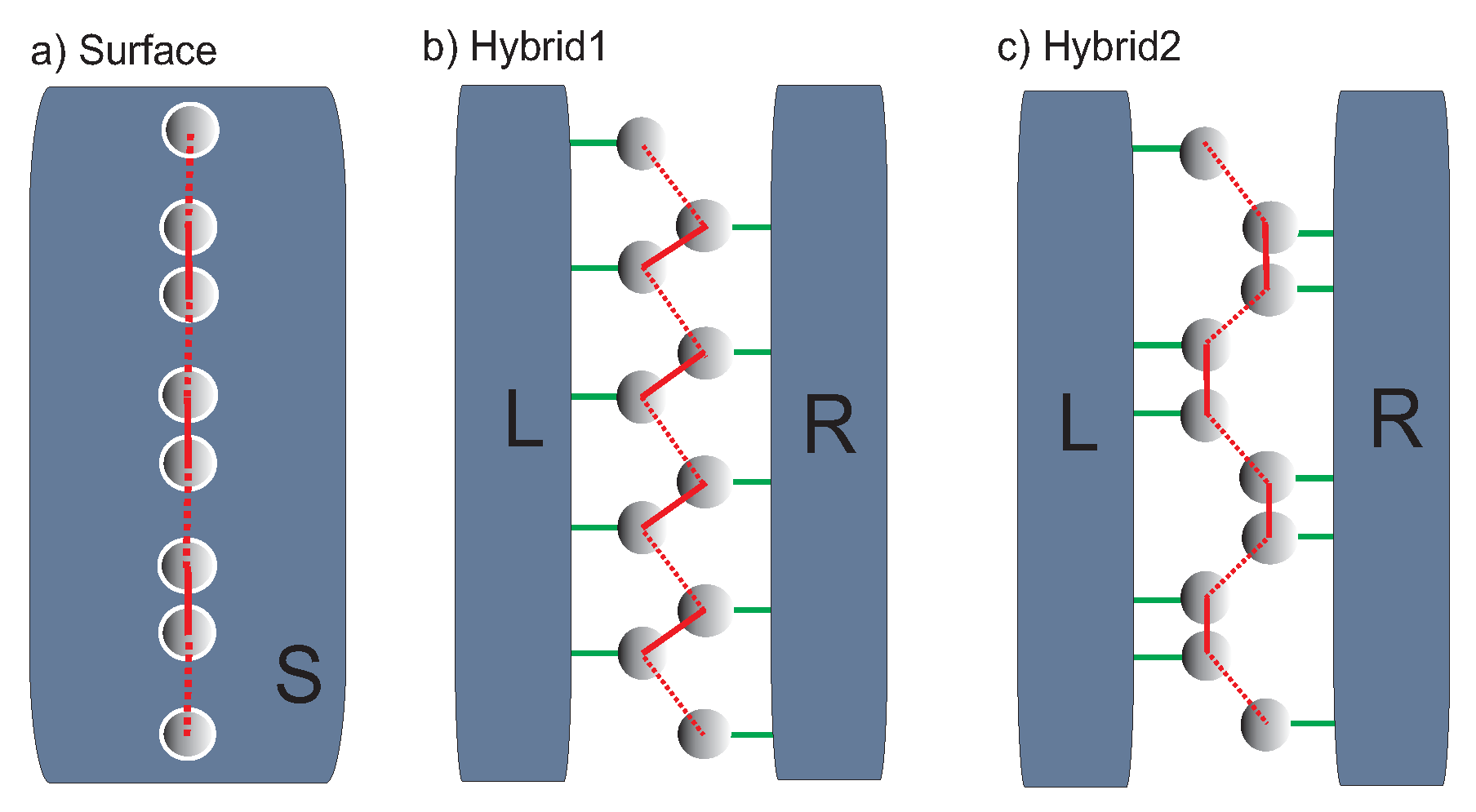
3.3. Zig-Zag and Armchair-Edge Chains between 2D Systems
4. Conclusions
- Surface with singularities in DOS essentially influences the spectral density function (local DOS) along the chain and is responsible for strong asymmetry in the topological chain energetic structure. It leads to the particle-hole symmetry breaking in the system.
- The surface van Hove singularities can split the SSH topological state of the chain. On the other hand dips in the surface DOS lead to dispersionless strongly localized states (topological or normal) in the chain.
- There was also discovered that topological mid-gap states can exist outside the surface band boundaries. It is important that when the chain on-site energies lie near the surface DOS edges topological state reveals partially localized behaviour with both wide dispersion due to continuous band states and sharp localized peak which comes from the surface band boundaries.
- Different geometries of the SSH atomic chain between two 2D electrodes systems show spatial and energetic asymmetry in the structure of chain DOS which leads to different energies of both topological edge states at the chain ends.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B

References
- Yu, B. Graphene nanoelectronics: Overview from post-silicon perspective. In Proceedings of the 2012 IEEE 11th International Conference on Solid-State and Integrated Circuit Technology, Xi’an, China, 29 October–1 November 2012; pp. 1–2. [Google Scholar] [CrossRef]
- Shore, K.A. Introduction to Graphene-Based Nanomaterials: From Electronic Structure to Quantum Transport, by Luis E.F. Foa Torres, Stephan Roche and Jean-Christophe Charlier. Contemp. Phys. 2014, 55, 344–345. [Google Scholar] [CrossRef]
- Li, D.; Liu, T.; Yu, X.; Wu, D.; Su, Z. Fabrication of graphene–biomacromolecule hybrid materials for tissue engineering application. Polym. Chem. 2017, 8, 4309–4321. [Google Scholar] [CrossRef]
- Lieber, C.M. One-dimensional nanostructures: Chemistry, physics and applications. Solid State Commun. 1998, 107, 607–616. [Google Scholar] [CrossRef]
- Saxena, S.K.; Nyodu, R.; Kumar, S.; Maurya, V.K. Current Advances in Nanotechnology and Medicine. In NanoBioMedicine; Saxena, S.K., Khurana, S.M.P., Eds.; Springer: Singapore, 2020; pp. 3–16. [Google Scholar] [CrossRef]
- Auslaender, O.M.; Steinberg, H.; Yacoby, A.; Tserkovnyak, Y.; Halperin, B.I.; Baldwin, K.W.; Pfeiffer, L.N.; West, K.W. Spin-Charge Separation and Localization in One Dimension. Science 2005, 308, 88–92. [Google Scholar] [CrossRef] [PubMed]
- Kwapiński, T.; Taranko, R. Spin and charge pumping in a quantum wire: The role of spin-flip scattering and Zeeman splitting. J. Phys. Condens. Matter 2011, 23, 405301. [Google Scholar] [CrossRef]
- Nadj-Perge, S.; Drozdov, I.K.; Li, J.; Chen, H.; Jeon, S.; Seo, J.; MacDonald, A.H.; Bernevig, B.A.; Yazdani, A. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 2014, 346, 602–607. [Google Scholar] [CrossRef] [PubMed]
- Pawlak, R.; Kisiel, M.; Klinovaja, J.; Meier, T.; Kawai, S.; Glatzel, T.; Loss, D.; Meyer, E. Probing atomic structure and Majorana wavefunctions in mono-atomic Fe chains on superconducting Pb surface. NPJ Quantum Inf. 2016, 2, 16035. [Google Scholar] [CrossRef]
- Shin, J.S.; Ryang, K.D.; Yeom, H.W. Finite-length charge-density waves on terminated atomic wires. Phys. Rev. B 2012, 85, 073401. [Google Scholar] [CrossRef]
- Kurzyna, M.; Kwapiński, T. Non-local electron transport through normal and topological ladder-like atomic systems. J. Appl. Phys. 2018, 123, 194301. [Google Scholar] [CrossRef]
- Kwapiński, T. Conductance oscillations and charge waves in zigzag shaped quantum wires. J. Phys. Condens. Matter 2010, 22, 295303. [Google Scholar] [CrossRef]
- van der Wiel, W.G.; De Franceschi, S.; Elzerman, J.M.; Fujisawa, T.; Tarucha, S.; Kouwenhoven, L.P. Electron transport through double quantum dots. Rev. Mod. Phys. 2002, 75, 1–22. [Google Scholar] [CrossRef]
- Fujisawa, T.; Tokura, Y.; Hirayama, Y. Transient current spectroscopy of a quantum dot in the Coulomb blockade regime. Phys. Rev. B 2001, 63, 081304. [Google Scholar] [CrossRef]
- Hayashi, T.; Fujisawa, T.; Cheong, H.D.; Jeong, Y.H.; Hirayama, Y. Coherent Manipulation of Electronic States in a Double Quantum Dot. Phys. Rev. Lett. 2003, 91, 226804. [Google Scholar] [CrossRef] [PubMed]
- Arkinstall, J.; Teimourpour, M.H.; Feng, L.; El-Ganainy, R.; Schomerus, H. Topological tight-binding models from nontrivial square roots. Phys. Rev. B 2017, 95. [Google Scholar] [CrossRef]
- Jürß, C.; Bauer, D. High-harmonic generation in Su-Schrieffer-Heeger chains. Phys. Rev. B 2019, 99. [Google Scholar] [CrossRef]
- Huneke, J.; Platero, G.; Kohler, S. Steady-State Coherent Transfer by Adiabatic Passage. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef]
- Kohler, S.; Lehmann, J.; Hänggi, P. Driven quantum transport on the nanoscale. Phys. Rep. 2005, 406, 379–443. [Google Scholar] [CrossRef]
- Kurzyna, M.; Kwapiński, T. Electron Pumping and Spectral Density Dynamics in Energy-Gapped Topological Chains. Appl. Sci. 2021, 11, 772. [Google Scholar] [CrossRef]
- Wilczek, F. Quantum Time Crystals. Phys. Rev. Lett. 2012, 109, 160401. [Google Scholar] [CrossRef]
- Sacha, K. Modeling spontaneous breaking of time-translation symmetry. Phys. Rev. A 2015, 91, 033617. [Google Scholar] [CrossRef]
- Sacha, K.; Zakrzewski, J. Time crystals: A review. Rep. Prog. Phys. 2017, 81, 016401. [Google Scholar] [CrossRef]
- Kurzyna, M.; Kwapiński, T. Nontrivial dynamics of a two-site system: Transient crystals. Phys. Rev. B 2020, 102, 245414. [Google Scholar] [CrossRef]
- Lindner, N.H.; Refael, G.; Galitski, V. Floquet topological insulator in semiconductor quantum wells. Nat. Phys. 2011, 7, 490–495. [Google Scholar] [CrossRef]
- Perez-Piskunow, P.M.; Usaj, G.; Balseiro, C.A.; Torres, L.E.F.F. Floquet chiral edge states in graphene. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
- Kraus, C.V.; Dalmonte, M.; Baranov, M.A.; Läuchli, A.M.; Zoller, P. Majorana Edge States in Atomic Wires Coupled by Pair Hopping. Phys. Rev. Lett. 2013, 111, 173004. [Google Scholar] [CrossRef] [PubMed]
- Kurzyna, M.; Kwapiński, T. Edge-state dynamics in coupled topological chains. Phys. Rev. B 2020, 102, 195429. [Google Scholar] [CrossRef]
- Pérez-González, B.; Bello, M.; Gómez-León, Á.; Platero, G. SSH model with long-range hoppings: Topology, driving and disorder. arXiv 2018, arXiv:1802.03973. [Google Scholar]
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698–1701. [Google Scholar] [CrossRef]
- Jałochowski, M.; Krawiec, M. Antimonene on Pb quantum wells. 2D Mater. 2019, 6, 045028. [Google Scholar] [CrossRef]
- Stpniak-Dybala, A.; Dyniec, P.; Kopciuszyski, M.; Zdyb, R.; Jałochowski, M.; Krawiec, M. Planar Silicene: A New Silicon Allotrope Epitaxially Grown by Segregation. Adv. Funct. Mater. 2019, 29, 1906053. [Google Scholar] [CrossRef]
- Drost, R.; Ojanen, T.; Harju, A.; Liljeroth, P. Topological states in engineered atomic lattices. Nat. Phys. 2017, 13, 668–671. [Google Scholar] [CrossRef]
- Le, N.H.; Fisher, A.J.; Curson, N.J.; Ginossar, E. Topological phases of a dimerized Fermi–Hubbard model for semiconductor nano-lattices. NPJ Quantum Inf. 2020, 6, 24. [Google Scholar] [CrossRef]
- Crain, J.N.; McChesney, J.L.; Zheng, F.; Gallagher, M.C.; Snijders, P.C.; Bissen, M.; Gundelach, C.; Erwin, S.C.; Himpsel, F.J. Chains of gold atoms with tailored electronic states. Phys. Rev. B 2004, 69, 125401. [Google Scholar] [CrossRef]
- Kopciuszyński, M.; Dyniec, P.; Krawiec, M.; Łukasik, P.; Jałochowski, M.; Zdyb, R. Pb nanoribbons on the Si(553) surface. Phys. Rev. B 2013, 88, 155431. [Google Scholar] [CrossRef]
- Baski, A.; Saoud, K.; Jones, K. 1-D nanostructures grown on the Si(5 5 12) surface. Appl. Surf. Sci. 2001, 182, 216–222. [Google Scholar] [CrossRef]
- Hensgens, T.; Fujita, T.; Janssen, L.; Li, X.; Van Diepen, C.J.; Reichl, C.; Wegscheider, W.; Das Sarma, S.; Vandersypen, L.M.K. Quantum simulation of a Fermi–Hubbard model using a semiconductor quantum dot array. Nature 2017, 548, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Zwanenburg, F.A.; Dzurak, A.S.; Morello, A.; Simmons, M.Y.; Hollenberg, L.C.L.; Klimeck, G.; Rogge, S.; Coppersmith, S.N.; Eriksson, M.A. Silicon quantum electronics. Rev. Mod. Phys. 2013, 85, 961–1019. [Google Scholar] [CrossRef]
- Huda, M.N.; Kezilebieke, S.; Ojanen, T.; Drost, R.; Liljeroth, P. Tuneable topological domain wall states in engineered atomic chains. NPJ Quantum Mater. 2020, 5, 17. [Google Scholar] [CrossRef]
- Ji, J.; Song, X.; Liu, J.; Yan, Z.; Huo, C.; Zhang, S.; Su, M.; Liao, L.; Wang, W.; Ni, Z.; et al. Two-dimensional antimonene single crystals grown by van der Waals epitaxy. Nat. Commun. 2016, 7, 13352. [Google Scholar] [CrossRef]
- Sun, X.; Song, Z.; Liu, S.; Wang, Y.; Li, Y.; Wang, W.; Lu, J. Sub-5 nm Monolayer Arsenene and Antimonene Transistors. ACS Appl. Mater. Interfaces 2018, 10, 22363–22371. [Google Scholar] [CrossRef] [PubMed]
- Jałochowski, M.; Kwapinski, T.; Łukasik, P.; Nita, P.; Kopciuszyński, M. Correlation between morphology, electron band structure, and resistivity of Pb atomic chains on the Si(553)-Au surface. J. Phys. Condens. Matter 2016, 28, 284003. [Google Scholar] [CrossRef]
- Krawiec, M.; Kwapiński, T.; Jałochowski, M. Double nonequivalent chain structure on a vicinal Si(557)-Au surface. Phys. Rev. B 2006, 73, 075415. [Google Scholar] [CrossRef]
- Kwapiński, T.; Kohler, S.; Hänggi, P. Electron transport across a quantum wire in the presence of electron leakage to a substrate. Eur. Phys. J. B 2010, 78, 75–81. [Google Scholar] [CrossRef]
- Asboth, J.K.; Oroszlany, L.; Palyi, A. A Short Course on Topological Insulators; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Li, L.; Yang, C.; Chen, S. Winding numbers of phase transition points for one-dimensional topological systems. EPL 2015, 112, 10004. [Google Scholar] [CrossRef][Green Version]
- Li, L.; Xu, Z.; Chen, S. Topological phases of generalized Su-Schrieffer-Heeger models. Phys. Rev. B 2014, 89, 085111. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge Studies in Semiconductor Physics and Microelectronic Engineering; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar] [CrossRef]
- Podloucky, R.; Desjonquères, M.C.; Spanjaard, D. Concepts in Surface Physics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1996; ISBN 978-3-540-58622-7. [Google Scholar]
- Newns, D.; Read, N. Mean-field theory of intermediate valence/heavy fermion systems. Adv. Phys. 1987, 36, 799–849. [Google Scholar] [CrossRef]
- Kwapiński, T. Conductance oscillations of a quantum wire disturbed by an adatom. J. Phys. Condens. Matter 2007, 19, 176218. [Google Scholar] [CrossRef] [PubMed]
- Choy, T.C. Density of states for a two-dimensional Penrose lattice: Evidence of a strong Van-Hove singularity. Phys. Rev. Lett. 1985, 55, 2915–2918. [Google Scholar] [CrossRef] [PubMed]
- Horiguchi, T. Lattice Green’s Functions for the Triangular and Honeycomb Lattices. J. Math. Phys. 1972, 13, 1411–1419. [Google Scholar] [CrossRef]
- Katsnelson, M.I. Graphene: Carbon in Two Dimensions; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Kogan, E.; Gumbs, G. Green’s Functions and DOS for Some 2D Lattices. Graphene 2021, 10, 1–12. [Google Scholar] [CrossRef]
- Yuhara, J.; Shichida, Y. Epitaxial growth of two-dimensional Pb and Sn films on Al(111). Thin Solid Film. 2016, 616, 618–623. [Google Scholar] [CrossRef]
- Feng, H.; Liu, C.; Zhou, S.; Gao, N.; Gao, Q.; Zhuang, J.; Xu, X.; Hu, Z.; Wang, J.; Chen, L.; et al. Experimental Realization of Two-Dimensional Buckled Lieb Lattice. Nano Lett. 2020, 20, 2537–2543. [Google Scholar] [CrossRef]
- Yuhara, J.; Schmid, M.; Varga, P. Two-dimensional alloy of immiscible metals: Single and binary monolayer films of Pb and Sn on Rh(111). Phys. Rev. B 2003, 67, 195407. [Google Scholar] [CrossRef]
- Kurzyna, M.; Kwapiński, T. Electronic properties of atomic ribbons with spin-orbit couplings on different substrates. J. Appl. Phys. 2019, 125, 144301. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwapiński, T.; Kurzyna, M. Topological Atomic Chains on 2D Hybrid Structure. Materials 2021, 14, 3289. https://doi.org/10.3390/ma14123289
Kwapiński T, Kurzyna M. Topological Atomic Chains on 2D Hybrid Structure. Materials. 2021; 14(12):3289. https://doi.org/10.3390/ma14123289
Chicago/Turabian StyleKwapiński, Tomasz, and Marcin Kurzyna. 2021. "Topological Atomic Chains on 2D Hybrid Structure" Materials 14, no. 12: 3289. https://doi.org/10.3390/ma14123289
APA StyleKwapiński, T., & Kurzyna, M. (2021). Topological Atomic Chains on 2D Hybrid Structure. Materials, 14(12), 3289. https://doi.org/10.3390/ma14123289