Cancellation of Auxetic Properties in F.C.C. Hard Sphere Crystals by Hybrid Layer-Channel Nanoinclusions Filled by Hard Spheres of Another Diameter
Abstract
1. Introduction
2. The Model
3. Method
3.1. Theory
3.2. Simulations
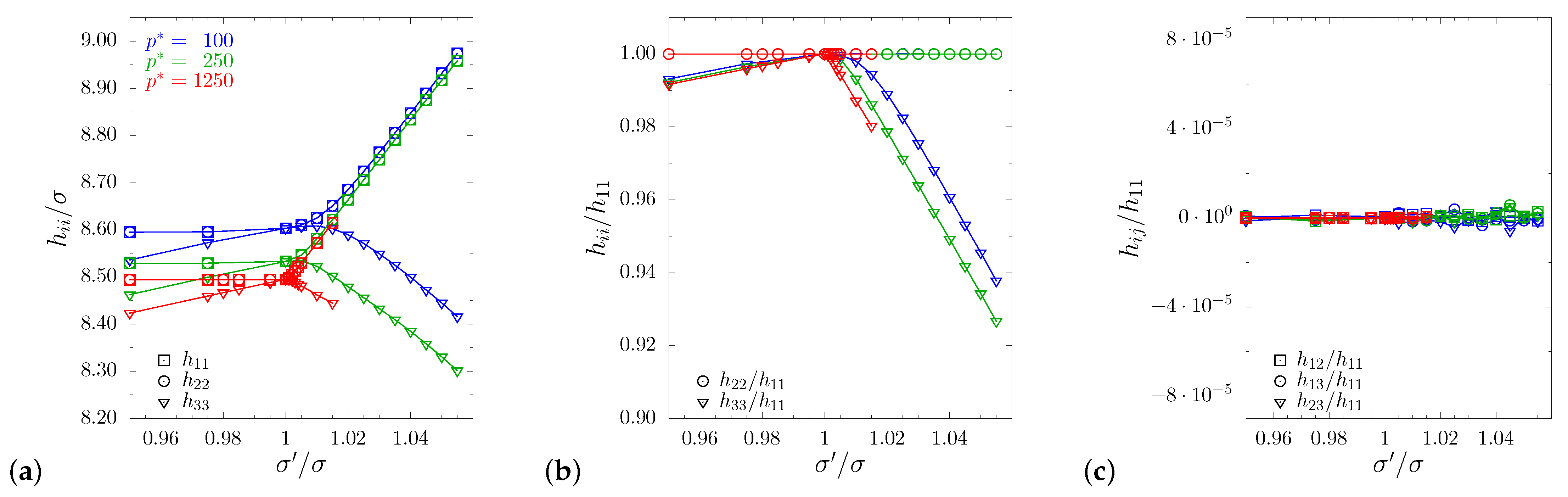
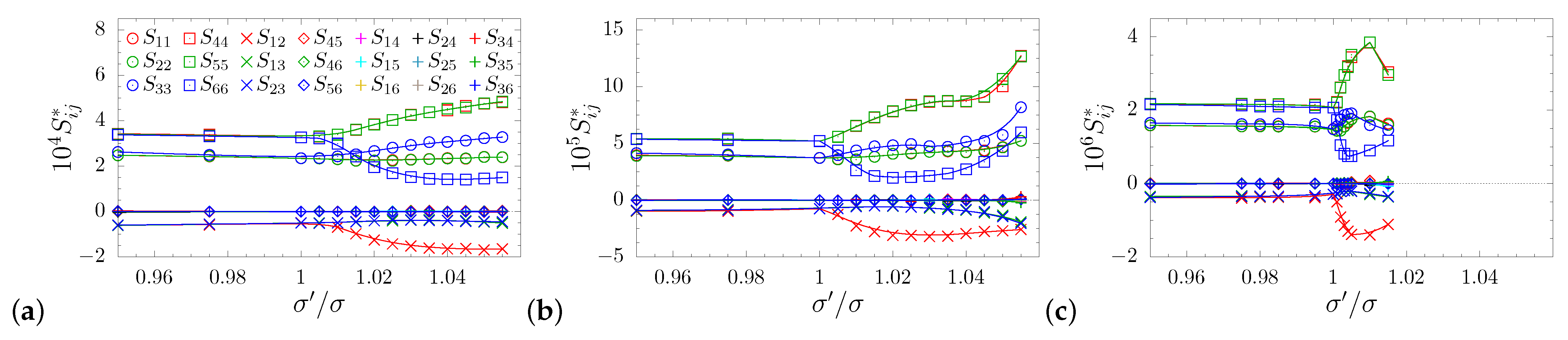
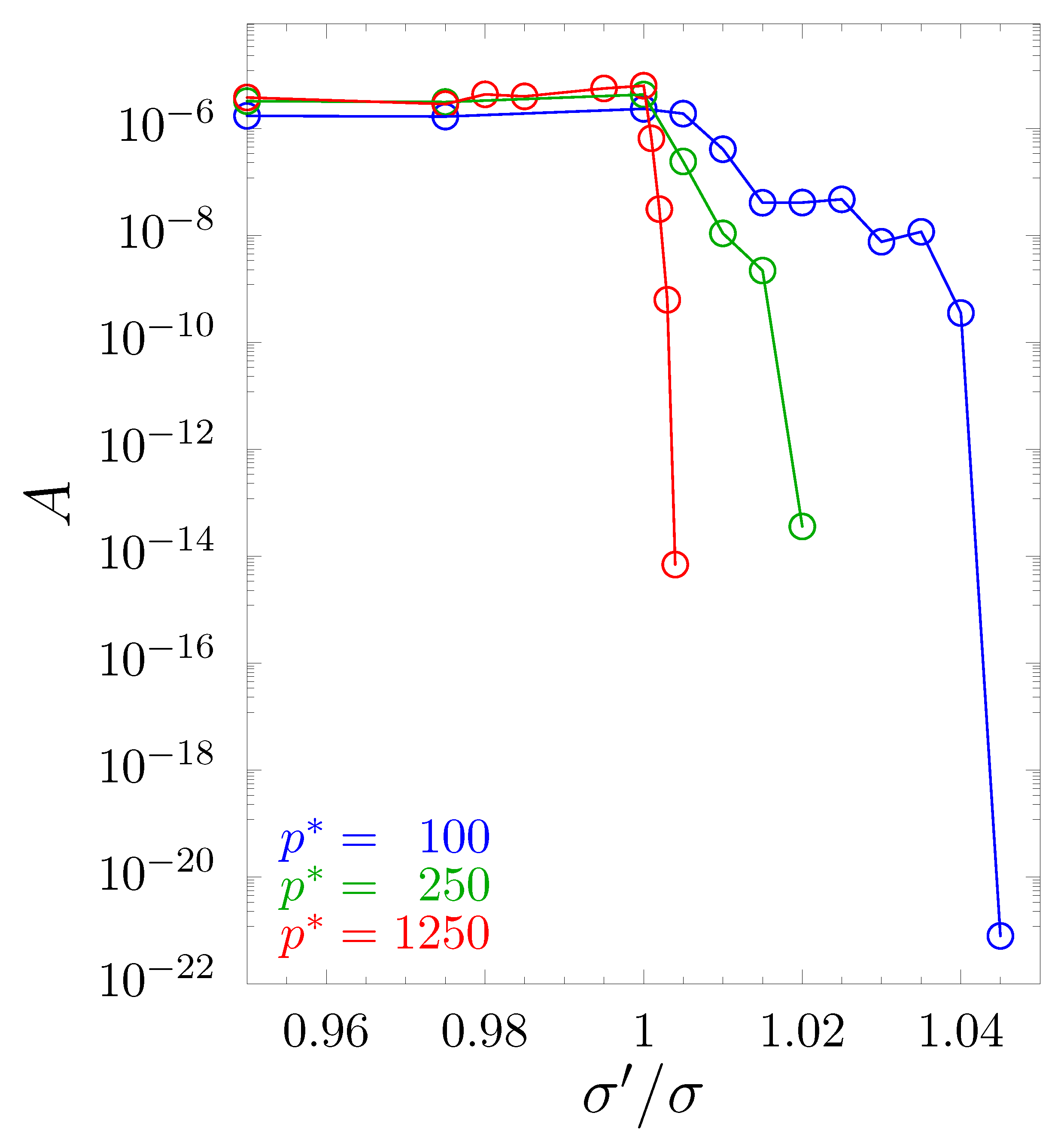
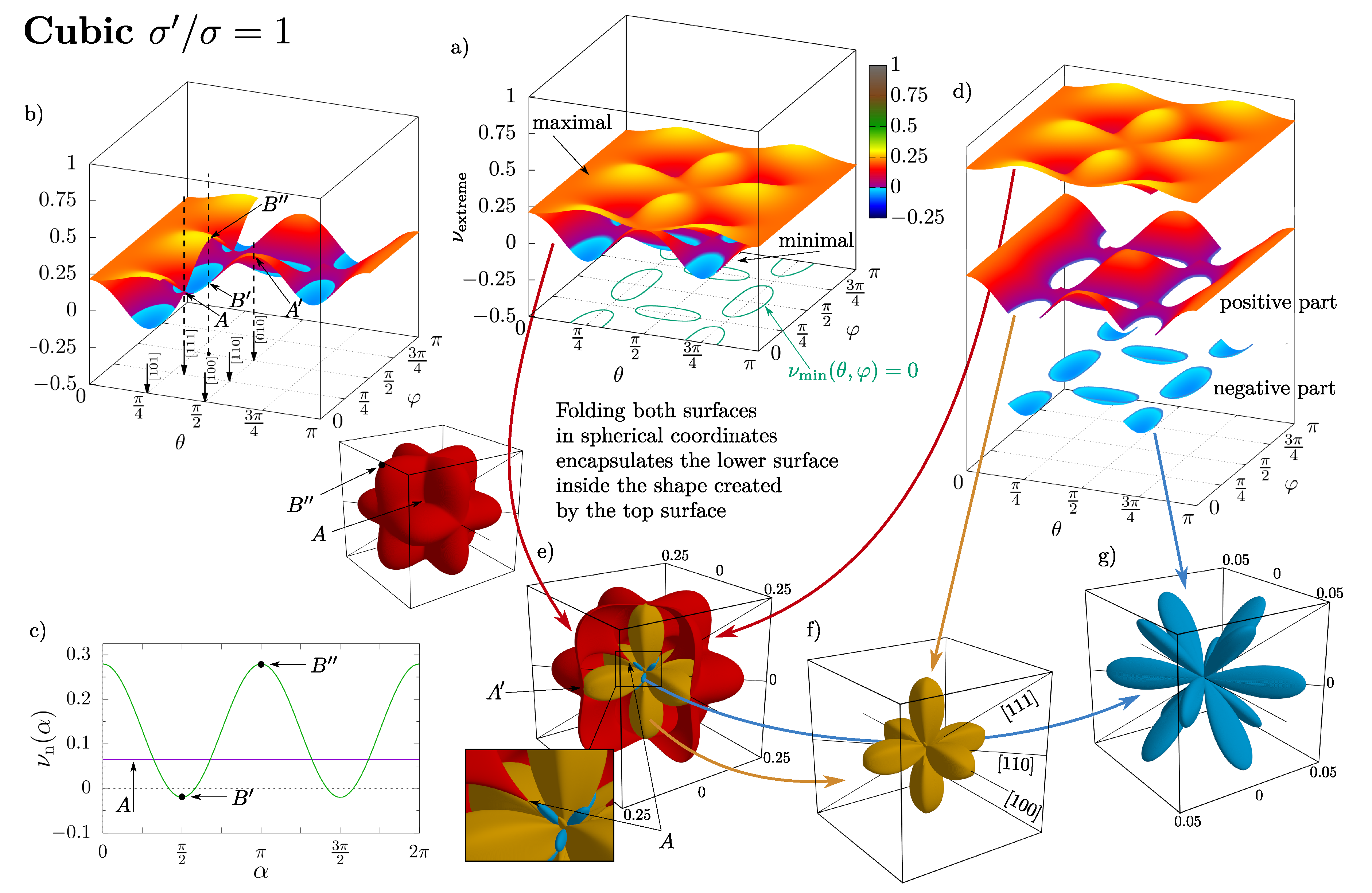
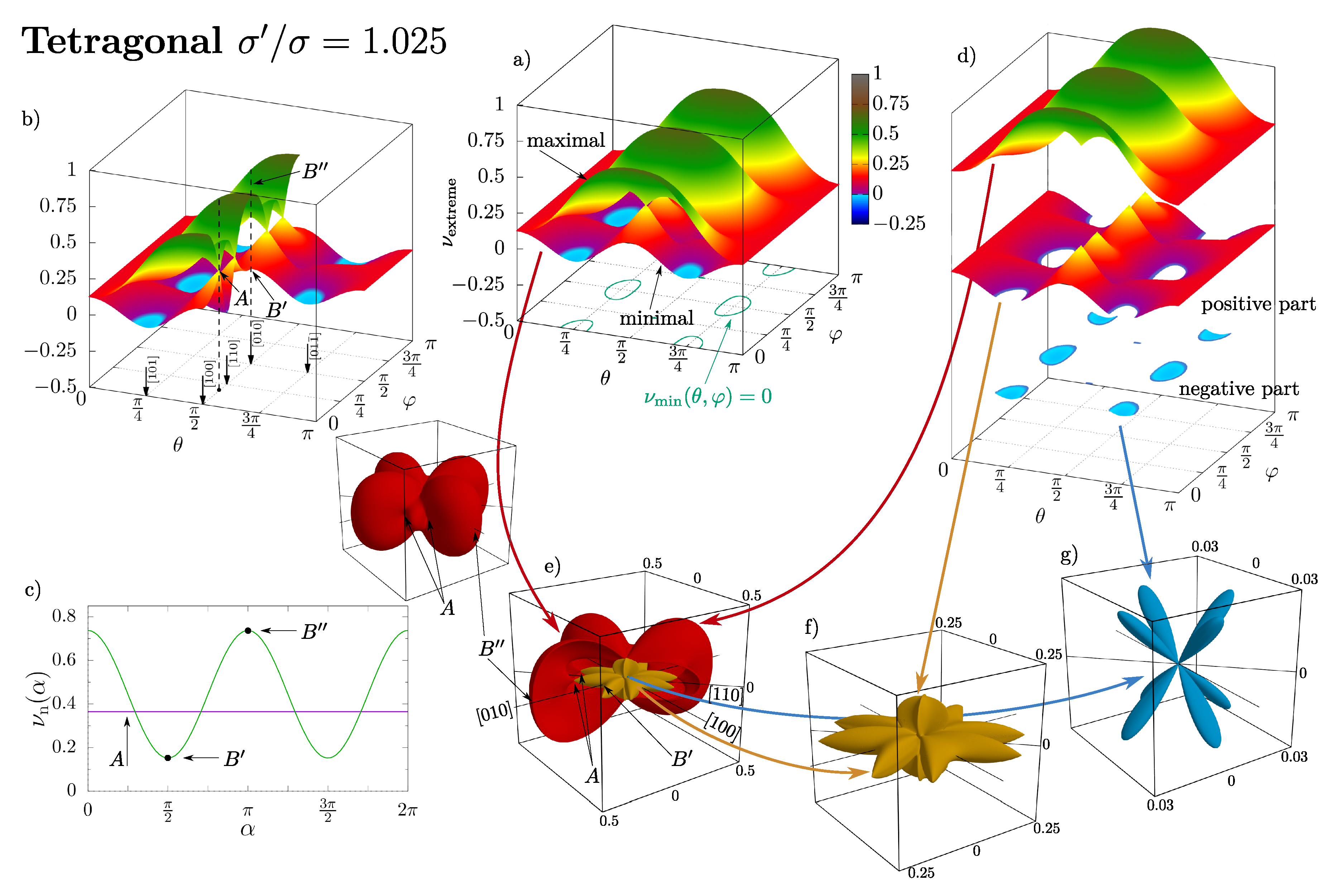
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PR | Poisson’s ratio |
| HS | hard sphere (potential) |
| MC | Monte Carlo |
References
- Evans, K.E. Auxetic polymers: A new range of materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity; Pergamon Press: London, UK, 1986. [Google Scholar]
- Lakes, R.S. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Pergamon Press: Oxford, UK, 1988. [Google Scholar]
- Wojciechowski, K.W. Two-dimensional isotropic model with a negative Poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Rothenburg, L. Note on a random isotropic granular material with negative Poisson’s ratio. Int. J. Eng. Sci. 1988, 26, 373–383. [Google Scholar] [CrossRef]
- Sigmund, O. Materials with prescribed constitutive parameters—An inverse homogenization problem. Int. J. Solids Struct. 1994, 31, 2313–2329. [Google Scholar] [CrossRef]
- Bowick, M.; Cacciuto, A.; Thorleifsson, G.; Travesset. Universal negative Poisson ratio of self-avoiding fixed-connectivity membranes. Phys. Rev. Lett. 2001, 87, 148103. [Google Scholar] [CrossRef]
- Hoover, W.G.; Hoover, C.G. Searching for auxetics with DYNA3D and ParaDyn. Phys. Status Solidi B-Basic Solid State Phys. 2005, 242, 585–594. [Google Scholar] [CrossRef]
- Tretiakov, K.V. Negative Poisson’s ratio of two-dimensional hard cyclic tetramers. J. Non-Cryst. Solids 2009, 355, 1435–1438. [Google Scholar] [CrossRef]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Saxena, K.K.; Das, R.; Calius, E.P. Three Decades of Auxetics Research—Materials with Negative Poisson’s Ratio: A Review. Adv. Eng. Mater. 2016, 18, 1847–1870. [Google Scholar] [CrossRef]
- Kadic, M.; Bueckmann, T.; Schittny, R.; Wegeneret, M. Metamaterials beyond electromagnetism. Rep. Prog. Phys. 2013, 76, 126501. [Google Scholar] [CrossRef]
- Huang, C.; Chen, L. Negative Poisson’s Ratio in Modern Functional Materials. Adv. Mater. 2016, 28, 8079–8096. [Google Scholar] [CrossRef]
- Dudek, K.K.; Gatt, R.; Dudek, M.R.; Grima, J.N. Controllable Hierarchical Mechanical Metamaterials Guided by the Hinge Design. Materials 2021, 14, 758. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R.S. Advances in negative Poisson’s ratio materials. Adv. Mater. 1993, 5, 293–296. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, A. Auxetic Materials: Functional Materials and Structures from Lateral Thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafstrom, S. Negative Poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Brańka, A.C.; Heyes, D.M.; Wojciechowski, K.W. Auxeticity of cubic materials. Phys. Status Solidi B-Basic Solid State Phys. 2009, 246, 2063–2071. [Google Scholar] [CrossRef]
- Krasavin, V.V.; Krasavin, A.V. Auxetic properties of cubic metal single crystals. Phys. Status Solidi B-Basic Solid State Phys. 2014, 251, 2314–2320. [Google Scholar] [CrossRef]
- Ho, D.T.; Kim, H.; Kwon, S.Y.; Kim, S.Y. Auxeticity of face–centered cubic metal (001) nanoplates. Phys. Status Solidi B-Basic Solid State Phys. 2015, 252, 1492–1501. [Google Scholar] [CrossRef]
- Goldstein, R.V.; Gorodtsov, V.A.; Volkov, D.S.L.M.A. Two-Layered Tubes from Cubic Crystals: Auxetic Tubes. Phys. Status Solidi B-Basic Solid State Phys. 2017, 254, 1600815. [Google Scholar] [CrossRef]
- Ho, D.T.; Park, S.; Kwon, S.; Han, T.; Kim, S.Y. Negative Poisson’s ratio in cubic materials along principal directions. Phys. Status Solidi B-Basic Solid State Phys. 2016, 253, 1288–1294. [Google Scholar] [CrossRef]
- Lisovenko, D.S.; Baimova, J.A.; Rysaeva, L.K.; Gorodtsov, V.A.; Rudskoy, A.I.; Dmitriev, S.V. Equilibrium diamond-like carbon nanostructures with cubic anisotropy: Elastic properties. Phys. Status Solidi B-Basic Solid State Phys. 2016, 253, 1295–1302. [Google Scholar] [CrossRef]
- Pozniak, A.A.; Wojciechowski, K.W. Poisson’s ratio of rectangular anti-chiral structures with size dispersion of circular nodes. Phys. Status Solidi B-Basic Solid State Phys. 2014, 251, 367–374. [Google Scholar] [CrossRef]
- Mohanraj, H.; Ribeiro, S.L.M.F.; Panzera, T.H.; Scarpa, F.; Farrow, I.R.; Jones, R.; Davies-Smith, A.; Remillat, C.D.L.; Walters, P.; Peng, H.X. Hybrid auxetic foam and perforated plate composites for human body support. Phys. Status Solidi B-Basic Solid State Phys. 2016, 253, 1378–1386. [Google Scholar] [CrossRef]
- Airoldi, A.; Bettini, P.; Panichelli, P.; Oktem, M.F.; Sala, G. Chiral topologies for composite morphing structures? Part I: Development of a chiral rib for deformable airfoils. Phys. Status Solidi B-Basic Solid State Phys. 2015, 252, 1435–1445. [Google Scholar] [CrossRef]
- Ho, V.H.; Ho, D.T.; Kwon, S.; Kim, S.Y. Negative Poisson’s ratio in periodic porous graphene structures. Phys. Status Solidi B-Basic Solid State Phys. 2016, 253, 1303–1309. [Google Scholar] [CrossRef]
- Chen, S.; Ryu, S.C. Design and characterization of rounded reentrant honeycomb patterns for lightweight and rigid auxetic structures. Smart Mater. Struct. 2017, 24, 115026. [Google Scholar] [CrossRef]
- Lim, T.C. Auxetic and negative thermal expansion structure based on interconnected array of rings and sliding rods. Phys. Status Solidi B-Basic Solid State Phys. 2017, 254, 1600775. [Google Scholar] [CrossRef]
- Lim, T.C. An accurate design equation for the maximum deflection in a class of auxetic sectorial plates. Phys. Status Solidi B-Basic Solid State Phys. 2017, 254, 1600784. [Google Scholar] [CrossRef]
- Hou, J.; Li, D.; Dong, L. Mechanical behaviors of hierarchical cellular structures with negative Poisson’s ratio. J. Mater. Sci. 2018, 53, 10209–10216. [Google Scholar] [CrossRef]
- Wang, Y.C.; Shen, M.W.; Liao, S.M. Microstructural effects on the Poisson’s ratio of star-shaped two-dimensional systems. Phys. Status Solidi B-Basic Solid State Phys. 2017, 254, 1700024. [Google Scholar] [CrossRef]
- Ho, D.T.; Ho, V.H.; Park, H.S.; Kim, S.Y. Negative in-plane Poisson’s ratio for single layer black phosphorus: An atomistic simulation study. Phys. Status Solidi B-Basic Solid State Phys. 2017, 254, 1700285. [Google Scholar] [CrossRef]
- Malfa, F.L.; Puce, S.; Rizzi, F.; Vittorio, M.D. A Flexible Carbon Nanotubes-Based Auxetic Sponge Electrode for Strain Sensors. Nanomaterials 2020, 10, 2365. [Google Scholar] [CrossRef] [PubMed]
- Attard, D.; Caruana-Gauci, R.; Gatt, R.; Grima, J.N. Negative linear compressibility from rotating rigid units. Phys. Status Solidi B-Basic Solid State Phys. 2016, 253, 1410–1418. [Google Scholar] [CrossRef]
- Ha, C.S.; Plesha, M.E.; Lakes, R.S. Chiral three-dimensional isotropic lattices with negative Poisson’s ratio. Phys. Status Solidi B-Basic Solid State Phys. 2016, 253, 1243–1251. [Google Scholar] [CrossRef]
- Desmoulins, A.; Zelhofer, A.J.; Kochmann, D.M. Auxeticity in truss networks and the role of bending versus stretching deformation. Smart Mater. Struct. 2016, 25, 054003. [Google Scholar] [CrossRef]
- Dudek, K.K.; Gatt, R.; Mizzi, L.; Dudek, M.R.; Attard, D.; Evans, K.E.; Grima, J.N. On the dynamics and control of mechanical properties of hierarchical rotating rigid unit auxetics. Sci. Rep. 2017, 7, 46529. [Google Scholar] [CrossRef]
- Li, D.; Yin, J.; Dong, L. Numerical analysis of a two-dimensional open cell topology with tunable Poisson’s ratio from positive to negative. Phys. Status Solidi-Rapid Res. Lett. 2018, 12, 1700374. [Google Scholar] [CrossRef]
- Mizzi, L.; Grima, J.N.; Gatt, R.; Attard, D. Analysis of the Deformation Behavior and Mechanical Properties of Slit-Perforated Auxetic Metamaterials. Phys. Status Solidi B-Basic Solid State Phys. 2019, 256, 1800153. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Wojciechowski, K.W. Poisson’s ratio of the fcc hard sphere crystal at high densities. J. Chem. Phys. 2005, 123, 074509. [Google Scholar] [CrossRef] [PubMed]
- Bielejewska, N.; Brańka, A.C.; Pieprzyk, S.; Yevchenko, T. Another Look at Auxeticity of 2D Square Media. Phys. Status Solidi B-Basic Solid State Phys. 2020, 257, 2000485. [Google Scholar] [CrossRef]
- Fozdar, D.Y.; Soman, P.; Lee, J.W.; Han, L.H.; Chen, S.C. Three-dimensional polymer constructs exhibiting a tunable negative Poisson’s ratio. Adv. Funct. Mater. 2011, 21, 2712–2720. [Google Scholar] [CrossRef] [PubMed]
- Alderson, K.; Nazaré, S.; Alderson, A. Large-scale extrusion of auxetic polypropylene fibre. Phys. Status Solidi B-Basic Solid State Phys. 2016, 253, 1279–1287. [Google Scholar] [CrossRef]
- Alderson, K.L.; Simkins, V.R.; Coenen, V.L.; Davies, P.J.; Alderson, A.; Evans, K.E. How to make auxetic fibre reinforced composites. Phys. Status Solidi B-Basic Solid State Phys. 2005, 242, 509–518. [Google Scholar] [CrossRef]
- Duncan, O.; Alderson, A.; Allen, T. Fabrication, characterization and analytical modeling of gradient auxetic closed cell foams. Smart Mater. Struct. 2021, 30, 035014. [Google Scholar] [CrossRef]
- Allen, T.; Hewage, T.; Newton-Mann, C.; Wang, W.; Duncan, O.; Alderson, A. Fabrication of Auxetic Foam Sheets for Sports Applications. Phys. Status Solidi B-Basic Solid State Phys. 2017, 254, 1700596. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Li, T.T.; Scarpa, F.; Wang, L.F. Lattice metamaterials with mechanically tunable Poisson’s ratio for vibration control. Phys. Rev. Appl. 2017, 7, 024012. [Google Scholar] [CrossRef]
- Usta, F.; Scarpa, F.; Turkmen, H.S.; Johnson, P.; Perriman, A.W.; Chen, Y.Y. Multiphase lattice metamaterials with enhanced mechanical performance. Smart Mater. Struct. 2021, 30, 025014. [Google Scholar] [CrossRef]
- Grima, J.N.; Attard, D.; Caruana-Gauci, R.; Gatt, R. Negative linear compressibility of hexagonal honeycombs and related systems. Scr. Mater. 2011, 65, 565–568. [Google Scholar] [CrossRef]
- Chetcuti, E.; Ellul, B.; Manicaro, E.; Brincat, J.P.; Attard, D.; Gatt, R.; Grima, J.N. Modeling auxetic foams through semi-rigid rotating triangles. Phys. Status Solidi B-Basic Solid State Phys. 2014, 251, 297–306. [Google Scholar] [CrossRef]
- Czarnecki, S.; Lukasiak, T. Recovery of the Auxetic Microstructures Appearing in the Least Compliant Continuum Two-Dimensional Bodies. Phys. Status Solidi B-Basic Solid State Phys. 2020, 257, 1900676. [Google Scholar] [CrossRef]
- Azzopardi, K.M.; Brincat, J.P.; Grima, J.N.; Gatt, R. Advances in the study of the deformation mechanism of stishovite. Phys. Status Solidi B-Basic Solid State Phys. 2015, 252, 1486–1491. [Google Scholar] [CrossRef]
- Rysaeva, L.K.; Baimova, J.A.; Lisovenko, D.S.; Gorodtsov, V.A.; Dmitriev, S.V. Elastic Properties of Fullerites and Diamond-Like Phases. Phys. Status Solidi B-Basic Solid State Phys. 2019, 256, 1800049. [Google Scholar] [CrossRef]
- Verma, P.; He, C.B.; Griffin, A.C. Implications for Auxetic Response in Liquid Crystalline Polymers: X-ray Scattering and Space-Filling Molecular Modeling. Phys. Status Solidi B-Basic Solid State Phys. 2020, 257, 2000261. [Google Scholar] [CrossRef]
- Iftekhar, H.; Khan, R.M.W.U.; Nawab, Y.; Hamdani, S.T.A.; Panchal, S. Numerical Analysis of Binding Yarn Float Length for 3D Auxetic Structures. Phys. Status Solidi B-Basic Solid State Phys. 2020, 257, 2000440. [Google Scholar] [CrossRef]
- Gambin, D.; Dudek, K.K.; Dudek, M.R.; Grima, J.N.; Gatt, R. The mechanical properties of ice “X” with particular emphasis on its auxetic potential. J. Phys. Chem. Solids 2021, 150, 109717. [Google Scholar] [CrossRef]
- Czarnecki, S.; Lewinski, T. Pareto optimal design of non-homogeneous isotropic material properties for the multiple loading conditions. Phys. Status Solidi B-Basic Solid State Phys. 2017, 254, 1600821. [Google Scholar] [CrossRef]
- Bacigalupo, A.; Lepidi, M.; Gnecco, G.; Gambarotta, L. Optimal design of auxetic hexachiral metamaterials with local resonators. Smart Mater. Struct. 2016, 25, 054009. [Google Scholar] [CrossRef]
- Liu, Q. Literature Review: Materials with Negative Poisson’s Ratios and Potential Applications to Aerospace and Defence; DSTO Defence Science and Technology Organisation: Fishermans Bend, VIC, Australia, 2006.
- Ma, Y.; Scarpa, F.; Zhang, D.; Zhu, B.; Chen, L.; Hong, J. A nonlinear auxetic structural vibration damper with metal rubber particles. Smart Mater. Struct. 2013, 22, 084012. [Google Scholar] [CrossRef]
- Smardzewski, J.; Klos, R.; Fabisiak, B. Design of small auxetic springs for furniture. Mater. Des. 2013, 51, 723–728. [Google Scholar] [CrossRef]
- Mizzi, L.; Attard, D.; Casha, A.; Grima, J.N.; Gatt, R. On the suitability of hexagonal honeycombs as stent geometries. Phys. Status Solidi B-Basic Solid State Phys. 2014, 251, 328–337. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Phuong, T.; Ngo, T.; Xie, Y.M. Auxetic nail: Design and experimental study. Comp. Struct. 2018, 184, 288–298. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lai, H.W.; Ren, J.X. Enhanced Auxetic and Viscoelastic Properties of Filled Reentrant Honeycomb. Phys. Status Solidi B-Basic Solid State Phys. 2020, 257, 1900184. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Ren, X. A Simple Methodology to Generate Metamaterials and Structures with Negative Poisson’s Ratio. Phys. Status Solidi B-Basic Solid State Phys. 2020, 257, 2000439. [Google Scholar] [CrossRef]
- Pasternak, E.; Shufrin, I.; Dyskin, A.V. Thermal stresses in hybrid materials with auxetic inclusions. Comp. Struct. 2016, 138, 313–321. [Google Scholar] [CrossRef]
- Ho, D.T.; Nguyen, C.T.; Kwon, S.Y.; Kim, S.Y. Auxeticity in metals and periodic metallic porous structures induced by elastic instabilities. Phys. Status Solidi B-Basic Solid State Phys. 2018, 256, 1800122. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W.; Tretiakov, K.V.; Smardzewski, J.; Scarpa, F.; Piglowski, P.M.; Kowalik, M.; Imre, A.R.; Bilski, M. Auxetic properties of a f.c.c. crystal of hard spheres with an array of [001]-nanochannels filled by hard spheres of another diameter. Phys. Status Solidi B-Basic Solid State Phys. 2019, 256, 1800611. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W. Poisson’s ratio of the f.c.c. hard sphere crystals with periodically stacked (001)-nanolayers of hard spheres of another diameter. Materials 2019, 12, 700. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Tretiakov, K.V.; Kowalik, M. Elastic properties of dense solid phases of hard cyclic pentamers and heptamers in two dimensions. Phys. Rev. E 2003, 67, 036121. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystalls, Their Representation by Tensors and Matrices; Clarendon Press: Oxford, UK, 1957. [Google Scholar]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Strain fluctuations and elastic constants. J. Chem. Phys. 1982, 76, 2662–2666. [Google Scholar] [CrossRef]
- Tokmakova, S.P. Stereographic projections of Poisson’s ratio in auxetic crystals. Phys. Status Solidi B-Basic Solid State Phys. 2005, 242, 721–729. [Google Scholar] [CrossRef]
- Weiner, J.H. Statistical Mechanics of Elasticity; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Piglowski, P.M.; Narojczyk, J.W.; Wojciechowski, K.W.; Tretiakov, K.V. Auxeticity enhancement due to size polydispersity in fcc crystals of hard-core repulsive Yukawa particles. Soft Matter 2017, 13, 7916–7921. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D. Order through entropy. Nat. Mater. 2015, 14, 9–12. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narojczyk, J.W.; Wojciechowski, K.W.; Smardzewski, J.; Imre, A.R.; Grima, J.N.; Bilski, M. Cancellation of Auxetic Properties in F.C.C. Hard Sphere Crystals by Hybrid Layer-Channel Nanoinclusions Filled by Hard Spheres of Another Diameter. Materials 2021, 14, 3008. https://doi.org/10.3390/ma14113008
Narojczyk JW, Wojciechowski KW, Smardzewski J, Imre AR, Grima JN, Bilski M. Cancellation of Auxetic Properties in F.C.C. Hard Sphere Crystals by Hybrid Layer-Channel Nanoinclusions Filled by Hard Spheres of Another Diameter. Materials. 2021; 14(11):3008. https://doi.org/10.3390/ma14113008
Chicago/Turabian StyleNarojczyk, Jakub W., Krzysztof W. Wojciechowski, Jerzy Smardzewski, Attila R. Imre, Joseph N. Grima, and Mikołaj Bilski. 2021. "Cancellation of Auxetic Properties in F.C.C. Hard Sphere Crystals by Hybrid Layer-Channel Nanoinclusions Filled by Hard Spheres of Another Diameter" Materials 14, no. 11: 3008. https://doi.org/10.3390/ma14113008
APA StyleNarojczyk, J. W., Wojciechowski, K. W., Smardzewski, J., Imre, A. R., Grima, J. N., & Bilski, M. (2021). Cancellation of Auxetic Properties in F.C.C. Hard Sphere Crystals by Hybrid Layer-Channel Nanoinclusions Filled by Hard Spheres of Another Diameter. Materials, 14(11), 3008. https://doi.org/10.3390/ma14113008








