Biomechanical Properties of Bone and Mucosa for Design and Application of Dental Implants
Abstract
1. Introduction
2. Literature Data Assessment
2.1. Reported Bone Properties
2.2. Reported Oral Soft Tissues Properties
2.3. Other Parameters of Clinical Importance
3. Methods
3.1. Bone Stiffness Approximation
3.2. Soft Tissues Stiffness Approximation
3.3. Statistical Method and Data Visualization
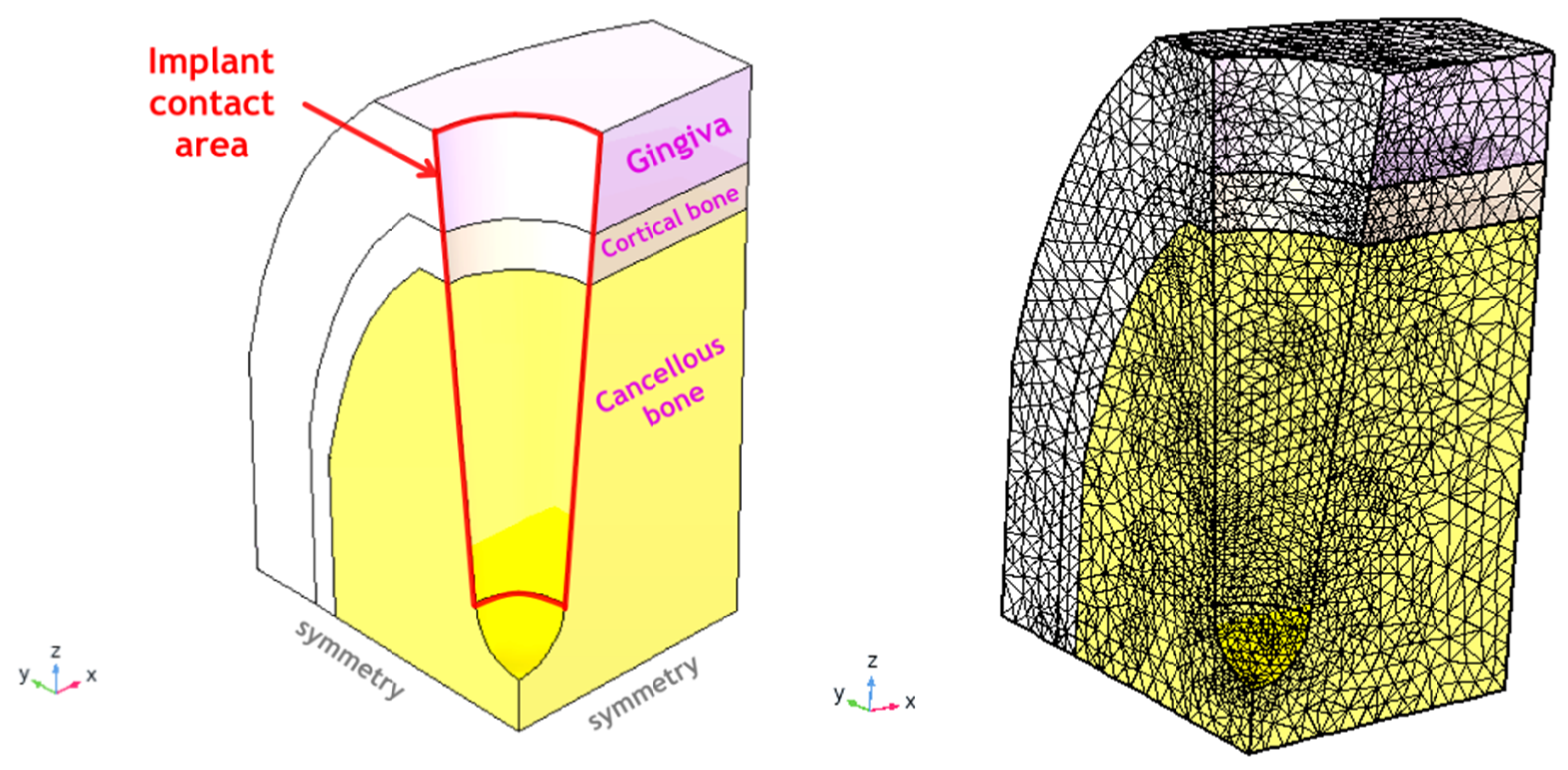
3.4. Clinical Case Simulation
4. Results
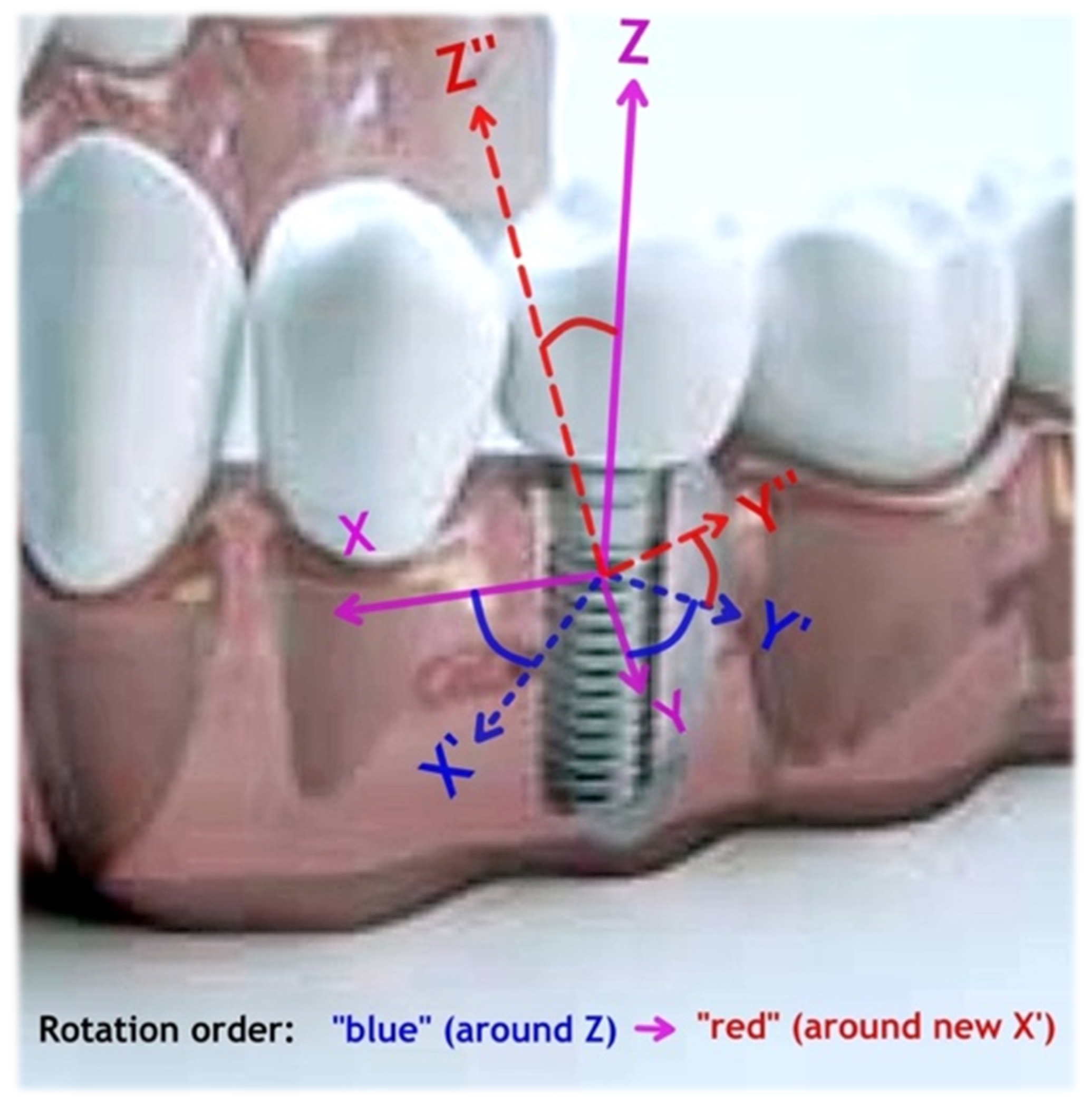
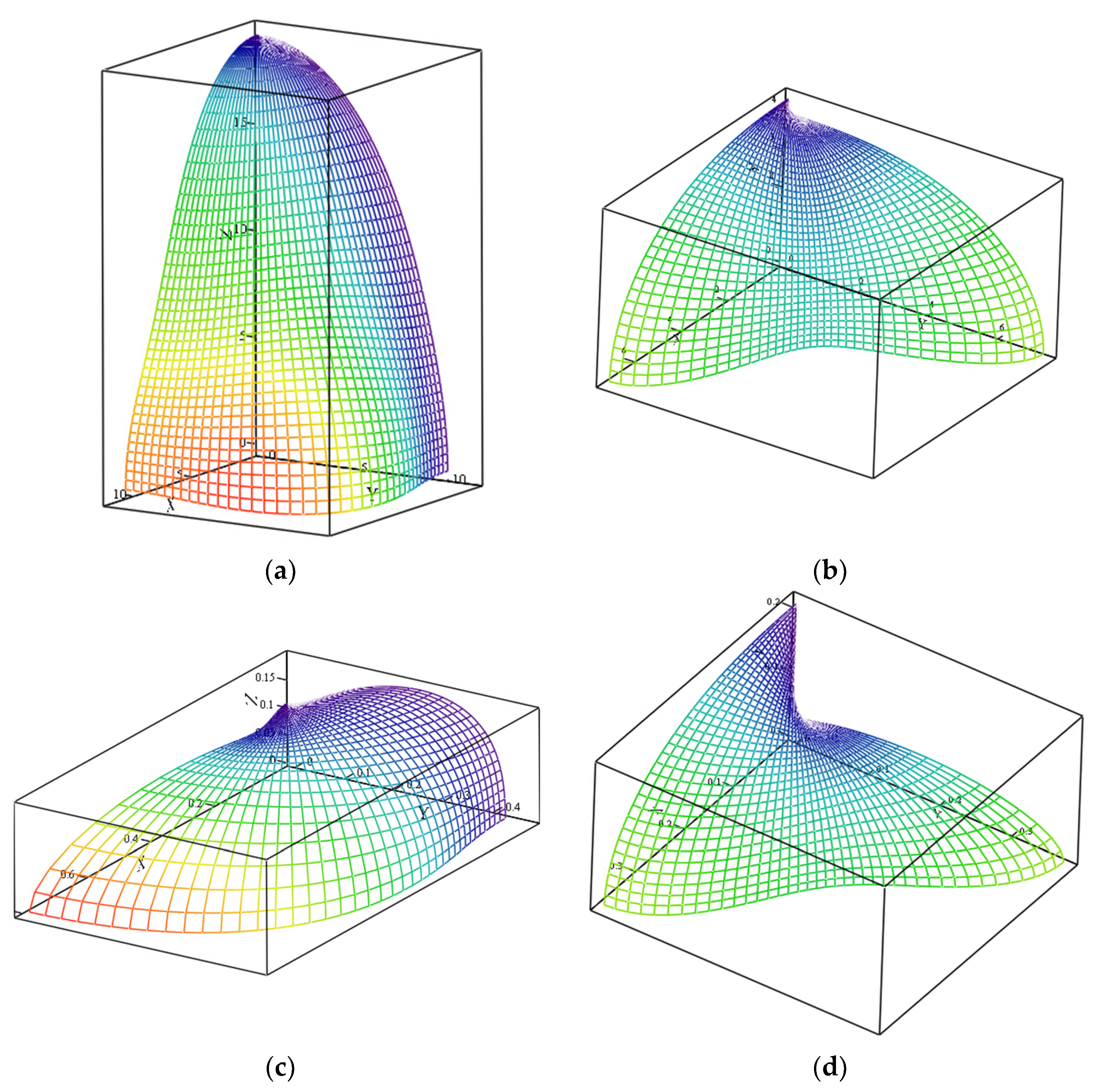
4.1. Stiffness Estimation and Visualization for an Arbitrary Direction
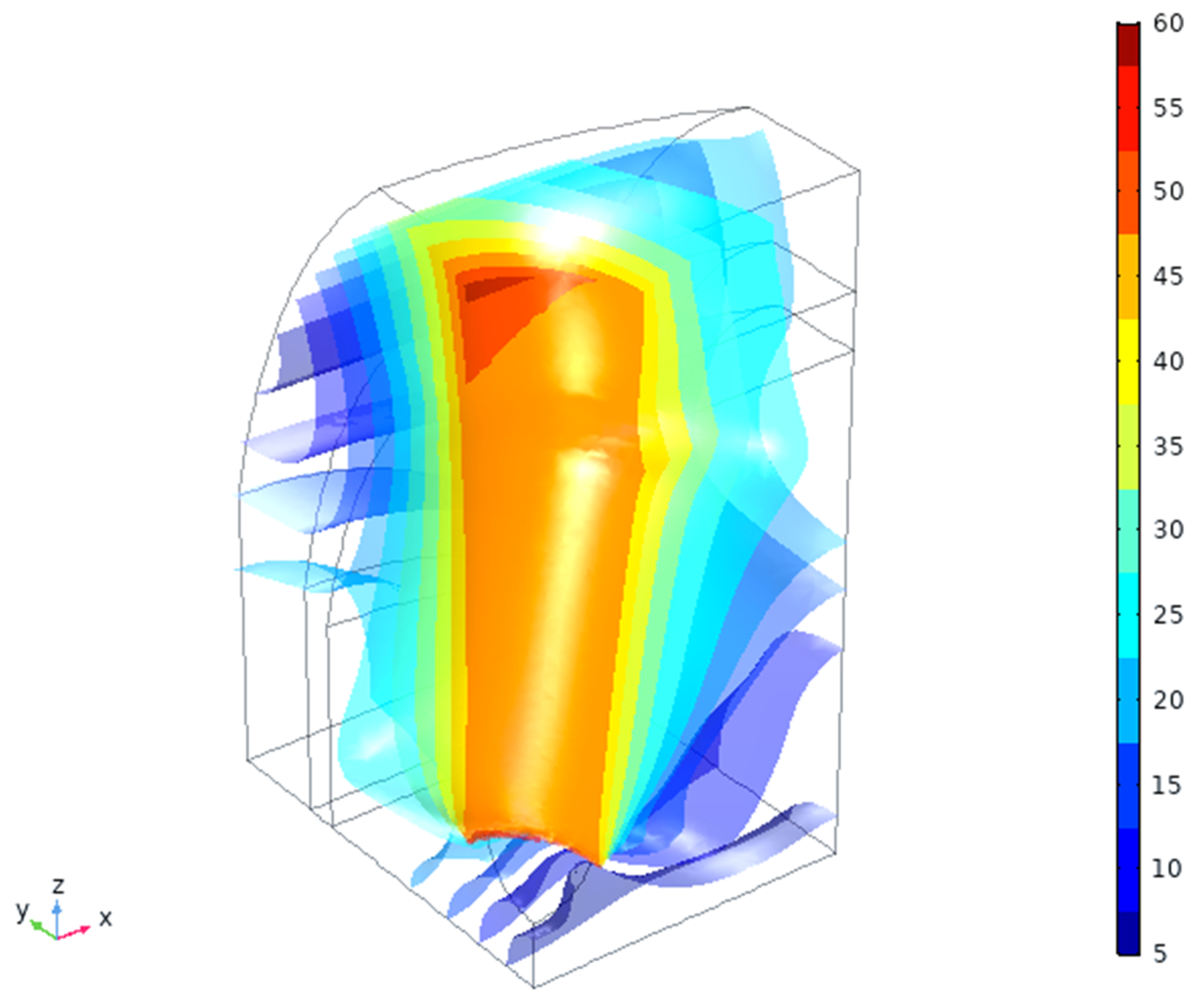
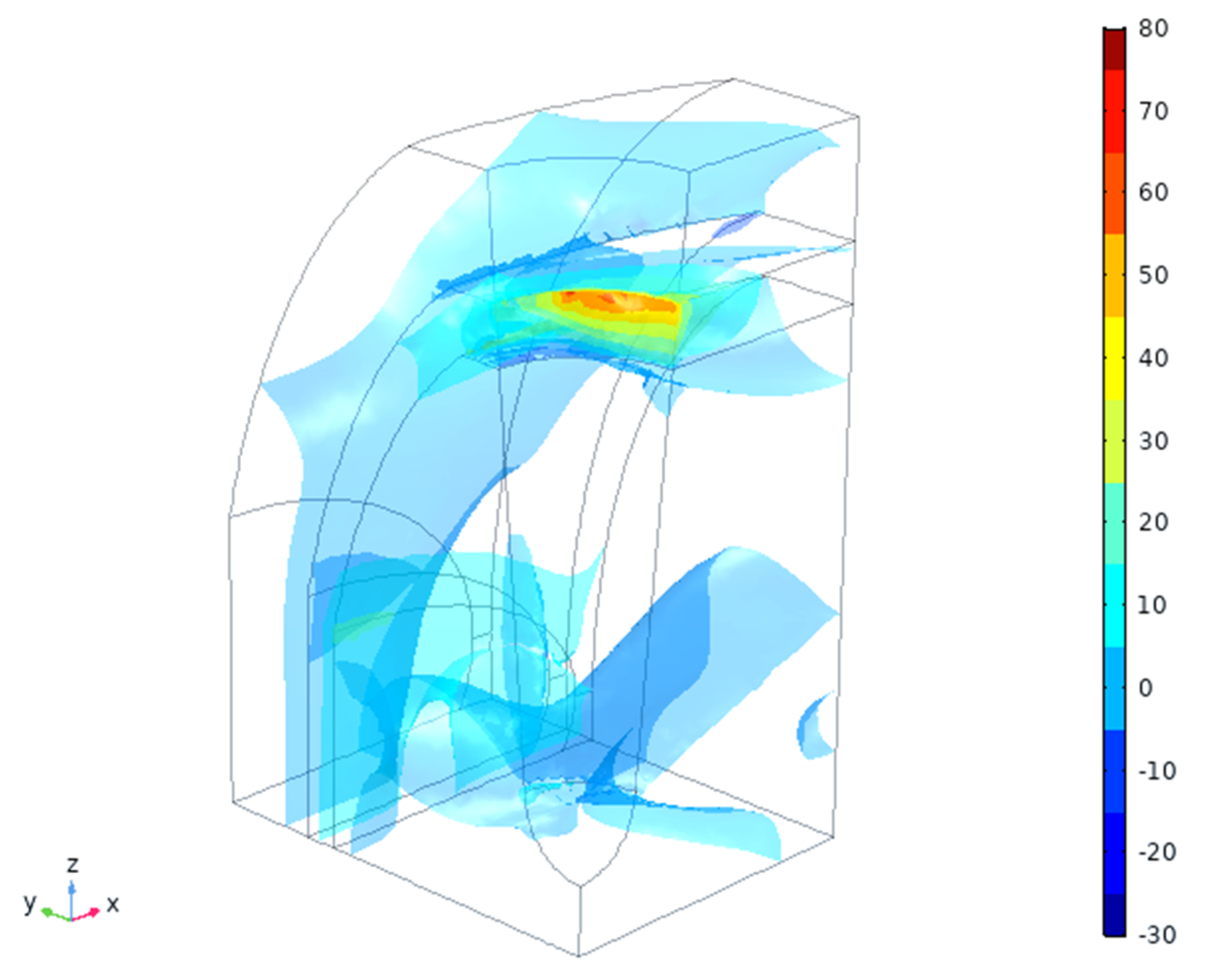
4.2. In Silico Simulation
5. Discussion
- Transitions from the single “elastic modulus” values towards true stiffness matrix components, which are real material functions of density, strain, time, frequency, etc. give a more precise and comprehensive description of the tissues with patient-specific data (such as bone density in loco).
- Visualized rotation and generated 3D plots can be of an assistance of identification of the weaker and stronger directions in the X-Y-Z coordinates that may help the digital planning of surgery (for example, where the lowest stiffness part might coincide with thinner or lighter bone in that direction).
- For soft tissues (gingiva, mucosa), invariant values (modulus E, characteristic time τ and material memory α) have shown being extracted from experimental data without the assumption of a material model. The same can be made for bone, if viscoelastic effects need to be considered without the need of complex numbers processing.
- In the case shown, the data used were obtained closer to the physiological range, allowed to mimic the behavior without needs to break down the values into specific tissue components. These invariant values comprise time-convoluted data and are better predictors for materials performance comparison than traditional stiffness (stress/strain ratios).
- Non-linear viscostiffness data can be placed into software packages for a detailed simulation, and there, the directional rotations are performed automatically. Here, the detailed simulation of the implant screw and abutment is not always necessary—the imprint surface transferring the load is of the greatest interest as a boundary condition. By changing the patient-specific parameters, a user can simulate a number of relevant scenarios in a short time to see whether a specific implant in that location would potentially have risky zones. This can simplify calculations for more realistic clinical cases with 3D implant placement planning and outcome estimation.
- Examining the patient and determination of the bone/tissues status (quality) and parameters for the implantation site.
- Selection of the implant type (dictated by the general considerations and safety).
- Entering the patient’s parameters and implant geometry into the 3D model.
- Setting up “normal” (a nearly perfect osseointegration) or “worst case” (e.g., absence of cohesion between the screw or the abutment) scenarios and performing numerical calculations.
- Post-processing the results, leading to the identification of potential risk zones and parameters.
- In the case of need, adjustment or changing the implant type, shape, thread geometry, etc. and repeating the computation for the optimal outcome.
6. Conclusions
- Correct biomechanical description of oral tissues has to be based on realistic stiffness matrix components, being functions of density, strain, time, frequency etc.—and not on a single value of “elastic modulus”.
- Consistent invariant values (modulus, characteristic time, material memory) can be extracted from experimental data without the assumption of a material model, when these experiments are carried out closer to physiological range (mimicking the behavior of the tissue, implant or tissue-implant assembly). Such invariant values are better predictors for the performance comparison than traditional stiffness (stress/strain ratios).
- Known non-linear viscostiffness data can be placed into commercial software for a detailed simulation with automatic directional rotations to obtain the distribution of stresses, strains, strain energy density, pressure etc. for better decision-making.
- The approach based on a combined application of non-linear anisotropic tissue descriptions, as a reduced order “model-free” method (i.e., not linked to a priori chosen model), is capable of a very quick operation (“data compression”) for an adequate computation of multi-tissue behavior in the contact with the dental implant in real-time dynamics. The approach can be expended to real screw and abutment geometry for securing better outcomes in planning dental implant operations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malet, J.; Mora, F.; Bouchard, F. Implant Dentistry at-a-Glance; John Wiley & Sons: Oxford, UK, 2012; 144p. [Google Scholar]
- Greenstein, G.; Cavallaro, J.; Romanos, G.; Tarnow, D. Clinical recommendations for avoiding and managing surgical complications associated with implant dentistry: A review. J. Periodontol. 2008, 79, 1317–1329. [Google Scholar] [CrossRef]
- Matinlinna, J.P. (Ed.) Handbook of Oral Biomaterial; Pan Stanford Publishing Pte. Ltd.: Singapore, 2014. [Google Scholar]
- Haanaes, H.R. Implants and infections with special reference to oral bacteria. J. Clin. Periodontol. 1990, 17, 516–524. [Google Scholar] [CrossRef]
- Rimondini, L.; Gasik, M. Bacterial attachment and biofilm formation on biomaterials: The case of dental and orthopaedic implants. In Biomaterials and Immune Response: Complications, Mechanisms and Immunomodulation; Vrana, E.N., Ed.; CRC Press: Boca Raton, FL, USA, 2018; 249p. [Google Scholar]
- Pereira, J.; Tavares, F.P.; Lima, K.C.; Carreiro, A.F.P.; Henriques, B.; Silva, F.S.; Nascimento, R.M.; Lopez-Lopez, J.; Souza, J.C.M. Relation between dental implant joint surfaces and biofilm formation. Dentistry 2015, 5, 296. [Google Scholar] [CrossRef]
- Nogueira, A.V.B.; Nokhbehsaim, M.; Eick, S.; Bourauel, C.; Jäger, A.; Jepsen, S.; Rossa, C., Jr.; Deschner, J.; Cirelli, J.A. Biomechanical loading modulates proinflammatory and bone resorptive mediators in bacterial-stimulated PDL cells. Mediat. Inflamm. 2014, 2014, 425421. [Google Scholar] [CrossRef] [PubMed]
- Gasik, M.; Van Mellaert, L.; Pierron, D.; Braem, A.; Hofmans, D.; De Waelheyns, E.; Anné, J.; Harmand, M.-F.; Vleugels, J. Reduction of biofilm infection risks and promotion of osteointegration for optimized surfaces of titanium implants. Adv. Healthc. Mater. 2012, 1, 117–127. [Google Scholar] [CrossRef] [PubMed]
- Gasik, M. Understanding biomaterial-tissue interface quality: Combined in vitro evaluation. Sci. Technol. Adv. Mater. 2017, 18, 550–562. [Google Scholar] [CrossRef]
- Shahramian, K.; Gasik, M.; Kangasniemi, I.; Walboomers, F.; Willberg, J.; Abdulmajeed, A.; Närhi, T. Zirconia implants with improved attachment to the gingival tissue. J. Periodontol. 2020, 91, 1213–1224. [Google Scholar] [CrossRef]
- Rompen, E.; Domken, O.; Degidi, M.; Pontes, A.E.P.; Piattelli, A. The effect of material characteristics, of surface topography and of implant components and connections on soft tissue integration: A literature review. Clin. Oral Implants Res. 2006, 17, 55–67. [Google Scholar] [CrossRef]
- Lindhe, J.; Karring, T.; Lang, N.P. (Eds.) Clinical Periodontology and Implant Dentistry, 4th ed.; Blackwell Munksgaard: Copenhagen, Denmark, 2003; 1055p. [Google Scholar]
- Delize, V.; Bouhy, A.; Lambert, F.; Lamy, M. Intrasubject comparison of digital vs. conventional workflow for screw-retained single-implant crowns: Prosthodontic and patient-centered outcomes. Clin. Oral Implants Res. 2019, 30, 892–902. [Google Scholar] [CrossRef]
- Lambert, F.; Bacevic, M.; Layrolle, P.; Schupbach, P.; Drion, P.; Rompen, E. Impact of biomaterial microtopography on bone regeneration: Comparison of three hydroxyapatites. Clin. Oral Implants Res. 2017, 28, e201–e207. [Google Scholar] [CrossRef]
- Lord, J.D.; Morrell, R. Elastic modulus measurement. In Measurement Good Practice Guide No. 98; NPL: Teddington, UK, 2006; 100p. [Google Scholar]
- Vrana, N.E.; Knopf-Marques, H.; Barthes, J. (Eds.) Biomaterials for Organ and Tissue Regeneration: New Technologies and Future Prospects; Woodhead Publishing: Cambridge, UK, 2020; 828p. [Google Scholar]
- Chen, J.; Ahmad, R.; Li, W.; Swain, M.; Li, Q. Biomechanics of oral mucosa. J. R. Soc. Interface 2015, 12, 20150325. [Google Scholar] [CrossRef] [PubMed]
- Rees, J.S.; Jacobsen, P.H. Elastic modulus of the periodontal ligament. Biomaterials 1997, 18, 995–999. [Google Scholar] [CrossRef]
- Sanctuary, C.S.; Anselm Wiskott, H.W.; Justiz, J.; Botsis, J.; Belser, U.C. In vitro time-dependent response of periodontal ligament to mechanical loading. J. Appl. Physiol. 2005, 99, 2369–2378. [Google Scholar] [CrossRef] [PubMed]
- Gasik, M. Biomechanical characterization of engineered tissues and implants for tissue/organ replacement applications. In Biomaterials for Organ and Tissue Regeneration; Vrana, N.E., Knopf-Marques, H., Barthes, J., Eds.; Woodhead Publishing: Cambridge, UK, 2020; pp. 599–627. [Google Scholar]
- Van Mow, C.; Huiskes, R. Basic Orthopedic Biomechanics and Mechanobiology; Lippincott, Williams & Wilkins: Philadelphia, PA, USA, 2005; 720p. [Google Scholar]
- Natali, A.N.; Pavan, P.G.; Scarpa, C. Numerical analysis of tooth mobility: Formulation of a non-linear constitutive law for the periodontal ligament. Dent. Mater. 2004, 20, 623–629. [Google Scholar] [CrossRef] [PubMed]
- Görke, U.J.; Günther, H.; Nagel, T.; Wimmer, M.A. A large strain material model for soft tissues with functionally graded properties. J. Biomech. Eng. 2010, 132, 074502. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H. Invariant characteristic representations for classical and micropolar anisotropic elasticity tensors. J. Elast. 1995, 40, 239–265. [Google Scholar] [CrossRef]
- Morresia, A.L.; D’Amario, M.; Capogreco, M.; Gattob, R.; Marzo, G.; D’Arcangelo, C.; Monaco, A. Thermal cycling for restorative materials: Does a standardized protocol exist in laboratory testing? A literature review. J. Mech. Behav. Biomed. Mater. 2014, 29, 295–308. [Google Scholar] [CrossRef]
- Żmudzki, J.; Chladek, G.; Kasperski, J. Biomechanical factors related to occlusal load transfer in removable complete dentures. Biomech. Model. Mechanobiol. 2015, 14, 679–691. [Google Scholar] [CrossRef]
- Gasik, M.; Bilotsky, Y. In Vitro Method for Measurement and Model-Free Evaluation of Time-Invariant Biomaterials Functions. U.S. Patent 10,379,106 B2, 13 August 2019. [Google Scholar]
- Shibata, Y.; Tanimoto, Y.; Maruyama, N.; Nagakura, M. A review of improved fixation methods for dental implants. Part II: Biomechanical integrity at bone-implant interface. J. Prosthdont. Res. 2015, 59, 84–85. [Google Scholar] [CrossRef]
- Almeida, E.O.; Freitas Júnior, A.C.; Rocha, E.P.; Pessoa, P.S.; Gupta, N.; Tovar, N.; Coelho, P.G. Critical aspects for mechanical simulation in dental implantology. In Finite Element Analysis: From Biomedical Applications to Industrial Developments; Moratal, D., Ed.; IntechOpen: Rijeka, Croatia, 2012; pp. 81–96. [Google Scholar]
- Tada, S.; Stegaroiu, R.; Kitamura, E.; Miyakawa, O.; Kusakari, H. Influence of implant design and bone quality on stress/strain distribution in bone around implants: A 3-dimensional finite element analysis. Int. J. Oral Maxillofac. Implants 2003, 18, 357–368. [Google Scholar]
- Katz, J.L.; Misra, A.; Marangos, O.; Ye, Q.; Spencer, P. Mechanics of hard tissue. In Biomechanics: Principles & Practices; Peteson, D.R., Bronzino, J.D., Eds.; CRC Press: Boca Raton, FL, USA, 2015; Volume 1, pp. 1–26. [Google Scholar]
- Sugiura, T.; Yamamoto, K.; Horita, S.; Murakami, K.; Tsutsumi, S.; Kirita, T. The effects of bone density and crestal cortical bone thickness on micromotion and peri-implant bone strain distribution in an immediately loaded implant: A nonlinear finite element analysis. J. Periodontal Implant Sci. 2016, 46, 152–165. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.; Li, Q.; Li, W.; Swain, M. Dental implant induced bone re-modelling and associated algorithms. J. Mech. Behav. Biomed. Mater. 2009, 2, 410–432. [Google Scholar] [CrossRef] [PubMed]
- Kydd, W.L.; Daly, C.H. The biologic and mechanical effects of stress on oral mucosa. J. Prosthet. Dent. 1982, 47, 317–329. [Google Scholar] [CrossRef]
- Kydd, W.L.; Daly, C.H.; Wheeler, J.B. The thickness measurement of masticatory mucosa in vivo. Int. Dent. J. 1971, 21, 430–441. [Google Scholar]
- Inoue, K.; Arikawa, H.; Fujii, K.; Shinohara, N.; Kawahata, N. Viscoelastic properties of oral soft tissue: A method of determining elastic modulus of oral soft tissue. Dent. Mater. J. 1985, 4, 47–53. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cheng, S.; Gandevia, S.C.; Green, M.; Sinkus, R.; Bilston, L.E. Viscoelastic properties of the tongue and soft palate using MR elastography. J. Biomech. 2011, 44, 450–454. [Google Scholar] [CrossRef] [PubMed]
- Lacoste-Ferré, M.-H.; Demont, P.; Dandurand, J.; Dantras, E.; Duran, D.; Lacabanne, C. Dynamic mechanical properties of oral mucosa: Comparison with polymeric soft denture liners. J. Mech. Behav. Biomed. Mater. 2011, 4, 269–274. [Google Scholar] [CrossRef]
- Choi, J.E.; Zwirner, J.; Ramani, R.S.; Ma, S.; Hussaini, H.M.; Waddell, J.N.; Hammer, N. Mechanical properties of human oral mucosa tissues are site dependent: A combined biomechanical, histological and ultrastructural approach. Clin. Dent. Exp. Res. 2020, 6, 602–611. [Google Scholar] [CrossRef]
- Goktas, S.; Dmytryk, J.J.; McFetridge, P.S. Biomechanical behavior of oral soft tissues. J. Periodontol. 2011, 82, 1178–1186. [Google Scholar] [CrossRef]
- Kydd, W.L.; Mandley, J. Stiffness of palatal mucoperiosteum. J. Prosthet. Dent. 1967, 18, 116–121. [Google Scholar] [CrossRef]
- Kishi, M. Experimental studies on the relation between area and displacement of loading surfaces in connection with displaceability in the mucosa of edentulous alveolar ridge under pressure. Shika Gakuho Dent. Sci. Rep. 1972, 72, 1043–1071. [Google Scholar]
- Menzel, A. Modelling of anisotropic growth in biological tissues: A new approach and computational aspects. Biomech. Model. Mechanobiol. 2005, 3, 147–171. [Google Scholar] [CrossRef] [PubMed]
- Taber, L.A. Biomechanics of growth, remodeling, and morphogenesis. Appl. Mech. Rev. 1995, 48, 487–545. [Google Scholar] [CrossRef]
- Tsai, S.W.; Melo, J.D.D. Composite Materials Design and Testing: Unlocking Mystery with Invariants; Stanford University: Stanford, CA, USA, 2015; 450p. [Google Scholar]
- Zühlke, A.; Gasik, M.; Shahramian, K.; Närhi, T.; Bilotsky, Y.; Kangasniemi, I. Enhancement of gingival tissue adherence of zirconia implant posts: In vitro study. Materials 2021, 14, 455. [Google Scholar] [CrossRef] [PubMed]
- Ashton, H. Effect of increased tissue pressure on blood flow. Clin. Orthopaed. Relat. Res. 1975, 113, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Kocabalkan, E.; Turgut, M. Variation in blood flow of supporting tissue during use of mandibular complete dentures with hard acrylic resin base and soft relining: A preliminary study. Int. J. Prosthodont. 2005, 18, 210–213. [Google Scholar] [PubMed]
- DeWitt, R. Elastic constants and thermal expansion averages of a nontextured polycrystal. J. Mech. Mater. Struct. 2008, 3, 195–212. [Google Scholar] [CrossRef]
- Gasik, M. Elastic properties of lamellar Ti-Al alloys. Comp. Mater. Sci. 2009, 47, 206–212. [Google Scholar] [CrossRef]
- Hvid, I.; Bentzen, S.M.; Linde, F.; Mosekilde, L.; Pongsoipetch, B. X-ray quantitative computed tomography: The relations to physical properties of proximal tibial trabecular bone specimens. J. Biomech. 1989, 22, 837–844. [Google Scholar] [CrossRef]
- Park, H.S.; Lee, Y.J.; Jeong, S.H.; Kwon, T.G. Density of the alveolar and basal bones of the maxilla and the mandible. Am. J. Orthodont. Dentofac. Orthoped. 2008, 133, 30–37. [Google Scholar] [CrossRef]
- O’Mahony, A.M.; Williams, J.L.; Katz, J.O.; Spencer, P. Anisotropic elastic properties of cancellous bone from a human edentulous mandible. Clin. Oral Implants Res. 2000, 11, 415–421. [Google Scholar] [CrossRef] [PubMed]
- Rho, J.Y.; Hobatho, M.C.; Ashman, R.B. Relations of mechanical-properties to density and CT numbers in human bone. Med. Eng. Phys. 1995, 17, 347–355. [Google Scholar] [CrossRef]
- Oliveira, H.; Velasco, A.B.; Ríos-Santos, J.-V.; Sánchez Lasheras, F.; Lemos, B.F.; Gil, F.J.; Carvalho, A.; Herrero-Climent, M. Effect of different implant designs on strain and stress distribution under non-axial loading: A three-dimensional finite element analysis. Int. J. Environ. Res. Public Health 2020, 17, 4738. [Google Scholar] [CrossRef] [PubMed]
- Gasik, M.; Zühlke, A.; Haaparanta, A.M.; Muhonen, V.; Laine, K.; Bilotsky, Y.; Kellomäki, M.; Kiviranta, I. The importance of controlled mismatch of biomechanical compliances of implantable scaffolds and native tissue for articular cartilage regeneration. Front. Bioeng. Biotechnol. 2018, 6, 187. [Google Scholar] [CrossRef] [PubMed]
- Gasik, M.; Ivanov, R.; Kazantseva, J.; Bilotsky, Y.; Hussainova, I. Biomechanical features of graphene-augmented inorganic nanofibrous scaffolds and their physical interaction with viruses. Materials 2021, 14, 164. [Google Scholar] [CrossRef]
- Maslov, V. The characteristics of pseudo-differential operators and difference schemes. Actes Congrès Int. Math. 1970, 2, 755–769. [Google Scholar]
- Rodríguez, R.F.; Salinas-Rodríguez, E.; Fujioka, J. Fractional time fluctuations in viscoelasticity: A comparative study of correlations and elastic moduli. Entropy 2018, 20, 28. [Google Scholar] [CrossRef]
- Litvinov, G.L.; Maslov, V.P. (Eds.) Idempotent Mathematics and Mathematical Physics; Contemporary Mathematics; AMS: Providence, RI, USA, 2005; 377p. [Google Scholar]
- Mason, T.G.; Weitz, D.A. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Phys. Rev. Lett. 1995, 74, 1250–1253. [Google Scholar] [CrossRef]
- Neumark, S. Concept of complex stiffness applied to problems of oscillations with viscous and hysteretic damping. In Aeronautical Research Council Reports 3269; Ministry of Aviation: London, UK, 1962; 36p. [Google Scholar]
- Ewoldt, R.H.; Johnston, M.T.; Caretta, L.M. Experimental challenges of shear rheology: How to avoid bad data. In Complex Fluids in Biological Systems; Spagnolie, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Nelson, L.S. The Anderson-Darling test for normality. J. Qual. Tech. 1998, 30, 298–299. [Google Scholar] [CrossRef]
- Manzoni, A.; Quateroni, A.; Rozza, G. Model reduction techniques for fast blood flow simulation in parameterized geometries. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 604–625. [Google Scholar] [CrossRef]
- Niroomandi, S.; Alfaro, I.; Gonzalez, D.; Cueto, E.; Chinesta, F. Real-time simulation of surgery by reduced-order modelling and x-FEM techniques. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 574–588. [Google Scholar] [CrossRef]
- Hollenstein, M.; Bajka, M.; Röhrnbauer, B.; Badir, S.; Mazza, E. Measuring the in vivo behavior of soft tissue and organs using the aspiration device. Stud. Mechanobiol. Tissue Eng. Biomater. 2012, 11, 201–228. [Google Scholar]

| Method [Reference] | Tissue | Results * | Comments |
|---|---|---|---|
| Various data [28] | Cortical bone | 14.0 | Data adopted for finite element analysis (FEA), bone density 1.3–2.0 g/cm3 |
| 13.0 | |||
| 13.7 | |||
| Various data [31] | Cortical bone | 11.4~14.1 | Buckling |
| 5.72 | Bending | ||
| 13.0~14.8 | Ultrasound (human) | ||
| 10.9 | Ultrasound (bovine) | ||
| 10.4 | Tensile | ||
| 15.0~19.4 | Nanoindentation | ||
| 17.4~17.5 | Acoustic microscopy | ||
| [29] | Cortical bone | 12.6~19.4 | Orthotropic formulations |
| Shear 4.85~5.7 | |||
| [32] | Cortical bone | 13.98 | Poisson ratio 0.30 |
| Calculated and analyzed in [33] | Cortical bone | 13.7~15 | At density 1.8 g/cm3 |
| 15~20 | Infero-superior direction (Z) | ||
| 8~10 | Bucco-lingual direction (Y) | ||
| 9.8~10 | Mesio-distal direction (X) | ||
| Assigned by bone density [30] | Bone type I | 9.5 | Mandible (anterior) |
| Bone Type II | 5.5 | Mandible & maxilla (anterior) | |
| Bone Type III | 1.6 | Mandible (posterior), maxilla (anterior) | |
| Bone Type IV | 0.69 | Maxilla (posterior) | |
| Various data [31] | Trabecular bone | 0.76 | Uniaxial tension |
| Various data [28] | Cancellous bone | 0.49 | Data adopted for finite element analysis (FEA), density 1.0 g/cm3 |
| 1.37 | |||
| 0.50 | |||
| 0.69 | |||
| [32] | Medullar bone | 0.259 | For low density (150 HU) |
| 3.507 | For high density (850 HU) | ||
| Adopted in [29] | Cancellous bone | 0.210~1.148 | Orthotropic formulations |
| Shear 0.068~0.434 | |||
| Calculated and analyzed in [33] | Cancellous bone | 0.20~0.25 | At density 1.0 g/cm3 |
| 0.30~0.33 | Infero-superior direction (Z) | ||
| 1.0~1.7 | Bucco-lingual direction (Y) | ||
| 3~4 | Mesio-distal direction (X) |
| Method [Reference] | Tissue | Results | Comments |
|---|---|---|---|
| Tension at 22 °C with stress/strain analysis (20 mm/min) [39] | Gingiva (H) | 37.36 ± 17.36 | No data about calculation. Preconditioning 0.5–2.0 N with 20 cycles. Specimens from Thiel-embalmed cadavers |
| B. mucosa (H) | 18.13 ± 4.51 | ||
| Hard palate (H) | 8.33 ± 5.78 | ||
| Tension with preload 3 mN (5 mm/min) [40] | L. attached gingiva (P) | 18.83 ± 5.98 | Preconditioning with 5 cycles before load to failure |
| B. attached gingiva (P) | 19.75 ± 6.20 | ||
| L. alveolar mucosa (P) | 4.79 ± 2.54 | ||
| B. alveolar mucosa (P) | 5.74 ± 1.15 | ||
| B. mucosa (P) | 2.48 ± 0.37 | ||
| Compression at 0.1–1 Hz, 10–15% strain [40] | B. attached gingiva (P) | ‘Instant’ 7.81 ± 1.11 | Preconditioning: 25 cycles + 5 min relaxation. Computed at the peak stress (1st and last cycle) |
| ‘Steady’ 0.86 ± 0.09 | |||
| Compressive creep 0.36 kPa, 37 °C in 5 min [38] | Hydrated mucosa (P) | 2.72 | Creep and relaxation were not analyzed in detail |
| Dehydrated mucosa (P) | E’ 2.0~4.5 | Data for E’ at 1 Hz, 37 °C | |
| E’ 0.2~0.35 | - | ||
| Various data [17] | Mucosa (H) | Creep: 0.04~2.35 | Data from different sources |
| Initial: 0.083 ± 0.020 | not all Initial values is creep for 1st Prony series | ||
| Linear: 0.1~680 | Poisson ratios: 0.30~0.49 | ||
| Others: 1~10, 19.6 | - | ||
| Standard linear solid: 1.1, 1.2 | For two spring elements | ||
| In vivo MRE [37] | Soft palate (H) | G’ 2.53 ± 0.31 | Shear moduli from the MRE displacements |
| G” 0.90 ± 0.22 | |||
| Various data [26] | Mucosa (H) | 0.91~5.93 | Measured by ultrasound |
| 0.37~5.80 | Mechanical measurements | ||
| 0.41~2.67 | - | ||
| 0.66~4.36 | - | ||
| 2.75~5.03 | - | ||
| 0.37~0.59 | Kelvin–Voigt model | ||
| 1.41 | Maxwell model | ||
| Various data [19]; mechanical tests | PDL (P) | 0.070~1750 | Different measurements |
| 5.5 ± 2.1 | At strain rate 0.002 L/s | ||
| 12.5 ± 4.2 | At strain rate 0.04 L/s | ||
| 19.0 ± 6.3 | At strain rate 1.2 L/s |
| Parameter (Purpose) | Preferred Values | Maximal (Short-Term) Values | Refs. |
|---|---|---|---|
| PPT (minimize pain) | <100 | <400 | [17] |
| IFP (minimize anoxia/ischaemia) | <4 | <13 | [17,47,48] |
| Pressure (minimize residual ridge resorption) | <7 | <20 | [17,46] |
| Type | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 | ν12 | ν23 | ν31 | ν21 | ν32 | ν13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bovine femur | 14.1 | 18.4 | 25.0 | 7.00 | 6.30 | 5.28 | 6.34 | 4.84 | 6.94 | 0.38 | 0.206 | 0.306 | 0.303 | 0.109 | 0.204 |
| Human tibia | 11.6 | 14.4 | 22.5 | 4.91 | 3.56 | 2.41 | 7.95 | 6.10 | 6.92 | 0.61 | 0.316 | 0.306 | 0.495 | 0.119 | 0.142 |
| Human femur | 20.0 | 21.7 | 30.0 | 6.56 | 5.85 | 4.74 | 10.9 | 11.5 | 11.5 | 0.021 | 0.474 | 0.426 | 0.019 | 0.376 | 0.375 |
| Bovine femur Haversian | 21.2 | 21.0 | 29.0 | 6.30 | 6.30 | 5.40 | 11.7 | 12.7 | 11.1 | 0.437 | 0.434 | 0.281 | 0.408 | 0.282 | 0.191 |
| Bovine femur plexiform | 22.4 | 25.0 | 35.0 | 8.20 | 7.10 | 6.10 | 14.0 | 15.8 | 13.6 | 0.515 | 0.562 | 0.229 | 0.399 | 0.297 | 0.156 |
| [33] | 15.73 | 18.59 | 26.91 | 4.63 | 4.31 | 3.81 | 8.16 | 9.68 | 9.73 | 0.381 | 0.445 | 0.328 | 0.309 | 0.249 | 0.224 |
| [29] | 17.38 | 17.38 | 27.02 | 5.7 | 5.7 | 4.85 | 7.69 | 6.34 | 6.34 | 0.30 | 0.253 | 0.253 | 0.30 | 0.39 | 0.39 |
| References | Measurements | Results | Comments |
|---|---|---|---|
| [34,35] | Creep at 83 kPa | E0c = 73 ± 21 kPa τ0c = 17 ± 3 s | Only one creep stress |
| [38] | Creep at 0.36 kPa in compression, 37 °C | E0c = 262.8 kPa τ0c = 13.2 s | Only one stress used; limited test time (5 min) |
| [40] | Dynamic compression at 1 Hz and 0.1 strain | E0ω = 272.7 kPa τ0ω = ~0.02 ms? | Only 0.1 strain data shown; large data scatter |
| [46] | Special shear simulating abutment load at 1 Hz and 37 °C | E0ω = 117 ± 8 kPa τ0ω = 23 s | Gingiva attached to the bone support; up to 50 μm displacement |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gasik, M.; Lambert, F.; Bacevic, M. Biomechanical Properties of Bone and Mucosa for Design and Application of Dental Implants. Materials 2021, 14, 2845. https://doi.org/10.3390/ma14112845
Gasik M, Lambert F, Bacevic M. Biomechanical Properties of Bone and Mucosa for Design and Application of Dental Implants. Materials. 2021; 14(11):2845. https://doi.org/10.3390/ma14112845
Chicago/Turabian StyleGasik, Michael, France Lambert, and Miljana Bacevic. 2021. "Biomechanical Properties of Bone and Mucosa for Design and Application of Dental Implants" Materials 14, no. 11: 2845. https://doi.org/10.3390/ma14112845
APA StyleGasik, M., Lambert, F., & Bacevic, M. (2021). Biomechanical Properties of Bone and Mucosa for Design and Application of Dental Implants. Materials, 14(11), 2845. https://doi.org/10.3390/ma14112845







