Multi-Layer Wear and Tool Life Calculation for Forging Applications Considering Dynamical Hardness Modeling and Nitrided Layer Degradation
Abstract
1. Introduction
2. Materials and Methods
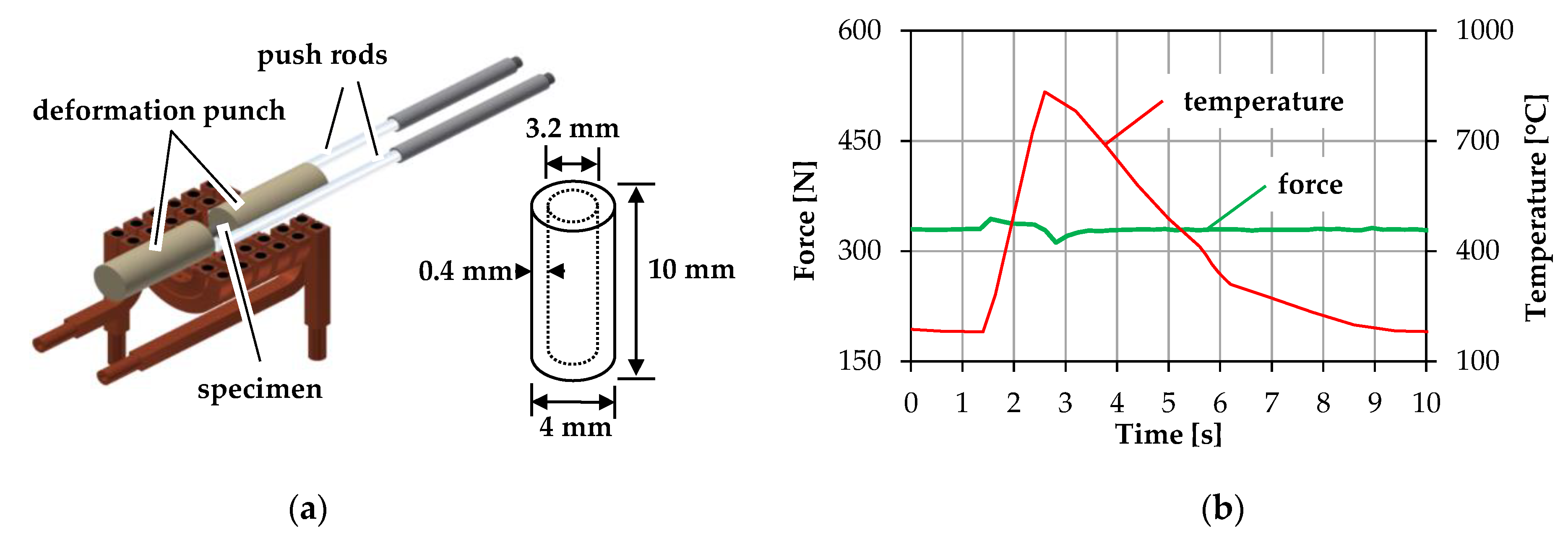
2.1. Material Modeling
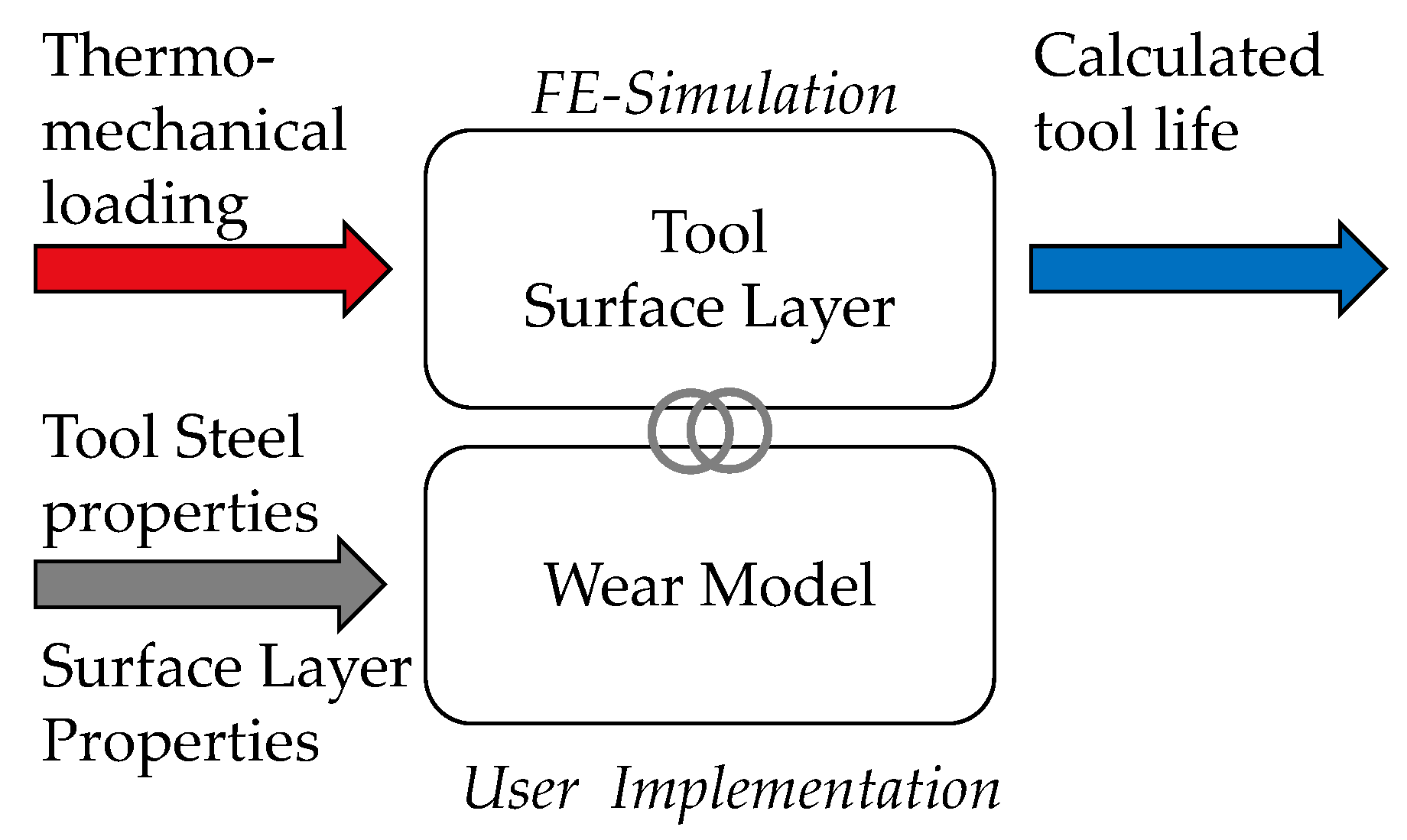
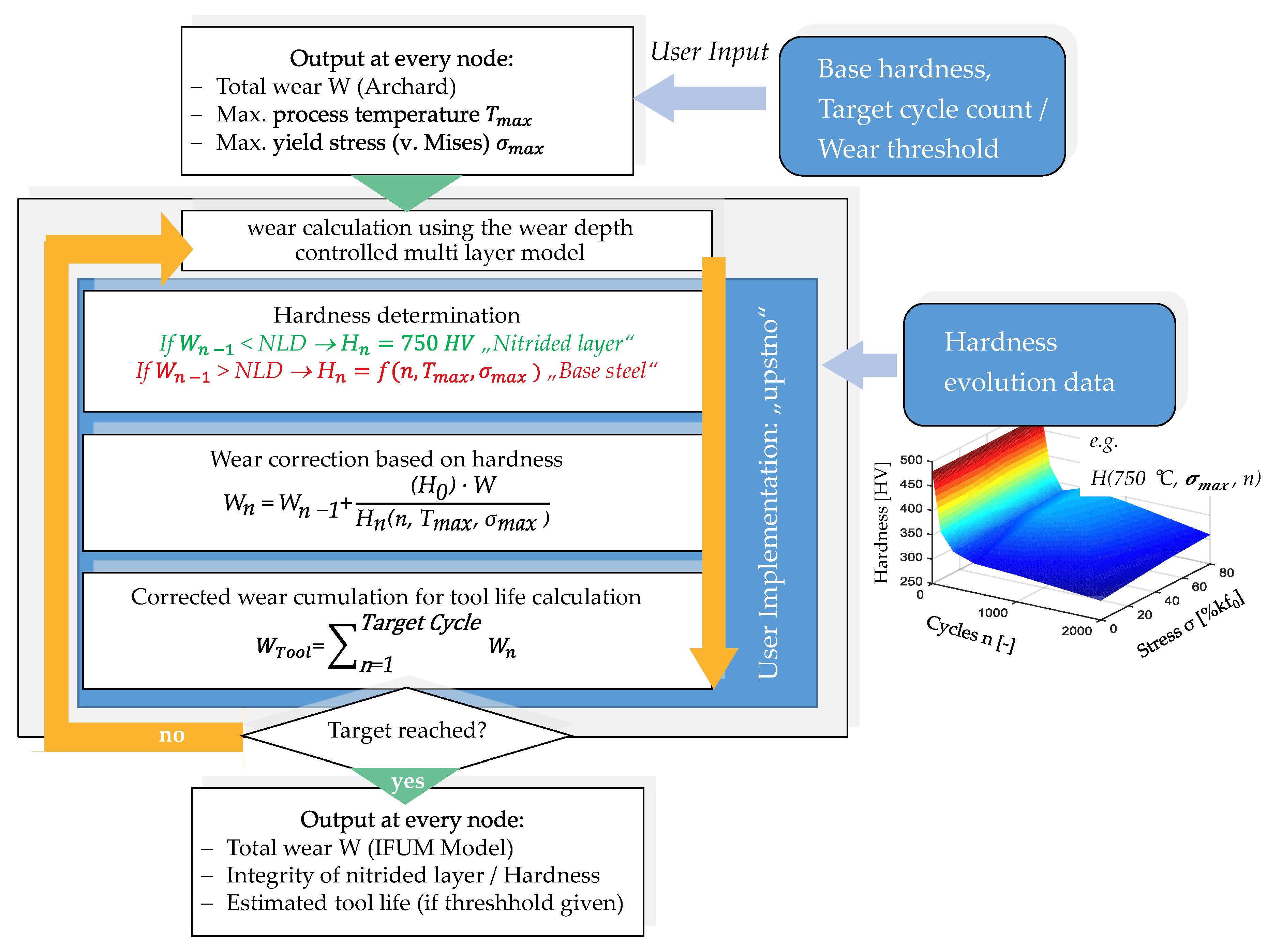
2.2. Wear Modeling and Implementation
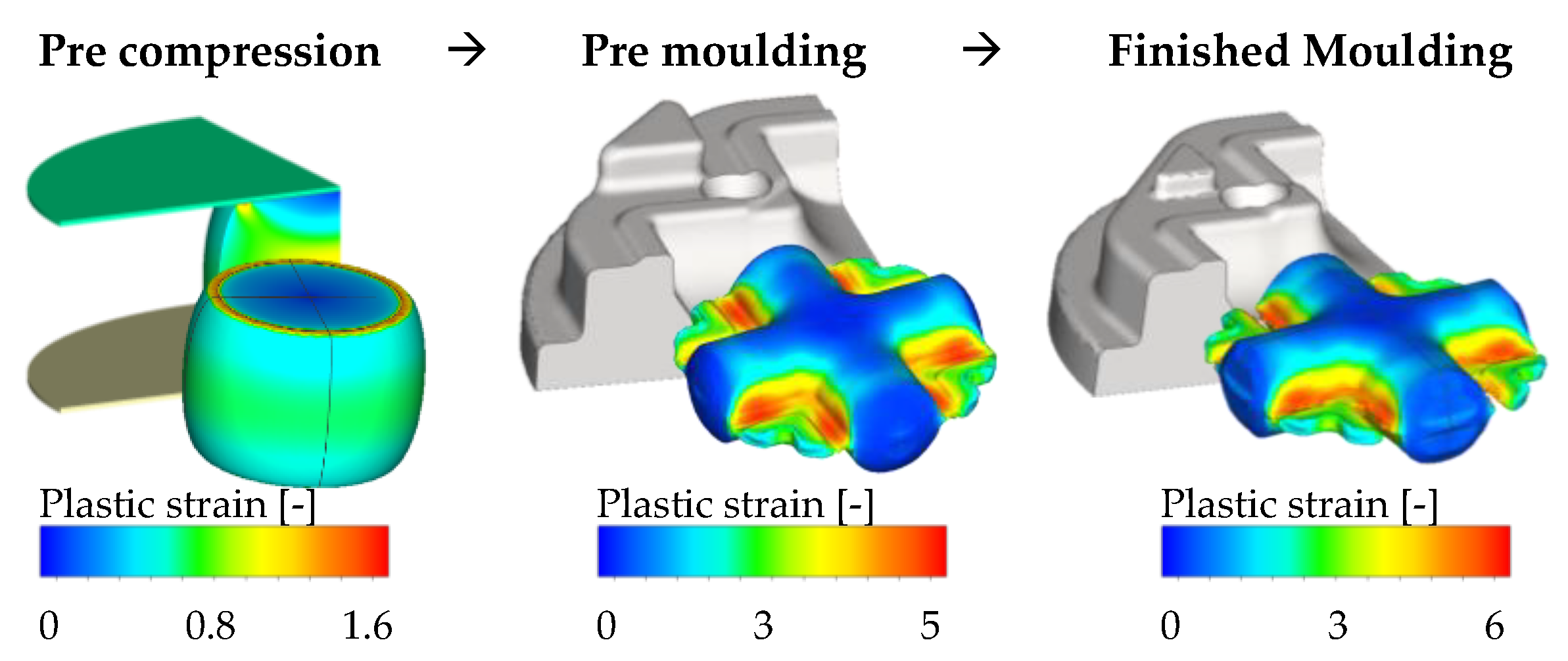
2.3. Industrial Validation Process
3. Results
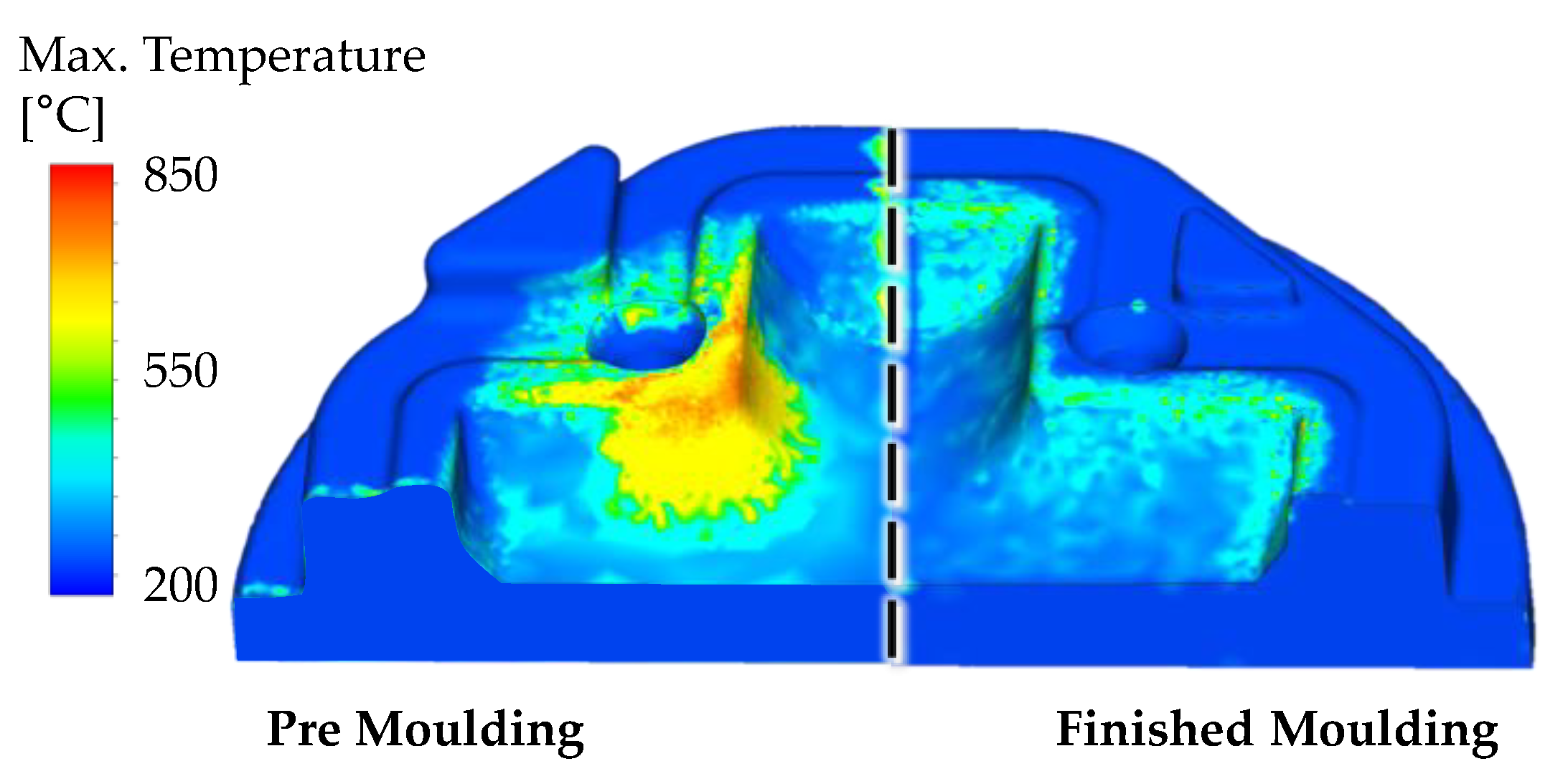
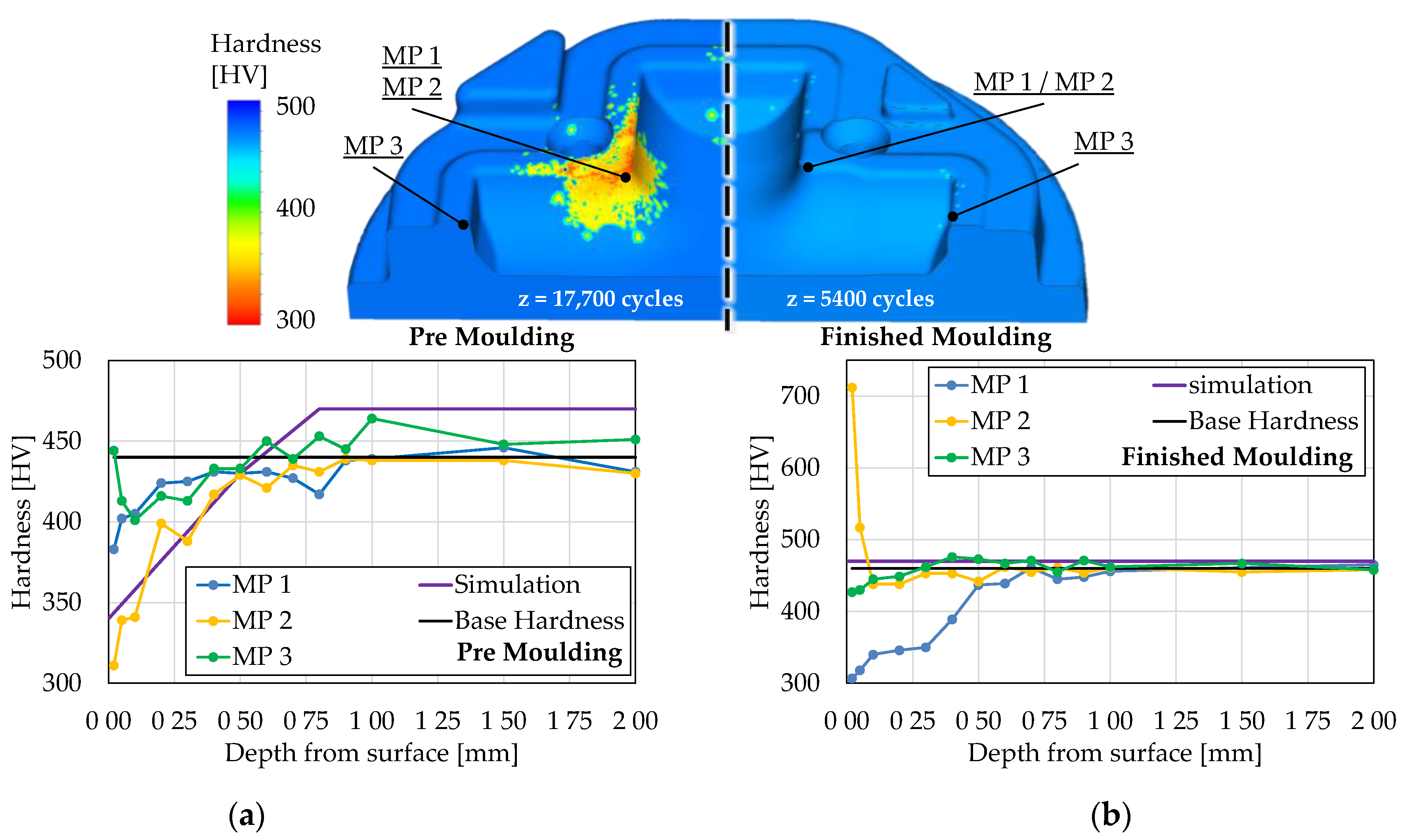
3.1. Tool Hardness Calculation
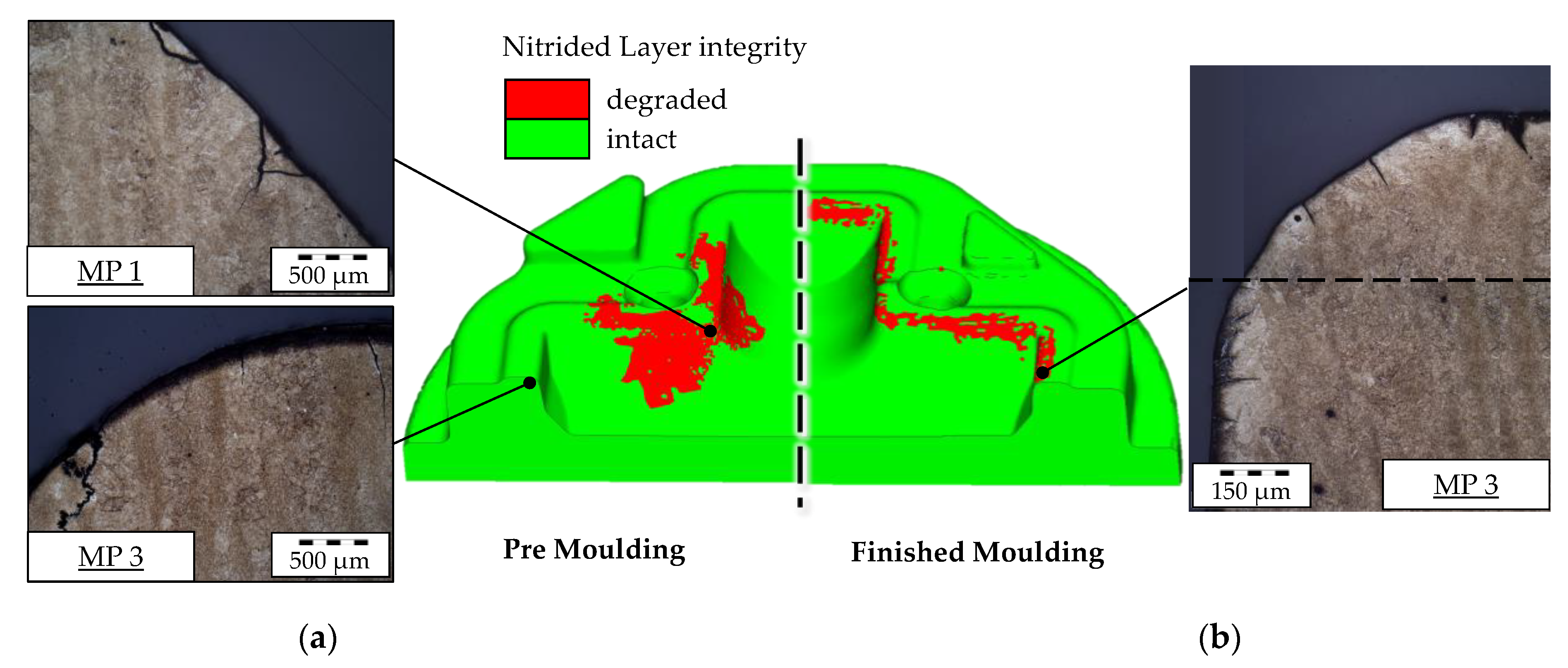
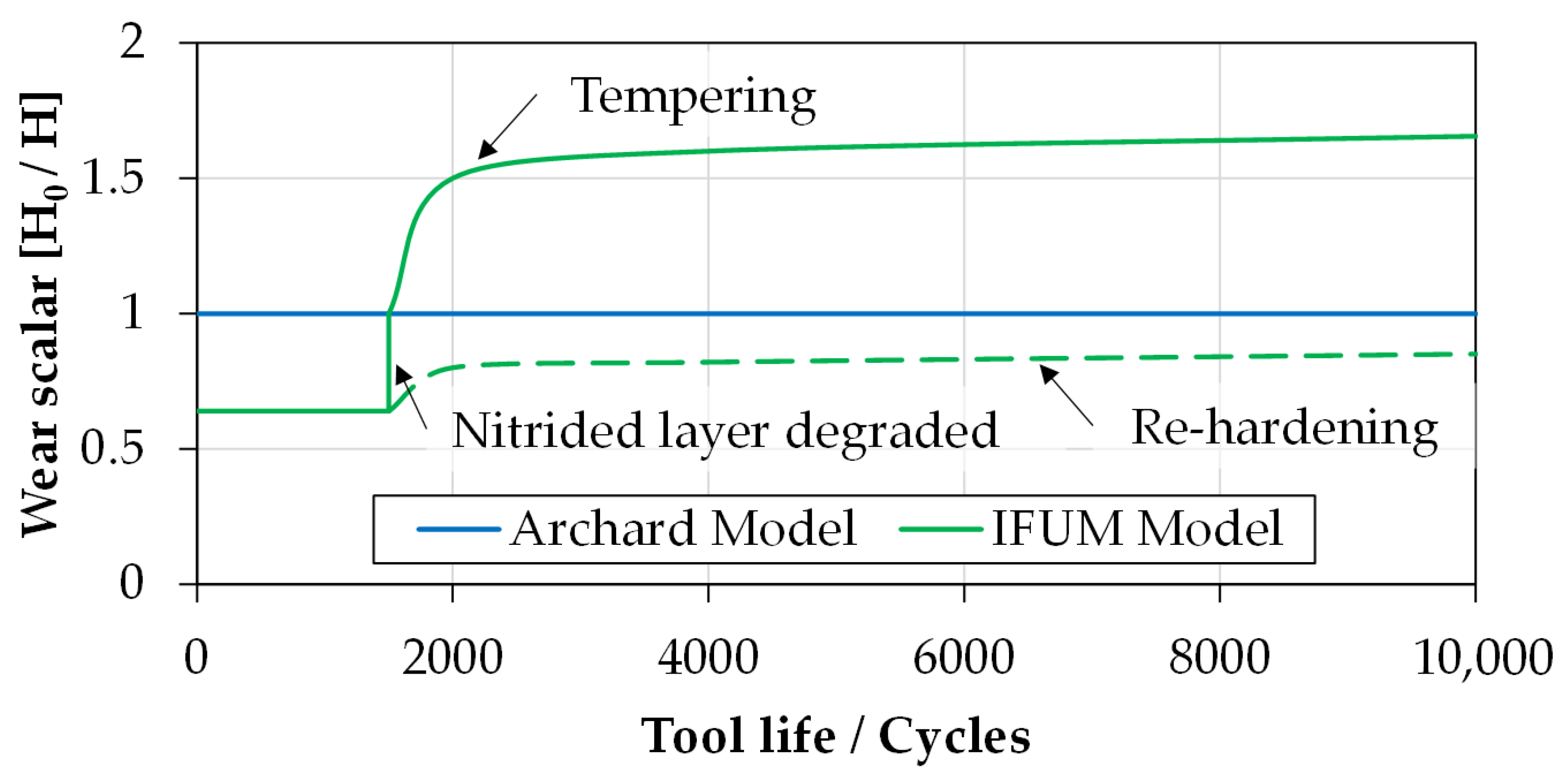
3.2. Wear Calculation and Nitrided Layer Integrity
- The measurements of the real tools are showing an increased amount of wear close to the contour next to ejector hole. To reduce the complexity of the calculation model, these holes were covered with analytical rigid parts leading to a minor deviation of the part material flow. Consequently, the calculated wear is underestimated at this location.
- By closer inspection of the finished molding, a high, homogenous amount of wear is found at the central corner of the mold using the optical measurements. An analysis of the calculated contact pressure and the sliding velocity at this region shows that the die is exposed to high mechanical pressure, but also that there is almost no material flow. It must therefore be assumed that the measured contour deviation cannot be explained by wear, but by deformation of the die.
- The corners of die are subject to a low amount of wear following the calculation results. The optical measurements are unclear in this region. While one corner is showing a comparable amount of wear, the other corner shows almost no wear. This finding could be explained with deviations of the insertion position during the industrial forming which are not displayable by the FE-calculation.
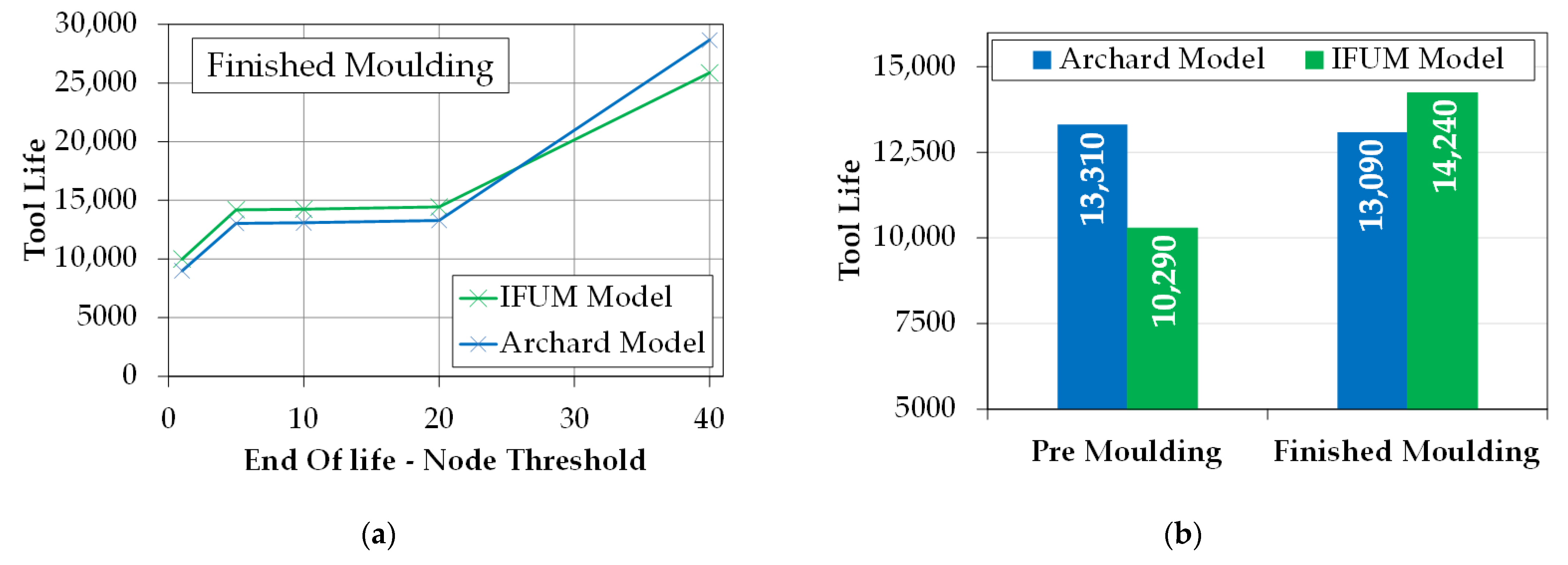
3.3. Tool Life Calculation
4. Discussion
4.1. Hardness Calculation
4.2. Wear Calculation
4.3. Tool Life Estimation
5. Conclusions
6. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| C | Cr | Mo | V | Si |
|---|---|---|---|---|
| 0.37 | 5.0 | 3.0 | 0.6 | 0.3 |
| C | Cr | Mo | V | Si |
|---|---|---|---|---|
| 0.37 | 5.0 | 1.25 | 0.4 | 1.0 |
| C | Mn | P | S |
|---|---|---|---|
| 0.45 | 0.75 | Max. 0.04 | Max. 0.05 |
References
- Summerville, E.; Venkatesan, K.; Subramanian, C. Wear processes in hot forging press tools. Mater. Des. 1995, 16, 289–294. [Google Scholar] [CrossRef]
- Gronostajski, Z.; Kaszuba, M.; Polak, S.; Zwierzchowski, M.; Niechajowicz, A.; Hawryluk, M. The failure mechanisms of hot forging dies. Mater. Sci. Eng. A 2016, 657, 147–160. [Google Scholar] [CrossRef]
- Bariani, P.F.; Berti, G.; D’Angelo, L. Tool Cost Estimating at the Early Stages of Cold Forging Process Design. CIRP Ann. Manuf. Technol. 1993, 42, 279–282. [Google Scholar] [CrossRef]
- Fila, P.; Balcar, M.; Martinek, L.; Suchmann, P.; Krejcik, J.; Jelen, L.; Psik, E. Development of new types of tool steels designed for forging dies. MM Sci. J. 2010, 2010, 222–224. [Google Scholar] [CrossRef]
- Archard, J.F. The wear of metals under unlubricated conditions. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 236, 397–410. [Google Scholar]
- Castro, G.; Vicente, A.F.; Cid, J. Influence of the nitriding time in the wear behaviour of an AISI H13 steel during a crankshaft forging process. Wear 2007, 263, 1375–1385. [Google Scholar] [CrossRef]
- Habig, K.-H. Wear protection of steels by boriding, vanadizing, nitriding, carburising, and hardening. Mater. Des. 1980, 2, 83–92. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Holm, R.; Holm, E. Elektrische Kontakte/Electric Contacts Handbook; Springer: Berlin/Heidelberg, Germany, 1958. [Google Scholar]
- Tabe, T. Location of Crack Occurrence in Tools; Jernkonteret: Borlänge, Sweden, 2004. [Google Scholar]
- Painter, B.; Shivpuri, R.; Altan, T. Prediction of die wear during hot-extrusion of engine valves. J. Mater. Process. Technol. 1996, 59, 132–143. [Google Scholar] [CrossRef]
- Choi, C.; Mendez, J.G.; Groseclose, A. Estimation of Die Stresses and Wear in Warm Forging of Steel Pinion Shafts, ERC for Net Shape Manufacturing, Report No. ERC/NSM-08-R-34; The Ohio State University: Columbus, OH, USA, 2009. [Google Scholar]
- Bobke, T. Randschichtphänomene bei Verschleißvorgängen an Gesenkschmiedewerkzeugen; Universität Hannover Dissertation: Hannover, Germany, 1991. [Google Scholar]
- Behrens, B.-A. New Developments in the FE Simulation of Closed Die Forging Processes. In Proceedings of the NAMRI/SME 2012, Notre Dame, IN, USA, 4–8 June 2012; p. 40. [Google Scholar]
- Choi, C.; Groseclose, A.; Altan, T. Estimation of plastic deformation and abrasive wear in warm forging dies. J. Mater. Process. Technol. 2012, 212, 1742–1752. [Google Scholar] [CrossRef]
- Leskovšek, V.; Podgornik, B.; Jenko, M. A PACVD duplex coating for hot-forging applications. Wear 2009, 266, 453–460. [Google Scholar] [CrossRef]
- Hubicki, R.; Richert, M.; Wiewióra, M. An Experimental Study of Temperature Effect on Properties of Nitride Layers on X37CrMoV51 Tool Steel Used in Extrusion Aluminium Industry. Materials (Basel) 2020, 13, 2311. [Google Scholar] [CrossRef] [PubMed]
- Klassen, A.; Bouguecha, A.; Behrens, B.A. Wear Prediction for Hot Forging Dies under Consideration of Structure Modification in the Surface Layer. Adv. Mater. Res. 2014, 1018, 341–348. [Google Scholar] [CrossRef]
- Müller, F.; Malik, I.; Wester, H.; Behrens, B.-A. Experimental Characterisation of Tool Hardness Evolution Under Consideration of Process Relevant Cyclic Thermal and Mechanical Loading During Industrial Forging. In Production at the Leading Edge of Technology. Lecture Notes in Production Engineering; Behrens, B.-A., Brosius, A., Hintze, W., Ihlenfeldt, S., Wulfsberg, J.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 3–12. [Google Scholar]
- Malik, I.Y.; Lorenz, U.; Chugreev, A.; Behrens, B.-A. Microstructure and wear behaviour of high alloyed hot-work tool steels 1.2343 and 1.2367 under thermo-mechanical loading. Proc. IOP Conf. Ser. Mater. Sci. Eng. 2019, 629, 12011. [Google Scholar] [CrossRef]
- Mehrer, H. Diffusion in Solids. Fundamentals, Methods, Materials, Diffusion-Controlled Processes. In Springer Series in Solid-State Sciences; Springer GmbH: Berlin/Heidelberg, Germany, 2007; p. 155. [Google Scholar]
- Niederhofer, P.; Eger, K.; Schwingenschlögl, P.; Merklein, M. Properties of Tool Steels for Application in Hot Stamping. Steel Res. Int. 2020, 91, 1900422. [Google Scholar] [CrossRef]
- Hafenstein, S.; Werner, E.; Wilzer, J.; Theisen, W.; Weber, S.; Sunderkötter, C.; Bachmann, M. Einfluss der Temperatur und des Vergütungszustands auf die Wärmeleitfähigkeit von Warmarbeitsstählen für das Presshärten. HTM J. Heat Treat. Mater. 2017, 72, 81–86. [Google Scholar] [CrossRef]
- Landolt, D.; Mischler, S. Tribocorrosion of Passive Metals and Coatings. In Metals and Surface Engineering; Woodhead Publishing: Cambridge, UK, 2011. [Google Scholar]
- Jarfors, A.; Castagne, S.; Danno, A.; Zhang, X. Tool Wear and Life Span Variations in Cold Forming Operations and Their Implications in Microforming. Technologies 2017, 5, 3. [Google Scholar] [CrossRef]
- Surech, K.; Regalla, S.P. Effect of Time Scaling and Mass Scaling in Numerical Simulation of Incremental Forming. Appl. Mech. Mater. 2014, 612, 105–110. [Google Scholar] [CrossRef]
- DIN, E.N. ISO 6507-2:2018-07:2018. Metallic Materials—Vickers Hardness Test—Part 2: Verification and Calibration of Testing Machines (ISO 6507-2:2018); German Version EN ISO 6507-2; Beuth: Berlin, Germany, 2018. [Google Scholar]
- Meidert, M.; Hänsel, M. Net shape cold forging to close tolerances under QS 9000 aspects. J. Mater. Process. Technol. 2000, 98, 150–154. [Google Scholar] [CrossRef]
- Basquin, O.H. The Exponential Law of Endurance Tests. Am. Soc. Test. Mater. Proc. 1910, 10, 625–630. [Google Scholar]
- Budynas, R.G.; Nisbett, J.K. Diseño en Ingeniería Mecánica de Shigley; México, D.F., Ed.; McGraw-Hill: New York, NY, USA, 2012. [Google Scholar]
- Behrens, B.-A.; Chugreev, A.; Hootak, M. Application of the Sehitoglu’s Model for the Calculation of Tool Life in Thixoforging of Steel Parts. In AIP Conference Proceedings, Proceedings of the 22nd Internatonal ESAFORM Conference on Material Forming: ESAFORM 2019, Vitoria-Gasteiz, Spain, 8–10 May 2019; AIP Publishing: Melville, NY, USA, 2019; p. 40009. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behrens, B.-A.; Brunotte, K.; Wester, H.; Rothgänger, M.; Müller, F. Multi-Layer Wear and Tool Life Calculation for Forging Applications Considering Dynamical Hardness Modeling and Nitrided Layer Degradation. Materials 2021, 14, 104. https://doi.org/10.3390/ma14010104
Behrens B-A, Brunotte K, Wester H, Rothgänger M, Müller F. Multi-Layer Wear and Tool Life Calculation for Forging Applications Considering Dynamical Hardness Modeling and Nitrided Layer Degradation. Materials. 2021; 14(1):104. https://doi.org/10.3390/ma14010104
Chicago/Turabian StyleBehrens, Bernd-Arno, Kai Brunotte, Hendrik Wester, Marcel Rothgänger, and Felix Müller. 2021. "Multi-Layer Wear and Tool Life Calculation for Forging Applications Considering Dynamical Hardness Modeling and Nitrided Layer Degradation" Materials 14, no. 1: 104. https://doi.org/10.3390/ma14010104
APA StyleBehrens, B.-A., Brunotte, K., Wester, H., Rothgänger, M., & Müller, F. (2021). Multi-Layer Wear and Tool Life Calculation for Forging Applications Considering Dynamical Hardness Modeling and Nitrided Layer Degradation. Materials, 14(1), 104. https://doi.org/10.3390/ma14010104






