Material Flow in Infeed Rotary Swaging of Tubes
Abstract
1. Introduction
2. Methods
2.1. FE Model
2.2. Experiments
3. Results of Simulation
3.1. Geometry Features
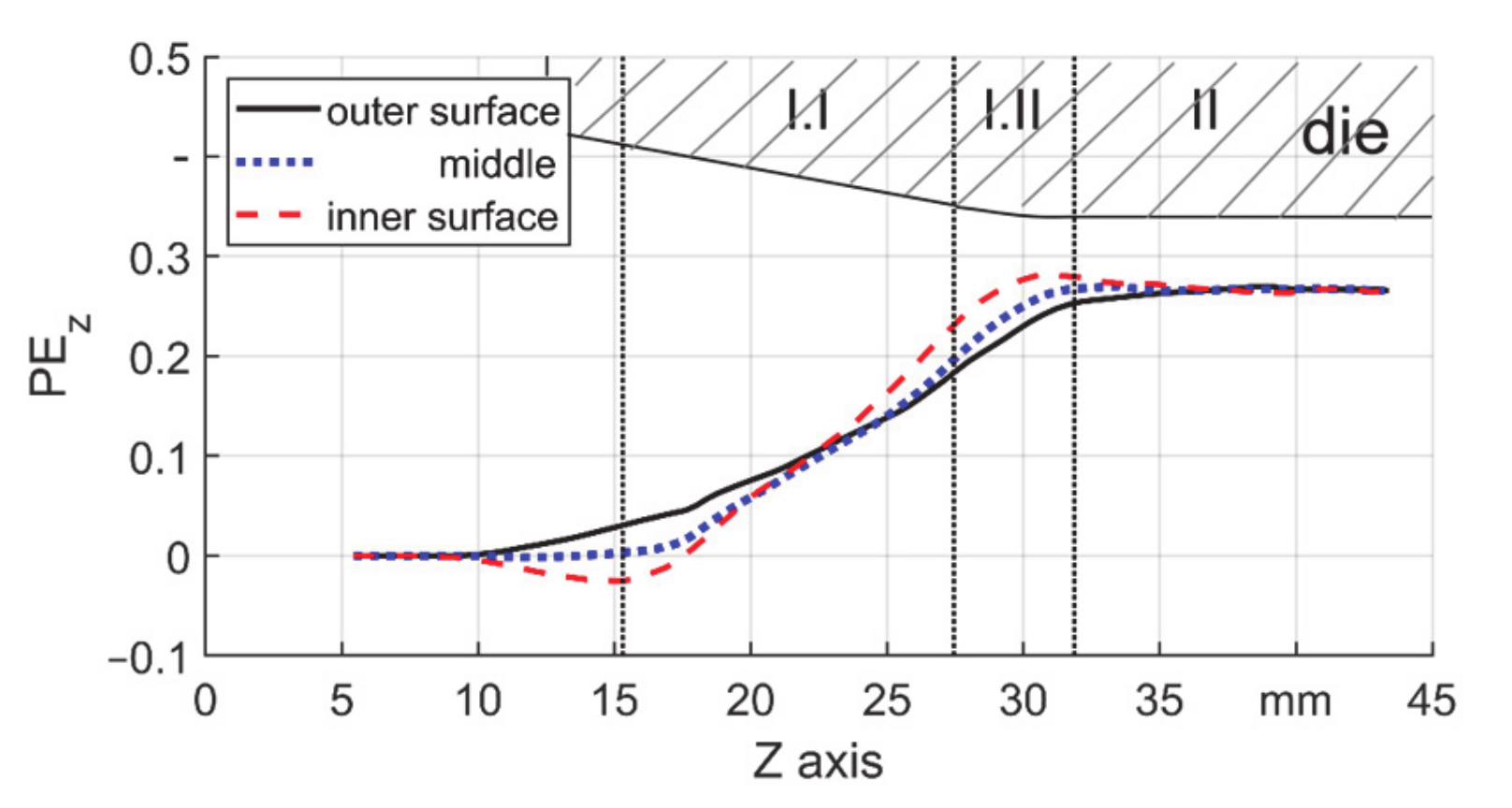
- Before the contact of die and workpiece (left of zone I.I)–the wall thickness of the workpiece shows an increase especially for low μ;
- The wall thickness increased in zone I.I, but on the locations with a changing profile of the die, i.e., the location of first contact (zone I.I) and the boundary between zones I.I and I.II, the wall thickness tended to reduce. This was more obvious in thicker tubes;
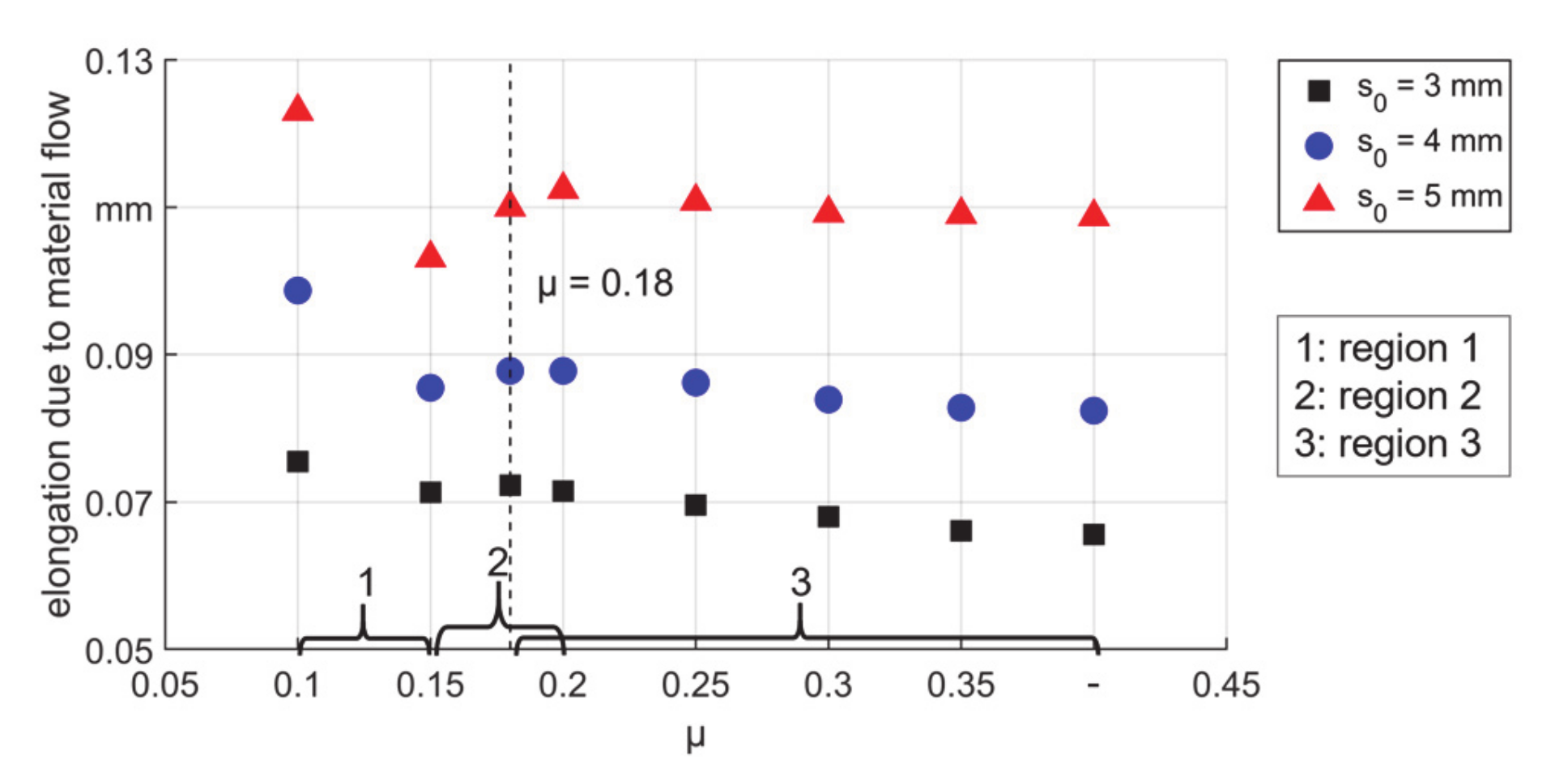
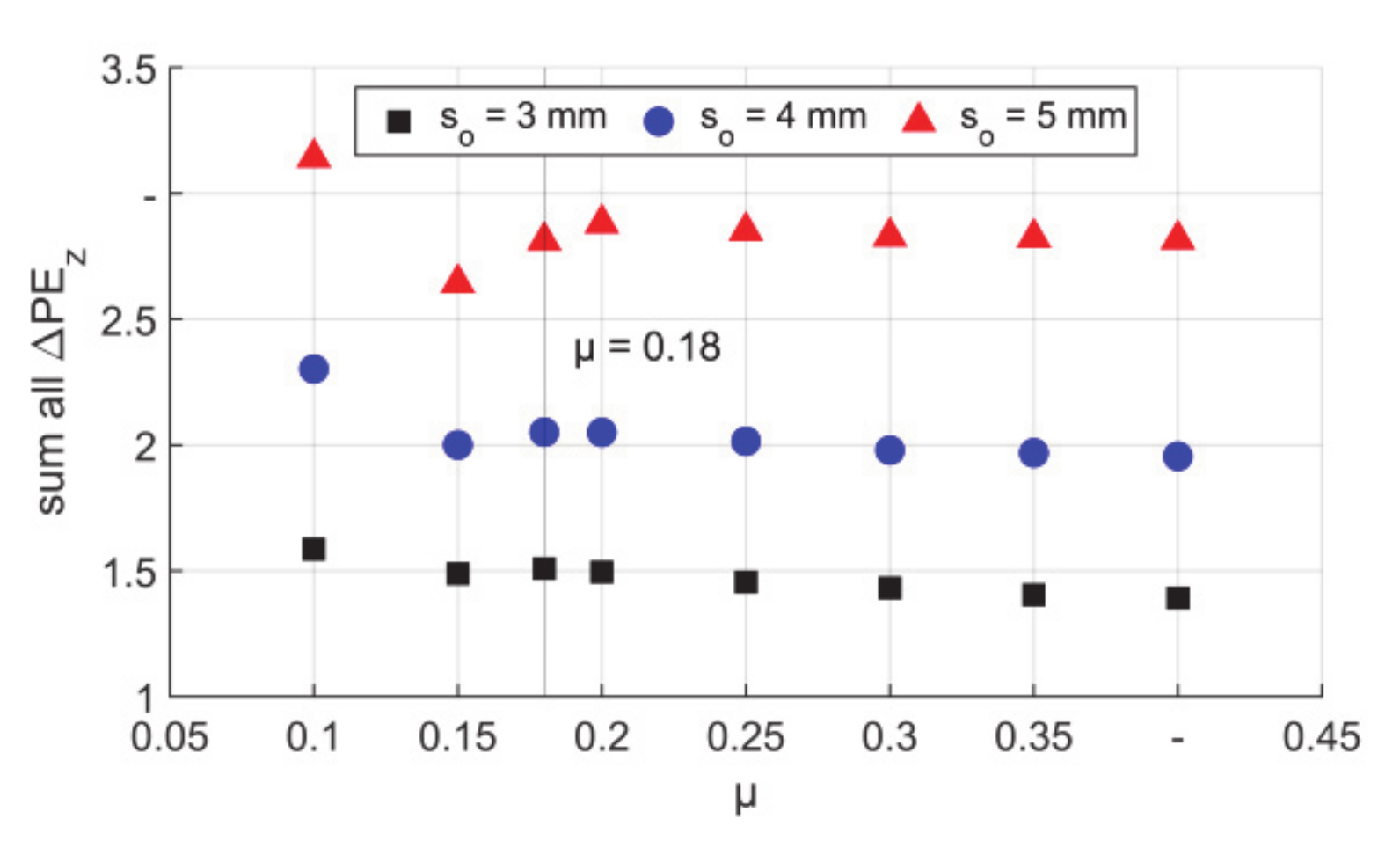
- The final wall thickness changed depending on friction coefficient. As could be seen, there was a certain friction coefficient (μ = 0.18), which led to the thinnest wall (longest workpiece).
3.2. Field Features in One Stroke
3.3. Axial Plastic Strain Development
4. Experimental Results and Validation
5. Conclusions and Outlook
- (1)
- The material on the outer surface experiences radial cyclic deformation while the material on the inner surface experienced axial cyclic deformation. Thus, it is necessary to generate a combined hardening model;
- (2)
- On the locations where redirected material flow appeared, the wall thickness tended to reduce due to stress concentration. This phenomenon was more obvious in thick tubes;
- (3)
- To reduce back shifting and backward material flow, the friction coefficient on the contact zone should be even higher than the self–locking value;
- (4)
- The material near the inner surface was deformed with higher amplitude of axial plastic strain, which could be reduced by increasing friction coefficient. This reduced amplitude could lead to a more homogeneous deformation in the workpiece;
- (5)
- The self–locking friction condition enabled maximum elongation of the workpiece thus the thinnest wall after the process.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vollertsen, F.; Friedrich, S.; Kuhfuß, B.; Maaß, P.; Thomy, C.; Zoch, H.-W. Cold Micro Metal Forming: Research Report of the Collaborative Research Center “Micro Cold Forming”(SFB 747), Bremen, Germany; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Nowak, J.; Madej, L.; Ziolkiewicz, S.; Plewinski, A.; Grosman, F.; Pietrzyk, M. Recent development in orbital forging technology. Int. J. Mater. Form. 2008, 1, 387–390. [Google Scholar] [CrossRef][Green Version]
- Macháčková, A.; Krátká, L.; Petrmichl, R.; Kunčická, L.; Kocich, R. Affecting Structure Characteristics of Rotary Swaged Tungsten Heavy Alloy Via Variable Deformation Temperature. Materials 2019, 12, 4200. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Huang, A.; Gao, L.; Li, Y.; Huang, C. Promising Tensile and Fatigue Properties of Commercially Pure Titanium Processed by Rotary Swaging and Annealing Treatment. Materials 2018, 11, 2261. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.J.; Choi, H.J.; Na, K.H.; Lee, C.H. Dimensional Characteristics of Products Using Rotary Swaging Machine with Four–Dies. Solid State Phenom. 2007, 124–126, 1645–1648. [Google Scholar] [CrossRef]
- Lahoti, G.D.; Liuzzi, L.; Altan, T. Design of dies for radial forging of rods and tubes. J. Mech. Work. Technol. 1977, 1, 99–109. [Google Scholar] [CrossRef]
- Zhang, Q.; Jin, K.; Mu, D. Tube/tube joining technology by using rotary swaging forming method. J. Mater. Process. Technol. 2014, 214, 2085–2094. [Google Scholar] [CrossRef]
- Liu, Y.; Herrmann, M.; Schenck, C.; Kuhfuss, B. Axial and Radial Material Flow Analysis in Infeed Rotary Swaging of Tubes; EDP Sciences: Les Ulis, France, 2018; Volume 190, p. 4003. [Google Scholar]
- Ghaei, A.; Movahhedy, M.R.; Karimi Taheri, A. Finite element modelling simulation of radial forging of tubes without mandrel. Mater. Des. 2008, 29, 867–872. [Google Scholar] [CrossRef]
- Li, Y.; He, T.; Zeng, Z. Numerical simulation and experimental study on the tube sinking of a thin–walled copper tube with axially inner micro grooves by radial forging. J. Mater. Process. Technol. 2013, 213, 987–996. [Google Scholar] [CrossRef]
- Fan, L.; Wang, Z.; Wang, H. 3D finite element modeling and analysis of radial forging processes. J. Manuf. Process. 2014, 16, 329–334. [Google Scholar] [CrossRef]
- Pantalé, O.; Gueye, B. Influence of the Constitutive Flow Law in FEM Simulation of the Radial Forging Process. J. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Abaqus, I. Defining Plasticity in Abaqus. Available online: https://abaqus-docs.mit.edu/2017/English/SIMACAEGSARefMap/simagsa-c-matdefining.htm (accessed on 12 October 2020).
- Jang, D.Y.; Liou, J.H. Study of stress development in axi–symmetric products processed by radial forging using a 3–D non–linear finite–element method. J. Mater. Process. Technol. 1998, 74, 74–82. [Google Scholar] [CrossRef]
- Liu, Y.; Herrmann, M.; Schenck, C.; Kuhfuss, B. Plastic Deformation Components in Mandrel Free Infeed Rotary Swaging of Tubes. Procedia Manuf. 2019, 27, 33–38. [Google Scholar] [CrossRef]
- Wu, Y.; Dong, X.; Yu, Q. Upper bound analysis of axial metal flow inhomogeneity in radial forging process. Int. J. Mech. Sci. 2015, 93, 102–110. [Google Scholar] [CrossRef]
- Sanjari, M.; Saidi, P.; Karimi Taheri, A.; Hossein–Zadeh, M. Determination of strain field and heterogeneity in radial forging of tube using finite element method and microhardness test. Mater. Des. 2012, 38, 147–153. [Google Scholar] [CrossRef]
- Moumi, E.; Ishkina, S.; Kuhfuss, B.; Hochrainer, T.; Struss, A.; Hunkel, M. 2D–simulation of Material Flow During Infeed Rotary Swaging Using Finite Element Method. Procedia Eng. 2014, 81, 2342–2347. [Google Scholar] [CrossRef]
- Ishkina, S.; Schenck, C.; Herrmann, M.; Kuhfuss, B. Visualization of Axial Material Flow by Eccentric Thread Swaging. Procedia Manuf. 2020, 47, 1339–1344. [Google Scholar] [CrossRef]
- Liu, Y.; Herrmann, M.; Kuhfuss, B.; Schenck, C. Plastic Deformation History in Infeed Rotary Swaging Process. In Proceedings of the 20th Anniversary of the International ESAFORM Conference on Material Forming, Dublin, Ireland, 26–28 April 2017. [Google Scholar]
- Abaqus, I. Models for Metals Subjected to Cyclic Loading. Available online: http://130.149.89.49:2080/v2016/books/usb/default.htm?startat=pt05ch23s02abm18.html#usb-mat-chardening (accessed on 22 October 2020).
- Sun, E.Q. Shear locking and hourglassing in MSC Nastran, ABAQUS, and ANSYS. In Proceedings of the Msc Software Users Meeting, Huntington Beach, CA, USA, 17–19 July 2006; pp. 1–9. [Google Scholar]
- Zhang, Q.; Jin, K.; Mu, D.; Ma, P.; Tian, J. Rotary Swaging Forming Process of Tube Workpieces. Procedia Eng. 2014, 81. [Google Scholar] [CrossRef]
- Ghiotti, A.; Bruschi, S. Tribological behaviour of DLC coatings for sheet metal forming tools. Wear 2011, 271, 2454–2458. [Google Scholar] [CrossRef]
- Singh, G.; Kalita, B.; Vishnu Narayanan, K.; Arora, U.K.; Mahapatra, M.M.; Jayaganthan, R. Finite Element Analysis and Experimental Evaluation of Residual Stress of Zr–4 alloys Processed through Swaging. Metals 2020, 10, 1281. [Google Scholar] [CrossRef]
- Hasselbruch, H.; Herrmann, M.; Heidhoff, J.; Böhmermann, F.; Riemer, O.; Mehner, A.; Kuhfuss, B. Potentials of Dry Rotary Swaging. Dry Met. Form. Open Access J. 2020. [Google Scholar] [CrossRef]
- Abaqus, I. Energy Balance. Available online: http://130.149.89.49:2080/v6.8/books/stm/default.htm?startat=ch01s05ath12.html (accessed on 22 October 2020).
- Ishkina, S.; Charni, D.; Herrmann, M.; Liu, Y.; Epp, J.; Schenck, C.; Kuhfuss, B.; Zoch, H.-W. Influence of Process Fluctuations on Residual Stress Evolution in Rotary Swaging of Steel Tubes. Materials 2019, 12, 855. [Google Scholar] [CrossRef] [PubMed]





















| σs (mPa) | Q (mPa) | b | C1 | γ1 | C2 | γ2 | C3 | γ3 |
|---|---|---|---|---|---|---|---|---|
| 170.50 | 168.16 | 14.82 | 1614.1 | 41.947 | 1543.2 | 40.704 | 239.00 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, J.; Herrmann, M.; Schenck, C.; Kuhfuss, B. Material Flow in Infeed Rotary Swaging of Tubes. Materials 2021, 14, 58. https://doi.org/10.3390/ma14010058
Liu Y, Liu J, Herrmann M, Schenck C, Kuhfuss B. Material Flow in Infeed Rotary Swaging of Tubes. Materials. 2021; 14(1):58. https://doi.org/10.3390/ma14010058
Chicago/Turabian StyleLiu, Yang, Jing Liu, Marius Herrmann, Christian Schenck, and Bernd Kuhfuss. 2021. "Material Flow in Infeed Rotary Swaging of Tubes" Materials 14, no. 1: 58. https://doi.org/10.3390/ma14010058
APA StyleLiu, Y., Liu, J., Herrmann, M., Schenck, C., & Kuhfuss, B. (2021). Material Flow in Infeed Rotary Swaging of Tubes. Materials, 14(1), 58. https://doi.org/10.3390/ma14010058





