C-S-H Pore Size Characterization Via a Combined Nuclear Magnetic Resonance (NMR)–Scanning Electron Microscopy (SEM) Surface Relaxivity Calibration
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Pore Size Evaluation
2.2.1. Determination of the Surface Relaxivity from Monolayer H2O Coverage
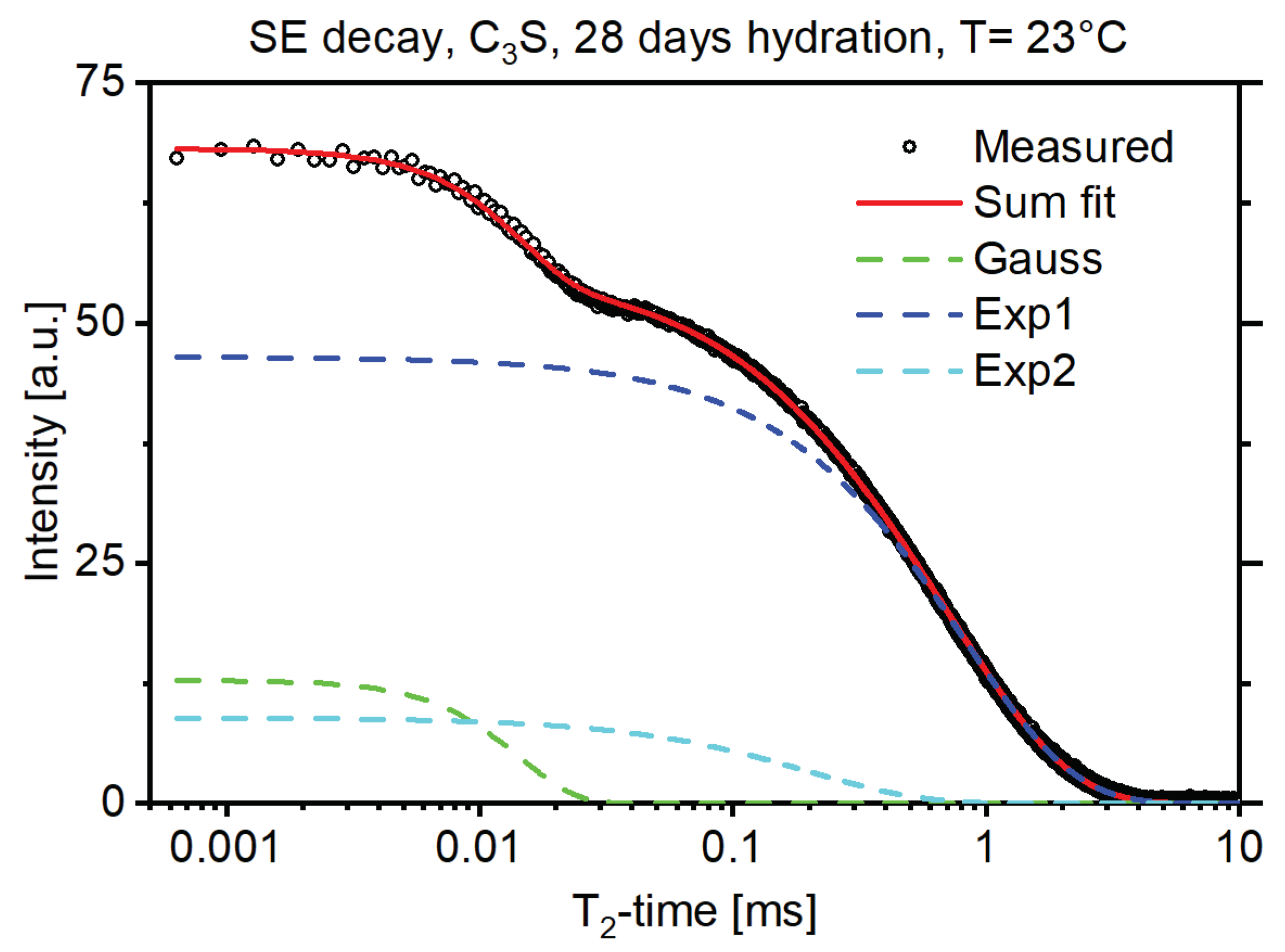
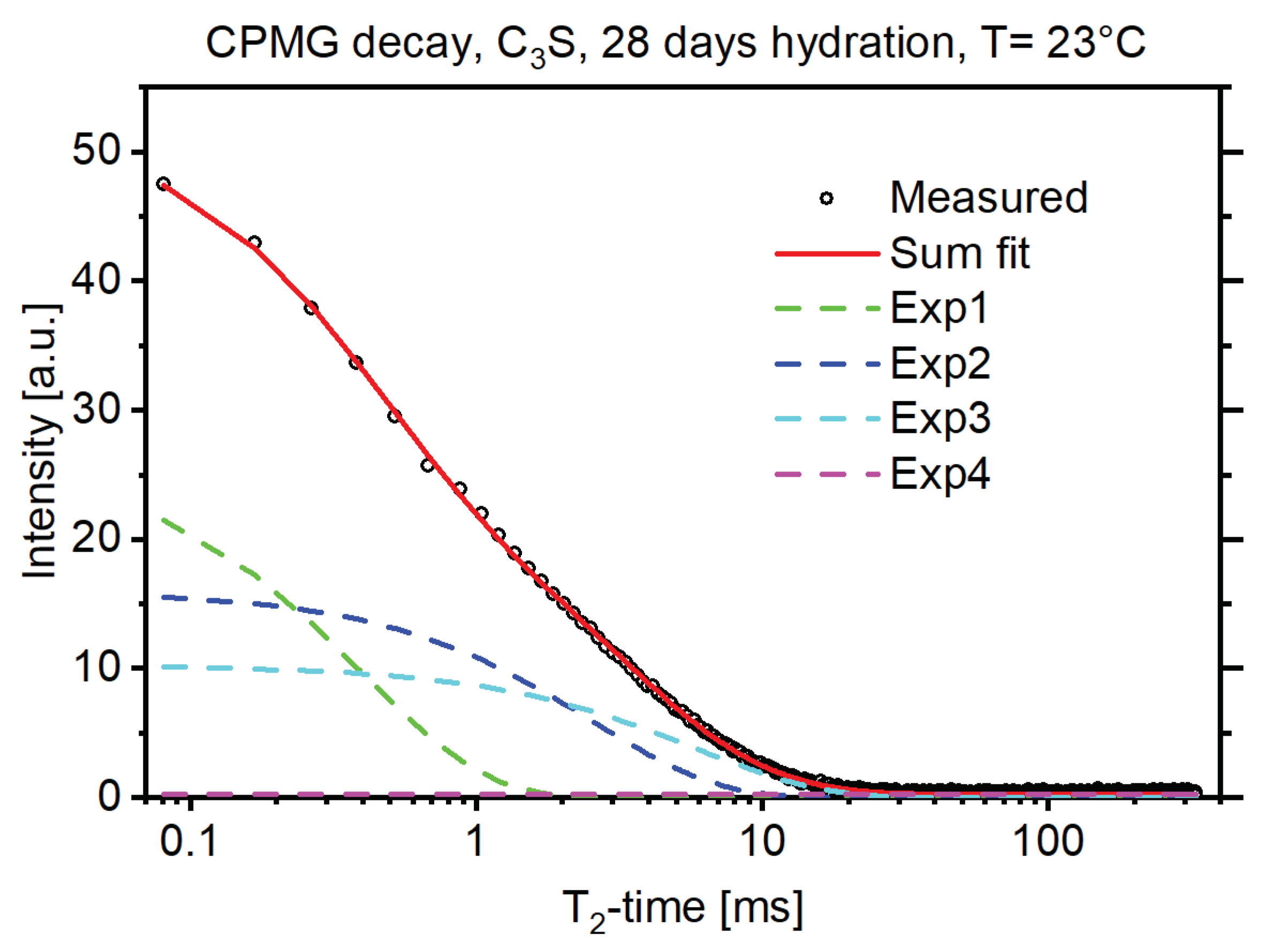
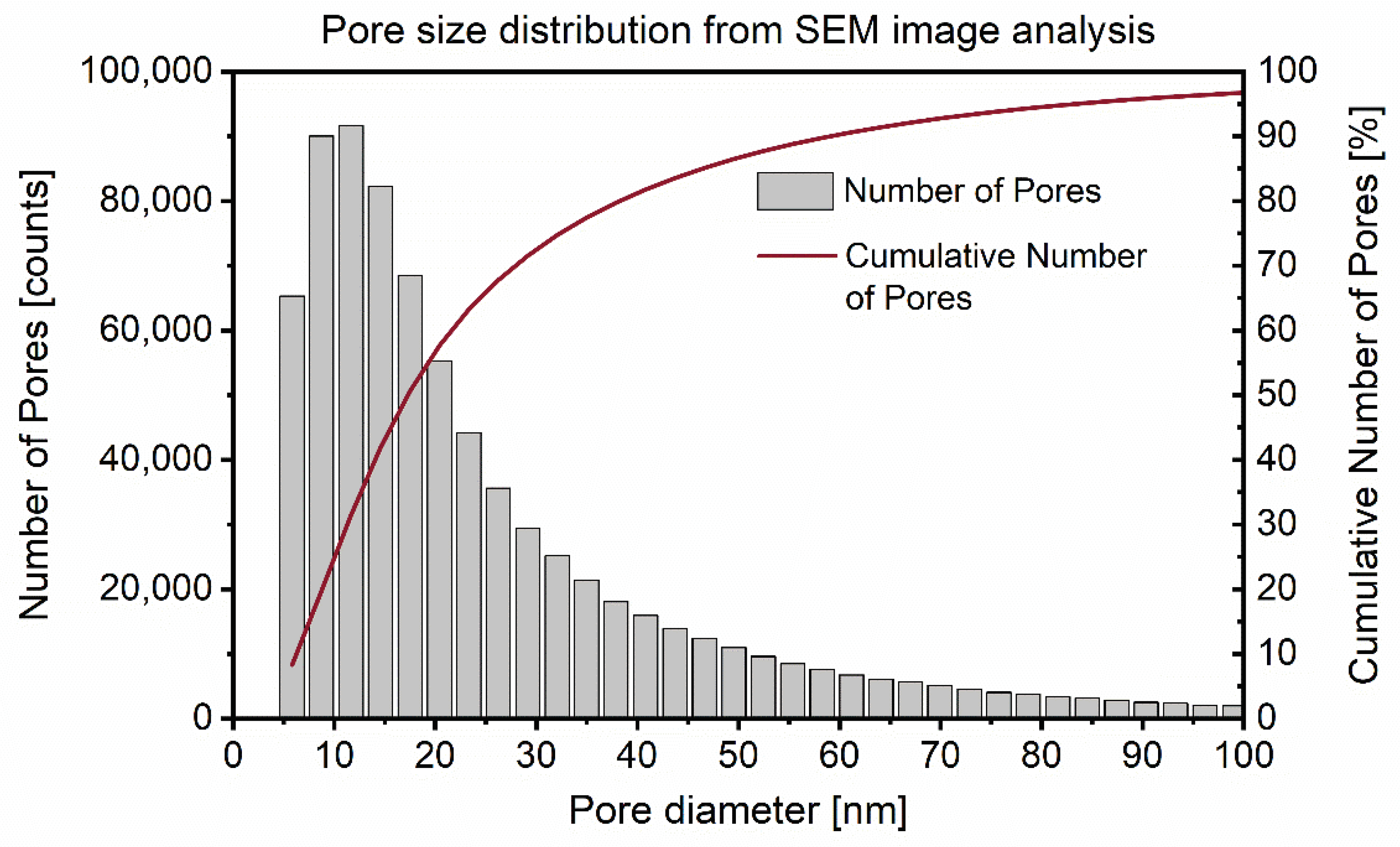
2.2.2. Combination of TD-NMR and SEM
3. Results and Discussion
3.1. Monolayer H2O Coverage Relaxation
3.2. Combination of SEM and TD-NMR
3.3. Comparison of the Two Methods Employed for Surface Relaxivity Calibration
4. Conclusions
- -
- The new method for the NMR surface relaxivity calibration presented in this work relies on a combined analysis of SEM images and 1H-TD-NMR measurements.
- -
- Argon broad ion beam sectioning allowed us to preserve and image the interhydrate pore space of hydrated tricalcium silicate with high resolution.
- -
- The acquired results were comparable to the results obtained by an already established drying method, assuming monolayer H2O coverage.
- -
- In contrast to this established method, the new method presented does not solely rely on NMR measurements and assumptions about the physico-chemical conditions of the sample surface.
- -
- -
- Apart from being relevant for fundamental research, the method presented could also help in the design of new mortar and concrete formulations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Muller, A.C.A.; Scrivener, K.L. A reassessment of mercury intrusion porosimetry by comparison with 1H NMR relaxometry. Cem. Concr. Res. 2017, 100, 350–360. [Google Scholar] [CrossRef]
- Zhang, J.; Scherer, G.W. Comparison of methods for arresting hydration of cement. Cem. Concr. Res. 2011, 41, 1024–1036. [Google Scholar] [CrossRef]
- Muller, A.C.A.; Scrivener, K.L.; Gajewicz, A.M.; McDonald, P.J. Use of bench-top NMR to measure the density, composition and desorption isotherm of C-S-H in cement paste. Microporous Mesoporous Mater. 2013, 178, 99–103. [Google Scholar] [CrossRef]
- McDonald, P.J.; Rodin, V.; Valori, A. Characterisation of intra-and inter-C-S-H gel pore water in white cement based on an analysis of NMR signal amplitudes as a function of water content. Cem. Concr. Res. 2010, 40, 1656–1663. [Google Scholar] [CrossRef]
- Ectors, D.; Goetz-Neunhoeffer, F.; Hergeth, W.D.; Dietrich, U.; Neubauer, J. In situ 1H-TD-NMR: Quantification and microstructure development during the early hydration of alite and OPC. Cem. Concr. Res. 2016, 79, 366–372. [Google Scholar] [CrossRef]
- Jansen, D.; Naber, C.; Ectors, D.; Lu, Z.; Kong, X.-M.; Goetz-Neunhoeffer, F.; Neubauer, J. The early hydration of OPC investigated by in-situ XRD, heat flow calorimetry, pore water analysis and1H NMR: Learning about adsorbed ions from a complete mass balance approach. Cem. Concr. Res. 2018, 109. [Google Scholar] [CrossRef]
- Brownstein, K.R.; Tarr, C.E. Importance of classical diffusion in NMR studies of water in biological cells. Phys. Rev. A. 1979, 19, 2446–2453. [Google Scholar] [CrossRef]
- Cohen, M.H.; Mendelson, K.S. Nuclear magnetic relaxation and the internal geometry of sedimentary rocks. J. Appl. Phys. 1982, 53, 1127–1135. [Google Scholar] [CrossRef]
- Desbois, G.; Urai, J.L.; Kukla, P.A.; Konstanty, J.; Baerle, C. High-resolution 3D fabric and porosity model in a tight gas sandstone reservoir:A new approach to investigate microstructures from mm-to nm-scale combining argon beam cross-sectioning and SEM imaging. J. Pet. Sci. Eng. 2011, 78, 243–257. [Google Scholar] [CrossRef]
- McDonald, P.J.; Gajewicz, A.M.; Morrell, R. The characterisation of cement based materials using T2 1H nuclear magnetic resonance relaxation analysis. 2017. Available online: http://eprintspublications.npl.co.uk/7365/ (accessed on 9 April 2020).
- Yermakou, V. Study of the transport of water in the nanopores of C-S-H by 1H NMR. Ph.D. Thesis, Department of Mechanical Engineering and Sciences, University of Surrey, Guildford, UK, 2017. [Google Scholar]
- D’Orazio, F.; Bhattacharja, S.; Halperin, W.P.; Eguchi, K.; Mizusaki, T. Molecular diffusion and nuclear-magnetic-resonance relaxation of water in unsaturated porous silica glass. Phys. Rev. B. 1990, 42, 9810–9818. [Google Scholar] [CrossRef] [PubMed]
- Powles, J.G.; Strange, J.H. Zero time resolution nuclear magnetic resonance transient in solids. Proc. Phys. Soc. 1963, 82, 6–15. [Google Scholar] [CrossRef]
- Carr, H.Y.; Purcell, E.M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 1954, 94, 630–638. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 1958, 29, 688–691. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Elevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Kleiner, F. GitHub Profile. 2019. Available online: https://github.com/kleinerELM/supported_manual_segmentation (accessed on 9 April 2020).
- Phansalkar, N.; More, S.; Sabale, A.; Joshi, M. Adaptive local thresholding for detection of nuclei in diversity stained cytology images. In Proceedings of the ICCSP 2011: International Conference on Communications and Signal Processing, Calicut, India, 10–12 February 2011; pp. 218–220. [Google Scholar] [CrossRef]
- Torquato, S. Random Heterogeneous Materials; Springer New York: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Möser, B.; Rössler, C.; Ludwig, H.-M. Recent Developments in Analytical SEM Techniques Combined with Focused Ion Beam Sectioning to Image the 3D Nanostructure of Hydrated Cements. In Proceedings of the 15th International Congress on the Chemistry of Cement (ICCC 2019), Prague, Czech Republic, 16–20 September 2019. [Google Scholar]
- Etzold, M.A.; McDonald, P.J.; Routh, A.F. Growth of sheets in 3D confinements—A model for the C-S-H meso structure. Cem. Concr. Res. 2014, 63, 137–142. [Google Scholar] [CrossRef]
- Nguyen-Tuan, L.; Etzold, M.A.; Rößler, C.; Ludwig, H.-M. Growth and porosity of C-S-H phases using the sheet growth model. Cem. Concr. Res. 2020, 129, 105960. [Google Scholar] [CrossRef]
| Oxides [wt.%] | C3S |
|---|---|
| SiO2 | 26.5 |
| TiO2 | 0.03 |
| Al2O3 | 0.34 |
| Fe2O3 | 0.07 |
| Mn2O3 | 0.02 |
| MgO | 2.02 |
| CaO | 70.3 |
| Na2O | 0.04 |
| K2O | 0.03 |
| P2O5 | 0.13 |
| LOI | 0.46 |
| ∑ [wt.%] | 99.8 |
| H Reservoir | H Fraction [at. %] | T2 [µs] |
|---|---|---|
| Portlandite (CH) | 18.4 ± 0.3 | 14.1 ± 0.1 |
| C-S-H interlayer | 40.8 ± 0.2 | 407 ± 10 |
| C-S-H gel pores | 24.5 ± 0.2 | 2694 ± 110 |
| Interhydrate pores | 15.9 ± 0.3 | 6089 ± 151 |
| Calibration Method | Surface Relaxivity [nm/µs] | C-S-H Interlayer [nm] | C-S-H Gel Pores [nm] | Interhydrate Pores [nm] |
|---|---|---|---|---|
| Monolayer H2O coverage | 9.0 × 10−4 | 0.72 | 4.9 | 33 |
| Combination SEM-NMR | 1.49 × 10−3 | 1.2 | 8.1 | 54 |
| From Muller et al. [3] | 3.73 × 10−3 | 0.94 | 3.1 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naber, C.; Kleiner, F.; Becker, F.; Nguyen-Tuan, L.; Rößler, C.; Etzold, M.A.; Neubauer, J. C-S-H Pore Size Characterization Via a Combined Nuclear Magnetic Resonance (NMR)–Scanning Electron Microscopy (SEM) Surface Relaxivity Calibration. Materials 2020, 13, 1779. https://doi.org/10.3390/ma13071779
Naber C, Kleiner F, Becker F, Nguyen-Tuan L, Rößler C, Etzold MA, Neubauer J. C-S-H Pore Size Characterization Via a Combined Nuclear Magnetic Resonance (NMR)–Scanning Electron Microscopy (SEM) Surface Relaxivity Calibration. Materials. 2020; 13(7):1779. https://doi.org/10.3390/ma13071779
Chicago/Turabian StyleNaber, Christoph, Florian Kleiner, Franz Becker, Long Nguyen-Tuan, Christiane Rößler, Merlin A. Etzold, and Jürgen Neubauer. 2020. "C-S-H Pore Size Characterization Via a Combined Nuclear Magnetic Resonance (NMR)–Scanning Electron Microscopy (SEM) Surface Relaxivity Calibration" Materials 13, no. 7: 1779. https://doi.org/10.3390/ma13071779
APA StyleNaber, C., Kleiner, F., Becker, F., Nguyen-Tuan, L., Rößler, C., Etzold, M. A., & Neubauer, J. (2020). C-S-H Pore Size Characterization Via a Combined Nuclear Magnetic Resonance (NMR)–Scanning Electron Microscopy (SEM) Surface Relaxivity Calibration. Materials, 13(7), 1779. https://doi.org/10.3390/ma13071779





