2.1. Anisotropic Continuum Plasticity
In order to describe the elastic-plastic deformation of a material, we introduce the strain tensor
that describes the deformation of the material and the stress tensor
that describes the forces acting on the surface of the material. Note that tensorial quantities with rank
are typeset in bold letters, whereas scalar quantities are represented by standard characters. In the elastic regime, Hooke’s law is used as constitutive relation between stress and strain, such that
where
is the fourth-rank elasticity tensor of the material. To describe plastic deformation, the yield function of the material is introduced as
which takes negative values if the equivalent stress
is smaller than the yield strength
of the material, i.e., in the elastic regime. When
plastic yielding sets in, and in case of work hardening,
should be considered as flow stress after this point. Since this work only deals with the onset of plastic yielding, ideal plasticity will be assumed throughout, such that
is a constant, irrespective of the deformation history of the material. Denoting the principal stresses of the stress tensor
as
with
, the equivalent stress takes the form
which—following the definition of von Mises (see, e.g., the translation of the original work by D. H. Delphenich [
20])—is based on the second invariant of the stress deviator (J2). In conjunction with the yield function of Equation (
2), it describes the onset of plastic yielding for isotropic materials. Note that the formulation in Equation (
3) is intrinsically independent of hydrostatic stress components
and thus does not require to explicitly calculate the deviatoric stress
where
is the unit tensor. By this definition of the equivalent stress, it is inherently assumed that hydrostatic stress components do not affect the plastic flow behavior of the considered material, which is typically fulfilled for metals, but not for polymers or rocks, such that the method formulated here, will mainly apply to metallic materials or, more generally, to materials, where hydrostatic stresses do not influence the plastic behavior.
As described in the introduction, many materials exhibit a directionally dependent yield strength, such that anisotropic flow rules need to be introduced. A first definition of such anisotropic flow rules was introduced by Hill [
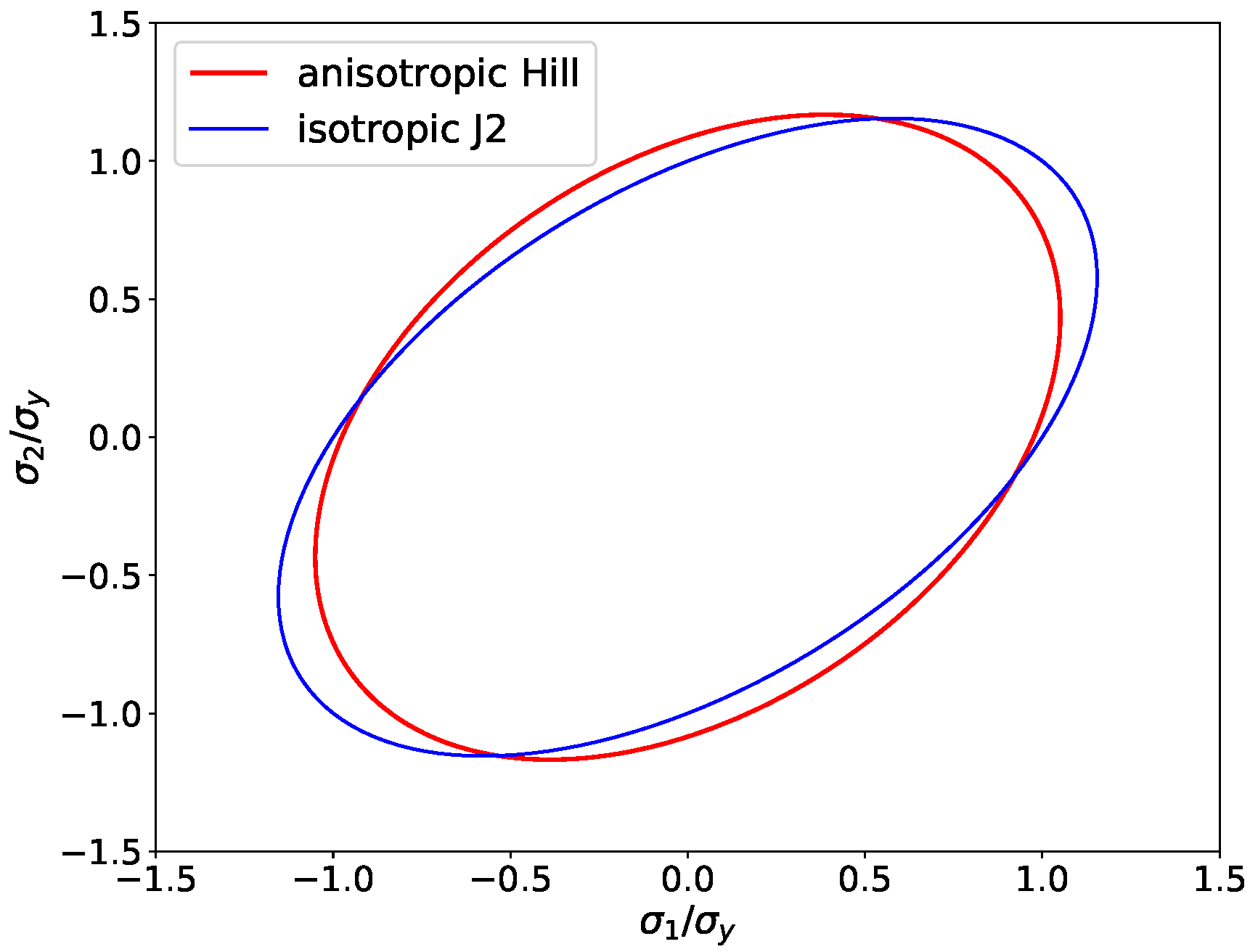
2], who used a generalized definition of the equivalent stress to achieve a directionally dependent mapping of the equivalent stresses to maintain a constant yield strength. Hence, in this formulation, the anisotropy is considered in the stress rather than in the yield strength. Since the mathematical formulations in this work are purely based on principal stresses, we use a simplified version of the Hill definition and introduce a Hill-like anisotropic definition of the equivalent stress as
with only three material parameters
and
, whereas in his original work, Hill introduced three more parameters for an orthotropic material to scale also the shear stress components. Since for orthotropic materials loaded along the main material axes there is no mutual influence of shear and normal components of stress and strain, the formulation introduced here is restricted to loading situations that only produce normal stresses and strains, and where consequently all off-diagonal components of stress and strains tensors remain zero. Furthermore, it is assumed that the loading axes and the main axes of the orthotropic material coincide. Hence, this formalism is currently only valid for a small subset of loading conditions for materials with orthotropic flow anisotropy. The definition of the equivalent stress following Hill can be considered as a generalization of the J2 equivalent stress, because for isotropy, i.e.,
, both definitions are equal.
The restrictions applied in this work, allow the mathematical notation to be simplified by only considering principal stresses. In future work, it is intended to render the formulation more general by exploiting that for any stress state, there exists a coordinate system in which the given stress tensor becomes a diagonal tensor composed of the principal stresses
. This coordinate system is given by the eigenvectors of the stress, representing the principal directions, such that the coordinate system of the original stress tensor—and with it the material axes—can be rotated into the coordinate system of the eigenvectors of the stress tensor. In this orientation the stress tensor becomes a diagonal tensor, and Equation (
5) can be evaluated with parameters
in the rotated state of the material axes.
The thus defined yield function can be used to determine whether a given stress state results in a purely elastic or rather in an elastic-plastic deformation of a material. The condition
relates stresses lying on a specific hyperplane in stress space, the so-called the yield-locus. Since a material does not sustain any stresses larger than the yield stress (for ideal plasticity) or the flow stress (in case of work hardening), acceptable stress states either produce a negative value of the yield function (elasticity) or lie on the yield locus (plasticity), which should be a convex hull of the elastic stress states. Hence, if a predictor step in finite element analysis (FEA) produces a stress outside the yield locus, a plastic strain increment must be calculated that leads again to an accepted stress state on the yield locus. The return mapping algorithm to calculate such strain increments has been described in many text books on continuum plasticity and non-linear FEA, such that here only a very brief summary based on [
1] is reproduced. According to the Prandtl–Reuss flow rule, the plastic strain increment for a given time step can be calculated as
where
is the normal vector to the yield locus, defined by the gradient of the yield function
, and
is the so-called plastic strain multiplier that can be evaluated as
where
is the total strain increment of the FEA predictor step that leads to a stress state outside the yield locus and which is consequently decomposed into the plastic strain increment, given by Equation (
6), and the elastic strain increment or stress increment given by
with the tangent stiffness tensor
where “⊗” denotes the tensorial product in the form
.
The gradient of the yield function with respect to the principal stresses can be evaluated analytically as
Note that in the case of isotropic plasticity (
), the gradient takes the simple form
This section served the purpose to introduce the main physical quantities in the notation used in this work. For further details of continuum plasticity or FEA, the reader is referred to standard textbooks, as for example [
1]. In the following, the formalism for the data-oriented constitutive model based on a machine learning (ML) yield function is laid out.
2.2. Stress Space in Cylindrical Coordinates
Since plastic deformation in most metals does not depend on hydrostatic stress components, it is useful to transform principal stresses from their representation as a 3-dimensional (3D) Cartesian vector of principal stresses
into a cylindrical coordinate system with
, where the equivalent stress
represents the norm of the stress deviator
, and the polar angle
lies in the deviatoric plane normal to the hydrostatic axis
p, which has already been used by Hill [
2]. This coordinate transformation improves the efficiency of the training, because only two-dimensional data for the equivalent stress and the polar angle need to be used as training features, whereas the hydrostatic component is disregarded. Hence, by exploiting basic physical principles, we effectively reduce the dimensionality of the problem from 6 independent components of an arbitrary stress tensor to 2 degrees of freedom, without loosing the generality of the formulation. As the polar angle
can be considered a generalized Lode angle [
21], it is noted that the Lode angle, by definition, describes the axiality of a loading state in a way that uniaxial loads in different directions result in the same Lode angle. Since our formulation aims at describing anisotropy in the plastic deformation, uniaxial stresses in different directions must possess different angles. To achieve this, we introduce a complex-valued deviatoric stress
where
i is the imaginary unit, such that the polar angle
with the unit vectors
and
that span the plane normal to the hydrostatic axis
.
To transform the gradient of the yield function from this cylindrical stress space back to the principle stress space, in which form it is used to calculate the direction of the plastic strain increments in the return mapping algorithm of the plasticity model, we introduce the Jacobian matrix for this coordinate transformation as
where
is given in Equation (
10),
and
With this Jacobian, the gradient can be calculated as
2.3. Data-Oriented Yield Function
While the concept of mapping the equivalent stress in describing anisotropic flow behavior has been applied successfully in the approaches of Hill [
2,
3] and Barlat [
4], for a data-oriented yield function, it is impracticable to calculate the necessary parameters for this stress mapping explicitly. Hence, it is of advantage to reformulate the flow rule in such a way that the yield strength is considered to be directionally dependent, whereas the equivalent stress is formulated in an objective way, without prior knowledge of the material behavior. This is achieved by using the J2 equivalent stress in the flow rule and formally considering the flow stress to be a function of the polar angle in the deviatoric plane, such that
A further advantage of this formulation is that the dependence of the yield function on the two degrees of freedom of the cylindrical stress notation is separated into two independent terms. Furthermore, for symmetry reasons, it is required that the yield strength is a periodic function of the polar angle with periodicity
. The gradient of the ML yield function w.r.t. the cylindrical coordinates reads
It is seen that in the cylindrical stress space
and
, under the condition that plasticity is independent of hydrostatic stress components. Hence, the only non-constant component of the gradient is
, which simplifies the numerical implementation of the method. For isotropic J2 plasticity,
, and in this case it is particularly easy to calculate the gradient and to see that the formulations in both coordinate systems result in the same gradient. The transformation of this gradient into the principal stress space is achieved by multiplication with the Jacobian, according to Equation (
16).
To establish a data-oriented formulation, we introduce a yield function in the form of a machine learning (ML) algorithm, rather than in a mathematically closed form with a number of model parameters that need to be fitted to the data. This enables us to use the available data directly for the training of the ML algorithm. Furthermore, ML methods allow for the use of higher dimensional feature vectors such that in future work, information about the material properties and the microstructure of the material can be directly used as input into one single ML yield function able to handle different microstructures.
In this work, Support Vector Classification (SVC) is applied to categorize data sets consisting of principal stresses into the classes “elastic” and “plastic”. During training, SVC constructs a hyperplane in stress space, which separates the two regions from each other. Consequently, this hyperplane, defined by the zeros of the so-called SVC decision function, is the equivalent to the yield locus, defined by the zeros of the yield function, and it is constructed such that it has the largest distance to the nearest training data points of both classes. The SVC decision function is defined as [
15]
where
n is the number of support vectors identified during the training process and
is the radial basis function (RBF) kernel of the SVC, which is well suited for non-linear problems, with the parameter
that determines how fast the influence of one support vector decays in stress space. The support vectors
, the dual coefficients
, and the intercept
are determined during the training. There are essentially two parameters that control the training process and thus the quality of the obtained decision function: (i)
is a parameter of the RBF kernel function and controls how far-reaching the influence of each support vector is: the larger the value of
, the more short-ranged and local the influence; (ii)
is a parameter that is used only during the training to regularize the decision function, but that does not directly enter the decision function (
18). The larger the value of
C, the more flexible but irregular the decision function will become by approximating the shape of the training data more accurately. The choice if these training parameters is critical for the successful use of the decision function in a flow rule. In short, the larger both values are, the more flexible and sensitive to local values the resulting decision function will become. Thus, too small values will result in a smooth but not accurate approximation of the true yield function, whereas too large values will result in a noisy yield function that cannot be used in FEA. The numerical example presented later on will demonstrate this effect and provide examples for values producing accurate yet sufficiently smooth results for the yield function.
For the supervised training, a set of
feature vectors
has to be provided together with the result vector
with
, which takes values only in two categories:
for those training data points
in the “elastic” regime and
for training data in the “plastic” regime. This training data are within the core of the method outlined here, because during the training process they are directly used to define the support vectors that in turn determine the plastic properties of the material. It is, therefore, essential to have sufficiently many training data points in close proximity to the yield locus to approximate it accurately. However, the SVC training will create support vectors only in the region covered by the training data, and outside this region the decision function drops to zero, which could produce erroneous results if the elastic predictor step of the return mapping algorithm falls into such a region. Hence, data points that lie deeper within the elastic and plastic regions are required to prevent the decision function (
18) from falling back to zero. Such data points, however, can be constructed from available raw data lying close to the yield locus simply by linearly scaling principal stresses in the elastic region towards smaller values, such that they stay within the elastic region, and, likewise in the plastic region, scaling principal stress data towards higher values. Thus, the raw data can be spread throughout the stress space, even without knowing the strain value associated with each data point. Only the knowledge of its class “elastic” or “plastic” is required as knowledge for this data extension step improving the training process. This property of the formalism introduced in this work is of critical importance, because it enables the creation of large volumes of training data from relatively few raw data points close to the yield locus, as demonstrated below.
As seen from Equation (
18), the decision function is a continuous function constructed in a way to reproduce this category, i.e., the sign of the training data in the respective regions in the optimal way. To make predictions about the elastic or plastic material behavior at any given stress, the sign of the value of the decision function
at the given stress is evaluated. Furthermore, the yield locus of the material can be obtained in the same way as for traditional yield functions, simply by finding the zeros of the continuous function. In this way, furthermore, the distance of any point in stress space to the yield locus can be evaluated, which is important for making efficient predictor steps during FEA and for calculating plastic strain increments for the return mapping algorithm. In particular, as described in the previous section, the gradient to the yield locus needs to be known in order to calculate plastic strain increments, that bring the stress back to the yield surface, because the plastic material does not support any stresses outside. Due to the definition of the ML yield function as convolution sum over the support vectors, the gradient to the SVC decision function can be calculated analytically as
with
The gradient of the yield function in the 3D principle stress space is obtained by multiplication of the gradient in the cylindrical stress space with the Jacobian defined in Equation (
14). Thus, the formulation of the data-oriented yield function based on the SVC algorithm can be used directly as ML yield function in FEA, with the same formalism for plasticity as for standard yield functions.