A Data-Driven Learning Method for Constitutive Modeling: Application to Vascular Hyperelastic Soft Tissues
Abstract
1. Introduction
2. Material and Methods
2.1. A GENERIC Approach to the Learning Procedure
2.2. Treatment of Dispersion and Noise in Data
2.3. Pseudo-Experimental Data—Learning a Visco-Hyperelastic Response
2.4. Learning the Constitutive Model of Porcine Carotid Tissue
3. Results
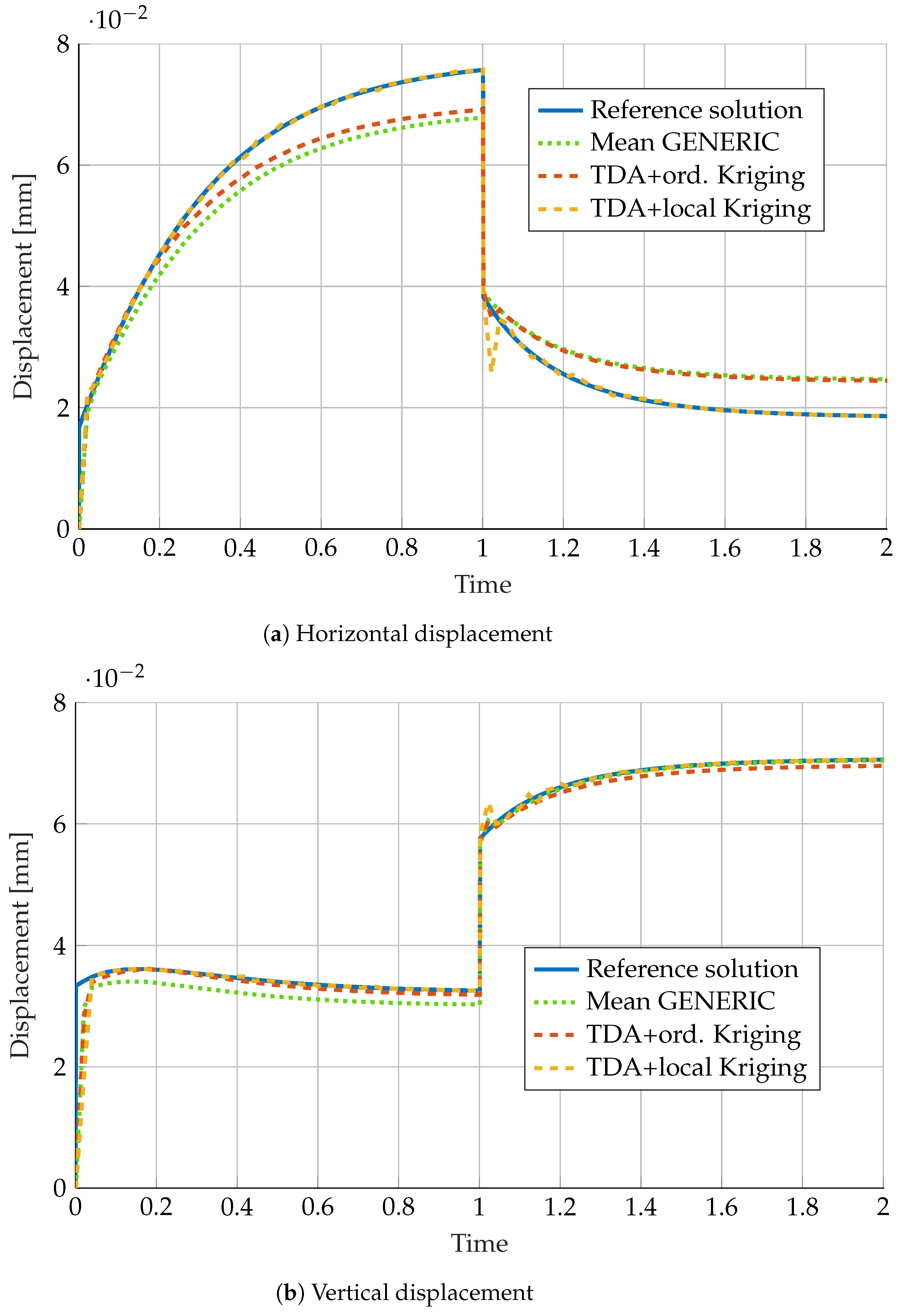
3.1. Numerical Fitting of the Pseudo-Experimental Data Set
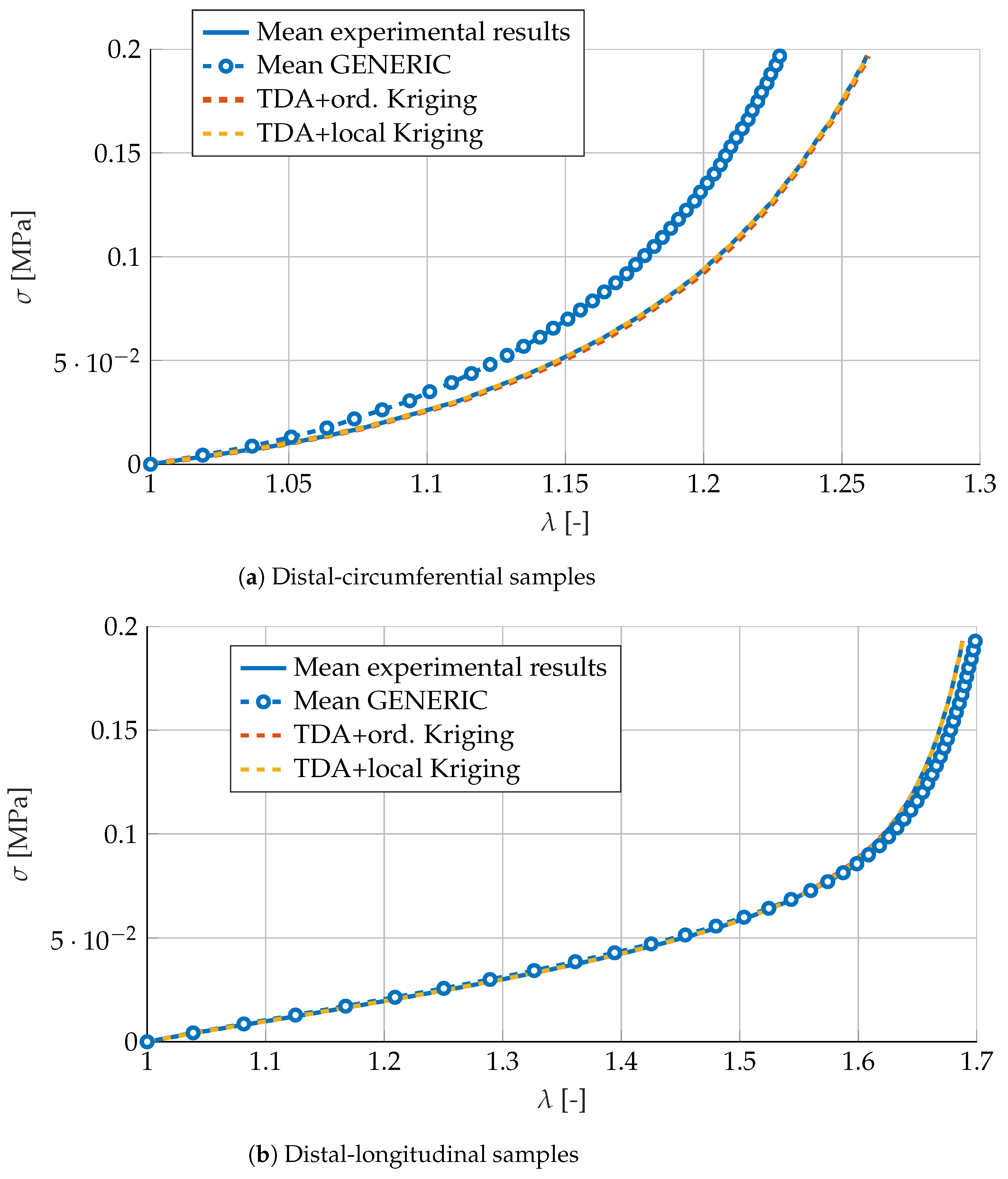
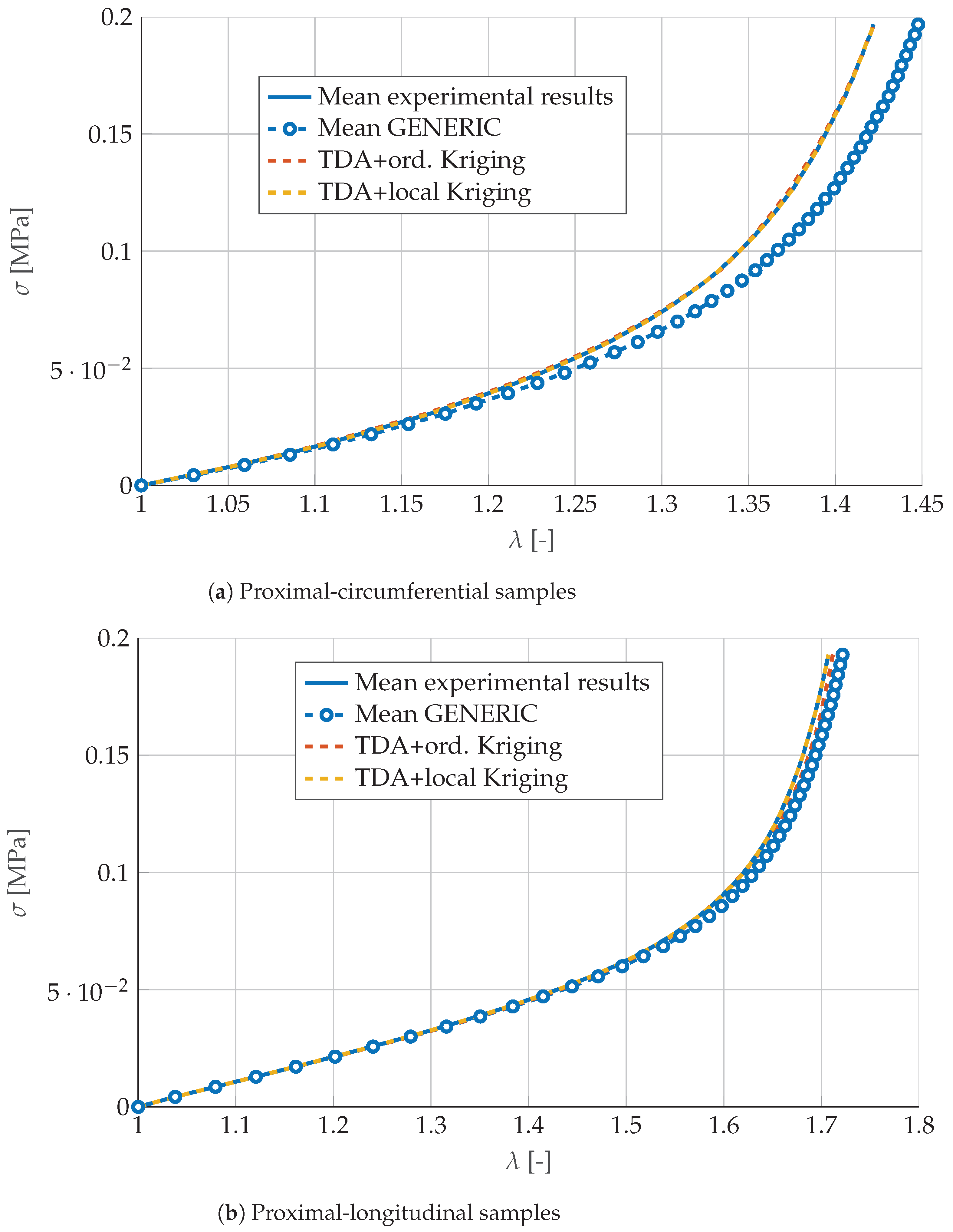
3.2. Numerical Fitting of Porcine Carotid Tissue
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kirchdoerfer, T.; Ortiz, M. Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 2016, 304, 81–101. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Bessa, M.; Liu, W.K. Self-consistent clustering analysis: An efficient multi-scale scheme for inelastic heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2016, 306, 319–341. [Google Scholar] [CrossRef]
- Ibañez, R.; Borzacchiello, D.; Aguado, J.V.; Abisset-Chavanne, E.; Cueto, E.; Ladeveze, P.; Chinesta, F. Data-driven non-linear elasticity: Constitutive manifold construction and problem discretization. Comput. Mech. 2017, 60, 813–826. [Google Scholar] [CrossRef]
- Latorre, M.; Montáns, F.J. What-You-Prescribe-Is-What-You-Get orthotropic hyperelasticity. Comput. Mech. 2014, 53, 1279–1298. [Google Scholar] [CrossRef]
- Bessa, M.; Bostanabad, R.; Liu, Z.; Hu, A.; Apley, D.W.; Brinson, C.; Chen, W.; Liu, W.K. A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Comput. Methods Appl. Mech. Eng. 2017, 320, 633–667. [Google Scholar] [CrossRef]
- Ibanez, R.; Abisset-Chavanne, E.; Aguado, J.V.; Gonzalez, D.; Cueto, E.; Chinesta, F. A manifold learning approach to data-driven computational elasticity and inelasticity. Arch. Comput. Methods Eng. 2018, 25, 47–57. [Google Scholar] [CrossRef]
- Latorre, M.; Peña, E.; Montáns, F.J. Determination and Finite Element Validation of the WYPIWYG Strain Energy of Superficial Fascia from Experimental Data. Ann. Biomed. Eng. 2017, 45, 799–810. [Google Scholar] [CrossRef]
- Cilla, M.; Martinez, J.; Pena, E.; Martínez, M.Á. Machine Learning Techniques as a Helpful Tool Toward Determination of Plaque Vulnerability. IEEE Trans. Biomed. Eng. 2012, 59, 1155–1161. [Google Scholar] [CrossRef]
- Kevrekidis, I.G.; Gear, C.W.; Hummer, G. Equation-free: The computer-aided analysis of complex multiscale systems. AIChE J. 2004, 50, 1346–1355. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data Driven Computing with noisy material data sets. Comput. Methods Appl. Mech. Eng. 2017, 326, 622–641. [Google Scholar] [CrossRef]
- Ayensa-Jiménez, J.; Doweidar, M.H.; Sanz-Herrera, J.A.; Doblaré, M. A new reliability-based data-driven approach for noisy experimental data with physical constraints. Comput. Methods Appl. Mech. Eng. 2018, 328, 752–774. [Google Scholar] [CrossRef]
- García, A.; Martínez, M.A.; Peña, E. Viscoelastic properties of the passive mechanical behavior of the porcine carotid artery: Influence of proximal and distal positions. Biorheology 2012, 49, 271–288. [Google Scholar] [CrossRef] [PubMed]
- García, A.; Peña, E.; Laborda, A.; Lostalé, F.; De Gregorio, M.; Doblaré, M.; Martínez, M. Experimental study and constitutive modelling of the passive mechanical properties of the porcine carotid artery and its relation to histological analysis: Implications in animal cardiovascular device trials. Med. Eng. Phys. 2011, 33, 665–676. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Pandolfi, A.; Holzapfel, G.A. Three-Dimensional Modeling and Computational Analysis of the Human Cornea Considering Distributed Collagen Fibril Orientations. J. Biomech. Eng. 2008, 130, 061006. [Google Scholar] [CrossRef]
- Peña, J.; Martínez, M.; Peña, E. A formulation to model the nonlinear viscoelastic properties of the vascular tissue. Acta Mech. 2011, 217, 63–74. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Sommer, G.; Gasser, C.T.; Regitnig, P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am. J. Physiol.-Heart Circ. Physiol. 2005, 289, H2048–H2058. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2005, 3, 15–35. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of arteries. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1551–1597. [Google Scholar] [CrossRef]
- Ibañez, R.; Abisset-Chavanne, E.; Gonzalez, D.; Duval, J.; Cueto, E.; Chinesta, F. Hybrid constitutive modeling: Data-driven learning of corrections to plasticity models. Int. J. Mater. Form. 2018, in press. [Google Scholar]
- Eggersmann, R.; Kirchdoerfer, T.; Reese, S.; Stainier, L.; Ortiz, M. Model-free data-driven inelasticity. Comput. Methods Appl. Mech. Eng. 2019, 350, 81–99. [Google Scholar] [CrossRef]
- Zhang, M.; Benítez, J.M.; Montáns, F.J. Capturing yield surface evolution with a multilinear anisotropic kinematic hardening model. Int. J. Solids Struct. 2016, 81, 329–336. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Sun, W. A deep learning approach to estimate chemically-treated collagenous tissue nonlinear anisotropic stress-strain responses from microscopy images. Acta Biomater. 2017, 63, 227–235. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Wang, J.X.; Wu, J.L.; Xiao, H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2017, 2, 034603. [Google Scholar] [CrossRef]
- Russo, A.; Durán-Olivencia, M.A.; Kevrekidis, I.G.; Kalliadasis, S. Deep learning as closure for irreversible processes: A data-driven generalized Langevin equation. arXiv 2019, arXiv:1903.09562. [Google Scholar]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620–6632. [Google Scholar] [CrossRef]
- Öttinger, H.C. Beyond Equilibrium Thermodynamics; John Wiley Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Pavelka, M.; Klika, V.; Grmela, M. Multiscale thermodynamics; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- González, D.; Chinesta, F.; Cueto, E. Thermodynamically consistent data-driven computational mechanics. Contin. Mech. Thermodyn. 2018. submitted. [Google Scholar]
- Gonzalez, D.; Chinesta, F.; Cueto, E. Learning corrections for hyperelastic models from data. Front. Mater. 2019, 6, 14. [Google Scholar] [CrossRef]
- Weinan, E. A Proposal on Machine Learning via Dynamical Systems. Commun. Math. Stat. 2017, 5, 1–11. [Google Scholar] [CrossRef]
- Li, Q.; Chen, L.; Tai, C.; Weinan, E. Maximum Principle Based Algorithms for Deep Learning. J. Mach. Learn. Res. 2018, 18, 1–29. [Google Scholar]
- Español, P. Statistical Mechanics of Coarse-Graining. In Novel Methods in Soft Matter Simulations; Karttunen, M., Lukkarinen, A., Vattulainen, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 69–115. [Google Scholar] [CrossRef]
- Lopez, E.; Gonzalez, D.; Aguado, J.V.; Abisset-Chavanne, E.; Cueto, E.; Binetruy, C.; Chinesta, F. A Manifold Learning Approach for Integrated Computational Materials Engineering. Arch. Comput. Methods Eng. 2016, 1–10. [Google Scholar] [CrossRef]
- Romero, I. A characterization of conserved quantities in non-equilibrium thermodynamics. Entropy 2013, 15, 5580–5596. [Google Scholar] [CrossRef]
- Wasserman, L. Topological Data Analysis. Annu. Rev. Stat. Its Appl. 2018, 5, 501–532. [Google Scholar] [CrossRef]
- Munch, E. A User’s Guide to Topological Data Analysis. J. Learn. Anal. 2017, 4, 47–61. [Google Scholar] [CrossRef]

| Mean GENERIC | 2.24% |
| Simple Kriging | 16.46% |
| Ordinary Kriging | 1.82% |
| Local Kriging | 0.38% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González, D.; García-González, A.; Chinesta, F.; Cueto, E. A Data-Driven Learning Method for Constitutive Modeling: Application to Vascular Hyperelastic Soft Tissues. Materials 2020, 13, 2319. https://doi.org/10.3390/ma13102319
González D, García-González A, Chinesta F, Cueto E. A Data-Driven Learning Method for Constitutive Modeling: Application to Vascular Hyperelastic Soft Tissues. Materials. 2020; 13(10):2319. https://doi.org/10.3390/ma13102319
Chicago/Turabian StyleGonzález, David, Alberto García-González, Francisco Chinesta, and Elías Cueto. 2020. "A Data-Driven Learning Method for Constitutive Modeling: Application to Vascular Hyperelastic Soft Tissues" Materials 13, no. 10: 2319. https://doi.org/10.3390/ma13102319
APA StyleGonzález, D., García-González, A., Chinesta, F., & Cueto, E. (2020). A Data-Driven Learning Method for Constitutive Modeling: Application to Vascular Hyperelastic Soft Tissues. Materials, 13(10), 2319. https://doi.org/10.3390/ma13102319







