Fracture Models and Effect of Fibers on Fracture Properties of Cementitious Composites—A Review
Abstract
1. Introduction
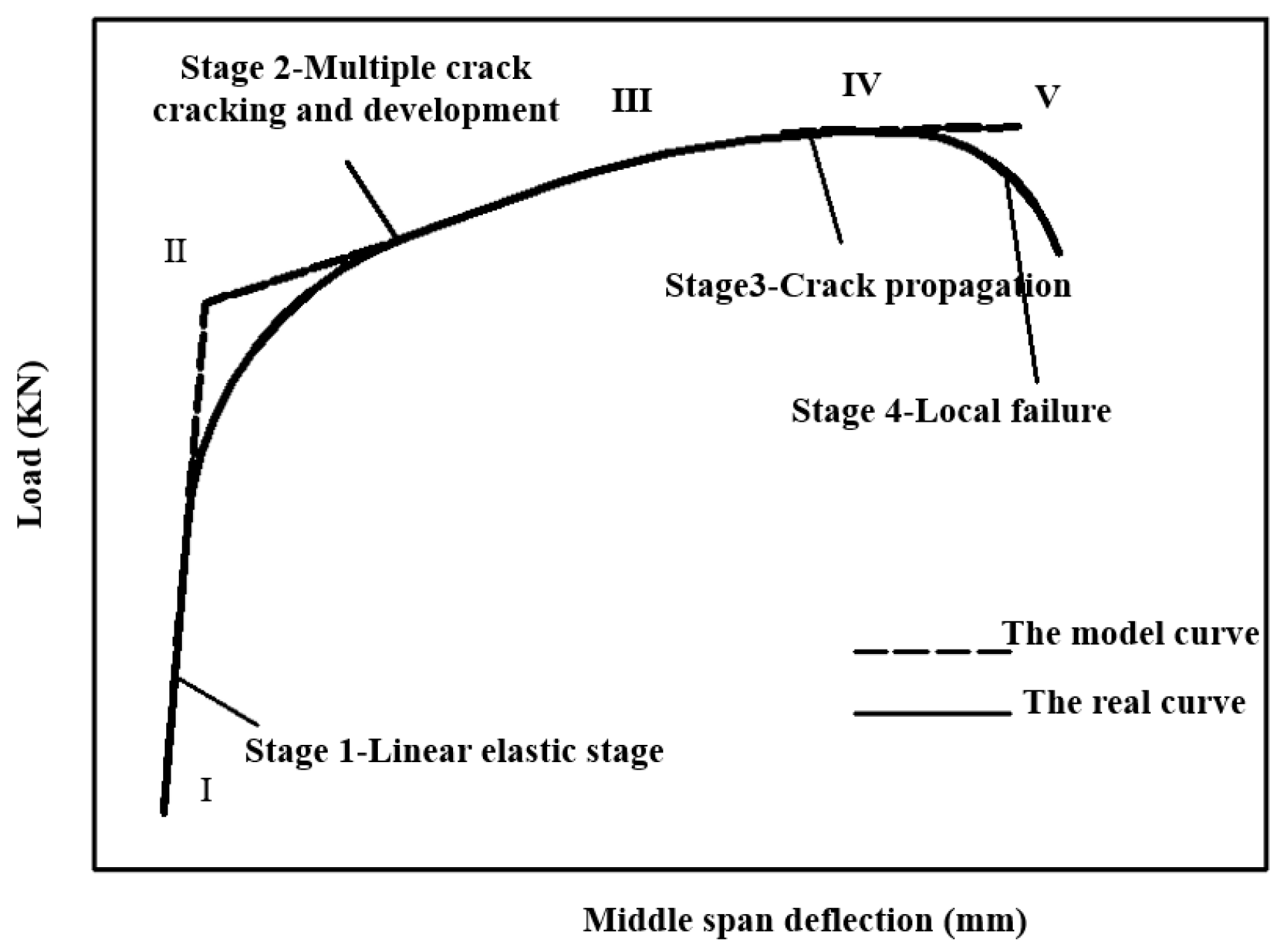
2. Fracture Models
2.1. ACK Model
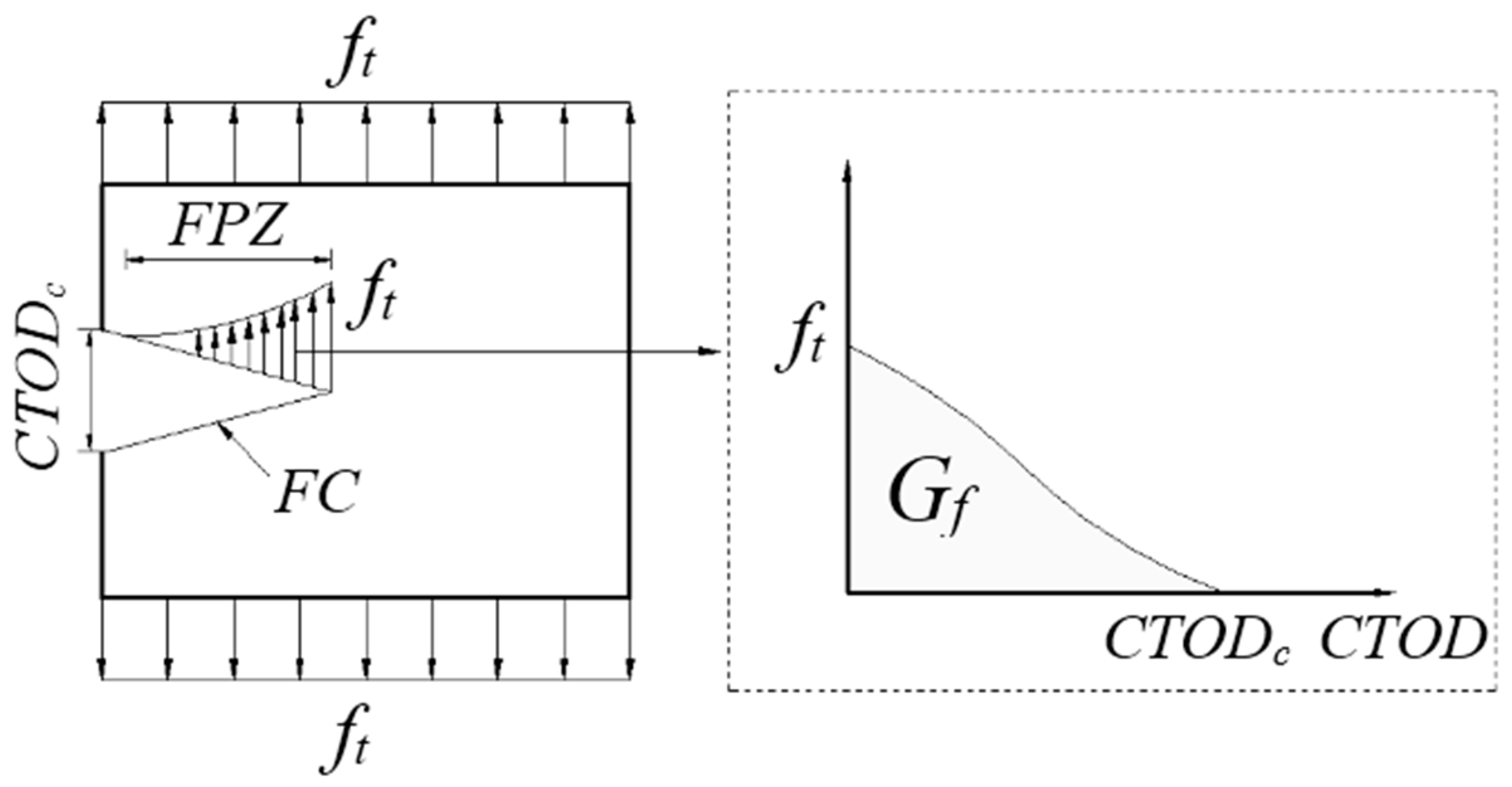
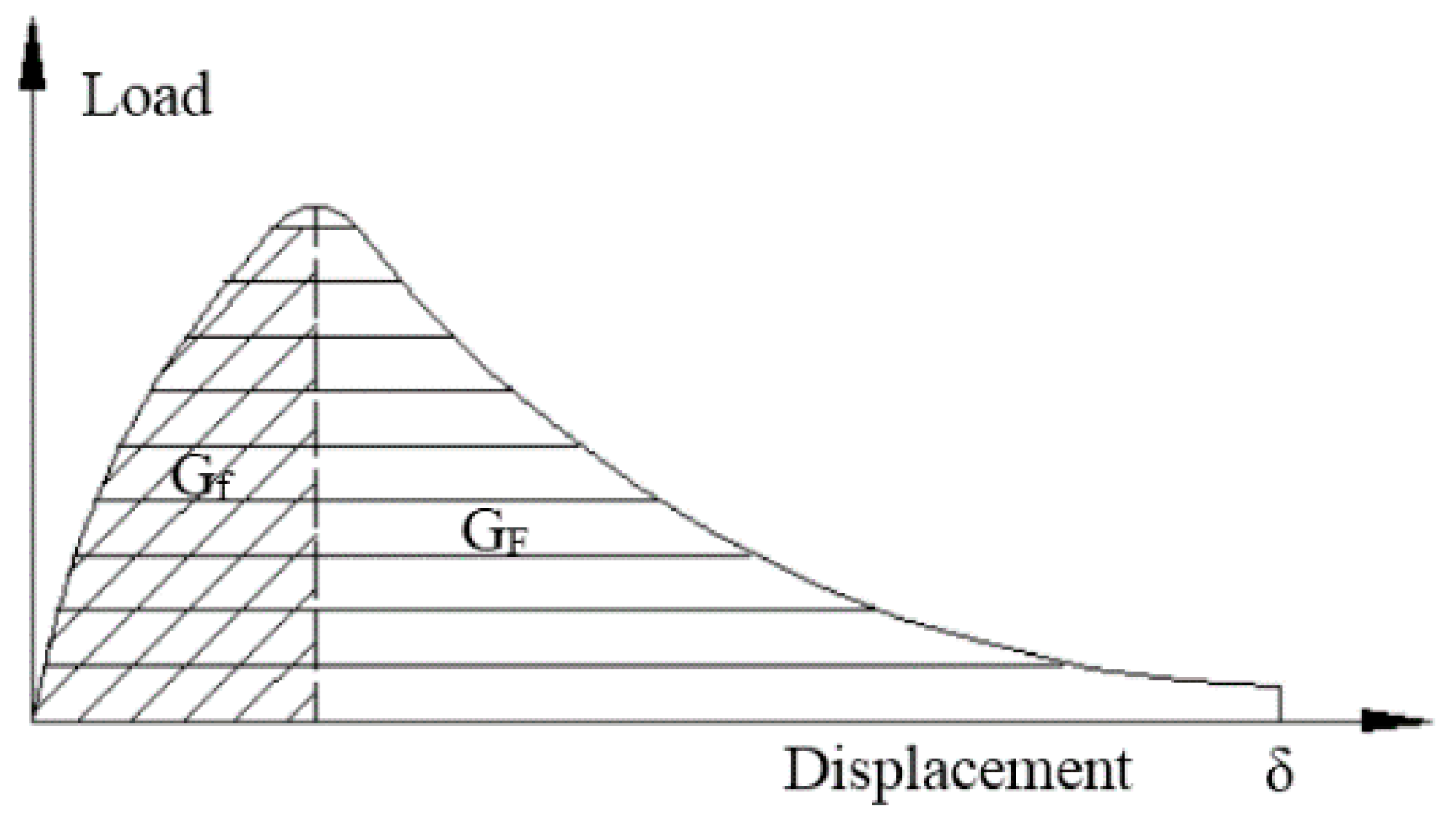
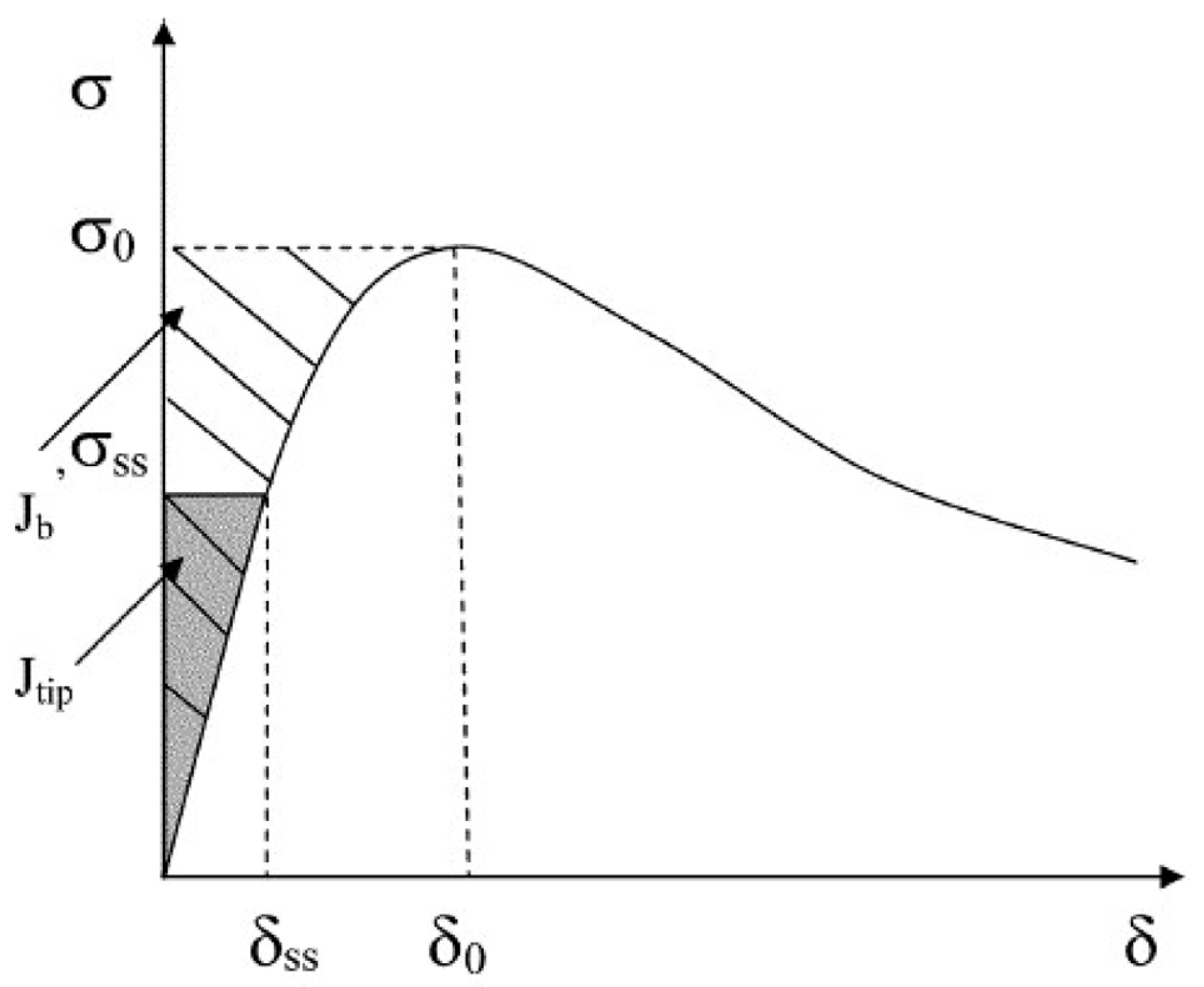
2.2. FC Model
2.3. CB Model
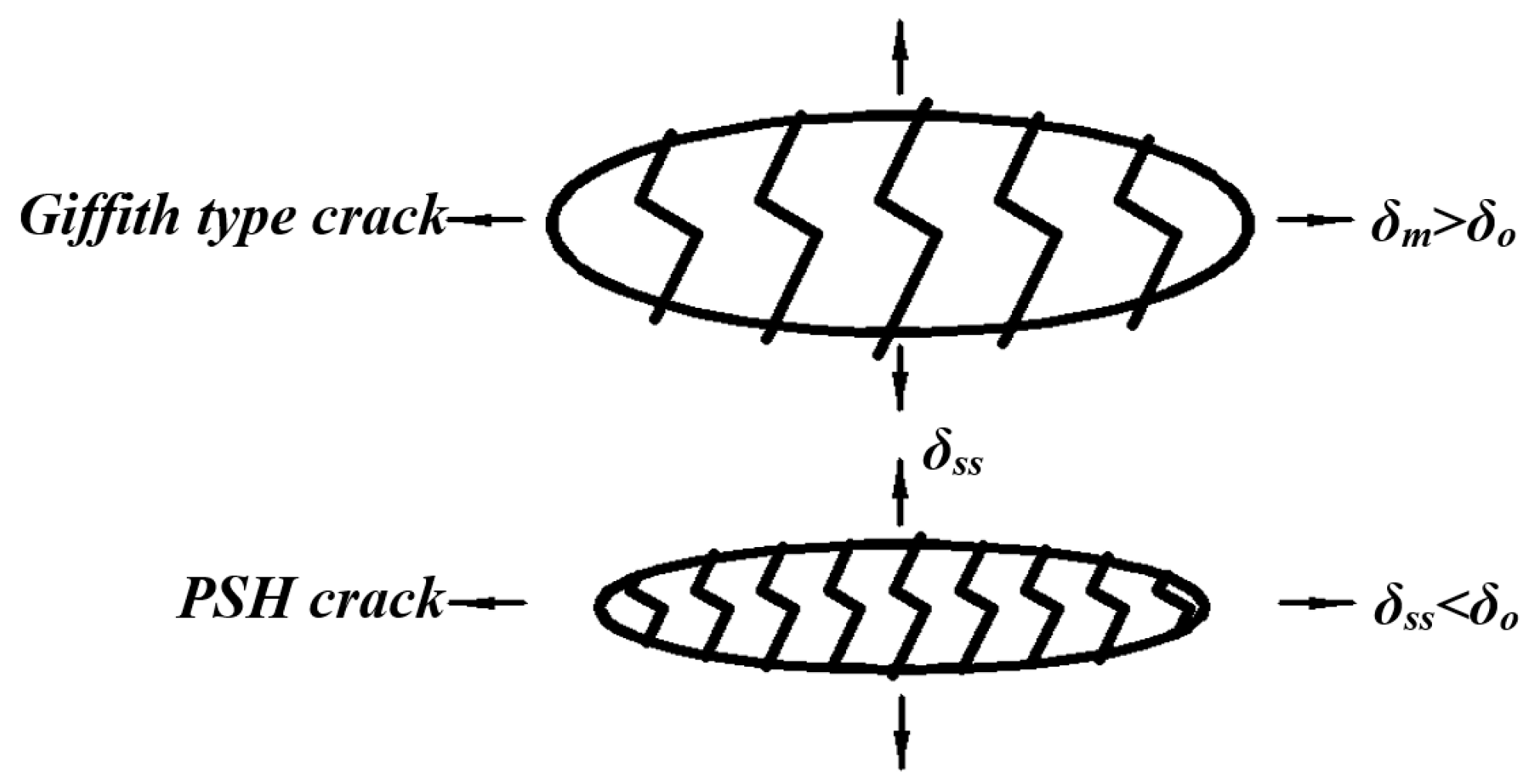
2.4. PSH Model
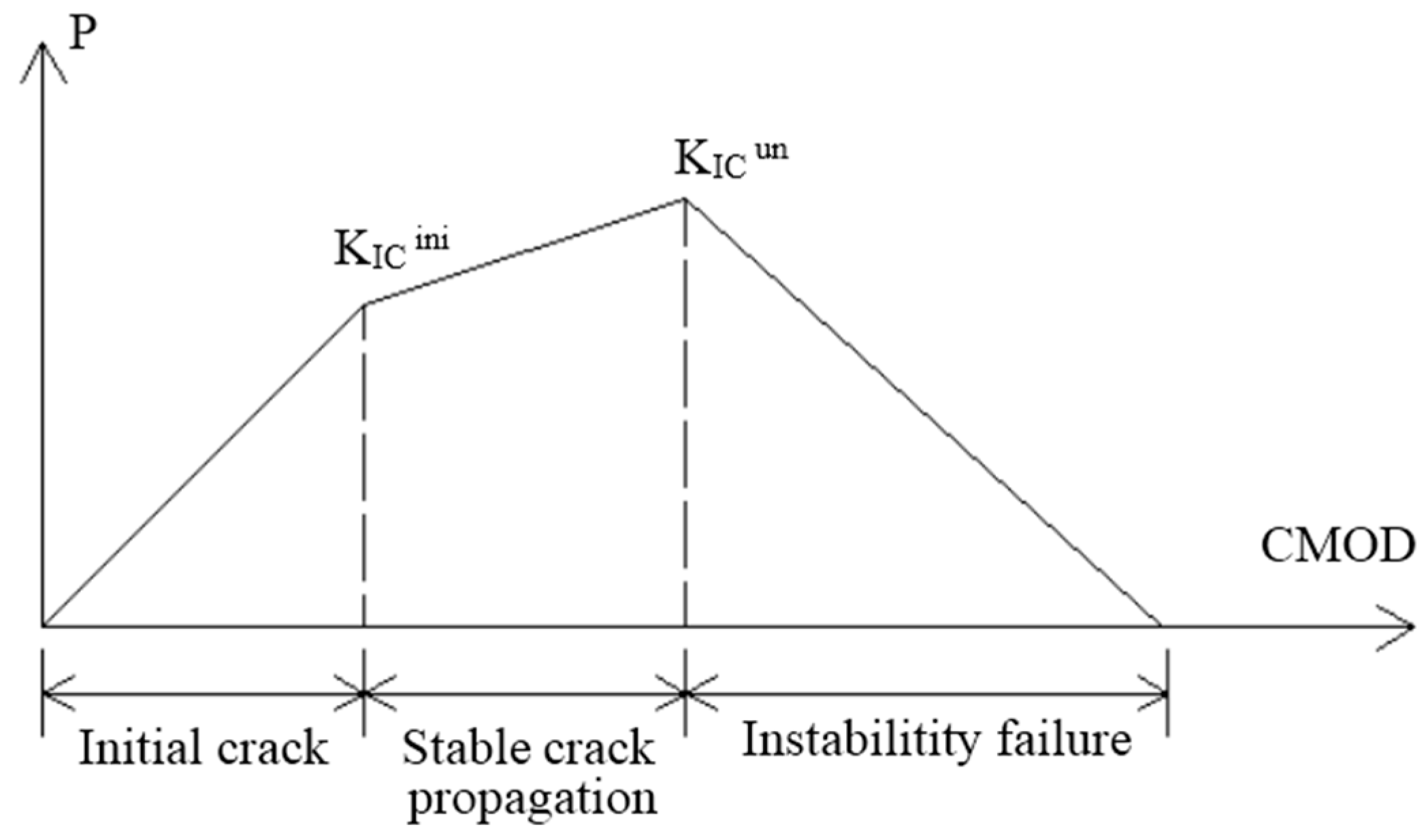
2.5. DKF Model
| Elastic Stage; No Crack | |
| Crack initiation | |
| Crack stable propagation | |
| Crack begins to destabilize and expand | |
| Crack instability propagation |
3. Effect of PVA Fiber on Fracture Properties
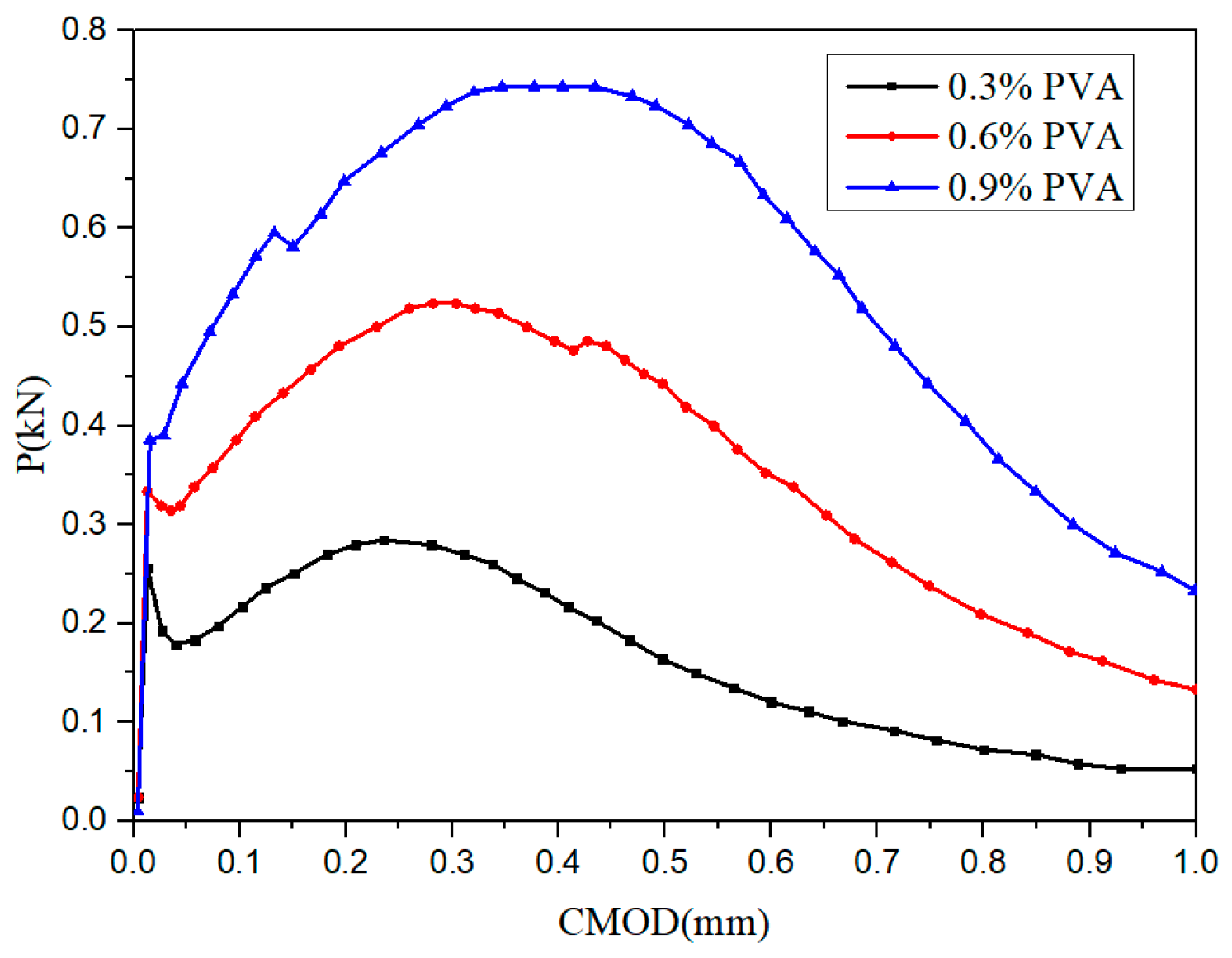
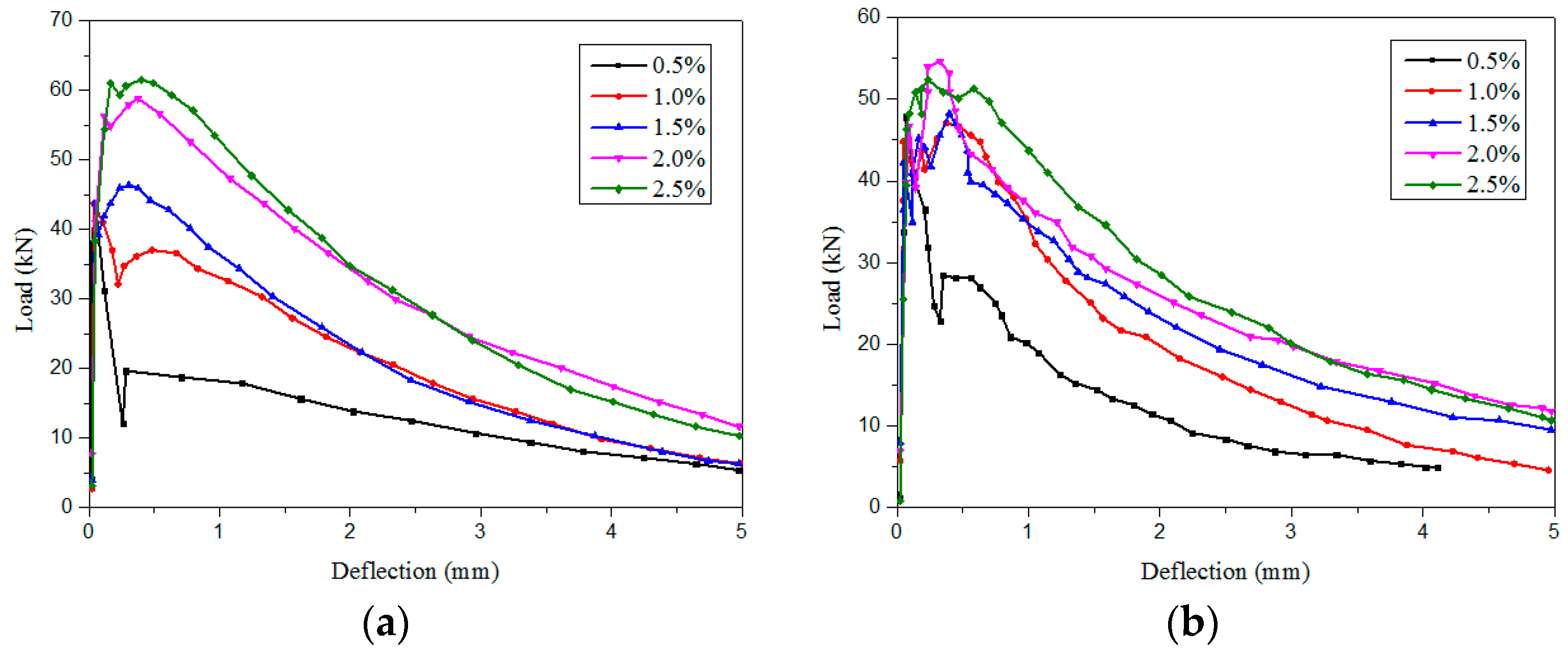
3.1. Effect of Fiber Content on Fracture Properties
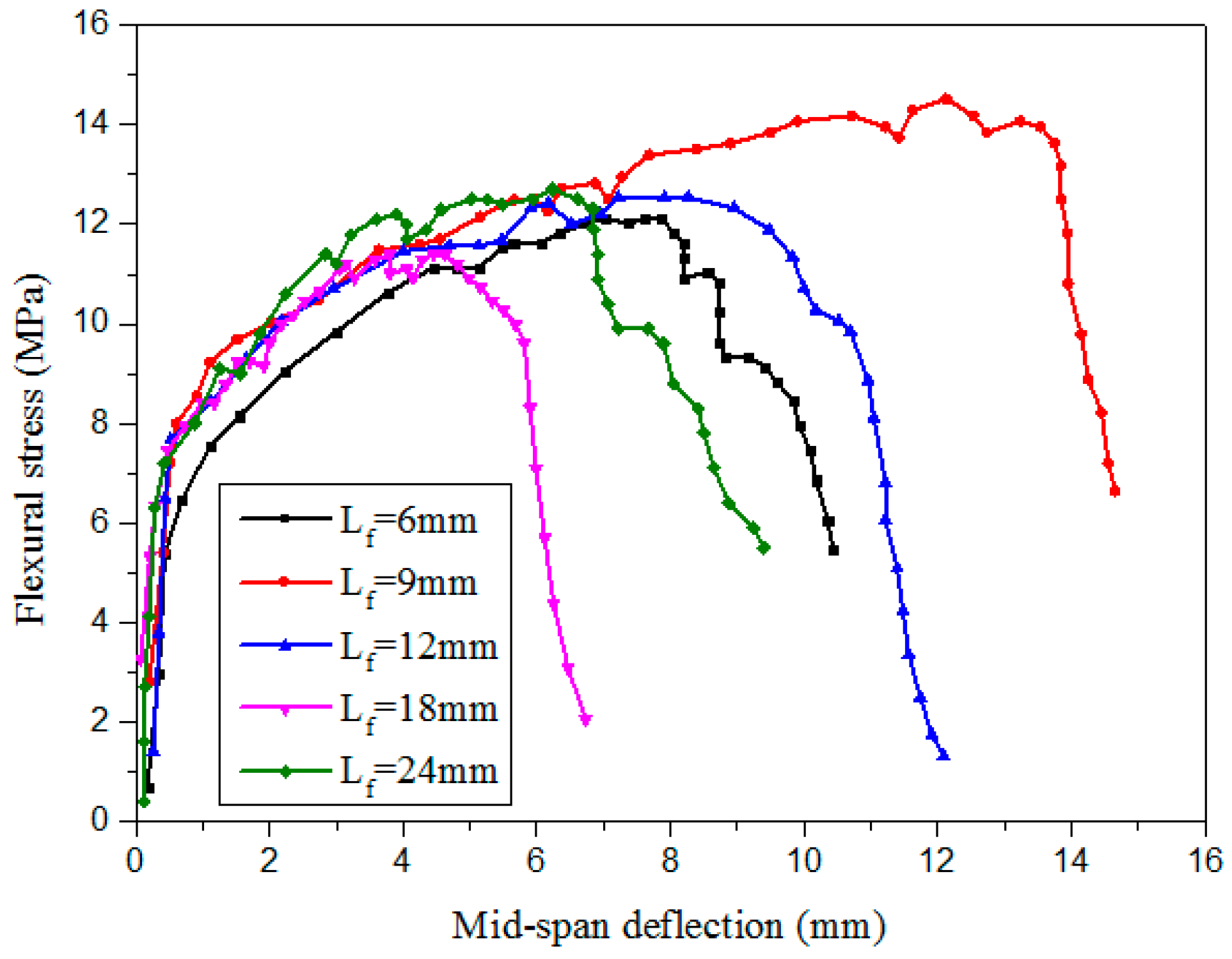
3.2. Effect of Fiber Length on Fracture Properties
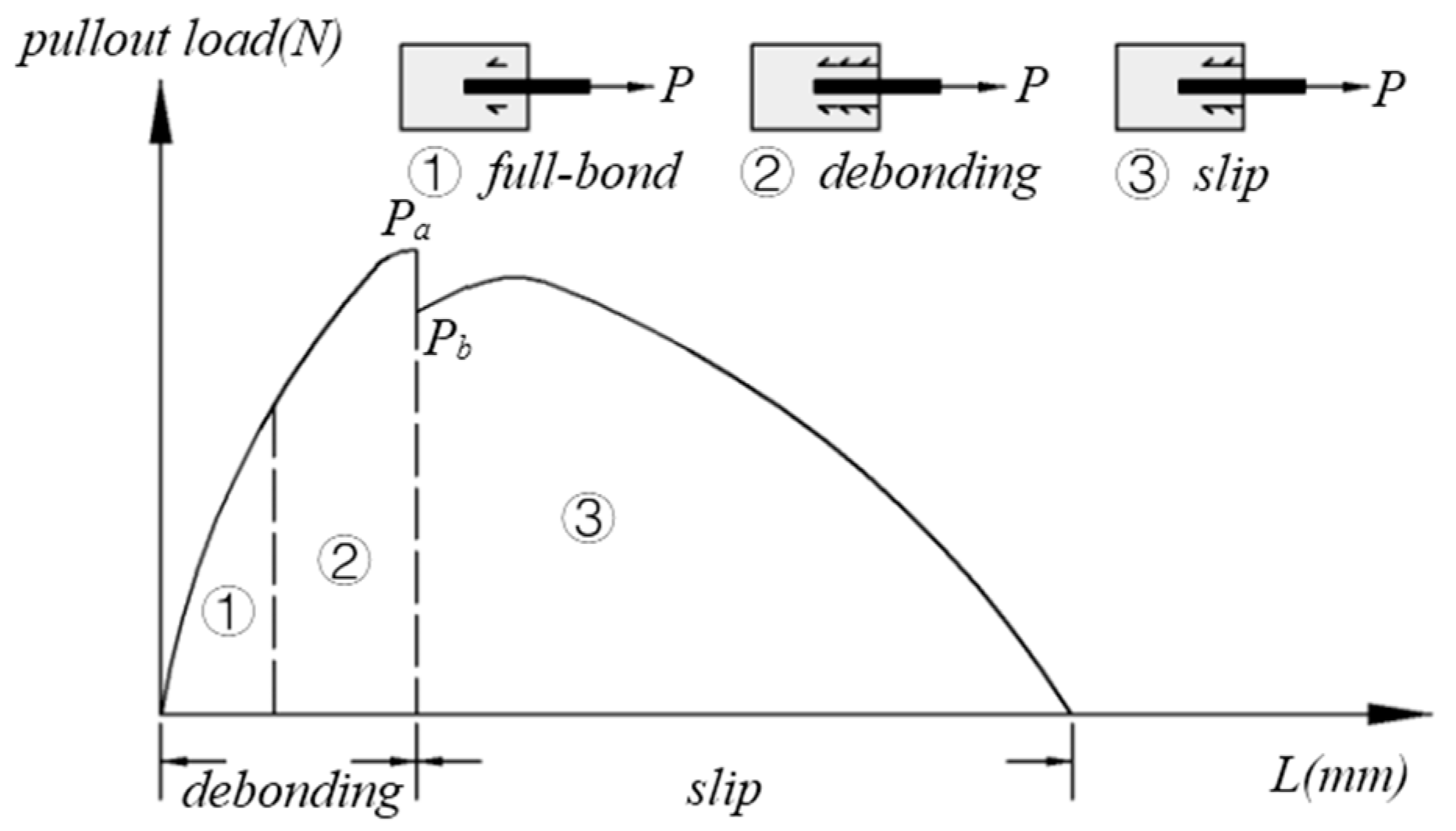
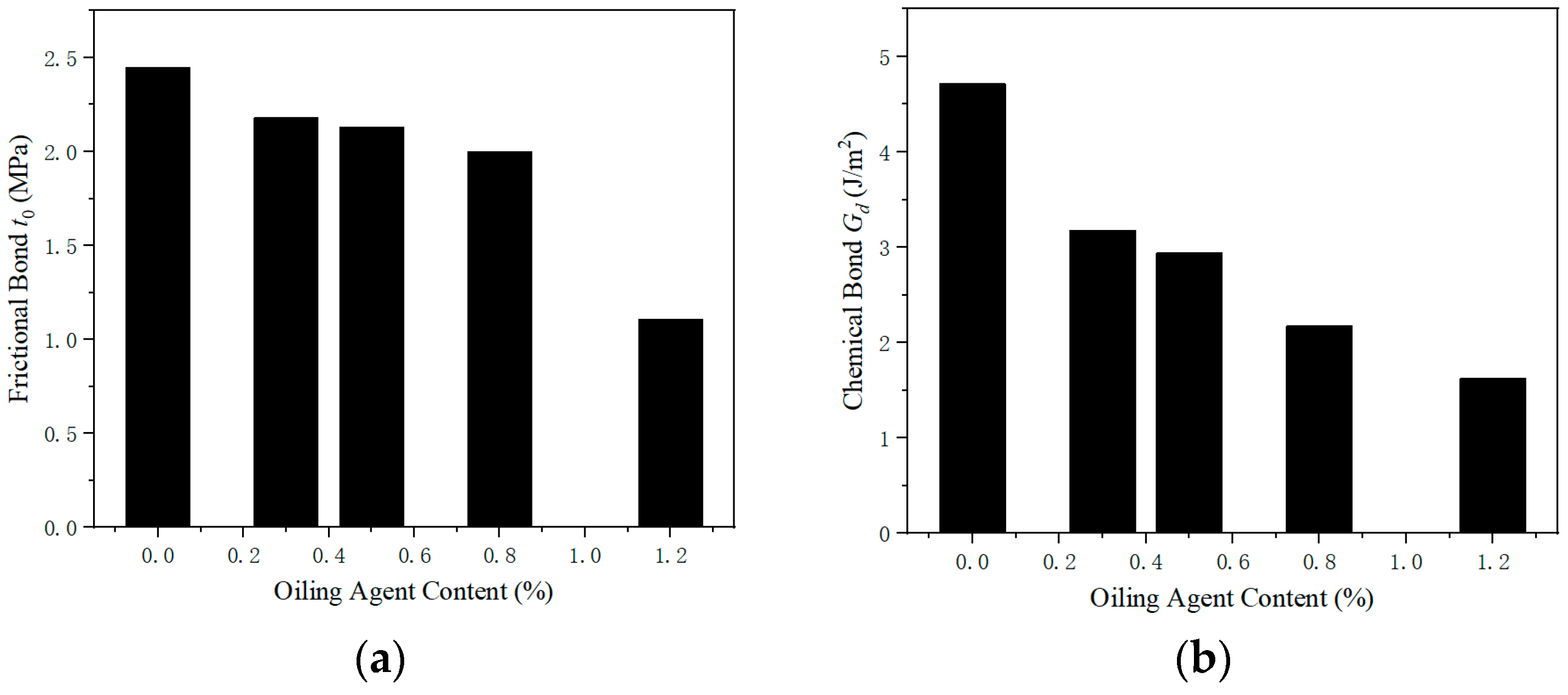
3.3. Effect of Fiber Surface Oiling on Bond Performance
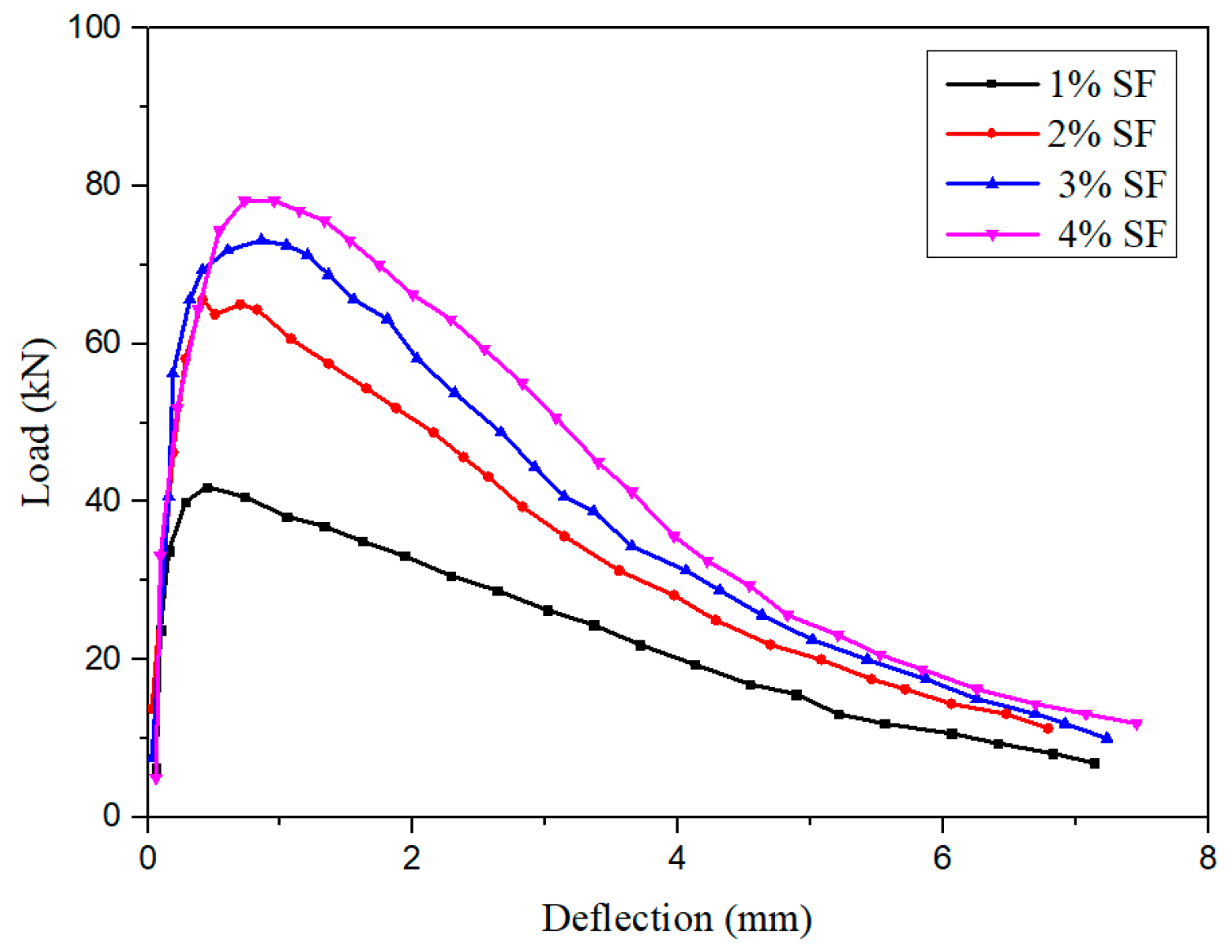
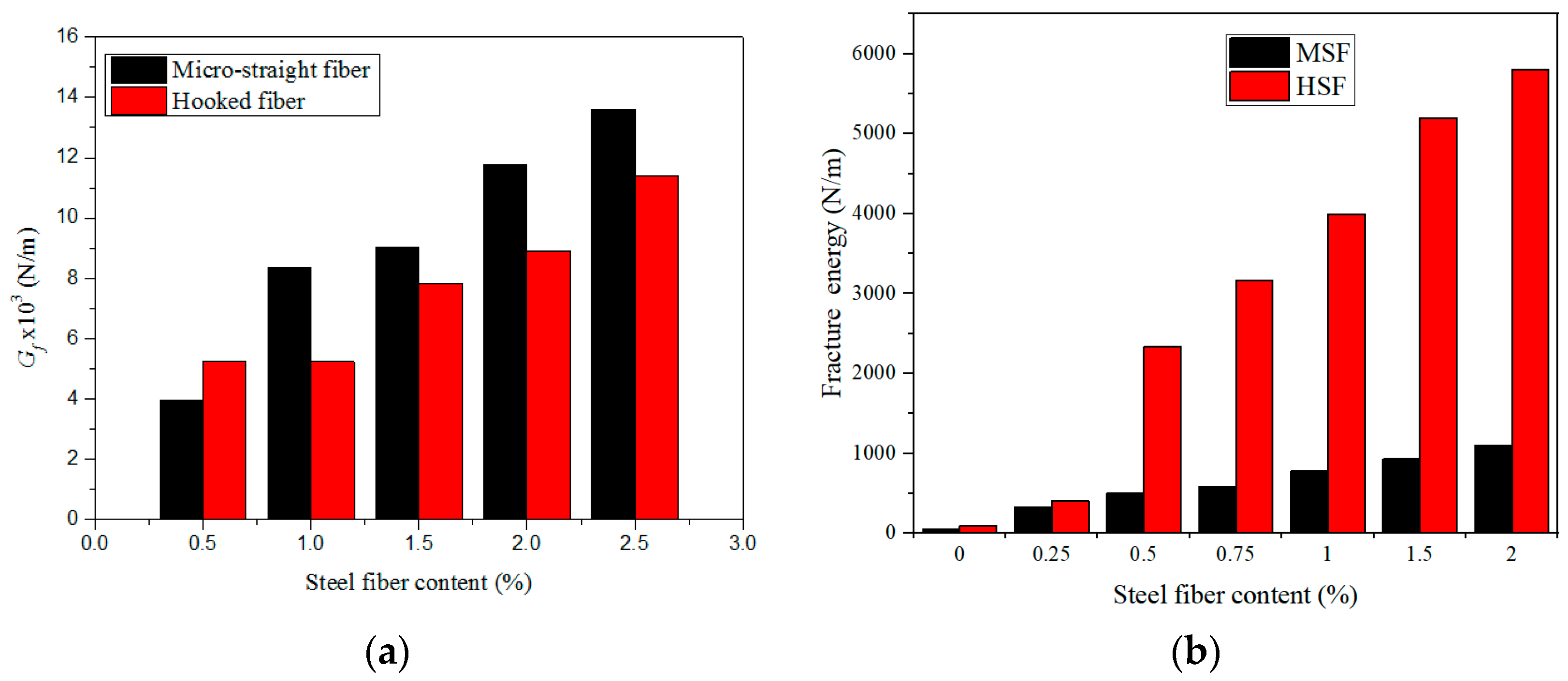
4. Effect of SFs on Fracture Properties
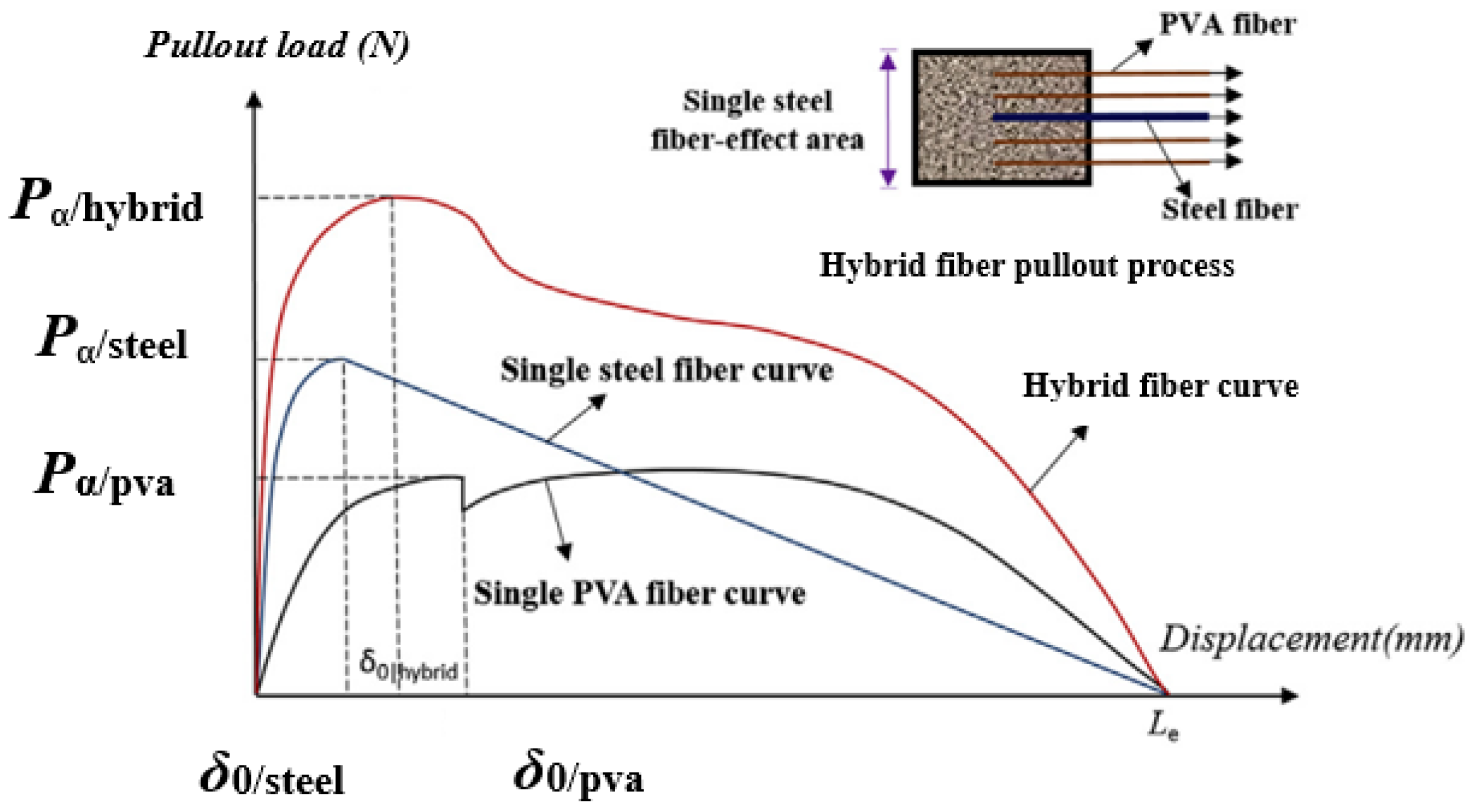
5. Effects of Hybrid Fibers on Fracture Performance
6. Conclusions
- (1)
- The fracture model of the cementitious composite, the ACK model, and the PSH model are used mainly for ductile cementitious composites. ACK model can determine the optimal fiber content of matrix, PVA fiber generally no more than is the basic condition for the quasi-strain hardening of cementitious composites, while a large value of can realize the cracking of multi-saturated cracks in the matrix. The FC, BC, and DKF models are mainly applied to semi-brittle material–concrete composites. Both FC and BC models are based on tensile softening of concrete, and the value of can be expressed as the ability of concrete to resist crack propagation. The FC model can directly simulate the concrete with nonlinear characteristics by using the finite element method. The DKF model has the advantages of the FC and BC models, and is widely used in practical engineering. The DKF model can judge the whole process of concrete failure according to , , and parameters.
- (2)
- The fracture energy and toughness of the cementitious composite can be increased by adding an appropriate amount of PVA fibers (1.2–2.0%) with an appropriate (16 mm) fiber length. The main objectives of PVA fiber surface oiling (approximately 1.2%) are to weaken the adhesion between the PVA fibers and the matrix, reduce the friction during fiber pullout, and prevent the fracture of PVA fibers.
- (3)
- The stiffness of SFs is higher than that of PVA fibers; thus, SFs have a better strengthening effect on the cementitious composite. SF fibers of appropriate length have a good bridging effect on macroscopic cracks in the matrix, and SFs can also absorb fracture energy. The mixing amount of SF in is cementitious composite 4%, which can greatly improve the fracture property of the matrix. In the pullout process, the SF is easily pulled out, whereas the PVA fiber is easily broken. SF and PVA fibers can be mixed in the matrix simultaneously. The pullout load displacement of the fibers is the synergistic effect of the two. Generally, adding 1.5% SFs and 1.0% PVA fiber to the matrix can greatly improve the fracture performance of the matrix. Thus, adding appropriate amounts of PVA fibers and SFs can improve the mechanical and fracture properties of the matrix.
7. Outlook
- (1)
- For comparison with the ACK model, the PSH, FC, BC, and DKF models are reviewed and analyzed. Although all the models have advantages, there are deficiencies for practical engineering that must be resolved.
- (2)
- However, when PVA fiber and SFs fiber are mixed, the optimal effect of SF and PVA fiber on the fracture property, mechanical property, and durability of the matrix is not discussed in depth. In the study of SFs and PVA fiber mixing, too much range of water–binder ratio was not set, and too much research on its high-temperature performance was not carried out. The pullout of a single fiber’s load–displacement curves of polypropylene fibers and SF single fibers were also not analyzed. To improve the mechanical properties of cementitious composites with low fiber contents, further research should be performed in these areas.
- (3)
- The fracture properties of fiber-reinforced cementitious composites are studied and analyzed only with regard to the basic properties and mechanisms. Therefore, it is necessary to further study the practical application of cementing composites and the freezing–thawing environment in which the cementing materials are located, as well as the wet, hot, and salt environment in saline and alkaline areas and coastal areas.
Author Contributions
Funding
Conflicts of Interest
References
- Li, V.C.; Leung, C.K.Y. Steady state and multiple cracking of short random fiber composites. J. Eng. Mech. 1992, 188, 2264. [Google Scholar] [CrossRef]
- Li, V.C.; Mishra, D.K.; Wu, H.C. Matrix design for pseudo strain-hardening fiber reinforced cementitious composites. Mater. Struct. 1995, 28, 586–595. [Google Scholar] [CrossRef]
- Li, V.C.; Mishra, D.K.; Naaman, A.E.; Wight, J.K.; Inada, Y. On the shear behavior of engineered cementitious composites. Adv. Cem. Based Mater. 1994, 1, 142–149. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Stroeven, M.; Sluys, L.J. Multiscale failure modeling of concrete: Micromechanical modeling, discontinuous homogenization and parallel computations. Comput. Methods Appl. Mech. Eng. 2012, 201, 139–156. [Google Scholar] [CrossRef]
- Ghaffar, S.H.; Al-Kheetan, M.; Ewens, P.; Wang, T.; Zhuang, J. Investigation of the interfacial bonding between flax/wool twine and various cementitious matrices in mortar composites. Constr. Build. Mater. 2020, 239, 117833. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.X.; Yang, H.M.; Wang, Y.; Tang, S.W. Comparison of fly ash, PVA fiber, MgO and shrinkage-reducing admixture on the frost resistance of face slab concrete via pore structural and fractal analysis. Fractals 2020. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, X.W.; Chai, J.R.; Xu, Z.G.; Li, S.Y. Experimental study of compressive behavior of polypropylene-fiber-reinforced and polypropylene-fiber-fabric-reinforced concrete. Constr. Build. Mater. 2019, 194, 216–225. [Google Scholar] [CrossRef]
- Yu, K.Q.; Lu, Z.D.; Dai, J.G.; Shah, S.P. Direct tensile properties and stress-strain model of UHP-ECC. J. Mater. Civ. Eng. 2020, 32, 04019334. [Google Scholar] [CrossRef]
- Li, V.C. Tailoring ECC for special attributes: A review. Int. J. Concr. Struct. Mater. 2012, 6, 135–144. [Google Scholar] [CrossRef]
- Li, B.; Xiong, H.; Jiang, J.; Dou, X. Tensile behaviour of basalt textile grid reinforced engineered cementitious composites. Compos. Part B Eng. 2019, 156, 185–200. [Google Scholar] [CrossRef]
- Yang, Y.; Lepech, M.D.; Yang, E.H.; Li, V.C. Autogenous healing of engineered cementitious composites under wet-dry cycles. Cem. Concr. Res. 2009, 39, 382–390. [Google Scholar] [CrossRef]
- Xu, S.L.; Cai, X.R. Experimental study and theoretical models on compressive properties of ultrahigh toughness cementitious composites. J. Mater. Civ. Eng. 2010, 22, 1067–1077. [Google Scholar] [CrossRef]
- Li, L.; Cai, Z.; Yu, K.; Zhang, Y.X.; Ding, Y. Performance-based design of all-grade strain hardening cementitious composites with compressive strengths from 40 MPa to 120 MPa. Cem. Concr. Compos. 2019, 97, 202–217. [Google Scholar] [CrossRef]
- Yu, K.; Ding, Y.; Liu, J.; Bai, Y. Energy dissipation characteristics of all-grade polyethylene fiber-reinforced engineered cementitious composites (PE-ECC). Cem. Concr. Compos. 2020, 106, 103459. [Google Scholar] [CrossRef]
- Li, V.C. High performance fiber reinforced cementitious composites as durable material for concrete structure repair. Int. J. Restor. 2004, 10, 163–180. [Google Scholar]
- Rokugo, K.; Kanda, T.; Yokota, H.; Sakata, N. Applications and recommendations of high performance fiber reinforced cement composites with multiple fine cracking (HPFRCC) in Japan. Mater. Struct. 2009, 42, 1197–1208. [Google Scholar] [CrossRef]
- Krouma, A.; Syed, Z.I. A review on the use of engineered cementitious composite in bridges. Mater. Sci. Forum 2016, 860, 125–134. [Google Scholar] [CrossRef]
- Kaplan, M.F. Crack propagation and the fracture of concrete. Am. Concr. Inst. 1961, 8, 591–610. [Google Scholar]
- Xu, S.L.; Zhang, X.F. Determination of fracture parameters for crack propagation in concrete using an energy approach. Eng. Fract. Mech. 2008, 75, 4292–4308. [Google Scholar] [CrossRef]
- Yu, X.M.; Ren, Q.W. Fracture release energy for ordinary concrete with freeze-thaw cycles. J. Hohai Univ. Nat. Sci. 2010, 38, 80–82. (In Chinese) [Google Scholar]
- Akkaya, Y.; Shah, S.P.; Ankenman, B. Effect of fiber dispersion on multiple cracking of cement composites. J. Eng. Mech. 2001, 127, 311–316. [Google Scholar] [CrossRef]
- Aveston, J.; Cooper, G.A.; Kelly, A. Single and Multiple Fracture; IPC Science and Technology Press: London, UK, 1971; pp. 15–26. [Google Scholar]
- Feng, P.; Cheng, S.; Bai, Y.; Ye, L.P. Mechanical behavior of concrete-filled square steel tube with FRP-confined concrete core subjected to axial compression. Compos. Struct. 2015, 123, 312–324. [Google Scholar] [CrossRef]
- Zhao, J.J.; Yan, C.W.; Liu, S.G.; Zhang, J.; Li, S.; Yan, Y. Effect of solid waste ceramic on uniaxial tensile properties and thin plate bending properties of polyvinyl alcohol engineered cementitious composite. J. Clean. Prod. 2020, 268, 122329. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Barpi, F.; Valente, S. Cohesive crack model description of ductile to brittle size-scale transition: Imensional analysis vs. renormalization group theory. Eng. Fract. Mech. 2003, 70, 1809–1839. [Google Scholar] [CrossRef]
- Elices, M.; Planas, J. Fracture mechanics parameters of concrete: An overview. Adv. Cem. Based Mater. 1996, 4, 116–127. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Cornetti, P. A scale-invariant cohesive crack model for quasi-brittle materials. Eng. Fract. Mech. 2002, 69, 207–217. [Google Scholar] [CrossRef]
- Choubey, R.K.; Kumar, S.; Rao, C.M. Modeling of fracture parameters for crack propagation in recycled aggregate concrete. Constr. Build. Mater. 2016, 106, 168–178. [Google Scholar] [CrossRef]
- Khalilpour, S.; BaniAsad, E.; Dehestani, M. A review on concrete fracture energy and effective parameters. Cem. Concr. Res. 2019, 120, 294–321. [Google Scholar] [CrossRef]
- Yang, I.H.; Joh, C.; Kim, B.S. Flexural response predictions for ultra-high-performance fiber-reinforced concrete beams. Mag. Concr. Res. 2012, 64, 113–127. [Google Scholar] [CrossRef]
- Fantilli, A.P.; Mihashi, F.H.; Nishiwaki, T. Tailoring hybrid strain-hardening cementitious composites. ACI Mater. J. 2014, 111, 211–218. [Google Scholar] [CrossRef]
- Dziemian, R. Guide to Stability Design Criteria for Metal Structures, 6th ed.; Wiley: New York, NY, USA, 2010. [Google Scholar]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Mater. Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Bažant, Z.P. Concrete fracture models: Testing and practice. Eng. Fract. Mech. 2002, 69, 165–205. [Google Scholar] [CrossRef]
- Kanda, T.; Li, V.C. New micromechanics design theory for pseudo strain hardening cementitious composite. J. Eng. Mech. 2002, 125, 373–381. [Google Scholar] [CrossRef]
- Li, V.C. Engineered Cementitious Composites (ECC): Bendable Concrete for Sustainable and Resilient Infrastructure; Springer: Berlin Heidelberg, Germany, 2019. [Google Scholar]
- Zhang, Z.G.; Zhang, Q.; Li, V.C. Multiple-scale investigations on self-healing induced mechanical property recovery of ECC. Cem. Concr. Compos. 2019, 103, 293–302. [Google Scholar] [CrossRef]
- Marshall, D.B.; Cox, B.N. A J-integral method for calculating steady-state matrix cracking stresses in composites. Mech. Mater. 1988, 7, 127–133. [Google Scholar] [CrossRef]
- Lu, C.; Leung, C.K.Y. A new model for the cracking process and tensile ductility of strain hardening cementitious composites (SHCC). Cem. Concr. Res. 2016, 79, 353–365. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, Y.; Qian, S. Influence of bacterial incorporation on mechanical properties of engineered cementitious composites (ECC). Constr. Build. Mater. 2019, 196, 195–203. [Google Scholar] [CrossRef]
- Kanda, T.; Li, V.C. Practical design criteria for saturated pseudo strain hardening behavior in ECC. J. Adv. Concr. Technol. 2006, 4, 59. [Google Scholar] [CrossRef]
- Li, V.C.; Wu, C.; Wang, S.; Ogawa, A.; Saito, T. Interface tailoring for strain-hardening polyvinyl alcohol-engineered cementitious composite (PVA-ECC). ACI Mater. J. 2002, 99, 463–472. [Google Scholar]
- Lin, Z.; Kanda, T.; Li, V.C. On interface property characterization and performance of fiber reinforced cementitious composites. Concr. Sci. Eng. 1999, 1, 173–184. [Google Scholar]
- Redon, C.; Li, V.C.; Wu, C.; Hoshiro, H.; Saito, T.; Ogawa, A. Measuring and modifying interface properties of PVA fibers in ECC matrix. J. Mater. Civ. Eng. 2001, 13, 399–406. [Google Scholar] [CrossRef]
- Yu, J.; Lu, C.; Chen, Y.; Leung, C.K.Y. Experimental determination of crack-bridging constitutive relations of hybrid-fiber strain-hardening cementitious composites using digital image processing. Constr. Build. Mater. 2018, 173, 359–367. [Google Scholar] [CrossRef]
- Wang, S.X.; Li, V.C. Engineered cementitious composites with high-volume fly ash. ACI Mater. J. 2007, 104, 233–241. [Google Scholar]
- Xu, S.L.; Reinhardt, H.W. Crack extension resistance and fracture properties of quasi-brittle softening materials like concrete based on the complete process of fracture. Int. J. Fract. 1998, 92, 71–99. [Google Scholar] [CrossRef]
- Xu, S.L.; Reinhardt, H.W. Determination of double-K criterion for crack propagation in quasi-brittle fracture. Part Ⅱ: Analytical evaluating and practical measuring methods for three-point bending notched beams. Int. J. Fract. 1999, 98, 151–177. [Google Scholar] [CrossRef]
- Wu, X.; Tian, J.; Ma, H.; Zheng, Y.; Hu, S.; Wang, W.; Du, Y.; Huang, W.; Sun, C.; Zhu, Z. Investigation on interface fracture properties and nonlinear fracture model between ECC and concrete subjected to salt freeze-thaw cycles. Constr. Bulid. Mater. 2020, 259, 119785. [Google Scholar] [CrossRef]
- Zhang, X.F.; Xu, S.L. A comparative study on five approaches to evaluate double-K fracture toughness parameters of concrete and size effect analysis. Eng. Fract. Mech. 2011, 78, 2115–2138. [Google Scholar] [CrossRef]
- Xu, S.L.; Reinhardt, H.W. Determination of double-K criterion for crack propagation in quasi-brittle fracture. Part Ⅰ: Experimental investigation of crack propagation. Int. J. Fract. 1999, 98, 111–149. [Google Scholar] [CrossRef]
- Liu, X.Y.; Li, Z.C. Determining double-K fracture parameters of concrete only by the measured peak load. Theor. Appl. Fract. Mech. 2016, 85, 412–423. [Google Scholar] [CrossRef]
- Kumar, S.; Barai, S.V. Determining double-K fracture parameters of concrete for compact tension and wedge splitting tests using weight function. Eng. Fract. Mech. 2009, 76, 935–948. [Google Scholar] [CrossRef]
- Kumar, S.; Barai, S.V. Determining the double-K fracture parameters for three-point bending notched concrete beams using weight function. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 645–660. [Google Scholar] [CrossRef]
- Yu, K.Q.; Lu, Z.D. Determining residual double-K fracture toughness of post-fire concrete using analytical and weight function method. Mater. Struct. 2014, 47, 839–852. [Google Scholar] [CrossRef]
- Hu, S.W.; Zhang, X.F.; Xu, S.L. Effects of loading rates on concrete double-K fracture parameters. Eng. Fract. Mech. 2015, 149, 58–73. [Google Scholar] [CrossRef]
- Rong, H.; Dong, W.; Zhang, X.F.; Zhang, B.S. Size effect on fracture properties of concrete after sustained loading. Mater. Struct. 2019, 52, 16. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, S.W.; Fan, X.Q.; Lu, J. Effect of water pressure on fracture parameters of concrete. Constr. Build. Mater. 2019, 199, 613–623. [Google Scholar] [CrossRef]
- Kumar, S.; Barai, S.V. Size effect prediction from the double-K fracture model for notched concrete beam. Int. J. Damage Mech. 2010, 19, 473–497. [Google Scholar] [CrossRef]
- Shah, S.P.; Swartz, S.E.; Ouyang, C. Fracture Mechanics of Concrete: Applications of Fracture Mechanics to Concrete, Rock and Other Quasi-Brittle Materials; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Xu, B.W.; Ju, J.W.; Shi, H.S. Progressive micromechanical modeling for pullout Energy of hooked-end steel Fiber in cement-based composites. Int. J. Damage Mech. 2010, 20, 922–938. [Google Scholar] [CrossRef]
- Toutanji, H.; Xu, B.; Gilbert, J.; Lavin, T. Properties of poly(vinyl alcohol) fiber reinforced high-performance organic aggregate cementitious material: Converting brittle to plastic. Constr. Build. Mater. 2010, 24, 1–10. [Google Scholar] [CrossRef]
- Qin, Y.; Zhang, X.W.; Chai, J.R. Damage performance and compressive behavior of early-age green concrete with recycled nylon fiber fabric under an axial load. Constr. Build. Mater. 2019, 209, 105–114. [Google Scholar] [CrossRef]
- Li, Y.L.; Li, W.G.; Deng, D.; Wang, K.; Duan, W.H. Reinforcement effects of polyvinyl alcohol and polypropylene fibers on flexural behaviors of sulfoaluminate cement matrices. Cem. Concr. Compos. 2018, 88, 139–149. [Google Scholar] [CrossRef]
- Lin, C.; Kayali, O.; Morozov, E.V.; Sharp, D.J. Sharp Influence of fibre type on flexural behaviour of self-compacting fibre reinforced cementitious composites. Cem. Concr. Compos. 2014, 51, 27–37. [Google Scholar] [CrossRef]
- Ling, Y.; Zhang, P.; Wang, J.; Chen, Y. Effect of PVA fiber on mechanical properties of cementitious composite with and without nano-SiO2. Constr. Build. Mater. 2019, 229, 117068. [Google Scholar] [CrossRef]
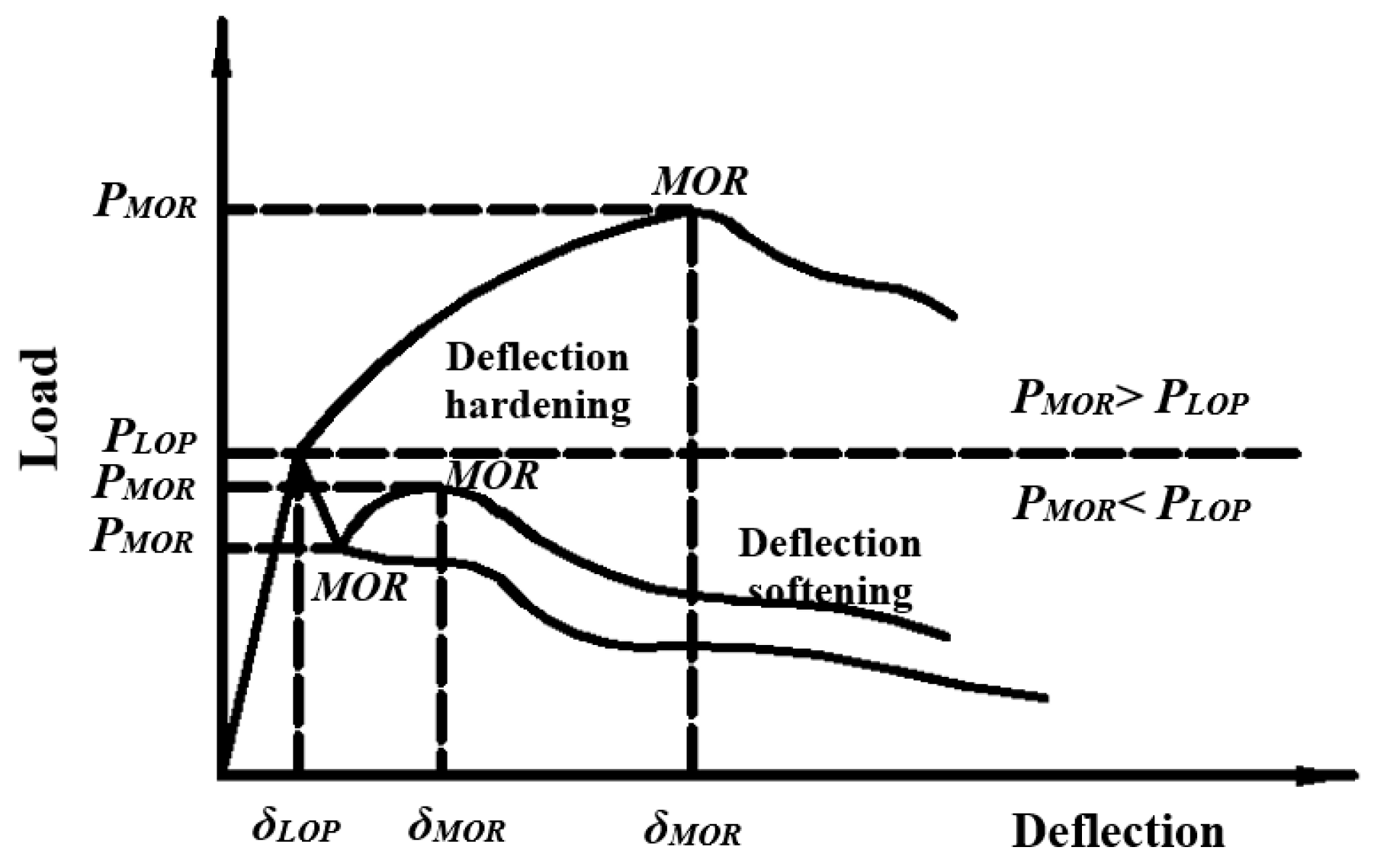
- Nematollahi, B.; Sanjayan, J.; Shaikh, F.U.A. Comparative deflection hardening behavior of short fiber reinforced geopolymer composites. Constr. Build. Mater. 2014, 70, 54–64. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, T.; Wang, W. Effect of PVA fiber content on creep property of fiber reinforced high-strength concrete columns. AIP Conf. Proc. 2018, 1955, 020026. [Google Scholar]
- Maalej, M.; Li, V.C.; Hashida, T. Effect of fiber rupture on tensile properties of short fiber composites. J. Eng. Mech. 1995, 121, 903–913. [Google Scholar] [CrossRef]
- Li, V.C.; Obla, K.H. Effect of fiber diameter variation on properties of cement-based matrix fiber reinforced composites. Compos. Part B Eng. 1996, 27, 275–284. [Google Scholar] [CrossRef]
- Ding, C.; Guo, L.P.; Chen, B. An optimum polyvinyl alcohol fiber length for reinforced high ductility cementitious composites based on theoretical and experimental analyses. Constr. Build. Mater. 2020, 259, 119824. [Google Scholar] [CrossRef]
- Sasmal, S.; Avinash, G. Investigations on mechanical performance of cementitious composites micro-engineered with polyvinyl alcohol fibers. Constr. Build. Mater. 2016, 128, 136–147. [Google Scholar] [CrossRef]
- Kucko, N.W.; Petre, D.G.; Ruiter, M.D. Micro- and macro-mechanical characterization of the influence of surface-modification of poly(vinyl alcohol) fibers on the reinforcement of calcium phosphate cements. J. Mech. Behav. Biomed. Mater. 2020, 109, 103776. [Google Scholar] [CrossRef]
- Yang, E.H.; Li, V.C. Strain-hardening fiber cement optimization and component tailoring by means of a micromechanical model. Constr. Build. Mater. 2010, 24, 130–139. [Google Scholar] [CrossRef]
- Wang, Q.; Lai, M.H.; Zhang, J.; Wang, Z.; Ho, J. Greener engineered cementitious composite (ECC)—The use of pozzolanic fillers and unoiled PVA fibers. Constr. Build. Mater. 2020, 247, 118211. [Google Scholar] [CrossRef]
- Tahenni, T.; Chemrouk, M.; Lecompte, T. Effect of steel fibers on the shear behavior of high strength concrete beams. Constr. Build. Mater. 2016, 105, 14–28. [Google Scholar] [CrossRef]
- Frazão, C.; Camões, A.; Barros, J.; Goncalves, D. Durability of steel fiber reinforced self-compacting concrete. Constr. Build. Mater. 2015, 80, 155–166. [Google Scholar] [CrossRef]
- Song, P.S.; Hang, S. Mechanical properties of high-strength steel fiber-reinforced concrete. Constr. Build. Mater. 2004, 18, 669–673. [Google Scholar] [CrossRef]
- Mai, Y.W.; Lawn, B.R. Crack stability and toughness characteristics in brittle materials. Annu. Rev. Mater. Res. 2003, 16, 415–439. [Google Scholar] [CrossRef]
- Mertol, H.C.; Baran, E.; Bello, H.J. Flexural behavior of lightly and heavily reinforced steel fiber concrete beams. Constr. Build. Mater. 2015, 98, 185–193. [Google Scholar] [CrossRef]
- Lee, S.-J.; Hong, Y.; Eom, A.-H.; Won, J.-P. Effect of steel fibers on fracture parameters of cementitious composites. Compos. Struct. 2018, 204, 658–663. [Google Scholar] [CrossRef]
- Lee, S.-J.; Eom, A.-H.; Ryu, S.-J.; Won, J.-P. Optimal dimension of arch-type steel fiber reinforced cementitious composite for shotcrete. Compos. Struct. 2016, 152, 600–606. [Google Scholar] [CrossRef]
- Ren, G.M.; Wu, H.; Fang, Q.; Liu, J.Z. Effects of steel fiber content and type on static mechanical properties of UHPCC. Constr. Build. Mater. 2018, 163, 826–839. [Google Scholar] [CrossRef]
- Wu, Z.M.; Shi, C.J.; He, W.; Wu, L.M. Effects of steel fiber content and shape on mechanical properties of ultra-high performance concrete. Constr. Build. Mater. 2016, 103, 8–14. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Lee, J.H.; Yoon, Y.S. Effect of fiber content on mechanical and fracture properties of ultra-high performance fiber reinforced cementitious composites. Compos. Struct. 2013, 106, 742–753. [Google Scholar] [CrossRef]
- Kim, D.J.; Naaman, A.E.; El-Tawil, S. Comparative flexural behavior of four fiber reinforced cementitious composites. Cem. Concr. Compos. 2008, 30, 917–928. [Google Scholar] [CrossRef]
- Won, J.-P.; Hong, B.-T.; Choi, T.-J.; Lee, S.-J.; Kang, J.-W. Flexural behaviour of amorphous micro-steel fiber-reinforced cement composites. Compos. Struct. 2012, 94, 1443–1449. [Google Scholar] [CrossRef]
- Gesoglu, M.; Güneyisi, E.; Muhyaddin, G.F.; Asaad, D.S. Strain hardening ultra-high performance fiber reinforced cementitious composites: Effect of fiber type and concentration. Compos. Part B Eng. 2016, 103, 74–83. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H.J. Static properties and impact resistance of a green ultra-high performance hybrid fiber reinforced concrete (UHPHFRC): Experiments and modeling. Constr. Build. Mater. 2014, 68, 158–171. [Google Scholar] [CrossRef]
- Soe, K.T.; Zhang, Y.; Zhang, L. Material properties of a new hybrid fiber reinforced engineered cementitious composite. Constr. Build. Mater. 2013, 43, 399–407. [Google Scholar] [CrossRef]
- Li, V.C.; Wang, S.; Wu, C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (PVA-ECC). ACI Mater. J. 2001, 98, 483–492. [Google Scholar]
- Ahmed, S.F.U.; Maalej, M.; Paramasivam, P. Strain-hardening behavior of hybrid fiber reinforced cement composites. J. Ferrocem. 2003, 33, 172–182. [Google Scholar]
- Yao, W.; Li, J.; Wu, K. Mechanical properties of hybrid fiber-reinforced concrete at low fiber volume fraction. Cem. Concr. Res. 2003, 33, 27–30. [Google Scholar] [CrossRef]
- Nehdi, M.; Ladanchuk, J.D. Fiber synergy in fiber-reinforced self-consolidating concrete. ACI Mater. J. 2004, 101, 508–517. [Google Scholar]
- El-Mal, H.S.S.A.A.; Sherbini, S.; Sallam, H.E.M. Mode II fracture toughness of hybrid FRCs. Int. J. Concr. Struct. Mater. 2015, 9, 475–486. [Google Scholar] [CrossRef]
- Banthia, N.; Gupta, R. Hybrid fiber reinforced concrete (HyFRC): Fiber synergy in high strength matrices. Mater. Struct. 2004, 37, 707–716. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.B.; Wang, Q.; Gao, Y. Simulation and test of flexural performance of polyvinyl alcohol-steel hybrid fiber reinforced cementitious composite. J. Compos. Mater. 2016, 50, 4291–4305. [Google Scholar] [CrossRef]
- Ahmed, S.F.U.; Maalej, M.; Paramasivam, P. Flexural responses of hybrid steel-polyethylene fiber reinforced cement composites containing high volume fly ash. Constr. Build. Mater. 2007, 21, 1088–1097. [Google Scholar] [CrossRef]
- Li, Q.H.; Gao, X.; Xu, S.L. Multiple effects of nano-SiO2 and hybrid fibers on properties of high toughness fiber reinforced cementitious composites with high volume fly ash. Cem. Concr. Compos. 2016, 72, 201–212. [Google Scholar] [CrossRef]
- Standard Test Method for Flexural Toughness and First Crack Strength of Fiber Reinforced Concrete (Using Beam with Third-Point Loading); ASTM C1018-97; ASTM International: Conshohocken, PA, USA, 1997.







| Model | Crack Criterion | Mechanical Treatment of Micro-Fissure Zone | Numerical Method Used |
|---|---|---|---|
| ACK model [22] | Stress–strain curve | Integral method | |
| FC model [27] | Bilinear (or nonlinear) strain softening curve | Finite-element method | |
| CB model [34] | Micro-cracks are uniformly distributed and parallel and the damage degree is expressed by the reduction of the elastic modulus | Finite-element method | |
| PSH model [39] | Energy under quasi-stress strain | Integral method | |
| DFK model [52] | Load–CMOD curve | Weight functions and other numerical calculation methods |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Yang, Y.; Wang, J.; Jiao, M.; Ling, Y. Fracture Models and Effect of Fibers on Fracture Properties of Cementitious Composites—A Review. Materials 2020, 13, 5495. https://doi.org/10.3390/ma13235495
Zhang P, Yang Y, Wang J, Jiao M, Ling Y. Fracture Models and Effect of Fibers on Fracture Properties of Cementitious Composites—A Review. Materials. 2020; 13(23):5495. https://doi.org/10.3390/ma13235495
Chicago/Turabian StyleZhang, Peng, Yonghui Yang, Juan Wang, Meiju Jiao, and Yifeng Ling. 2020. "Fracture Models and Effect of Fibers on Fracture Properties of Cementitious Composites—A Review" Materials 13, no. 23: 5495. https://doi.org/10.3390/ma13235495
APA StyleZhang, P., Yang, Y., Wang, J., Jiao, M., & Ling, Y. (2020). Fracture Models and Effect of Fibers on Fracture Properties of Cementitious Composites—A Review. Materials, 13(23), 5495. https://doi.org/10.3390/ma13235495







