Stribeck Curve of Magnetorheological Fluid within Pin-on-Disc Configuration: An Experimental Investigation
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement Method of COF
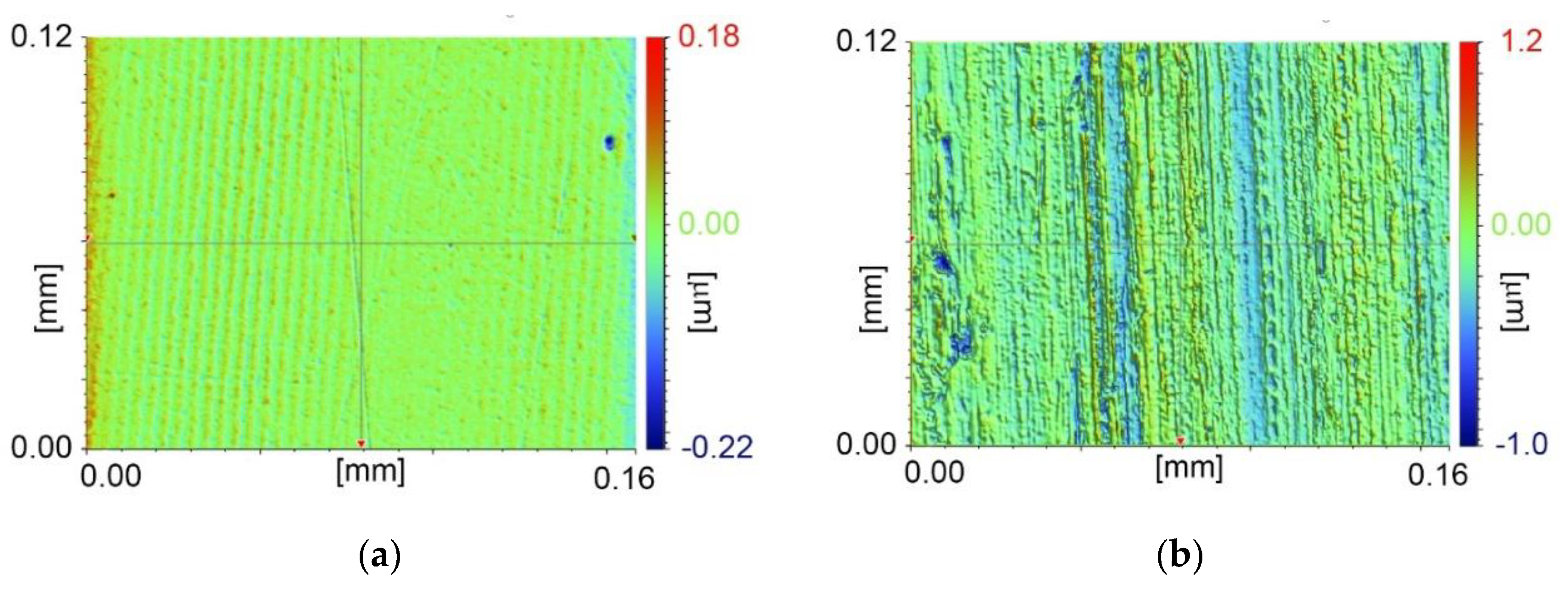
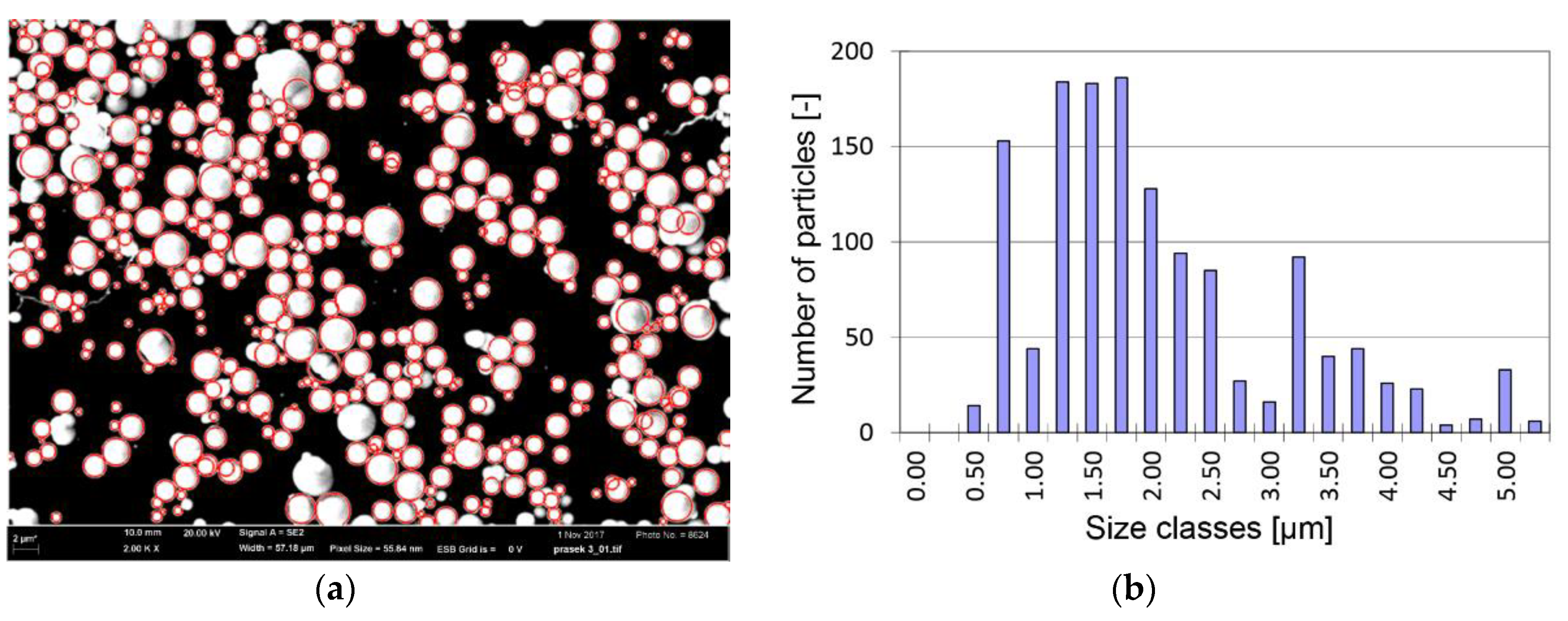
2.2. Testing Samples
3. Results and Discussion
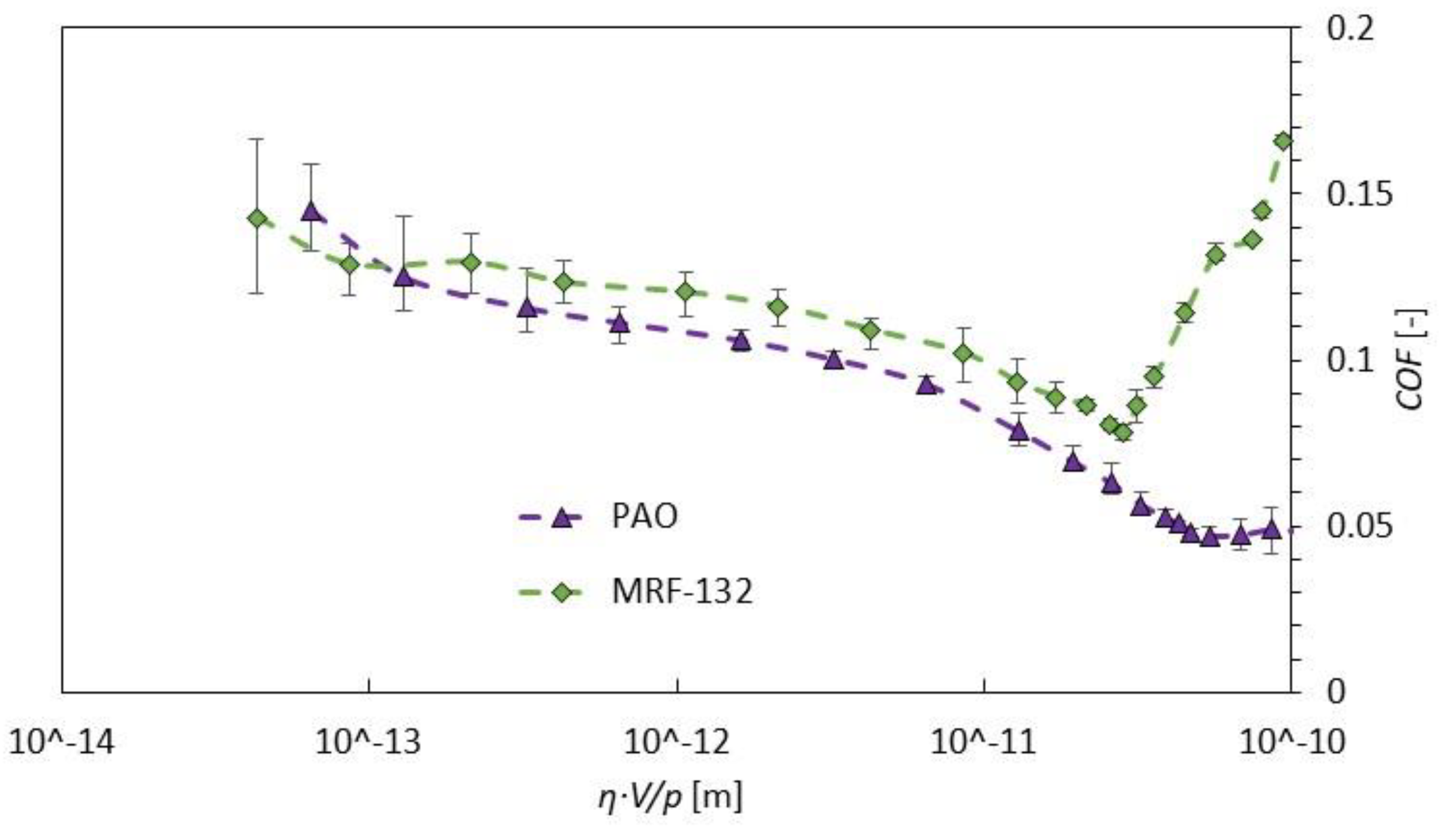
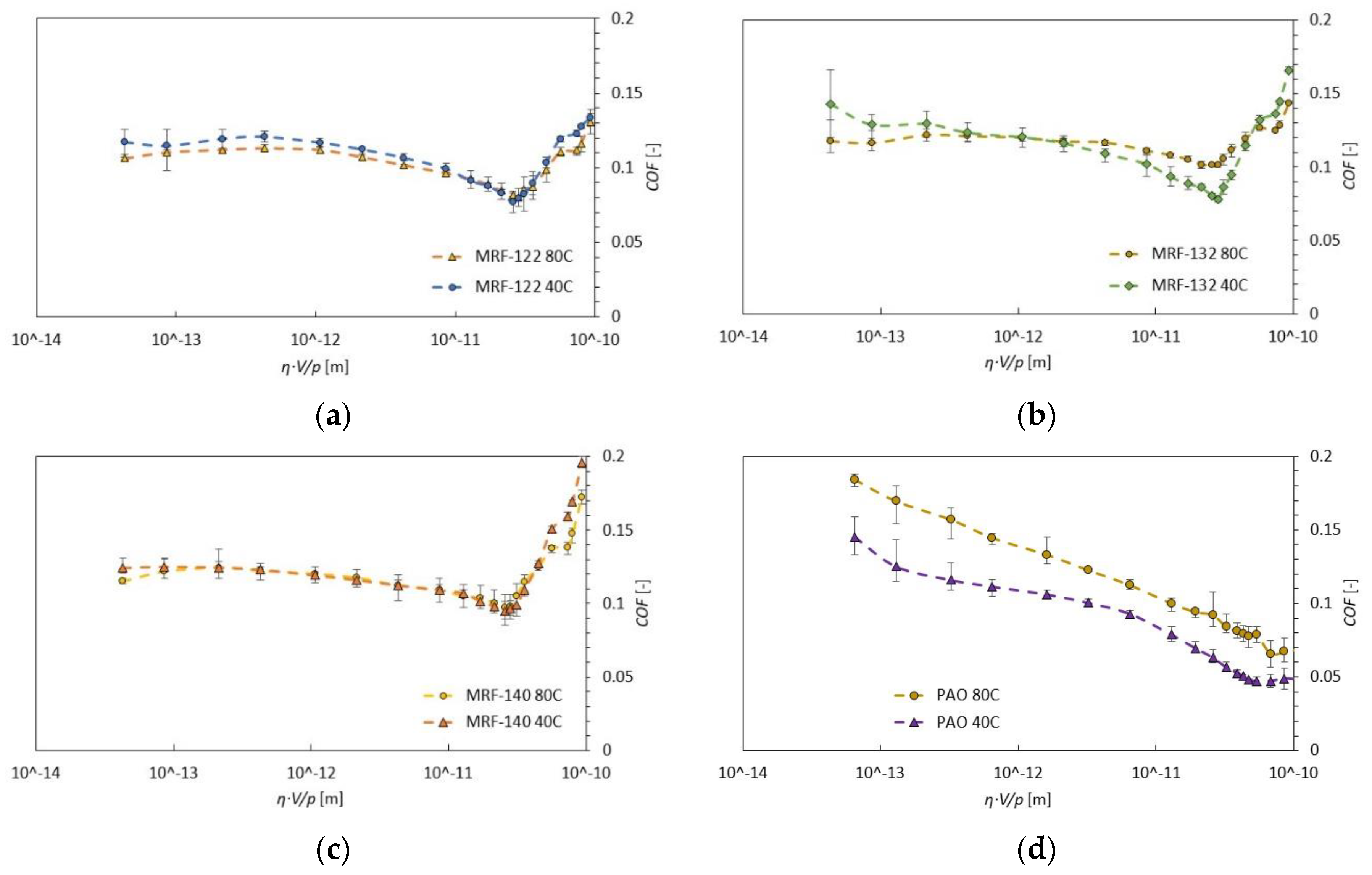
3.1. COF Comparison of Oils and MR Fluid
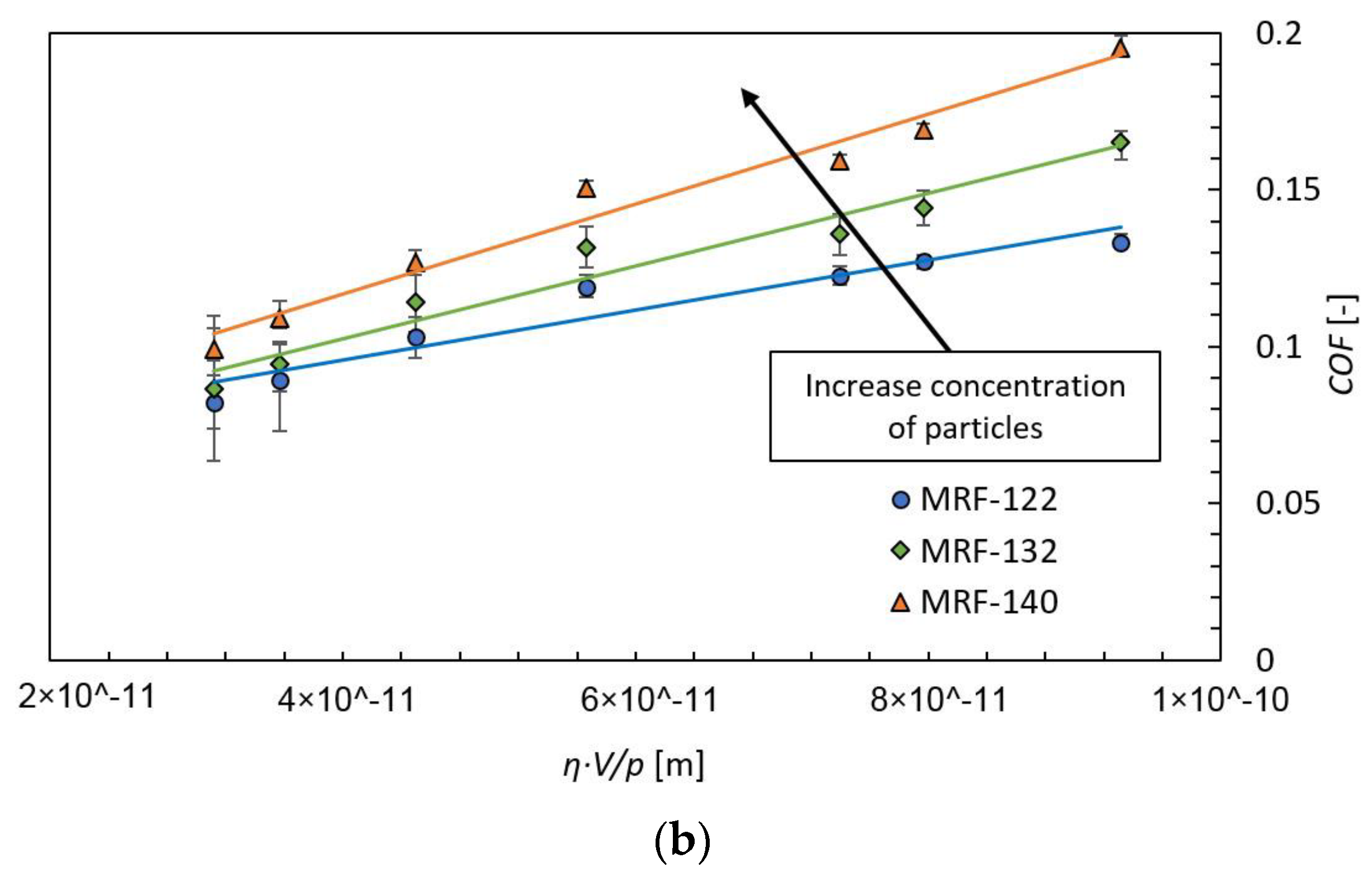
3.2. Particle Concentration Effect
3.3. Temperature Effect
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goncalves, F.D.; Ahmadian, M.; Carlson, J.D. Investigating the magnetorheological effect at high flow velocities. Smart Mater. Struct. 2005, 15, 75–85. [Google Scholar] [CrossRef]
- Pappas, Y.; Klingenberg, D.J. Simulations of magnetorheological suspensions in Poiseuille flow. Rheol. Acta. 2006, 45, 621–629. [Google Scholar] [CrossRef]
- Goldasz, J. Magnetostatic study of a dual-gap MR valve. In Proceedings of the 20th International Conference on Research and Education in Mechatronics (REM), Wels, Austria, 23–24 May 2019. [Google Scholar]
- Strecker, Z.; Kubik, M.; Vitek, P.; Roupec, J.; Paloušek, D.; Šreibr, V. Structured magnetic circuit for magnetorheological damper made by selective laser melting technology. Smart Mater. Struct. 2019, 28, 055016. [Google Scholar] [CrossRef]
- Kubík, M.; Goldasz, J. Multiphysics Model of an MR Damper including Magnetic Hysteresis. Shock Vib. 2019, 2019. [Google Scholar] [CrossRef]
- Chen, S.; Yang, J. Probing Slip Differential Heat of Magnetorheological Fluids Subjected to Shear Mode Operation and Its Effect on the Structure. Materials (Basel) 2019, 12, 1860. [Google Scholar] [CrossRef] [PubMed]
- Li, W.H.; Du, H. Design and Experimental Evaluation of a Magnetorheological Brake. Int. J. Adv. Manuf. Technol. 2003, 21, 508–515. [Google Scholar] [CrossRef]
- Park, E.J.; Stoikov, D.; Falcao da Luz, L.; Suleman, A. A performance evaluation of an automotive magnetorheological brake design with a sliding mode controller. Mechatronics 2006, 16, 405–416. [Google Scholar] [CrossRef]
- Kubík, M.; Pavlíček, D.; Macháček, O.; Strecker, Z.; Roupec, J. A magnetorheological fluid shaft seal with low friction torque. Smart Mater. Struct. 2019, 28, 047002. [Google Scholar] [CrossRef]
- Szczȩch, M. Experimental Study on the Pressure Distribution Mechanism Among Stages of the Magnetic Fluid Seal. IEEE Trans. Magn. 2018, 54, 1–7. [Google Scholar] [CrossRef]
- Choi, S.-B.; Hong, S.R.; Choi, Y.T.; Wereley, N.M. Vibration control of flexible structures using MR and piezoceramic mounts. In Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE), Proceedings of Smart Structures and Materials 2004, San Diego, CA, USA, 15–18 March 2004; Flatau, A.B., Ed.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2004; Volume 5390, pp. 127–134. [Google Scholar]
- Song, B.-K.; Yoon, J.-Y.; Hong, S.-W.; Choi, S.-B. Field-Dependent Stiffness of a Soft Structure Fabricated from Magnetic-Responsive Materials: Magnetorheological Elastomer and Fluid. Materials 2020, 13, 953. [Google Scholar] [CrossRef]
- Rich, J.P.; Doyle, P.S.; McKinley, G.H. Magnetorheology in an aging, yield stress matrix fluid. Rheol. Acta. 2012, 51, 579–593. [Google Scholar] [CrossRef]
- Roupec, J.; Berka, P.; Mazůrek, I.; Strecker, Z.; Kubík, M.; Macháček, O.; Andani, M.T. A novel method for measurement of MR fluid sedimentation and its experimental verification. Smart Mater. Struct. 2017, 26, 107001. [Google Scholar] [CrossRef]
- Mazůrek, I.; Roupec, J.; Klapka, M.; Strecker, Z. Load and rheometric unit for the test of magnetorheological fluid. Meccanica 2013, 48, 631–641. [Google Scholar] [CrossRef]
- Carlson, J.D. Critical factors for MR fluids in vehicle systems. Int. J. Veh. Des. 2003, 33, 207. [Google Scholar] [CrossRef]
- Iyengar, V.R.; Robert, T. Foister Durable Magnetorheological Fluid Compositions. US Patent 6,599,439, 29 July 2003. [Google Scholar]
- Utami, D.; Ubaidillah; Mazlan, S.; Imaduddin, F.; Nordin, N.; Bahiuddin, I.; Abdul Aziz, S.; Mohamad, N.; Choi, S.-B. Material Characterization of a Magnetorheological Fluid Subjected to Long-Term Operation in Damper. Materials (Basel) 2018, 11, 2195. [Google Scholar]
- Jolly, M.R.; Bender, J.W.; Carlson, J.D. Properties and Applications of Commercial Magnetorheological Fluids. J. Intell. Mater. Syst. Struct. 1999, 10, 5–13. [Google Scholar]
- Song, W.-L.; Choi, S.-B.; Choi, J.-Y.; Lee, C.-H. Wear and Friction Characteristics of Magnetorheological Fluid under Magnetic Field Activation. Tribol. Trans. 2011, 54, 616–624. [Google Scholar] [CrossRef]
- Shahrivar, K.; Ortiz, A.L.; de Vicente, J. A comparative study of the tribological performance of ferrofluids and magnetorheological fluids within steel–steel point contacts. Tribol. Int. 2014, 78, 125–133. [Google Scholar] [CrossRef]
- Rosa, W.O.; Vereda, F.; de Vicente, J. Tribological Behavior of Glycerol/Water-Based Magnetorheological Fluids in PMMA Point Contacts. Front. Mater. 2019, 6, 1–11. [Google Scholar] [CrossRef]
- Zhang, P.; Lee, K.-H.; Lee, C.-H. Friction behavior of magnetorheological fluids with different material types and magnetic field strength. Chin. J. Mech. Eng. 2016, 29, 84–90. [Google Scholar] [CrossRef]
- Leung, W.C.; Bullough, W.A.; Wong, P.L.; Feng, C. The effect of particle concentration in a magneto rheological suspension on the performance of a boundary lubricated contact. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2004, 218, 251–263. [Google Scholar] [CrossRef]
- Sohn, J.W.; Choi, S.B.; Lee, C.H.; Cho, M.W. Wear Characteristics of Magnetorheological Fluid under Boundary Lubrication. Adv. Mater. Res. 2009, 79, 83–86. [Google Scholar] [CrossRef]
- Song, W.-L.; Lee, C.-H.; Choi, S.-B. Sliding wear behavior of magnetorheological fluid for brass with and without magnetic field. Trans. Nonferrous Met. Soc. China 2013, 23, 400–405. [Google Scholar] [CrossRef]
- Wong, P.; Bullough, W.; Feng, C.; Lingard, S. Tribological performance of a magneto-rheological suspension. Wear 2001, 247, 33–40. [Google Scholar] [CrossRef]
- Lee, C.H.; Lee, D.W.; Choi, J.Y.; Choi, S.B.; Cho, W.O.; Yun, H.C. Tribological Characteristics Modification of Magnetorheological Fluid. J. Tribol. 2011, 133. [Google Scholar] [CrossRef]
- Zhang, P.; Lee, K.-H.; Lee, C.-H. Reciprocating friction characteristics of magneto-rheological fluid for aluminum under magnetic field. Trans. Nonferrous Met. Soc. China 2014, 24, 171–176. [Google Scholar] [CrossRef]
- Yakubov, G.E.; Branfield, T.E.; Bongaerts, J.H.H.; Stokes, J.R. Tribology of particle suspensions in rolling-sliding soft contacts. Biotribology 2015, 3, 1–10. [Google Scholar] [CrossRef]


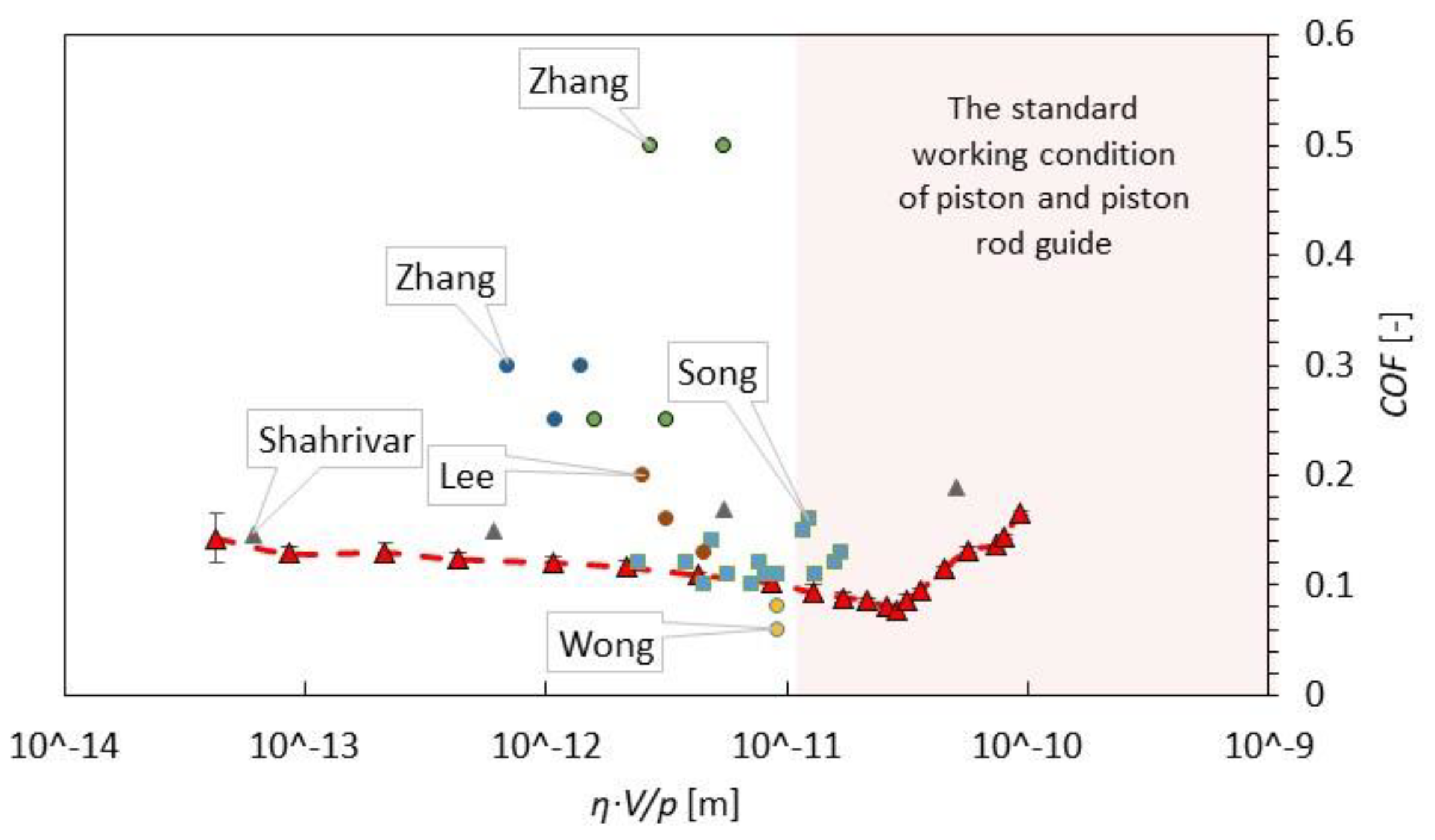
| Author | Geometry | Relative Speed [mm/s] | Normal Force [N] | Contact Pair | Viscosity [mPa.s] | COF [-] | Contact Pressure [GPa] |
|---|---|---|---|---|---|---|---|
| Sohn | Block on ring | 950 | 40 | S45C/S45C | 14.2 | 0.8 | 1.433 |
| Song | pin on disc | 780 | 50 | brass/brass | 14.2 | 0.13 | 0.012 |
| Song | pin on disc | 780 | 20 | steel/steel | 13.6 | 0.12 | 1.367 |
| 780 | 50 | steel/steel | 13.6 | 0.11 | 1.855 | ||
| 780 | 100 | steel/steel | 13.6 | 0.1 | 2.337 | ||
| 780 | 20 | brass/brass | 13.6 | 0.16 | 0.862 | ||
| 780 | 100 | brass/brass | 13.6 | 0.1 | 1.474 | ||
| 780 | 20 | alu/alu | 13.6 | 0.12 | 0.673 | ||
| 780 | 50 | alu/alu | 13.6 | 0.15 | 0.913 | ||
| 780 | 100 | alu/alu | 13.6 | 0.11 | 1.150 | ||
| 330 | 50 | steel/steel | 13.6 | 0.12 | 1.855 | ||
| 1120 | 50 | steel/steel | 13.6 | 0.11 | 1.855 | ||
| 330 | 50 | brass/brass | 13.6 | 0.12 | 1.170 | ||
| 1120 | 50 | brass/brass | 13.6 | 0.11 | 1.170 | ||
| 330 | 50 | alu/alu | 13.6 | 0.14 | 0.913 | ||
| 1120 | 50 | alu/alu | 13.6 | 0.13 | 0.913 | ||
| Wong | block on ring | 1623 | 292 | steel/steel | 15.1 | 0.06 | 2.658 |
| 1623 | 292 | steel/steel | 15.1 | 0.08 | 26.585 | ||
| Zhang | pin on disk | 31.25 | 1 | alu/alu | 13.6 | 0.5 | 0.156 |
| 31.25 | 5 | alu/alu | 13.6 | 0.25 | 0.267 | ||
| 62.5 | 1 | alu/alu | 13.6 | 0.5 | 0.156 | ||
| 62.5 | 5 | alu/alu | 13.6 | 0.25 | 0.267 | ||
| Zhang | pin on disk | 31.25 | 10 | steel/steel | 15.1 | 0.3 | 0.683 |
| 31.25 | 10 | alu/alu | 15.1 | 0.3 | 0.336 | ||
| 31.25 | 10 | brass/brass | 15.1 | 0.25 | 0.336 | ||
| Lee | pin on disc | 390 | 50 | steel/steel | 15.1 | 0.16 | 1.855 |
| 390 | 100 | steel/steel | 15.1 | 0.2 | 2.337 | ||
| 560 | 50 | steel/steel | 15.1 | 0.13 | 1.855 | ||
| Shahrivar | ball-on-three plates | 0.06 | 10 | steel/steel | 13.6 | 0.15 | 0.224 |
| 0.1 | 10 | steel/steel | 13.6 | 0.14 | 0.224 | ||
| 1 | 10 | steel/steel | 13.6 | 0.145 | 0.224 | ||
| 10 | 10 | steel/steel | 13.6 | 0.15 | 0.224 | ||
| 100 | 11 | steel/steel | 13.6 | 0.17 | 0.224 | ||
| 1000 | 12 | steel/steel | 13.6 | 0.19 | 0.269 |
| Step | Fz (N) | v (mm/s) | Step | Fz (N) | v (mm/s) |
|---|---|---|---|---|---|
| 1 | 20 | 5 | 11 | 20 | 2500 |
| 2 | 20 | 10 | 12 | 20 | 3000 |
| 3 | 20 | 25 | 13 | 20 | 3300 |
| 4 | 20 | 50 | 14 | 15 | 3300 |
| 5 | 20 | 125 | 15 | 10 | 3300 |
| 6 | 20 | 250 | 16 | 5 | 3300 |
| 7 | 20 | 500 | 17 | 2.5 | 3300 |
| 8 | 20 | 1000 | 18 | 2 | 4000 |
| 9 | 20 | 1500 | 19 | 1.6 | 4000 |
| 10 | 20 | 2000 | 20 | 1 | 4000 |
| Parameter | MRF-122EG | MRF-132DG | MRF-140CG | PAO4 |
|---|---|---|---|---|
| Viscosity at 40 °C (Pa.s) | 0.042 ± 0.02 | 0.112 ± 0.02 | 0.28 ± 0.07 | 0.014 |
| Density (g/cm3) | 2.28–2.48 | 2.95–3.15 | 3.54–3.74 | 0.82 |
| Solids content of weight (%) | 72 | 80.98 | 85.44 | 0 |
| Solids content of volume (%) | 22 | 32 | 40 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roupec, J.; Jeniš, F.; Strecker, Z.; Kubík, M.; Macháček, O. Stribeck Curve of Magnetorheological Fluid within Pin-on-Disc Configuration: An Experimental Investigation. Materials 2020, 13, 4670. https://doi.org/10.3390/ma13204670
Roupec J, Jeniš F, Strecker Z, Kubík M, Macháček O. Stribeck Curve of Magnetorheological Fluid within Pin-on-Disc Configuration: An Experimental Investigation. Materials. 2020; 13(20):4670. https://doi.org/10.3390/ma13204670
Chicago/Turabian StyleRoupec, Jakub, Filip Jeniš, Zbyněk Strecker, Michal Kubík, and Ondřej Macháček. 2020. "Stribeck Curve of Magnetorheological Fluid within Pin-on-Disc Configuration: An Experimental Investigation" Materials 13, no. 20: 4670. https://doi.org/10.3390/ma13204670
APA StyleRoupec, J., Jeniš, F., Strecker, Z., Kubík, M., & Macháček, O. (2020). Stribeck Curve of Magnetorheological Fluid within Pin-on-Disc Configuration: An Experimental Investigation. Materials, 13(20), 4670. https://doi.org/10.3390/ma13204670





