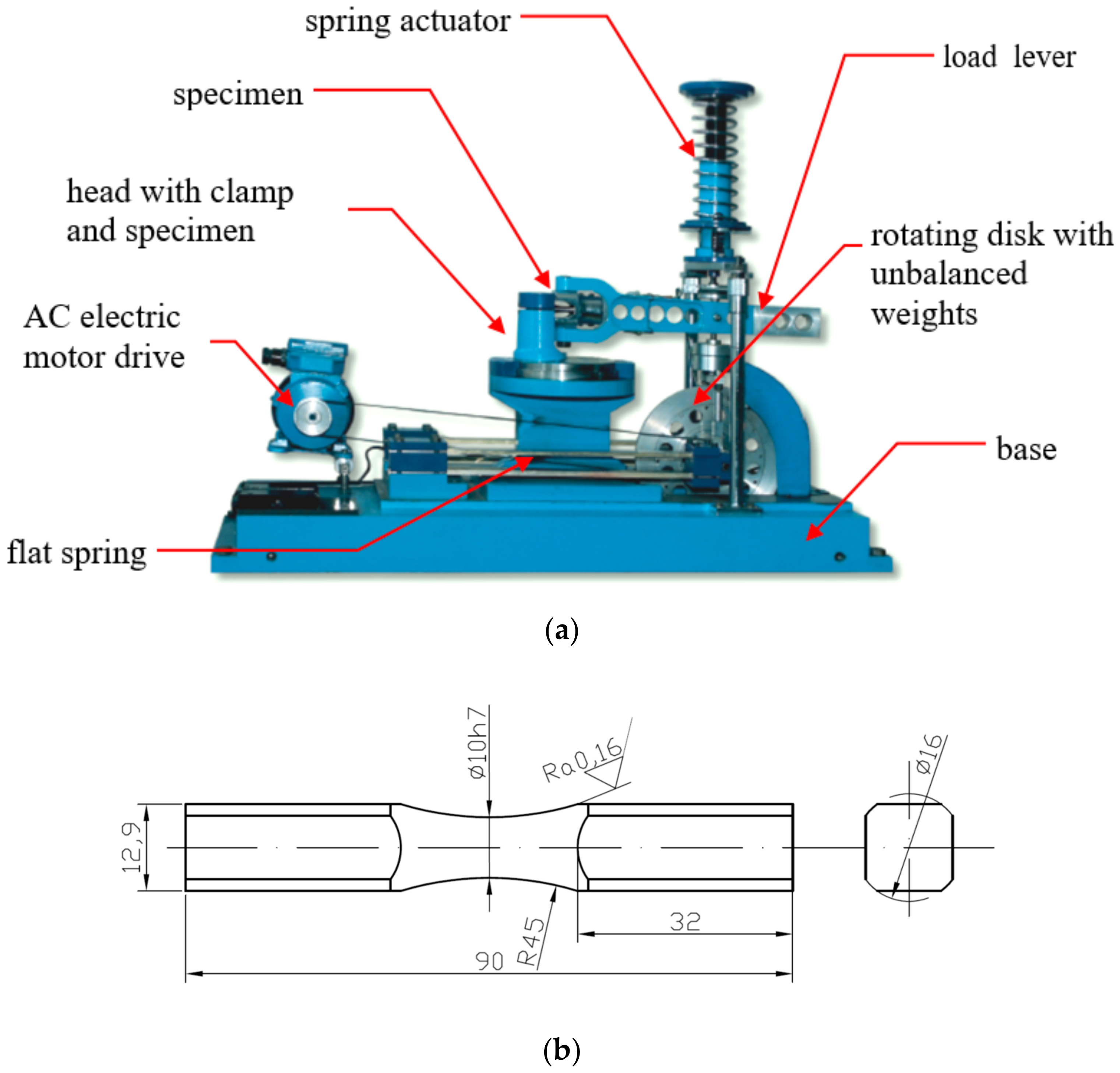
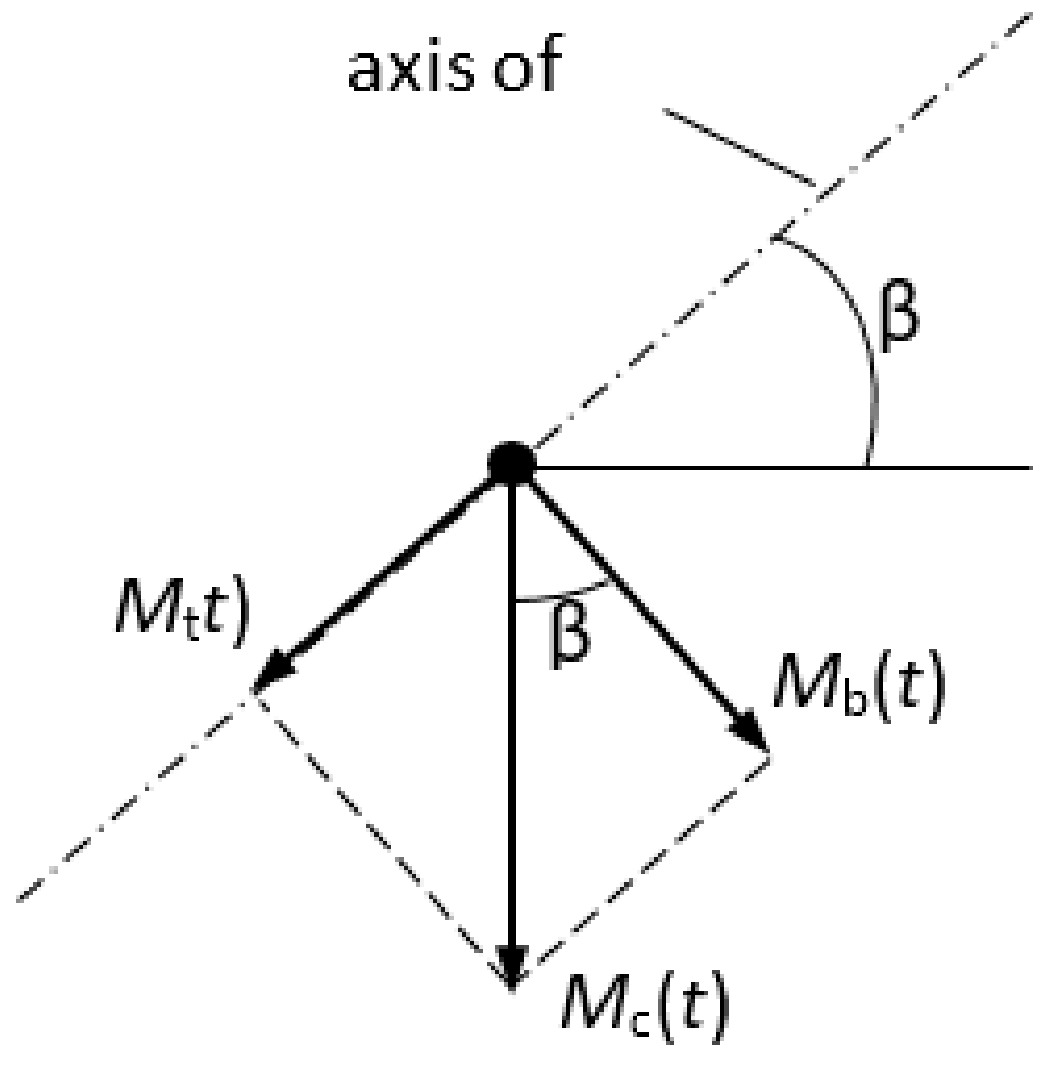
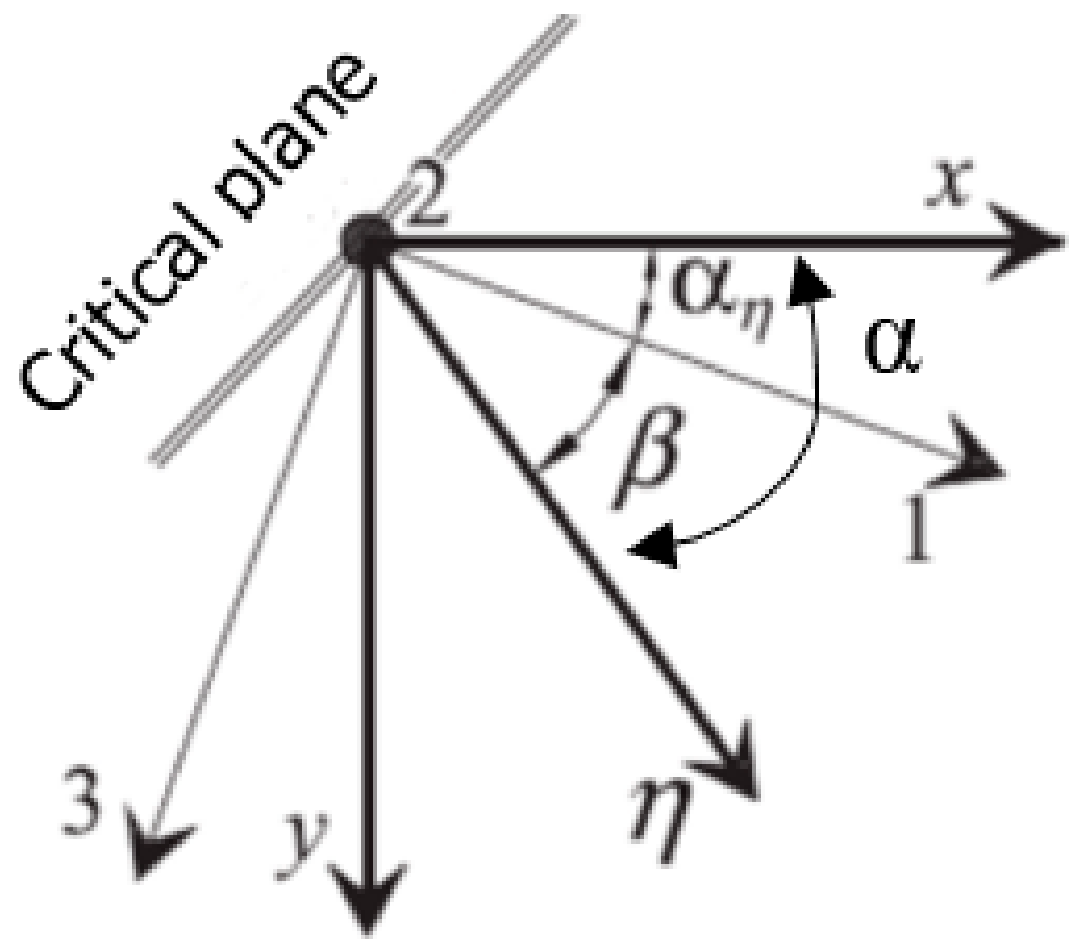
1. Introduction
Currently, the approach to assessing the fatigue life of machinery and equipment components is similar in many areas of civil engineering. Examples include the design of airplanes and rockets, road and rail vehicles, ships and offshore drilling platforms, turbines, land structures, chemical and process equipment, working machinery and other equipment. The proper estimation of the fatigue life of these facilities is a very important problem of modern technology, and incorrect assessments can be the cause of disasters [
1,
2,
3].
The phenomenon of fatigue has been a current topic of research on structural materials for nearly two hundred years, due to fatigue failure, which causes enormous material losses and an increase in the safety risk for working people every year. Many tragic accidents were caused by the appearance of fatigue cracks in structural elements, which in effect made it impossible to carry the loads and led to complete destruction of the entire structure. Therefore, the proper aim of all research conducted on the phenomenon of fatigue is to design and construct safe components of structures and machines.
The complex nature of fatigue processes has resulted in a large number of fatigue hypotheses, which are the basic tools in fatigue life prediction. These hypotheses reduce the dimensional stress state to an equivalent uniaxial stress state. The criteria of multiaxial fatigue originating in the above-mentioned hypotheses can be divided according to the physical nature of the failure parameter into stress criteria, strain criteria, and energy (stress-strain) criteria.
Stress formulation is applied for a large number of cycles, strain formulation is most often used for a small number of cycles, and energy formulation allows the components of stress and strain state to be taken into account simultaneously and can be used for both a small and large number of cycles.
The problem of estimating the fatigue life of various materials is not new. With the development of research on the phenomenon of fatigue, many models have been developed to estimate fatigue life [
4,
5,
6]. A number of steps have been taken to define an algorithm to determine with the greatest possible accuracy the durability of machines or equipment subjected to alternating loads. The first work on the algorithm for estimating fatigue life under random loads in terms of stress was started by Prof. Macha in 1979 [
7]. The algorithm developed by Macha for the general dimensional state of stress has already been modified many times and presented in various works [
8,
9,
10,
11,
12].
Safety regulations and environmental protection standards force industries to look for the most efficient materials. Aluminium has been in ever-wider use from as early as the 1970s. Due to their characteristics, aluminium alloys are slowly replacing popular structural materials such as steel, plastic, and copper.
In the subject literature, we can also find a number of works dealing with various aspects of forecasting the fatigue strength of aluminium alloys [
13,
14,
15]. Fatigue strength properties of pure aluminium are relatively low, hence the use of alloys that can be even several times as strong when adequately heat-treated. Aluminium alloys have a desirable structural parameter, i.e., the ratio of fatigue strength to specific weight, which is higher than that of steel. Furthermore, their impact strength does not decrease as temperature is lowered, so they exhibit a higher impact strength in lower temperatures than steel. Aluminium alloys are being increasingly used in the production of either machine components or entire structures working under operating loads that are not always of constant amplitude.
In [
16], the author summarized the attempt at evaluating the fatigue strength of various materials subjected to proportionate and disproportionate loads. One of the materials was the LY12CZ aluminium alloy; in this case, the fatigue strength was calculated using a method based on the critical plane concept, with the stress-correlated factor taken into account. Article, where the authors study pipe couplings made of aluminium alloys A1Si1MgMn (EN AW 6082 T6) and AlMg3.5Mn (EN AW 5042) under disproportionate load conditions is worth noticing as well [
17]. The fatigue behavior of elements was evaluated using the notch stress concept with the reference radius r
ref = 0.05 mm, while equivalent stresses were determined based on the stress space curve hypothesis. In [
18], readers will find a broad analysis of crack surface changes and micro-mechanism formation in relation to both particle topology and the orientation and size of grains in the 7075-T651 rolled alloy. A new fatigue model for aluminium–silicon alloys with a low copper content was put forward in [
19]. Renault has adopted a methodology for estimating the fatigue strength while taking the effect of thermal aging into account. It is also worth noting that aluminium alloys have found application in the selective laser melting (SLM) method. In this case as well, the fatigue strength is estimated [
20,
21] and crack propagation is observed [
22]. A new proposition for estimating the fatigue strength, based on factoring in the variability in material parameters, was presented in [
10,
23]. In these works, the models were verified based on the findings from studies on fatigue in aluminium alloys.
The analysis of the resulting hypotheses shows that there is no universal algorithm to determine the fatigue life, taking into account both the type of material of the tested item and the nature of the load. These algorithms are often modified due to particular fatigue dependent variables. However, there are still difficulties in determining the fatigue life resulting from the impossibility to determine it using a single equation. The main advantage of the theoretical models is the significant time saving in trying to determine the fatigue life of materials or structures exposed to random loads without performing long-term experimental studies.
An additional advantage is that theoretical models can be used in reverse analysis in this case to determine critical load conditions. Examples of application of theoretical models can also be found in other works [
24,
25,
26,
27,
28].
It should also be mentioned that theoretical models are often used to optimize machines or structures [
29,
30].
The main objective of this work is to find a method that will allow estimation of the fatigue life of elements subjected to multiaxial loads already at the design and construction stage of machinery and equipment parts. The proposed new fatigue life estimation model will take into account the different angles of critical plane orientation for chosen aluminium alloys under multiaxial load conditions. Based on the results of experimental research, a new method of computing the angle of the critical plane orientation will be developed, which will be implemented into the algorithm for estimating the fatigue life of materials under a complex load condition.
The aluminium alloy group analyzed consists of six materials: 6082-T6 [
31], 2017A-T4 [
32], D-30 [
33], and three types of Al-Zn-Mg type alloys in grade 7003 for plastic working after the low-temperature heat-plastic treatment [
34,
35,
36]. The results were used to analyze the correctness of the proposed model of fatigue life estimation.
Aluminium alloys are characterized by a very good specific strength, i.e., the ratio of tensile strength to density. Due to their properties, especially their lightness, they are used in structures in which the weight of the structure is an important factor, namely in aircraft, cars, rolling stock, energy industry, and construction, as well as the food and chemical industry. A drawback of aluminium alloys is their low melting point, which results in a rapid deterioration of mechanical properties with an increase in temperature. They are also characterized by very high plasticity, high electrical and thermal conductivity, good corrosion resistance, and high abrasion resistance.
4. Discussion
Any new model or formula requires verification, during which the assumptions made should be confirmed. In order to verify the model, the scatter analysis of the estimated fatigue life was used, both in respect to the proposed angle and the value of the ratio of normal stresses to shear stresses. As well as the scatter analysis, this paper proposes two conditions that will be used for model verification and further analysis of the obtained results according to
Section 2.
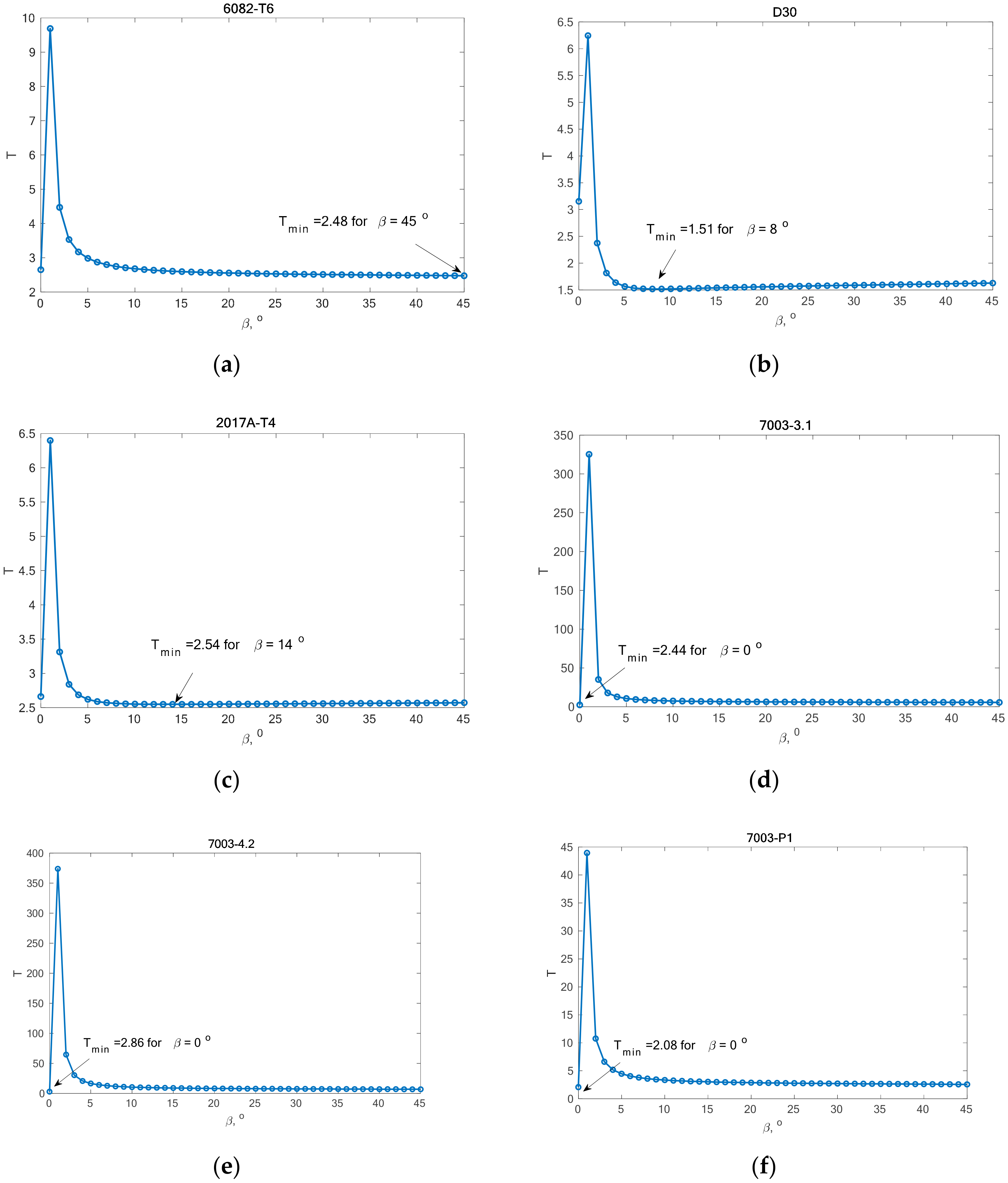
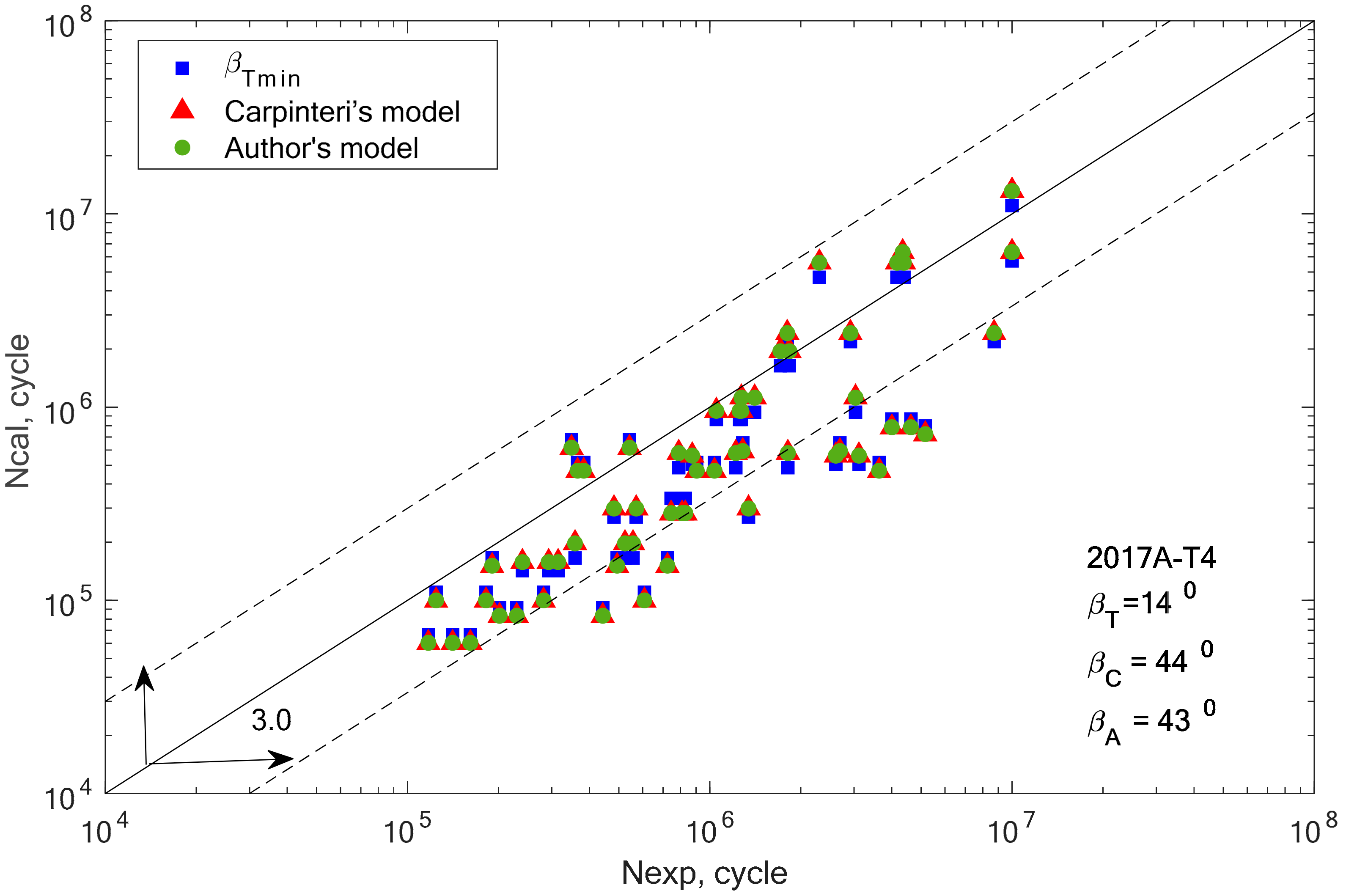
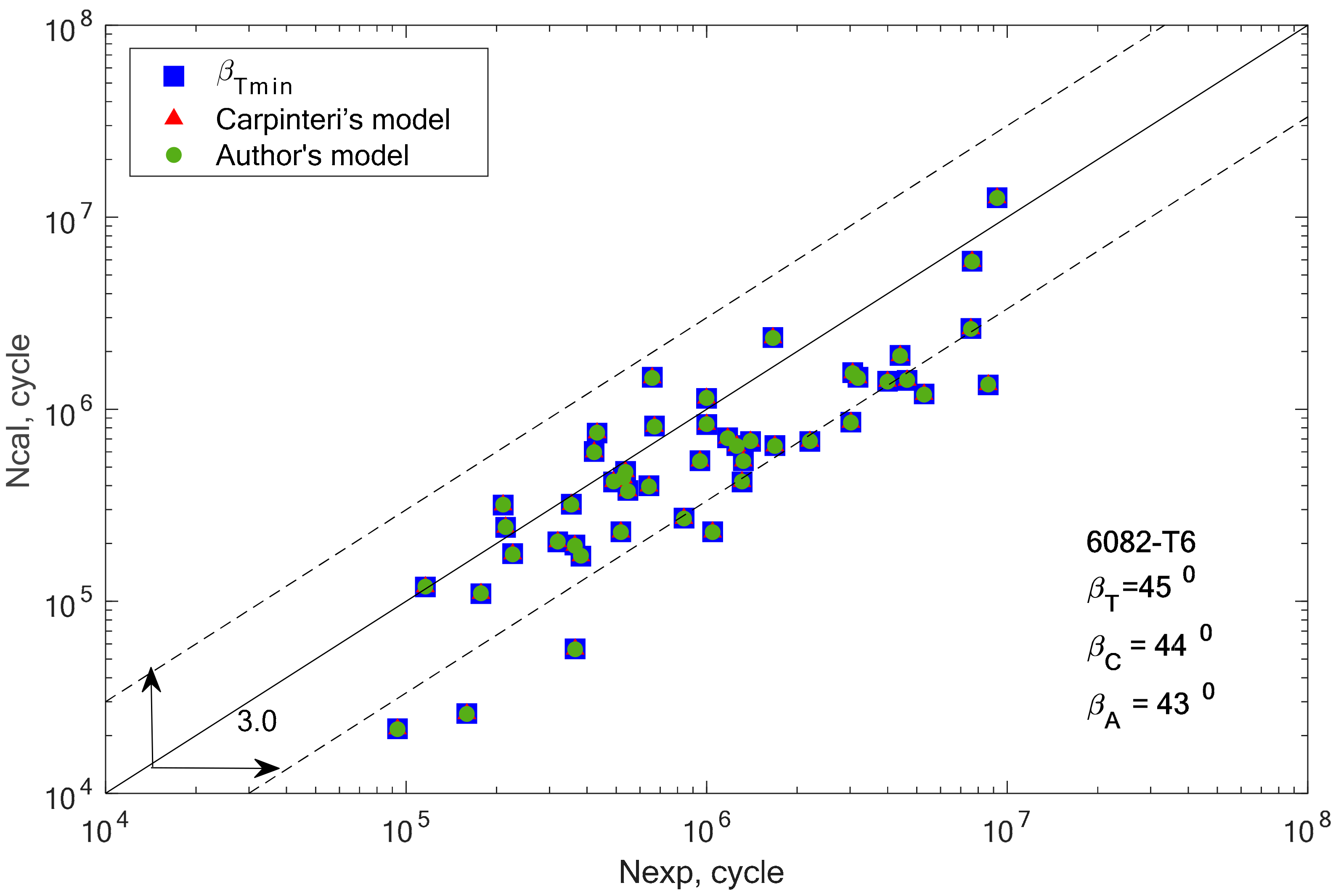
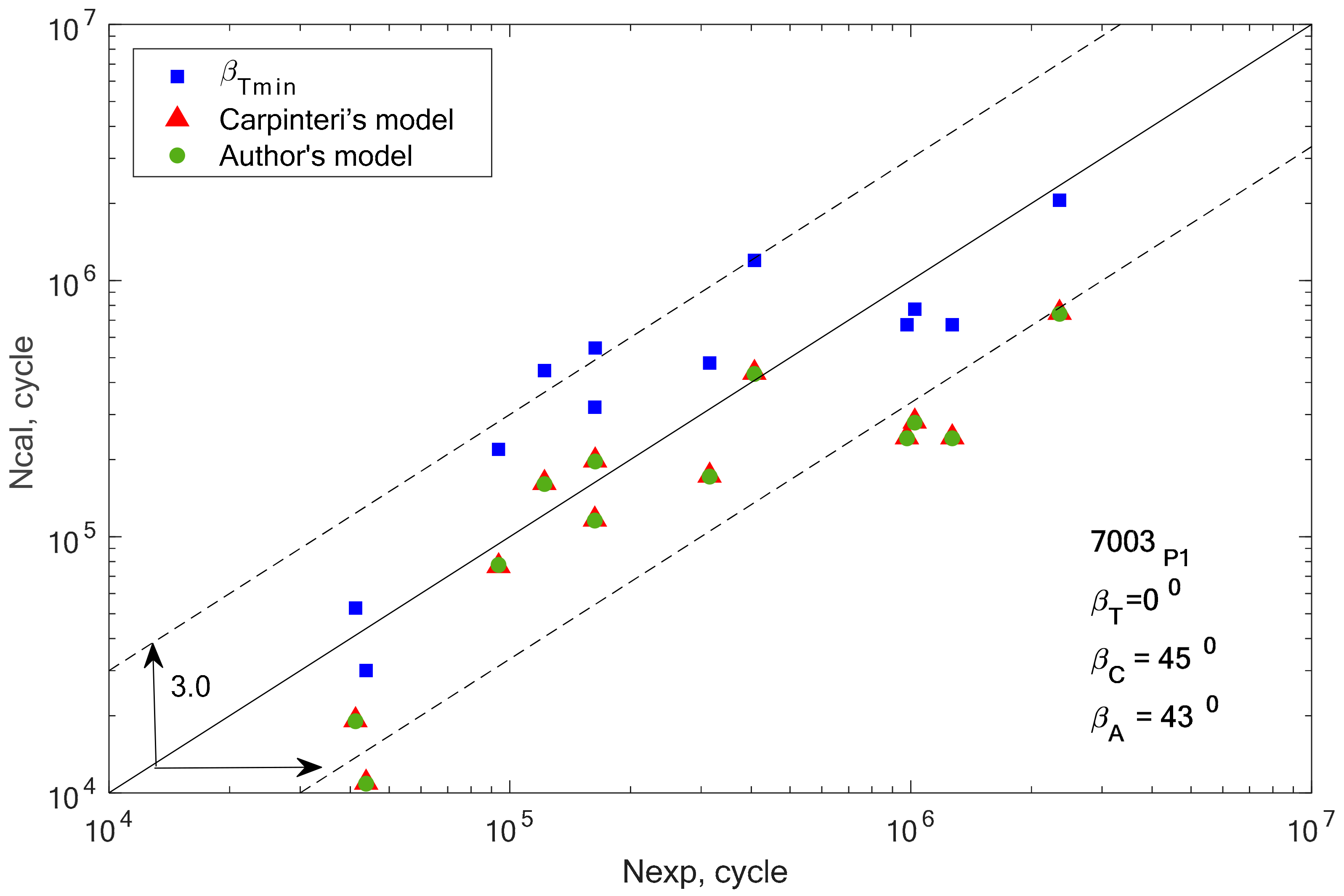
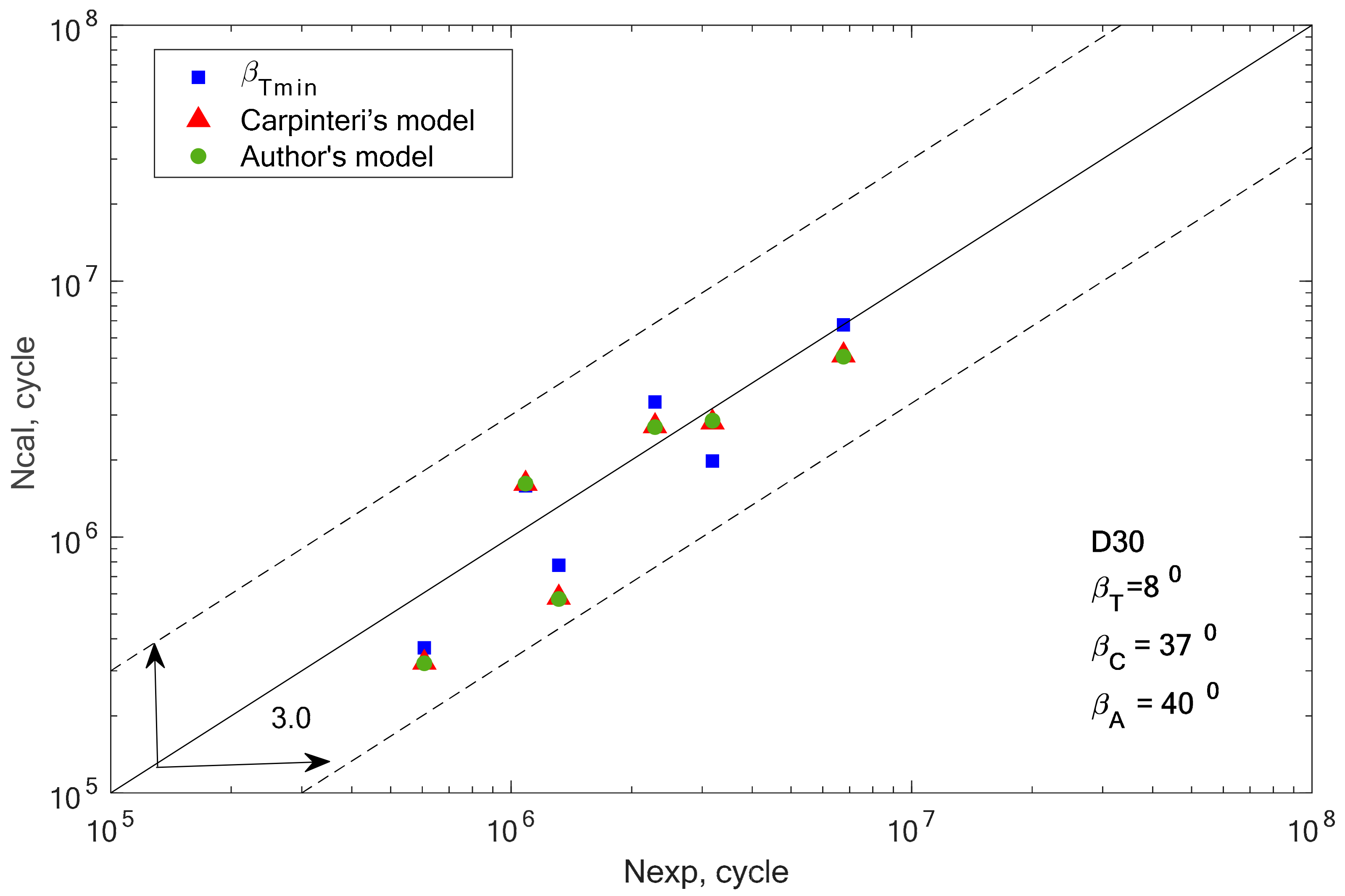
In the group of aluminium alloys, it can be observed that the two analyzed models gave very similar fatigue life results. For two aluminium alloys 2017A-T4 and 6082-T6, these computational points coincide with the results obtained for the βT angle. In other cases, the results calculated using Equations (19) and (32) are similar, but with a greater scatter than those obtained for βT.
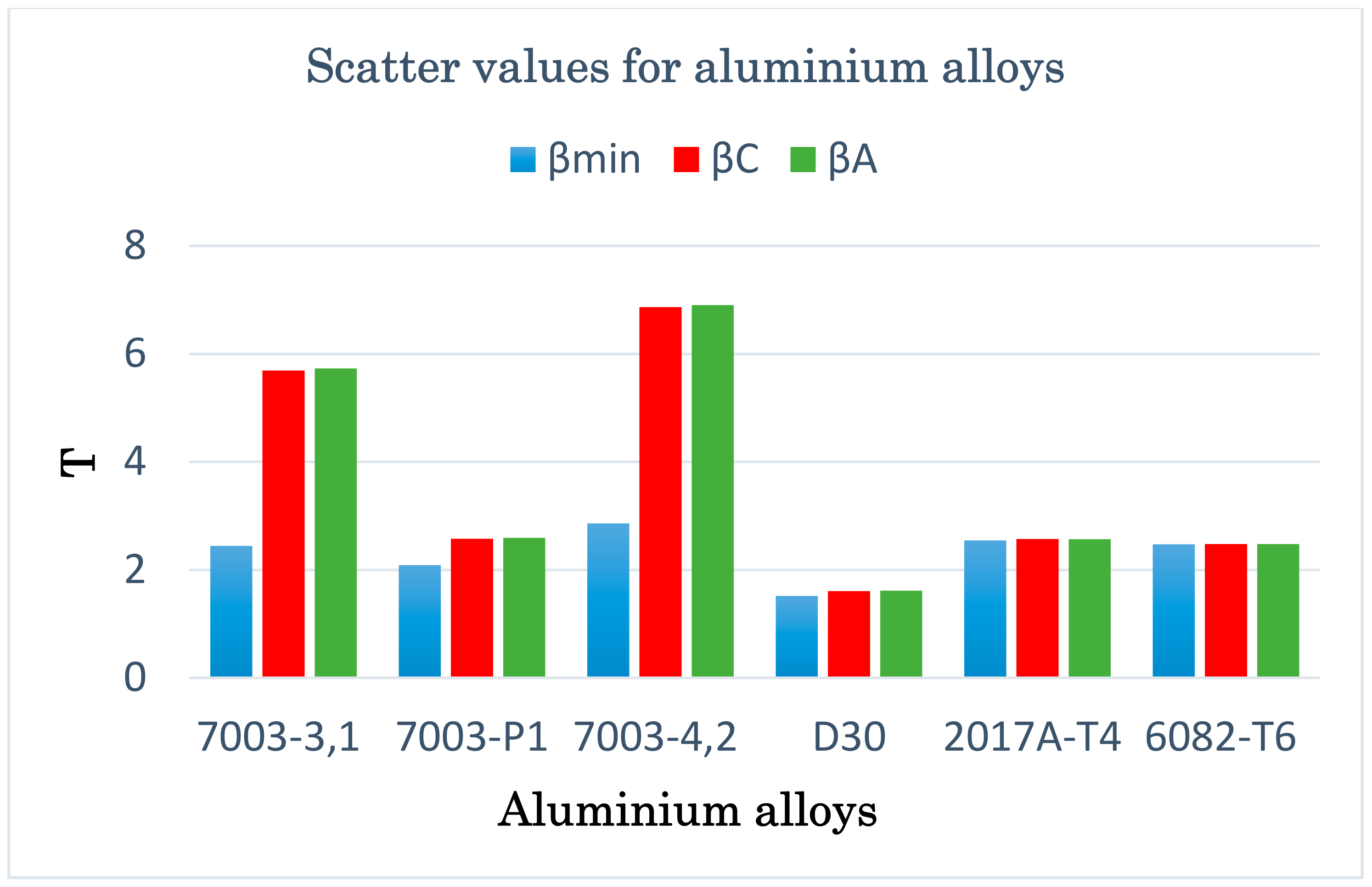
Apart from the graphical verification of the proposed model, it is also necessary to calculate the fatigue life scatter for each of the analyzed computation methods. Using the formula for logarithmic correlations of experimental and computational fatigue life, the scatter was calculated for all analyzed materials and applied models, and the results are presented in graphic form in
Figure 14.
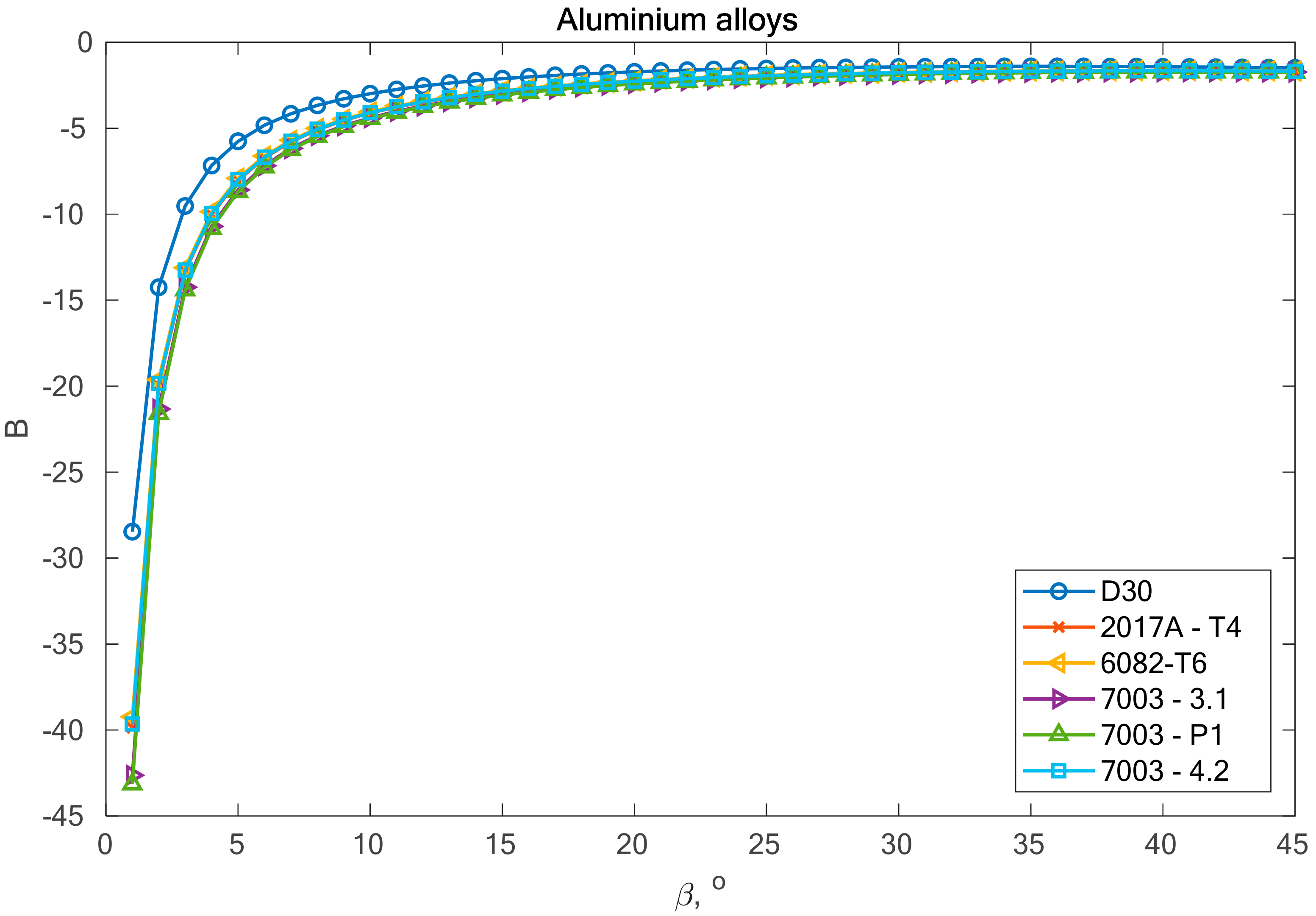
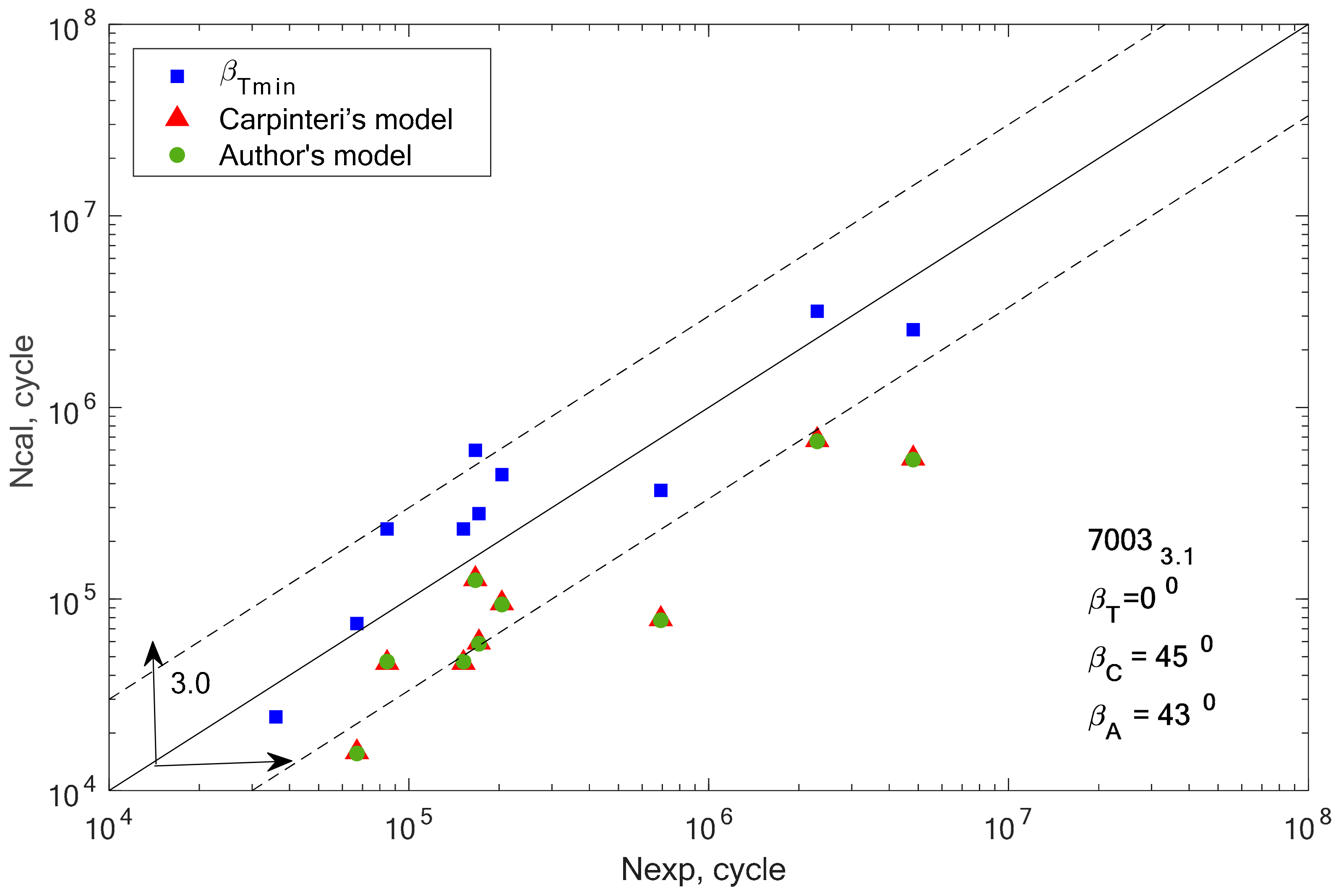
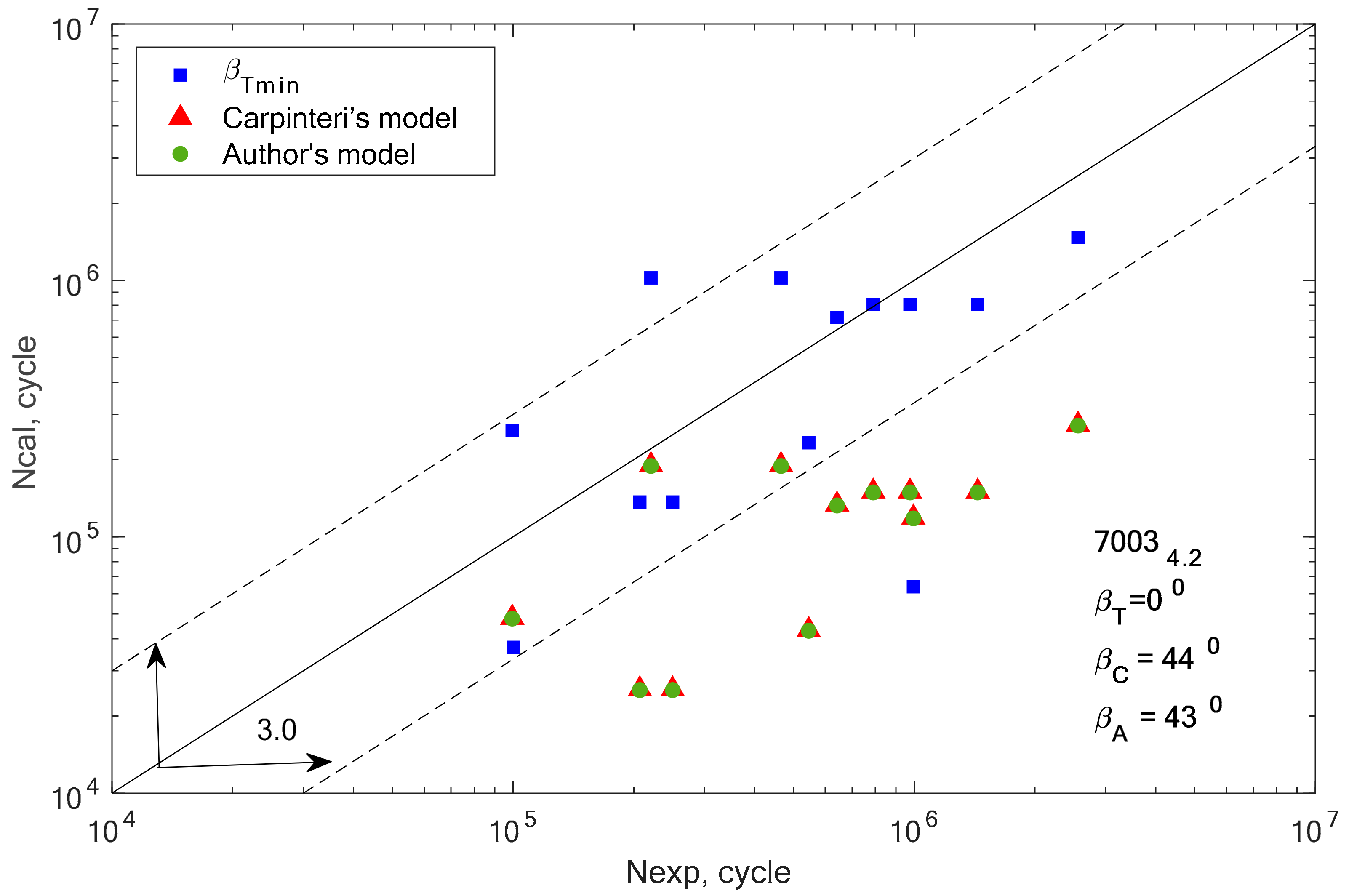
In the case of alloys 7003-3.1 and 7003-4.2, only one value (β = 0°) meets this condition. This can be the cause of very high scattering and inconsistent results. In addition, we can link these incompatibilities to the plastic working. These alloys were additionally cold rolled in contrast to alloy 7003_P1.
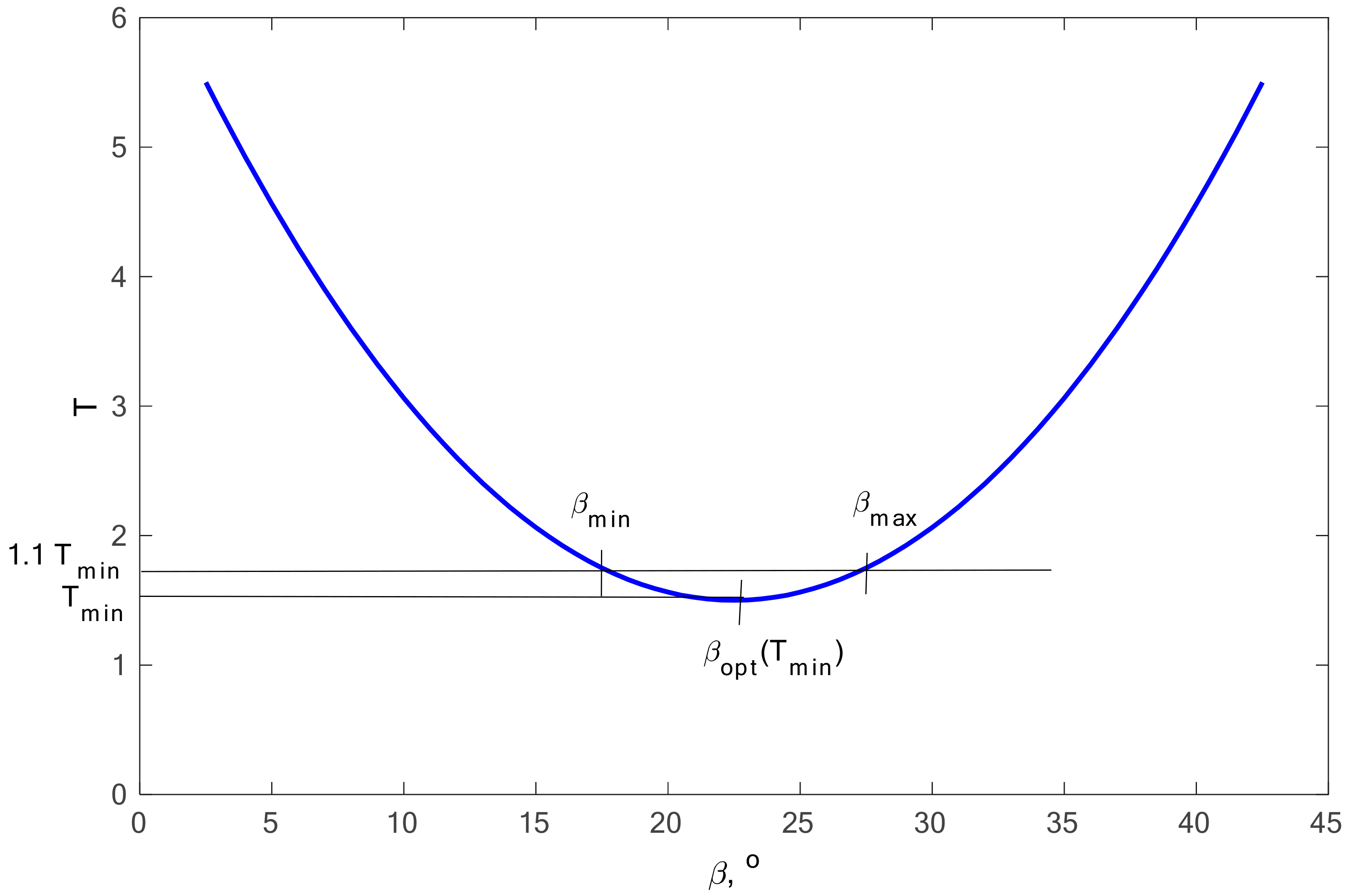
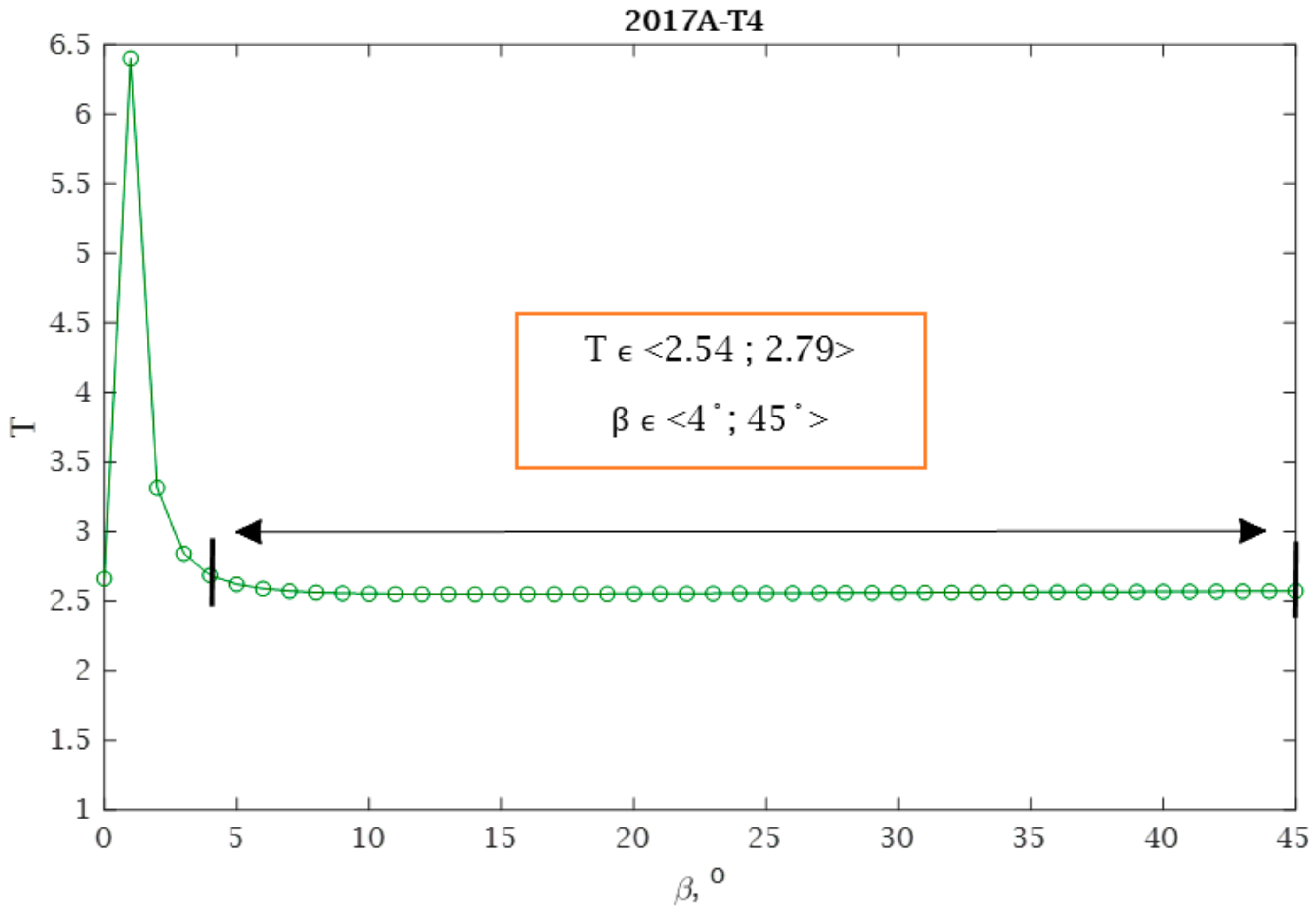
For all aluminum alloys analyzed, calculations were carried out in accordance with the proposed conditions presented in
Section 2.4. Using Equation (34), the optimum angle
β was calculated and an example of the distribution for the selected material is shown in
Figure 15.
Table 5 summarizes detailed calculations concerning condition I.
By analyzing the presented graph and values from
Table 5, it can be noticed that the scatter values vary depending on the value of the
β angle. The assumption is that the scatter value can vary by up to 10%, taking a different form depending on the material. For example, for the 2017-T4 aluminium alloy, the assumption is fulfilled for angles
β within the range β ϵ <4°,45°>. This means that the fatigue life results calculated for angles within this range will have similar values. With 7003-3.1 and 7003-4.2, only one angle value
β = 0° satisfies this requirement.
The analysis for the proposed Condition II was conducted for all aluminium alloys and a detailed summary was presented in
Table 6. Values of scatter for oscillatory bending (
Tσ) and bilateral torsion
(Tτ) were also included in the table.
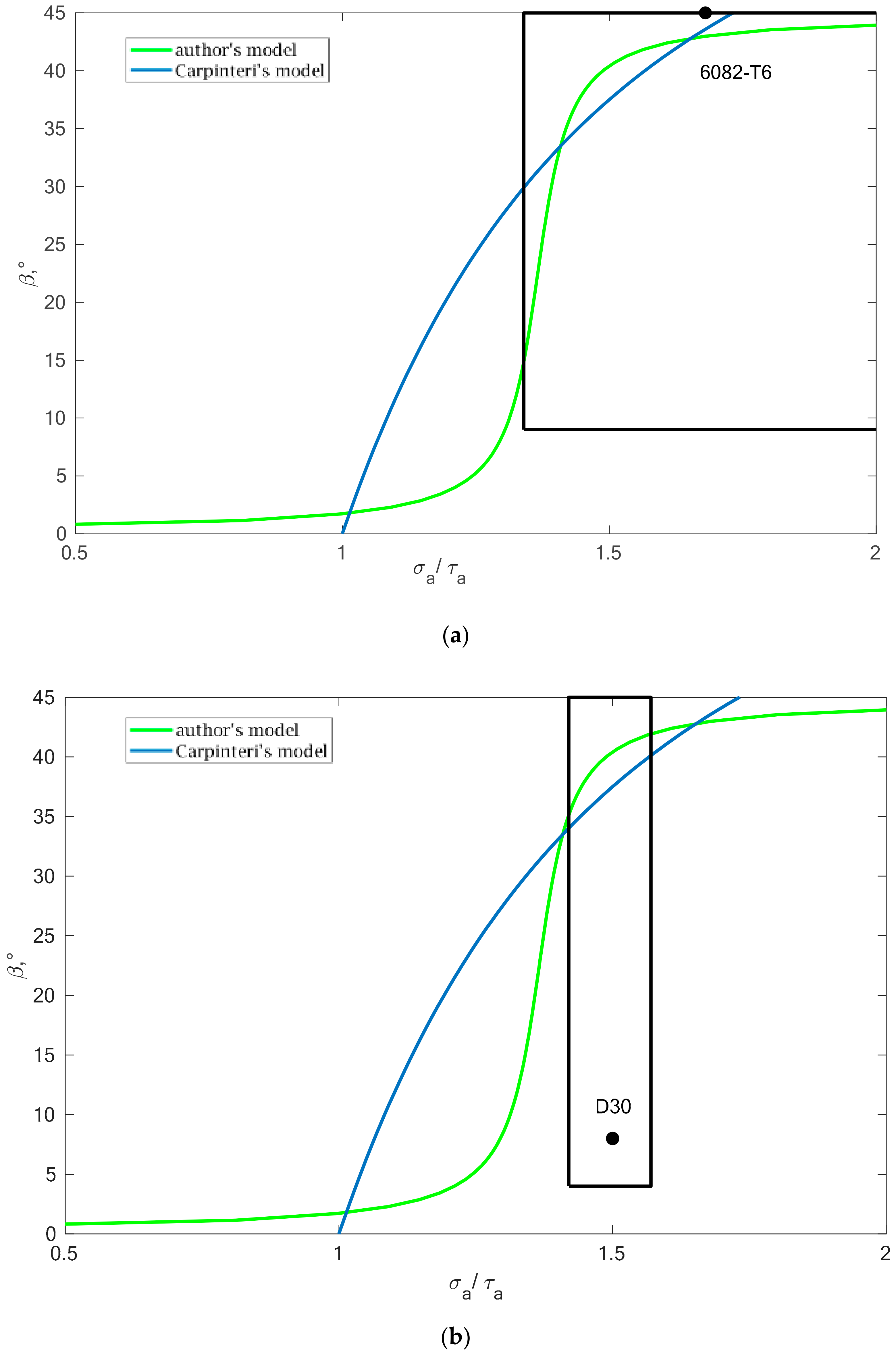
Using the data presented in
Table 5 and
Table 6, in terms of the relationship between the
β angle value and the ratio of normal to tangent stresses (
B2), the fields were marked with where the obtained results of design fatigue life will be similar. The analysis for two selected materials is presented in
Figure 16.