Fatigue Life Appraisal and Its Corrected Stress Intensity Factor for Repaired Off-CentrallyCracked Aluminum Plates
Abstract
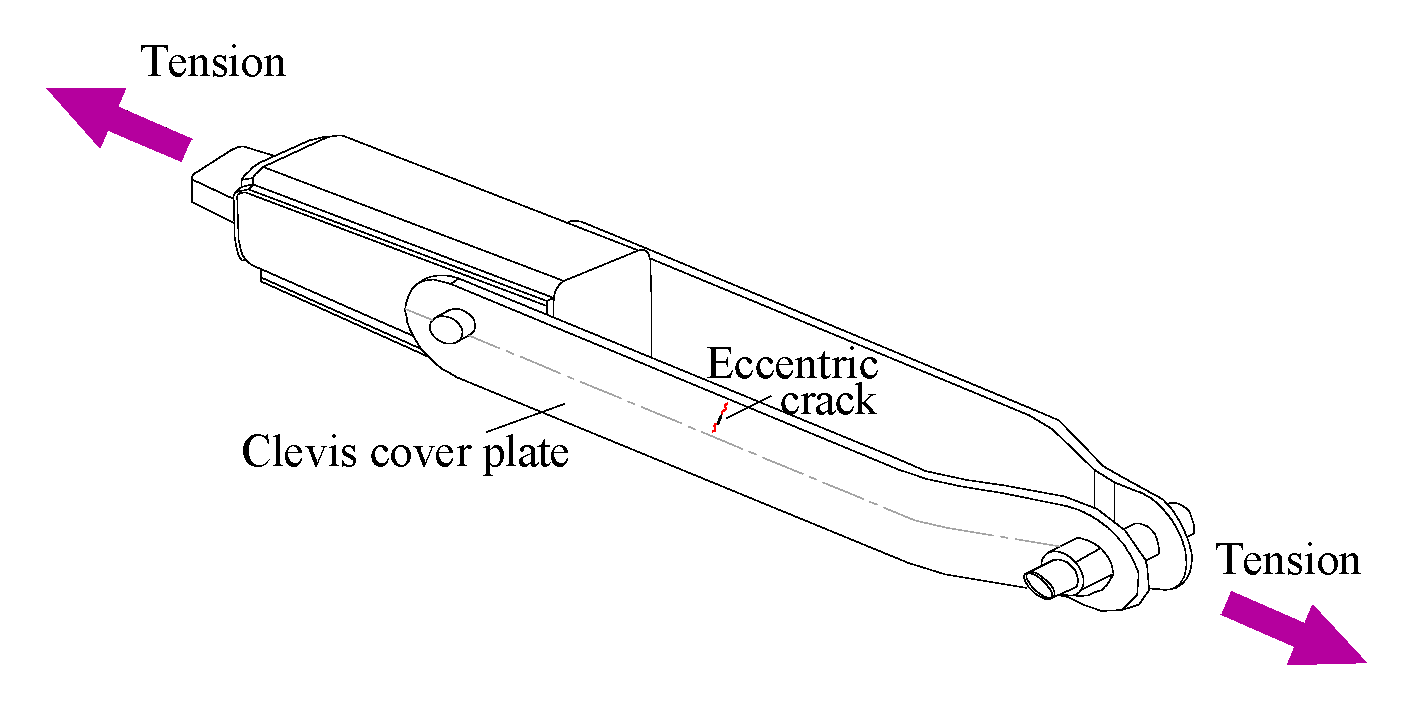
1. Introduction
2. Experimental Procedure and Results
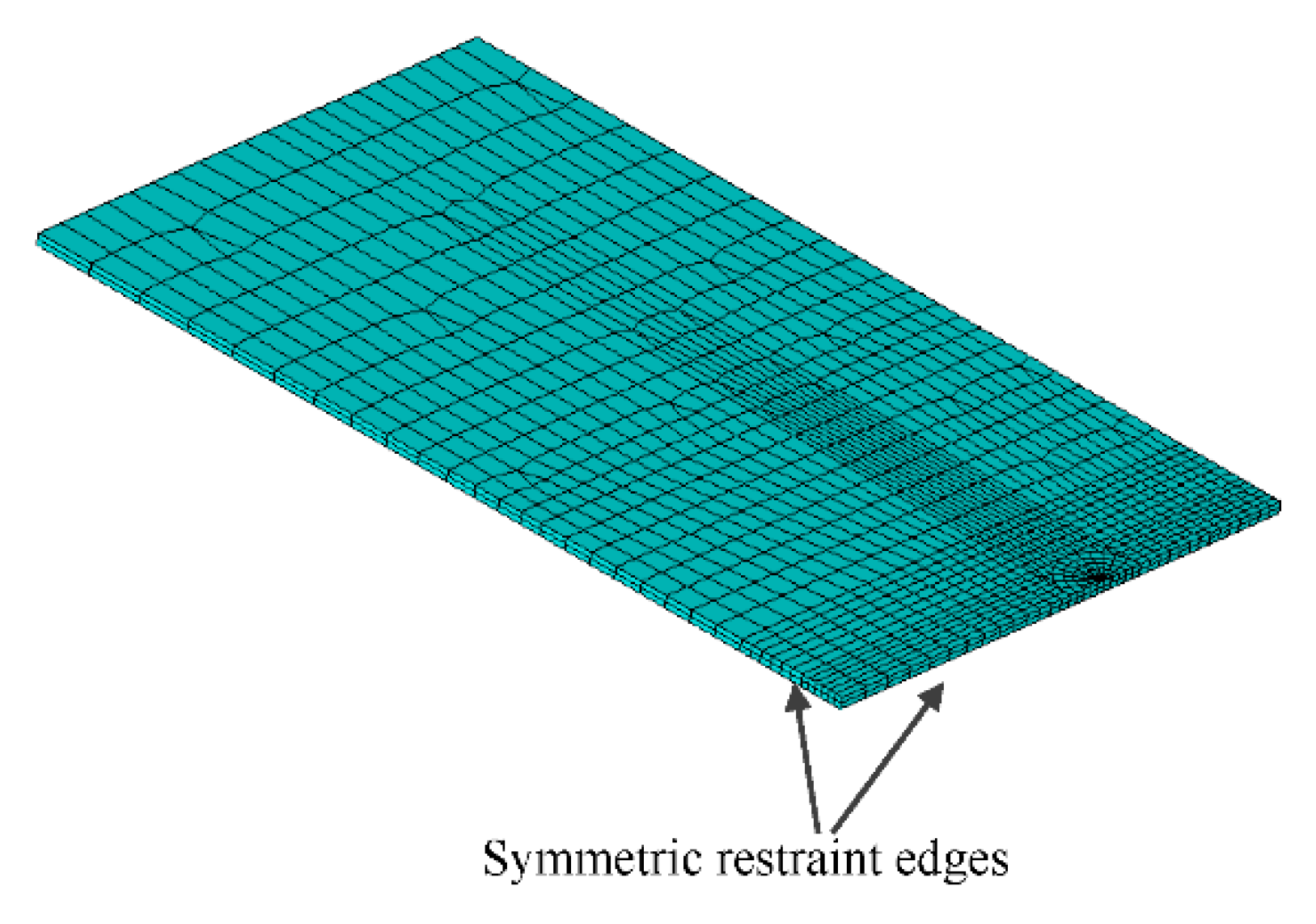
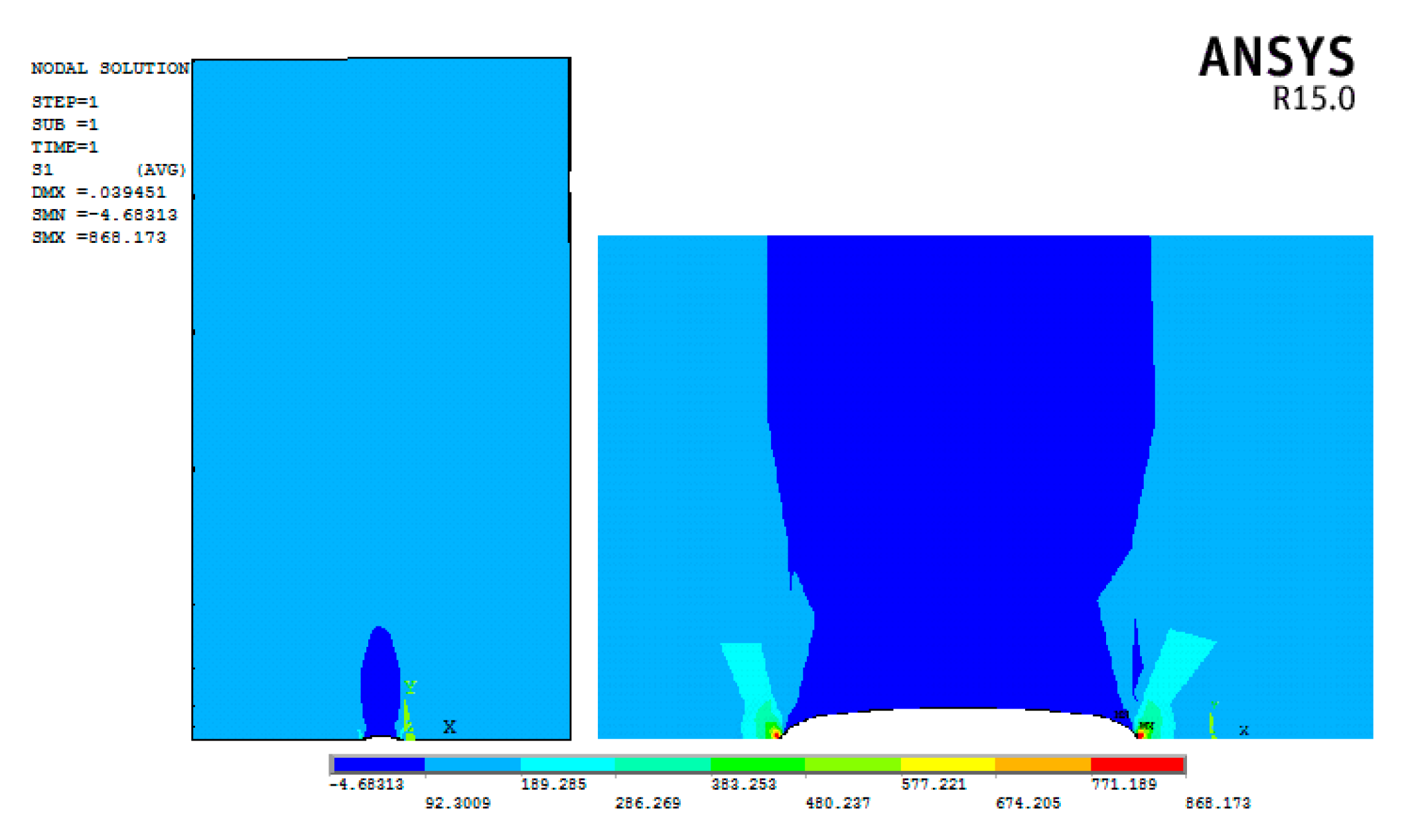
3. Finite Element Analysis
4. Results and Discussion
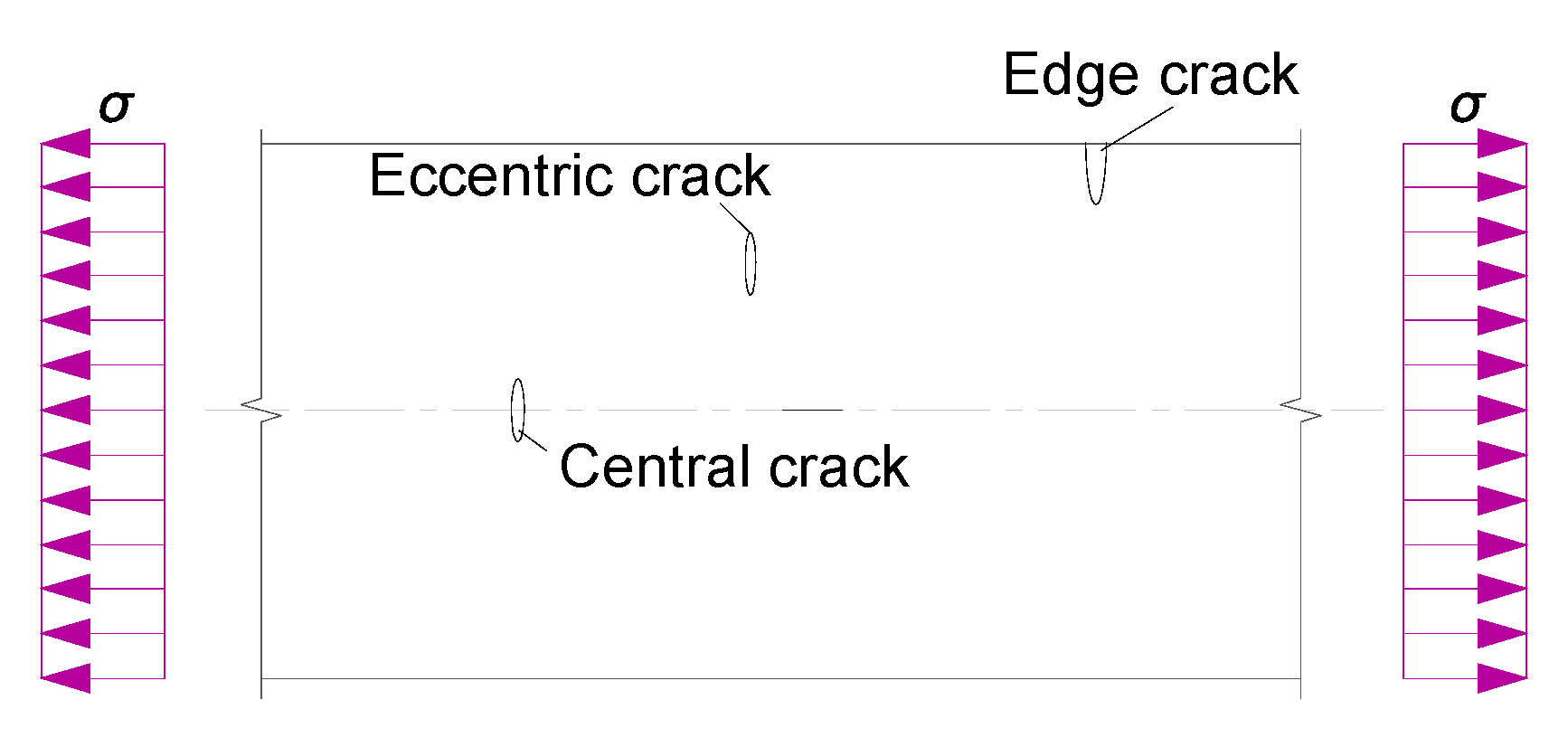
4.1. Summary of KI and Fw Theoretical Equations for Off-Central, Central and Edge Cracks
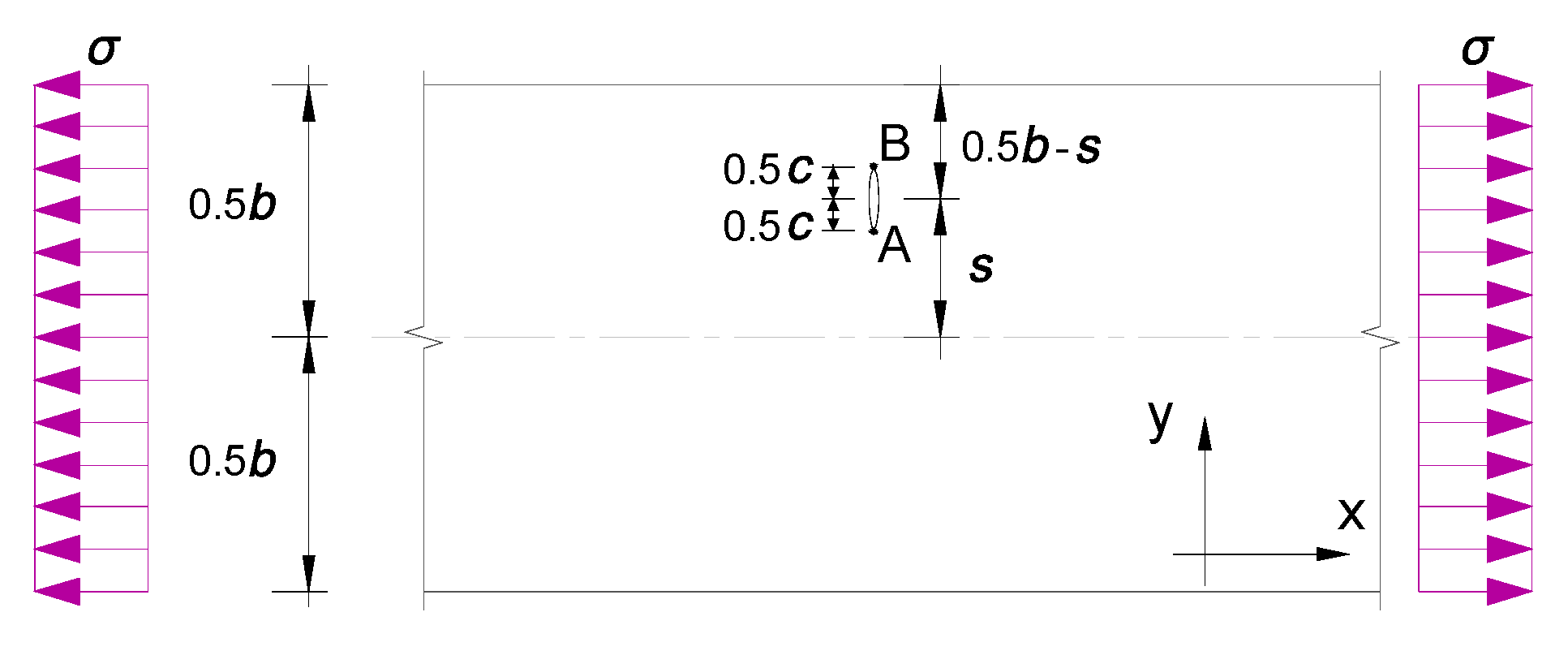
4.1.1. Crack Line Stress Field Method for Off-Centrally Cracked Case
4.1.2. The Westergaard Function Based Method for Off-Centrally Cracked Case
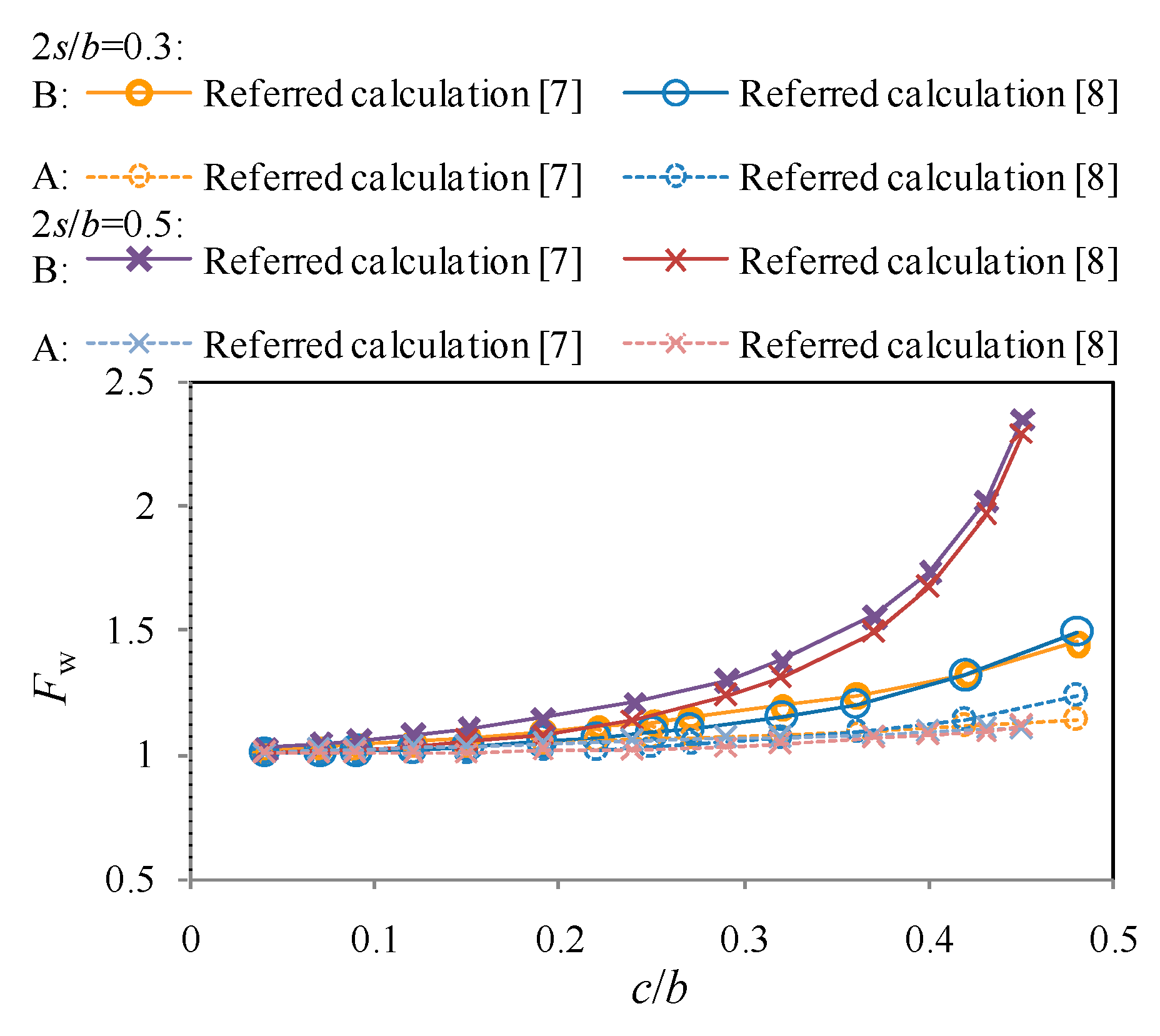
4.1.3. Comparison of Referred Calculations]
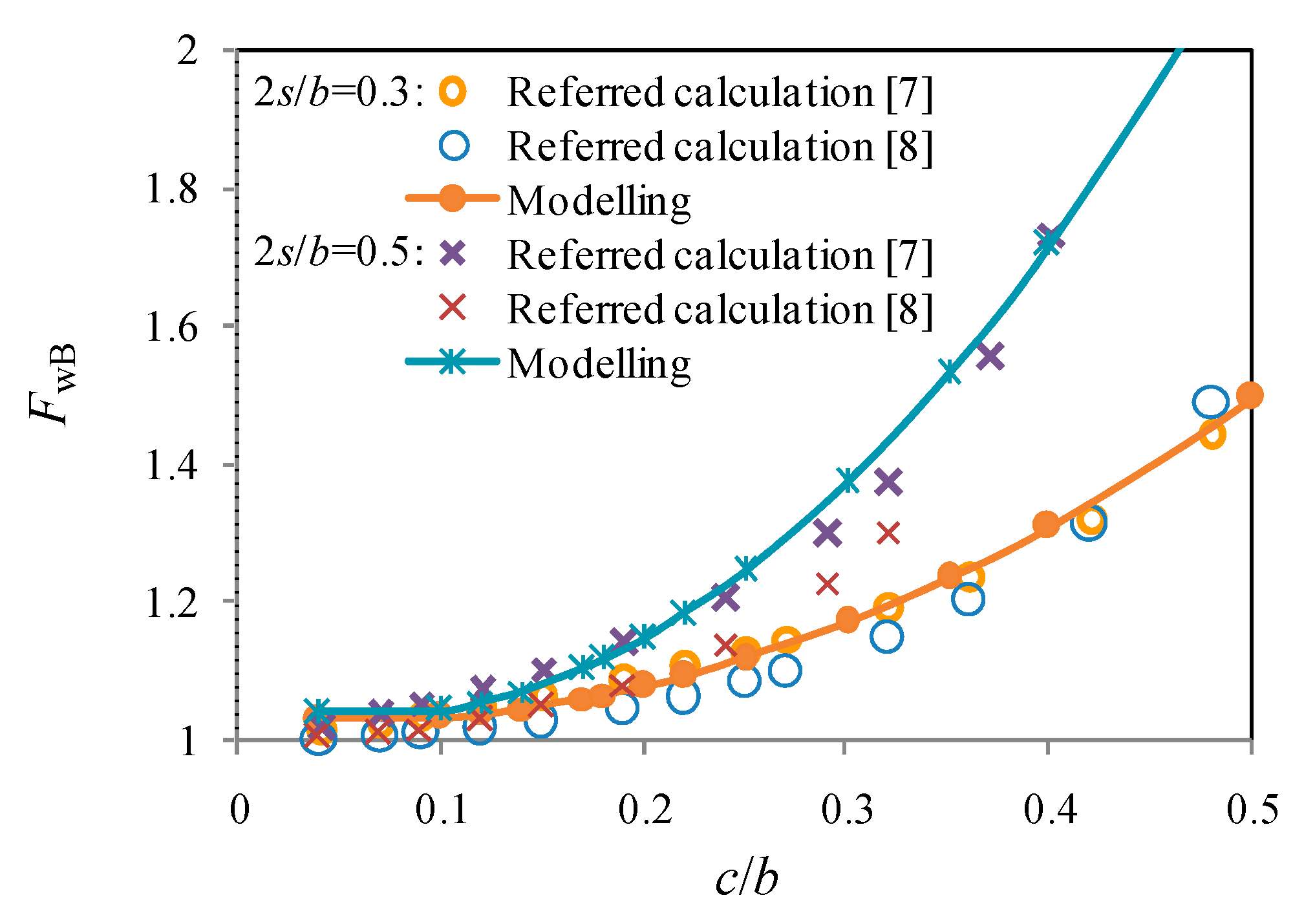
4.2. Finite Element Analysis Based Evaluation of Fw for Off-Centrally Cracked Plates
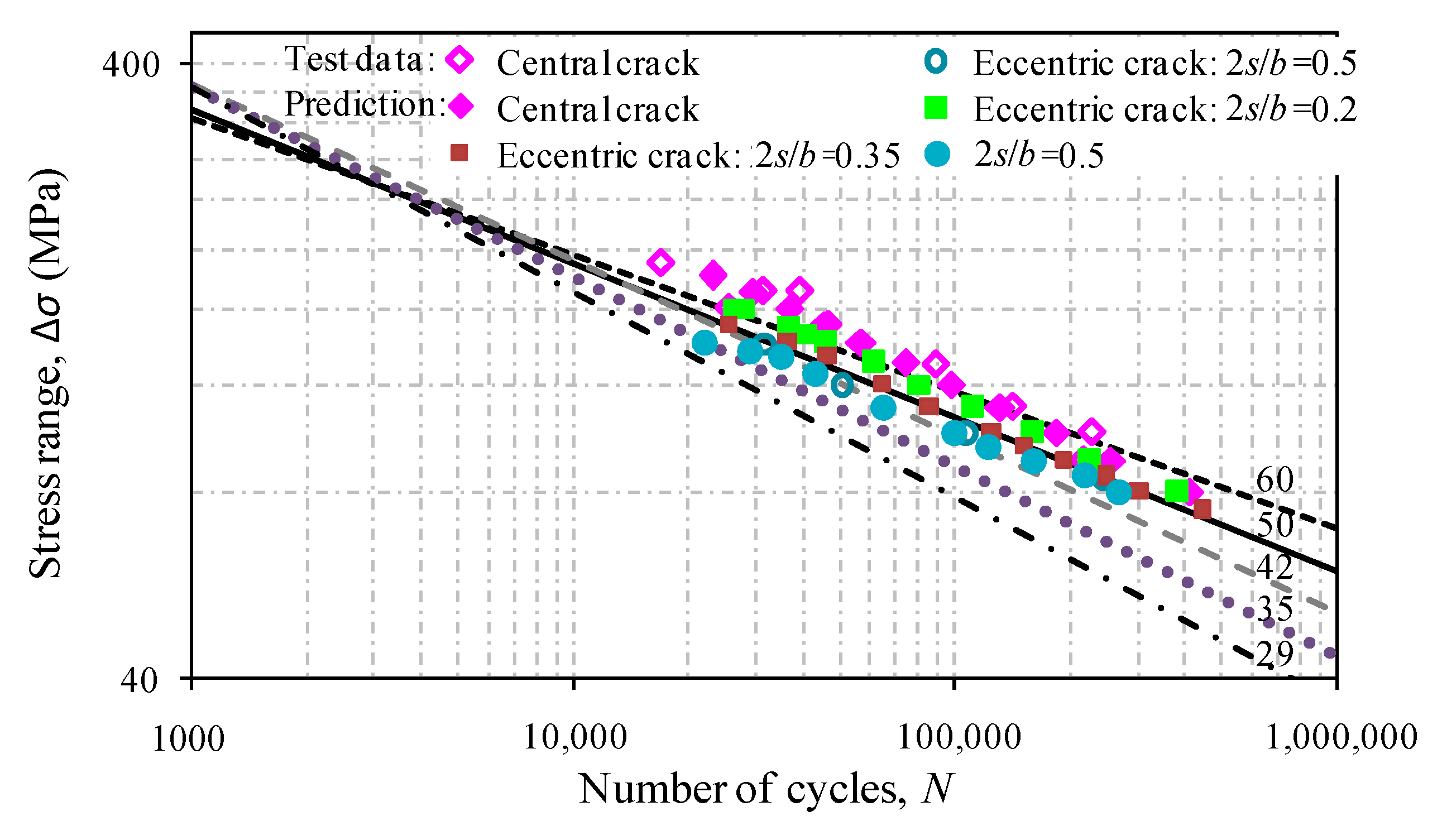
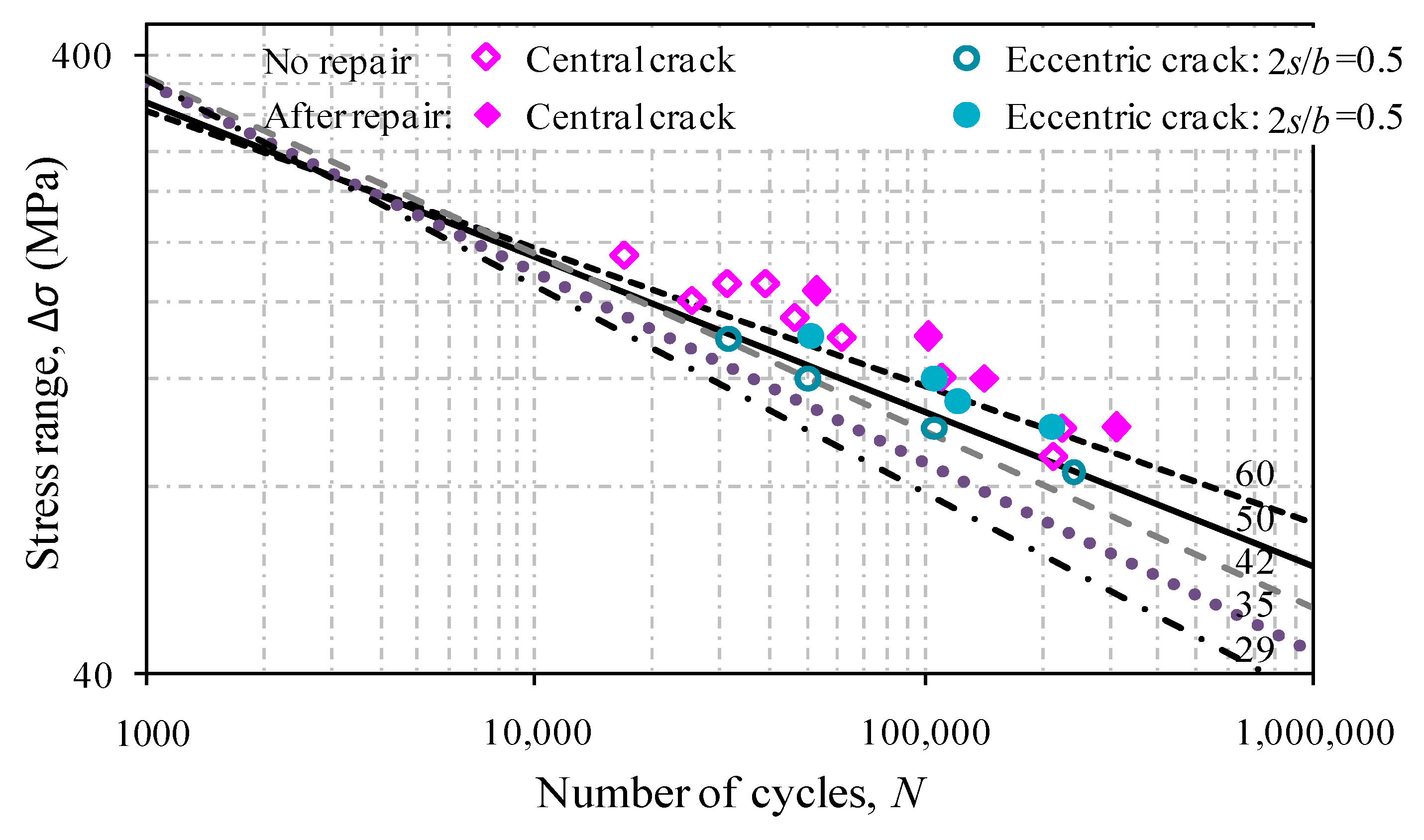
4.3. Fatigue Life Evaluation
5. Concluding Remarks
- The developed finite element parametric study-based poly-fit equation for the boundary correction coefficient incorporating the eccentricity ratio and the crack size ratio is demonstrated to agree well with referred calculations. Moreover, it fits in well between centrally cracked cases and edge crack casesfor the off-centrally cracked aluminum plates.
- The fatigue life prediction on the basis ofthe Forman equation accounting for the crack in linear growth and accelerated growth is shown to correlate well with the test results of aluminum plates with central cracks and off-central cracks. The corresponding S-N curves are also comparable to those suggested by codified curves.
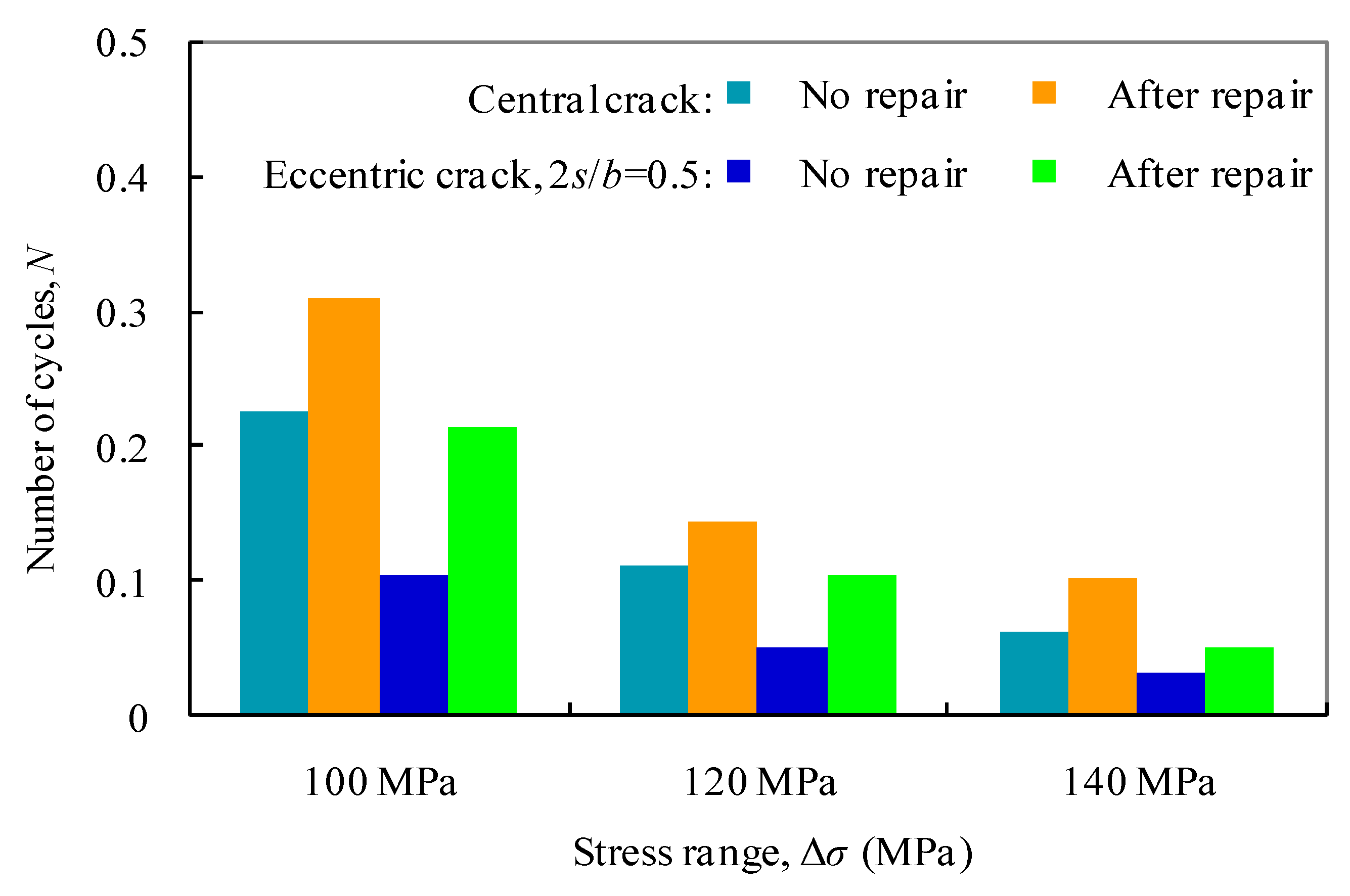
- The beneficial effect of patched laminate repair can be identified from the increase in test fatigue lives by 30–60% and 90–120% for centrally cracked and off-centrally cracked aluminum plates, respectively. Thus, the repair at the crack tip close to the plate edge is deemed to be effective in the fatigue life improvement for off-centrally crack aluminum plates.The strengthening effect of patched laminate repair, however, was not modelled in detail, and therefore requires more experimental work in furthering the correction of defined parameters in the fatigue life prediction.
Author Contributions
Funding
Conflicts of Interest
References
- Cho, J.G.; Kim, J.W.; Koo, J.S. A Study on Fatigue Strength Improvement for Tension Clampof Railway Using Work Hardening. IOP Conf. Ser. Mater. Sci. Eng. 2019, 491, 012028. [Google Scholar] [CrossRef]
- Park, Y.C.; An, C.; Sim, H.; Kim, M.; Hong, J.-K. Failure analysis of fatigue cracking in the tension clamp of a rail fastening system. Int. J. Steel Struct. 2019, 19, 1570–1577. [Google Scholar] [CrossRef]
- Huliraj, R.V.; Janardhana, H.L. Aircraft Mechanical Systems. In Aerospace Materials and Material Technologies; Indian Institute of Metals Series; Prasad, N., Wanhill, R., Eds.; Springer: Singapore, 2017. [Google Scholar]
- Skorupa, A.; Skorupa, M. Riveted Lap Joints in Aircraft Fuselage: Design, Analysis and Properties; Springer: Dordrecht, The Netherlands; Berlin/Heidelberg, Germany; New York, NY, USA; London, UK, 2012. [Google Scholar]
- Research Institute of Aviation. The Handbook of Stress Intensity Factors; Science Press: Beijing, China, 1981. (In Chinese) [Google Scholar]
- Isida, M. Stress-intensity factors for the tension of a neccentrically cracked strip. J. Appl. Mech. 1966, 33, 674–675. [Google Scholar] [CrossRef]
- Wang, Q. A simple expression of SIF for a neccentrically cracked plate. Mech. Eng. 1997, 19, 31–32. (In Chinese) [Google Scholar]
- Wang, W.; Rans, C.; Benedictus, R. Analytical solutions for crack opening displacements of eccentric cracks in thin-walled metallic plates. Thin-Walled Struct. 2018, 123, 371–381. [Google Scholar] [CrossRef]
- Wang, F.; Huang, X.P.; Cui, W.C. Stress intensity factor and ultimate tensile strength analysis of eccentrically cracked plates. J. Ship Mech. 2005, 3, 97–110. [Google Scholar]
- Ismail, A.E. Stress Intensity Factors of Eccentric Cracks in Bi-Material Plates. Appl. Mech. Mater. 2014, 663, 98–102. [Google Scholar] [CrossRef]
- Han, Q.; Wang, Y.; Yin, Y.; Wang, D. Determination of stress in tensity factor for modeI fatigue crack based on finite element analysis. Eng. Fract. Mech. 2015, 138, 118–126. [Google Scholar] [CrossRef]
- He, X.; Dong, Y.; Yang, B.; Li, Y. A wide range stress in tensity factor solution for aneccentrically cracked middle tension specimen with clam pedends. Eng. Fract. Mech. 2018, 191, 461–475. [Google Scholar] [CrossRef]
- Ayatollahi, M.; Hashemi, R. Mixed mode fracture in an inclined center crack repaired by composite patching. Compos. Struct. 2007, 81, 264–273. [Google Scholar] [CrossRef]
- KhanMohammed, S.M.A.; BachirBouiadjra, B.; Benyahia, F.; Albedah, A. Analysis of the single over load effect on fatigue crack growth in AA2024-T3 plates repaired with composite patch. Eng. Fract. Mech. 2018, 202, 147–161. [Google Scholar]
- Wang, Z.Y.; Wang, Q.Y. Fatigue strength of CFRP strengthened welded joints with corrugated steel plates. Compos. Part B Eng. 2015, 72, 30–39. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, Q.Y.; Liu, Y. Evaluation of fatigue strength improvement by CFRP laminates and shot peening onto the tension flanges joining corrugated steelwebs. Materials 2015, 8, 5348–5362. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.Y.; Zhang, N.; Wang, Q.Y. Tensile behaviour of open-hole and bolted steel plate srein forced by CFRP strips. Compos. Part B 2016, 100, 101–113. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, Q.Y.; Li, L.; Zhang, N. Fatigue behaviour of CFRP strengthened open-hole steel plates. Thin-Walled Struct. 2017, 115, 176–187. [Google Scholar] [CrossRef]
- Wang, Z.-Y.; Zhang, T.; Li, X.; Wang, Q.-Y.; Huang, W.; Shen, M. Characterization of the effect of CFRP reinforcement on the fatigue strength of aluminium alloy plates with fastener holes. Eng. Struct. 2018, 177, 739–752. [Google Scholar] [CrossRef]
- Seo, D.C.; Lee, J.J. Fatigue crack growth behaviour of cracked aluminium plate repaired with composite patch. Compos. Struct. 2003, 57, 323–330. [Google Scholar] [CrossRef]
- HosseiniToudeshky, H.; Sadeghi, G.; Daghyani, H.R. Experimental fatigue crack growth and crack-front shape analysis of a symmetric repaired aluminium panels with glass–epoxy composite patches. Compos. Struct. 2005, 71, 401–406. [Google Scholar] [CrossRef]
- Lanciotti, A.; Polese, C. Fatigue properties of monolithic and metal-laminated aluminium open-hole specimens. Fatigue Fract. Eng. Mater. Struct. 2008, 31, 911–917. [Google Scholar] [CrossRef]
- Pastor, M.L.; Balandraud, X.; Robert, J.L.; Grédiac, M. Lifetime prediction of aluminium structures reinforced with composite patches. Int. J. Fatigue 2009, 31, 850–858. [Google Scholar] [CrossRef]
- Li, D.; Han, L.; Thornton, M.; Shergold, M.; Williams, G. The influence of fatigue on the stiffness and remaining static strength of self-piercing riveted aluminium joints. Mater. Des. 2014, 54, 301–314. [Google Scholar] [CrossRef]
- Duncheva, G.V.; Maximov, J.T.; Ganev, N. A new conception for enhancement of fatigue life of large number of fastener holes in air craft structures. Fatigue Fract. Eng. Mater. Struct. 2017, 40, 176–189. [Google Scholar] [CrossRef]
- Feddersen, C.E. Discussion in planes train crack toughness testing of metallic materials, ASTMSTP410. ASTM 1976, 1, 77–79. [Google Scholar]
- Bs Group. BS 7910 2005: Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures; Bs Group: London, UK, 2005. [Google Scholar]
- Su, C.; Wei, Y.J.; Anand, L. Anelastic–plastic interface constitutive model: Application to adhesive joints. Int. J. Plast. 2004, 20, 2063–2081. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Wang, Q.Y. Fatigue assessment of welds joining corrugated steel webst of lange plates. Eng. Struct. 2014, 73, 1–12. [Google Scholar] [CrossRef]
- BSI. BS 8118-1: 1991: Structural Use of Aluminium-Part 1: Code of Practice for Design; BSI Group: London, UK, 1999. [Google Scholar]


| Material | Yield Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (MPa) | Elongation (%) | Critical Stress Intensity Factor (MPa·mm0.5) |
|---|---|---|---|---|---|
| Aluminum | 307 | 445 | 7.2 × 105 | 15 | 1181 |
| Carbon Fiber | - | 4216 | 2.52 × 105 | 1.76 | - |
| Adhesive | - | 30 | 4.5 × 103 | 0.9 | - |
| Specimen Series | Test Number | Crack Mode | Repair | 2s/b | c/b |
|---|---|---|---|---|---|
| T1 | 9 | Centrally | × | 0 | 0.15–0.45 |
| T2 | 4 | Centrally | √ | 0 | 0.3 |
| T3 | 4 | Off-Centrally | × | 0.5 | 0.3 |
| T4 | 4 | Off-Centrally | √ | 0.5 | 0.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, X.; Wang, Z.; Zhou, X.; Liu, Z.; Jiang, R.; Gai, W. Fatigue Life Appraisal and Its Corrected Stress Intensity Factor for Repaired Off-CentrallyCracked Aluminum Plates. Materials 2020, 13, 4014. https://doi.org/10.3390/ma13184014
You X, Wang Z, Zhou X, Liu Z, Jiang R, Gai W. Fatigue Life Appraisal and Its Corrected Stress Intensity Factor for Repaired Off-CentrallyCracked Aluminum Plates. Materials. 2020; 13(18):4014. https://doi.org/10.3390/ma13184014
Chicago/Turabian StyleYou, Xiang, Zhiyu Wang, Xiafang Zhou, Zifeng Liu, Ruijuan Jiang, and Weiming Gai. 2020. "Fatigue Life Appraisal and Its Corrected Stress Intensity Factor for Repaired Off-CentrallyCracked Aluminum Plates" Materials 13, no. 18: 4014. https://doi.org/10.3390/ma13184014
APA StyleYou, X., Wang, Z., Zhou, X., Liu, Z., Jiang, R., & Gai, W. (2020). Fatigue Life Appraisal and Its Corrected Stress Intensity Factor for Repaired Off-CentrallyCracked Aluminum Plates. Materials, 13(18), 4014. https://doi.org/10.3390/ma13184014





