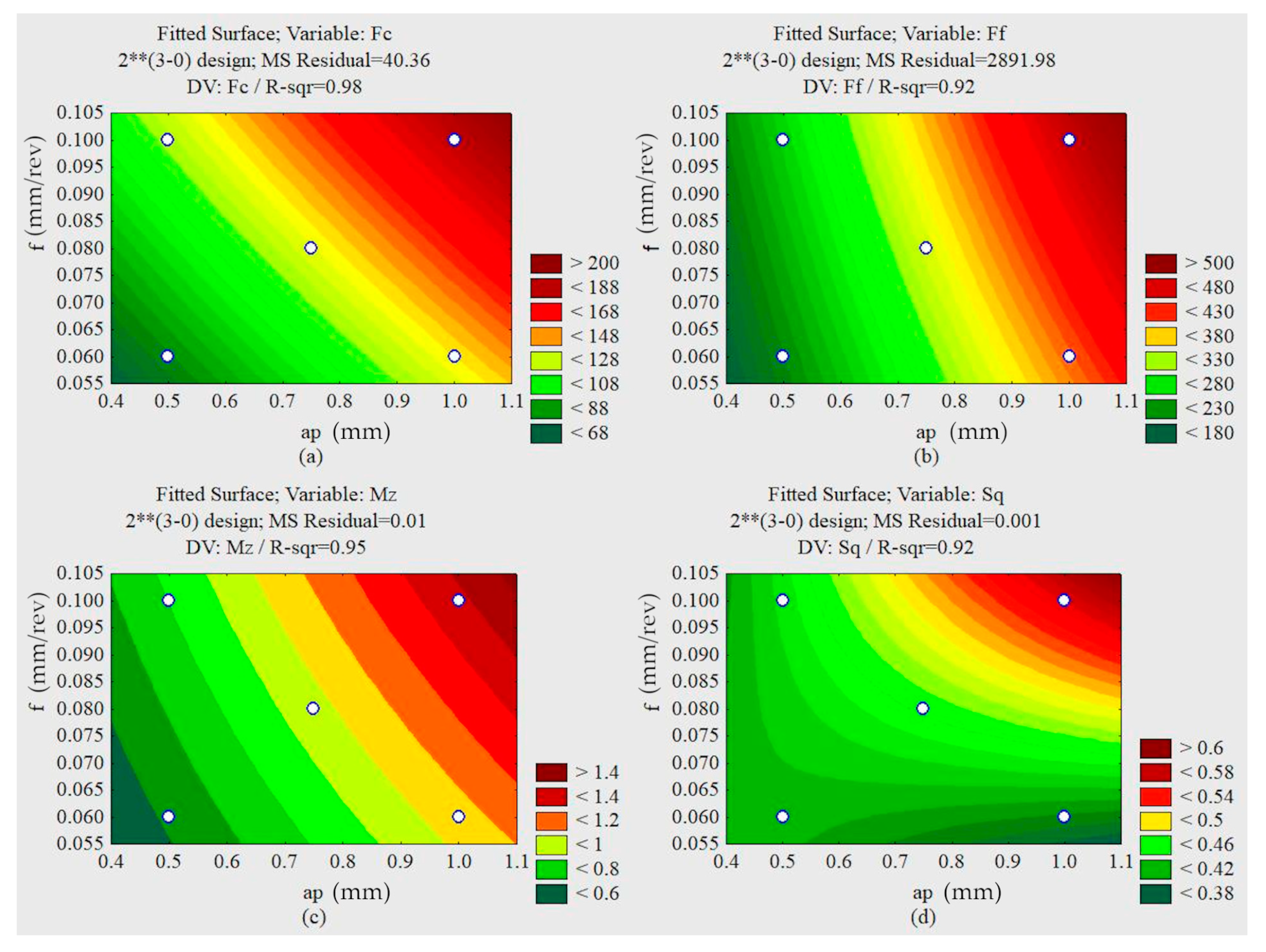
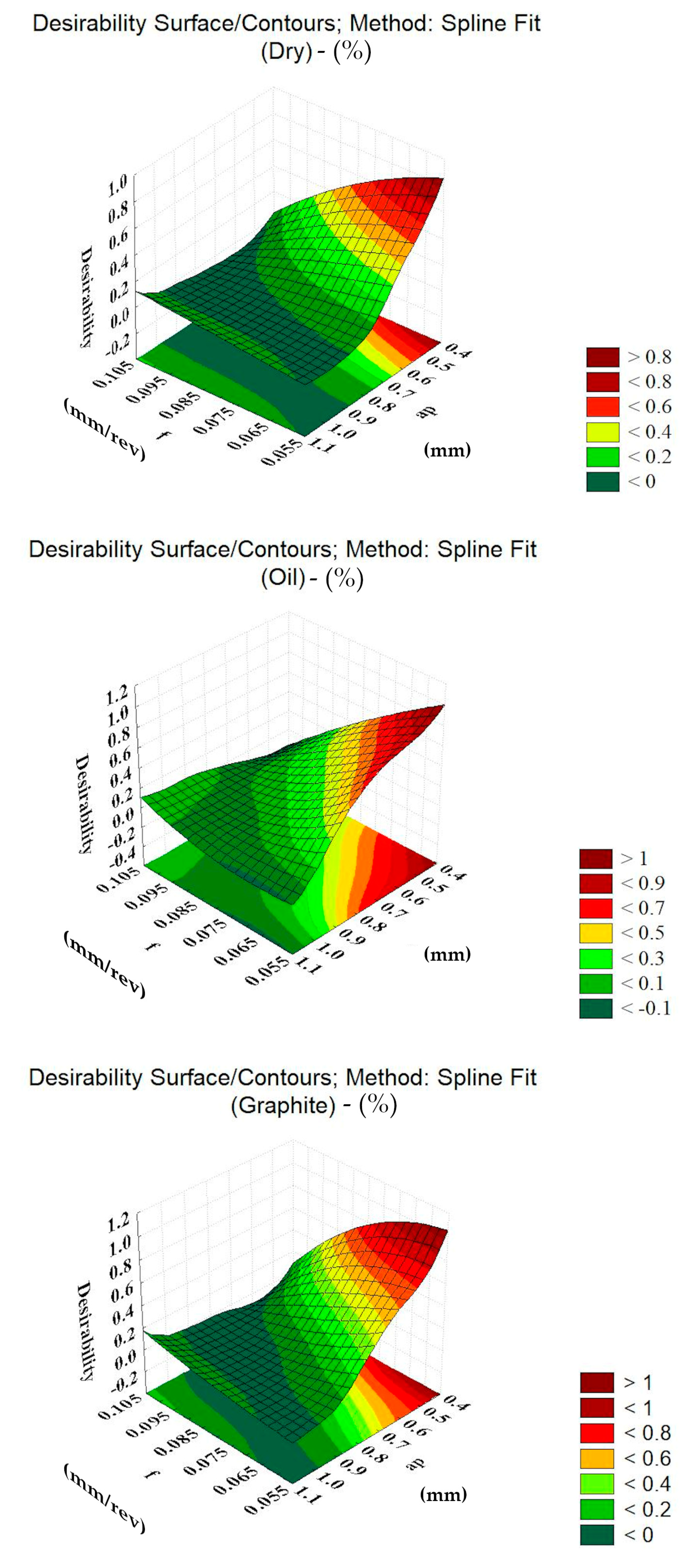
1. Introduction
Machining processes, such as turning, boring, drilling, and milling, are some of the most important techniques used in industries [
1]. In these processes, the material is separated from the original body by the chips, creating a new shape, and it is estimated that it contributes to approximately 5% of the GDP in developed countries [
2]. This removal of wanted parts leads to plastic deformations of work specimens, and most of the fed energy is converted into heat [
3].
Considering the importance of these processes in the industry, mainly in aerospace, which is highly specialized, it is necessary to keep resources and developments to meet the demand when it arises [
4]. Most materials used in the aerospace industry are hard to machine [
5]. The Ti-6Al-4V alloy with an α-β microstructure is estimated to account for 50% of the global titanium metal production, and 80% of this corresponds to the aerospace and medical industries [
6,
7]. According to [
8], 14% of the aerostructure of the Airbus A350-900 XWB [
2], 15% of the Boeing 787 [
3], and 25% of the GE CF6 aeroengine is made from titanium alloys. In addition to the aerospace industry, titanium is also used in the marine, biomedicine, energy, automobile, and chemical industries [
9,
10]. The main properties of titanium are a high hot strength and hardness, and a superior corrosion resistance and fracture toughness when compared with other materials. It has the highest strength-to-weight ratio amongst all structural materials, excellent creep and biocompatibility, a low elastic modulus, and chemical inertness at room temperature [
11]. As a result of these properties, titanium is considered a hard-to-cut material [
12], and the main problems include the fact that the high chemical reactivity makes chips easily adhere to the tool-cutting edge, and the low thermal conductivity (1/6 of that for steel) increases the temperature at the tool’s cutting edge (which can easily reach beyond 1000 °C) [
13,
14,
15,
16]. A low modulus of elasticity and an extreme strength at high temperature generate long ductile chips, a relatively large contact length between the chip and the cutting tool, and a high compressive stress, leading to a poor tool life, or to higher cutting forces [
17].
Since heat generated during machining is a major problem, it is important to choose an adequate lubrication/cooling condition, to improve the machinability of a difficult-to-cut material [
12,
18]. The minimum quantity lubrication (MQL) is an attractive alternative solution for floods, which have occurred for decades and bring health risks to workers [
17,
19], and for dry machining, which can accelerate tool wear and the degradation of piece surface integrity [
11]. This technique has also been used more often, due to pressure from governments, law enforcement, and environmental agencies that have compelled manufacturers to adopt it [
20]. It uses a small amount of cutting fluid in the form of an oil mist that is directly sprayed to the contact zone, helping to reduce friction and cutting forces, and decreasing the surface’s crumple zone by a large amount (~50%) when compared with dry cutting [
21]. Consequently, MQL reduces tool wear [
22,
23]. This technique combines the lubrication from the cutting fluid and the cooling from the air pressure, sometimes reducing the thermal shock caused by flood lubrication [
24], and can be used in drilling, milling, turning, and others. Studies conducted by [
25] also showed a minimization in vibrations along with radial force during turning.
Artificial neural networks (ANNs) model the complex nonlinear relationships between input and output parameters by observing datasets and identifying patterns, without the need to write explicit programs [
4]. An ANN is inspired by the way biological nerves, such as the brain, work to solve problems, and the first artificial neuron was produced in 1943 by McCulloch and the logician Walter Pits [
26,
27]. The ANN and the genetic algorithm (GA) are important alternatives to be used in machining processes, due to their high complexity in optimizing cutting parameters. They have become very popular in recent years due to their capability of learning nonlinear behavior [
28], with many studies conducted. The authors in [
27] studied ANNs to predict the material removal rate and surface roughness in the CNC milling of P20 steel and the results indicating a successful application. The authors in [
9] used a backpropagation neural network (BPNN), and optimized the overall cutting performance during the high-speed turning of the Ti-6Al-4V alloy, and the results achieved a balance among all studied responses. The authors in [
18] investigated the characteristics of different nano-cutting fluids, molybdenum disulfide, and graphite under MQL conditions, using Box–Cox transformation, normal probability plots, and analysis of variance (ANOVA) tests. The best choice for the application was chosen, and the machining characteristics of the Inconel-800 alloy were improved. The authors in [
17] studied turning tests with a combination of cooling techniques on titanium (Grade 2). The surface quality measurements, force values, and tool wear were investigated using a combination of ANOVA, and the correlations were established with a success rate of 90%. The authors in [
28] used regression analysis and an ANN to predict the surface roughness during the hard turning of AISI 52100, and found superior results in the ANN application. The authors in [
4] used the friction force computed for 648 experimental trials to develop and optimize ANN architecture prediction during turning with different materials and cutting parameters, and obtained a 12.5% difference between the estimated and measured values. The results obtained in [
24] were even better, with variations from 1% to 4% during a comparative experimental study in three different machining environments (dry air cooling, flood cooling, and minimum quantity cutting fluid). The authors in [
29] studied the dry machining of hardened steel En31 to identify the influence of input parameters (speed, feed rate, and the depth of cut) on the surface roughness, and it was possible to analyze the process sensitivity. The authors in [
30] used an ANN to predict the cutting force by monitoring the spindle and the individual drives, obtaining success in application during 2.5D milling in E355 steel. The authors in [
31] also used an ANN and a GA to predict the minimum surface roughness and chose the best cutting parameters to achieve it. The authors in [
32] described numerous papers in which an ANN was developed using this modern technique for many applications besides machining, showing its versatility.
Over time, statistical tools have been applied and have helped to assist in the process of analyzing problems and making decisions. The design of experiments (DOE) has often been used to design a specific experiment or to define data in a methodology. The collection and organization of data for the experiment should ensure that the process has the best possible yield and that there is safety or a minimal difference in the empirical results related to the collected data.
As demonstrated by a growing number of articles published in the last decade, many researchers in the manufacturing field explore ways of applying artificial neural networks to control or to perform an estimation of a product’s critical quality, and to optimize production processes [
33]. In this respect, many authors use DOE techniques to implement and optimize ANN parameters. According to authors in [
34] the combination of multilayer perceptron with DOE has proven to be an appropriate tool in modeling and problem analysis. Chromium layer thickness predictions on hard chrome plating processes´ results suggest that DOE may be successfully used for the optimization of ANNs´ backpropagation parameters. In another paper on turning, DOE was employed to determine factor levels that benefit network forecasting skills, concluding that the DOE methodology constitutes a better approach to the design of RBF networks for roughness prediction than most trial and error common approaches [
35]. Authors in [
36] comment that an efficient methodology is needed to obtain optimal values for various parameters in artificial neural networks. In their paper, authors used the Gray–Taguchi method to determine the optimal value of various ANN model input parameters trained by different algorithms in a 2.5D milling process modeling.
The results showed that the combination with RNA presents a better performance. In the search for better prediction values, some studies compare statistical methodologies to ANNs. Authors in [
37] studied the AISI316L steel dry turning surface roughness prediction, by comparing ANNs to multiple regression methods. The results found by the methods indicate a better artificial neural networks accuracy. A study involving the prediction of surface roughness in red brass turning was developed using a comparison between a complete factorial planning and ANN. The finding was that, based on ANN percentage error and the regression model, the artificial neural network was considered more accurate than the regression model [
38]. Authors in [
39] developed a model to investigate C23000 turning cutting parameter effects. Artificial neural networks and multiple regression models were used to model cutting forces based on cutting parameters, using variance analysis. It was concluded that the ANN model was more accurate than the regression model. Another study compared the mathematical regression with ANN, in order to predict the wear of the AISI 304 cutting tool. Experimental design includes four factors at five levels. According to the authors, the artificial neural network model was capable of better tool wear predictions [
40]. A tool wear prediction by artificial neural networks in the Aluminum 7075 milling was proposed by [
41]. Authors subdivided the research using the Taguchi model and ANNs. It was found that ANN prediction correlates very well with experimental results. In a turning paper, DOE was employed to select factor levels that benefit network prediction skills, concluding that the DOE methodology constitutes a better approach to the design of RBF networks for roughness prediction than most trial and error approaches. However, a frequently cited ANN disadvantage is the lack of a systematic way to design high-performance networks [
35]. Another study deals with AISI 1040 steel machining. Response surface and ANN approaches were used. According to the authors, both approaches predict surface roughness accurately [
42]. The authors in [
43] reviewed several publications dealing with modeling and roughness by ANNs in machining processes. The review showed that most of the paper had a roughness (R
a) average prediction, and that little attention was given to the efficiency of the training. Researchers point out the definition of the ideal network topology as the main problem in roughness modeling. Optimization efforts are detected in a small number of publications, and comparisons between topology definition approaches are hardly found. Moreover, with regard to validation, most publications neglect or make this ability unclear. The use of the third validation data set can be found in only a few studies. The use of statistical evaluation to compare trained networks can be found in only one fifth of the peer-reviewed papers, in addition to the lack of a statistical evaluation comparing ANN-based models and models obtained by other methods. According to authors, the ANNs models´ accuracy are points that require more attention and many papers are presented only in graphic forms, thus lacking information as to the results’ reproduction. There is no standard procedure for choosing more appropriate ANN settings, thus becoming a difficult task that depends on many variables. The trial and error method is the procedure most commonly used to identify the best settings [
44]. Based on the peer-reviewed literature, some areas of improvement are suggested, such as the no need to transform or change data, that reveal non-regular periodic movement. In addition, papers focus on network characteristics in a specification phase, with tests being performed to determine errors and R oscillations, and to validate a performance optimization model [
45].
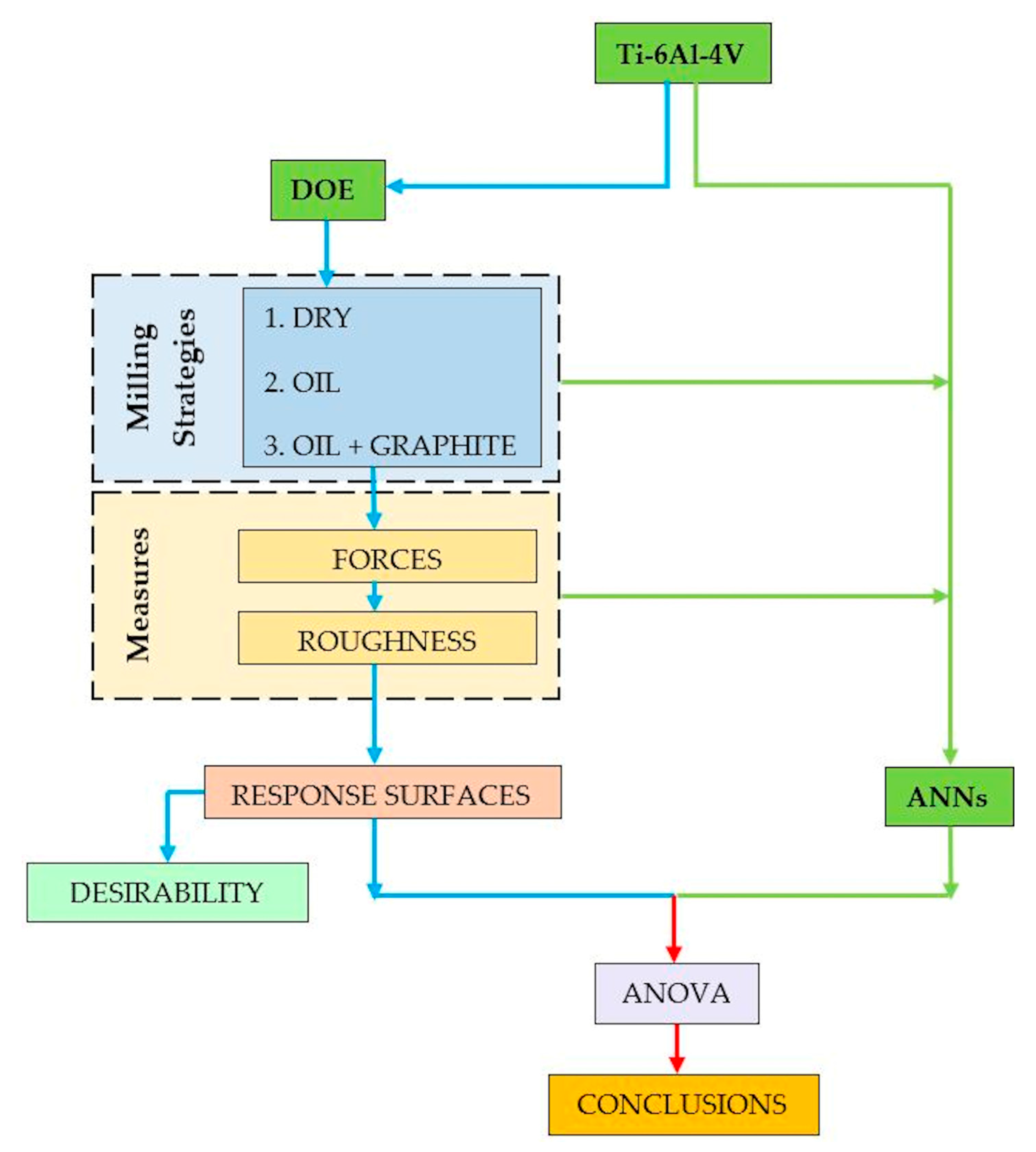
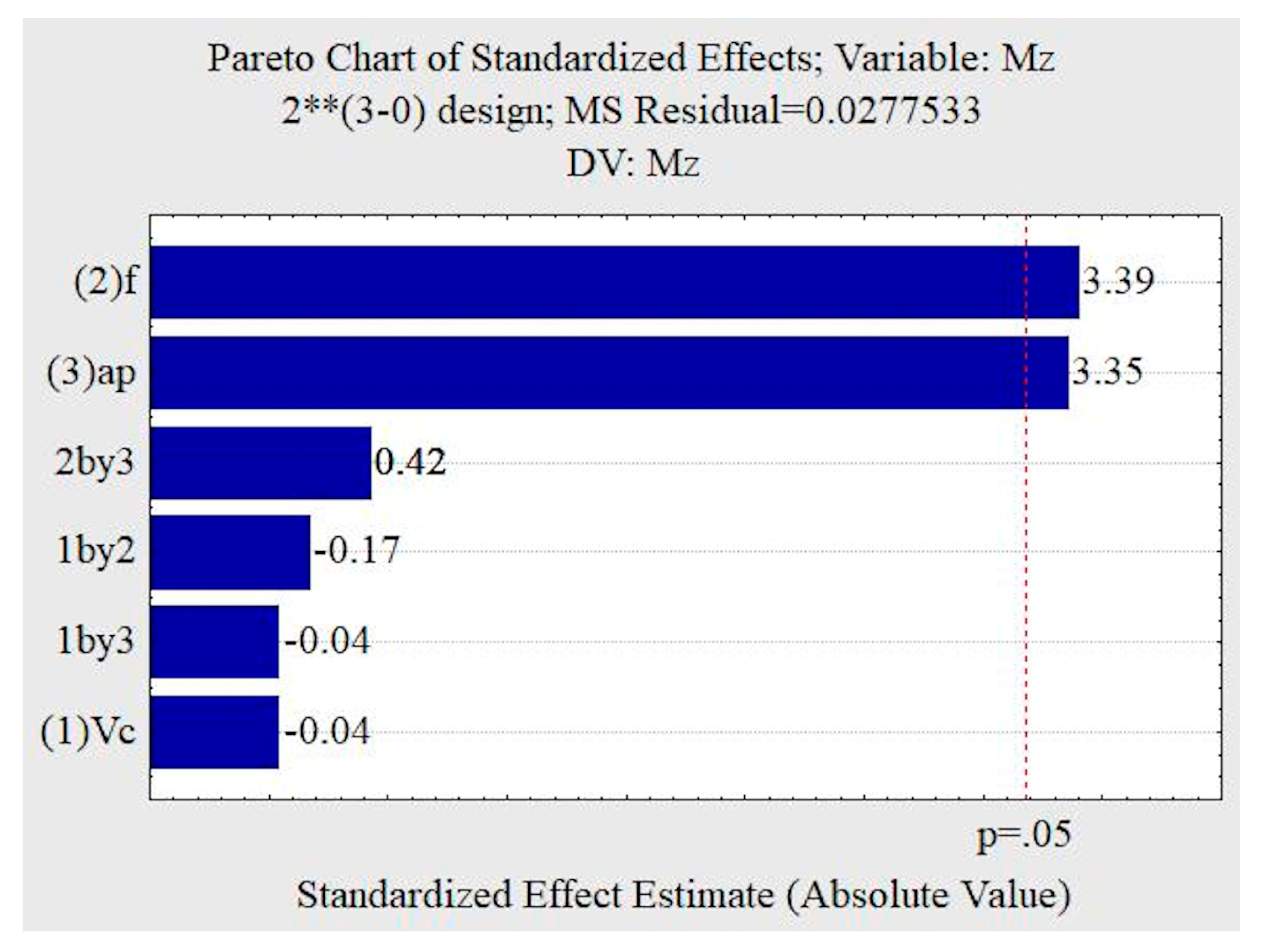
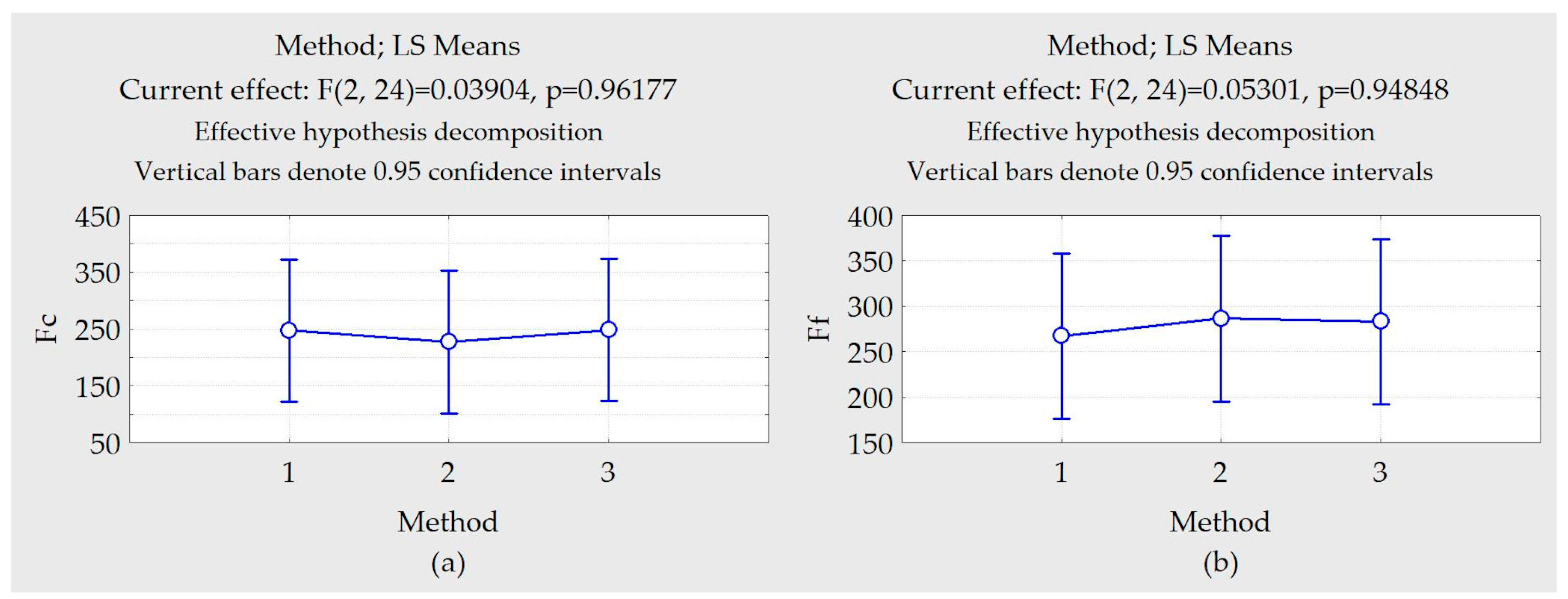
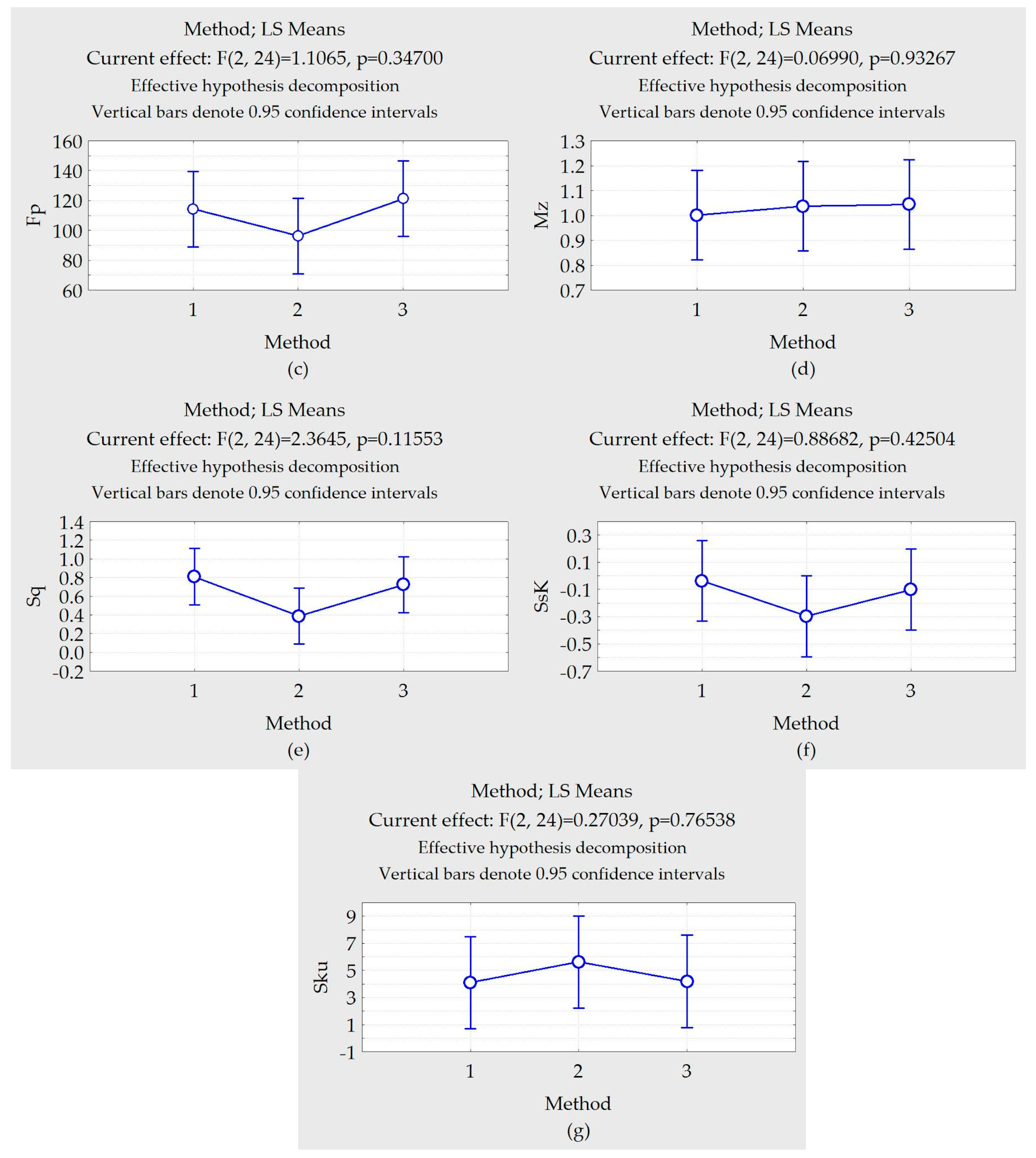
The objective of this paper is to evaluate the application of different MQL strategies in Ti-6Al-4V alloy machining, and to study whether the prediction of results between the ANNs approaches and factorial design describe similar values. The classical DOE approach and its comparison with a high number of different neural network architectures have not yet been studied. The number of comparative analysis studies between the DOE and ANN approaches is still limited. This paper includes training and testing of 15,000 artificial neural networks to minimize a systematic trial and error in the top milling of a Ti-6Al-4V alloy. An MQL valve was built for this purpose.