Multiscale Characterizations of Surface Anisotropies
Abstract
1. Introduction
2. Materials and Methods
2.1. Surfaces and Measurements
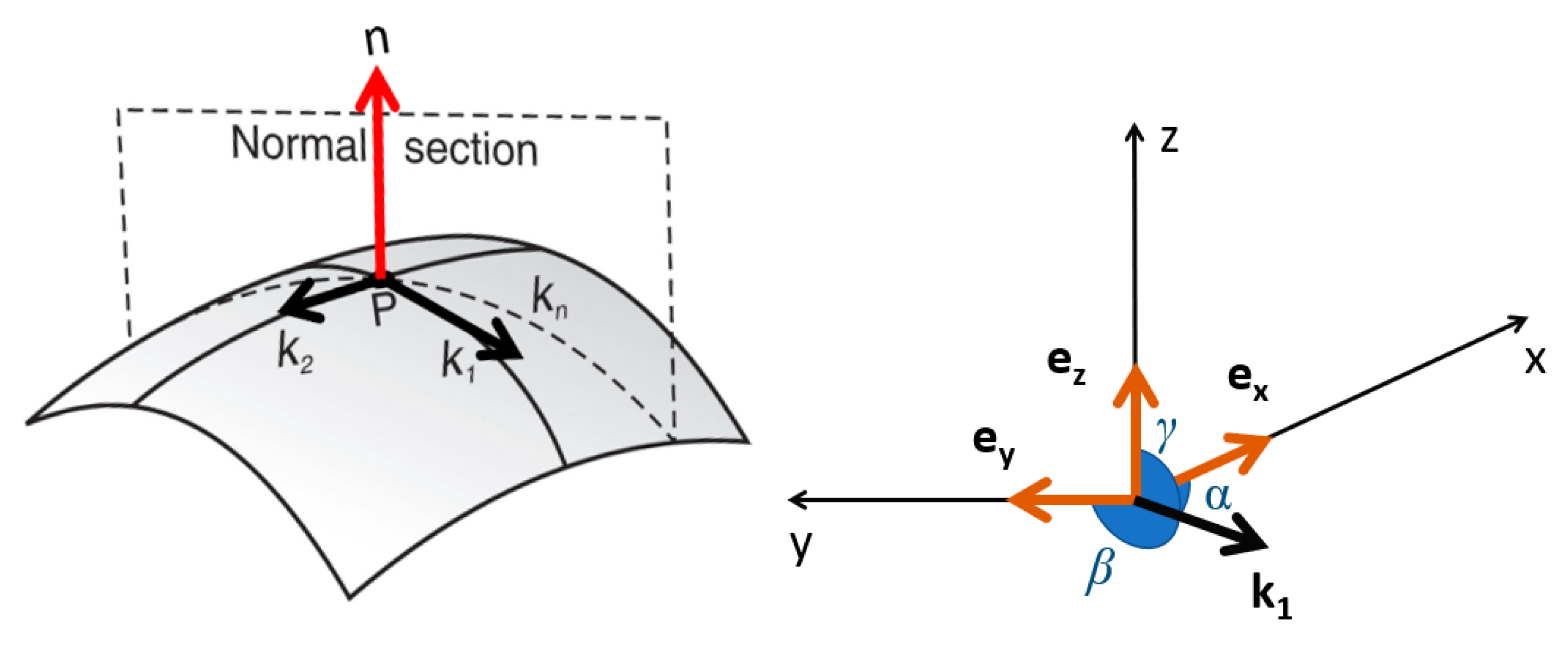
2.2. Multiscale Curvature Tensor Calculations
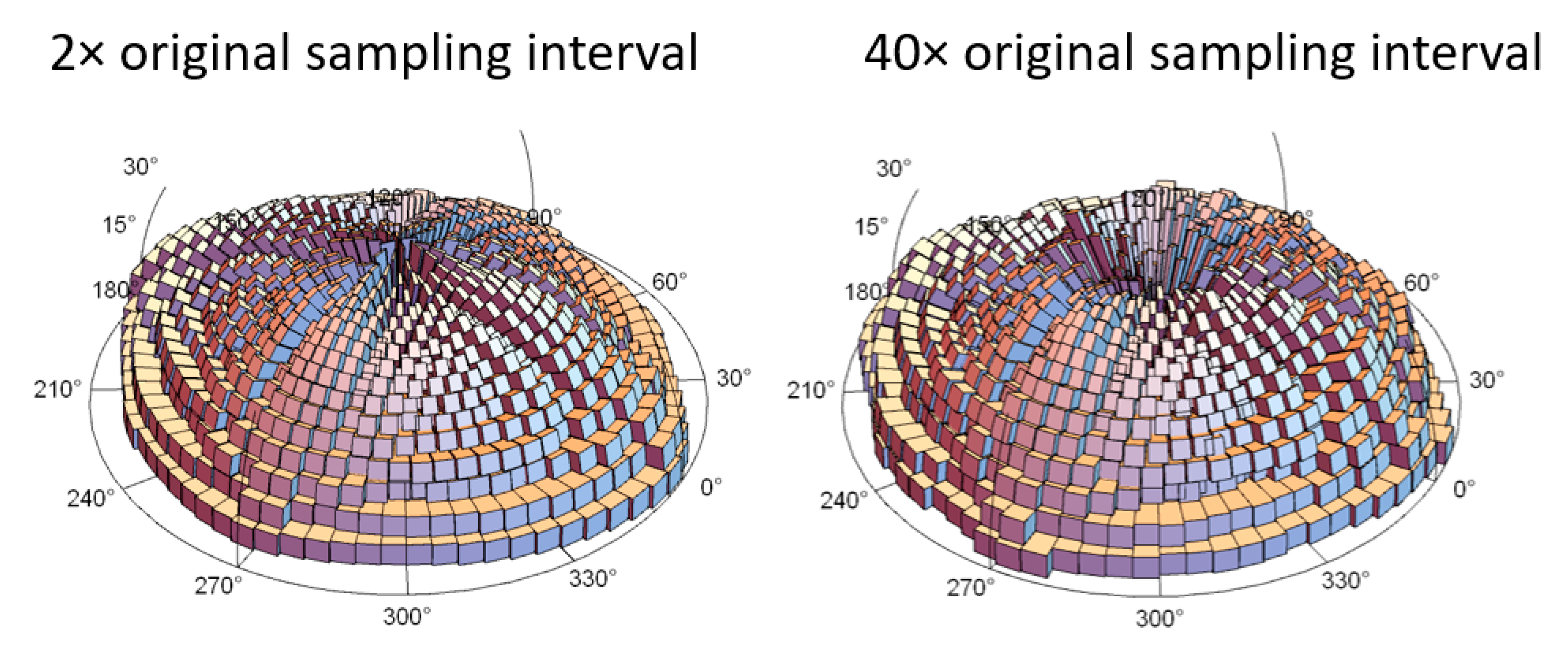
2.3. Bandpass Filtering for Multiscale Analyses
Step 1: Defining spatial frequency bands (scales) for bandpass filters and filtering.
Step 2: Calculating conventional topographic characterization parameters.
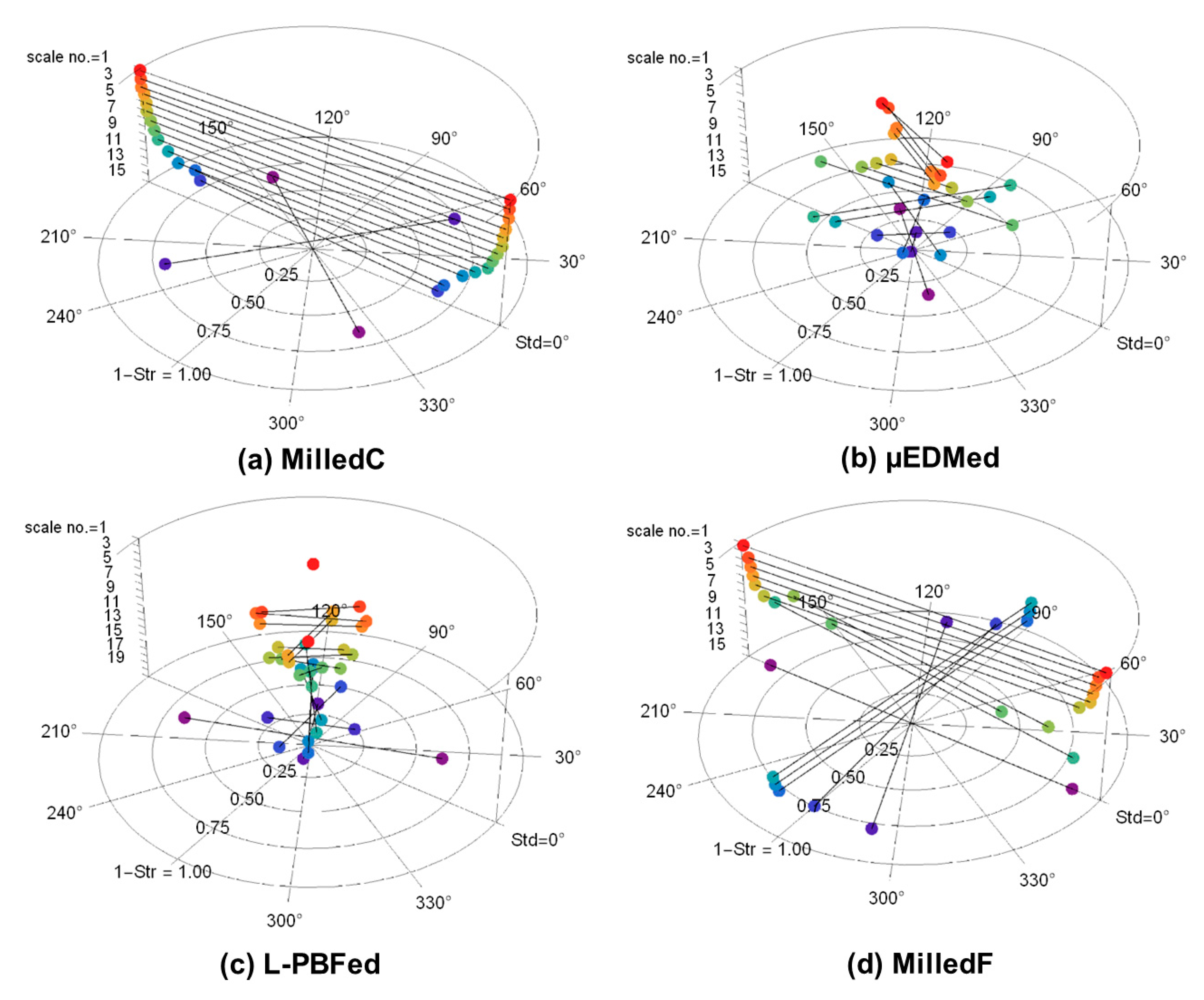
Step 3: Creating polar plots from conventional topographic characterization parameters.
3. Results
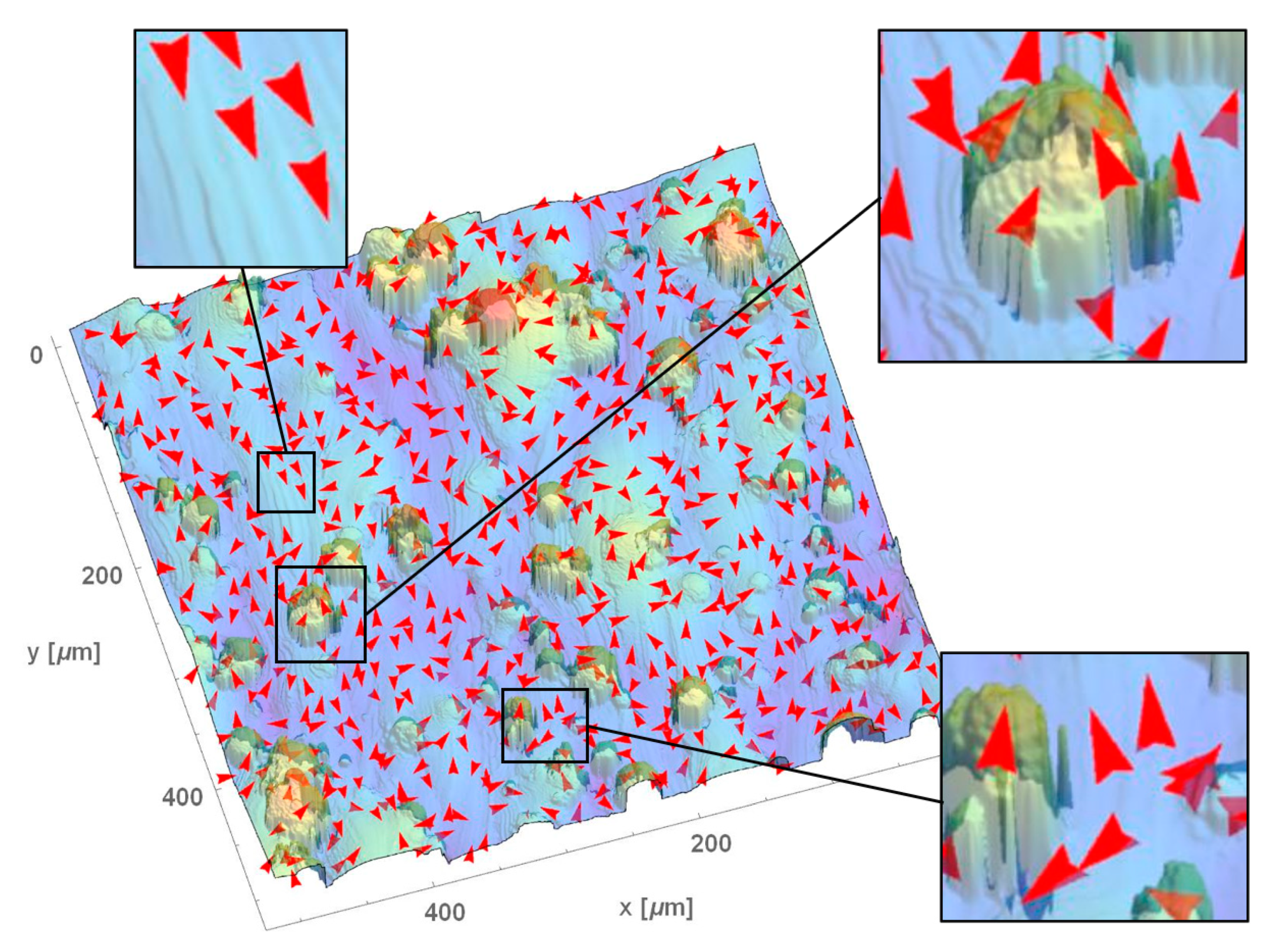
3.1. Visual Impressions of Anisotropy
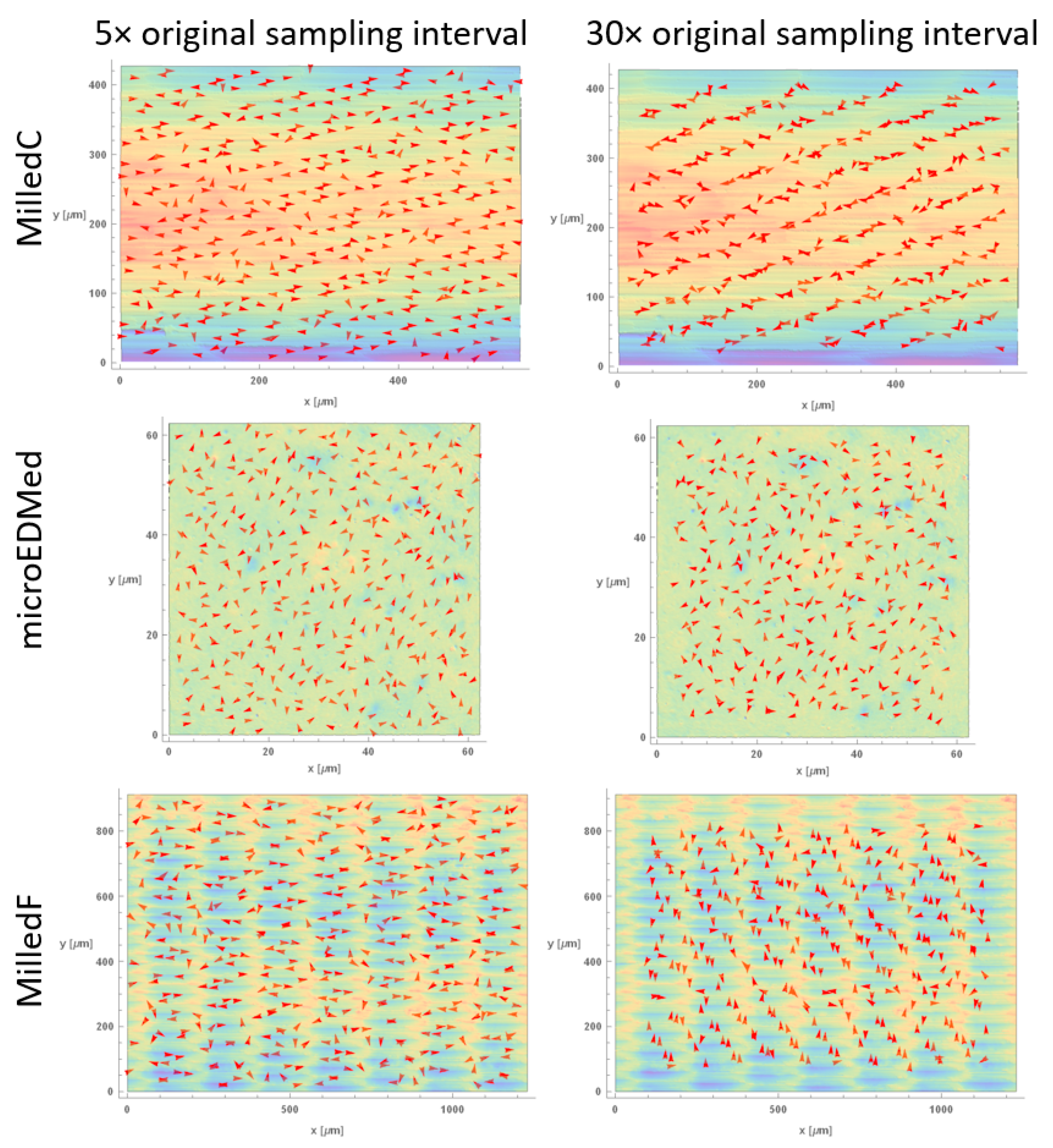
3.2. Multiscale Characterizations of Surface Anisotropies by Bandpass Filtering
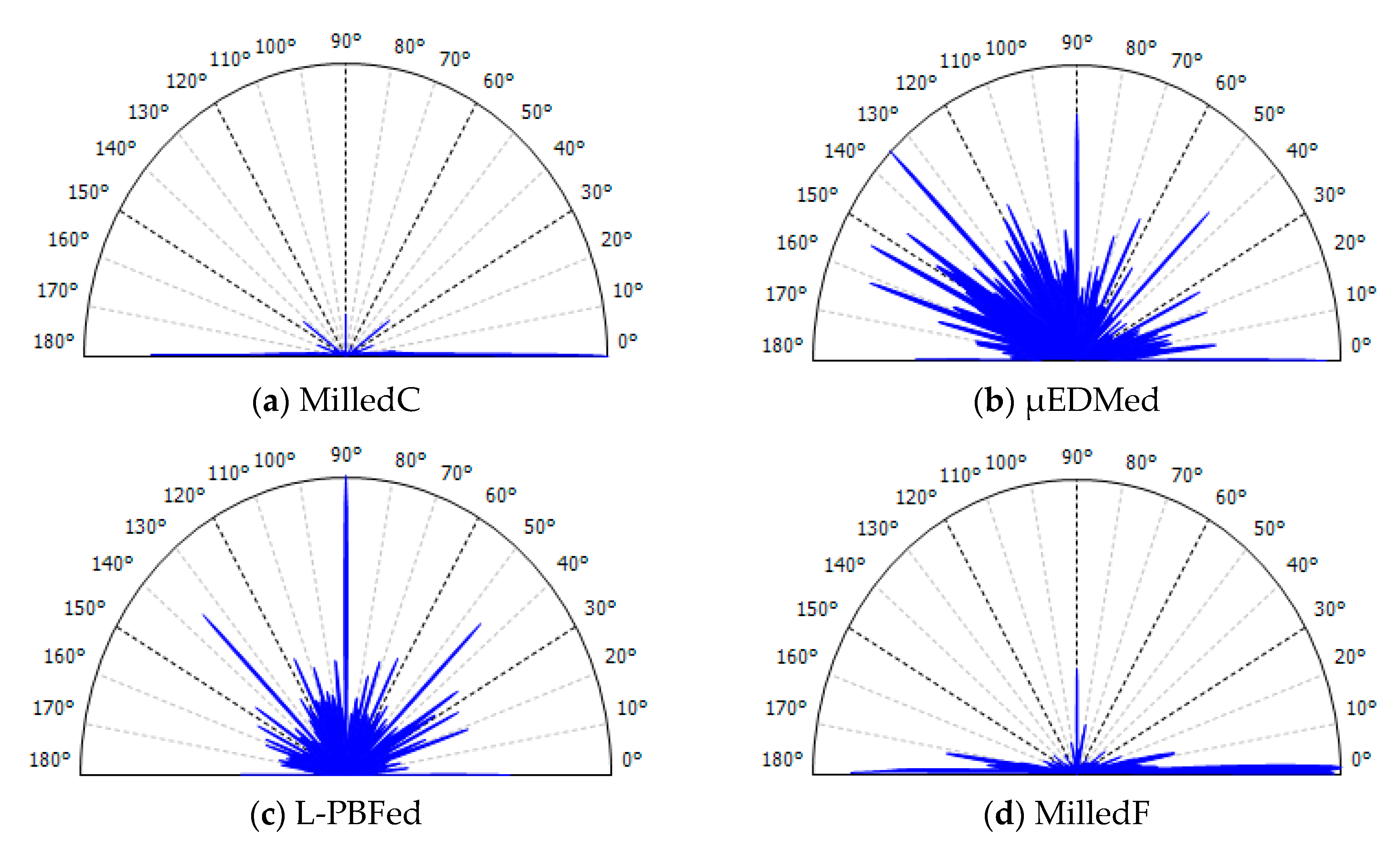
3.3. Multiscale Characterizations of Surface Anisotropie by the Direction of Maximum Curvature
3.4. Conventional Approach Based on Fourier Transform in Polar Coordinates
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Organization for Standardization. ISO 25178-2. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2, Terms, Definitions and Surface Texture Parameters; International Organization for Standardization: Geneva, Switzerland, 2010. [Google Scholar]
- Brown, C.A.; Hansen, H.N.; Jiang, X.J.; Blateyron, F.; Berglund, J.; Senin, N.; Bartkowiak, T.; Dixon, B.; Le Goic, G.; Quinsat, Y.; et al. Multiscale analyses and characterizations of surface topographies. CIRP Ann. 2018, 67, 839–862. [Google Scholar] [CrossRef]
- Kirchmayr, H. Magnetic Anisotropy. In Encyclopedia of Materials: Science and Technology; Elsevier: Amsterdam, The Netherlands, 2001; pp. 4754–4757. [Google Scholar]
- American National Standards Institute; American Society of Mechanical Engineers. Surface Texture (Surface Roughness, Waviness, and Lay); ASME B46.1; American Society of Mechanical Engineers: New York, NY, USA, 2003. [Google Scholar]
- Townsend, A.; Senin, N.; Blunt, L.; Leach, R.K.; Taylor, J.S. Surface texture metrology for metal additive manufacturing: A review. Precis. Eng. 2016, 46, 34–47. [Google Scholar] [CrossRef]
- Lou, S.; Pagani, L.; Zeng, W.; Jiang, X.; Scott, P.J. Watershed segmentation of topographical features on freeform surfaces and its application to additively manufactured surfaces. Precis. Eng. 2020, 63, 177–186. [Google Scholar] [CrossRef]
- Bush, A.W.; Gibson, R.D.; Keogh, G.P. Strongly anisotropic rough surfaces. Trans. ASME J. Lubr. Technol. 1979, 101, 15–20. [Google Scholar] [CrossRef]
- Wallach, J.; Hawley, J.K.; Moore, H.B.; Rathbun, F.V.; Gitzen-danner, L.G. Calculation of Leakage between Metallic Sealing Surfaces; American Society of Mechanical Engineers Series 68-Lub-15; ASME: New York, NY, USA, 1968. [Google Scholar]
- Thomas, T.R.; Rosén, B.-G.; Amini, N. Fractal Characterisation of the Anisotropy of Rough Surfaces. Wear 1999, 232, 41–50. [Google Scholar] [CrossRef]
- Bartkowiak, T. Characterization of 3D surface texture directionality using multiscale curvature tensor analysis. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition IMECE17, Tampa, FL, USA, 3–9 November 2017. [Google Scholar]
- Berglund, J.; Agunwamba, C.; Powers, B.; Brown, C.A.; Rosén, B.-G. On Discovering Relevant Scales in Surface Roughness Measurement—An Evaluation of a Band-Pass Method. Scanning 2010, 32, 244–249. [Google Scholar] [CrossRef]
- Boulanger, J. The “Motifs” method: An interesting complement to ISO parameters for some functional problems. Int. J. Mach. Tools Manuf. 1992, 32, 203–209. [Google Scholar] [CrossRef]
- Lou, S.; Jiang, X.; Scott, P.J. Correlating motif analysis and morphological filters for surface texture analysis. Measurement 2013, 46, 993–1001. [Google Scholar] [CrossRef][Green Version]
- Zahouani, H. Spectral and 3D motifs identification of anisotropic topographical components. Analysis and filtering of anisotropic patterns by morphological rose approach. Int. J. Mach. Tools Manuf. 1998, 38, 615–623. [Google Scholar] [CrossRef]
- Michalski, J. Surface topography of the cylindrical gear tooth flanks after machining. Int. J. Adv. Manuf. Technol. 2009, 43, 513–528. [Google Scholar] [CrossRef]
- Jacobs, T.D.B.; Junge, T.; Pastewka, L. Quantitative characterization of surface topography using spectral analysis. Surf. Topogr. Metrol. Prop. 2017, 5, 013001. [Google Scholar] [CrossRef]
- Krolczyk, G.M.; Maruda, R.W.; Nieslony, P.; Wieczorowski, M. Surface morphology analysis of duplex stainless steel (DSS) in clean production using the power spectral density. Measurement 2016, 94, 464–470. [Google Scholar] [CrossRef]
- Mishra, V.; Khan, G.S.; Chattopadhyay, K.D.; Nand, K.; Sarepaka, R.G.V. Effects of tool overhang on selection of machining parameters and surface finish during diamond turning. Measurement 2014, 55, 353–361. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, S. Effects of Feed per Tooth and Radial Depth of Cut on Amplitude Parameters and Power Spectral Density of a Machined Surface. Materials 2020, 13, 1323. [Google Scholar] [CrossRef] [PubMed]
- Kubiak, K.J.; Bigerelle, M.; Mathia, T.G.; Dubois, A.; Dubar, L. Dynamic evolution of interface roughness during friction and wear processes. Scanning 2014, 36, 30–38. [Google Scholar] [CrossRef]
- Vulliez, M.; Gleason, M.A.; Souto-Lebel, A.; Quinsat, Y.; Lartigue, C.; Kordell, S.P.; Lemoine, A.C.; Brown, C.A. Multi-scale curvature analysis and correlations with the fatigue limit on steel surfaces after milling. Procedia CIRP 2014, 13, 308–313. [Google Scholar] [CrossRef]
- Gleason, M.A.; Kordell, S.; Lemoine, A.; Brown, C.A. Profile Curvatures by Heron’s Formula as a Function of Scale and Position on an Edge Rounded by Mass Finishing. In Proceedings of the 14th International Conference on Metrology and Properties of Engineering Surfaces, Taipei, Taiwan, 17–21 June 2013; paper TS4-01. Volume 22. [Google Scholar]
- Gleason, M.A.; Morgan, C.; Lemoine, A.; Brown, C.A. Multi-scale calculation of curvatures from an aspheric lens profile using Heron’s formula. In Proceedings of the ASPE/ASPEN Summer Topical Meeting, Manufacture and Metrology of Freeform and Off-Axis Aspheric Surfaces, Kohala, HI, USA, 26–27 June 2014; pp. 98–102. [Google Scholar]
- Bartkowiak, T.; Lehner, J.T.; Hyde, J.; Wang, Z.; Pedersen, D.B.; Hansen, H.N.; Brown, C.A. Multi-scale areal curvature analysis of fused deposition surfaces. In Proceedings of the ASPE Spring Topical Meeting on Achieving Precision Tolerances in Additive Manufacturing, Raleigh, NC, USA, 26–29 April 2015; pp. 77–82. [Google Scholar]
- Bartkowiak, T.; Brown, C.A. Multiscale 3D Curvature Analysis of Processed Surface Textures of Aluminum Alloy 6061 T6. Materials 2019, 12, 257. [Google Scholar] [CrossRef]
- Bartkowiak, T.; Staniek, R. Application of multi-scale areal curvature analysis to contact problem, Insights and Innovations in Structural Engineering, Mechanics and Computation. In Proceedings of the 6th International Conference on Structural Engineering, Mechanics and Computation, SEMC, Cape Town, South Africa, 5–7 September 2016; pp. 1823–1829. [Google Scholar]
- Wiklund, D.; Liljebgren, M.; Berglund, J.; Bay, N.; Kjellsson, K.; Rosén, B.-G. Friction in sheet metal forming: A Comparison between milled and manually polished surfaces. In Proceedings of the 4th International Conference on Tribology in Manufacturing Processes, ICTMP, Nice, France, 13–15 June 2010; Volume 2, pp. 613–622. [Google Scholar]
- Barre, F.; Lopez, J. On a 3D extension of the MOTIF method (ISO 12085). Int. J. Mach. Tools Manuf. 2001, 41, 1873–1880. [Google Scholar] [CrossRef]
- Lehner, J.T.; Brown, C.A. Wear of abrasive particles in slurry during lapping. In Proceedings of the ASME 2014 International Manufacturing Science and Engineering Conference, MSEC 2014 Collocated with the JSME 2014 International Conference on Materials and Processing and the 42nd North American Manufacturing Research Conference, Detroit, MI, USA, 9–13 June 2014; Volume 45813, p. V002T02A017. [Google Scholar]
- Scott, R.S.; Ungar, P.S.; Bergstrom, T.S.; Brown, C.A.; Grine, F.E.; Teaford, M.F.; Walker, A. Dental microwear texture analysis shows within-species diet variability in fossil hominins. Nature 2005, 436, 693–695. [Google Scholar] [CrossRef]
- Arman, S.D.; Ungar, P.S.; Brown, C.A.; DeSantis, L.R.G.; Schmidt, C.; Prideaux, G.J. Minimizing inter-microscope variability in dental microwear texture analysis. Surf. Topogr. Metrol. Prop. 2016, 4, 024007. [Google Scholar] [CrossRef]
- Stemp, W.J.; Childs, B.E.; Vionnet, S.; Brown, C.A. Quantification and discrimination of lithic use-wear: Surface profile measurements and length-scale fractal analysis. Archaeometry 2009, 51, 366–382. [Google Scholar] [CrossRef]
- Stemp, W.J.; Morozov, M.; Key, A.J.M. Quantifying lithic microwear with load variation on experimental basalt flakes using LSCM and area-scale fractal complexity (Asfc). Surf. Topogr. Metrol. Prop. 2015, 3, 1–20. [Google Scholar] [CrossRef]
- Le Goïc, G.; Brown, C.A.; Favreliere, H.; Samper, S.; Formosa, F. Outlier filtering: A new method for improving the quality of surface measurements. Meas. Sci. Technol. 2013, 24, 015001. [Google Scholar] [CrossRef]
- Theisel, H.; Rossi, C.; Zayer, R.; Seidel, H.-P. Normal based estimation of the curvature tensor for triangular meshes. In Proceedings of the 12th Pacific Conference on Computer Graphics and Applications, Seoul, Korea, 6–8 October 2004; pp. 288–297. [Google Scholar]
- Clarke, A.E.; Roy, D. Astronomy Principles and Practice, 4th ed.; Institute of Physics Pub.: Bristol, PA, USA, 2003; p. 59. ISBN 9780750309172. [Google Scholar]
- Berglund, J.; Wiklund, D.; Rosén, B.-G. A method for visualization of surface texture anisotropy in different scales of observation. Scanning 2011, 33, 325–331. [Google Scholar] [CrossRef] [PubMed]
- Maleki, I.; Wolski, M.; Woloszynski, T.; Podsiadlo, P.; Stachowiak, G. A comparison of multiscale surface curvature characterization methods for tribological surfaces. Tribol. Online 2019, 14, 8–17. [Google Scholar] [CrossRef]
- Cain, M.K.; Zhang, Z.; Yuan, K. Univariate and multivariate skewness and kurtosis for measuring nonnormality: Prevalence, influence and estimation. Behav. Res. 2017, 49, 1716–1735. [Google Scholar] [CrossRef]
- Tay, F.E.; Sikdar, S.K.; Mannan, M.A. Topography of the flank wear surface. J. Mater. Process. Technol. 2002, 120, 243–248. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z. Tool wear behaviors and corresponding machined surface topography during high-speed machining of Ti-6Al-4V with fine grain tools. Tribol. Int. 2018, 121, 321–332. [Google Scholar] [CrossRef]
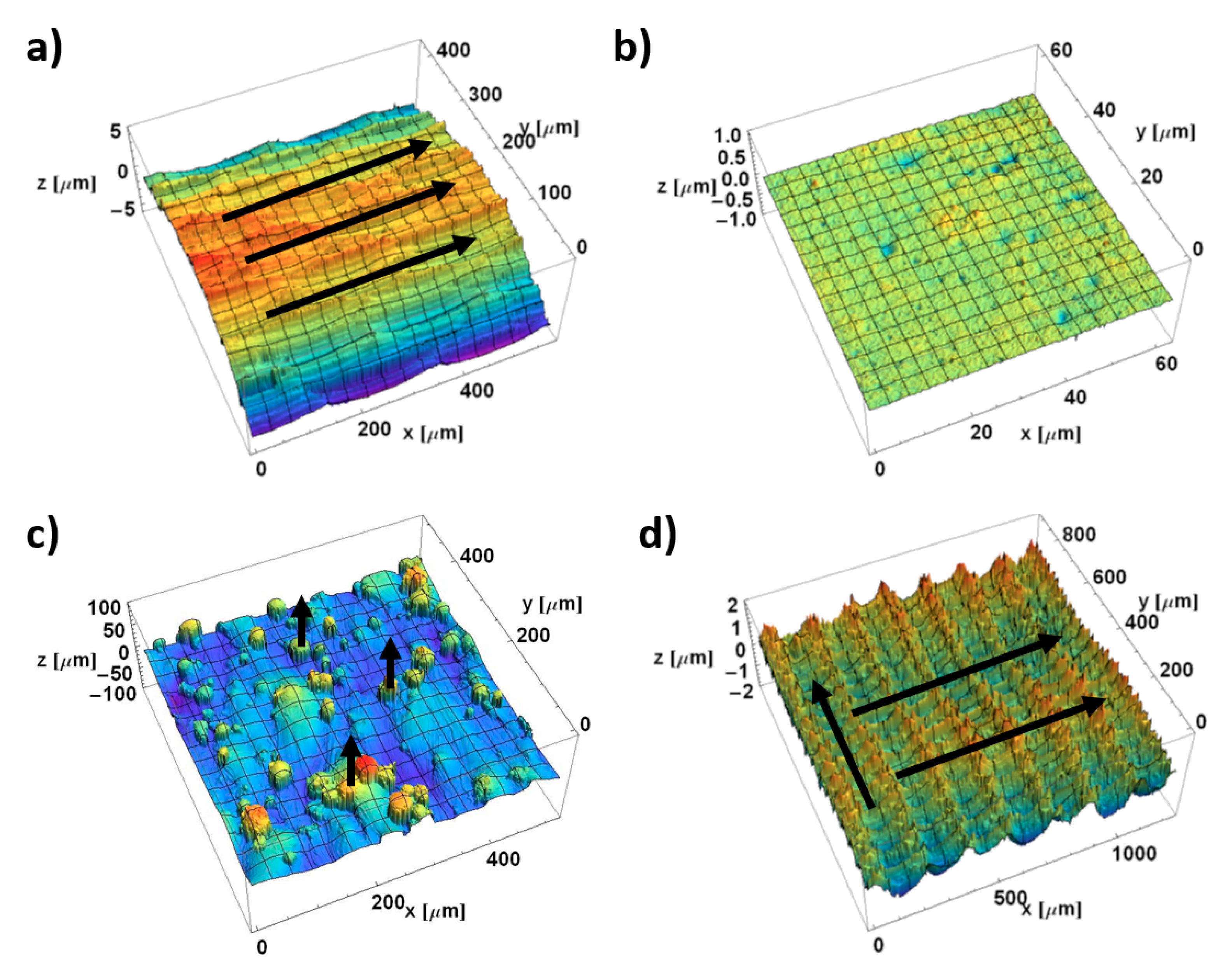


| Surface | MilledC | MilledF | µEDMed | L-PBFed |
|---|---|---|---|---|
| Original sampling interval [µm] | 0.790 | 2.000 | 0.125 | 0.260 |
| 5× original sampling interval [µm] | 3.950 | 10.000 | 0.625 | 1.300 |
| 20× original sampling interval [µm] | 15.800 | 40.000 | 2.500 | 5.200 |
| 25× original sampling interval [µm] | 19.750 | 50.000 | 3.125 | 6.500 |
| 40× original sampling interval [µm] | 31.600 | 80.000 | 5.000 | 10.400 |
| MilledC | µEDMed | L-PBFed | MilledF | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Center | Low | High | Center | Low | High | Center | Low | High | Center | Low | High |
| 1 | 3.0 | - | 4.0 | 0.422 | - | 0.563 | 1.1 | - | 1.5 | 6 | - | 8 |
| 2 | 4.5 | 3.0 | 6.0 | 0.563 | 0.375 | 0.750 | 1.5 | 1.0 | 2.0 | 9 | 6 | 12 |
| 3 | 6.0 | 4.0 | 8.0 | 0.844 | 0.563 | 1.125 | 2.3 | 1.5 | 3.0 | 12 | 8 | 16 |
| 4 | 9.0 | 6.0 | 12.0 | 1.125 | 0.750 | 1.500 | 3.0 | 2.0 | 4.0 | 18 | 12 | 24 |
| 5 | 12.0 | 8.0 | 16.0 | 1.688 | 1.125 | 2.250 | 4.5 | 3.0 | 6.0 | 24 | 16 | 32 |
| 6 | 18.0 | 12.0 | 24.0 | 2.250 | 1.500 | 3.000 | 6.0 | 4.0 | 8.0 | 36 | 24 | 48 |
| 7 | 24.0 | 16.0 | 32.0 | 3.375 | 2.250 | 4.500 | 9.0 | 6.0 | 12.0 | 48 | 32 | 64 |
| 8 | 36.0 | 24.0 | 48.0 | 4.500 | 3.000 | 6.000 | 12.0 | 8.0 | 16.0 | 72 | 48 | 96 |
| 9 | 48.0 | 32.0 | 64.0 | 6.750 | 4.500 | 9.000 | 18.0 | 12.0 | 24.0 | 96 | 64 | 128 |
| 10 | 72.0 | 48.0 | 96.0 | 9.000 | 6.000 | 12.000 | 24.0 | 16.0 | 32.0 | 144 | 96 | 192 |
| 11 | 96.0 | 64.0 | 128.0 | 13.500 | 9.000 | 18.000 | 36.0 | 24.0 | 48.0 | 192 | 128 | 256 |
| 12 | 144.0 | 96.0 | 192.0 | 18.000 | 12.000 | 24.000 | 48.0 | 32.0 | 64.0 | 270 | 192 | 348 |
| 13 | 192.0 | 128.0 | 256.0 | 27.000 | 18.000 | 36.000 | 72.0 | 48.0 | 96.0 | 384 | 256 | 512 |
| 14 | 270.0 | 192.0 | 348.0 | 36.000 | 24.000 | 48.000 | 96.0 | 64.0 | 128.0 | 522 | 348 | 696 |
| 15 | 384.0 | 256.0 | - | 48.000 | 32.000 | - | 144.0 | 96.0 | 192.0 | 768 | 512 | - |
| 16 | N/A | N/A | N/A | N/A | N/A | N/A | 192.0 | 128.0 | 256.0 | N/A | N/A | N/A |
| 17 | N/A | N/A | N/A | N/A | N/A | N/A | 288.0 | 192.0 | 384.0 | N/A | N/A | N/A |
| 18 | N/A | N/A | N/A | N/A | N/A | N/A | 384.0 | 256.0 | 512.0 | N/A | N/A | N/A |
| 19 | N/A | N/A | N/A | N/A | N/A | N/A | 576.0 | 384.0 | - | N/A | N/A | N/A |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartkowiak, T.; Berglund, J.; Brown, C.A. Multiscale Characterizations of Surface Anisotropies. Materials 2020, 13, 3028. https://doi.org/10.3390/ma13133028
Bartkowiak T, Berglund J, Brown CA. Multiscale Characterizations of Surface Anisotropies. Materials. 2020; 13(13):3028. https://doi.org/10.3390/ma13133028
Chicago/Turabian StyleBartkowiak, Tomasz, Johan Berglund, and Christopher A. Brown. 2020. "Multiscale Characterizations of Surface Anisotropies" Materials 13, no. 13: 3028. https://doi.org/10.3390/ma13133028
APA StyleBartkowiak, T., Berglund, J., & Brown, C. A. (2020). Multiscale Characterizations of Surface Anisotropies. Materials, 13(13), 3028. https://doi.org/10.3390/ma13133028







