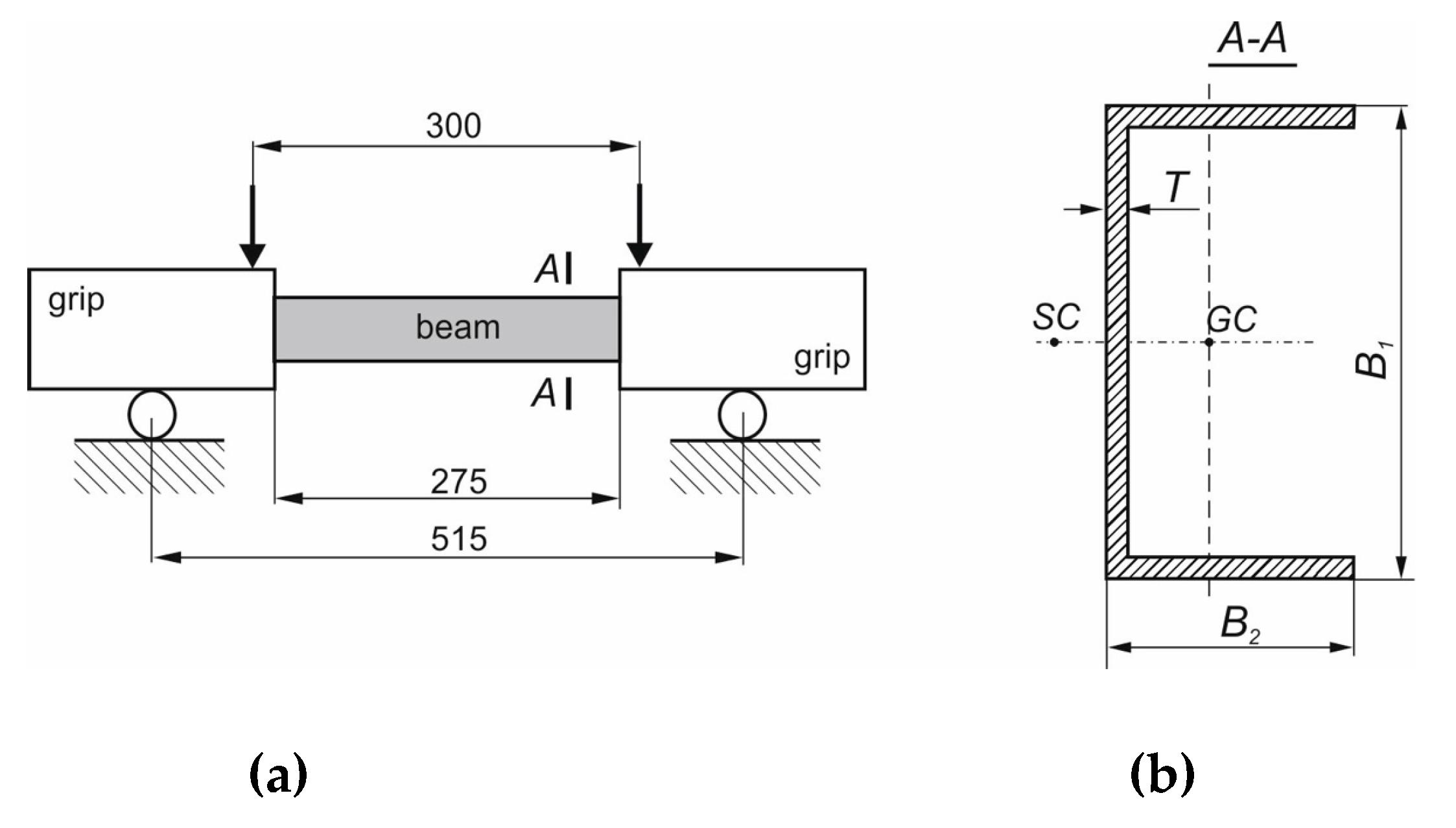
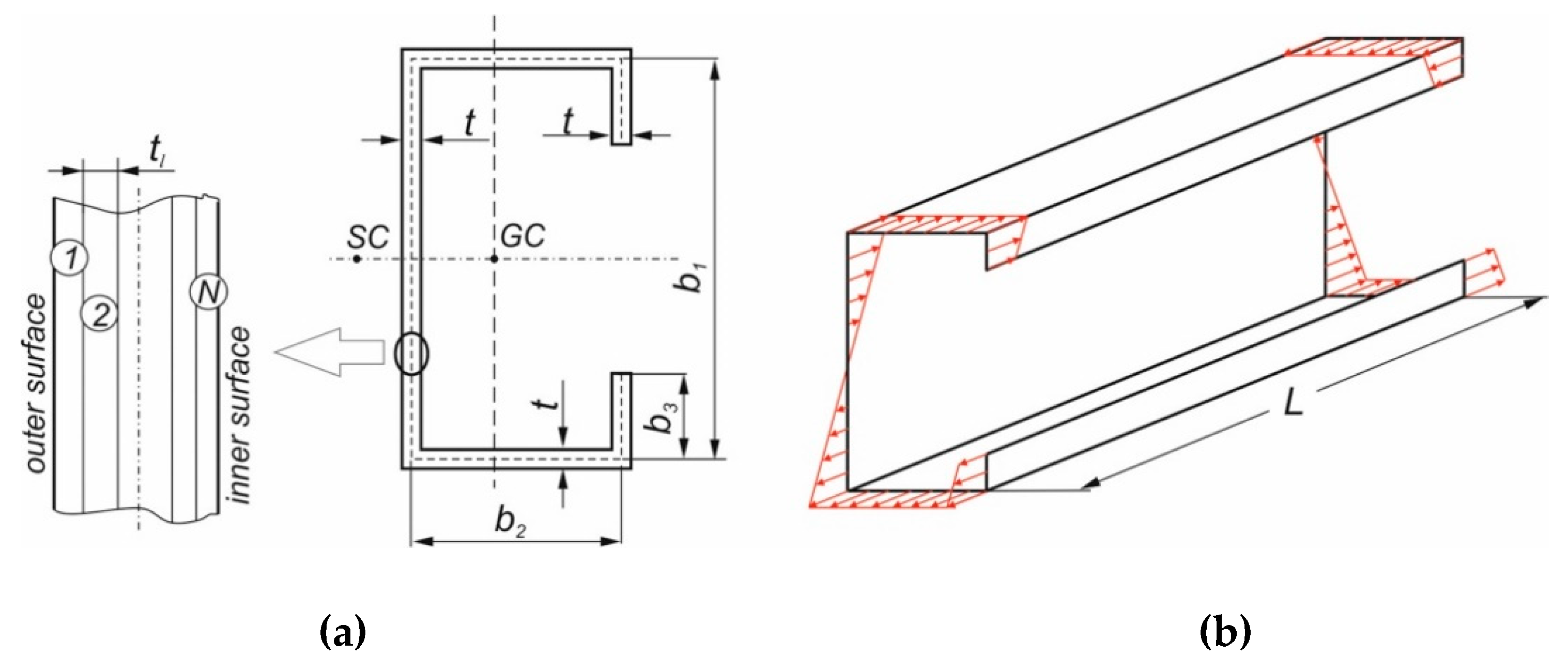
Figure 1.
(a) Scheme of four-point bending test performed experimentally. (b) Considered cross-section.
Figure 1.
(a) Scheme of four-point bending test performed experimentally. (b) Considered cross-section.
Figure 2.
(a) Experimental test stand. (b) The load and the support in four-point bending test. (c) Aramis software view with depicted points (d) Zoom of points depicted in left grip.
Figure 2.
(a) Experimental test stand. (b) The load and the support in four-point bending test. (c) Aramis software view with depicted points (d) Zoom of points depicted in left grip.
Figure 3.
(a) The considered laminate beam dimensions with layer arrangement and (b) type of the load.
Figure 3.
(a) The considered laminate beam dimensions with layer arrangement and (b) type of the load.
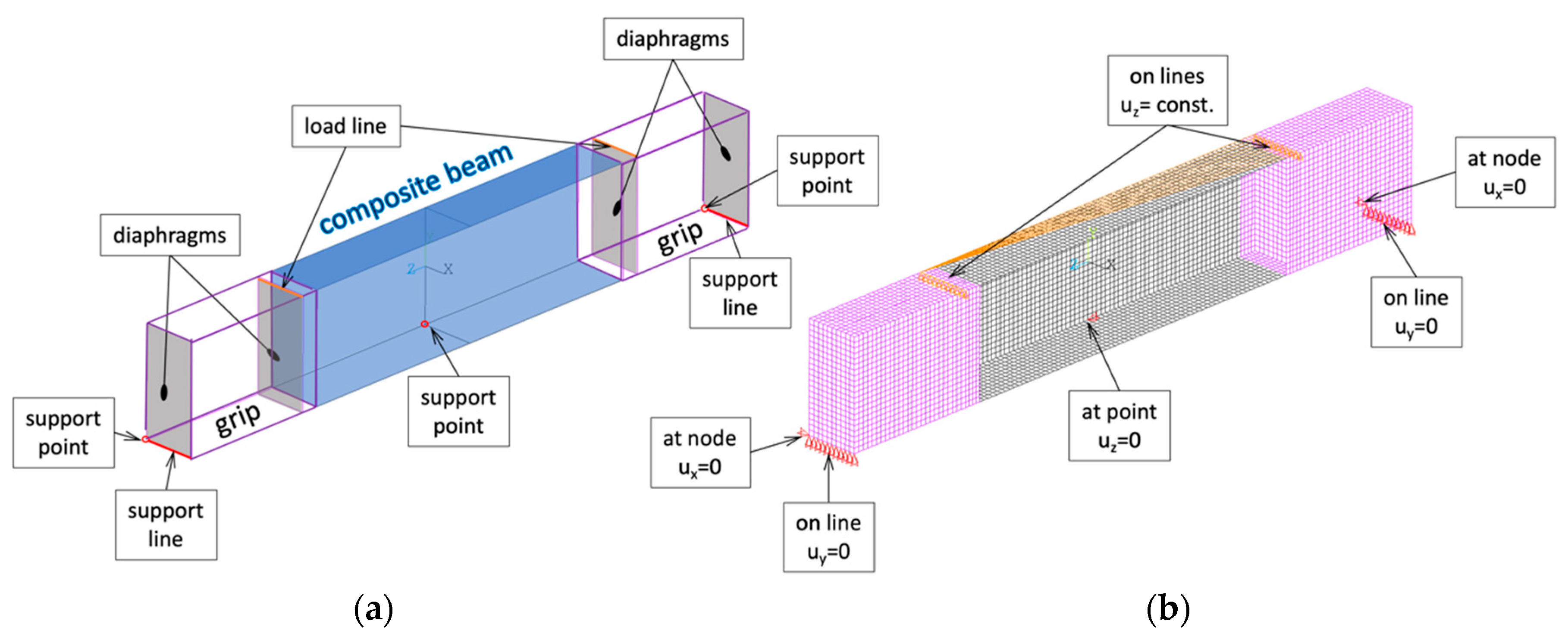
Figure 4.
(a) Geometry of numerical model; (b) discrete model with applied boundary condition and load.
Figure 4.
(a) Geometry of numerical model; (b) discrete model with applied boundary condition and load.
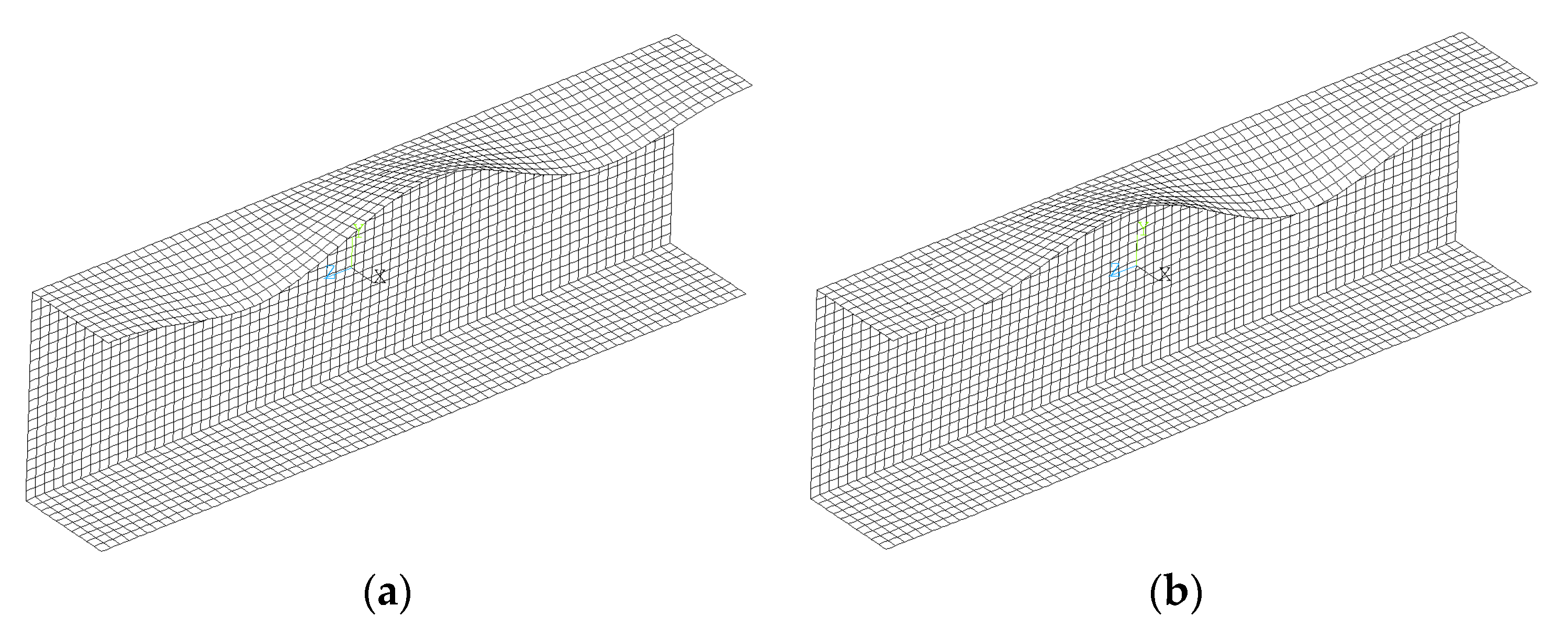
Figure 5.
Buckling modes corresponding to the lowest buckling loads for the beams with the layer arrangement: (a) [0/90/0/90]S and [45/−45/45/−45]S; (b) [45/−45/90/0]S.
Figure 5.
Buckling modes corresponding to the lowest buckling loads for the beams with the layer arrangement: (a) [0/90/0/90]S and [45/−45/45/−45]S; (b) [45/−45/90/0]S.
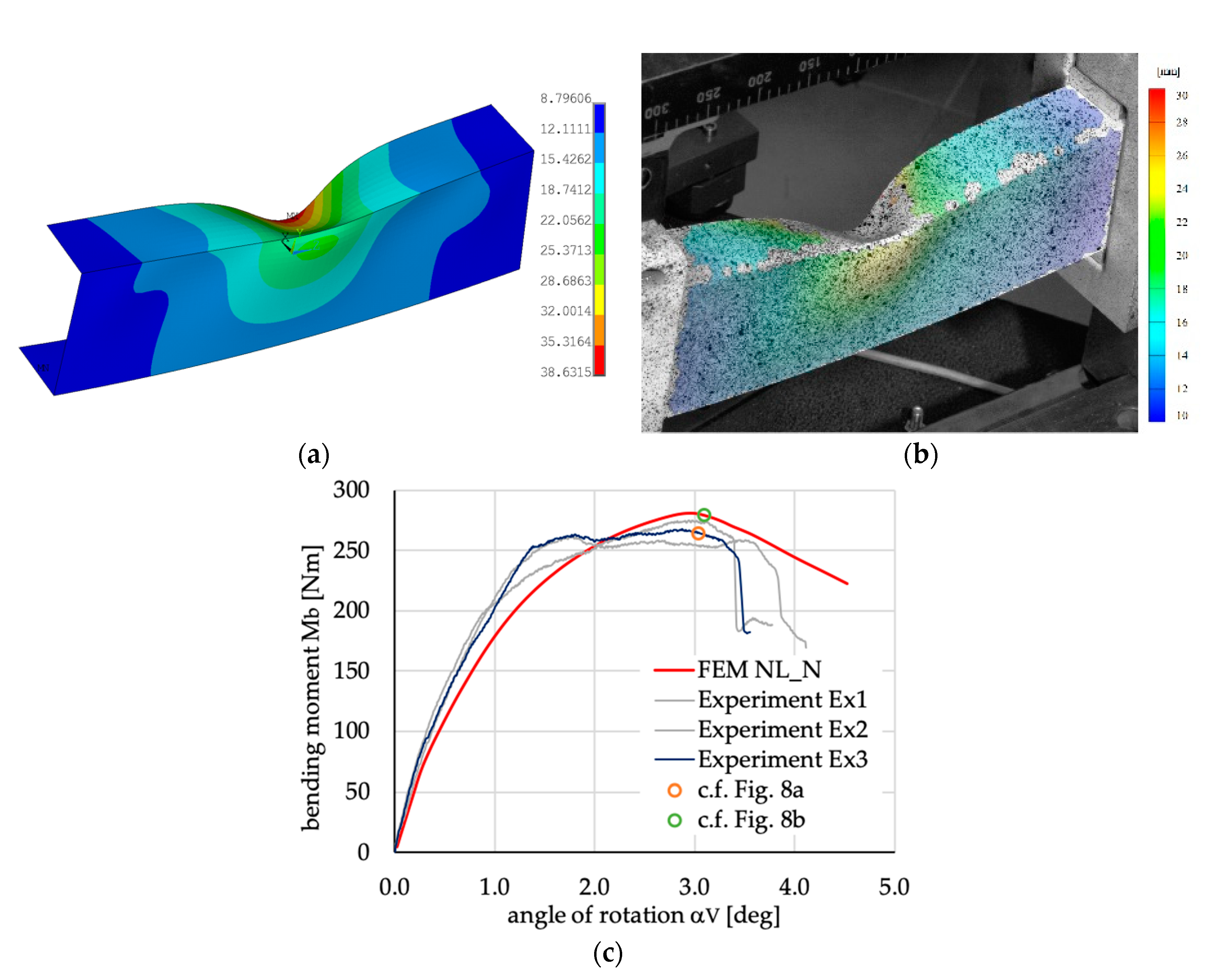
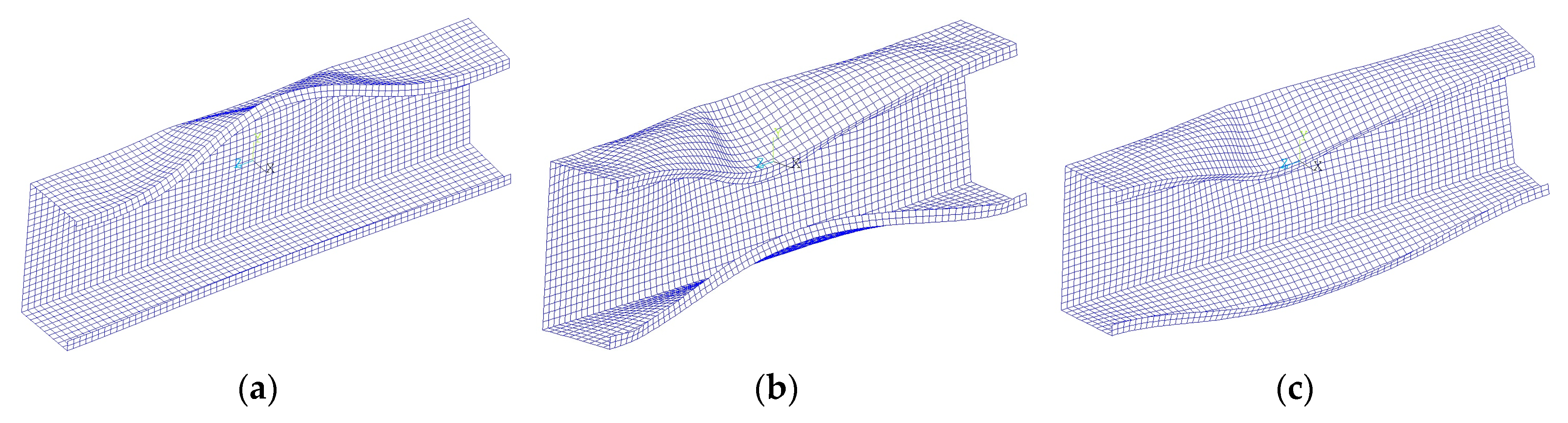
Figure 6.
Comparison of beams deflection for case [45/−45/45/−45]S obtained (a) numerically with model NL_N; and (b) experimentally; (c) the load-displacements comparison of curves obtained experimentally and numerically.
Figure 6.
Comparison of beams deflection for case [45/−45/45/−45]S obtained (a) numerically with model NL_N; and (b) experimentally; (c) the load-displacements comparison of curves obtained experimentally and numerically.
Figure 7.
The influence of amplitude of initial geometric imperfection on bending moment vs. angle of rotation αV, curves for beams with layer arrangement: (a) [45/−45/90/0]S; (b) [0/90/0/90]S; (c) [45/−45/45/−45]S. FE 0—numerical analysis without imperfection, FE −0.01 t—numerical analysis with the imperfection equal to −1% of thickness, FE −0.1 t—numerical analysis with the imperfection equal to −10% of thickness, FE −0.5 t—numerical analysis with the imperfection equal to −50% of thickness, Ex1—experimental results of first specimen, Ex2—experimental results of second specimen.
Figure 7.
The influence of amplitude of initial geometric imperfection on bending moment vs. angle of rotation αV, curves for beams with layer arrangement: (a) [45/−45/90/0]S; (b) [0/90/0/90]S; (c) [45/−45/45/−45]S. FE 0—numerical analysis without imperfection, FE −0.01 t—numerical analysis with the imperfection equal to −1% of thickness, FE −0.1 t—numerical analysis with the imperfection equal to −10% of thickness, FE −0.5 t—numerical analysis with the imperfection equal to −50% of thickness, Ex1—experimental results of first specimen, Ex2—experimental results of second specimen.
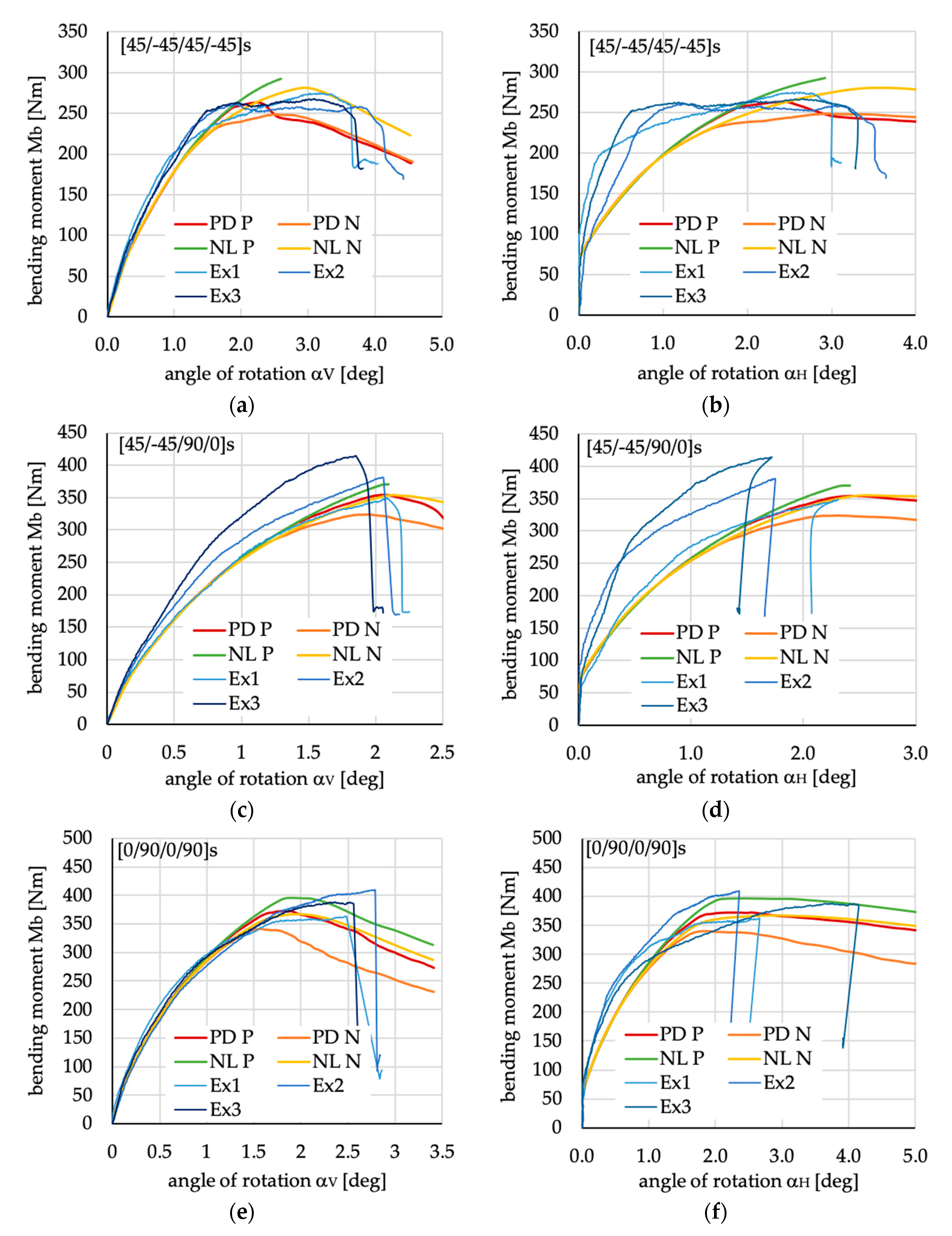
Figure 8.
Bending moment vs. angles of rotations Mb(αV) and Mb(αH) for all analyzed cases—comparison of numerical results with experimental ones. (a) Mb(αV) for [45/−45/90/0]S; (b) Mb(αH) for [45/−45/90/0]S; (c) Mb(αV) for [0/90/0/90]S; (d) Mb(αH) for [0/90/0/90]S; (e) Mb(αV) for [45/−45/45/−45]S; (f) Mb(αH) for [45/−45/45/−45]S. PD P—progressive damage algorithm analysis with positive imperfection; PD N—progressive damage algorithm analysis with positive imperfection; NL P—nonlinear analysis with positive imperfection; NL N - nonlinear analysis with negative imperfection; Ex1—experimental results of first specimen; Ex2—experimental results of second specimen; Ex3—experimental results of first specimen.
Figure 8.
Bending moment vs. angles of rotations Mb(αV) and Mb(αH) for all analyzed cases—comparison of numerical results with experimental ones. (a) Mb(αV) for [45/−45/90/0]S; (b) Mb(αH) for [45/−45/90/0]S; (c) Mb(αV) for [0/90/0/90]S; (d) Mb(αH) for [0/90/0/90]S; (e) Mb(αV) for [45/−45/45/−45]S; (f) Mb(αH) for [45/−45/45/−45]S. PD P—progressive damage algorithm analysis with positive imperfection; PD N—progressive damage algorithm analysis with positive imperfection; NL P—nonlinear analysis with positive imperfection; NL N - nonlinear analysis with negative imperfection; Ex1—experimental results of first specimen; Ex2—experimental results of second specimen; Ex3—experimental results of first specimen.
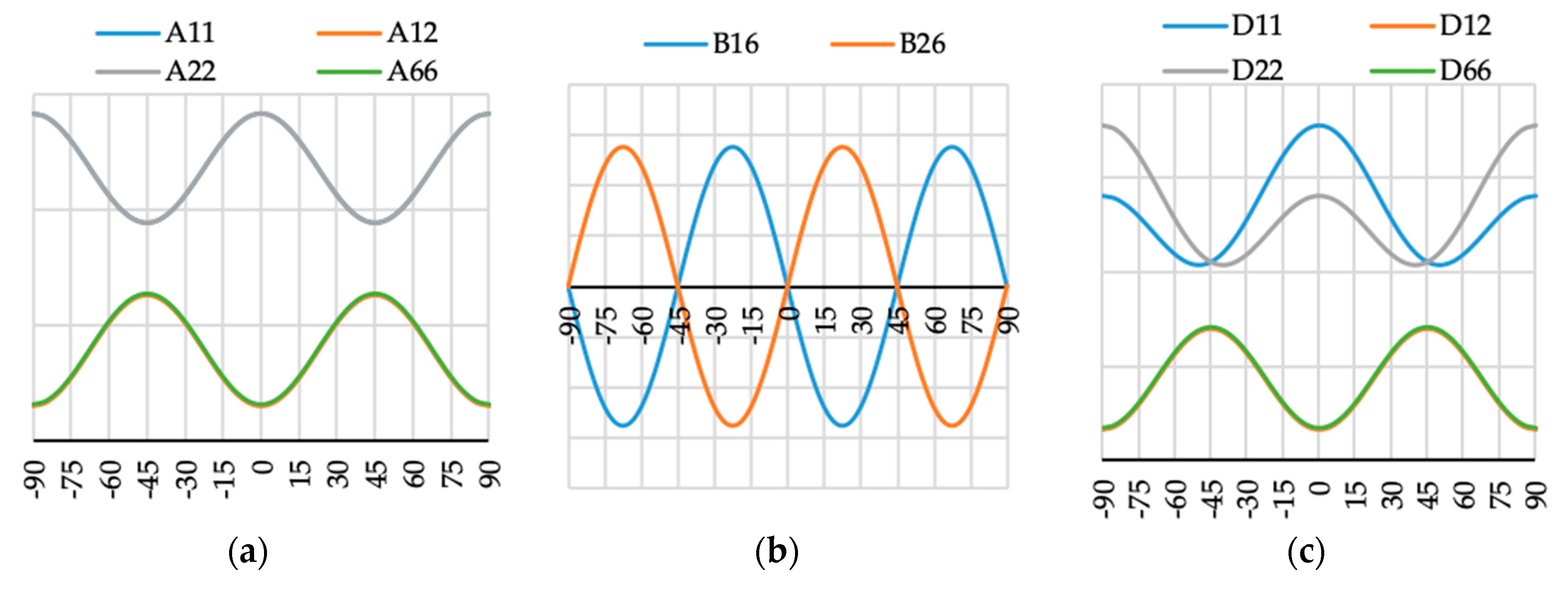
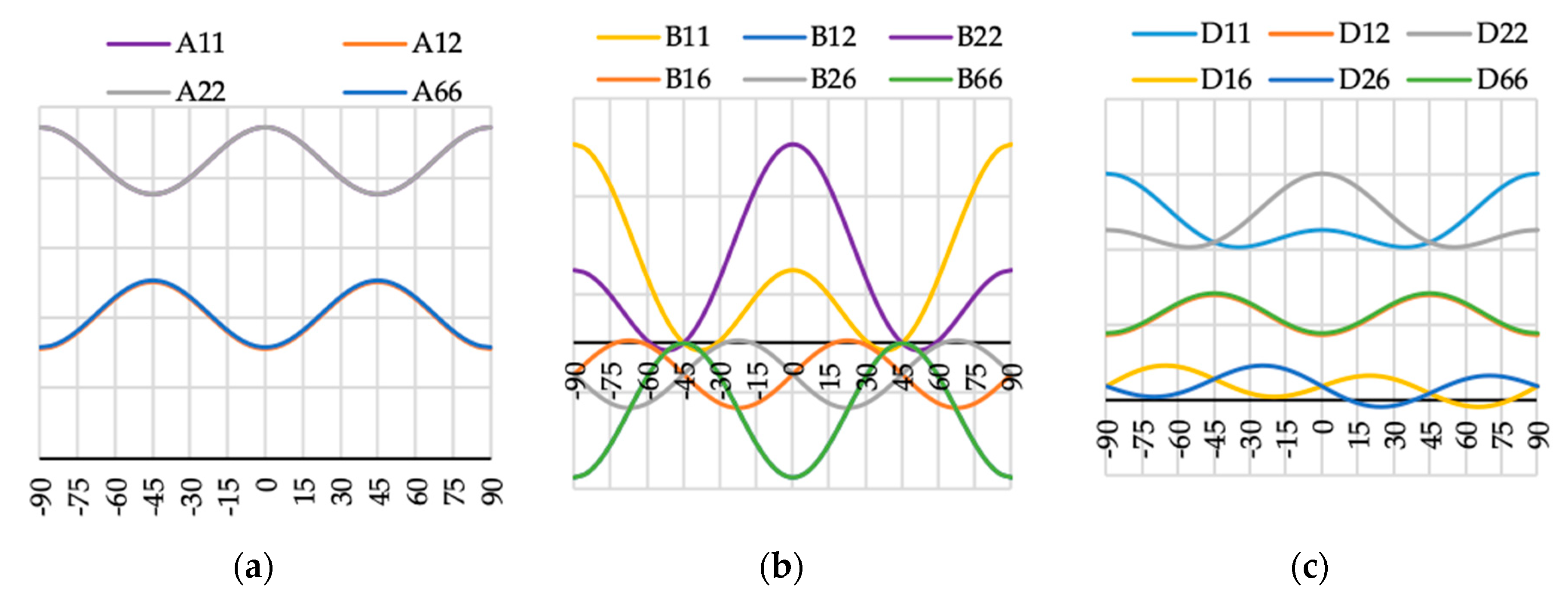
Figure 9.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case A1(θ).
Figure 9.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case A1(θ).
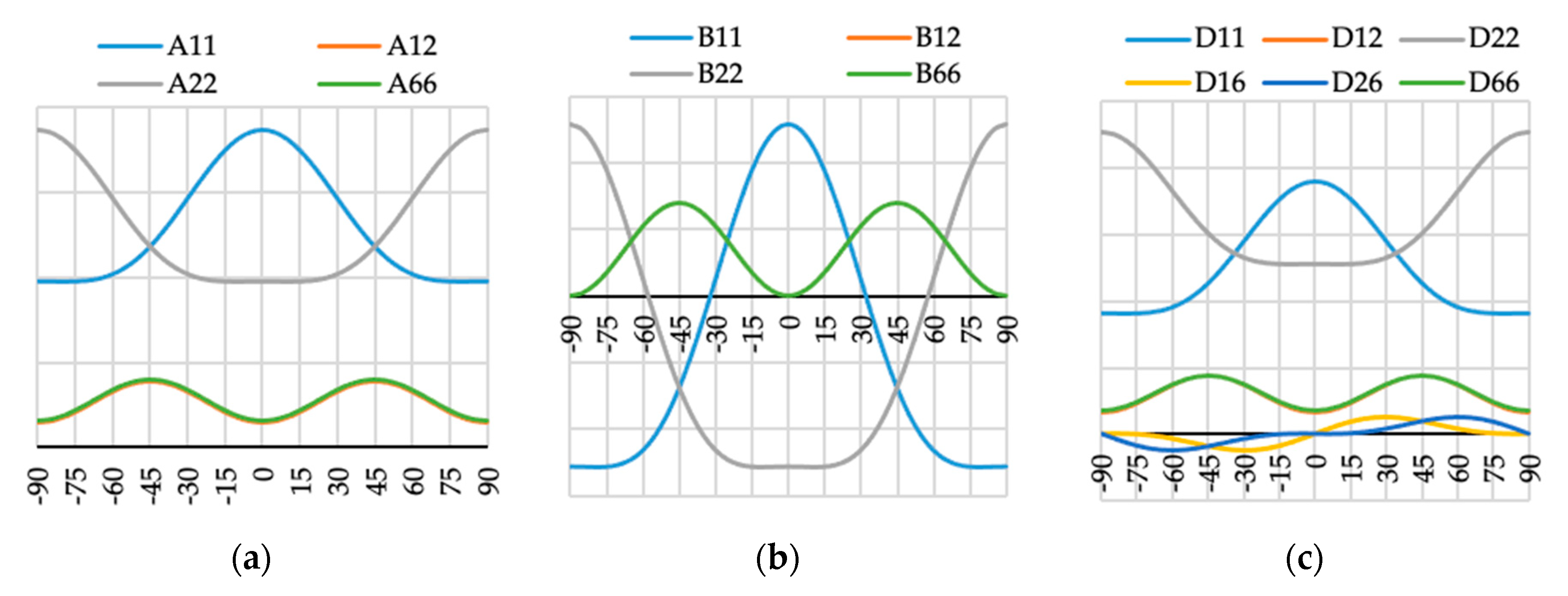
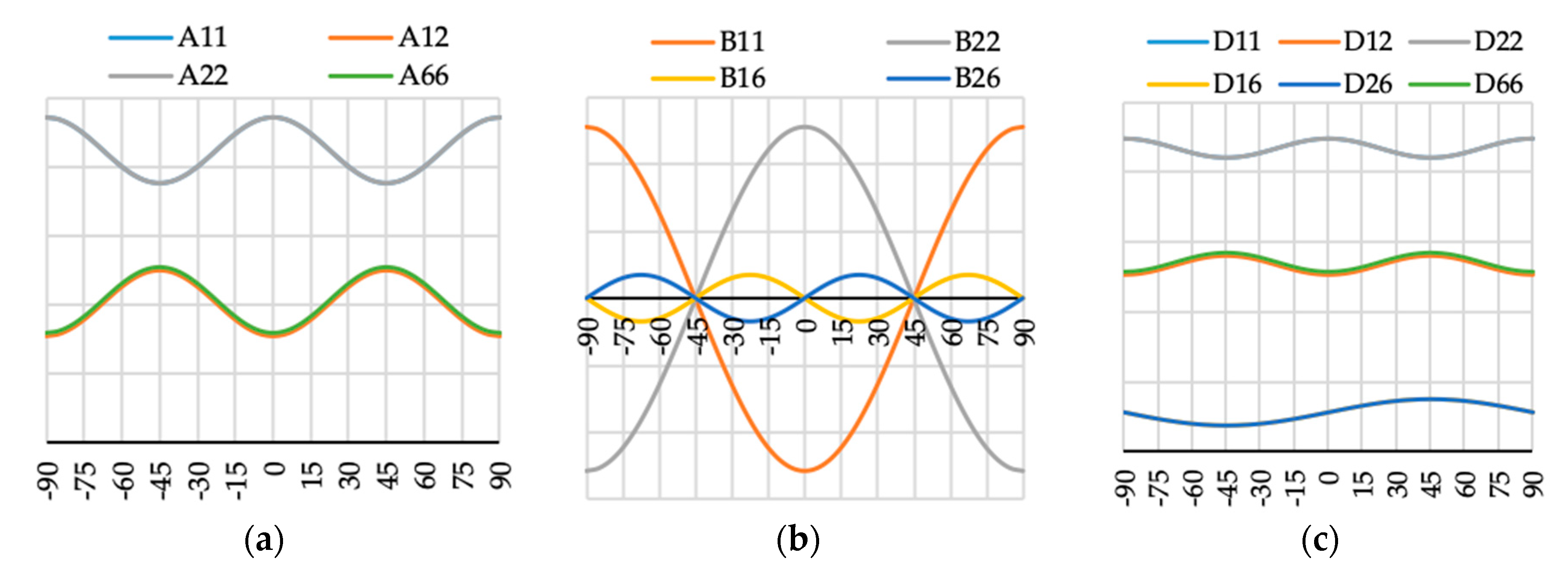
Figure 10.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N3(θ).
Figure 10.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N3(θ).
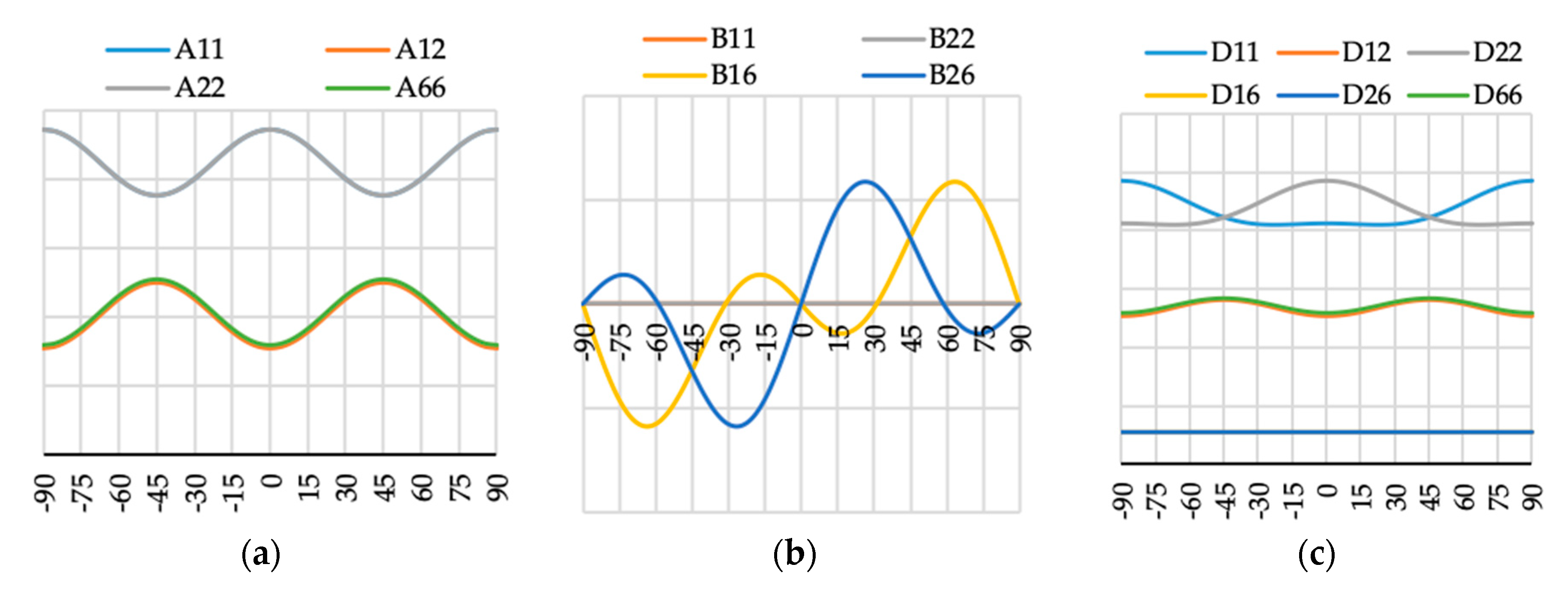
Figure 11.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case A2(θ).
Figure 11.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case A2(θ).
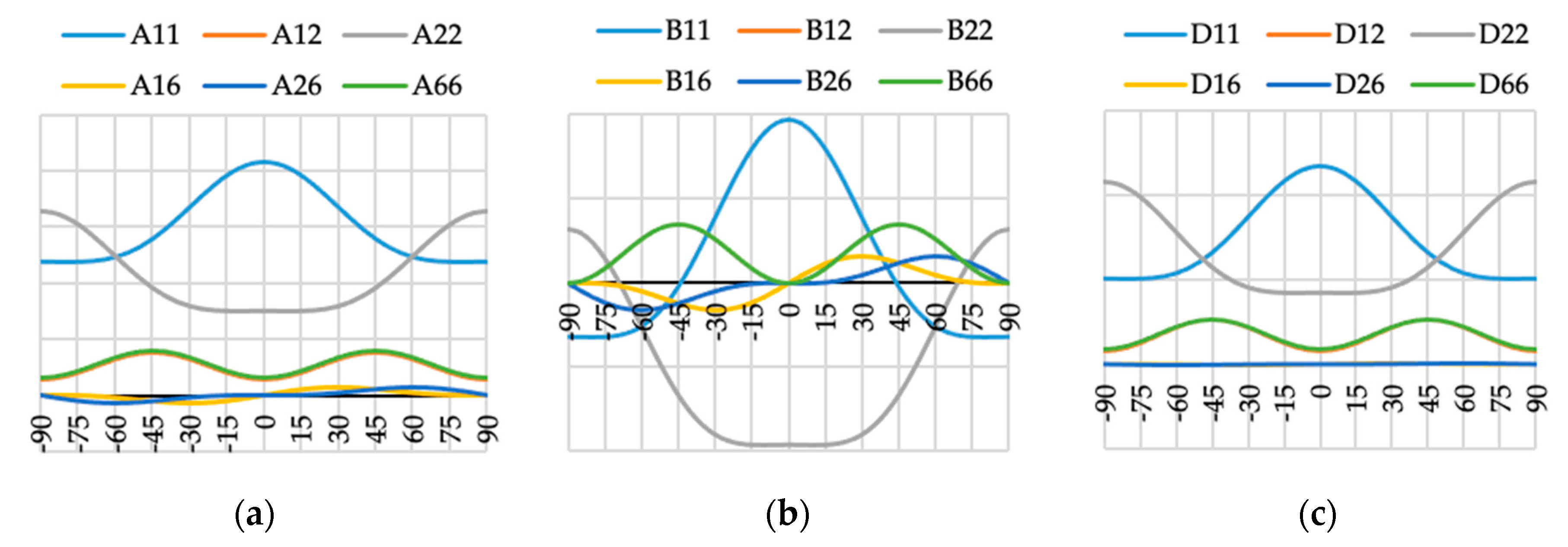
Figure 12.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N4(θ).
Figure 12.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N4(θ).
Figure 13.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N5(θ).
Figure 13.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N5(θ).
Figure 14.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N6(θ).
Figure 14.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N6(θ).
Figure 15.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N16(θ).
Figure 15.
Elements (a) [A], (b) [B] and (c) [D] of laminate stiffness matrix value for case N16(θ).
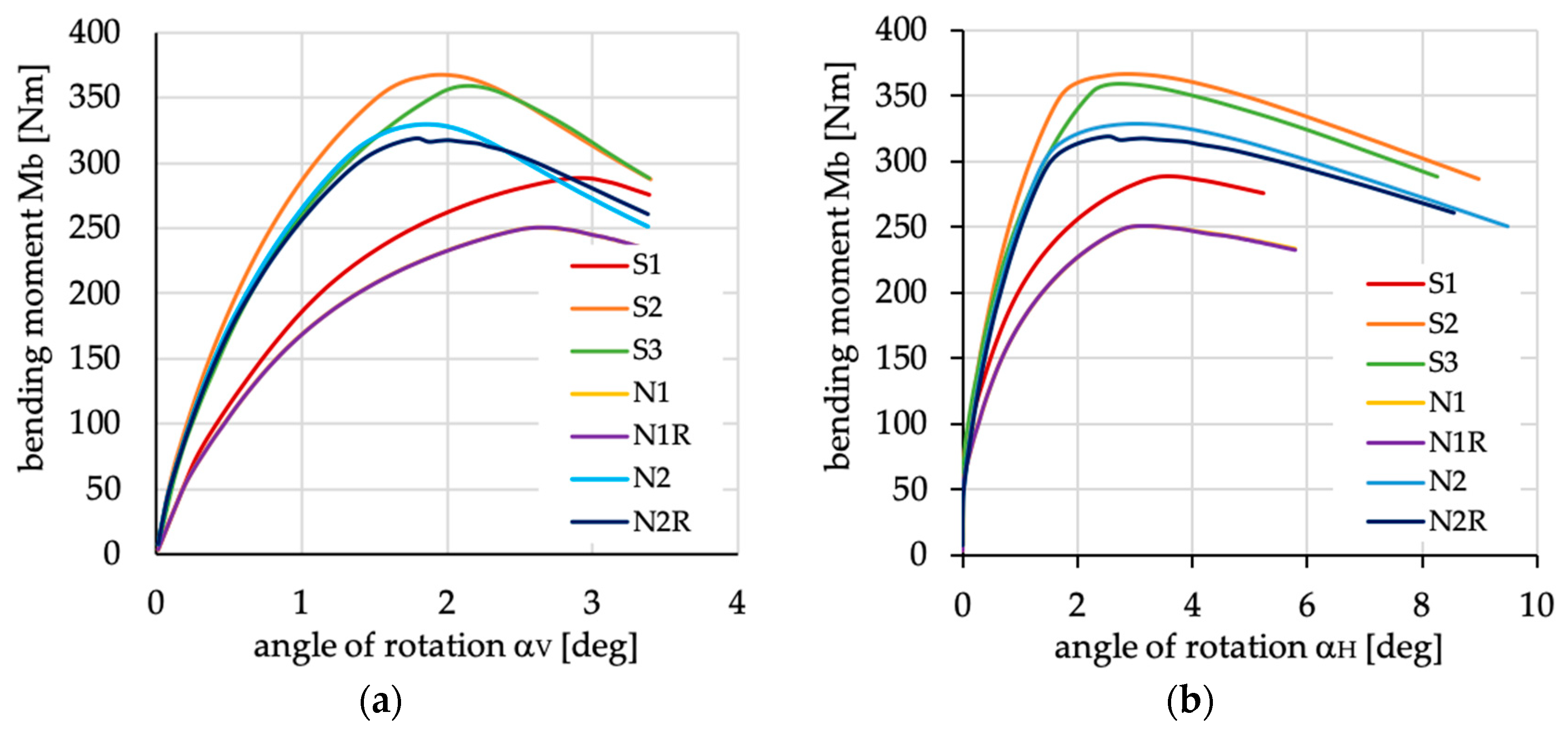
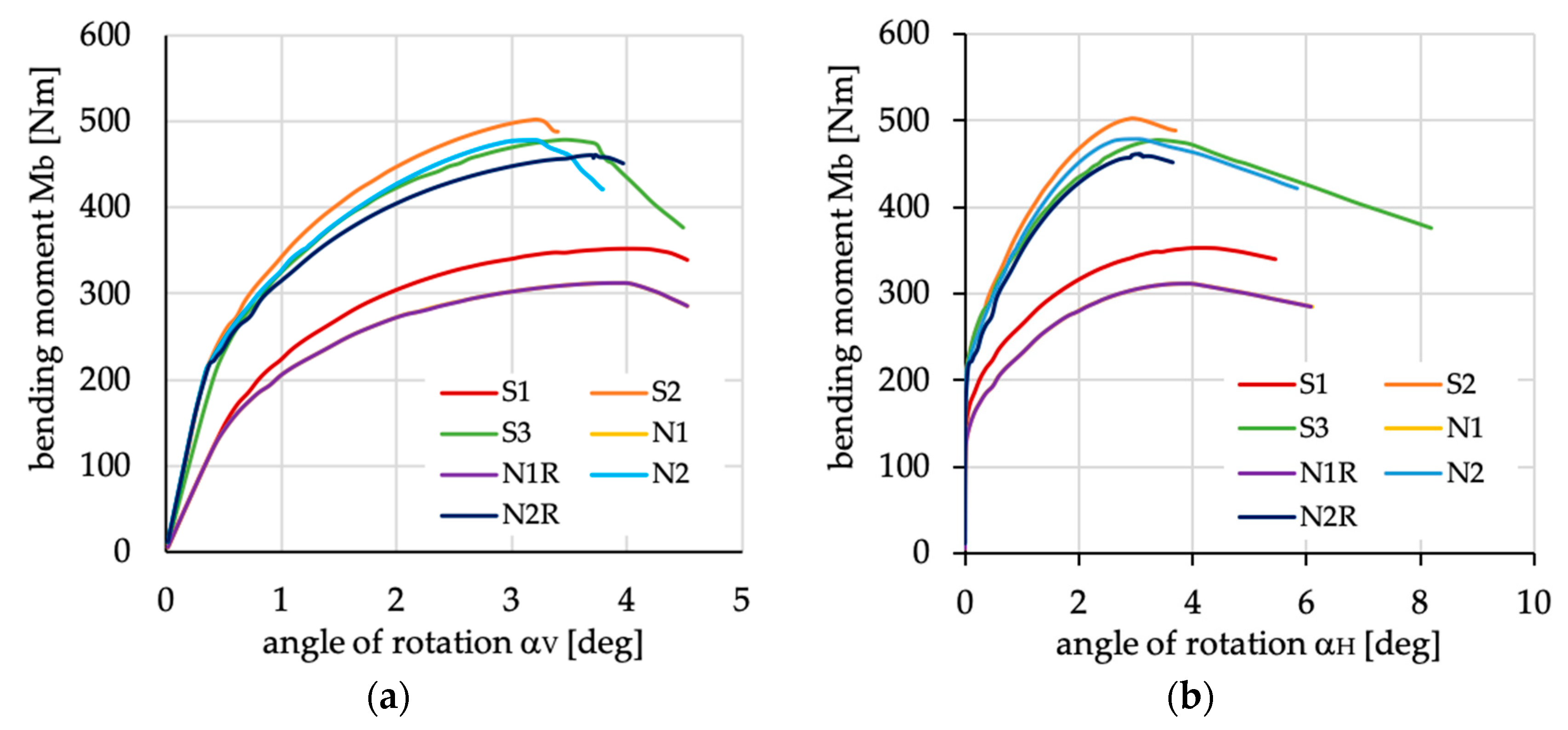
Figure 16.
Bending moment vs. angles of rotations in (a) vertical and (b) horizontal plane for channel section beams with layups denoted as S1, S2, S3, N1, N1R, N2 and N2R.
Figure 16.
Bending moment vs. angles of rotations in (a) vertical and (b) horizontal plane for channel section beams with layups denoted as S1, S2, S3, N1, N1R, N2 and N2R.
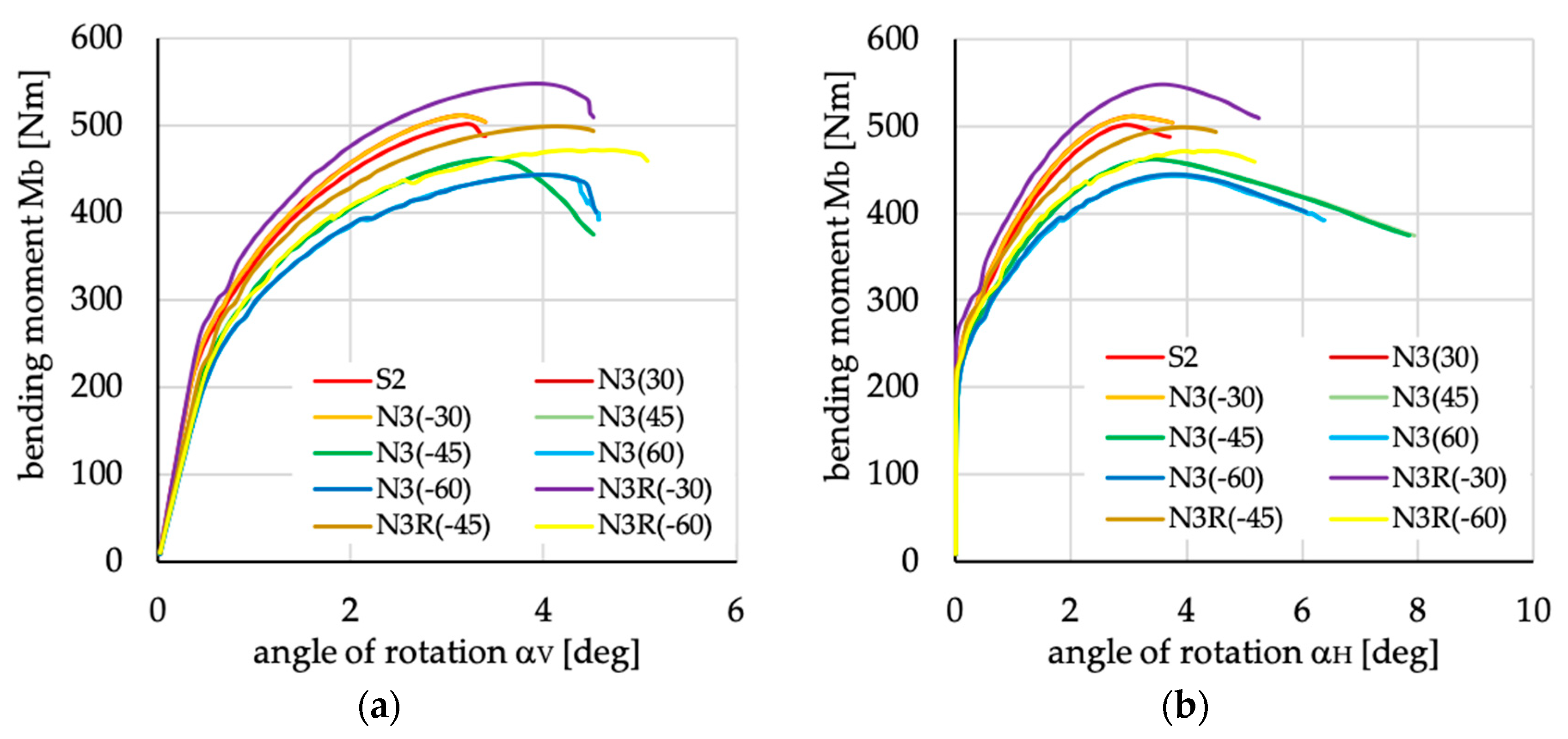
Figure 17.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as N3(θ) and N3R(θ).
Figure 17.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as N3(θ) and N3R(θ).
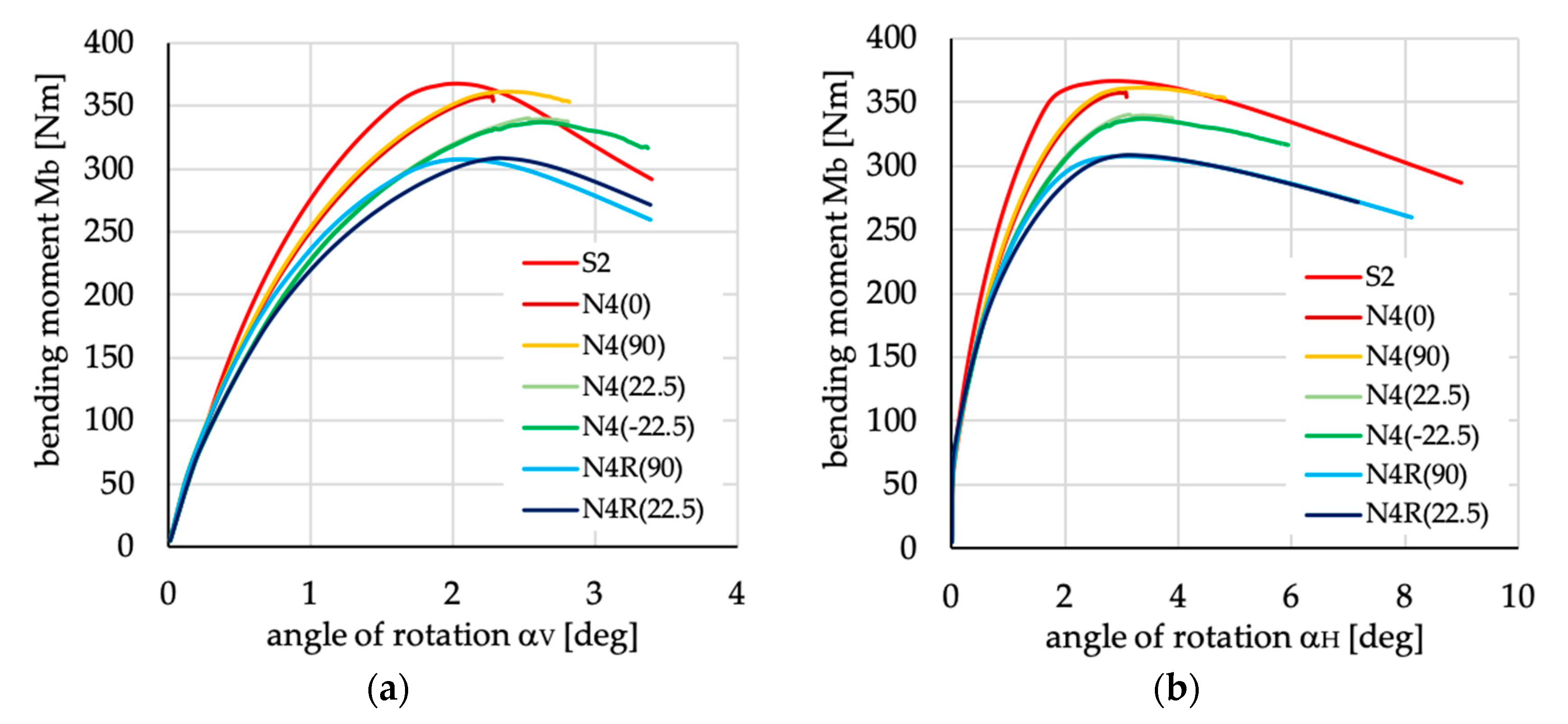
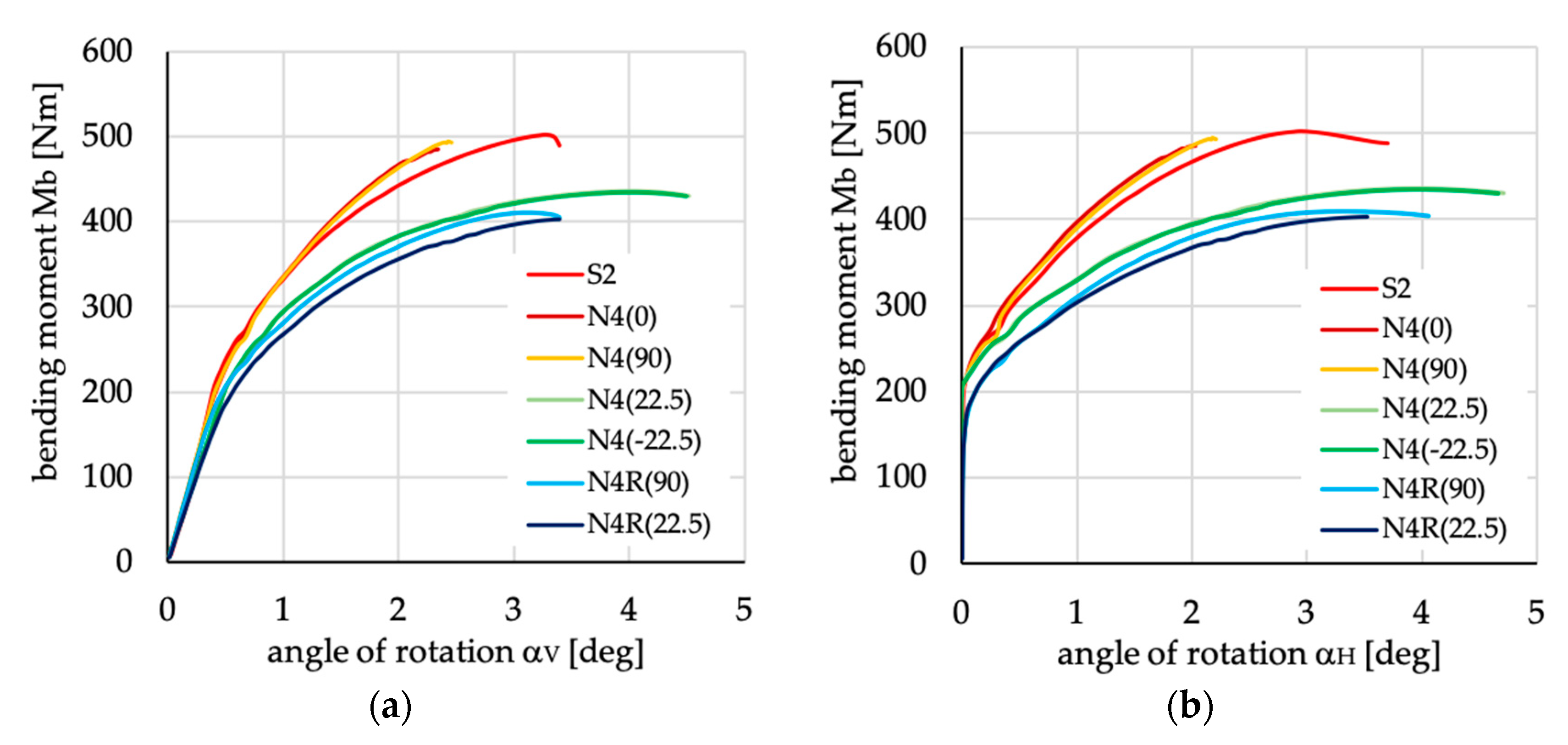
Figure 18.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as N4(θ) and N4R(θ).
Figure 18.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as N4(θ) and N4R(θ).
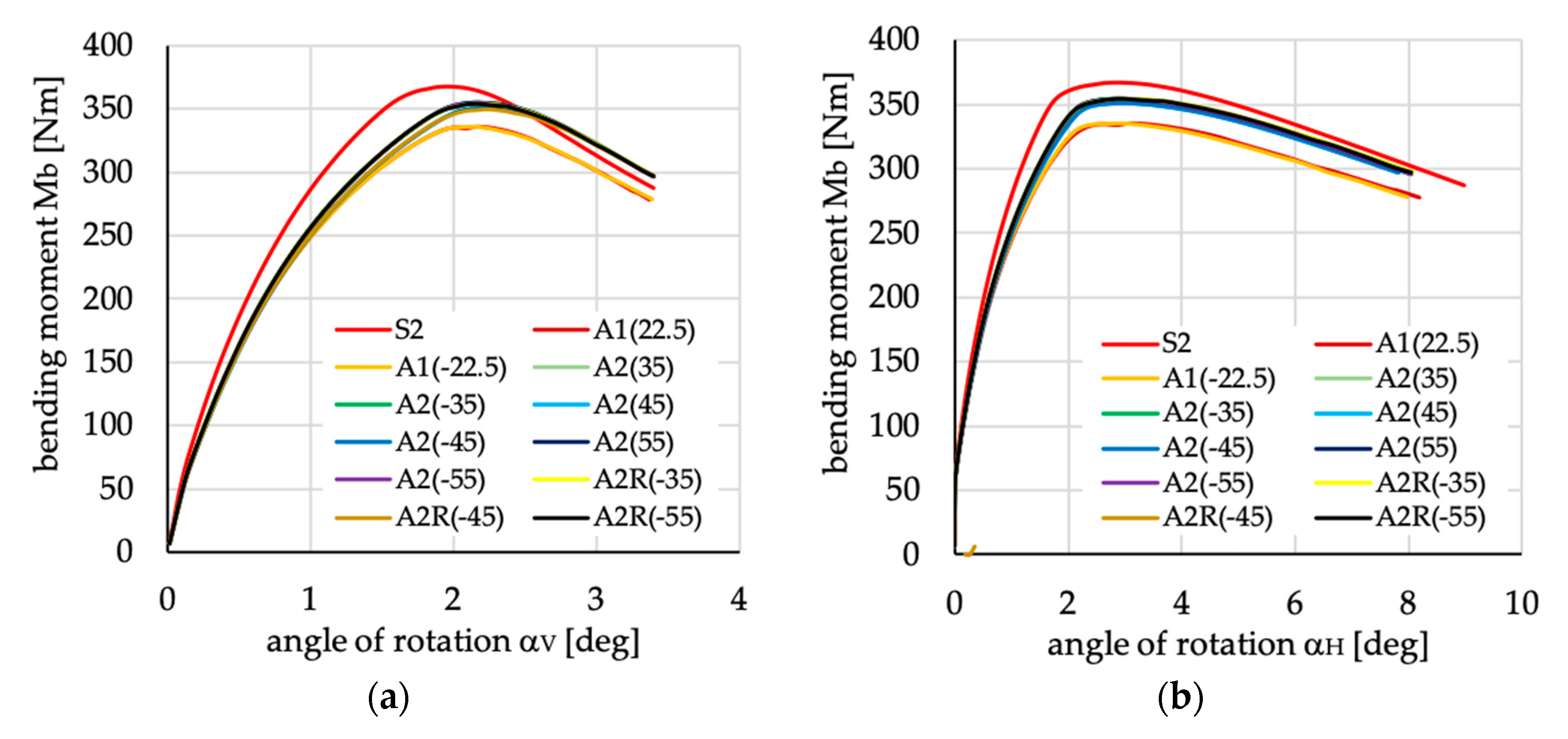
Figure 19.
Bending moment vs. angles of rotations in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as A1(θ), A2(θ) and A2R(θ).
Figure 19.
Bending moment vs. angles of rotations in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as A1(θ), A2(θ) and A2R(θ).
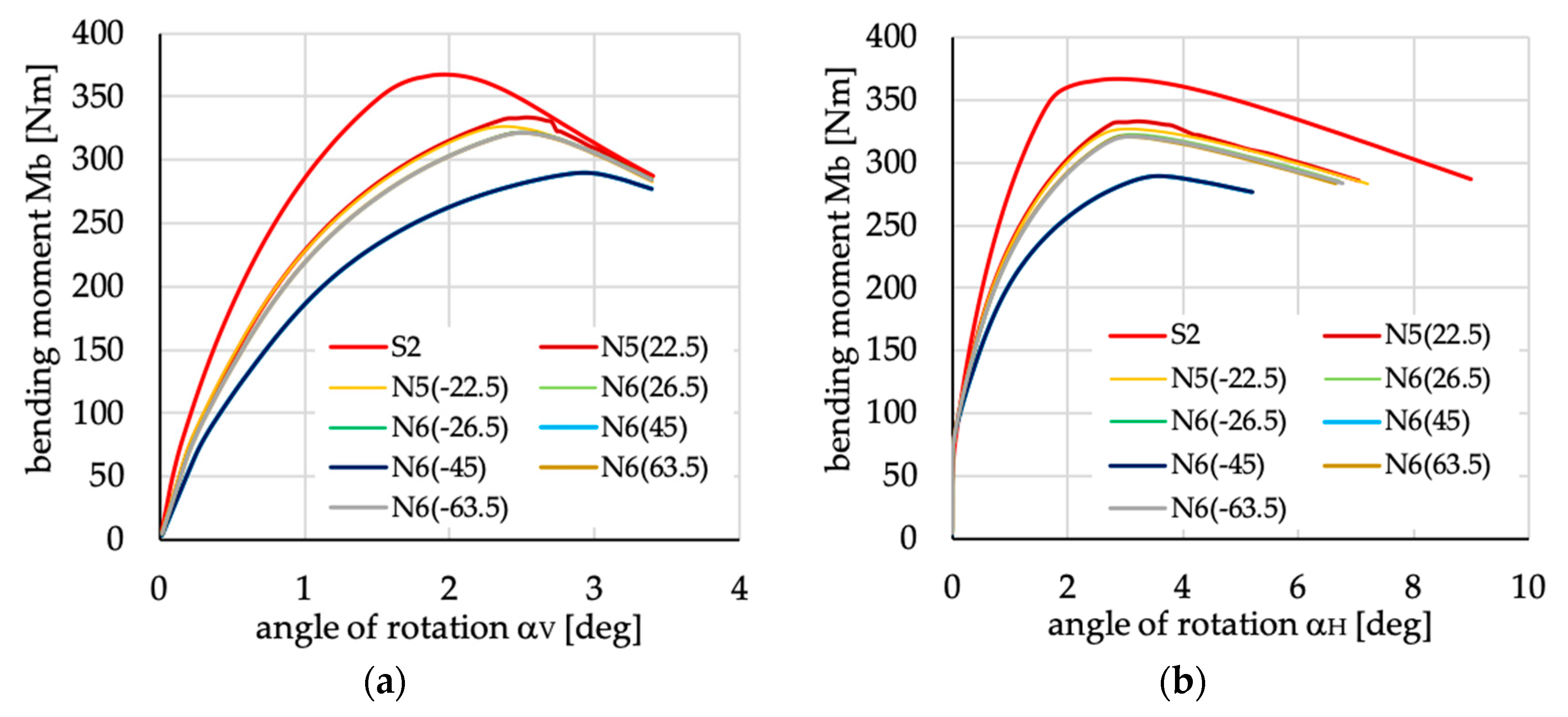
Figure 20.
Bending moment vs. angles of rotations in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as N5(θ) and N6(θ).
Figure 20.
Bending moment vs. angles of rotations in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as N5(θ) and N6(θ).
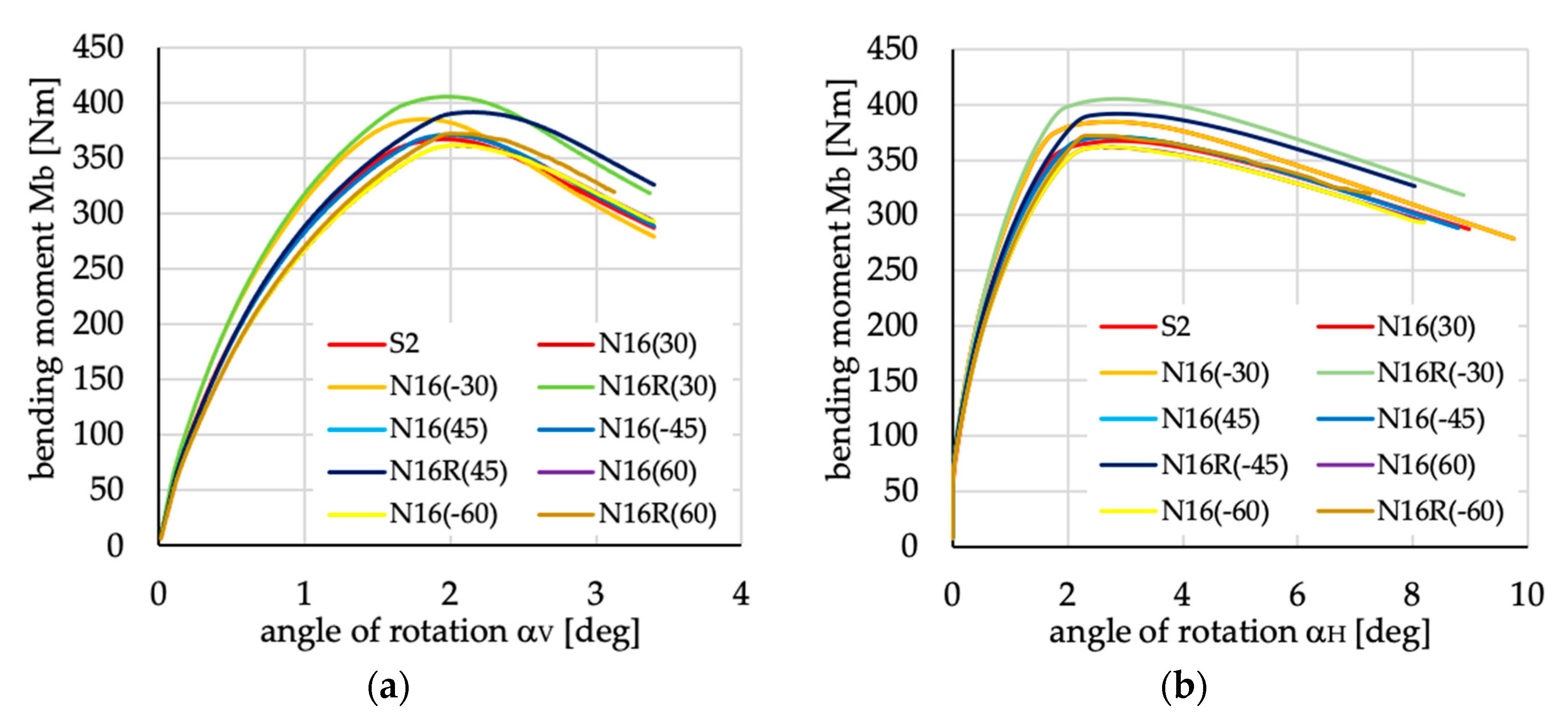
Figure 21.
Bending moment vs. angles of rotations in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as N16(θ) and N16R(θ).
Figure 21.
Bending moment vs. angles of rotations in: (a) vertical; and (b) horizontal planes for channel section beams with layups denoted as N16(θ) and N16R(θ).
Figure 22.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as S1, S2, S3, N1, N1R, N2 and N2R.
Figure 22.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as S1, S2, S3, N1, N1R, N2 and N2R.
Figure 23.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as N3(θ) and N3R(θ).
Figure 23.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as N3(θ) and N3R(θ).
Figure 24.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as N4(θ) and N4R(θ).
Figure 24.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as N4(θ) and N4R(θ).
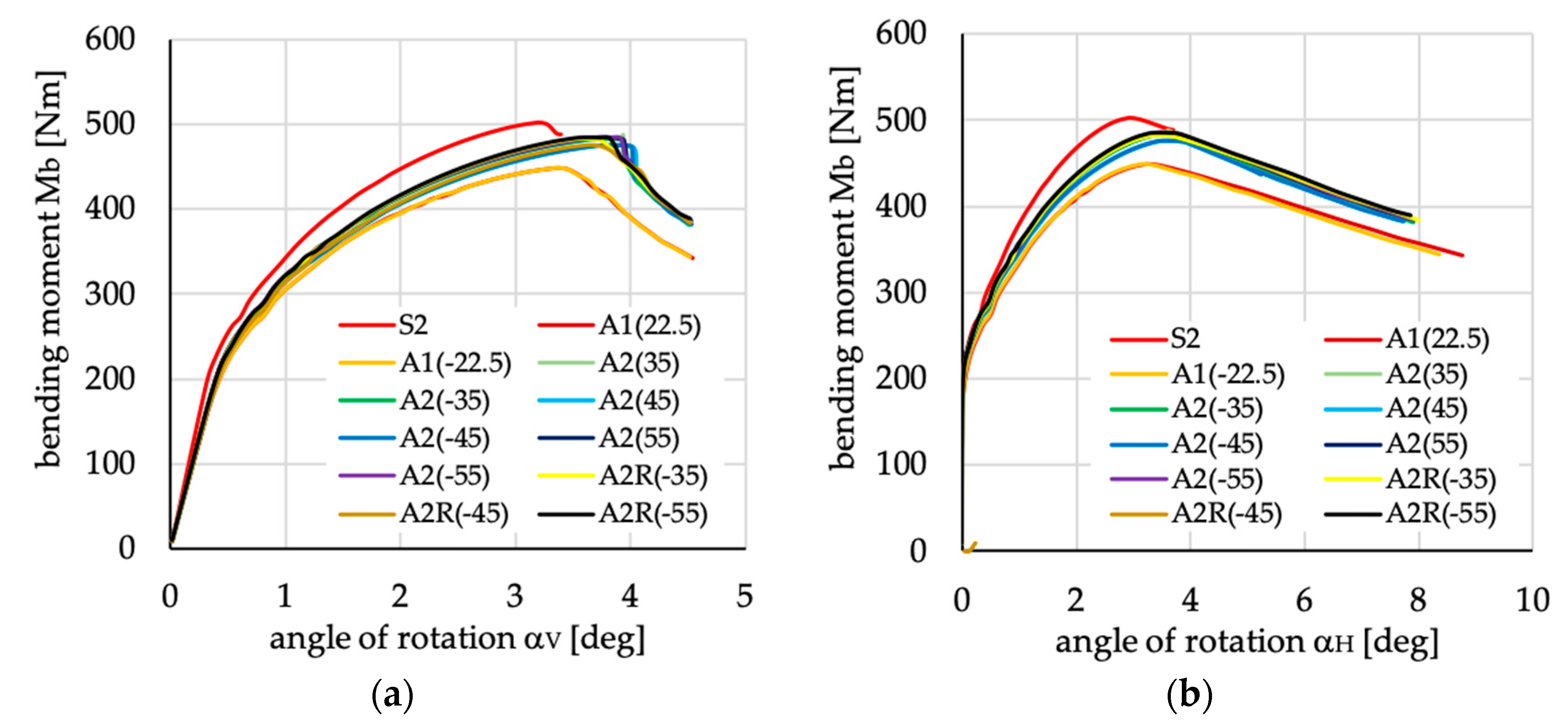
Figure 25.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as A1(θ), A2(θ) and A2R(θ).
Figure 25.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as A1(θ), A2(θ) and A2R(θ).
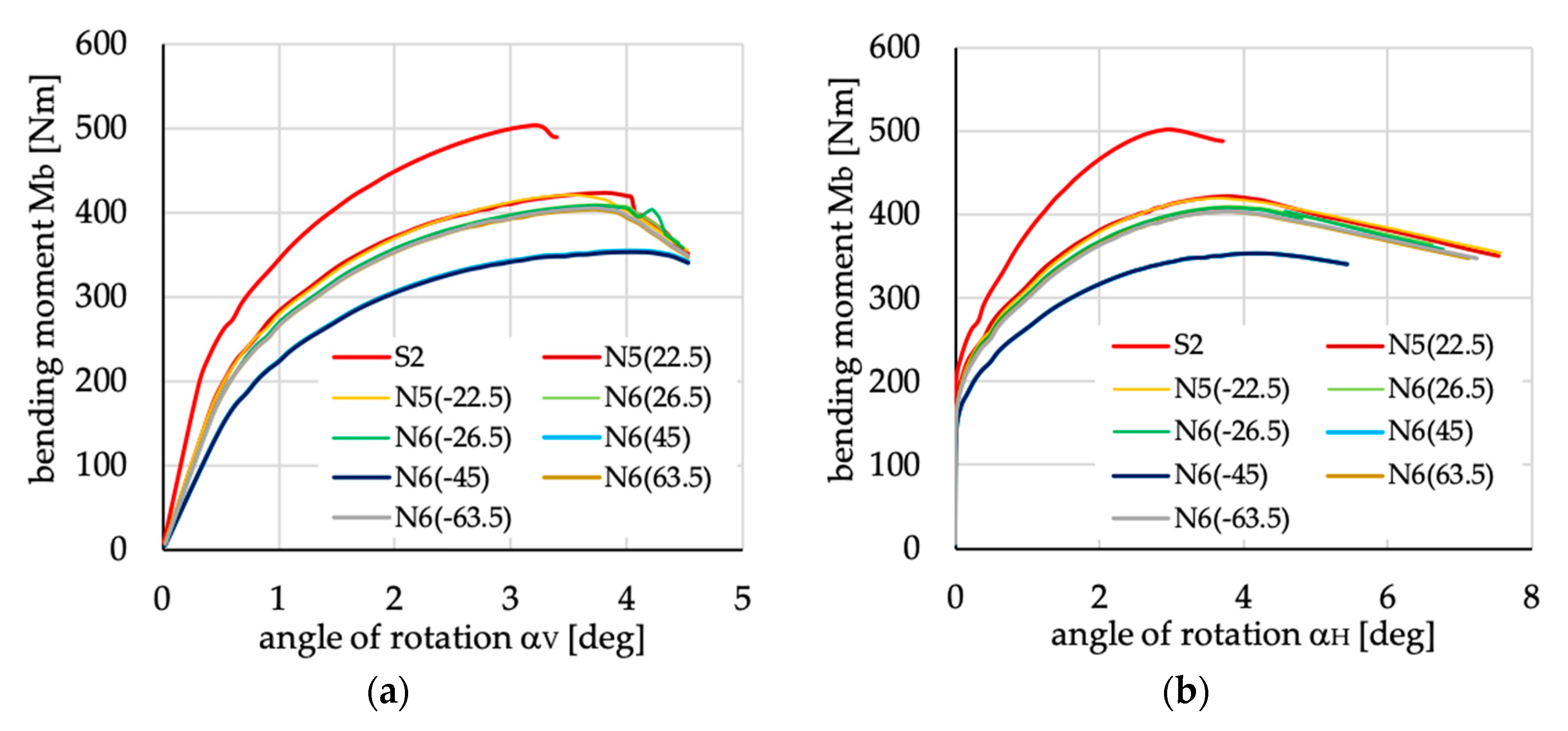
Figure 26.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as N5(θ) and N6(θ).
Figure 26.
Bending moment vs. angles of rotation in: (a) vertical; and (b) horizontal planes for lipped section beams with layups denoted as N5(θ) and N6(θ).
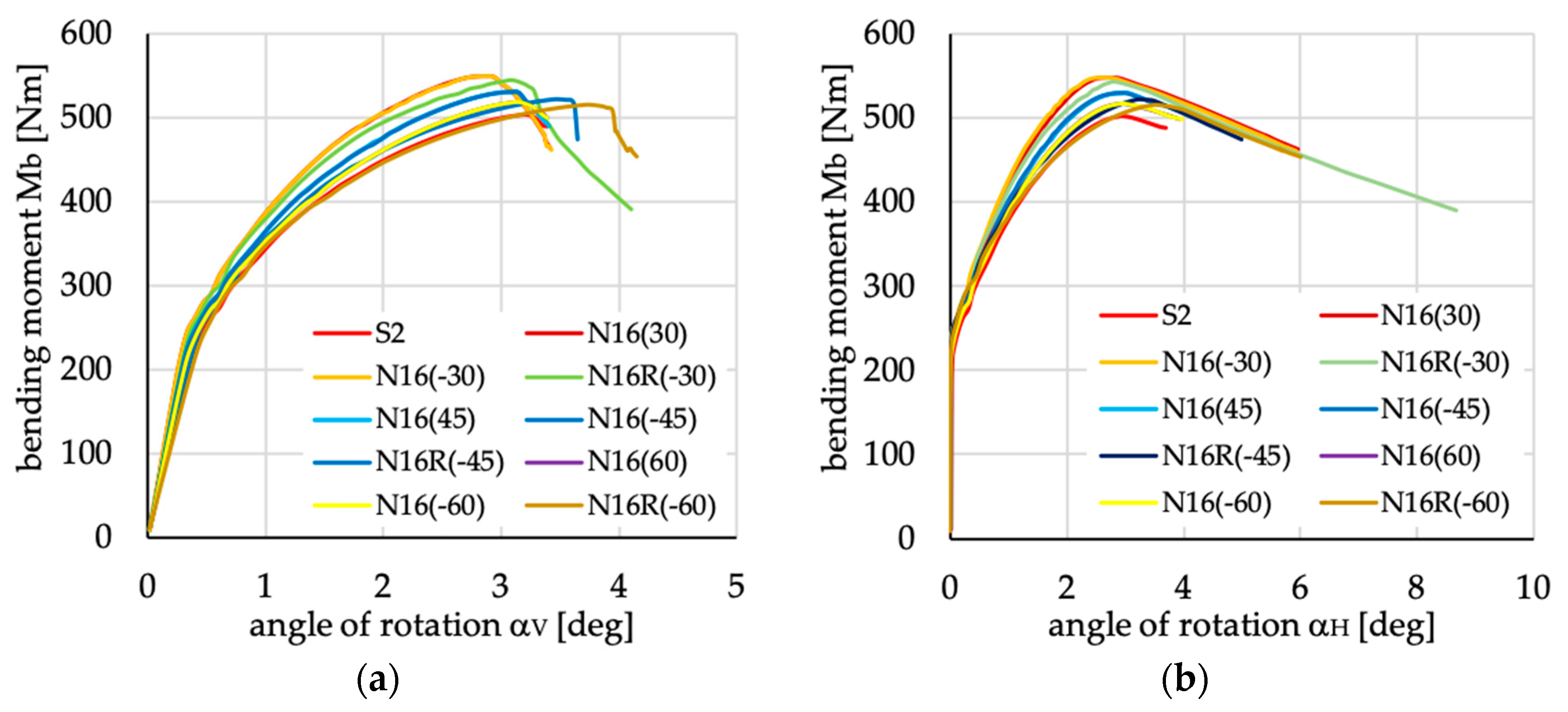
Figure 27.
Bending moment vs. angles of rotation in: (a) vertical and (b) horizontal planes for lipped section beams with layups denoted as N16(θ) and N16R(θ).
Figure 27.
Bending moment vs. angles of rotation in: (a) vertical and (b) horizontal planes for lipped section beams with layups denoted as N16(θ) and N16R(θ).
Figure 28.
Lipped channel section beam deflection for: (a) layups N4(0) and N4(90); (b) layups N4(±22.5); (c) remaining layer arrangements.
Figure 28.
Lipped channel section beam deflection for: (a) layups N4(0) and N4(90); (b) layups N4(±22.5); (c) remaining layer arrangements.
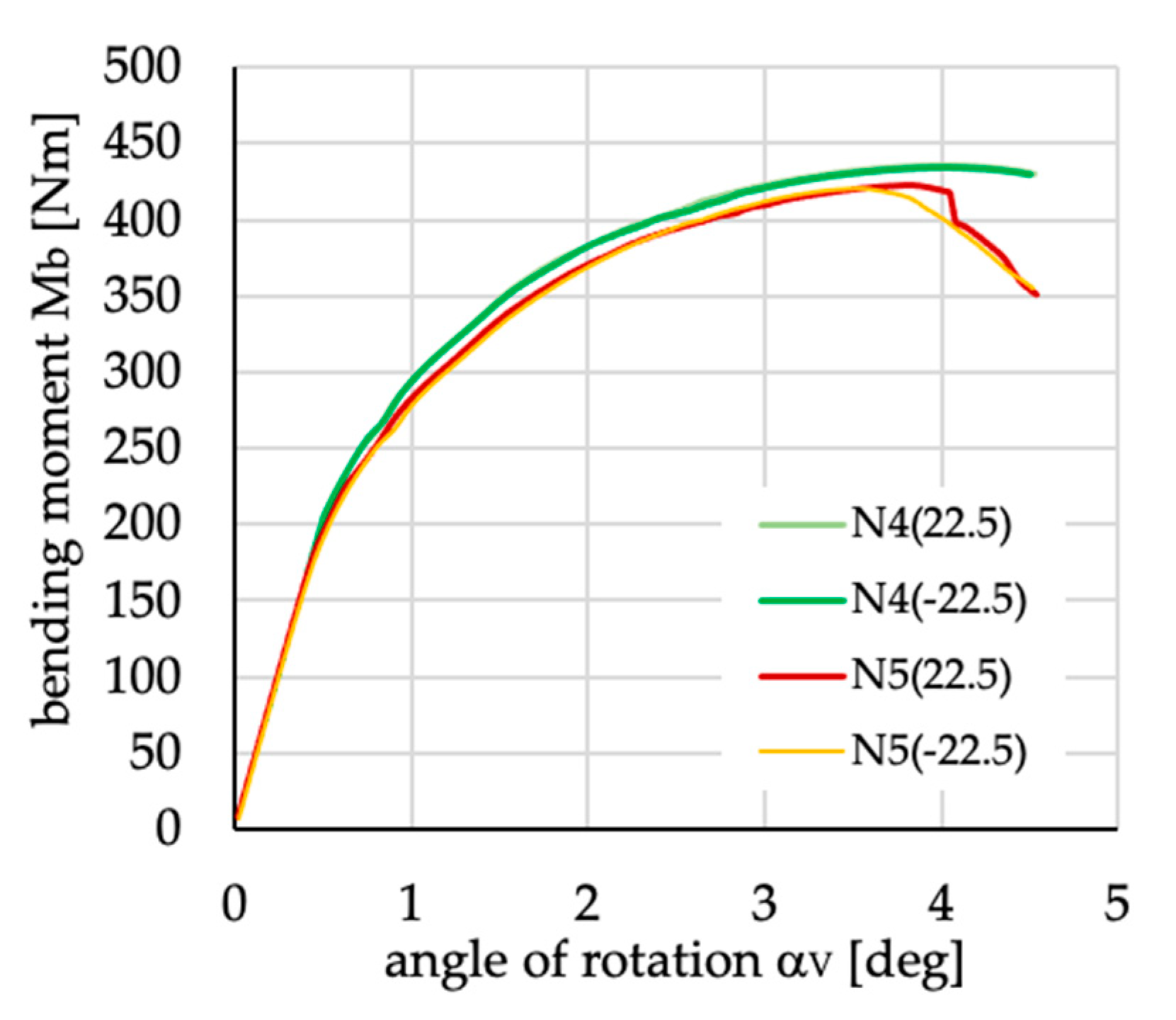
Figure 29.
Differences in the course of curves presenting bending moment vs. angle of rotation αV for positive and negative angles of fiber inclination for layups denoted as N4(±22.5) and N5(±22.5).
Figure 29.
Differences in the course of curves presenting bending moment vs. angle of rotation αV for positive and negative angles of fiber inclination for layups denoted as N4(±22.5) and N5(±22.5).
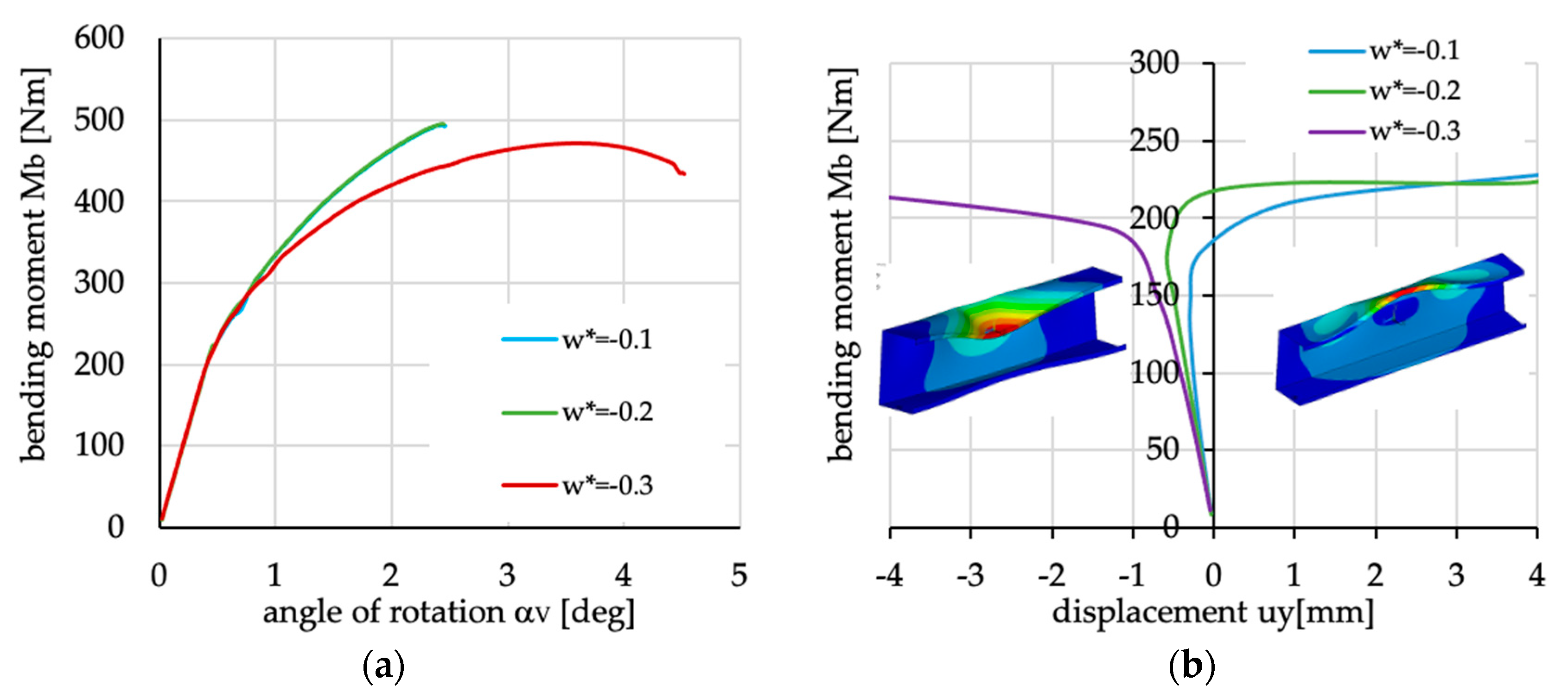
Figure 30.
Bending moment vs. (a) angle of rotation and (b) upper flange displacement.
Figure 30.
Bending moment vs. (a) angle of rotation and (b) upper flange displacement.
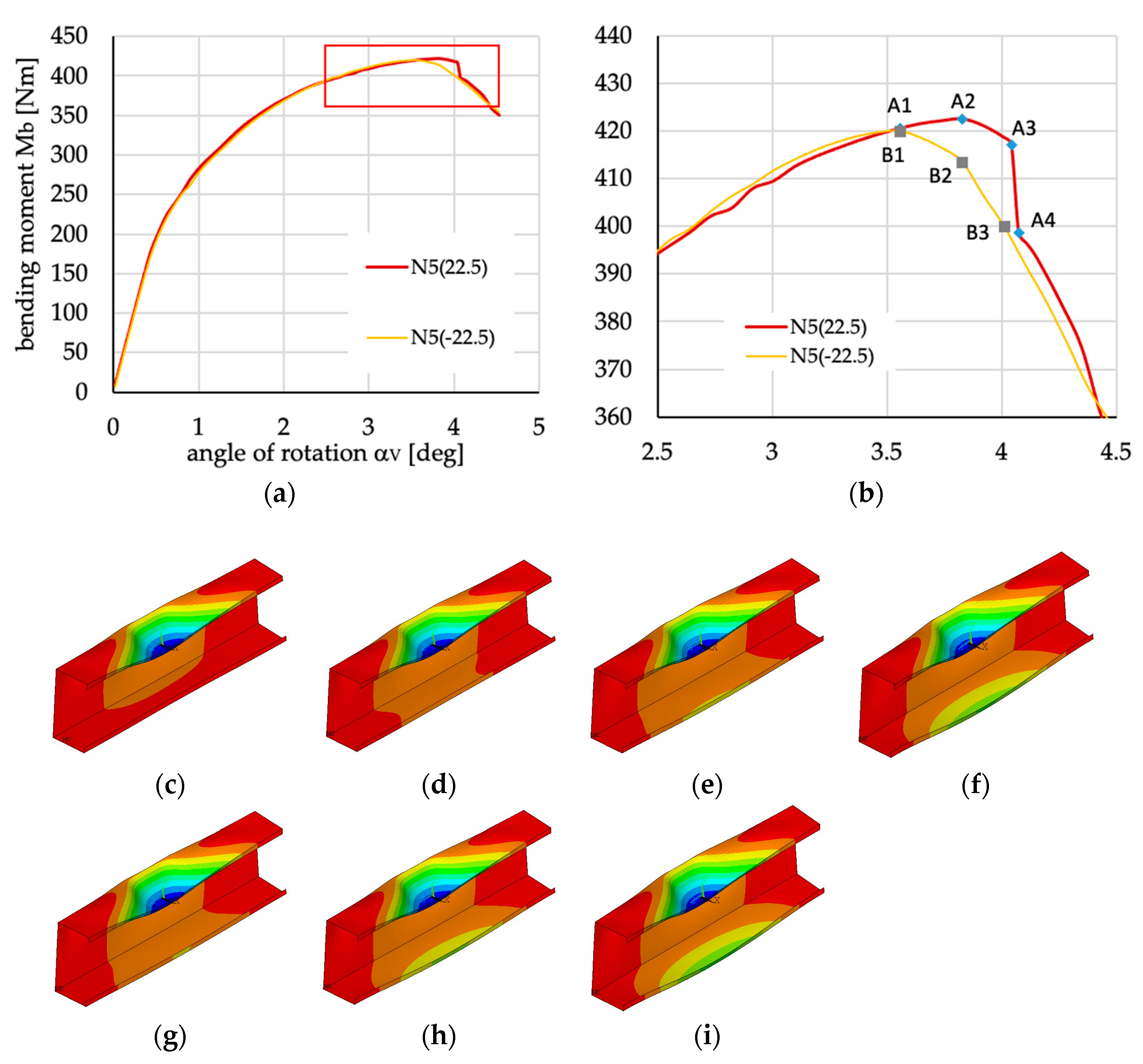
Figure 31.
(a) Bending moment vs. angle of rotation αV. (b) Zoom of sub-figure (a). Shape of beam deflection from points depicted in sub-figure (b): (c) from point A1; (d) from point A2; (e) point A3, (f) point A4, (g) point B1, (h) point B2, (i) point B3.
Figure 31.
(a) Bending moment vs. angle of rotation αV. (b) Zoom of sub-figure (a). Shape of beam deflection from points depicted in sub-figure (b): (c) from point A1; (d) from point A2; (e) point A3, (f) point A4, (g) point B1, (h) point B2, (i) point B3.
Table 1.
The material properties laminate under consideration.
Table 1.
The material properties laminate under consideration.
| | E1 | E2 | G12 | ν12 | XT | YT | XC | YC | S |
|---|
| [GPa] | [GPa] | [GPa] | [-] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] |
|---|
| Data | 39.0 | 9.0 | 2.7 | 0.28 | 1250 | 43 | 620 | 140 | 112 |
| SD | 0.4 | 0.7 | 0.1 | 0.003 | 78 | 4 | 62 | 5 | 1 |
Table 2.
Cross-section dimension of channel section beams for experimental tests.
Table 2.
Cross-section dimension of channel section beams for experimental tests.
| Layer Arrangement | [0/90/0/90]S | [45/−45/90/0]S | [45/−45/45/−45]S |
|---|
| Specimen No. | B1 | B2 | T | B1 | B2 | T | B1 | B2 | T |
|---|
| [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] |
|---|
| 1 | 82.1 | 41.0 | 1.18 | 82.3 | 41.1 | 1.15 | 82.4 | 41.2 | 1.15 |
| 2 | 82.1 | 41.0 | 1.20 | 82.3 | 41.0 | 1.17 | 82.3 | 41.2 | 1.15 |
| 3 | 82.1 | 41.0 | 1.18 | 82.3 | 41.1 | 1.16 | 82.3 | 41.4 | 1.17 |
| average: | 82.1 | 41.00 | 1.19 | 82.3 | 41.1 | 1.16 | 82.3 | 41.3 | 1.16 |
Table 3.
Notation of ABD matrix components of laminates under consideration.
Table 3.
Notation of ABD matrix components of laminates under consideration.
| Subscript Notation ESDU (1994) [40] | Description of Load Response Coupling | Stiffness Submatrices |
|---|
| AS | simple laminate no in-plane coupling | |
| AF | shear-extension coupling | |
| Bt | extension-twisting and shear-bending | |
| Bl | extension-bending | |
| Blt | extension-bending; extension-twisting; shearing-bending | |
| BS | extension-bending and shear-twisting | |
| BF | all in-plane with out-of-plane coupling | |
| DS | simple laminate no out-of-plane coupling | |
| DF | twisting-bending coupling | |
Table 4.
The layer arrangements of laminates under consideration.
Table 4.
The layer arrangements of laminates under consideration.
| Case ID | Number of Layers | Layer Arrangement | Laminate Type [40] | Considered θ [deg] |
|---|
| S1 | 8 | 45/−45/45/−45/−45/45/−45/45 | ASB0DF | - |
| S2 | 8 | 0/90/0/90/90/0/90/0 | AS B0DS | - |
| S3 | 8 | 45/−45/90/0/0/90/−45/45 | AS B0DF | - |
| N1 | 8 | 45/45/45/45/−45/−45/−45/−45 | ASBtDS | - |
| N2 | 8 | 90/90/90/90/0/0/0/0 | ASBlDS | - |
| A1(θ) [41] | 8 | θ/(θ−90)2/θ/−θ/(90−θ)2/−θ | ASBtDS | ±22.5 |
| A2(θ) | 8 | 0/90/θ/90−θ/θ−90/−θ/0/90 | ASBltDS | ±35, ±45, ±55 |
| A2R(θ) | 8 | 90/0/−θ/θ−90/90−θ/θ/90/0 | ASBltDS | −35, −45, −55 |
| N3(θ) [1] | 8 | 90/0/θ/−θ/0/90/−θ/θ | ASBSDF | ±30, ±45, ±60 |
| N3R(θ) | 8 | θ/−θ/90/0/−θ/θ/0/90 | ASBSDF | −30, −45, −60 |
| N4(θ) | 8 | 45/−45/45/−45/−θ/90−θ/θ/θ−90 | ASBFDF | 0, 90, ±22.5 |
| N4R(θ) | 8 | θ−90/θ/90−θ/−θ/−45/45/−45/45 | ASBFDF | 90, 22.5 |
| N5(θ) | 8 | 45/−45/θ/−θ/θ−90/90−θ/−45/45 | ASBltDF | ±22.5 |
| N6(θ) | 8 | 45/−45/θ−90/θ/−θ/90−θ/−45/45 | ASBtDF | ±26.5, ±45, ±63.5 |
| N16(θ) [1] | 16 | −θ/90/θ/0/0/θ/0/0/90/−θ/0/−θ/θ/0/−θ/θ | AFBFDF | ±30, ±45, ±60 |
| N16R(θ) | 16 | θ/−θ/0/θ/−θ/0/−θ/90/0/0/θ/0/0/θ/90/−θ | AFBFDF | −30, −45, −60 |
Table 5.
Buckling and ultimate loads with corresponding angles of rotation for considered cases.
Table 5.
Buckling and ultimate loads with corresponding angles of rotation for considered cases.
| Case ID | θ | C-Section Beam | Lipped Section Beam |
|---|
| Mcr | Mu | (αV)u | (αH)u | Mcr | Mu | (αV)u | (αH)u |
|---|
| [Nm] | [Nm] | [deg] | [deg] | [Nm] | [Nm] | [deg] | [deg] |
|---|
| S1 | – | 78.4 | 288.5 | 2.94 | 3.63 | 190.6 | 352.8 | 4.01 | 4.15 |
| S2 | 60.8 | 367.2 | 1.96 | 2.88 | 291.4 | 502.6 | 3.22 | 2.96 |
| S3 | 76.4 | 358.9 | 2.12 | 2.65 | 248.5 | 477.9 | 3.46 | 3.39 |
| A1(θ) | ±22.5 | 60.8 | 335.7 | 2.15 | 3.07 | 223.8 | 449.2 | 3.37 | 3.27 |
| A2(θ) | ±35 | 59.7 | 354.6 | 2.16 | 2.89 | 236.3 | 487.7 | 3.94 | 3.6 |
| ±45 | 59.9 | 350.8 | 2.23 | 2.99 | 233.1 | 475.6 | 3.83 | 3.58 |
| ±55 | 59.4 | 354.6 | 2.16 | 2.89 | 238.8 | 485.6 | 3.74 | 3.45 |
| A2R(θ) | ±35 | 59.8 | 354 | 2.16 | 2.96 | 241.2 | 482.7 | 3.55 | 3.34 |
| ±45 | 59.9 | 350.1 | 2.23 | 3.07 | 238.3 | 475.3 | 3.64 | 3.46 |
| ±55 | 59.5 | 354.3 | 2.16 | 2.96 | 243.8 | 485.2 | 3.65 | 3.47 |
| N1 | – | 58.2 | 250.7 | 2.67 | 3.23 | 160.3 | 311.5 | 3.92 | 3.89 |
| N1R | 58.3 | 250.8 | 2.67 | 3.19 | 160.3 | 311.6 | 3.92 | 3.86 |
| N2 | 52.4 | 329.3 | 1.87 | 3.09 | 239.4 | 477.9 | 3.15 | 2.96 |
| N2R | 45.8 | 319.2 | 1.81 | 2.56 | 216 | 460.5 | 3.71 | 3.05 |
| N3(θ) | ±30 | 66 | 369.5 | 1.96 | 2.96 | 267.2 | 512.2 | 3.15 | 3.09 |
| ±45 | 66.2 | 338.8 | 2.12 | 2.92 | 246.8 | 462.7 | 3.46 | 3.43 |
| ±60 | 61.6 | 320.5 | 2.26 | 2.96 | 240.4 | 444.1 | 3.98 | 3.79 |
| N3R(θ) | ±30 | 65.7 | 396 | 2.16 | 3.15 | 263.6 | 512.3 | 3.15 | 3.08 |
| ±45 | 66 | 367 | 2.32 | 3 | 248.6 | 499.4 | 4.1 | 3.89 |
| ±60 | 61.5 | 341.4 | 2.42 | 3.11 | 246.9 | 472 | 4.5 | 4.22 |
| N4(θ) | 0 | 58.4 | 357.9 | 2.28 | 3.08 | 234.1 | – | – | – |
| 90 | 60 | 361.7 | 2.39 | 3.35 | 225.9 | – | – | – |
| 22.5 | 71.1 | 340.3 | 2.53 | 3.14 | 220.4 | 436 | 4.01 | 3.96 |
| −22.5 | 69.9 | 336.7 | 2.61 | 3.33 | 219.2 | 434.4 | 4.04 | 3.99 |
| N4R(θ) | 90 | 60.2 | 307.3 | 2.05 | 3.02 | 218.3 | 410 | 3.14 | 3.38 |
| 22.5 | 70.1 | 308.8 | 2.32 | 3.11 | 221 | 405.3 | 3.46 | 3.65 |
| N5(θ) | ±22.5 | 76.7 | 329.9 | 2.53 | 3.21 | 219.4 | 421.2 | 3.69 | 3.74 |
| N6(θ) | ±26.5 | 77.2 | 322.1 | 2.53 | 3.18 | 215.6 | 410.2 | 3.74 | 3.79 |
| ±45 | 79.1 | 289.6 | 2.94 | 3.6 | 191 | 353.8 | 4.01 | 4.15 |
| ±63.5 | 77.6 | 321.1 | 2.53 | 3.15 | 210.6 | 403.7 | 3.74 | 3.82 |
| N16(θ) | ±30 | 71.4 | 385 | 1.82 | 2.76 | 270.2 | 548.6 | 2.87 | 2.76 |
| ±45 | 73.8 | 370.6 | 1.98 | 2.74 | 262.8 | 529.5 | 3.08 | 2.9 |
| ±60 | 68.4 | 361.7 | 2.02 | 2.6 | 260.4 | 518 | 3.15 | 2.95 |
| N16R(θ) | ±30 | 71.2 | 405.5 | 2 | 2.93 | 265.8 | 543.6 | 3.09 | 2.81 |
| ±45 | 73.7 | 391.4 | 2.16 | 2.92 | 258.9 | 522.2 | 3.46 | 3.24 |
| ±60 | 68.3 | 371.4 | 2.03 | 2.42 | 262.8 | 515.9 | 3.74 | 3.52 |
Table 6.
Nondimensional value of ABD laminate stiffness matrix for laminates used in channel section beam for which the extremal buckling and ultimate load were obtained.
Table 6.
Nondimensional value of ABD laminate stiffness matrix for laminates used in channel section beam for which the extremal buckling and ultimate load were obtained.
| Sub-Matrix | Minimal Mcr | Maximal Mcr | Minimal Mu | Maximal Mu |
|---|
| N2R | N6(±45) | N1, N1R | N16R(±30) |
|---|
| A | | | | |
| B | | | | |
| D | | | | |
Table 7.
Nondimensional value of ABD laminate stiffness matrix for laminates used in lipped section beam for which the extremal buckling and ultimate load were obtained.
Table 7.
Nondimensional value of ABD laminate stiffness matrix for laminates used in lipped section beam for which the extremal buckling and ultimate load were obtained.
| Sub-Matrix | Minimal Mcr | Maximal Mcr | Minimal Mu | Maximal Mu |
|---|
| N1, N1R | S2 | N1 | N16(±30) |
|---|
| A | | | | |
| B | | | | |
| D | | | | |