Numeric Analysis on Shear Behavior of High-Strength Concrete Single-Keyed Dry Joints with Fixing Imperfections in Precast Concrete Segmental Bridges
Abstract
:1. Introduction
2. Materials and Methods
2.1. Concrete Damage Plasticity Model
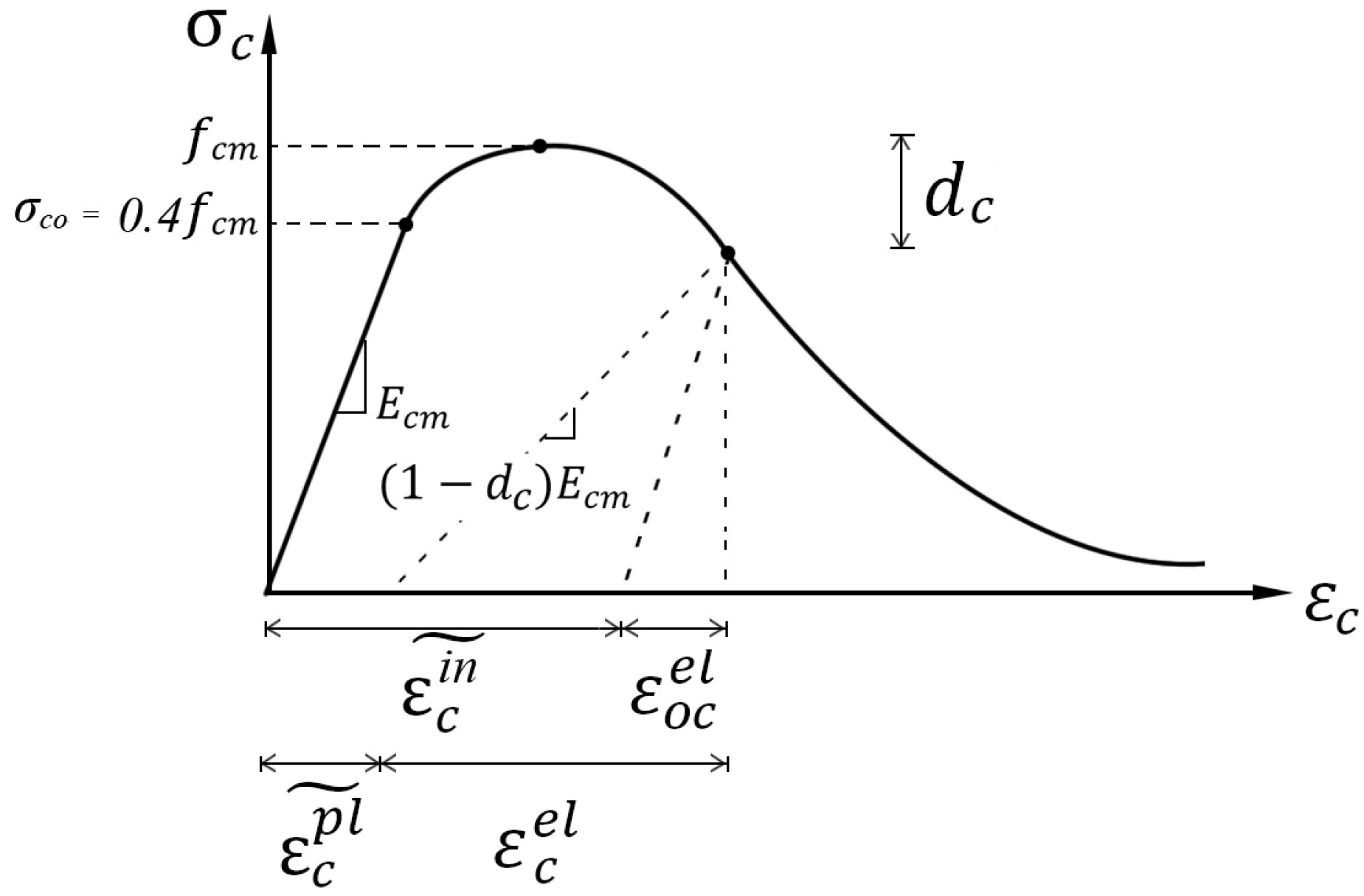
2.2. Concrete Constitutive Relation under Uniaxial Compression
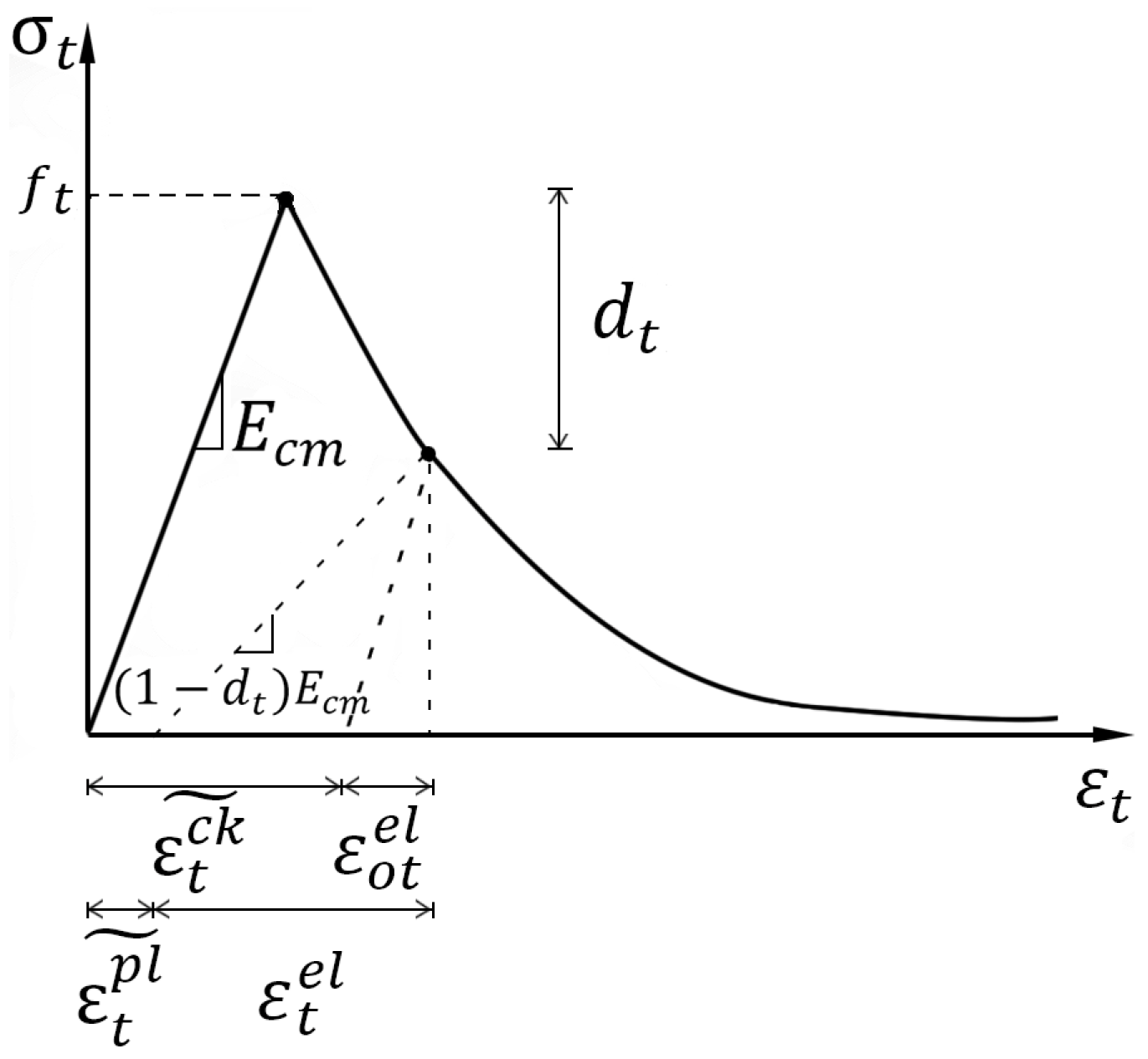
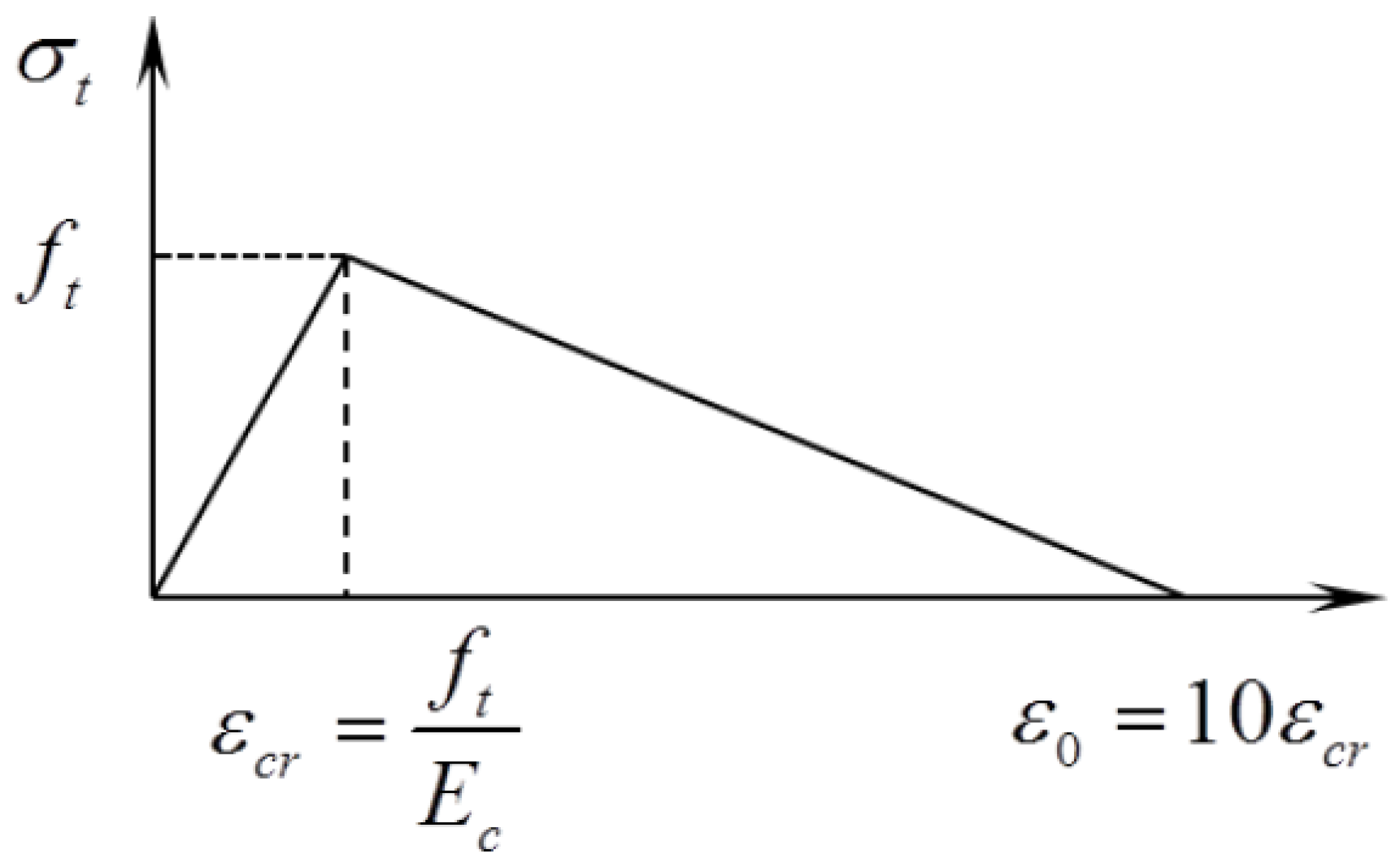
2.3. Concrete Constitutive Relation under Uniaxial Tension
2.4. Crack Detection of CDP in Numeric Analysis
2.5. Material Properties for Reinforcement Bar and Steel Plate
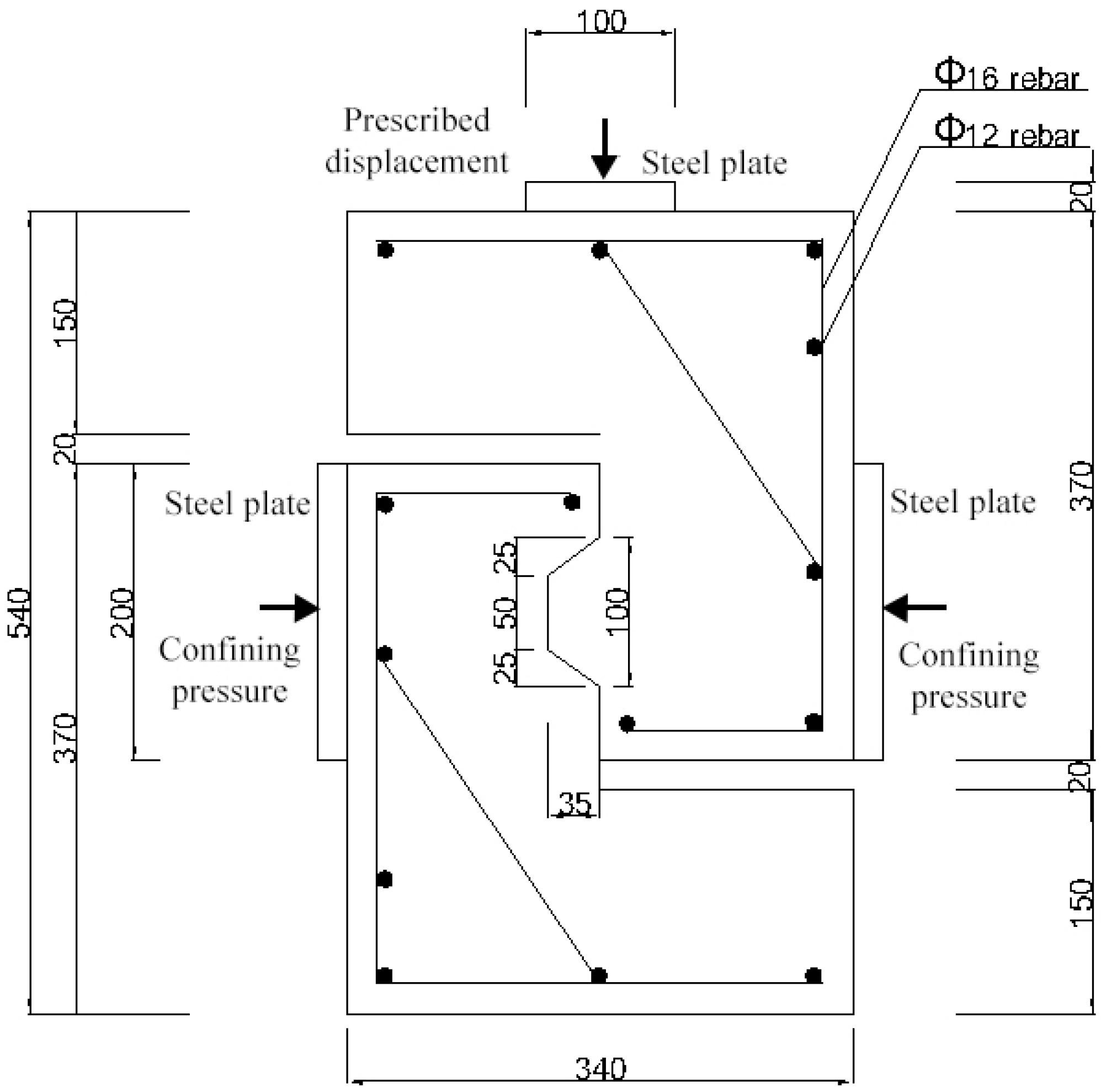
2.6. Numeric Simulation
3. FE Analysis Results
3.1. Shear Capacity
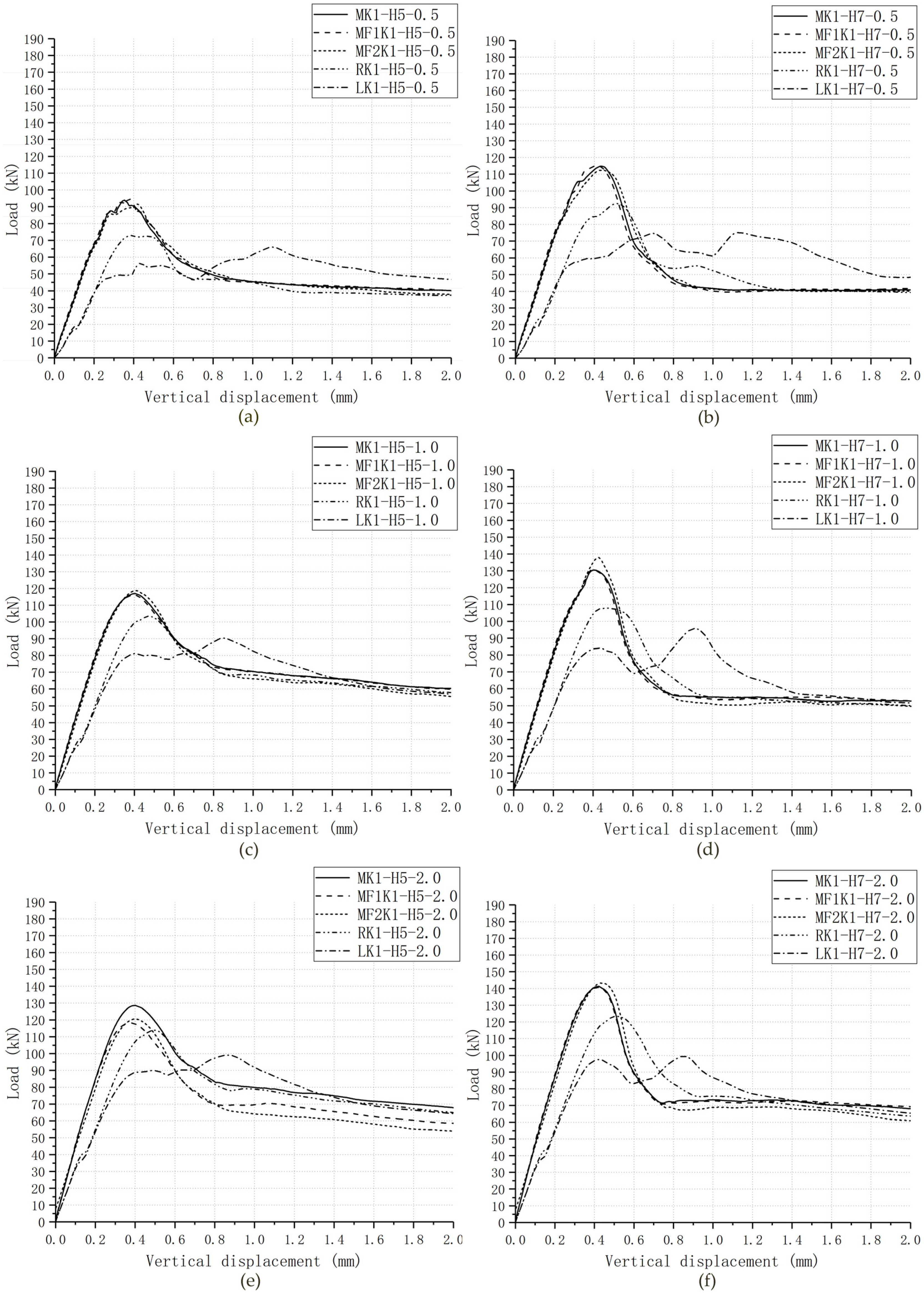
3.2. Load–Displacement Relationship
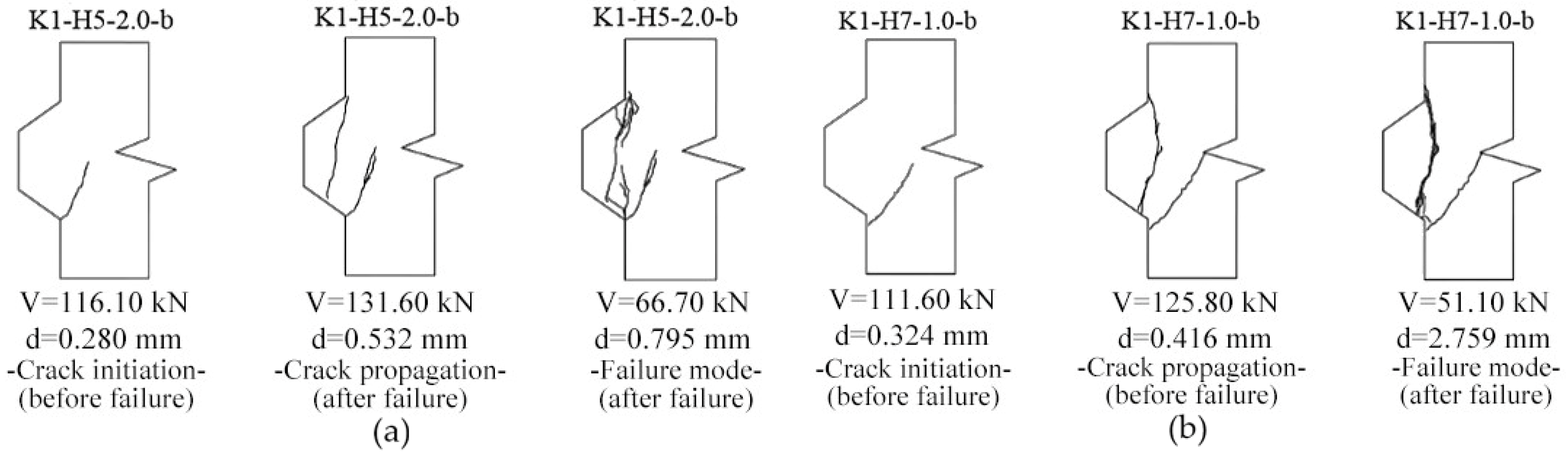
3.3. Crack Patterns
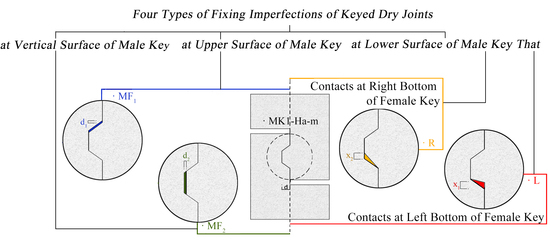
4. Parametric Study: Fixing Imperfections in Shear Key
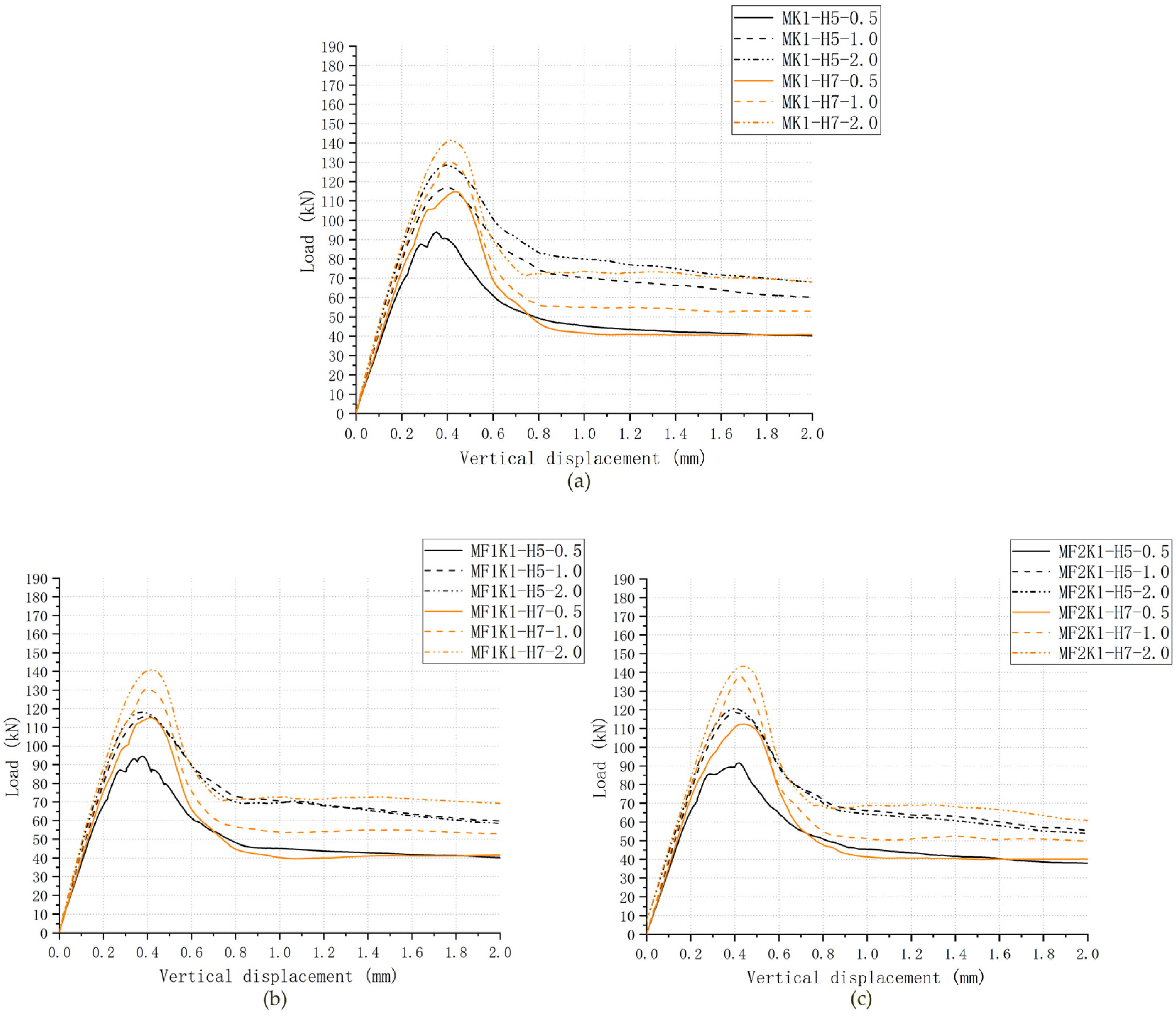
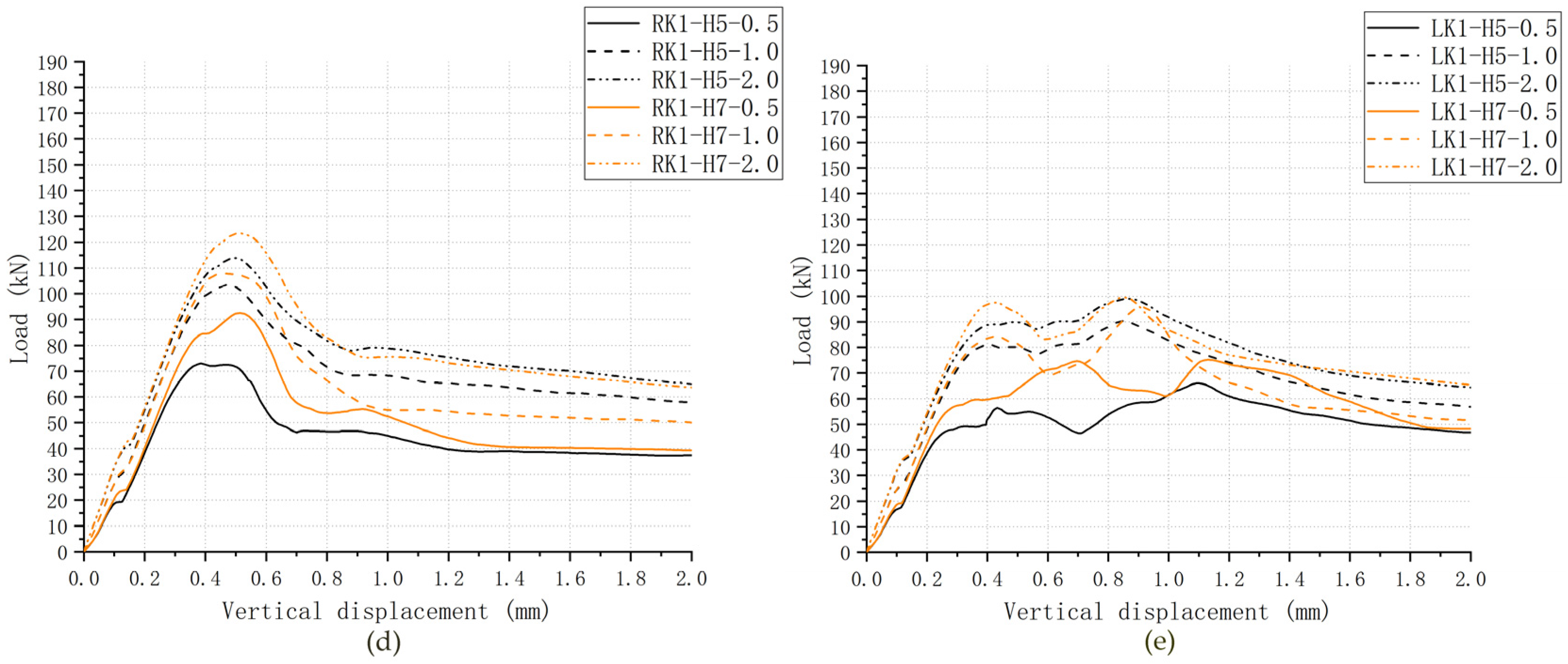
4.1. Effects of Fixing Imperfections of Keys on Shear Capacity and Load–Displacement Relationship
4.2. Effects of Fixing Imperfections of Keys on Crack Patterns
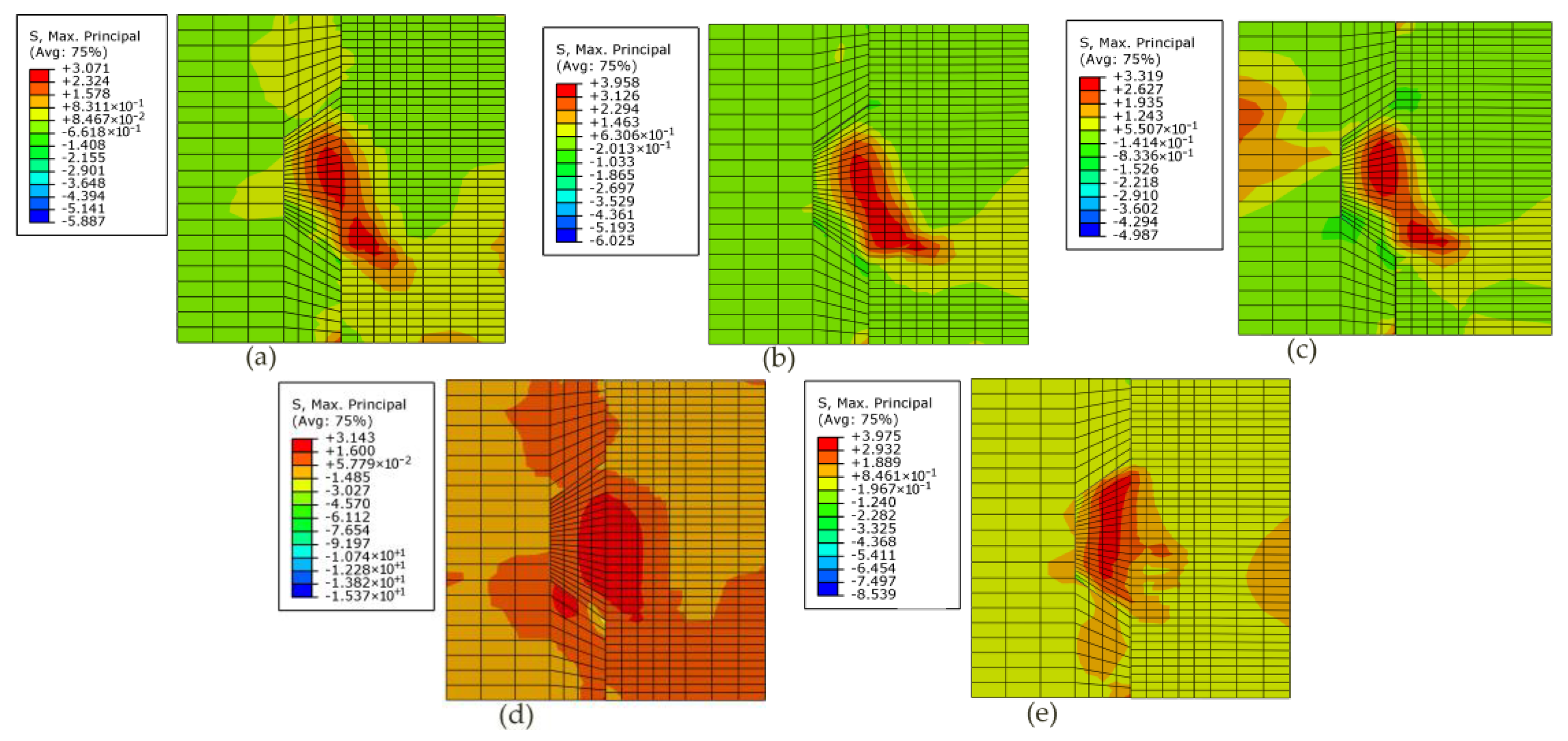
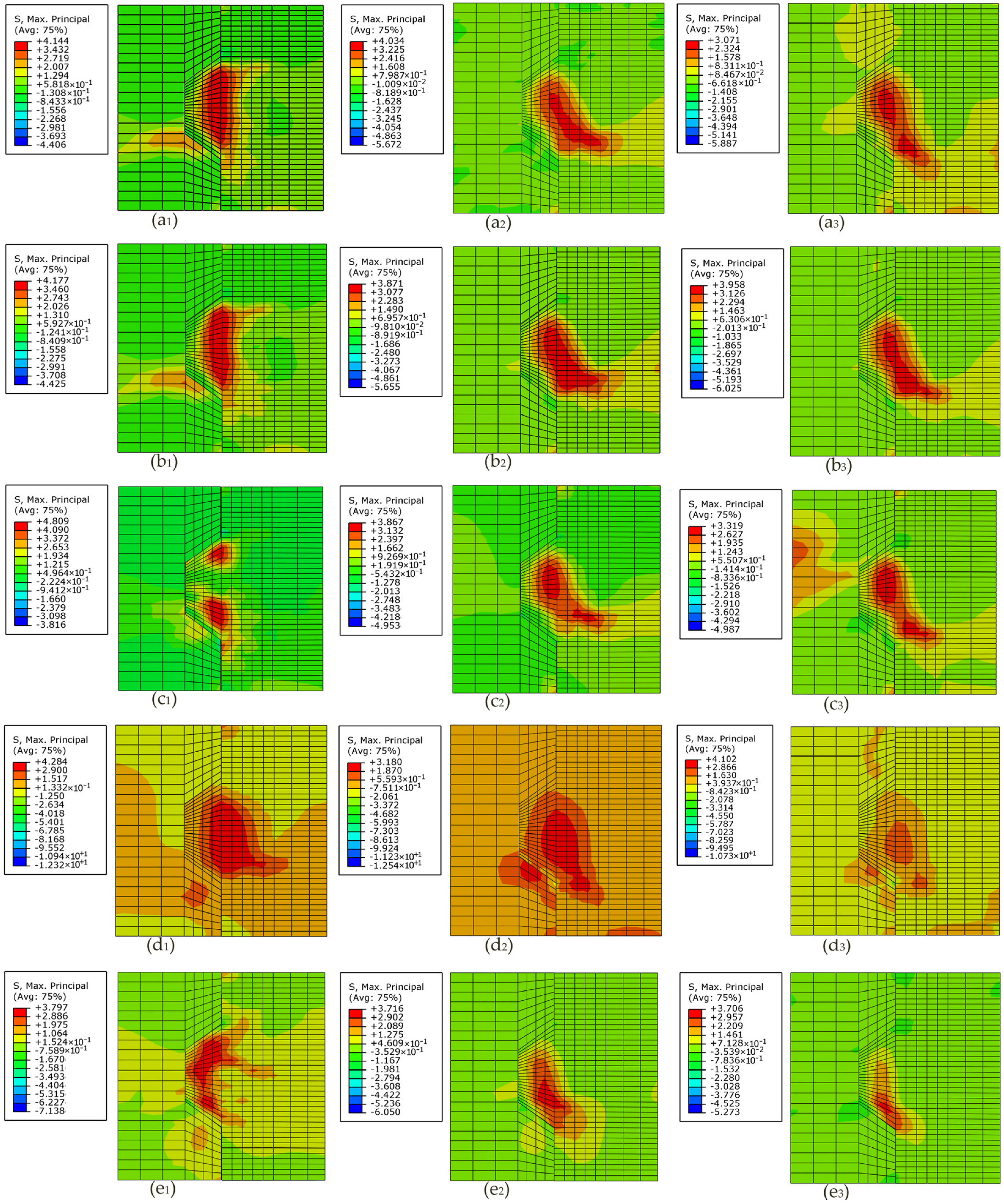
4.3. Effects of Fixing Imperfections of Keys on the Contour Plot of the Maximum Principal Stress Contour
5. Parametric Study: Confining Pressure
5.1. Effects of Confining Pressure on Shear Capacity and Load–Displacement Relationship
5.2. Effects of Confining Pressure on the Contour Plot of the Maximum Principal Stress Contour
6. Parametric Study: Concrete Strength
6.1. Effects of Concrete Strength on Shear Capacity and Load–Displacement Relationship
6.2. Effects of Concrete Strength on the Contour Plot of the Maximum Principal Stress Contour
7. Comparisons between Numeric Analysis and AASHTO
7.1. A Correction Factor of Direct-Shear Strength Based on AASHTO and This Numeric Study
7.2. Modified Formula for Multiple-Keyed Dry Joints Based on AASHTO and This Numeric Study
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jongho, P.; Jinwoong, C.; Yongjoon, J.; Sun-Kyu, P.; Hong, S. An Experimental and Analytical Study on the Deflection Behavior of Precast Concrete Beams with Joints. Appl. Sci. 2017, 7, 1198–1208. [Google Scholar]
- Xiong, Z.; Cai, Q.; Liu, F.; Li, L.; Long, Y. Dynamic performance of RAC-filled double-skin tubular columns subjected to cyclic axial compression. Constr. Build. Mater. 2020, 248, 118665. [Google Scholar] [CrossRef]
- Valikhnai, A.; Jahromi, A.J.; Mantawy, I.M.; Azizinamini, A. Numerical Modelling of concrete-to-UHPC Bond Strength. Materials 2020, 13, 1379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bae, J.; Hwang, H.; Park, S. Structural Safety Evaluation of Precast, Prestressed Concrete Deck Slabs Cast Using 120-MPa High-Performance Concrete with a Reinforced Joint. Materials 2019, 12, 3040. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poston, R.W.; Wouters, J.P. Durability of Precast Segmental Bridges: Final Report; Nchrp Web Document: Washington, DC, USA, 1998. [Google Scholar]
- Wium, D.J.W.; Buyukozturk, O. Precast segmental bridges—Status and future directions. Civ. Eng. Pract. Des. Eng. 1984, ACSE 3, 59–79. [Google Scholar]
- Koseki, K.; Breen, J.E. Exploratory Study of Shear Strenght of Joints for Precast Segmental Bridges; Texas State Department of Highways and Public Transportation; Transportation Planning Division: Center for Transportation Research, The University of Texas at Austin: Austin, TX, USA, 1983; pp. 1–93. [Google Scholar]
- Ramos, G.; Aparicio, A.C. Ultimate Analysis of Monolithic and Segmental Externally Prestressed Concrete Bridges. J. Bridge Eng. 1996, 1, 10–17. [Google Scholar] [CrossRef]
- Issa, M.A.; Abdalla, H.A. Structural Behavior of Single Key Joints in Precast Concrete Segmental Bridges. J. Bridge Eng. 2007, 12, 315–324. [Google Scholar] [CrossRef]
- Zhou, X.; Mickleborough, N.; Li, Z. Shear Strength of Joints in Precast Concrete Segmental Bridges. Aci. Struct. J. 2005, 102, 3–11. [Google Scholar]
- Buyukozturk, O.; Bakhoum, M.M.; Michael Beattie, S. Shear Behavior of Joints in Precast Concrete Segmental Bridges. J. Struct. Eng. 1990, 116, 3380–3401. [Google Scholar] [CrossRef]
- Zhi, Q.; Xiong, X.; Yang, W.; Liu, S.; Xiong, J. Experimental Study on the Shear Behavior of Precast Wall Concrete Joints with/without Dowel Reinforcement. Materials 2020, 13, 1726. [Google Scholar] [CrossRef] [Green Version]
- Yuan, A.; Yang, C.; Wang, J.; Chen, L.; Lu, R. Shear Behavior of Epoxy Resin Joints in Precast Concrete Segmental Bridges. J. Bridge Eng. 2019, 24, 04019009. [Google Scholar] [CrossRef]
- Chen, G.; Fang, Z.; Wang, S.; Jiang, H.; Liang, H. Numerical Analysis on Shear Behavior of Joints under Low Confining and Eccentric Loads. Adv. Civ. Eng. 2019, 2019, 4589824. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Shear behavior of dry and epoxied joints in precast concrete segmental box girder bridges under direct shear loading. Eng. Struct. 2019, 182, 89–100. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Influence of intensity & eccentricity of posttensioning force and concrete strength on shear behavior of epoxied joints in segmental box girder bridges. Constr. Build. Mater. 2019, 197, 117–129. [Google Scholar] [CrossRef]
- Turmo, J.; Ramos, G.; Aparicio, J.A. Shear strength of match cast dry joints of precast concrete segmental bridges: Proposal for Eurocode 2. Mater. Constr. 2006, 56, 45–52. [Google Scholar]
- Forestieri, G.; Marseglia, G.; Galiano, G. Recovery and Optimization of A Former Railway Transport Track. In Wit Transactions on the Built Environment; Wit Press: Aveiro, Portuga, 2019; Volume 186, pp. 47–57. ISBN 1743-3509. [Google Scholar]
- Moustafa Saad, E. Ultimate Load Test of A segmentally Constructed Prestressed concrete I-beam. PCIJ 1974, 19, 54–75. [Google Scholar] [CrossRef]
- Rabbat Basile, G.; Sowlat, K. Testing of Segmental Concrete Girders With External Tendons. PCIJ 1987, 32, 86–106. [Google Scholar] [CrossRef]
- Abdel-Halim, M.; Mcclure, R.M.; West, H.H. Overload Behavior of an Experimental Precast Prestressed Concrete Segmental Bridge. PCI J. 1987, 32, 102–123. [Google Scholar] [CrossRef]
- Kashima, S. Construction and Load Tests of a Segmental Precast Box Girder Bridge Model. Cantilevers 1975, 121, 6. [Google Scholar]
- Liu, T.; Wang, Z.; Guo, J.; Wang, J. Shear Strength of Dry Joints in Precast UHPC Segmental Bridges: Experimental and Theoretical Research. J. Bridge Eng. 2018, 24, 04018100. [Google Scholar] [CrossRef]
- AASHTO (American Association of State Highway and Transportation Officials). 2003 Interim Revisions to the Guide Specifications for Design and Construction of Segmental Concrete Bridges, 2nd ed.; AASHTO: Washington, DC, USA, 2003; p. 93. [Google Scholar]
- Fang, Z.; Shangguan, P. Discussion on the mechanical behavior of prestressed concrete continuous beams with external cable. J. Fuzhou Univ. 1996, 24, 16–21. (In Chinese) [Google Scholar]
- Li, G. Calculating Method for Design of Externally Prestressed Concrete Bridge; Tongji University: Shanghai, China, 2007. (In Chinese) [Google Scholar]
- Rombach, G.A. Precast Segmental Box Girder Bridges with External Prestressing-Design and Construction. Segm. Bridges 2002, 19, 1–15. [Google Scholar]
- Macgregor, R.J.F.; Kreger, M.E.; John, E.B. Strength and Ductility of a Three-Span Externally Post-Tensioned Segmental Box Girder Bridge Model. ACI Symp. Publ. 1989, 120, 315–338. [Google Scholar] [CrossRef]
- Mattock, A.H. Shear Transfer in Reinforced Concrete-Recent Research. J. PCI 1972, 17, 55–75. [Google Scholar] [CrossRef]
- Turmo, J.; Ramos, G.; Aparicio, A.C. Shear strength of dry joints of concrete panels with and without steel fibres: Application to precast segmental bridges. Eng. Struct. 2006, 28, 23–33. [Google Scholar] [CrossRef]
- Jiang, H.; Ying, C.; Liu, A.; Wang, T.; Fang, Z. Effect of high-strength concrete on shear behavior of dry joints in precast concrete segmental bridges. Steel Compos. Struct. 2016, 22, 1019–1038. [Google Scholar] [CrossRef]
- Chen, L. Research on Shear Behavior of Dry Joints in Precast Segmental Concrete Bridges; Gruangdong University of Technology: Guangzhou, China, 2013. [Google Scholar]
- Wei, R. Rongbin Research on Shear Behavior of Multiple-Keyed Dry Joint of C40 SFR Concrete; Guangdong University of Technology: Guangzhou, China, 2016. [Google Scholar]
- Rombach, G.A. Segmentbrücken; Beton-Kalender: Berlin, Germany, 2004; Volume Teil 1, Verlag Ernst und Sohn. (In German) [Google Scholar]
- Turmo, J.; Ramos, G.; Aparicio, A.C. Towards a model of dry shear keyed joints: Modelling of panel tests. Comput. Concr. 2012, 10, 469–487. [Google Scholar] [CrossRef]
- Alcalde, M.; Cifuentes, H.; Medina, F. Influence of the number of keys on the shear strength of post-tensioned dry joints. Mater. Constr. 2013, 63, 297–307. [Google Scholar] [CrossRef] [Green Version]
- Shamass, R.; Zhou, X.; Alfano, G. Finite-Element Analysis of Shear-Off Failure of Keyed Dry Joints in Precast Concrete Segmental Bridges. J. Bridge Eng. 2015, 20, 04014084. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.H.; Kim, Y.J.; Jin, B.M.; Shin, H.M. Numerical study on the joints between precast post-tensioned segments. Int. J. Concr. Struct. Mater. 2007, 19, 3–9. [Google Scholar]
- Jiang, H.; Li, C.; Ma, Z.J.; Feng, W. Shear Behavior of Dry Joints with Castellated Keys in Precast Concrete Segmental Bridges. J. Bridge Eng. 2015, 20, 04014062. [Google Scholar] [CrossRef]
- Zou, L.; Jiang, H.; Wei, C.; Yin, W.; Yang, M. Finite-element analysis on shear behavior of joints in precast concrete segmental box girder bridges. J. Ind. Constr. 2011, 041, 92–95. [Google Scholar]
- Simulia, D.C.S. Abaqus 6.11 Analysis User’s Manual; Dassault Systemes Simulia Corp.: Providence, RI, USA, 2011. [Google Scholar]
- Zhao, J.; Liu, L.; Qiu, H.; Zhu, A.; Wang, X.; Ke, C.; Fan, Z.; Xu, Y.; Huang, X.; Li, Y. Specification for Design of Concrete Structure (GB 50010-2010). PRC Minist. Constr. 2015. (In Chinese) [Google Scholar] [CrossRef]
- Song, C.; Liu, J.; Ai, T.; Li, Z. The Study on Damage Factors in Concrete Plastic Damage Model of ABAQUS. Eng. Constr. 2017, 49, 1–5. [Google Scholar]
- ACI. Building Code Requirements for Structural Concrete; ACI 318-14: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Cairns, J. Model Code 2010 First Complete Draft Volume 1; Technical Report, Bulletin 55; Fédération Internationale du Béton: Lausanne, Switzerland, 2010. [Google Scholar]
- CJJT 293-2019 Technical Standard for Prestressed Precast Concrete Segmental Bridges in Urban Rail Transit; 204 Huanshi Xi Lu: Guangzhou, China, 2010.







| (N/mm2) | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (10−6) | 1470 | 1560 | 1640 | 1720 | 1790 | 1850 | 1920 | 1980 | 2030 | 2080 | 2130 | 2190 | 2240 |
| 0.74 | 1.06 | 1.36 | 1.65 | 1.94 | 2.21 | 2.48 | 2.74 | 3.00 | 3.25 | 3.50 | 3.75 | 3.99 | |
| 3.0 | 2.6 | 2.3 | 2.1 | 2.0 | 1.9 | 1.9 | 1.8 | 1.8 | 1.7 | 1.7 | 1.7 | 1.6 |
| (N/mm2) | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
|---|---|---|---|---|---|---|---|
| (10−6) | 65 | 81 | 95 | 107 | 118 | 128 | 137 |
| 0.31 | 0.70 | 1.25 | 1.95 | 2.81 | 3.82 | 5.00 |
| Test Name | (MPa) | Average (kN) (1) | (kN) (2) | Appearance of the First Crack (Male Part; Numeric Value) | Appearance of Shear-off Crack (Numeric Value) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Angle (°) | Load (kN) (3) | (%) | Angle (°) | Load (kN) (4) | (%) | |||||
| MK1-H5-0.5 | 59.9 | 87.3 | 93.9 | 1.08 | 62 | 43.6 | 46.5 | 95 | 89.7 | 95.5 |
| MK1-H5-1.0 | 59.9 | 123 | 117 | 0.955 | 45 | 58.4 | 49.9 | 95 | 111 | 94.9 |
| MK1-H5-2.0 | 59.9 | 139 | 129 | 0.923 | 27 | 67.2 | 52.2 | 95 | 125 | 97.3 |
| MK1-H7-0.5 | 70.3 | 105 | 115 | 1.09 | 66 | 54.0 | 47.1 | 95 | 113 | 98.3 |
| MK1-H7-1.0 | 70.3 | 134 | 130 | 0.976 | 51 | 65.8 | 50.4 | 90 | 129 | 99.3 |
| MK1-H7-2.0 | 70.3 | 165 | 141 | 0.859 | 48 | 80.7 | 57.0 | 90 | 140 | 99.0 |
| Average | 0.980 | / | / | 50.5 | / | / | 97.4 | |||
| Standard deviation | 0.078 | / | / | / | / | / | / | |||
| Specimen | Fixing Imperfections | (mm) | (mm) | (mm) | (mm) | Concrete Strength | Confining Pressure (MPa) |
|---|---|---|---|---|---|---|---|
| MK1-Ha-m | / | 0 | 0 | 0 | 0 | C70; C50 | 0.5; 1.0; 2.0 |
| MF1K1-Ha-m | MF1 | 0.5 | 0 | 0 | 0 | C70; C50 | 0.5; 1.0; 2.0 |
| MF2K1-Ha-m | MF2 | 0 | 0.5 | 0 | 0 | C70; C50 | 0.5; 1.0; 2.0 |
| RK1-Ha-m | R | 0 | 0 | 0 | 0.5 | C70; C50 | 0.5; 1.0; 2.0 |
| LK1-Ha-m | L | 0 | 0 | 0.5 | 0 | C70; C50 | 0.5; 1.0; 2.0 |
| Specimen | Numeric Ultimate Strength | AASHTO | Specimen | Numeric Ultimate Strength | AASHTO | ||||
|---|---|---|---|---|---|---|---|---|---|
| Value (kN) | Reduced by (%) | Value (kN) | Error (%) | Value (kN) | Reduced by (%) | Value (kN) | Error (%) | ||
| MK1-H5-0.5 | 93.9 | / | 83.2 | −12.8 | MK1-H7-0.5 | 114 | / | 93.5 | −22.8 |
| MF1K1-H5-0.5 | 94.5 | −0.682 | −13.6 | MF1K1-H7-0.5 | 115 | −0.331 | −23.2 | ||
| MF2K1-H5-0.5 | 91.7 | 2.38 | −10.1 | MF2K1-H7-0.5 | 112 | 2.10 | −20.2 | ||
| RK1-H5-0.5 | 73.0 | 22.2 | 12.3 | RK1-H7-0.5 | 92.5 | 19.4 | 1.05 | ||
| LK1-H5-0.5 | 66.0 | 29.7 | 20.7 | LK1-H7-0.5 | 74.6 | 35.0 | 20.2 | ||
| MK1-H5-1.0 | 117 | / | 93.7 | −24.9 | MK1-H7-1.0 | 130 | / | 105 | −24.3 |
| MF1K1-H5-1.0 | 116 | 0.752 | −24.0 | MF1K1-H7-1.0 | 131 | −0.184 | −24.6 | ||
| MF2K1-H5-1.0 | 119 | −1.46 | −26.7 | MF2K1-H7-1.0 | 138 | −5.77 | −31.5 | ||
| RK1-H5-1.0 | 104 | 11.5 | −10.5 | RK1-H7-1.0 | 108 | 17.3 | −2.84 | ||
| LK1-H5-1.0 | 90.4 | 22.8 | 3.53 | LK1-H7-1.0 | 95.8 | 26.6 | 8.77 | ||
| MK1-H5-2.0 | 129 | / | 115 | −12.2 | MK1-H7-2.0 | 141 | / | 128 | −10.7 |
| MF1K1-H5-2.0 | 118 | 8.05 | −3.18 | MF1K1-H7-2.0 | 141 | 0.474 | −10.2 | ||
| MF2K1-H5-2.0 | 121 | 6.25 | −5.20 | MF2K1-H7-2.0 | 143 | −1.32 | −12.2 | ||
| RK1-H5-2.0 | 114 | 11.4 | 0.602 | RK1-H7-2.0 | 123 | 12.8 | 3.45 | ||
| LK1-H5-2.0 | 99.1 | 23.0 | 13.6 | LK1-H7-2.0 | 99.7 | 29.5 | 22.0 | ||
| Concrete Strength (MPa) | Confining Pressure (MPa) | Direct-Shear Strength of Each Shear Key for Keyed Dry-Joint Specimens | (1)/(3) | (2)/(4) | (2)/(1) | |||
|---|---|---|---|---|---|---|---|---|
| Numeric Value | Experimental Value | |||||||
| (1) | (2) | (3) | (4) | |||||
| C50 | 0.5 | 90.9 | 80.8 | 84.3 | 70.5 | 1.08 | 1.15 | 0.889 |
| C50 | 1.0 | 111 | 103 | 116. | 83.8 | 0.957 | 1.23 | 0.929 |
| C50 | 2.0 | 117 | 104 | 127 | 98.9 | 0.916 | 1.05 | 0.893 |
| C70 | 0.5 | 112 | 98.9 | 102 | 88.6 | 1.09 | 1.12 | 0.885 |
| C70 | 1.0 | 124 | 115 | 128 | 100 | 0.975 | 1.14 | 0.920 |
| C70 | 2.0 | 130 | 118 | 153 | 134 | 0.848 | 0.877 | 0.909 |
| Average/ Standard deviation | 0.977/ 0.086 | 1.09/ 0.111 | 0.904 | |||||
| Specimen | Key Number | Ultimate Shear Strength | Error 1 (%) | Error 2 (%) | Error 3 (%) | Error 4 (%) | |||
|---|---|---|---|---|---|---|---|---|---|
| (Average) Experimental Value | (Average)Numeric Value | AASHTO (Equation (24)) | Modified Formula (Equation (25)) | ||||||
| (1) | (2) | (3) | (4) | ||||||
| Experimental specimens from Jiang et al. (2016) | |||||||||
| K3-H5-0.5 | 3 | 218 | / | 247 | 223 | 11.8 | / | 2.24 | / |
| K3-H5-1.0 | 3 | 263 | / | 275 | 249 | 4.30 | / | −5.82 | / |
| K3-H5-2.0 | 3 | 321 | / | 332 | 301 | 3.42 | / | −6.45 | / |
| K3-H7-0.5 | 3 | 272 | / | 277 | 250 | 2.10 | / | −8.51 | / |
| K3-H7-1.0 | 3 | 313 | / | 309 | 279 | −1.30 | / | −12.1 | / |
| K3-H7-2.0 | 3 | 427 | / | 371 | 337 | −15.0 | / | −26.8 | / |
| Average | 0.888 | / | −9.58 | / | |||||
| Experimental specimens from Jiang et al. (2016) and numeric specimens without fixing imperfections from this study | |||||||||
| K1-H5-0.5 | 1 | 87.3 | 93.9 | 83.2 | 75.2 | −4.90 | −12.8 | −16.1 | −24.9 |
| K1-H5-1.0 | 1 | 123 | 117 | 93.7 | 84.9 | −30.8 | −24.9 | −44.3 | −37.8 |
| K1-H5-2.0 | 1 | 139 | 129 | 115 | 104 | −21.6 | −12.2 | −33.6 | −23.3 |
| K1-H7-0.5 | 1 | 105 | 115 | 93.5 | 84.5 | −12.8 | −22.8 | −24.9 | −35.9 |
| K1-H7-1.0 | 1 | 134 | 130 | 105 | 95.1 | −27.4 | −24.3 | −40.7 | −37.3 |
| K1-H7-2.0 | 1 | 165 | 141 | 128 | 116 | −28.8 | −10.7 | −41.7 | −21.7 |
| Average | −21.1 | −18.0 | −33.5 | −30.1 | |||||
| Numeric single-keyed dry-joint specimens with or without fixing imperfections from this study | |||||||||
| K1-H5-0.5 | 1 | / | 83.8 | 83.2 | 75.2 | / | −0.721 | / | −11.5 |
| K1-H5-1.0 | 1 | / | 109 | 93.7 | 84.9 | / | −16.5 | / | −28.6 |
| K1-H5-2.0 | 1 | / | 116 | 115 | 104 | / | −1.29 | / | −11.3 |
| K1-H7-0.5 | 1 | / | 102 | 93.5 | 84.5 | / | −8.97 | / | −20.7 |
| K1-H7-1.0 | 1 | / | 121 | 105 | 95.1 | / | −14.9 | / | −26.9 |
| K1-H7-2.0 | 1 | / | 130 | 128 | 116 | / | −1.52 | / | −11.6 |
| Average | −7.32 | −18.4 | |||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Chen, M.; Sha, Z.; Xiao, J.; Feng, J. Numeric Analysis on Shear Behavior of High-Strength Concrete Single-Keyed Dry Joints with Fixing Imperfections in Precast Concrete Segmental Bridges. Materials 2020, 13, 2914. https://doi.org/10.3390/ma13132914
Jiang H, Chen M, Sha Z, Xiao J, Feng J. Numeric Analysis on Shear Behavior of High-Strength Concrete Single-Keyed Dry Joints with Fixing Imperfections in Precast Concrete Segmental Bridges. Materials. 2020; 13(13):2914. https://doi.org/10.3390/ma13132914
Chicago/Turabian StyleJiang, Haibo, Mingzhu Chen, Zhijun Sha, Jie Xiao, and Jiahui Feng. 2020. "Numeric Analysis on Shear Behavior of High-Strength Concrete Single-Keyed Dry Joints with Fixing Imperfections in Precast Concrete Segmental Bridges" Materials 13, no. 13: 2914. https://doi.org/10.3390/ma13132914
APA StyleJiang, H., Chen, M., Sha, Z., Xiao, J., & Feng, J. (2020). Numeric Analysis on Shear Behavior of High-Strength Concrete Single-Keyed Dry Joints with Fixing Imperfections in Precast Concrete Segmental Bridges. Materials, 13(13), 2914. https://doi.org/10.3390/ma13132914