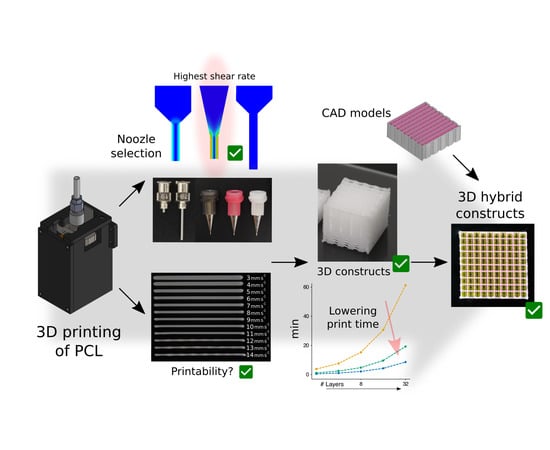
Efficient Fabrication of Polycaprolactone Scaffolds for Printing Hybrid Tissue-Engineered Constructs
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
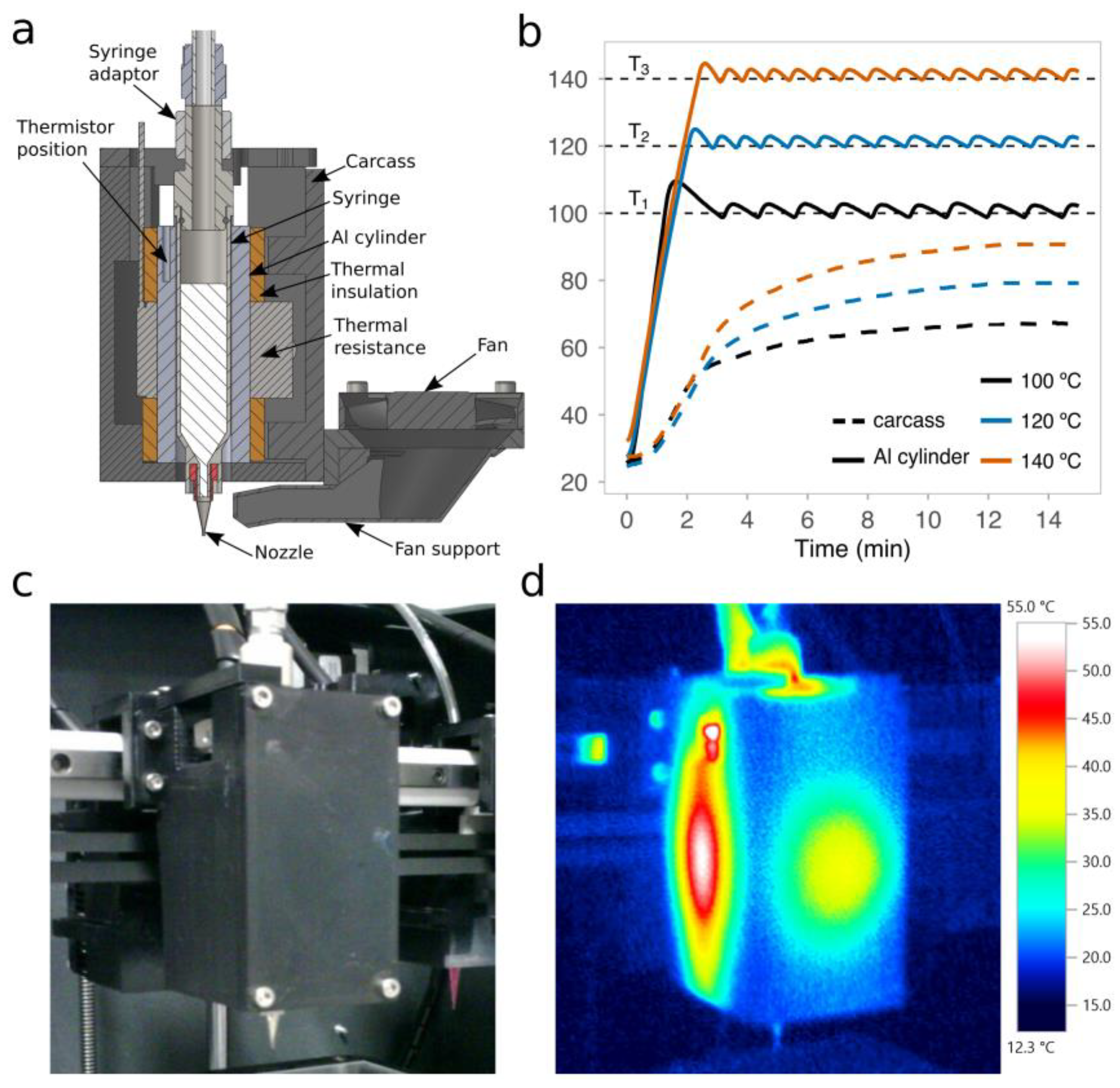
2.2. Open-Source High-Temperature Microextrusion-Based Printhead
2.3. Measurement of the Temperature Response in the Extrusion System
2.4. Open-Source 3D Printer Specifications and Main Configuration
2.5. G-Code Generation and Printing Software
2.6. 3D Scaffold Printing
2.7. Hybrid Construct Preparation
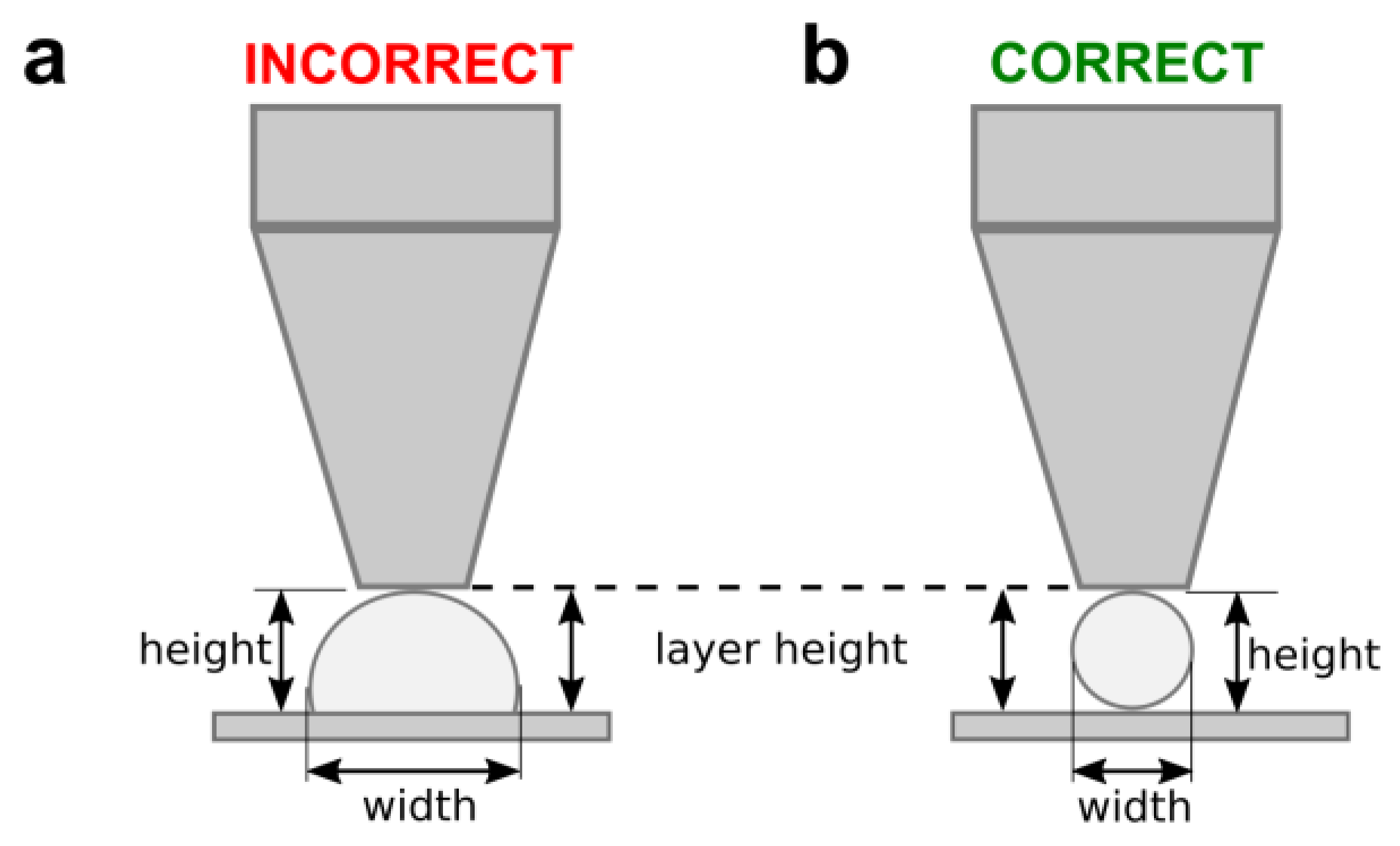
2.8. Printing Performance Metrics
2.9. Computational Fluid Dynamics Model
2.10. Constitutive Equations of the PCL
3. Results and Discussion
3.1. Control of the PCL Temperature
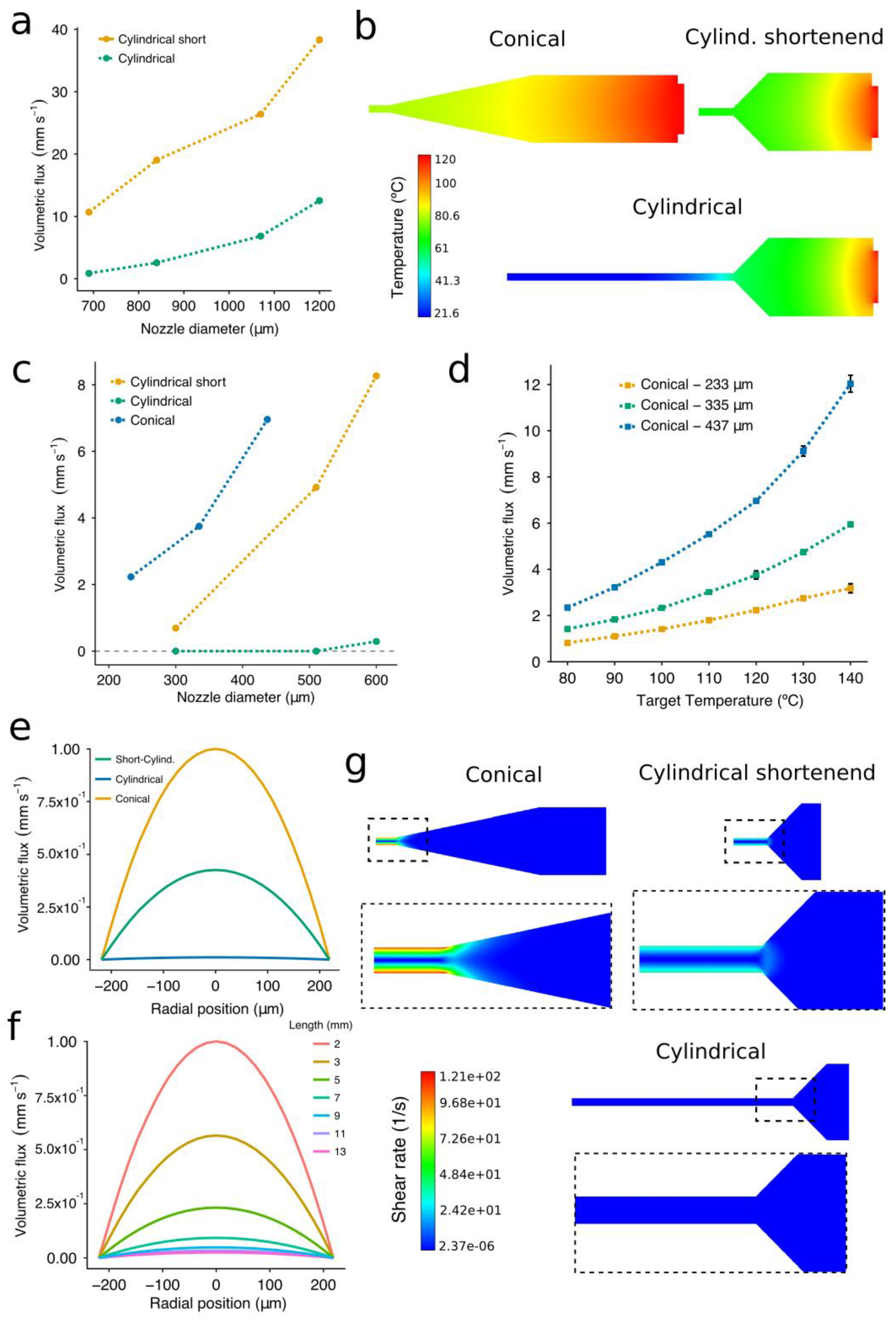
3.2. Influence of Temperature, Shape, and Diameter of Nozzles on the PCL Flow Rate
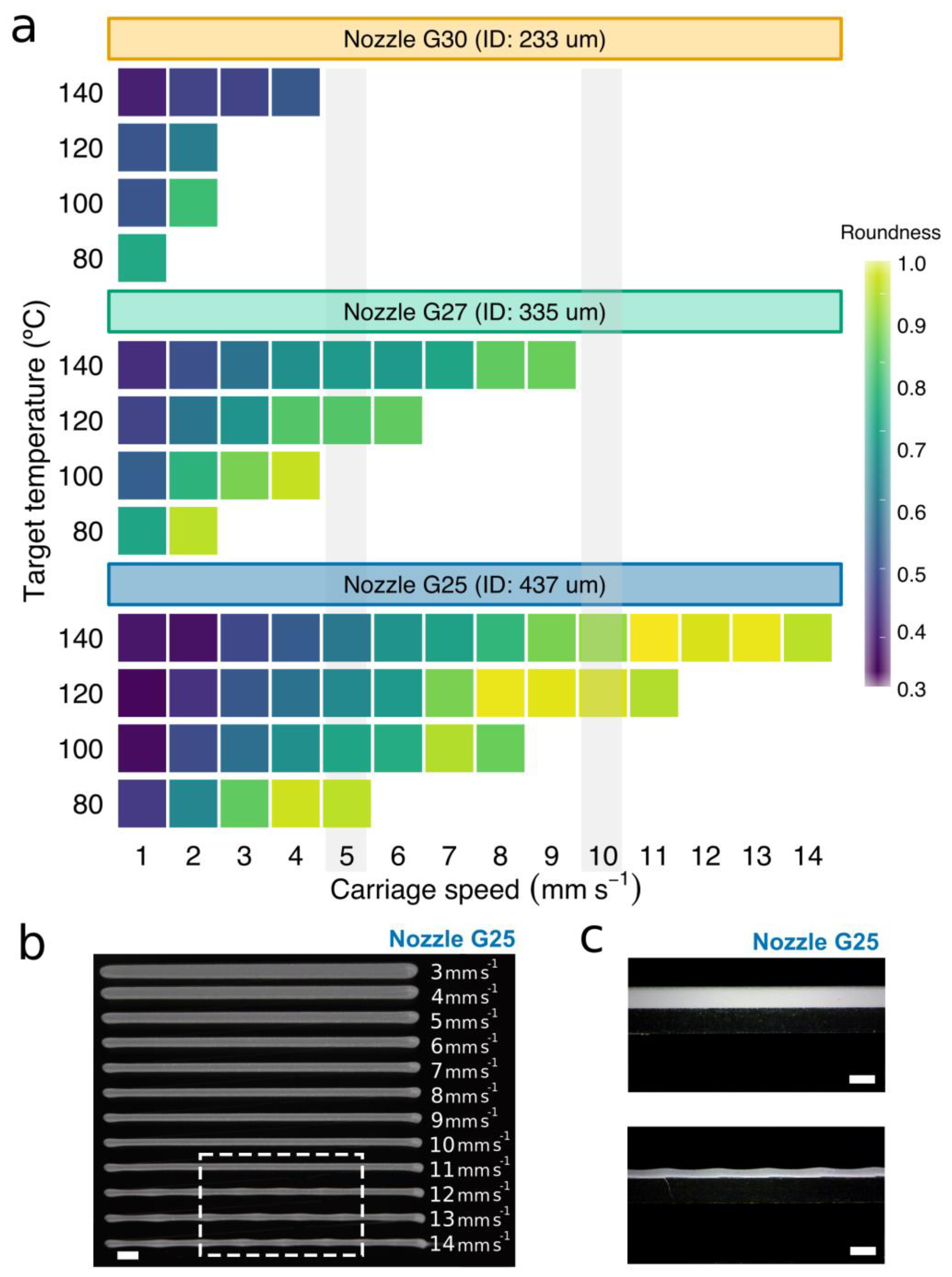
3.3. Determination of the Carriage Speeds for PCL Extrusion
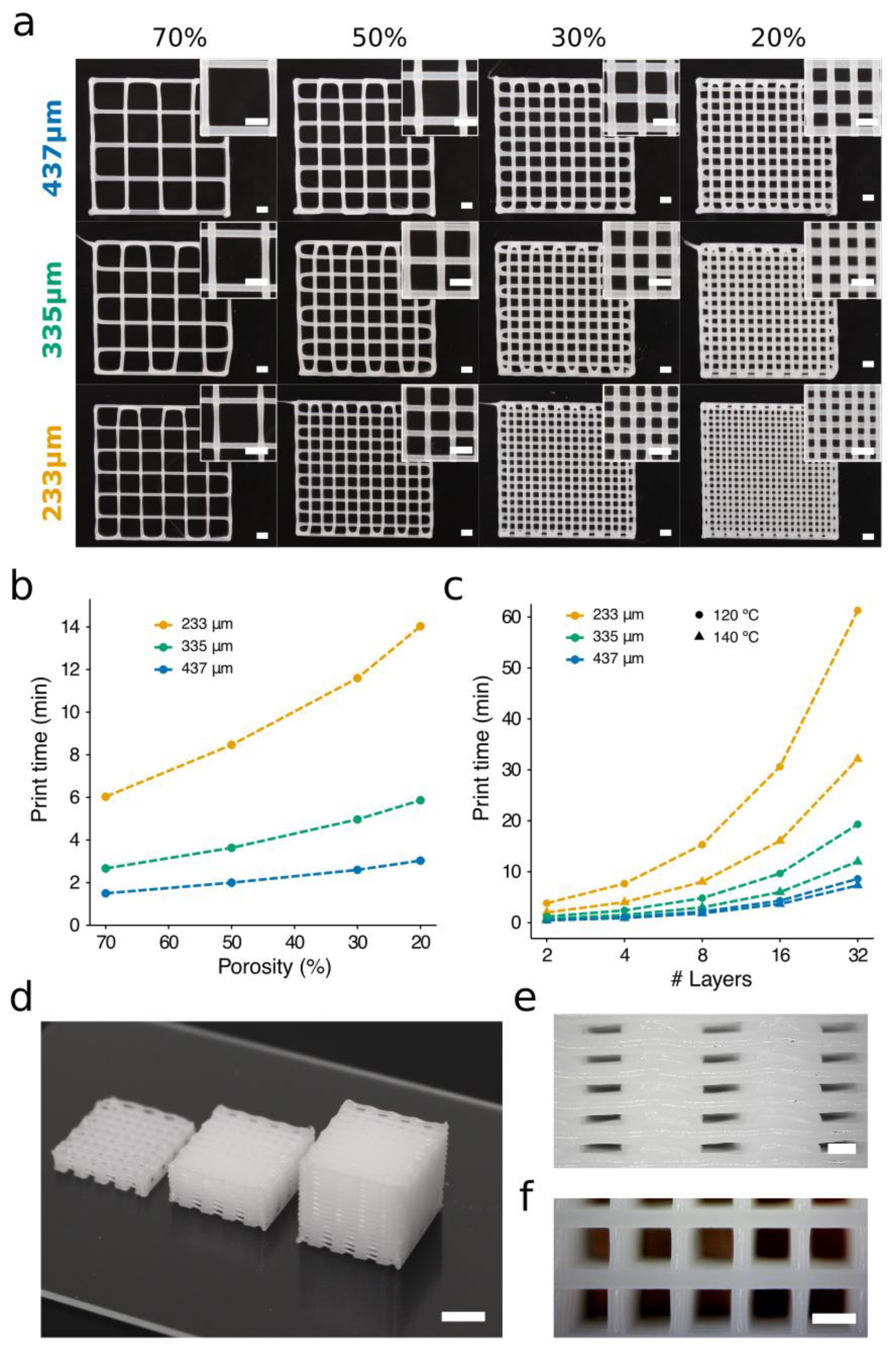
3.4. Evaluation of PCL Print Times
3.5. Proof of Concept of a Hybrid Construct using the Selected Print Parameters
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lam, C.X.; Hutmacher, D.W.; Schantz, J.T.; Woodruff, M.A.; Teoh, S.H. Evaluation of polycaprolactone scaffold degradation for 6 months in vitro and in vivo. J. Biomed. Mater. Res. Part A 2009, 90, 906–919. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, M.; Wei, X.; Hao, Y.; Wang, J. Evaluation of 3D-printed polycaprolactone scaffolds coated with freeze-dried platelet-rich plasma for bone regeneration. Materials 2017, 10, 831. [Google Scholar] [CrossRef] [PubMed]
- Mitsak, A.G.; Kemppainen, J.M.; Harris, M.T.; Hollister, S.J. Effect of polycaprolactone scaffold permeability on bone regeneration in vivo. Tissue Eng. Part A 2011, 17, 1831–1839. [Google Scholar] [CrossRef] [PubMed]
- Hendrikson, W.; Rouwkema, J.; Van Blitterswijk, C.; Moroni, L. Influence of PCL molecular weight on mesenchymal stromal cell differentiation. RSC Adv. 2015, 5, 54510–54516. [Google Scholar] [CrossRef]
- Lam, C.X.; Teoh, S.H.; Hutmacher, D.W. Comparison of the degradation of polycaprolactone and polycaprolactone–(β-tricalcium phosphate) scaffolds in alkaline medium. Polym. Int. 2007, 56, 718–728. [Google Scholar] [CrossRef]
- Lam, C.X.; Savalani, M.M.; Teoh, S.-H.; Hutmacher, D.W. Dynamics of in vitro polymer degradation of polycaprolactone-based scaffolds: Accelerated versus simulated physiological conditions. Biomed. Mater. 2008, 3, 034108. [Google Scholar] [CrossRef] [PubMed]
- Groll, J.; Burdick, J.; Cho, D.; Derby, B.; Gelinsky, M.; Heilshorn, S.; Jüngst, T.; Malda, J.; Mironov, V.; Nakayama, K. A definition of bioinks and their distinction from biomaterial inks. Biofabrication 2018, 11, 013001. [Google Scholar] [CrossRef]
- Li, W.J.; Danielson, K.G.; Alexander, P.G.; Tuan, R.S. Biological response of chondrocytes cultured in three-dimensional nanofibrous poly (ϵ-caprolactone) scaffolds. J. Biomed. Mater. Res. Part A 2003, 67, 1105–1114. [Google Scholar] [CrossRef]
- Park, A.S.; Lee, H.-J.; Kim, K.-S.; Lee, J.S.; Lee, J.-T.; Kim, S.-Y.; Chang, N.-H.; Park, S.-Y. In Vivo Evaluation of 3D-Printed Polycaprolactone Scaffold Implantation Combined with β-TCP Powder for Alveolar Bone Augmentation in a Beagle Defect Model. Materials 2018, 11, 238. [Google Scholar] [CrossRef]
- Woodruff, M.A.; Hutmacher, D.W. The return of a forgotten polymer—Polycaprolactone in the 21st century. Prog. Polym. Sci. 2010, 35, 1217–1256. [Google Scholar] [CrossRef]
- Gorodzha, S.N.; Muslimov, A.R.; Syromotina, D.S.; Timin, A.S.; Tcvetkov, N.Y.; Lepik, K.V.; Petrova, A.V.; Surmeneva, M.A.; Gorin, D.A.; Sukhorukov, G.B.; et al. A comparison study between electrospun polycaprolactone and piezoelectric poly(3-hydroxybutyrate-co-3-hydroxyvalerate) scaffolds for bone tissue engineering. Colloids Surf. B Biointerfaces 2017, 160, 48–59. [Google Scholar] [CrossRef] [PubMed]
- Shkarina, S.; Shkarin, R.; Weinhardt, V.; Melnik, E.; Vacun, G.; Kluger, P.J.; Loza, K.; Epple, M.; Ivlev, S.I.; Baumbach, T.; et al. 3D biodegradable scaffolds of polycaprolactone with silicate-containing hydroxyapatite microparticles for bone tissue engineering: High-resolution tomography and in vitro study. Sci. Rep. 2018, 8, 8907. [Google Scholar] [CrossRef] [PubMed]
- Mellor, L.F.; Huebner, P.; Cai, S.; Mohiti-Asli, M.; Taylor, M.A.; Spang, J.; Shirwaiker, R.A.; Loboa, E.G. Fabrication and Evaluation of Electrospun, 3D-Bioplotted, and Combination of Electrospun/3D-Bioplotted Scaffolds for Tissue Engineering Applications. Biomed. Res. Int. 2017, 2017, 6956794. [Google Scholar] [CrossRef] [PubMed]
- Guerra, J.A.; Cano, P.; Rabionet, M.; Puig, T.; Ciurana, J. 3D-Printed PCL/PLA Composite Stents: Towards a New Solution to Cardiovascular Problems. Materials 2018, 11, 1679. [Google Scholar] [CrossRef] [PubMed]
- Ramanath, H.; Chua, C.; Leong, K.; Shah, K. Melt flow behaviour of poly-ε-caprolactone in fused deposition modelling. J. Mater. Sci. Mater. Med. 2008, 19, 2541–2550. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Bissoyi, A.; Bit, A. A Review on 3D Printable Techniques for Tissue Engineering. BioNanoScience 2018, 1–16. [Google Scholar] [CrossRef]
- Zein, I.; Hutmacher, D.W.; Tan, K.C.; Teoh, S.H. Fused deposition modeling of novel scaffold architectures for tissue engineering applications. Biomaterials 2002, 23, 1169–1185. [Google Scholar] [CrossRef]
- Grosvenor, M.; Staniforth, J. The effect of molecular weight on the rheological and tensile properties of poly (ϵ-caprolactone). Int. J. Pharm. 1996, 135, 103–109. [Google Scholar] [CrossRef]
- Kim, G.H.; Son, J.G. 3D polycarprolactone (PCL) scaffold with hierarchical structure fabricated byáaápiezoelectric transducer (PZT)-assisted bioplotter. Appl. Phys. A 2009, 94, 781–785. [Google Scholar] [CrossRef]
- Seyednejad, H.; Gawlitta, D.; Dhert, W.J.; Van Nostrum, C.F.; Vermonden, T.; Hennink, W.E. Preparation and characterization of a three-dimensional printed scaffold based on a functionalized polyester for bone tissue engineering applications. Acta Biomater. 2011, 7, 1999–2006. [Google Scholar] [CrossRef]
- Trachtenberg, J.E.; Mountziaris, P.M.; Miller, J.S.; Wettergreen, M.; Kasper, F.K.; Mikos, A.G. Open-source three-dimensional printing of biodegradable polymer scaffolds for tissue engineering. J. Biomed. Mater. Res. Part A 2014, 102, 4326–4335. [Google Scholar] [CrossRef]
- Kundu, J.; Shim, J.H.; Jang, J.; Kim, S.W.; Cho, D.W. An additive manufacturing-based PCL–alginate–chondrocyte bioprinted scaffold for cartilage tissue engineering. J. Tissue Eng. Regen. Med. 2015, 9, 1286–1297. [Google Scholar] [CrossRef] [PubMed]
- Shim, J.-H.; Lee, J.-S.; Kim, J.Y.; Cho, D.-W. Bioprinting of a mechanically enhanced three-dimensional dual cell-laden construct for osteochondral tissue engineering using a multi-head tissue/organ building system. J. Micromech. Microeng. 2012, 22, 085014. [Google Scholar] [CrossRef]
- Kang, H.-W.; Lee, S.J.; Ko, I.K.; Kengla, C.; Yoo, J.J.; Atala, A. A 3D bioprinting system to produce human-scale tissue constructs with structural integrity. Nat. Biotechnol. 2016, 34, 312. [Google Scholar] [CrossRef] [PubMed]
- Visser, J.; Peters, B.; Burger, T.J.; Boomstra, J.; Dhert, W.J.; Melchels, F.P.; Malda, J. Biofabrication of multi-material anatomically shaped tissue constructs. Biofabrication 2013, 5, 035007. [Google Scholar] [CrossRef]
- Olubamiji, A.D.; Izadifar, Z.; Zhu, N.; Chang, T.; Chen, X.; Eames, B.F. Using synchrotron radiation inline phase-contrast imaging computed tomography to visualize three-dimensional printed hybrid constructs for cartilage tissue engineering. J. Synchrotron. Radiat. 2016, 23, 802–812. [Google Scholar] [CrossRef]
- Khademhosseini, A.; Langer, R. A decade of progress in tissue engineering. Nat. Protoc. 2016, 11, 1775. [Google Scholar] [CrossRef] [PubMed]
- Pati, F.; Shim, J.-H.; Lee, J.-S.; Cho, D.-W. 3D printing of cell-laden constructs for heterogeneous tissue regeneration. Manuf. Lett. 2013, 1, 49–53. [Google Scholar] [CrossRef]
- Skardal, A.; Atala, A. Biomaterials for integration with 3-D bioprinting. Ann. Biomed. Eng. 2015, 43, 730–746. [Google Scholar] [CrossRef]
- Riegel, J.; Mayer, W.; Havre, Y.V. FreeCAD, 0.16.6712. 2001. Available online: http://www.freecadweb.org (accessed on 1 March 2018).
- TELab. Printhead for 3D Printing of Polymers at High Temperature. 2018. Available online: https://3dprint.nih.gov/users/telab (accessed on 1 June 2018).
- Olubamiji, A.D.; Izadifar, Z.; Si, J.L.; Cooper, D.M.; Eames, B.F.; Chen, D.X. Modulating mechanical behaviour of 3D-printed cartilage-mimetic PCL scaffolds: Influence of molecular weight and pore geometry. Biofabrication 2016, 8, 025020. [Google Scholar] [CrossRef]
- Sodupe-Ortega, E.; Sanz-Garcia, A.; Escobedo-Lucea, C. Accurate Calibration in Multi-Material 3D Bioprinting for Tissue Engineering. Materials 2018, 11, 1402. [Google Scholar] [CrossRef] [PubMed]
- Rasband, W.S. ImageJ. Available online: http://rsb.info.nih.gov/ij/index.html (accessed on 15 February 2018).
- Carreau, P.J. Rheological equations from molecular network theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Carreau, P.J.; MacDonald, I.F.; Bird, R.B. A nonlinear viscoelastic model for polymer solutions and melts—II. Chem. Eng. Sci. 1968, 23, 901–911. [Google Scholar] [CrossRef]
- Arrhenius, S. Paper 2—On the reaction velocity of the inversion of cane sugar by acids. An extract, translated from the German, from an article in Zeitschrift für Physikalische Chemie, 4, 226 (1889). In Selected Readings in Chemical Kinetics; Back, M.H., Laidler, K.J., Eds.; Pergamon Press: Oxford, UK, 1967; pp. 31–35. [Google Scholar]
- Billiet, T.; Gevaert, E.; De Schryver, T.; Cornelissen, M.; Dubruel, P. The 3D printing of gelatin methacrylamide cell-laden tissue-engineered constructs with high cell viability. Biomaterials 2014, 35, 49–62. [Google Scholar] [CrossRef] [PubMed]
- Sheshadri, P.; Shirwaiker, R.A. Characterization of material–process–structure interactions in the 3D bioplotting of polycaprolactone. 3D Print. Addit. Manuf. 2015, 2, 20–31. [Google Scholar] [CrossRef]
- St-Pierre, J.-P.; Gauthier, M.; Lefebvre, L.-P.; Tabrizian, M. Three-dimensional growth of differentiating MC3T3-E1 pre-osteoblasts on porous titanium scaffolds. Biomaterials 2005, 26, 7319–7328. [Google Scholar] [CrossRef] [PubMed]
- Bidan, C.M.; Kommareddy, K.P.; Rumpler, M.; Kollmannsberger, P.; Bréchet, Y.J.M.; Fratzl, P.; Dunlop, J.W.C. How Linear Tension Converts to Curvature: Geometric Control of Bone Tissue Growth. PLOS ONE 2012, 7, e36336. [Google Scholar] [CrossRef]
- Murphy, S.V.; Atala, A. 3D bioprinting of tissues and organs. Nat. Biotechnol. 2014, 32, 773. [Google Scholar] [CrossRef]
- Shanjani, Y.; Pan, C.; Elomaa, L.; Yang, Y. A novel bioprinting method and system for forming hybrid tissue engineering constructs. Biofabrication 2015, 7, 045008. [Google Scholar] [CrossRef]



| Type | Inner Diameter (ID) μm and Gauge | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Conical | 233 | - | 335 | 437 | - | - | - | - | - | - |
| Cylindrical | - | 300 | - | - | 510 | 600 | 690 | 840 | 1070 | 1200 |
| G30 | G24 | G27 | G25 | G21 | G20 | G19 | G18 | G17 | G16 | |
| Bird–Carreau Parameters | Activation Energy (Ea) kJ mol−1 | ||
|---|---|---|---|
| Zero-Shear Viscosity (η0) Pa s | n | λ | |
| 291.3 | 0.8 | 0.0083 | 30.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sodupe Ortega, E.; Sanz-Garcia, A.; Pernia-Espinoza, A.; Escobedo-Lucea, C. Efficient Fabrication of Polycaprolactone Scaffolds for Printing Hybrid Tissue-Engineered Constructs. Materials 2019, 12, 613. https://doi.org/10.3390/ma12040613
Sodupe Ortega E, Sanz-Garcia A, Pernia-Espinoza A, Escobedo-Lucea C. Efficient Fabrication of Polycaprolactone Scaffolds for Printing Hybrid Tissue-Engineered Constructs. Materials. 2019; 12(4):613. https://doi.org/10.3390/ma12040613
Chicago/Turabian StyleSodupe Ortega, Enrique, Andres Sanz-Garcia, Alpha Pernia-Espinoza, and Carmen Escobedo-Lucea. 2019. "Efficient Fabrication of Polycaprolactone Scaffolds for Printing Hybrid Tissue-Engineered Constructs" Materials 12, no. 4: 613. https://doi.org/10.3390/ma12040613
APA StyleSodupe Ortega, E., Sanz-Garcia, A., Pernia-Espinoza, A., & Escobedo-Lucea, C. (2019). Efficient Fabrication of Polycaprolactone Scaffolds for Printing Hybrid Tissue-Engineered Constructs. Materials, 12(4), 613. https://doi.org/10.3390/ma12040613